Magnetic particle detection (MPD) for in-vitro dosimetry

Abstract

In-vitro tests intended for evaluating the potential health effects of magnetic nanoparticles generally require an accurate measure of cell dose to promote the consistent use and interpretation of biological response. Here, a simple low-cost inductive sensor is developed for quickly determining the total mass of magnetic nanoparticles that is bound to the plasma membrane and internalized by cultured cells. Sensor operation exploits an oscillating magnetic field (f₀ = 250 kHz) together with the nonlinear response of particle magnetization to generate a harmonic signal (f₃ = 750 kHz) that varies linearly with particulate mass (R² > 0.999) and is sufficiently sensitive for detecting ~100 ng of carboxyl-coated iron-oxide nanoparticles in under a second. When exploited for measuring receptor-mediated nanoparticle uptake in RAW 264.7 macrophages, results show that the achieved dosimetric performance is comparable with relatively expensive analytical techniques that are much more time-consuming and labor-intensive to perform. The described sensing is therefore potentially better suited for low-cost in-vitro assays that require fast and quantitative magnetic particle detection.

1. Introduction

Magnetic nanoparticles are of widespread interest for diagnostic imaging, targeted drug delivery, and cancer therapy (Banerjee et al., 2010). To optimize their biomedical use, material synthesis is routinely tailored to vary particle size, composition, and surface functionality (Hao et al., 2010; Krishnan, 2010). Unfortunately, once inside the body, there is a concern that engineered nanomaterials can have unintended consequences that adversely affect the patient health and outweigh possible benefits. The burgeoning field of nanotoxicology seeks to identify potential health risks through a tiered approach that currently employs in-vitro testing as an economical way to bridge the gap between known material properties and expensive safety evaluations in live animals (Oberdorster, 2010).

Unlike animal testing where dose has historically been based on the principle that response is proportional to the amount of material at the site of action, in-vitro studies routinely measure it in terms of exposure. The problem with this is that gravitational settling, diffusion, and particle agglomeration in culture media all influence the delivery of nanomaterials to the cell surface (Hinderliter et al., 2010; Teeguarden et al., 2007). Cell uptake is also mediated by active transport through different pathways that vary with cell type and particle properties (Hillaireau and Couvreur, 2009). Consequently, cells exposed to the same mass concentration in dosing media can interact with significantly different nanoparticle amounts. Actual measures of cell dose are therefore essential for the consistent toxicological use and interpretation of in-vitro tests (Soenen and De Cuyper, 2010).

Analytical methods to detect magnetic nanoparticles for in-vitro testing include atomic absorption spectroscopy (Settles et al., 2011), electron paramagnetic resonance (Gamarra et al., 2010; Wilhelm et al., 2002a), and inductively coupled plasma mass spectrometry (Huang et al., 2011). There are also several important sensor-based strategies that generally employ specialized designs to achieve more economical performance for rapid bioassays (Tamanaha et al., 2008). Magnetic particle detection (MPD) specifically exploits the nonlinearity of nanoparticle magnetization (Krause et al., 2007) and has been successfully used for sensitive immunoassays (Nikitin et al., 2007) as well as for real-time monitoring of nanoparticle kinetics in circulating blood (Nikitin et al., 2008). Its underlying detection strategy also forms the foundation for a new, noninvasive imaging technique that measures the amount and location of magnetic nanoparticles in biological tissues (Gleich and Weizenecker, 2005).

Despite growing biomedical interest in MPD, specific utilization for in-vitro dosimetry has not yet been described. This study therefore highlights its practical use, not only for measuring in-vitro dose kinetics, but also for understanding nanoparticle delivery and uptake mechanisms. Major emphasis is also placed on sensor design and testing to show explicitly, for the first time, that harmonic distortion serves as the practical limit for MPD sensitivity. This is in contrast with prior work where harmonic distortion in sensor electronics was not sufficiently considered to explain sensor performance or to account for discrepancies with simple theoretical projections (Goodwill et al., 2009; Krause et al., 2007). Here, gained insight provides new opportunities to further increase MPD sensitivity– even though presented results already demonstrate parity with alternative analytical methods that substantially require more time and labor to perform. Results therefore provide a firm foundation for rapid and economical in-vitro testing with magnetic nanomaterials.

2. Materials and methods

2.1. Nanoparticles and principles of sensor operation

In-vitro testing was performed using two different types of carboxyl-coated iron oxides. One was purchased commercially (Ocean NanoTech, Catalog # SHP-20–25, Lot # 072109, Spring-dale, AR) and the other was synthesized in-house using similar methods to those previously described (Lin et al., 2005). Table 1 summarizes the nanoparticle size, surface charge, and degree of agglomeration. Of particular importance for MPD is that iron-oxide cores are small enough to exhibit thermally unstable ferromagnetic behavior at room temperature (Krishnan, 2010). In this superparamagnetic regime, thermal energy is sufficient to randomize the orientation of individual ferromagnetic moments so no net particle magnetization (M) is observed in the absence of an external magnetizing force field (H). If, on the other hand, a field is applied, there is a natural tendency for moments to align and this gives rise to a finite particle magnetization that increases nonlinearly to approach ferromagnetic strength in strong H-fields (Ferguson et al., 2011). The sensor strategy illustrated in Fig. 1 exploits this nonlinear behavior simply by applying a oscillating H-field to induce a time-varying particle magnetization (M) that not only contains the applied field’s fundamental frequency (f₀) but also higher, odd-order harmonics (f_n) that result from the magnetization’s nonlinear field-dependence. Since the third harmonic is generally largest when no DC bias field is employed (Ferguson et al., 2009; Weaver et al., 2008), sensor circuitry is specifically tailored for f₃ detection using an inductively coupled receiver. Prior work specifically describes the magnetic properties for tested nanoparticles (Adolphi et al., 2010; Lin et al., 2005) as well as their general influence on third harmonic signal strength (Ferguson et al., 2011, 2009).

Table 1.

Size and surface charge for different carboxyl-coated iron-oxide nanoparticles when suspended in either water or RPMI culture media.

Particle source	Core diameter (nm)	Zeta potential (mv)	Hydrodynamic diameter4 (nm)
			Water5	Culture media
In-house	~121	−34.5 ± 2.92,a,c	154.7 ± 57.92,b	457 ± 1132,b
Ocean	~203	−51.953	34.8 ± 18.42,b	993 ± 2722,b
NanoTech			31.23

¹Measured by SEM (Zeiss, Merlin SEM).

²Determined by dynamic light scattering (^aZetaPlus analyzer,^bHome built, ^cIn water).

³Provided by manufacturer.

⁴Measured at 10 ug/ml.

⁵De-ionized (MilliQ, resistance > 18 MΩ cm).

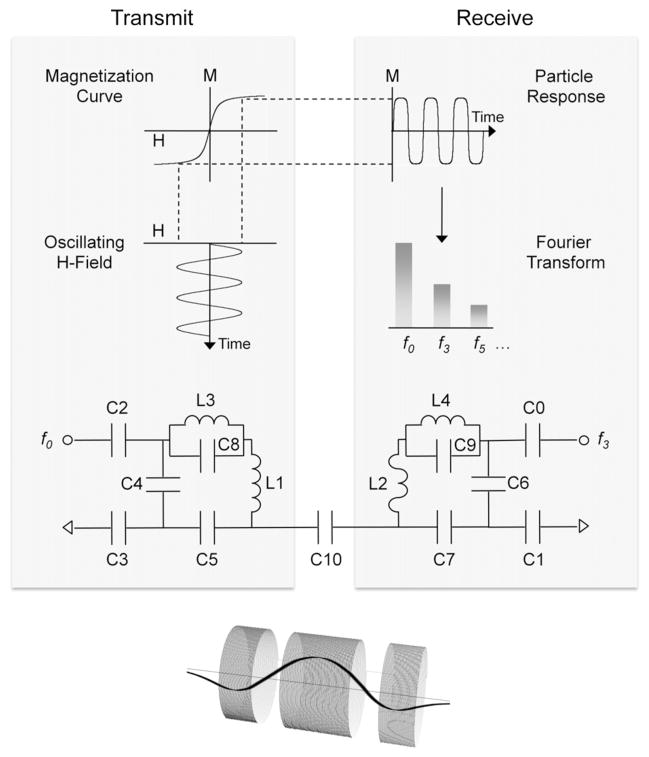
Fig. 1. Sensor operation and design.

Upper left: nanoparticle magnetization (M) varies nonlinearly when a magnetizing force field (H) is applied. Middle left: During sensor operation, an oscillating H-field drives particle magnetization at a fixed frequency (f₀). Right upper and middle: The time-varying particle response (M) then not only contains f₀ but also higher-order (odd) harmonics (f₃, f₅, etc …) due to nonlinear H-dependence. Transceiver circuit: H-field modulation is produced using a wire-wound solenoid (L1) and commercial capacitors that— (1) tune its resonant circuit to f₀ (C4–C5), and (2) match impedance to 50 Ω (C2–C3). Third order harmonics in particle magnetization (M) are then detected using a smaller receiver coil (L2) that resides inside the transmit coil (L1), is tuned (C6–C7) to f₃, and is also matched (C0–C1). Electrical isolation between transmit and receive channels is enhanced by capacitive decoupling (C10) and through LC-traps at f₃ (L3C8) and f₀ (L4C9). Coil inset: counter windings on opposite ends of the receiver coil (L2) further improve isolation but also introduce axial variations in the sensor’s sensitivity profile (bold curve).

2.2. Sensor design and function

Fig. 1 illustrates sensor circuitry in terms of distinct transmit and receive channels. The transmit circuit resonates at a fundamental frequency f₀ (250 kHz) and employs an air-cooled solenoid (L1) to produce a magnetizing force field (H) that oscillates with approximately 10 mT ${\mu }_0^{-1}$ when supplied with ~10 W of class-A power (T&C Power Conversion Inc., AG 1021, Rochester, NY). The solenoid itself is wound with 94 turns of 550 μm copper wire and has a diameter and length of 2.7 and 5.2 cm respectively. The large number of turns generally ensures that supplied power is efficiently dissipated in the transmitter coil and not inadvertently wasted by tuning and matching capacitors. This is demonstrated by the transmitter circuit’s quality factor (Q) since its measured value (33) is identical to theoretical estimates formulated by assuming all losses are determined solely by solenoid resistance (Minard and Wind, 2001a). It is also noted that specified solenoid dimensions are not critical but merely ensure a homogeneous H-field (Minard and Wind, 2001b) over inserted samples, which are cylindrical in shape, under 1 cm in diameter, and typically 100 μl or less.

The receiver circuit resonates at the transmitter’s third harmonic f₃ (750 kHz) and employs an air-cooled detector coil (L2) that surrounds the sample and is centered inside the transmitter (L1). The detector coil is illustrated in Fig. 1 and has a total length of 2 cm. It is composed of three 1 cm-diameter solenoids that are each wound with 114 μm copper wire and are separated along their symmetry axis by 3 mm gaps. All coils are connected in series but the central winding has 70 turns whereas each of outer has 35. Outer coils are also counter wound to reduce inductive coupling with L1. This generally improves electrical isolation between transmit and receive channels since the magnetic flux produced by L1 induces counter-rotating currents in the detector that tend to cancel one another. Of course, complete cancelation is never achieved, but if it were, harmonic distortion out of the amplifier would not contribute to the measured voltage at f₃. Conversely, any sample localized at the center of the detector coil is more tightly coupled with the detector’s middle solenoid than either of its outer two. The sample’s time-varying magnetization therefore induces a net voltage that is then measured by the receiver.

Because residual coupling between L1 and L2 is inevitable, small signals induced by nanoparticle magnetization must ultimately compete with amplifier distortion. To minimize this as much as possible, L3 and C8 form a parallel resonance at f₃, and this presents high impedance to third harmonic distortion from the amplifier. Injected amplifier distortion is further attenuated by using a third order, low-pass filter that is not shown in Fig. 1, but preconditions input power and provides approximately 55 dB of additional attenuation at the amplifier’s third harmonic (f₃ = 750 kHz). Capacitive decoupling is also employed at C10 and works by first reversing the phase of residual f₃ distortion in the transmitter. It then feeds the result directly into the receiver where it subtracts from any f₃ distortion induced by residual coupling between L1 and L2. Together, these different strategies provide ~145 dB of isolation when measured between transmit and receive channels at 750 kHz.

A theoretical estimate for receiver (L1) Q is formulated by: (1) neglecting mutual inductance between primary and counter windings, and (2) assuming their series resistance reflects total circuit losses. This predicts a Q of only ~10 and agrees fairly well with the measured value of 7. It is not surprising that the measured value is slightly smaller given that the close proximity of counter and primary windings means their respective H-fields overlap and subtract to varying degrees. Stored energy density (i.e. H²) is therefore actually less than calculated by assuming no mutual inductance. Since Q is just a measure of stored to dissipated energy, this then diminishes the actual circuit Q relative to formulated estimates. By virtue of the reciprocity principle, it is also noted that detector sensitivity varies with the H-field that would be produced if a unit current flowed through its respective coils (Minard and Wind, 2001a). Fig. 1 therefore shows how this quantity varies along the coil’s symmetry axis and highlights the importance of placing small samples inside the detector’s central winding where the H-field is most intense. Generally, field homogeneity inside the detector is sufficient to ensure quantitative analysis for samples up to~100 μl.

One potential drawback of using capacitor C10 for decoupling is that it also injects a small amount of f₀ into the receiver and, if left unchecked, this can saturate any pre-amp it employs. The L4C9 trap diminishes this problem to some degree since it is tuned to f₀. To further reduce unwanted f₀ voltage, output from the receiver is high-pass filtered (not shown) before being routed to a commercial pre-amp with ~26 dB of gain (Advanced Receiver Research, LF Broadband, Burlington, CT). After the pre-amp, signal is passed to a commercial spectrum analyzer (Rohde & Schwarz, Model FSL303, Munich Germany) so harmonic voltage at f₃ can be continuously measured as samples are inserted and removed for MPD analysis. To ensure ease of use, transmit and receive coils reside inside a grounded shield that has a small opening for sample access. During sensor operation the shield rests on top of a wooden desk along with the spectrum analyzer so induced harmonics are easily recorded. All other equipment is housed in a standard 19” rack that is adjacent to the desktop workspace.

2.3. In-vitro study design and cell culture

To test whether MPD is sufficiently sensitive to reveal cell–particle interactions, we compared total nanoparticle binding and uptake in wildtype RAW 264.7 mouse macrophages with stable mutants (RAW-S3) where the expression of macrophage scavenger receptor A (SR-A) is silenced by approximately 90%. For anionic silica nanoparticles, SR-A was recently shown to foster cellular uptake through a pathway characteristic of clathrin-mediated endocytosis (Orr et al., 2011). In macrophages, SR-A also participates during the phagocytic uptake of larger micron-sized particulates and bacteria (Arredouani et al., 2006; Kobzik, 1995). By either internalization route, the same underlying mechanism is thought to involve electrostatic interactions between anionic functional groups on the particle surface and positively charged regions on the extracellular receptor domain. We therefore test whether modulating cellular SR-A levels also alters the cellular adhesion and uptake of anionic iron oxides, and if MPD is sufficiently sensitivity to discern specific receptor-mediated differences.

Previous methods were used to culture wildtype RAW 264.7 and SR-A deficient RAW-S3 mutants (Orr et al. 2011). Both cell types were cultured in a humidified atmosphere of 37 °C and 5% CO₂ using 100 cm² dishes and RPMI media supplemented with 10% fetal bovine serum (Atlanta Biologicals), 2 mM L-glutamine (Gibco), and penicillin–streptomycin antibiotic (Gibco). Prior to nanoparticle exposure, cells were seeded into 6 cm culture dishes using 4 ml of total media and ~3 × 10⁶ cells/dish. Cells were then allowed to attach and divide for 24 h. The following day, dosing solution was prepared by mixing stock nanoparticle suspensions with 10% of the final volume of fetal bovine serum, vortexing briefly, and diluting to give complete media. All cells were then treated at 2 μg/ml using 6 ml per culture well. At this low concentration, no significant effect on cell viability was observed using either Alamar Blue reagent or trypan blue exclusion.

Prior to MPD analysis, exposed cells were washed three times with 4 ml of sterile phosphate buffered saline (PBS) to remove any particles that were not tightly bound on cell surfaces or internalized. After washing, cells were lysed by adding 0.3 ml of cold phosphate buffered saline containing 1% NP40 detergent. This was not generally necessary but proved quicker and easier than physically scraping plates to remove attached cells. Initial studies performed with either detachment method also showed no differences so the more convenient approach was routinely employed.

After cell detachment, the total lysate for each dish was transferred to a separate MPD sample tube (Block Scientific Inc., Product # 6500-Clear, Bohemia, NY). Each tube was then centrifuged at 800 rpm for 10 min so 200 μl of supernate could be removed to leave a total sample volume (100 μl) consistent with sensor design (see Section 2.2). To estimate the number of cells in each MPD sample, additional culture dishes were included so a hemacytometer could be used after otherwise identical exposure and washing.

3. Results

3.1. Sensor calibration and sensitivity

Sensor output is calibrated by analyzing separate standards that are serially diluted from stock nanoparticle suspensions to produce different samples with known particle mass. Results in Fig. 2 highlight sensor linearity and provide a direct measure of sensitivity that is 14.88 ± 0.02 ng/μv for Ocean NanoTech particles and 29.8 ± 0.3 ng/μv for in-house counterparts. Relative differences are generally expected since the iron-oxide core diameter for Ocean NanoTech particles (c.f. Table 1) is closer to the optimum value (~18 nm) that was recently found to maximize MPD sensitivity (Ferguson et al., 2011). The same work shows that MPD sensitivity depends strongly on the diameter of the iron-oxide core as well as its chemical composition and relaxation behavior. Other factors affecting sensor sensitivity include the size and geometry of the receiver coil (Ferguson et al., 2009; Krause et al., 2007), transmission frequency (f₀) and power (Ferguson et al., 2011), as well as harmonic number and whether or not a bias field is employed (Weaver et al., 2008).

Fig. 2. Sensor calibration and linearity.

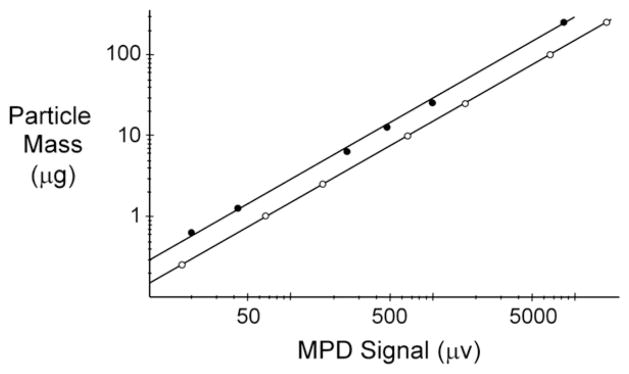
The known mass of Ocean NanoTech (○) and in-house (●) nanoparticles in calibration standards is plotted as a function of sensor output voltage. Data is well fit (R² ≥ 0.9996) to a straight line that has zero intercept and a slope that defines detection sensitivity. MPD analysis of all standards and cell samples containing Ocean NanoTech particles was performed using 14 W of transmitter power (at f₀), whereas, experiments with in-house counterparts only used 12 W. In each case, error bars representing the standard deviation from three replicates are all smaller than the actual symbols used to plot mean values and are therefore omitted on the log–log graph.

In the current study, slightly different transmitter power was employed for each particle type (c.f. Fig. 2 caption). This was not intentional but merely reflected different settings at the time measurements for each type of particle were performed. While expected to have a small influence on relative sensitivity, different settings are generally accounted for by sensor calibration and therefore have no direct effect on measured particle amounts.

3.2. Harmonic distortion and lower detection limits

Even with no sample inside the sensor, residual system harmonics produce about 1 μv of f₃ at the 50 Ω input of the spectrum analyzer. This corresponds to −110 dBm of RMS power that fundamentally limits the sensor’s minimum detection capability and is most likely due to harmonic (f₃) distortion in the transmitter. To identify this source, consider that the measured f₃ distortion out of the transmitter is 6 dBm when the power level at f₀ is 13 W (c.f. Fig. 2 caption). Electrical isolation between transmit and receive is also measured to be −145 dB @ f₃. Together with 26 dB of pre-amp gain, it is then seen that residual system harmonics (−110 dBm) are close to the −113 dBm of f₃ distortion that the transmitter is estimated to inject directly into the receiver (i.e. −113= 6 − 145+26). Assuming actual signal should be about 5 times stronger to ensure confident nanoparticle detection, measured sensitivity and residual system harmonics (i.e. 1 μv) set the lower limit of detection (LOD) at approximately 100 ng for tested nanoparticles. Since typical cell samples contained anywhere from 3 to 30 times this amount, confident in-vitro dosimetry was assured.

3.3. In-vitro dosimetry and kinetics

Fig. 3 shows the kinetics of cell dose during in-vitro exposures performed using different nanoparticles and cell types. Despite using identical nanoparticle concentration in culture media (2 μg/ml), results vary significantly for different particle-cell combinations. Indeed, it is for this reason that simple exposure metrics are generally insufficient to correctly understand cellular response, and why actual cell dose is needed for the consistent use of in-vitro toxicity assays (Soenen and De Cuyper, 2010; Teeguarden et al., 2007).

Fig. 3. In-vitro nanoparticle dosimetry.

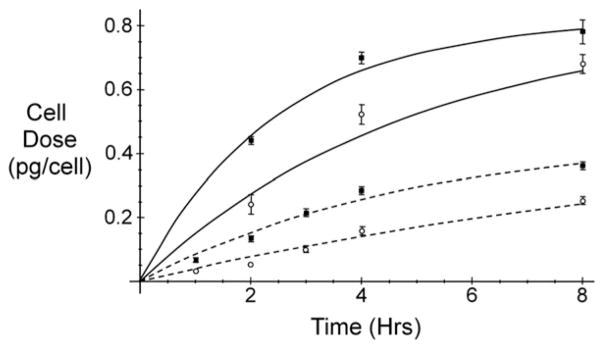
Average cell doses for wildtype (■) and SR-A deficient macrophages (○) are shown with error bars that represent standard deviations from three replicates. Numerical fitting to Eq. (1) summarizes time-dependent results during exposure to either Ocean NanoTech (—) or in-house nanoparticles (— —) described in Table 1.

For each particle-cell combination in Fig. 3, time-dependent cell dose (D) is well-described by a simple rate equation that asymptotically saturates (D_s) with a characteristic time (τ), such that:

$$D(t)=D_{\text{s}}(1-e^{-t/\tau })$$ (1)

The same kinetic behavior has been previously measured for human (Lunov et al., 2011) and mouse (Wilhelm et al., 2002a) macrophages when either cell type is exposed to other negatively charged iron-oxide nanoparticles. But unlike here, prior results employed either spectroscopic analysis (Lunov et al., 2011) or a combination of electron paramagnetic resonance (EPR) and cell magnetophoresis (Wilhelm et al., 2002a), all of which are more time-consuming and labor-intensive than MPD.

Kinetic parameters in Eq. (1) are derived from Fig. 3 using nonlinear regression, and estimated values are summarized in Table 2. Results show that wildtype RAW 264.7 and SR-A deficient cells both achieve similar saturation levels (D_s) when exposed to same nanoparticles. Differences in the characteristic time (τ) indicate, however, that SR-A deficient cells typically take about twice as long to accumulate the same saturating dose. Active transport mediated by SR-A binding is therefore responsible for approximately half the measured rate of particle loading in RAW 264.7 macrophages. This is similar to our previous findings measured using fluorescent nanoparticles of amorphous silica, but in that study cell dose was only monitored for 1 h (Orr et al., 2011). Prior linearity for measured kinetics is therefore expected and merely reflects the short-time behavior of Eq. (1).

Table 2.

Estimated kinetic parameters derived using nonlinear regression to fit Eq. (1) to data in Fig. 3. Parameter uncertainties reflect asymptotic standard error from nonlinear fitting.

Particle source	Cell line	Ds (pg)	τ (h)
In-house	Raw	0.45 ± 0.06	4.8 ± 1.1
	SR-A	0.45 ± 0.11	9.7 ± 3.3
Ocean NanoTech	Raw	0.82 ± 0.05	2.5 ± 0.4
	SR-A	0.89 ± 0.17	5.5 ± 1.9

For each cell line in Fig. 3, results in Table 2 show that cell dose is consistently higher for larger agglomerates (c.f. Table 1). One likely reason is that they simply settle out of suspension faster and, as a result, are delivered more quickly to the cell surface (Hinderliter et al., 2010). However, another contributing factor may be that larger agglomerates also bind more efficiently to the plasma membrane. This is not only because of their greater contact area (Champion et al., 2008) but also because electrostatic interactions are enhanced by the higher surface charge for their constituent nanoparticles (c.f. Table 1 and (Wilhelm et al., 2002b). In either case, MPD results are consistent with known effects stemming from agglomerate size and surface charge.

In addition to reflecting known dosimetric mechanisms, MPD results are also in qualitative agreement with anticipated mass–balance limitations. All D_s values are, for example, lower than the maximum possible cell dose (D_max) that is estimated in Table 3. Summarized values are formulated by assuming that all suspended nanomaterial in culture media is delivered to, and fully associated with, exposed cells. It is generally expected that D_s < D_max since: (1) cell cultures are not always 100% confluent, (2) loosely associated material is inevitably washed off, and (3) because particle settling is not necessary fast enough to ensure the delivery of all suspended nanomaterial to the cell surface during the allowed exposure time (Hinderliter et al., 2010; Teeguarden et al., 2007).

Table 3.

Maximum possible cell dose (D_max) estimated using known media concentration (2 ug/ml), media volume (6 ml), and measured cell counts at 8 h.

Particle source	Cell line	Dmax (pg)
In-house	Raw	0.9
	SR-A	1.2
Ocean NanoTech	Raw	1.5
	SR-A	1.7

4. Discussion

4.1. MPD’s potential utility for mechanistic studies of in-vitro dosimetry

In-vitro dosimetry in Fig. 3 is generally consistent with the known effects of agglomerate size and surface charge on cellular delivery and receptor-mediated uptake. However, the relative importance and combined influence of different dosimetric mechanisms is difficult to assess. This is especially challenging since theoretical descriptions of nanoparticle diffusion and the effects of agglomeration on gravitational settling have not yet considered active transport at the cell surface (Hinderliter et al., 2010; Teeguarden et al., 2007). Likewise, prior mathematical models of electrostatic binding on the plasma membrane assume a constant nanoparticle concentration and do not yet consider actual delivery to the cell surface (Lunov et al., 2011; Wilhelm et al., 2002b). Results in this study clearly identify the importance of both mechanisms and generally highlight the need for their integrated description. Differences in observed rates of particle association between wildtype cells and counterparts deficient in a major uptake pathway also provides confidence that the detected MPD signal is due to specific nanoparticle–cell interactions, and that employed cell washing was sufficient for minimizing possible signal contributions arising from nonspecific interactions with extracellular matrix. Together, these findings demonstrate the overall utility of MPD as a dosimetric platform that is easy and fast to use. Moreover, detected nanoparticles are widely available with a diverse range of physical and chemical properties that are ideal for mechanistic studies. This includes microspheres doped with magnetic nanoparticles since these are also easily detected (data not shown).

4.2. Relative MPD performance

Average in-vitro samples analyzed in this study each contained about six million cells and had roughly 1.4 μg of magnetic nanoparticles. Since the sensor’s LOD was approximately 100 ng, similar dosimetry should be achievable using as few as half million cells per sample. This is comparable to the one million cells and 1–20 μg of total nanoparticle mass typical for samples previously analyzed using much more expensive and time-consuming dosimetry based on either atomic absorption spectrometry (Settles et al., 2011) or electron paramagnetic resonance (Gamarra et al., 2010; Wilhelm et al., 2002a). Direct detection of particle magnetism with a super-conducting quantum interference device (SQUID) also requires similar cell and particulate amounts (Hashimoto et al., 2009; Levy et al., 2011). MPD, however, requires no expensive cryogens and is far simpler to operate. Furthermore, recent claims that 50 ng might be detectable with SQUID are unsubstantiated and are simply based on very optimistic extrapolation of instrument calibrations performed at microgram-levels (Oisjoen et al., 2010). Alternative sensors based on either AC susceptometry (de la Torre et al., 2011) or magnetic permeability (Kriz et al., 1996) also appear less sensitive than MPD - but neither has yet been used for in-vitro analysis so exact comparisons are difficult. Moreover, uneven cell coverage on the surface of magnetoresistive sensors seriously compromises their practical use for in-vitro dosimetry (Chen et al., 2011). By comparison, MPD is readily adapted for a wide range of different sample sizes and shapes, is easy to use, requires less than a second to perform, and is inexpensive to deploy and maintain.

4.3. Future directions in sensor design and use

Detailed electrical characterization in this study identifies the transmitter as an important source of harmonic distortion that currently limits MPD performance. We have found, however, that additional low-pass filtering to further condition transmitter signal does not significantly reduce residual system harmonics. This suggests that other low-level sources of harmonic distortion downstream from the transmitting amplifier now need to be considered to make further sensitivity improvements. The same conclusion was recently corroborated independently by others and has stimulated their own work to characterize the distortion properties of commercial capacitors that might be used for MPD transceiver circuitry (Zheng et al., 2012). More generally, the distortion behavior for all passive and active circuit elements needs to be more carefully considered. Other potentially important sources include: (1) eddy currents, (2) mechanical coil vibrations, and (3) inadvertent use of magnetic parts like steel screws.

Although not the focus of this study, it is anticipated that the introduction of recognition molecules on nanoparticle surfaces will enable future strategies for monitoring cellular function. Attached antibodies, for example, should inform about targeted protein expression on cell surfaces. In this case, small nanoparticles like those described here should be employed since their magnetic moment is relatively free to follow the excitation field and does not require physical particle rotation (Ferguson et al., 2011; Ferguson et al., 2009). A robust MPD response is therefore expected to be independent of whether nanoparticles are bound to the cell surface, or to what degree their hydrodynamic diameter is altered by required surface modification.

5. Conclusions

Magnetic particle detection (MPD) is a sensitive technique for measuring the amount of magnetic nanoparticles in small cell samples. For in-vitro bioassays, achieved detection performance is comparable to alternative analytical methods that are substantially more expensive, time-consuming, and labor-intensive to perform.