Modeling multi-system biological risk in young adults: the Coronary Artery Risk Development in Young Adults Study (CARDIA)

Abstract

Background

While much prior research has focused on identifying the roles of major regulatory systems in health risks, the concept of allostatic load (AL) focuses on the importance of a more multi-systems view of health risks. How best to operationalize allostatic load, however, remains the subject of some debate.

Aim

To test a hypothesized meta-factor model of allostatic load composed of a number of biological system factors, and to investigate model invariance across sex and ethnicity.

Subjects & Methods

Biological data from 782 men and women, aged 32–47, from the Oakland, CA and Chicago, IL sites of the Coronary Artery Risk Development in Young Adults Study (CARDIA) were collected as part of the Year 15 exam in 2000. These include measures of blood pressure, metabolic parameters (glucose, insulin, lipid profiles, and waist circumference), markers of inflammation (interleukin-6, C-reactive protein, and fibrinogen), heart rate variability, sympathetic nervous system activity (12 hr urinary norepinephrine and epinephrine) and hypothalamic-pituitary-adrenal axis activity (diurnal salivary free cortisol).

Results

A “meta-factor” model of AL as an aggregate measure of six underlying latent biological subfactors was found to fit the data, with the meta-factor structure capturing 84% of variance of all pairwise associations among biological subsystems. There was little evidence of model variance across sex and/or ethnicity.

Conclusions

These analyses extend work operationalizing AL as a multi-systems index of biological dysregulation, providing initial support for a model of AL as a meta-construct of inter-relationships among multiple biological regulatory systems, that varies little across sex or ethnicity.

INTRODUCTION

Despite an extensive literature linking various major physiological regulatory systems to health risks (Barrett-Connor and others 1986; Despres and others 1990; Eaton 2005; Forouhi and Sattar 2006; Fried and others 1998; Landsberg 1994; Munck and Guyre 1991; Reuben and others 2000; Simon and others 2006; Tsuji and others 1996), surprisingly little attention has been paid to the health impacts of the co-occurrence of physiological dysregulation across multiple systems. The concept of allostatic load (AL), first proposed by McEwen & Stellar (McEwen and Stellar 1993) and subsequently elaborated by McEwen (McEwen 2003), represents one attempt to conceptualize health risks from such a multi-systems perspective. Fundamental to the concept of AL is the fact that the body’s physiological regulatory systems are constantly adjusting to an ever-changing set of demands and stimuli as we (and our bodies) consciously and unconsciously respond to the world around us - a process that has been termed allostasis. (Sterling and Ever 1988) Over time, as this process of on-going adaptation continues, physiological systems can lose their ability to efficiently and effectively adapt (i.e., they begin to exhibit evidence of “wear and tear” or physiological dysregulation). The concept of allostatic load reflects an attempt to conceptualize such physiological dysregulation from a multi-systems perspective (i.e., as the cumulative physiologic toll or “price” that the body may ultimately pay for its adaptational efforts).

What distinguishes the concept of AL from other approaches to understanding physiological predictors of health risks is its focus on consideration of multiple physiological systems (and their attendant dysregulations) and their possible conjoint impacts on risks for various health outcomes. It is this multi-systems focus that sets allostatic load apart from the heretofore more common approach of focusing on risks associated with individual systems. Consistent with the idea that a cumulative, multi-systems view of biological risks is important to understanding health differentials, several studies have found that multiple biological factors, none of which were individually significant as predictors of major health events such as heart attacks and/or death, do contribute to significantly elevated risks when considered jointly (McEwen 1998; Schulkin 2004). Empirical work using various operational definitions of AL has also demonstrated that cumulative burdens of dysregulation are associated with significantly greater risks for cognitive and physical decline as well as mortality, even when individual, component biological measures were not significantly related to outcomes (Karlamangla and others 2002; Lynch and others 1996; Seeman and others 2004).

Prior research, however, has operationalized AL in terms of various summative indices (Karlamangla and others 2002; Seeman and others 2001). While useful as relatively simple approaches to estimating cumulative levels of physiological dysregulation, this work has not included explicit testing of the concept of allostatic load as a higher-order constellation of dysregulations across multiple major regulatory systems (e.g., cardiovascular, metabolic, endocrine, immune), with expected clustering of dysregulation both within each system (e.g., among various cardiovascular indicators) as well as across systems (i.e., as a function of inter-system dependencies). The present paper seeks to extend previous research on the measurement of AL through use of structural equation modeling to estimate three hypothesized structural/measurement models of AL and to evaluate the fit of a proposed “meta factor” model reflecting the shared (cumulative) variance across these systems.

Data from participants in the Coronary Artery Risk Development in Young Adults Study (CARDIA) also provide an opportunity to examine the patterning of these inter-relationships among various regulatory systems by sex and ethnicity (Whites vs. Blacks). The potential importance of examining sex and ethnic differences is suggested by a growing body of evidence for potentially important gender differences in biological responses to challenge (Taylor and others 2000), a pattern that could also result in differential patterns of dysregulation among physiological regulatory systems. Similarly, in light of known differences in the typical life experiences and challenges faced by Whites and Blacks in the US, with our history of social and economic disenfranchisement of Blacks, it is possible that the cumulative patterns of AL “wear and tear” seen across different regulatory systems will differ between Blacks and Whites. Indeed, Geronimus and colleagues (Geronimus and others 2006) have documented Black/White differences in overall AL using the nationally-representative NHANES III data. No prior work has directly tested for possible ethnic differences in patterning of associations among biological risk factors. The possibility of such differences is at least suggested by a mixed literature pointing to possible Black/White differences in links between cardiovascular risk factors and major health outcomes: some studies find similar effects of risk factors on coronary disease risks for Whites and Blacks (D'Agostino and others 2001; Vaccaro and others 1998) while others indicate differences in the relative impacts of different risk factors (Liao and others 1999; Paultre and Mosca 2006). In contrast to many studies where one or another ethnic group is sampled in only small numbers, the CARDIA sample design provides similar sample sizes for Whites and Blacks, allowing for stronger statistical comparisons within and between these groups.

METHODS

CARDIA is a bi-ethnic, prospective, multi-center epidemiological study of the evolution of cardiovascular risk beginning in young adulthood. In 1985–1986, 5115 black and white men and women, aged 18 to 30 years, were recruited at Birmingham, AL; Chicago, IL; Minneapolis, MN; and Oakland, CA, to achieve a balance at each site by race (black, white), gender, education (high school degree or less, more than high school), and age (18–24 years, 25–30 years) (Cutter and others 1991). Participants were examined at study entry and years 2, 5, 7, 10, and 15 with re-examination rates among surviving cohort members of 90.5%, 85.7%, 80.6%, 78.5%, and 73.5%, respectively. Compared with CARDIA subjects who participated in the Year 15 exam, those who did not participate were more likely to be African-American, younger, less educated and smokers (data not shown). Site institutional review committee approval and informed consent were obtained for each examination.

At the Year 15 exam, subjects seen at the Oakland, CA and Chicago, IL sites (and living within 50 miles of the clinic; N=721 and 615 respectively) were invited to participate in a sub-study of cumulative biological risk; 844 (63%) agreed to participate. Participation in the sub-study involved a second clinic visit to augment the core CARDIA biological measures with additional assessments of heart rate variability, and hypothalamic-pituitary-adrenal axis and sympathetic nervous system activity. At the second clinic visit, participants completed a 30-minute, computer-based assessment of heart rate variability (see details below) and received instructions for completion of a 12hr, over-night urine collection and collection of 6 saliva samples over the course of a single day. There were no significant differences between those subjects participating in the ancillary study and those from the Chicago and Oakland sites who did not participate in the ancillary study in terms of mean age or the gender distribution of subjects. However, those in the ancillary study were slightly more likely to be black and had slightly lower levels of education and income than those who did not participate in the ancillary study. Ancillary study participants who had completed two or more of four sets of physiological measurements (blood [as part of core CARDIA protocol], urinary, salivary, autonomic) were considered to have sufficient information on components of AL to be included in the current analyses (782 of the 844 enrolled [93%]).

Biological Risk

Measurements for 18 different biological parameters were available for analysis, including measures of metabolism, blood pressure, and inflammation from the core CARDIA exam, and measures of heart rate variability [HRV], sympathetic nervous system [SNS], and the hypothalamic-pituitary-adrenal [HPA] axis from the ancillary study protocol. Parameters considered as components of our assessment of overall, cumulative risk (i.e., AL) were selected to reflect the activity and functioning of major biological regulatory systems known to affect health (Barrett-Connor and others 1986; Despres and others 1990; Eaton 2005; Forouhi and Sattar 2006; Fried and others 1998; Landsberg 1994; McEwen 1998; McEwen and Stellar 1993; Munck and Guyre 1991; Reuben and others 2000; Simon and others 2006; Tsuji and others 1996).

Seated systolic and diastolic blood pressure were measured as the average of the second and third of three seated blood pressure readings assessed after a 5-minute rest period with a Hawksley random zero sphygmomanometer (W.A. Baum Company, Copiague, NY, USA).

Measures of inflammation included C-reactive protein (CRP), interleukin-6 (IL-6) and fibrinogen. CRP and fibrinogen were measured using the BNII nephelometer from Dade Behring utilizing a particle enhanced immunonephelometric assay. The assay range for CRP is 0.175 – 1100 mg/L; intra-assay CVs range from 2.3 – 4.4% and inter-assay CVs range from 2.1 – 5.7%. Fibrinogen intra-assay and inter-assay CVs were 2.7% and 2.6% respectively. IL-6 was measured by ultra-sensitive ELISA (R&D Systems, Minneapolis, MN), with a detection range of 0.156–10.0 pg/mL and a routine CV in the lab of 6.3%.

Measures of metabolism included waist circumference, and fasting measures of high-density lipoprotein (HDL-C) and low-density lipoprotein (LDL-C) cholesterol, triglycerides and glucose and insulin. Waist circumference was measured as the average of two measurements taken to the nearest 0.5 cm at the minimum abdominal girth, while participants were standing upright. Blood samples for total cholesterol, HDL-C and LDL-C cholesterol, insulin and glucose assays were drawn in the morning after an overnight fast. Blood was drawn into vacuum tubes from participants in the seated position and was centrifuged at 4C within 60 min. Serum and plasma were stored in cryovials (containing fluoride for the glucose assay) and then frozen at −70C for shipment to the Northwest Lipid Research Laboratories, University of Washington, Seattle. Total cholesterol was determined enzymatically on the Abbot Spectrum, within 6 weeks of collection (Warnick 1986). HDL-C was determined by precipitation with dextran sulfate/magnesium chloride (Warnick and others 1982). LDL-C was calculated using the Friedewald equation (Friedewald and others 1972). Glucose and insulin assays were conducted at Linco Research, Inc. Glucose measurements were assessed with a Cobas Mira Plus chemistry analyzer (Roche Diagnostic Systems) using the hexokinase ultraviolet method; insulin was measured by radioimmunoassay (RIA) using an overnight, equilibrium incubation format (Folsom and others 1996; Haffner and others 1994).

Heart rate variability (HRV) was assessed based on a 10-minute protocol during which subjects were asked to sit quietly without moving or talking. Details regarding the protocol have been previously reported (Sloan and others 2005). ECG electrodes were placed on the right shoulder, on the left anterior axillary line at the 10th intercostal space and in the right lower quadrant. The analog ECG signal was digitized at 500 Hz during a 10-min quiet, seated resting period. The ECG waveform was submitted to a specially written R-wave detection routine, resulting in a time series of RR intervals. Errors in marking of R-waves were corrected interactively. Spectral analysis to compute RR variability (RRV) was conducted on 5-min epochs using an interval method for computing Fourier transforms (DeBoer and others 1984). Power, i.e., variance (in msec2), over the low (0.04–0.15 Hz (LF)) and high (0.15–0.50 Hz (HF)) frequency bands was summed. Mean heart rate (HR) was computed for all subjects.

Integrated measurements of SNS activity were obtained from assays for norepinephrine (NOR) and epinephrine (EPI) from 12-hr over-night urine samples preserved with sodium metabisulfite. Aliquots to be assayed for NOR and EPI were acidified to pH of 3 or less and frozen at −80C until assayed. Samples were analyzed by HPLC with electrochemical detection (Macdonald and Lake 1985) and creatinine by the method of Baranowski and Westenfelder (Baranowski and Westenfelder 1986). The sensitivity of the assay as prepared was 1.0 ng/ml. The intra- and inter-assay CVs for NOR were 3.0% and 4.1% respectively; comparable statistics for EPI were 4.8% and 7.1%.

Diurnal cortisol activity was assessed based on a series of six saliva samples collected at wakening (“when your eyes open and you are ready to get up”), 45 minutes later, 1hr 45 min after that (i.e., 2.5 hrs after wakening), +5.5hrs (i.e., 8 hrs after wakening), +4 hrs (i.e., 12 hrs after wakening), and at bedtime (“right before getting into bed”). Participants were given 6 Salivettes (i.e., a small cotton roll in a plastic tube; Sarstedt, Rommelsdorft, Germany) at the conclusion of their Year 15 CARDIA clinic visit. Participants collected samples on a single weekday, recording the time they woke up and (on the tube label) the time each sample was collected. Participants returned the Salivettes to the clinic the following morning. Salivettes were stored frozen at each site until they were assayed by time-resolved immunoassay with fluorometric end point detection (Dressendorfer and others 1992). Nine samples with levels below the minimum detectable level (0.7 nmol/l) for this assay were assigned values of 0.5 nmol/l. Intra- and inter-assay variabilities were each less than 12%.

Two summary measures were developed and included in the current analyses to reflect diurnal rhythm: 1) Morning Rise – the difference between the wake-up sample and the sample collected 45 minutes later (after transforming both to logarithms; equivalent to the log of the ratio of the two samples) and 2) Diurnal slope – The slope of the decline of cortisol across the day was derived from a multilevel growth curve model (Adam and others 2006), treating the slope (of time elapsed since wake-up) and intercept as random coefficients. The second cortisol sample (+ 45 min after wake-up) was used as the starting point for estimation of slopes, thereby defining the slope as the average hourly rate of decline, following the morning rise, in logged cortisol. The empirical Bayes' best linear unbiased predictors (EBLUP) of the subject-specific slopes, derived from the multi-level model, were used in the analysis. Data were excluded for individuals who woke-up after twelve noon or whose timing of sample collections deviated by more than 15–30 minutes for first 2 samples (i.e., those measuring morning rise) and by more than 30–60 minutes for the subsequent 4 samples (i.e., those measuring afternoon decline and bedtime nadir).

Age. Sex and Ethnicity

At the time of this sub-study (i.e., CARDIA Year 15 exam), ages of participants could range from 32–49. As indicated previously, based on the original CARDIA sampling design, there are approximately equal numbers of Black and White men and women in the sample (White Females = 1031, Black Females = 1021; White Males = 911; Black Males = 709).

Analyses

Structural equation modelling (SEM) analyses was employed to estimate alternative models of the “structure” of AL and to test for factorial invariance of the final structural model across gender and ethnicity. SEM is a technique used to assess the “plausibility” of hypothesized-models of interrelationships among variables (Hu and Bentler 1999). With SEM, one can test whether an a priori hypothesized model fits observed sample data by comparing the estimated population covariance matrix of the hypothesized model to that of the observed sample data covariance matrix.

A first set of analyses examined the relative fit of three a priori models representing the inter-relationships among the biological measures and systems for which we had data. These analyses were designed to test the hypothesis that AL can be represented by a higher-order meta-construct reflecting dysregulation across multiple biological systems (modelled as sub-factors). The available biological data were hypothesized to represent six “latent” sub-factors (or domains) representing heart rate variability, blood pressure, inflammation, metabolism, sympathetic nervous system and hypothalamic-pituitary-adrenal axis activity. These six sub-factors were in turn hypothesized to represent various aspects or components of a meta “allostatic load” factor. The fit of this hypothesized AL meta-factor model was tested against two alternative models. One alternative was a “one-factor” model where all the biological variables were hypothesized to be indicators of a single “latent” AL factor (i.e., removing specification of separate biological subsystems). The second alternative was a correlated “6-factor” model in which the individual biological measures were hypothesized to reflect the same six underlying biological factors represented in the meta-factor model but relationships among these factors were represented by a series of paired correlations rather than through a meta “allostatic load” factor. The “one-factor” model is nested within the meta-factor model, and the latter, in turn, is nested within the “6-factor” model. While a nested model is more parsimonious than the less constrained model in which it is nested, it will also necessarily provide a poorer fit. The central question was how much better does the meta-factor model, reflecting a higher order constellation of shared biological dysregulations across our six sub-factors, fit when compared to the one-factor model, and how well does it capture the majority of the information contained in the less structured/constrained “6-factor” model.

To assess the relative fit of the “6-factor” and “meta factor” models, each was compared to a “null” model wherein the 6 factors were modelled as independent entities, unrelated to one another. While the latter model was not expected to fit well (since it cannot reflect the known relationships among these biological systems), it provides a standard against which to compare the relative improvements in fit achieved by the “meta-factor” versus the “6-factor” model.

The SEM literature has proposed an array of statistics for assessing whether a hypothesized model adequately “fits” one’s empirical data. For analyses testing model fit, we report the chi-square (χ²) test statistic, the chi-square to degrees of freedom (χ²/df) ratio, the comparative fit index (CFI), and the root mean square error of approximation (RMSEA). The χ² statistic is used to assess the extent to which the deviations between the model-implied covariance matrix and the observed covariance matrix exceeds chance expectation. However, χ² values are sensitive to sample size and even small deviations between model-implied and observed covariance matrices can lead to a large and statistically significant χ² value. The χ²/df ratio is an additional statistic that proves useful in such situations. χ²/df values less than 3.0 are desirable (Kline 1998). The CFI is an incremental fit index assessing improvement in fit of a hypothesized model compared to a restricted, nested baseline model (one in which all observed values are uncorrelated) (Bentler 1990; Hu and Bentler 1999). Values of .90 or greater are desired. RMSEA is an absolute fit index, which assesses the fit of a hypothesized model to observed sample data, with low values (≤ .06) desired, as this value represents the average discrepancy between the model-implied and observed covariance matrices. For comparisons of nested models, χ² difference tests were used to assess whether the change in model fit was statistically significant. Lagrange multiplier (LM) test statistics were examined to identify specific model parameters that when added to the model might improve model fit (e.g., the addition of a path between two model variables), including model parameters that should be freed from cross-group equality constraints (e.g., those parameters that would improve model fit if added to or “estimated freely” in the model; see below for description of multiple group analyses). After evaluating the relative fit of our “meta-factor” model of AL, we tested the factorial invariance of this model across four groups defined jointly by gender and ethnicity (i.e., White men and women and Black men and women).

Prior to model testing, each biological parameter was assessed for univariate normality and log transformations were made for glucose, insulin, triglycerides, CRP, IL-6, high and low frequency power, epinephrine, norepinephrine, and salivary cortisol measures. Despite improvements in univariate normality of biological parameters, computation of Mardia’s coefficient (e.g., Mardia’s = 35.10) in analyses using the EQS software indicated that the data displayed substantial multivariate non-normality. Thus, we used Satorra-Bentler Scaled Chi-Square statistics that are robust to violations of non-normality. And, for analyses assessing factorial invariance of the structure of AL across gender, ethnicity, and gender/ethnic groupings, chi-square difference tests correcting for the use of robust statistics (Satorra and Bentler 2001) were employed when comparing nested models. Also, since complete data were not available for all biological parameters, SEM analyses using EQS were computed using a complete data set produced from the maximum likelihood imputation method available within EQS (Jamshidian-Bentler EM algorithm) (Jamshidian and Bentler 1999). Analyses using listwise and pairwise estimation methods produced similar results to those reported here. All analyses were run using the EQS v6.1 software.

RESULTS

The mean age for the sample was 40 (range = 32–47; see Table 1). Reflecting the original CARDIA study design, gender and ethnicity exhibit approximately equal splits (57.9% female; 45.3% White). The lower portion of Table 1 provides descriptive statistics for each of the 18 biological parameters used to model AL.

Table 1.

Descriptive Statistics

	N	Mean (sd) or %	Variance- Transformed Mean (sd)	Imputed Mean (sd)
Age	782	40 (3.6)
Gender
Female (%)	453	57.9
Male (%)	329	42.1
Race
White (%)	354	45.3
Black (%)	428	54.7
Heart Rate (ln bpm)	721	72.6(11.7)	22.7 (3.6)	22.7 (3.5)
Low Freq. Power (ln ms2)	721	6.1 (1.1)	19.6 (3.6)	19.6 (3.5)
High Freq. Power (ln ms2)	721	5.9 (1.3)	18.8 (4.2)	18.8 (4.0)
Systolic BP (ln mmHg)	782	113.7 (14.3)	35.5 (4.5)	35.5 (4.5)
Diastolic BP (ln mmHg)	782	75.4 (10.7)	23.6 (3.3)	23.6 (3.3)
Triglycerides (ln mg/dL)	768	4.5 (0.6)	28.1 (3.5)	28.1 (3.5)
HDL-C (ln mg/dL)	768	50.3 (13.7)	15.7 (4.3)	15.7 (4.3)
LDL-C (ln mg/dL)	762	113.5 (32.3)	11.4 (3.2)	11.4 (3.2)
Waist Girth (ln cm)	779	89.8 (15.7)	28.1 (4.9)	28.1 (4.9)
Fasting Glucose (ln mg/dL)	768	4.4 (0.2)	88.7 (3.2)	88.7 (3.2)
Fasting Insulin (ln uU/mL)	766	2.5 (0.6)	15.8 (3.5)	15.8 (3.5)
Fibrinogen (ln mg/dL)	708	339.3 (79.2)	13.6 (3.2)	13.6 (3.1)
CRP (ln uG/mL)	760	1.1 (0.8)	4.6 (3.2)	4.6 (3.2)
IL-6 (ln pg/mL)	705	0.9 (0.4)	7.5 (3.5)	7.6 (3.4)
Norepinephrine (ln ug/g creatine)	725	3.4 (0.6)	21.3 (3.6)	21.3 (3.4)
Epinephrine (ln ug/g creatine)	681	1.5 (0.6)	9.2 (3.6)	9.3 (3.4)
AM rise – Salivary Cort. (ln nmol/L)	696	0.3 (0.6)	1.5 (3.4)	1.5 (3.2)
PM decline – Salivary Cort. (ln cort (nmol/L)/hour)	743	−0.03 (0.03)	−3.2 (3.6)	−3.1 (3.5)

Testing of the single-factor AL model revealed the expected poor fit to the data (χ² (135) = 2349.44, χ²/df = 17.40, CFI = .45, RMSEA = .15, Model AIC = 2079.44). Factor loadings for individual biological indicators are presented in Figure 1a.

Figure 1.

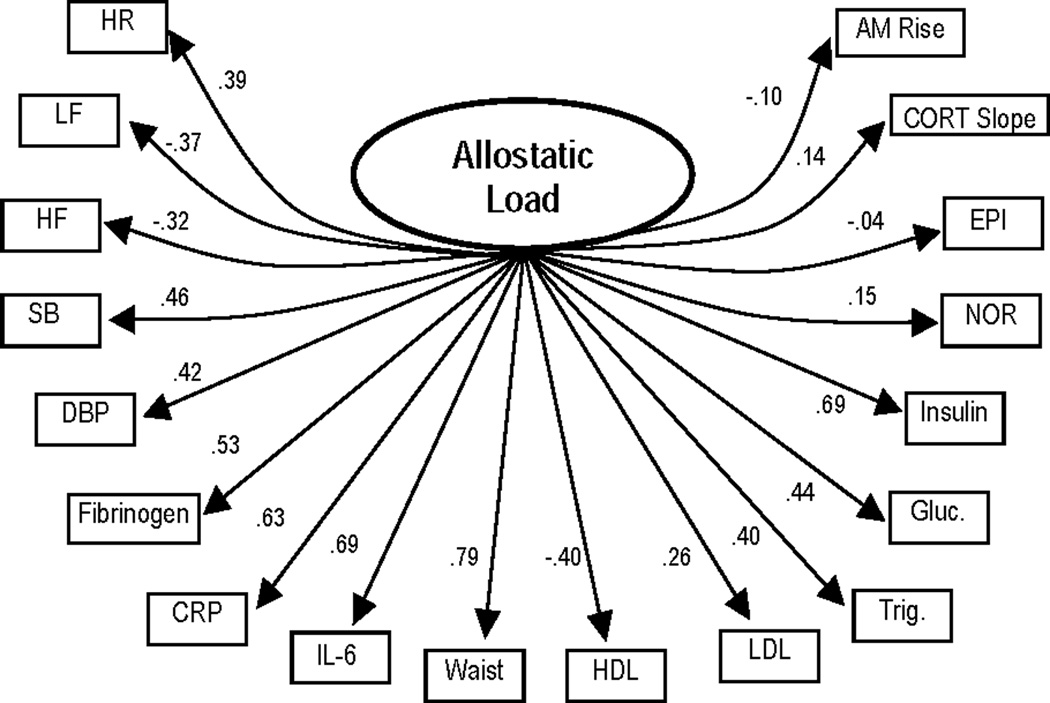
a. Results for final one-factor allostatic load model (model fit statistics: χ² (135) = 2349.44 χ²/df = 17.40, CFI = .45, RMSEA = .15, Model AIC = 2079.44). All parameter estimates are standardized and significant (p ≤ .05) except for path estimate for epinephrine (EPI). Estimates for error terms are not depicted.

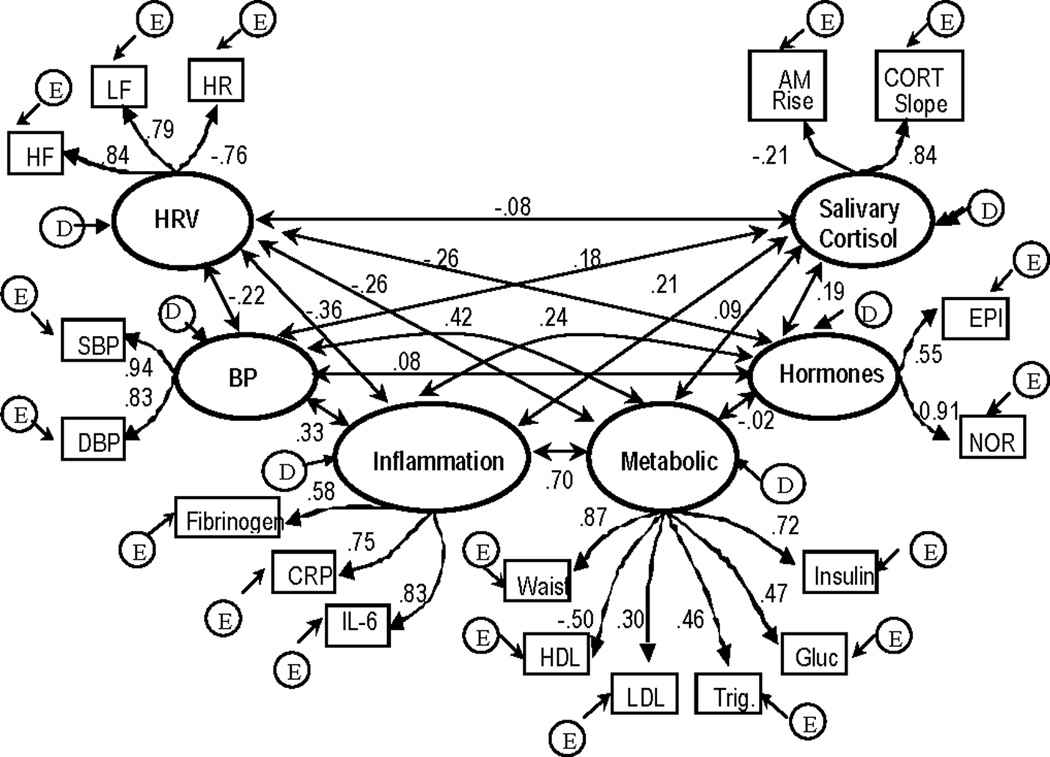
b. Results for “correlated 6 factor” allostatic load model (model fit statistics: χ² (120) = 568.89, χ²/df = 4.7, CFI = .89, RMSEA = .07, Model AIC = 328.89). All parameter estimates are standardized and significant (p ≤ .05) except for path estimate for AM rise, and correlations between blood pressure and hormone factors, metabolic and hormone factors, HRV and salivary cortisol factors, and metabolic and salivary cortisol factors. Estimates for error terms are not depicted.

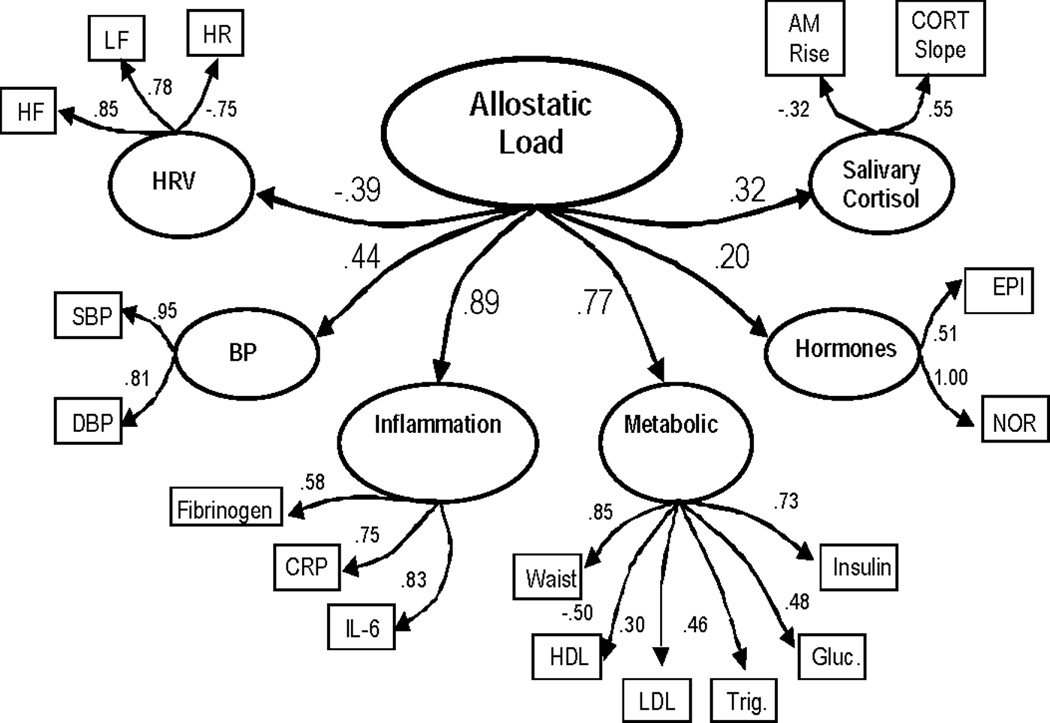
c. Results for meta-factor allostatic load model including epinephrine (model fit statistics: χ² (130) = 656.09, χ²/df = 5.0, CFI = .87, RMSEA = .07, Model AIC = 396). All parameter estimates are standardized and significant (p ≤ .05). Estimates for error terms are not depicted.

The correlated six-factor model provided a much better fit to the data (χ² (120) = 568.89, χ²/df = 4.7, CFI = .89, RMSEA = .07, Model AIC = 328.89). As shown in Figure 1b, with the exception of the measure of AM rise in salivary cortisol, all of the biological indicators loaded significantly on their respective “latent” factors. The pattern of correlations among the 6 factors was consistent with known associations among the various regulatory systems represented by these factors. The strongest correlations were those between metabolism and inflammation (0.70) and between metabolism and blood pressure (0.42); next in strength were those of inflammation with blood pressure (0.33) and HRV (−0.36).

As shown in Figure 1c, the hypothesized meta-factor AL model also provided a much better fit to the data than the one-factor AL model, albeit a significantly poorer fit than the correlated 6-factor model (χ ² (130) = 656.09, χ ²/df = 5.0, CFI = .87, RMSEA = .07, Model AIC = 396.1). As shown in Table 2, comparison of the improvements in fit of the meta-factor and 6-factor models relative to the “null” model - which hypothesized no relationships among the 6 factors - indicated that the improvement in fit associated with the meta-factor model (χ² difference relative to the “null” model = 471.65) represented 84% of that achieved by the less parsimonious “correlated 6-factor” model (χ ² difference relative to the “null” model = 558.85).

Table 2.

Relative model fit statistics

Model Fit Statistics	“Null” Model (6-factor uncorrelated)	6-Factor Model (Correlated)	Meta-Factor Model
CFI	.75	.89	.87
X2	1127.74	568.89	656.09
Df	135	120	130
X2/df	8.4	4.7	5.0
AIC	857.74	328.9	396.1
Difference in model X2 (from that of the Null Model)		558.85	471.65

A closer examination of the meta-factor model itself indicated that several modifications could be made to improve the fit. First, since the factor loading for norepinephrine on the hormone factor was 1.0 and analyses indicated that the removal of epinephrine did not alter the path estimate between the AL meta-factor and the single measure of norepinephrine, the hormone factor was replaced with the single measured norepinephrine variable (χ² (114) = 551.62, χ²/df = 4.8, CFI = .88, RMSEA = .07, Model AIC = 323.62). In addition, LM tests indicated that the addition of a parameter representing the covariance between the residual errors for HDL-C and triglycerides would lead to a very substantial improvement in the fit of this model (χ² (113) = 459.08, χ²/df = 4.1, CFI = .91, RMSEA = .06, Model AIC = 233.08). Figure 2 presents this final “refined” model.

Figure 2.

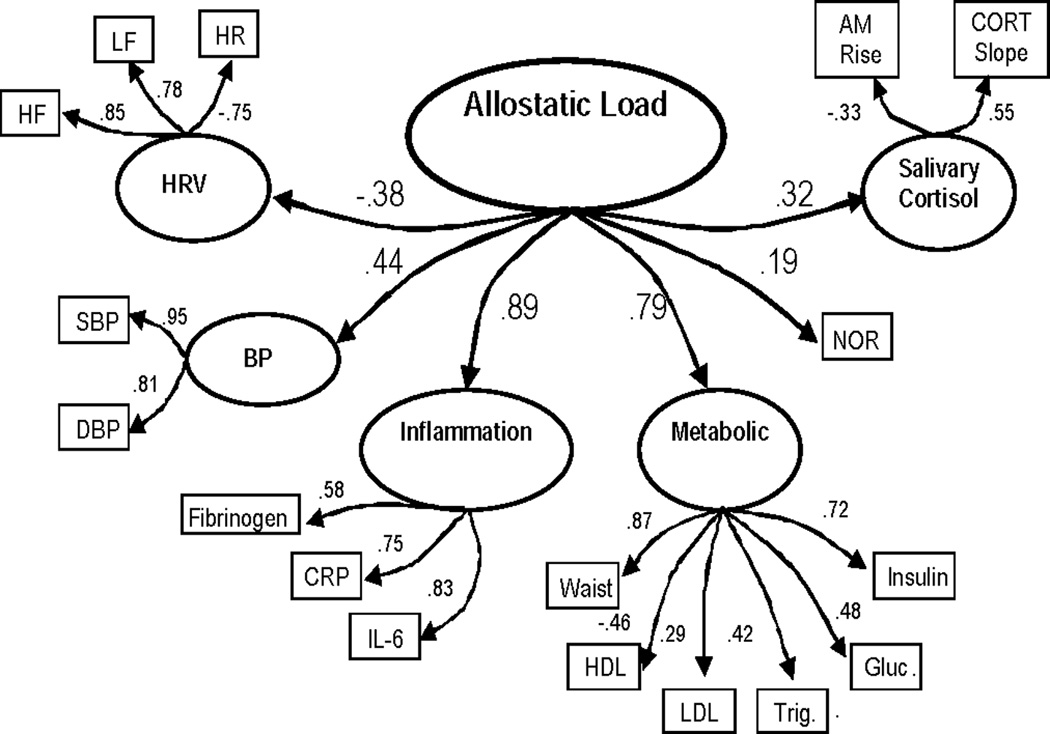
Results for final meta-factor allostatic load model (model fit statistics: χ² (113) = 459.08, χ²/df = 4.1, CFI = .91, RMSEA = .06, Model AIC = 233.08). All parameter estimates are standardized and significant (p ≤ .05). Estimates for error terms and the correlation between error terms for HDL-C and triglycerides (r = −.36) are not depicted.

Examination of the loadings for the various sub-factors on the AL meta-factor (range = .19 – .89) suggests that, in this relatively young population of Whites and Blacks, the core domains of the AL meta-factor are inflammation and metabolism. Loadings for each of the remaining systems are approximately 50% smaller, though still statistically significant and of moderate size. Examination of the individual sub-factors indicated that higher loadings on the HPA/salivary cortisol factor reflected those with a flatter diurnal rhythm while higher loadings on the metabolic factor reflected those with greater metabolic risk profiles (through positive contributions from all components except HDL-C). Likewise, higher scores on the inflammation and BP factors, respectively, reflected those with more elevated levels of the three markers of inflammation and/or higher blood pressure. Higher loadings on the HRV factor reflect both higher HF and LF and lower HR – a pattern previously associated with lower CVD risk (5, 42). As expected, sub-factor profiles, reflecting poorer patterns of blood pressure, inflammation, metabolic, and hormonal functioning (i.e., flatter diurnal rhythm of salivary cortisol; higher levels of SNS activity), load positively on the AL meta-factor while the HRV factor (reflecting better HRV) loads negatively on the meta-factor.

Factorial invariance across gender/ethnic groups

The CARDIA sampling design, with similar numbers of Black and White men and women, also allows for examination of possible gender-by-ethnicity variability in these models. A model in which all factor loadings and the correlation between the residual errors of HDL-C and triglycerides of the AL meta-factor model were constrained to be equal across the four gender/ethnic groups produced a significantly worse chi-square fit statistic (χ² (506) = 829. 92, p = <.0001) as compared to a multi-group model in which no equality constraints were imposed (χ² (455) = 712.78, p = <.0001, χ² difference (51) = 114.09, p=<.0001).¹ Examination of LM statistics for the improvement in fit provided by relaxing specific equality constraints indicated that a model in which the equality constraint for the norepinephrine factor loading on the AL factor was removed for white females, and the equality constraints for the inflammation factor loading on the AL meta-factor, as well as for the triglycerides, glucose, and waist circumference loadings on the metabolic factor and the association between errors for HDL and triglycerides were removed for white males would produce a model for which the chi-square fit statistic (modified model χ² (503) = 768.66, p = <.0001) was not significantly different from that of the unconstrained baseline model (χ² difference (48) = 56.26, p=.19).² Table 3 presents standardized factor loadings for the final model, with standardized values estimated based on pooled standard deviations across the four groups. Parameter estimates that were allowed to vary for a specific race/gender group are noted in parentheses. The only differences were for the metabolic factor where white men had significantly higher loadings for 3 of the 5 metabolic parameters – triglycerides, glucose, and waist circumference – and a stronger association between the residual errors of HDL and triglycerides, as well as for the inflammation factor loading on the AL factor, where white men had a lower value compared to the other groups. White women also had a lower and non-significant loading on the norepinephrine/SNS path on the AL factor. With these few exceptions, all other loadings were similar across the four sex-ethnic groups.

Table 3.

Standardized Factor Loadings for Final Multigroup Meta-Factor Model

	Standardized Factor Loading
HRV Factor
Heart rate	−.72
LF	.79
HF	.91
Blood Pressure Factor
SBP	.93
DBP	.82
Inflammation Factor
Fibrinogen	.55
CRP	.72
IL-6	.80
Metabolic Factor
Waist	.91 (.66 – White Males)
HDL-C	−.43
LDL-C	.27
Triglycerides	.38 (.71 – White Males)
Glucose	.34 (.86 – White Males)
Insulin	.71
Salivary Cortisol Factor
AM Rise	−.40
PM Decline	.47
Allostatic Load Meta-Factor (subscale loadings)
HRV	−.33
BP	.39
Inflammation	.91 (.66 – White Males)
Metabolic	.92
Norepinephrine	.23 (.02 – White Females)
Salivary Cortisol – PM Decline	.23
HDL-C/Triglyceride residual corr.	−.28 (−.51 - White Males)

Note. Values noted in parentheses reflect parameter estimates that were allowed to vary for the specific group noted.

In supplementary analyses we modelled mean levels of the AL meta-factor as well as mean levels of the 5 five AL subfactors. As shown on the far left in Figure 3, the lowest mean AL levels were seen in white females, followed by white males, then black males, with black females having the highest mean levels. Means for each group varied significantly from the others. Mean levels for the 5 subfactors are shown in the right-hand section of Figure 3. For the salivary cortisol subfactor, all groups were significantly different from each other except white males and black males. For the inflammation subfactor, all groups were significantly different from each other except white females and white males. For the metabolic subfactor, all groups were significantly different from each other except white males and black males. For the heart rate variability subfactor, black females were significantly different from white males. For the blood pressure subfactor, all groups were significantly different from each other except black females and black males. No single pattern of group differences emerged across the five subfactors. Whites had lower mean scores for all but the metabolic and heart rate variability subfactors where patterns reflected more male/female differences with relative male disadvantage with respect to metabolism but relative advantage with respect to heart rate variability. Consistent with the findings for total AL, white females generally have a more favourable profile of mean scores across the physiological subfactors.

Figure 3.

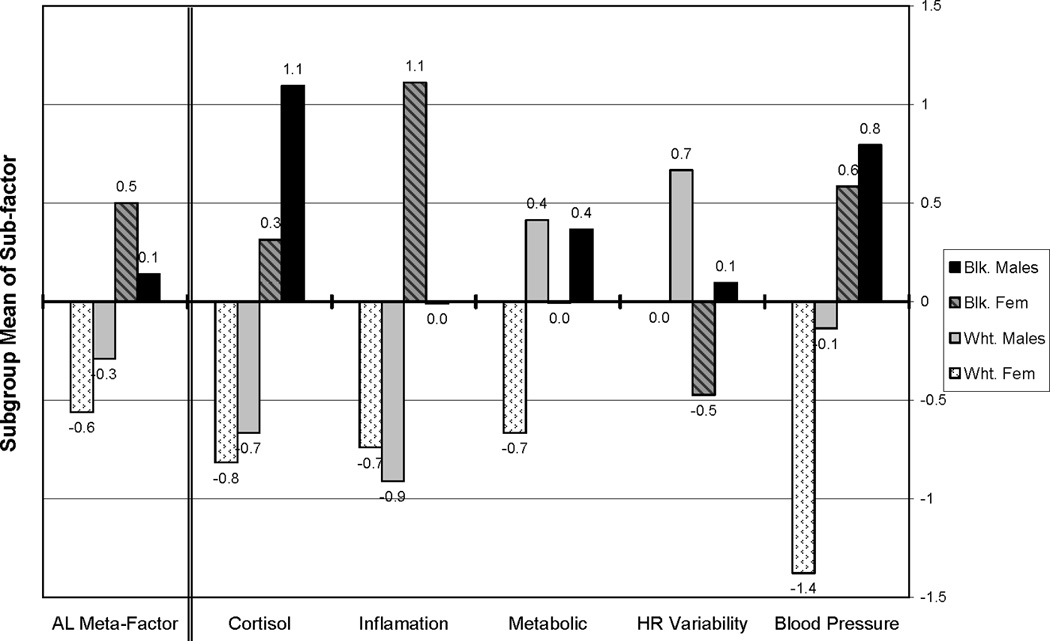
Estimated Allostatic Load & Sub-factor Mean Scores for White & Black Men and Women

DISCUSSION

Analyses presented here provide preliminary support for a hypothesized “meta-factor” model of allostatic load wherein the individual biomarkers load on a set of “latent” subfactors/domains, representing aspects of overall physiological integrity (i.e. HRV, BP, inflammation, metabolism, SNS and HPA axis), and the sub-factors in turn load on a meta-AL factor that reflects their shared variance (i.e., their constellation of shared, inter-relationships). While this model did not fit the data as well as the fully parameterised “6 factor” model representing all possible pairwise relationships among the 6 sub-factors, it did capture over 84% of the pattern of associations among the latter, suggesting that there is, indeed, a core of common or shared variance among these various biological factors.

In the current analyses of a relatively young population, all six domains were significantly related to the AL meta-factor, with metabolic and inflammation subfactors exhibiting the highest loadings. This is consistent with the observation that the correlation between the metabolic and inflammation subfactors, in the 6-factor model, was substantially greater than the other pairwise correlations. Future analyses of other samples, including those with a wider age range, should examine whether this pattern prevails in other age groups and for more comprehensive assessments of the various systems.

Overall, fit indices indicated that the six-factor and AL meta-factor models provided an adequate fit to the data (e.g., CFI values range from .87 – .91, RMSEA values from .06 – .07). Reasons for the lack of better fitting models may include the range of methodologies reflected in the data (i.e., measurements in blood, urine and saliva) as well as our inability to obtain an exhaustive battery of measures to represent each biological system in the context of this population-based study. We also explored only a limited number of model modifications to improve model fit, being more concerned with comparing the relative fit of our hypothesized models of allostatic load to gain a better understanding of associations between various biological regulatory systems, than with obtaining a more perfect-fitting model that may be less generalizable to other samples.

Analyses testing for possible differences in the structure of AL across the four race/gender groups available in CARDIA yielded evidence indicating a high degree of invariance with few significant differences in loadings for either individual biomarkers or the system-specific sub-factors. Though these population subgroups are known to experience differential health risks (e.g., higher mortality among men and among Blacks), such invariance in how system-specific measures relate to one another (reflected in our system-specific parameter loadings) and in how systems relate to one another (reflected in our system-level loadings on the AL factor) is perhaps not so surprising to the extent that our models are capturing inherent intra- and inter-system commonalities in how the human body’s regulatory systems operate. Where we do see evidence for significant difference by sex and/or ethnicity (i.e., white men had significantly higher loadings for triglycerides, glucose, and waist circumference on the metabolic factor and a lower loading for the inflammation factor on the allostatic load meta-factor), the patterning is consistent with other evidence pointing to greater contributions to overall AL levels from dysregulations in these same systems from studies of White and Asian men (Goldman and others 2004; Karlamangla and others 2005). Further work is needed to determine whether the lack of similar evidence in the Black men in CARDIA reflects a true difference among Black men in the general population with respect to these parameters or whether the lack of similar findings in the current analyses reflects unique characteristics of the sample of Black men participating in this study. Evidence that white women had a lower and non-significant loading for norepinephrine on the allostatic load factor is consistent with evidence suggesting that women may tend to be less “reactive” with respect to stress responsive systems such as the sympathetic nervous system (Seeman and McEwen 1996; Taylor and others 2000). The apparent disadvantage for Black women in this case may reflect their generally lower socio-economic status which has been shown to predict greater accumulation of AL (Geronimus and others 2006; Seeman and others 2008; Seeman and others 2004). More generally, and not unexpectedly, as the mean levels for the subfactors indicate, Blacks were found to exhibit relative disadvantage with respect to all factors except heart rate variability and metabolism. These findings parallel work by Geronimus and others (2006) for the nationally-representative National Health and Nutrition Survey (NHANES) III where Blacks had significantly higher levels of overall AL. These differences were not explained by poverty and, notably, the poor and non-poor Black women had the highest and second highest AL burdens. Thus, our findings and those of Geronimus and others (2006) suggest that Blacks in general, and Black women in particular, may be at highest risk for development of AL.

A strength of these analyses is the range of biomarkers available for modelling allostatic load; while not exhaustive, it was considerably broader than is frequently available in such community-based research. Biomarkers provided information on six major components of physiological regulation (HRV, blood pressure, inflammation, metabolism, SNS, and HPA axis activity), allowing for estimation of the relationship of each of these systems to an overall allostatic load construct within the CARDIA cohort. Using SEM, the relative fit of the proposed meta-factor AL model was compared with that of a non-specific model of pairwise relationships among the six factors represented in the available data. The sampling design of the CARDIA study also permitted a more complete evaluation of possible gender and ethnic differences in the structure of AL than has been possible in previous research.

There are also limitations to the available data. The data are cross-sectional, making it impossible to assess whether currently observed levels of AL reflect a cumulative process of increasing biological dysregulation over time. Available data are also more limited with respect to the range of parameters within some of the systems (e.g., there are more parameters measured for the metabolic and inflammation domains), resulting in potential differences in the comprehensiveness of assessment across these domains. Measures are also limited to static, single point in time assessments rather than measures of the dynamics of these various biological systems. The sole exception - the measurement of diurnal cortisol rhythm over the course of a day – is itself limited to only one day rather than the recommended multiple day protocol. The demographic characteristics of the CARDIA cohort also limit our ability to generalize these findings beyond the age range and major ethnic groups represented here (Whites and African Americans).

CONCLUSION

Despite these limitations, the current analyses extend previous research on allostatic load in important ways. First, structural equation modeling provides evidence, consistent with the original conceptualization of AL as a multi-systems index of cumulative dysregulation, that a meta-factor model reflecting a common core of inter-relationships among multiple systems provides a reasonable fit to the data. As demonstrated in the current analyses, each of the six factors or systems represented in the CARDIA data is related to the AL meta-factor. Second, the analyses provide the first test of the factorial invariance of these relationships across both gender and ethnicity, revealing little evidence that the structure of these relationships differs across such central demographic characteristics. Clearly, these analyses require further replication and extension, but such a meta-factor model of AL may be a particularly useful tool in efforts to assess the multiple physiological pathways through which factors such as socio-economic status or exposure to chronic stress impact health (i.e., taking a more global, multi-systems perspective on physiological parameters). Such an approach does not negate the value or necessity of efforts to understand the links between such factors and individual biological systems. However, by modeling the shared variance among these various biological systems, a meta-factor AL approach offers a way of conceptualizing and testing for more cumulative or simultaneous effects of such factors on not one system but on an array of multiple systems.

Glossary

CARDIA

Coronary Artery Risk Development in Young Adults Study

AL

Allostatic load

HPA

hypothalamic-pituitary adrenocortical

BMI

body mass index

SNS

sympathetic nervous system

HRV

heart rate variability

CRP

c-reactive protein

IL-6

interleukin 6

HDL-C

high density lipoprotein cholesterol

LDL-C

low density lipoprotein cholesterol

RIA

radioimmuno assay

RRV

beat-to-beat heart rate [RR] variability

LF

low frequency

HF

high frequency

HR

heart rate

NOR

norepinephrine

EPI

epinephrine

SEM

structural equation modeling

χ²

chi-square

CFI

comparative fit index

RMSE

root mean square error of approximation

LM

Lagrange multiplier