Robust Variable Selection with Exponential Squared Loss

Abstract

Robust variable selection procedures through penalized regression have been gaining increased attention in the literature. They can be used to perform variable selection and are expected to yield robust estimates. However, to the best of our knowledge, the robustness of those penalized regression procedures has not been well characterized. In this paper, we propose a class of penalized robust regression estimators based on exponential squared loss. The motivation for this new procedure is that it enables us to characterize its robustness that has not been done for the existing procedures, while its performance is near optimal and superior to some recently developed methods. Specifically, under defined regularity conditions, our estimators are $\sqrt{n}\text{-consistent}$ and possess the oracle property. Importantly, we show that our estimators can achieve the highest asymptotic breakdown point of 1/2 and that their influence functions are bounded with respect to the outliers in either the response or the covariate domain. We performed simulation studies to compare our proposed method with some recent methods, using the oracle method as the benchmark. We consider common sources of influential points. Our simulation studies reveal that our proposed method performs similarly to the oracle method in terms of the model error and the positive selection rate even in the presence of influential points. In contrast, other existing procedures have a much lower non-causal selection rate. Furthermore, we re-analyze the Boston Housing Price Dataset and the Plasma Beta-Carotene Level Dataset that are commonly used examples for regression diagnostics of influential points. Our analysis unravels the discrepancies of using our robust method versus the other penalized regression method, underscoring the importance of developing and applying robust penalized regression methods.

1. INTRODUCTION

Selecting important explanatory variables is one of the most important problems in statistical learning. To this end, there have been many important progresses in the use of penalized regression methods for variable selection. Those penalized regression methods have a unified framework for theoretical properties and enjoy great flexibility in allowing different choices of penalty such as the bridge regression (Frank and Friedman, 1993), LASSO (Tibshirani, 1996), SCAD (Fan and Li, 2001), and adaptive LASSO (Zou, 2006). It is important to note that many of those methods are closely related to the least squares method. It is well known that the least squares method is sensitive to outliers in the finite samples, and consequently, the outliers can present serious problems for the least squares based methods in variable selection. Therefore, in the presence of outliers, it is desirable to replace the least squares criterion with a robust one.

In a seminal work, Fan and Li (2001) introduced a general framework of penalized robust regression estimators, i.e., to minimize

$${\mathrm{\Gamma }}_n(\mathit{\beta })={\displaystyle \sum _{i=1}^n}\varphi (Y_i-{\mathbf{x}}_i^T\mathit{\beta })+n{\displaystyle \sum _{j=1}^p}{p}_{{\lambda }_{\mathit{\text{nj}}}}(|{\beta }_j|)$$ (1.1)

with respect to β, where ϕ(·) is the Huber’s function. Since then, penalized robust regression has attracted increased attention, and different loss functions ϕ(·) and different penalty functions have been proposed and examined. For example, Wang et al. (2007) proposed the LAD-LASSO where ϕ(t) = |t|, p_λnj (|β_j|) = λ_nj |β_j|; Wu and Liu (2009) introduced the penalized quantile regression when ϕ(t) = t{τ − I̱(t < 0)} with 0 ≤ τ ≤ 1, and p_λnj (|β_j|) is either the SCAD penalty or the adaptive LASSO penalty; Kai et al. (2011) studied the variable selection in semiparametric varying-coefficient partially linear model via a penalized composite quantile loss (Zou and Yuan, 2008); Johnson and Peng (2008) evaluated a rank-based variable selection; Wang and Li (2009) examined a weighted Wilcoxon-type SCAD method for robust variable selection; Leng (2010) presented the variable selection via regularized rank regression; and Bradic et al. (2011) investigated the penalized composite quasi-likelihood for ultrahigh dimensional variable selection.

Despite these progresses, to the best of our knowledge, the robustness (e.g., the breakdown point and influence function) of these variable selection procedures has not been well characterized or understood. For example, we do not know the answers to the basic questions: What is the breakdown point for a penalized robust regression estimator? Is its influence function bounded? In the regression setting, the choice of loss function determines the robustness of the resulting estimators. Thus, for model (1.1), the loss function ρ(·) is critical to the robustness, and for this reason, a loss function with a superior robustness performance is of great interest.

The motivation of this work is to study the robustness of variable selection procedures, which necessitates us to introduce a new robust variable selection procedure. As discussed above, the robustness has not been well characterized for the existing procedures. Besides the robustness, as presented below, our new procedure performs at a level that is near optimal and superior to two competing methods in practical settings. The numerical performance of our method is not entirely surprising, as the exponential loss function has been used in Adaboost for classification problem with similar success (Friedman et al., 2000).

We begin with the following loss function

$${\varphi }_{\gamma }(t)=1-\text{exp}(-t^2/\gamma ),$$

which is an exponential squared loss with a tuning parameter γ. The tuning parameter γ controls the degree of robustness for the estimators. When γ is large, ϕ_γ(t) ≈ t²/γ, and therefore the proposed estimators are similar to the least squares estimators in the extreme case. For a small γ, observations with large absolute values of $t_i=Y_i-{\mathbf{x}}_i^T\mathit{\beta }$ will result in large losses of ϕ_γ(t_i), and therefore have a small impact on the estimation of β. Hence, a smaller γ would limit the influence of an outlier on the estimators, although it could also reduce the sensitivity of the estimators.

In this paper, we discuss how to select γ so that the corresponding penalized regression estimators are robust and possess desirable finite and large sample properties. We show that our estimators satisfy selection consistency and asymptotic normality. We characterize the finite sample breakdown point and show that our estimators possess the highest asymptotic addition breakdown point for a wide range of penalties, including L_q penalty with q > 0, adaptive LASSO, and elastic net. In addition, we derive the influence functions and show that the influence functions of our estimators are bounded with respect to the outliers in either the response or the covariate domain.

The rest of this paper is organized as follows. In Section 2, we introduce the penalized robust regression estimators with the exponential squared loss, and investigate the sampling properties. In Section 3, we study the robustness properties by deriving the influence functions and finite sample breakdown point. In Section 4, numerical simulations are conducted to compare the performance of the proposed method with composite quantile loss and L₁ loss using the oracle method as the benchmark. We conclude with some remarks in Section 5. The proofs are given in the Appendix.

2. PENALIZED ROBUST REGRESSION ESTIMATOR WITH EXPONENTIAL SQUARED LOSS

Assume that {x_i, Y_i), i = 1, …, n} is a random sample from population (x, Y). Here, Y is a univariate response, x is a d-dimensional predictor, and (x, Y) has joint distribution F. Suppose that (x_i, Y_i) satisfying a linear regression model

$$Y_i={\mathbf{x}}_i^T\mathit{\beta }+{\epsilon }_i,i=1,\dots ,n,$$ (2.1)

where β is a d-dimensional vector of unknown parameters, and the error terms ε_i are i.i.d. with unknown distribution G, E(ε_i) = 0, and ε_i is independent of x_i. An intercept term is included if the first elements of all x_i’s are 1. Let D_i = (x_i, Y_i), and D_n = (D₁, ⋯, D_n) be the observed data. Variable selection is necessary because some of the coefficients in β are zero; that is, some of the variables in x_i do not contribute to Y_i. Without loss of generality, let $\mathit{\beta }={({\mathit{\beta }}_1^T,{\mathit{\beta }}_2^T)}^T$, where β₁ ∈ ℝ^s and β₂ ∈ ℝ^d−s. The true regression coefficients are ${\mathit{\beta }}_0={({\mathit{\beta }}_{01}^T,{\mathit{\beta }}_{02}^T)}^T$ with each element of β₀₁ being nonzero, and β₀₂ = 0. Let ${\mathbf{x}}_i={({\mathbf{x}}_{i1}^T,{\mathbf{x}}_{i2}^T)}^T$, where x_i1 and x_i2 are the covariates corresponding to β₁ and β₂.

The objective function of penalized robust regression consists of a loss function and a penalty term. In this paper, we propose maximizing

$${\ell }_n(\mathit{\beta })={\displaystyle \sum _{i=1}^n}\text{exp}\{-{(Y_i-{\mathbf{x}}_i^T\mathit{\beta })}^2/{\gamma }_n\}-n{\displaystyle \sum _{j=1}^d}{p}_{{\lambda }_{\mathit{\text{nj}}}}(|{\beta }_j|)$$ (2.2)

with respect to β, which is a special case of (1.1) for any γ_n ∈ (0, +∞). Because γ_n is a tuning parameter and needs to be chosen adaptively according to the data, our objective function (2.2) is distinct from (1.1). This additional feature is critical for our estimators to have a high breakdown point and high efficiency.

Let $\mathit{\beta ̂}={({\mathit{\beta ̂}}_{n1}^T,{\mathit{\beta ̂}}_{n2}^T)}^T$ be the resulting estimator of (2.2),

$$a_n=\text{max}\{p_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\beta }_{0j}|):{\beta }_{0j}\ne 0\},$$

$$b_n=\text{max}\{p_{{\lambda }_{\mathit{\text{nj}}}}^{″}(|{\beta }_{0j}|):{\beta }_{0j}\ne 0\},$$

and

$$I(\mathit{\beta },\gamma )=\frac{2}{\gamma }{\displaystyle \int }{\mathbf{\text{xx}}}^T{e}^{-r^2/\gamma }(\frac{2r^2}{\gamma }-1)\mathit{\text{dF}}(\mathbf{x},y),$$

where r = Y − x^Tβ.

We assume the following regularity condition:

• (C1) ∑ = E(xx^T) is positive definite, and E‖x‖³ < ∞.

Condition (C1) ensures that the main term dominates the remainder in the Taylor expansion. It warrants further examination as to whether this condition can be weakened. With these preparations, we present the following sampling properties for our proposed estimators.

Theorem 1 Assume that condition (C1) holds, b_n = o_p(1), and I(β₀, γ₀) is negative definite.

1. If γ_n − γ₀ = o_p(1) for some γ₀ > 0, there exists a local maximizer β̂_n such that ‖β̂_n − β₀‖ = O_p(n^−1/2 + a_n).

2. (Oracle property) If $\sqrt{n}{a}_n=O_p(1),1/{\text{min}}_{s+1\le j\le d}(\sqrt{n}{\lambda }_{\mathit{\text{nj}}})=o_p(1),\sqrt{n}({\gamma }_n-{\gamma }_0)=o_p(1)$, and with probability 1,

   $$\underset{n\to \mathrm{\infty }}{\text{lim}}\text{inf}\underset{t\to 0+}{\text{lim}}\text{inf}\{\underset{s+1\le j\le d}{\text{min}}{p}_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|t|)/{\lambda }_{\mathit{\text{nj}}}\}>0,$$ (2.3)

   then we have: (a) sparsity, i.e., β̂_n2 = 0 with probability 1; (b) asymptotic normality,

   $$\sqrt{n}(I_1({\mathit{\beta }}_{01},{\gamma }_0)+{\mathrm{\Sigma }}_1)\{{\mathit{\beta ̂}}_{n1}-{\mathit{\beta }}_{01}+{(I_1({\mathit{\beta }}_{01},{\gamma }_0)+{\mathrm{\Sigma }}_1)}^{-1}\mathrm{\Delta }\}\stackrel{D}{\to }N(\mathbf{0},{\mathrm{\Sigma }}_2),$$ (2.4)

   where ${\mathrm{\Sigma }}_1=\mathit{\text{diag}}\{p_{{\lambda }_{n1}}^{″}(|{\beta }_{01}|),\cdots ,p_{{\lambda }_{\mathit{\text{ns}}}}^{″}(|{\beta }_{0s}|)\},{\mathrm{\Sigma }}_2=\mathit{\text{cov}}(\text{exp}(-r^2/{\mathrm{\gamma }}_0)\frac{2r}{{\gamma }_0}{\mathbf{x}}_{i1})$,

   $$\mathrm{\Delta }={(p_{{\lambda }_{n1}}^{\prime }(|{\beta }_{01}|)\mathit{\text{sign}}({\beta }_{01}),\cdots ,p_{{\lambda }_{\mathit{\text{ns}}}}^{\prime }(|{\beta }_{0s}|)\mathit{\text{sign}}({\beta }_{0s}))}^T,$$

   $$I_1({\mathit{\beta }}_{01},{\gamma }_0)=\frac{2}{{\gamma }_0}E\left[\text{exp }\right(-r^2/{\gamma }_0\left)\right(\frac{2r^2}{{\gamma }_0}-1\left)\right](E{\mathbf{x}}_{i1}{\mathbf{x}}_{i1}^T).$$

Remark 1 Note that not all penalties satisfy the conditions in Theorem 1. For example, LASSO is inconsistent, and the oracle property does not hold. Zou (2006) proposed the adaptive LASSO, and showed that it enjoys the oracle property. The adaptive LASSO penalty has the form of p_λnj (|β_j|) = λ_nj |β_j| with λ_nj = τ_nj/|β̃_j|^k for some k > 0, where β̃ = (β̃₁, ⋯, β̃_d)^T is a $\sqrt{n}\text{-consistent}$ estimator of β₀, and τ _nj’s are the regularization parameters. With this penalty in the penalized robust regression (2.2), we can prove that our estimators are $\sqrt{n}\text{-consistent}$ and have the oracle property under the following condition (C2) in addition to the regularity condition (C1). The detailed proof is omitted here.

• (C2): ${\text{max}}_{1\le j\le s}(\sqrt{n}{\lambda }_{\mathit{\text{nj}}})=o_p(1)\text{ and }1/{\text{min}}_{s+1\le j\le d}(\sqrt{n}{\lambda }_{\mathit{\text{nj}}})=o_p(1)$.

In fact, ${\text{max}}_{1\le j\le s}(\sqrt{n}{\lambda }_{\mathit{\text{nj}}})=o_p(1)\mathit{\text{ implies }}\sqrt{n}{a}_n=O_p(1)$ by the definition of a_n. Note that some data-driven methods for selecting λ_nj, e.g., cross-validation, may not satisfy condition (C2). Here, we utilize a BIC criterion for which (C2) holds.

3. ROBUSTNESS PROPERTIES AND IMPLEMENTATION

3.1 Finite sample breakdown point

Finite sample breakdown point is used to measure the maximum fraction of outliers in a sample that an estimator can tolerate before returning arbitrary values. It is a global measurement of robustness in terms of resistance to outliers. Several definitions of the finite sample breakdown point have been proposed in literature [see Hampel (1971); Donoho (1982); Donoho and Huber (1983)].

Here, let us describe the addition measure defined by Donoho and Huber (1983). Recall the notations D_i = (x_i, Y_i), and D_n = (D₁, ⋯, D_n). We assume that D_n contains m bad points and n − m good points. Denote the bad points by D_m = {D₁, ⋯, D_m} and the good points by D_n−m = {D_m+1, ⋯, D_n}. The fraction of bad points in D_n is m/n. Let β̂(D_n) denote a regression estimator based on sample D_n. The finite sample addition breakdown point of an estimator is defined as

$$\mathit{\text{BP}}=({\mathit{\beta ̂}}_n;{\mathbf{D}}_{n-m})=\text{min }\{\frac{m}{n}:\underset{{\mathbf{D}}_m}{\text{sup}}\Vert \mathit{\beta ̂}({\mathbf{D}}_n)-\mathit{\beta ̂}({\mathbf{D}}_{n-m})\Vert =\mathrm{\infty }\},$$

where ‖ · ‖ is the Euclidean norm. In the regression setting, many estimators such as S-estimator (Rousseeuw and Yohai, 1984), MM-estimator, τ-estimator (Yohai and Zamar, 1988), and REWLS-estimator (Gervini and Yohai, 2002), can achieve the highest asymptotic breakdown point of 1/2.

Next, we derive the finite sample breakdown point for our proposed penalized robust estimators with the exponential squared loss. We first take an initial estimator β̃_n. For a contaminated sample D_n, let

$$\zeta ({\gamma }_n)=\frac{2m}{n}+\frac{2}{n}{\displaystyle \sum _{i=m+1}^n}{\varphi }_{{\gamma }_n}\{r_i({\mathit{\beta ̃}}_n)\},$$ (3.1)

where $r_i(\mathit{\beta })=Y_i-{\mathbf{x}}_i^T\mathit{\beta }$. It is easy to see that ζ(γ_n) is a real number ranged in (0, 2]. Let

$$a_{\mathit{\text{nm}}}={(n-m)}^{-1}\underset{\mathit{\beta }\in {ℝ}^d}{\text{max}}\#\{i:m+1\le i\le n\mathit{\text{ and }}{\mathbf{x}}_i^T\mathit{\beta }=0\}.$$

Note that if a set of d regressor variables is linearly independent, then a_nm = (d − 1)/(n − m). Denote by BP(β̂_n;D_n−m, γ_n) the breakdown point for the penalized robust regression estimators β̂_n with the tuning parameter γ_n.

Theorem 2 For any penalty function of the form p_λnj (|β_j|) = λ_njg(|β_j|), where g(·) is a strictly increasing and unbounded function defined on [0,∞], and the weight λ_nj is positive for all j = 1, ⋯, d. If m/n ≤ ε < (1−2a_nm)/(2−2a_nm), a_nm < 0.5, and ζ(γ_n) < (1−ε)(2−2a_nm) hold, then, for any initial estimator β̃_n of β₀, we have

$$\mathit{\text{BP}}=({\mathit{\beta ̂}}_n;{\mathbf{D}}_{n-m},{\gamma }_n)\ge \text{ min }\{\mathit{\text{BP}}({\mathit{\beta ̃}}_n;{\mathbf{D}}_{n-m}),\frac{1-2a_{\mathit{\text{nm}}}}{2-2a_{\mathit{\text{nm}}}},1-\frac{\zeta ({\gamma }_n)}{2-2a_{\mathit{\text{nm}}}}\}.$$ (3.2)

Theorem 2 provides the lower bound of breakdown point of the proposed penalized robust estimators. The breakdown point depends on the breakdown point of an initial estimate and the tuning parameter γ_n. If β̃_n is a robust estimator with asymptotic breakdown point 1/2, and γ_n is chosen such that ζ(γ_n) ∈ (0, 1], then BP(β̂_n;D_n−m, γ_n) is asymptotically 1/2. This observation guides us in selecting γ_n to reach the highest efficiency. We should note that the breakdown point is a limiting measure of the bias robustness (He and Simpson, 1993).

There are many commonly used penalties that utilize the penalty form of Theorem 2, such as LASSO, adaptive LASSO, the L_q penalty with q > 0, logarithm penalty, elastic-net penalty, and adaptive elastic-net penalty. Hence the breakdown point result holds for these penalized robust regression estimators. However, it is an open question to extend the result of Theorem 2 to bounded penalties such as SCAD (Fan and Li, 2001) and MCP (Zhang, 2010). As a practical solution, for those bounded penalties, we may employ the one-step or k-step local linear approximation (LLA) method proposed by Zou and Li (2008). Additional discussions will be given in Section 5.

3.2 Influence function

The influence function introduced by Hampel (1968) measures the stability of estimators given an infinitesimal contamination. Denote by δ_z the point mass probability distribution at a fixed point z = (x₀, y₀)^T ∈ ℝ^d+1. Given the distribution F of (x, Y) in ℝ^d+1 and proportion ε ∈ (0, 1), the mixture distribution of F and δ_z is F_ε = (1 − ε)F + εδ_z. Suppose that λ_nj’s have the limit point λ_0j’s, let

$${\mathit{\beta }}_0^{*}=\text{arg }\underset{\mathit{\beta }}{\text{min}}\left[\right\{{\displaystyle \int }(1-e^{-{(y-{\mathbf{x}}^T\mathit{\beta })}^2/{\gamma }_0})\mathit{\text{ dF}}\}+{\displaystyle \sum _{j=1}^d}{p}_{{\lambda }_{0j}}(|{\beta }_j|)],$$

$${\mathit{\beta }}_{\epsilon }^{*}=\text{arg }\underset{\mathit{\beta }}{\text{min}}\left[\right\{{\displaystyle \int }(1-e^{-{(y-{\mathbf{x}}^T\mathit{\beta })}^2/{\gamma }_0}){\mathit{\text{ dF}}}_{\epsilon }\}+{\displaystyle \sum _{j=1}^d}{p}_{{\lambda }_{0j}}(|{\beta }_j|)].$$

Note that ${\mathit{\beta }}_0^{*}$ is a shrinkage of the true coefficient β₀ to 0, and ${\mathit{\beta ̂}}_n\stackrel{P}{\to }{\mathit{\beta ̂}}_0^{*}$ under the conditions in Theorem 1. For the exponential-type penalized robust estimators, the influence function at a point z ∈ ℝ^d+1 is defined as $\mathit{\text{IF}}(\mathbf{z};{\mathit{\beta }}_0^{*})={\text{lim}}_{\epsilon \to 0+}({\mathit{\beta }}_{\epsilon }^{*}-{\mathit{\beta }}_0^{*})/\epsilon$, provided that the limit exists.

Theorem 3 For the penalized robust regression estimators with exponential squared loss, the j-th element of the influence function ${\mathit{\text{IF}}}_j(\mathbf{z};{\mathit{\beta }}_0^{*})$ has the following form:

$${\mathit{\text{IF}}}_j(\mathbf{z};{\mathit{\beta }}_0^{*})=\{\begin{array}{cc}0\hfill & \mathit{\text{if }}{\beta }_{0j}^{*}=0,\hfill \\ -{\mathrm{\Gamma }}_j\{2\text{ exp }(-r_0^2/{\gamma }_0)r_0{\mathbf{x}}_0/{\gamma }_0+{\nu }_2\},\hfill & \mathit{\text{otherwise}},\hfill \end{array}$$ (3.3)

where Γ_j denotes the j-th row of {2A(γ₀)/γ₀ − B}⁻¹, $r_0=y_0-{\mathbf{x}}_0^T{\mathit{\beta }}_0^{*}$,

$${\nu }_2={\{p_{{\lambda }_{01}}^{\prime }(|{\beta }_{01}^{*}|)\mathit{\text{sign}}({\beta }_{01}^{*}),\cdots ,p_{{\lambda }_{0d}}^{\prime }(|{\beta }_{0d}^{*}|)\mathit{\text{sign}}({\beta }_{0d}^{*})\}}^T,$$

$$B=\mathit{\text{diag}}\{p_{{\lambda }_{01}}^{″}(|{\beta }_{01}^{*}|),\cdots ,p_{{\lambda }_{0d}}^{″}(|{\beta }_{0d}^{*}|)\},$$

and

$$A(\gamma )={\displaystyle \int }{\mathbf{\text{xx}}}^T\text{ exp }\{-{(y-{\mathbf{x}}^T{\mathit{\beta }}_0^{*})}^2/\gamma \}\{\frac{2{(y-{\mathbf{x}}^T{\mathit{\beta }}_0^{*})}^2}{\gamma }-1\}\mathit{\text{ dF}}(\mathbf{x},y).$$ (3.4)

For the case of adaptive LASSO penalty, with the regularization parameter selected by the BIC described in Section 3.3, by the condition (C2), we have λ_0j = 0 for j = 1, ⋯, s, and λ_0j = +∞ for j = s + 1, ⋯, d. Therefore, the corresponding influence functions of the zero coefficients are zero. For the nonzero coefficients, the influence functions have the form

$${\mathit{\text{IF}}}_j(\mathbf{z};{\mathit{\beta }}_0^{*})=-{\mathrm{\Gamma }}_j\{2\text{ exp }(-r_0^2/{\gamma }_0)r_0{\mathbf{x}}_{01}/{\gamma }_0\}.$$ (3.5)

3.3 Algorithm and the choice of tuning parameters

The penalty function facilitates variable selection in regression. Theorem 2 implies that there may be many penalties that can facilitate robust variable selection; however, we believe it is a lesser issue to compare the performance of different penalties for a given type of loss function. A more important issue is to compare the performance of different loss functions for a given form of penalty.

In the simulations, we focus on the adaptive LASSO penalty p_λnj (|β_j|) = τ_nj |β_j|/|β̃_nj|^k with k = 1, λ_nj = τ_nj/|β̃_nj|, and β̃_nj is an initial robust regression estimator. The maximization of (2.2) with an adaptive LASSO penalty involves nonlinear weighted L₁ regularization. To facilitate the computation, we use a quadratic approximation to replace the loss function. Let

$${\ell }^{*}(\mathit{\beta })={\displaystyle \sum _{i=1}^n}\text{exp}\{-{(Y_i-{\mathbf{x}}_i^T\mathit{\beta })}^2/{\gamma }_n\}.$$ (3.6)

Suppose that β̃ is an initial estimator, then the loss function is approximated as ${\ell }^{*}(\mathit{\beta })\approx {\ell }^{*}(\mathit{\beta ̃})+\frac{1}{2}{(\mathit{\beta }-\mathit{\beta ̃})}^T{\nabla }^2{\ell }^{*}(\mathit{\beta ̃})(\mathit{\beta }-\mathit{\beta ̃})$. Next, we maximize

$$\frac{1}{2}{(\mathit{\beta }-\mathit{\beta ̃})}^T{\nabla }^2{\ell }^{*}(\mathit{\beta ̃})(\mathit{\beta }-\mathit{\beta ̃})-n{\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj }}}|{\beta }_j|/|{\mathrm{\beta ̃}}_j|$$

with respect to β, which leads to an approximated solution of (2.2).

There exist efficient computing algorithms for this L₁ regularization problem. Popular algorithms include the least angle regression (Efron et al., 2004) and coordinate descent procedures such as the pathwise coordinate optimization introduced by Friedman et al. (2007), coordinate descent algorithms proposed by Wu and Lange (2008), and the block coordinate gradient descent (BCGD) algorithm proposed by Tseng and Yun (2009). In our paper, we use BCGD algorithm for computation.

To implement our methodology, we need to select both types of tuning parameters λ_nj and γ_n. Since λ_nj and γ_n depend on each other, it could be treated as a bivariate optimization problem. In this paper, we consider a simple selection method for λ_nj, and a data-driven procedure for γ_n.

The choice of the regularization parameter λ_nj

In general, many methods can be used to select λ_nj, such as cross-validation, AIC, BIC. To reduce intensive computation, and guarantee consistent variable selection, we consider the regularization parameter by minimizing a BIC-type objective function (see Wang et al. (2007)):

$${\displaystyle \sum _{i=1}^n}[1-\text{exp}{\{-(Y_i-{\mathbf{x}}_i^T\mathit{\beta })}^2/{\gamma }_n\}]+n{\displaystyle \sum _{j=1}^d}{\tau }_{\mathit{\text{nj }}}|{\beta }_j|/|{\mathrm{\beta ̃}}_{\mathit{\text{nj}}}|-{\displaystyle \sum _{j=1}^d}\text{log}(0.5n{\tau }_{\mathit{\text{nj}}})\text{ log}(n).$$

This leads to λ_nj = τ̂_nj/|β̃_nj|, where

$${\mathrm{\tau ̂}}_{\mathit{\text{nj}}}=\frac{\text{log}(n)}{n}.$$

Note that this simple choice satisfies the conditions for oracle property of the adaptive LASSO, as described in the following corollary.

Corollary 1 If the regularization parameter is chosen as τ̂_nj = log(n)/n, then the solution of (2.2) with adaptive LASSO penalty possess the oracle property.

The choice of tuning parameter γ_n

The tuning parameter γ_n controls the degree of robustness and efficiency of the proposed robust regression estimators. To select γ_n, we propose a data-driven procedure which yields both high robustness and high efficiency simultaneously. We first determine a set of the tuning parameters such that the proposed penalized robust estimators have asymptotic breakdown point at 1/2, and then select the tuning parameter with the maximum efficiency. We describe the whole procedure in the following steps:

1. Find the pseudo outlier set of the sample

   Let D_n = {(x₁, Y₁), ⋯, (x_n, Y_n)}. Calculate ** and S_n = 1.4826 × median_i |r_i (β̂_n) − median_j(r_j(β̂n))|. Then, take the pseudo outlier set D_m = {(x_i, Y_i) : |r_i(β̂_n)| ≥ 2.5S_n}, set m = #{1 ≤ i ≤ n : |r_i(β̂_n)| ≤ 2.5S_n}, and D_n−m = D_n/D_m.

2. Update the tuning parameter γ_n

   Let γ_n be the minimizer of det(V̂ (γ)) in the set G = {γ : ζ(γ) ∈ (0, 1]}, where ζ(γ) is defined in (3.1), det(·) denotes the determinant operator, V̂(γ) = {Î₁(β̂_n)}⁻¹Σ̃₂{Î₁(β̂_n)}⁻¹, and

   $${Î}_1({\mathit{\beta ̂}}_n)=\frac{2}{\gamma }\{\frac{1}{n}{\displaystyle \sum _{i=1}^n}\text{exp }(-r_i^2({\mathit{\beta ̂}}_n)/\gamma )(\frac{2r_i^2({\mathit{\beta ̂}}_n)}{\gamma }-1\left)\right\}\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\mathbf{x}}_i{\mathbf{x}}_i^T\right),$$

   $${\mathrm{\Sigma ̃}}_2=\mathit{\text{cov}}\left\{\text{exp }\right(-r_1^2({\mathit{\beta ̂}}_n)/\gamma )\frac{2r_1({\mathit{\beta ̂}}_n)}{\gamma }{\mathbf{x}}_1,\cdots ,\text{exp }(-r_n^2({\mathit{\beta ̂}}_n)/\gamma \left)\frac{2r_n({\mathit{\beta ̂}}_n)}{\gamma }{\mathbf{x}}_n\right\}.$$

3. Update β̂_n:

   With fixed λ_nj = log(n)/(n|β̂_nj|), and the selected γ_n in step 2, and update β̂_n by maximizing (2.2).

In practice, we set the MM-estimator β̃_n as the initial estimate, i.e., β̂_n = β̃_n, then repeat Steps 1 − 3 until β̂_n and γ_n converges. Note that λ_nj is fixed within the iterations. One may update β̂_n in step 3 with λ_nj selected by cross-validation, however, this approach requires huge computation. See discussions in section 5.

Remark 2 In the initial cycle of our algorithm, we set β̂_n as the MM estimator and detect the outliers in step 1. This allows us to calculate ζ(γ_n) by (3.1). Based on Theorem 2, the proposed penalized robust estimators achieve asymptotic breakdown point 1/2 if two conditions hold: (1) the initial robust estimator possesses asymptotic breakdown point 1/2; and (2) the tuning parameter γ_n is chosen such that ζ(γ_n) ∈ (0, 1]. Therefore, β̂_n achieves the asymptotic breakdown point 1/2 at all iterations.

To attain high efficiency, we choose the tuning parameter γ_n by minimizing the determinant of asymptotic covariance matrix as in step 2. Since the calculation of of det(V̂ (γ)) depends on estimate β̂_n, we update β̂_n in step 3, and repeat the algorithm until convergence. Based on our limited experience in simulation, the computing algorithm converges very quickly. In practice, we repeat Steps 1–3 once.

4. SIMULATION AND APPLICATION

4.1 Simulation study

In this section, we conduct simulation studies to evaluate the finite-sample performance of our estimator. We first illustrate how to select the tuning parameter γ. We choose n = 200, d = 8, and β = (1, 1.5, 2, 1, 0, 0, 0, 0)^T. We generate x_i = (x_i1, ⋯, x_id)^T from a multi-normal distribution N(0, Ω₂), where the (i, j)-th element of Ω₂ is ρ^|i−j|, ρ = 0.5. The error term follows a Cauchy distribution.

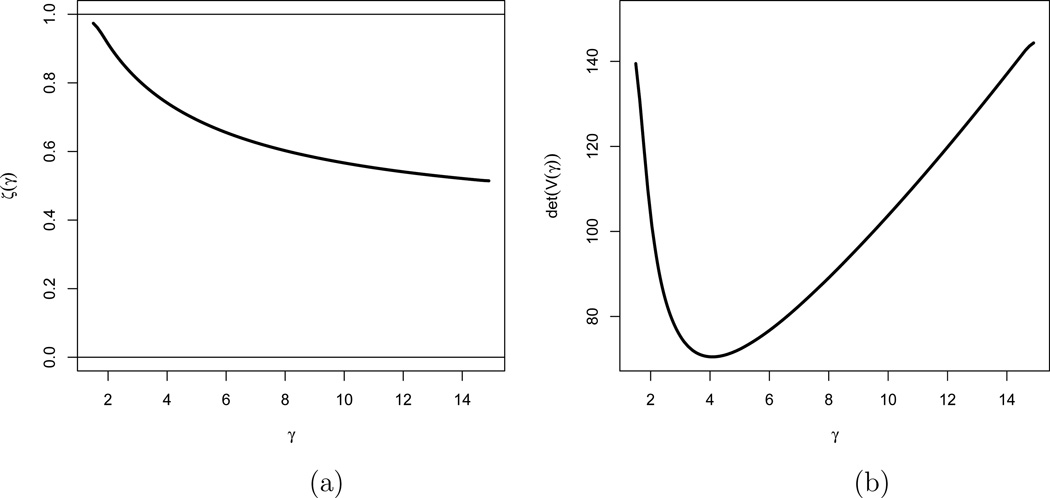
Following the procedure described in section 3.3, we obtain the values of ζ(γ) and det(V̂ (γ)), and plot them against the tuning parameter γ as depicted in Figure 1. Set G can be determined from Figure 1(a). The tuning parameter γ is selected by minimizing the det(V̂(γ)) over G as illustrated in Figure 1(b).

Figure 1.

(a) ζ(γ) against γ; (b) The determinant of matrix V̂(γ) against γ

Next, we evaluate the performance of various loss functions with different sample sizes. For each setting, we simulate 1000 data sets from model (2.1) with sample sizes of n = 100, 150, 200, 400, 600, 800. We choose d = 8 and β = (1, 1.5, 2, 1, 0, 0, 0, 0)^T. We use the following three mechanisms to generate influential points:

1. Influential points in the predictors. Covariate x_i follows a mixture of d-dimensional normal distributions 0.8N(0, Ω₁) + 0.2N(μ, Ω₂), Ω₁ = I_d×d, μ = 31_d, 1_d is d-dimensional vector of ones, and the error term follows a standard normal distribution;

2. Influential points in the response. Covariate x_i follows a multi-normal distribution N(0, Ω₂), and the error term follows a mixture normal distribution 0.8N(0, 1) + 0.2N(10, 6²);

3. Influential points in both the predictors and response. Covariate x_i follows a mixture of d-dimensional normal distributions 0.8N(0, Ω₁) + 0.2N(μ, Ω₂), and the error term follows a Cauchy distribution.

For each mechanism mentioned above, we compare the performance of four methods: CQR-LASSO (CQR is the shortening of the composite quantile regression introduced by Zou and Yuan (2008)); LAD-LASSO proposed by Wang et al. (2007); the oracle method based on MM-estimator; and our method (ESL-LASSO). For CQR-LASSO, we set the quantiles τ_k = k/10 for k = 1, 2, ⋯, 9. The performance is represented by the positive selection rate (PSR), the non-causal selection rate (NSR), and the median and median absolute deviation (MAD) of the model error advocated by Fan and Li (2001), where PSR(Chen and Chen, 2008) is the proportion of causal features selected by one method in all causal features, NSR(Fan and Li, 2001) is the average restricted only to the true zero coefficients, and the model error is defined by

$$\mathit{\text{ME}}={({\mathit{\beta ̂}}_n-{\mathit{\beta }}_0)}^{T}E[{\mathbf{\text{xx}}}^T]({\mathit{\beta ̂}}_n-{\mathit{\beta }}_0).$$

The tuning parameter γ is selected for each simulated sample, and γ̄_n and ζ̄(γ_n) are the averages of the selected values in 1000 simulations.

From Tables 1, 2, and 3, we find that ESL-LASSO yields larger model error than LAD-LASSO and CQR-LASSO when the sample size is small, because it involves some consistent estimators in its selection procedure. With the increase of the sample size, the medians and MADs of the model error decrease in all three settings. Especially in the view of the median of the model error, although ESL-LASSO’s is always larger than CQR-LASSO’s but shall be smaller than LAD-LASSO’s if the sample size is at least 200 in the first setting, while ESL-LASSO’s shall be smaller than both LAD-LASSO’s and CQR-LASSO’s if the sample size is large enough in the other two settings.

Table 1.

Simulation results in the first setting

						Model error
n	Method	γ̄n	ζ̄(γn)	PSR	NSR	Median	MAD
	ESL-LASSO	3.965	0.260	0.982	0.999	0.076	0.040
	CQR-LASSO	– –	– –	1.000	0.877	0.041	0.021
100	LAD-LASSO	– –	– –	1.000	0.581	0.057	0.030
	Oracle	– –	– –	1.000	1.000	0.034	0.018
	ESL-LASSO	4.303	0.282	0.999	1.000	0.038	0.020
	CQR-LASSO	– –	– –	1.000	0.906	0.026	0.013
150	LAD-LASSO	– –	– –	1.000	0.554	0.035	0.016
	Oracle	– –	– –	1.000	1.000	0.022	0.011
	ESL-LASSO	4.450	0.309	1.000	1.000	0.027	0.013
	CQR-LASSO	– –	– –	1.000	0.935	0.019	0.010
200	LAD-LASSO	– –	– –	1.000	0.539	0.028	0.012
	Oracle	– –	– –	1.000	1.000	0.017	0.009
	ESL-LASSO	4.500	0.331	1.000	1.000	0.012	0.006
	CQR-LASSO	– –	– –	1.000	0.966	0.010	0.005
400	LAD-LASSO	– –	– –	1.000	0.498	0.0142	0.007
	Oracle	– –	– –	1.000	1.000	0.009	0.005
	ESL-LASSO	4.500	0.337	1.000	1.000	0.008	0.004
	CQR-LASSO	– –	– –	1.000	0.980	0.006	0.003
600	LAD-LASSO	– –	– –	1.000	0.480	0.009	0.005
	Oracle	– –	– –	1.000	1.000	0.006	0.003
	ESL-LASSO	4.500	0.338	1.000	1.000	0.005	0.003
	CQR-LASSO	– –	– –	1.000	0.988	0.005	0.002
800	LAD-LASSO	– –	– –	1.000	0.498	0.007	0.003
	Oracle	– –	– –	1.000	1.000	0.004	0.002

Table 2.

Simulation results in the second setting

						Model error
n	Method	γ̄n	ζ̄(γn)	PSR	NSR	Median	MAD
	ESL-LASSO	4.315	0.454	0.939	1.000	0.352	0.231
	CQR-LASSO	– –	– –	1.000	0.781	0.066	0.033
100	LAD-LASSO	– –	– –	1.000	0.738	0.113	0.061
	Oracle	– –	– –	1.000	1.000	0.051	0.026
	ESL-LASSO	4.375	0.629	0.995	1.000	0.148	0.075
	CQR-LASSO	– –	– –	1.000	0.739	0.066	0.033
150	LAD-LASSO	– –	– –	1.000	0.737	0.070	0.034
	Oracle	– –	– –	1.000	1.000	0.035	0.017
	ESL-LASSO	4.449	0.633	1.000	1.000	0.080	0.039
	CQR-LASSO	– –	– –	1.000	0.789	0.046	0.023
200	LAD-LASSO	– –	– –	1.000	0.712	0.050	0.026
	Oracle	– –	– –	1.000	1.000	0.025	0.013
	ESL-LASSO	4.496	0.638	1.000	1.000	0.027	0.012
	CQR-LASSO	– –	– –	1.000	0.864	0.021	0.010
400	LAD-LASSO	– –	– –	1.000	0.686	0.023	0.011
	Oracle	– –	– –	1.000	1.000	0.012	0.006
	ESL-LASSO	4.499	0.642	1.000	1.000	0.015	0.007
	CQR-LASSO	– –	– –	1.000	0.897	0.015	0.007
600	LAD-LASSO	– –	– –	1.000	0.650	0.016	0.008
	Oracle	– –	– –	1.000	1.000	0.008	0.004
	ESL-LASSO	4.499	0.642	1.000	1.000	0.009	0.005
	CQR-LASSO	– –	– –	1.000	0.910	0.010	0.006
800	LAD-LASSO	– –	– –	1.000	0.633	0.011	0.005
	Oracle	– –	– –	1.000	1.000	0.006	0.003

Table 3.

Simulation results in the third setting

						Model error
n	Method	γ̄n	ζ̄(γn)	PSR	NSR	Median	MAD
	ESL-LASSO	4.565	0.662	1.000	0.989	0.174	0.101
	CQR-LASSO	– –	– –	1.000	0.675	0.173	0.097
100	LAD-LASSO	– –	– –	1.000	0.488	0.113	0.061
	Oracle	– –	– –	1.000	1.000	0.098	0.050
	ESL-LASSO	3.646	0.731	1.000	1.000	0.081	0.046
	CQR-LASSO	– –	– –	1.000	0.730	0.103	0.055
150	LAD-LASSO	– –	– –	1.000	0.492	0.067	0.036
	Oracle	– –	– –	1.000	1.000	0.066	0.036
	ESL-LASSO	3.654	0.722	1.000	1.000	0.058	0.030
	CQR-LASSO	– –	– –	1.000	0.778	0.068	0.031
200	LAD-LASSO	– –	– –	1.000	0.487	0.051	0.025
	Oracle	– –	– –	1.000	1.000	0.049	0.023
	ESL-LASSO	3.589	0.850	1.000	1.000	0.022	0.012
	CQR-LASSO	– –	– –	1.000	0.856	0.031	0.016
400	LAD-LASSO	– –	– –	1.000	0.459	0.023	0.011
	Oracle	– –	– –	1.000	1.000	0.023	0.011
	ESL-LASSO	3.590	0.717	1.000	1.000	0.014	0.007
	CQR-LASSO	– –	– –	1.000	0.897	0.020	0.010
600	LAD-LASSO	– –	– –	1.000	0.431	0.014	0.007
	Oracle	– –	– –	1.000	1.000	0.016	0.008
	ESL-LASSO	3.525	0.833	1.000	1.000	0.010	0.005
	CQR-LASSO	– –	– –	1.000	0.912	0.015	0.008
800	LAD-LASSO	– –	– –	1.000	0.435	0.011	0.005
	Oracle	– –	– –	1.000	1.000	0.012	0.006

The PSR is around 1 for all three methods in all settings. Therefore, the performance of the three methods are comparable in terms of the model error and PSR. What distinguishes ESL-LASSO from LAD-LASSO and CQR-LASSO is NSR. Indeed, the NSR of the ESL-LASSO estimator is as close 1 as that of the oracle estimator, while the NSR of the LAD-LASSO and CQR-LASSO ranges from 0.431 to 0.738, and from 0.675 to 0.988, respectively. These simulation experiments suggest that the ESL-LASSO estimator leads to a consistent variable selection in common situations where outliers result from either the response or the covariate domain.

So far, we only considered d = 8. Next, we run a simulation study for d = 100. The true coefficients are set to be β = (1, 1.5, 2, 1, 0_p)^T, where 0_p is p-dimensional row vector of zeros, and p = 96. Covariate x_i follows a multi-normal distribution N(0, Ω₂), and the error term follows a mixture normal distribution 0.7N(0, 1) + 0.3N(5, 3²). Since our proposed method requires that p is fixed and less than n, we take n = 1000. We replicate the simulation 500 times to evaluate the finite-sample performance of ESL-LASSO. The simulation results are summarized in Table 4. This table reveals that ESL-LASSO still performs better in variable selection and has much lower model error than LAD-LASSO and CQR-LASSO.

Table 4.

Simulation results when d = 100

						Model error
n	Method	γ̄n	ζ̄(γn)	PSR	NSR	Median	MAD
	ESL-LASSO	4.441	0.736	1.000	1.000	0.010	0.005
	CQR-LASSO	– –	– –	1.000	0.866	0.030	0.013
1000	LAD-LASSO	– –	– –	1.000	0.661	0.022	0.008
	Oracle	– –	– –	1.000	1.000	0.010	0.005

4.2 Applications

Example 1

We apply the proposed methodology to analyze the Boston Housing Price Dataset which is available on http://lib.stat.cmu.edu/datasets/boston. This dataset was presented by Harrison and Rubinfeld (1978), and is commonly used as an example for regression diagnostics (Belsley et al. (1980)).

The data contains the following 14 variables: crim (per capita crime rate by town), zn (proportion of residential land zoned for lots over 25,000 sq.ft), indus (proportion of non-retail business acres per town), chas (Charles River dummy variable: equal to 1 if tract bounds river; 0 otherwise), nox (nitrogen oxides concentration: parts per 10 million), rm (average number of rooms per dwelling), age (proportion of owner-occupied units built prior to 1940), dis (weighted mean of distances to five Boston employment centres), rad (index of accessibility to radial highways), tax (full-value property-tax rate per ten thousand dollar), ptratio (pupil-teacher ratio by town), black (1000(Bk − 0.63)², where Bk is the proportion of blacks by town), lstat (lower status of the population (percent)), and medv (median value of owner-occupied homes in thousand dollars). There are 506 observations in the dataset. The response variable is medv, and the rest are the predictors. In this section, the predictors are scaled to have mean zero and unit variance.

Table 5 compares the estimates of the regression coefficients from the MM method and ordinary least-squares (OLS) besides ESL-LASSO, CQR-LASSO and LAD-LASSO. The selected variables and their coefficients are clearly different among the five methods.

Table 5.

Estimated regression coefficients from the Boston Housing Price Data

			Method
Variable	ESL-LASSO	CQR-LASSO	LAD-LASSO	MM	OLS
crim	0	0	0	−0.097	−0.101
zn	0	0	0	0.072	0.118
indus	0	0	0	−0.005	0.015
chas	0	0	0	0.038	0.074
nox	0	0	0	−0.097	−0.224
rm	0.590	0.422	0.503	0.491	0.291
age	0	0	0	−0.117	0.002
dis	0	−0.057	−0.013	−0.235	−0.338
rad	0	0	0	0.156	0.290
tax	−0.105	−0.133	−0.058	−0.208	−0.226
ptratio	−0.076	−0.153	−0.155	−0.179	−0.224
black	0	0.040	0.085	0.124	0.092
lstat	−0.131	−0.334	−0.243	−0.174	−0.408

With the proposed ESL-LASSO procedure, Steps 1 and 2 of the selection procedure first chooses the tuning γ_n at 2.1, which corresponds to m = 8, the number of ”bad points” in the observations. Table 5 reveals that ESL-LASSO selects four of the six variables selected by both CQR-LASSO and LAD-LASSO. The four variables are rm, tax, ptratio, and lstat. The two variables selected by LAD-LASSO but not by CQR-LASSO and ESL-LASSO are dis and black.

Example 2

As another illustration, we analyze the Plasma Beta-carotene Level Dataset from a cross-sectional study. This dataset consists of 315 sample, in which there are 273 female patients, and can be downloaded at http://lib.stat.cmu.edu/datasets/Plasma Retinol.

In this example, we only analyze the 273 female patients. Of interest are to study the relationships between the plasma beta-carotene level (betaplasma) and the following 10 covariates: age, smoking status (smokstat), quetelet, vitamin use (vituse), number of calories consumed per day (calories), grams of fat consumed per day (fat), grams of fiber consumed per day (fiber), number of alcoholic drinks consumed per week (alcohol), cholesterol consumed (cholesterol), and dietary beta-carotene consumed (betadiet).

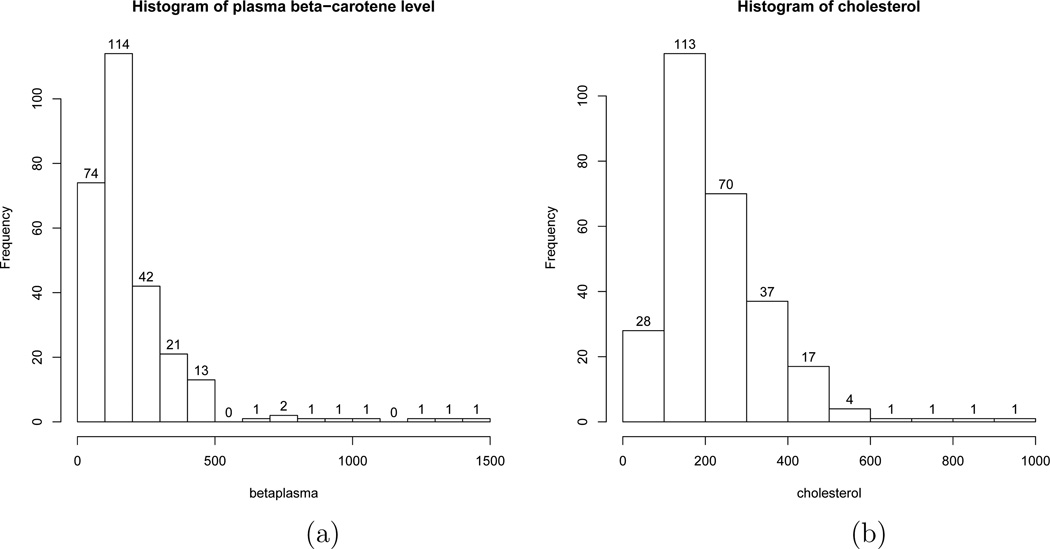
We plot a histogram of betaplasma and cholesterol in Figure 2. Figure 2 indicates that there are unusual points in either the response or the covariate domain. In the following, the predictors are scaled to have zero mean and unit variance. We use the first 200 sample as a training data set to fit the model, and then use the remaining 73 sample to evaluate the predictive ability of the selected model. The prediction performance is measured by the median absolute prediction error (MAPE).

Figure 2.

Histogram of betaplasma (a) and cholesterol (b).

Next, we apply ESL-LASSO, CQR-LASSO and LAD-LASSO to analyze the plasma beta-carotene level dataset. For ESL-LASSO, we first apply the proposed procedure to choose the tuning parameter γ_n, and obtain γ_n = 0.190. The results are summarized in Table 6. This table reveals that ESL-LASSO selects “fiber” that is also selected by CQR-LASSO and LAD-LASSO. In addition, CQR-LASSO selects “quetelet” and LAD-LASSO selects “batadiet”, and these two different choices are not selected by ESL-LASSO. Although ESL-LASSO selects one fewer covariate than LAD-LASSO, ESL-LASSO has a slightly smaller MAPE. ESL-LASSO also selects one fewer covariate than CQR-LASSO, the MAPE of ESL-LASSO is 10% higher.

Table 6.

Estimated regression coefficients from the plasma beta-carotene level data

		Method
Variable	ESL-LASSO	CQR-LASSO	LAD-LASSO
age	0	0	0
smokstat	0	0	0
quetelet	0	−0.057	0
vituse	0	0	0
calories	0	0	0
fat	0	0	0
fiber	0.114	0.077	0.058
alcohol	0	0	0
cholesterol	0	0	0
betadiet	0	0	0.075
MAPE	0.559	0.503	0.568

For further comparisons, we apply a combination of the bootstrap and cross validation Figure 2 method to obtain the standard errors of the estimates for the number of non-zeros and the model errors for two real datasets. For each bootstrap sample, we randomly split the 506 observations into training and testing sets in the Boston Housing Price Dataset of sizes 300 and 206, respectively. For the plasma beta-carotene level dataset, we randomly split the 273 observations into training and testing datasets of sizes 200 and 73, respectively. For ESL-LASSO, CQR-LASSO and LAD-LASSO, we calculate the median of absolute prediction error based on |y − x^Tβ̂| and MAD of prediction error based on y − x^Tβ̂ for the test set, respectively. The average errors and the average numbers of estimated nonzero coefficients over 200 repetitions are summarized in Table 7. The standard deviations are given in their corresponding parentheses. ESL-LASSO tends to select the fewest number of non-zeros.

Table 7.

Bootstrap results

			Model error
Dataset	Method	No. of non-zeros	Median	MAD
Boston Housing	ESL-LASSO	3.710(0.830)	0.381(0.021)	0.180(0.069)
Price	CQR-LASSO	7.025(1.015)	0.286(0.016)	0.258(0.020)
	LAD-LASSO	5.020(0.839)	0.277(0.017)	0.113(0.075)
Plasma Beta-	ESL-LASSO	0.305(0.462)	0.459(0.030)	0.180(0.054)
Carotene Level	CQR-LASSO	2.915(1.026)	0.453(0.032)	0.299(0.050)
	LAD-LASSO	2.570(1.020)	0.429(0.036)	0.176(0.161)

5. DISCUSSION

In this paper, we proposed a robust variable selection procedure via a penalized regression with the exponential squared loss. We investigated the sampling properties and studied the robustness properties of the proposed estimators. Through the theoretical and simulation results, we demonstrate the merits of our proposed method. We also illustrate that our proposed method can result in notable difference in real data analysis. Specifically, we show that our estimators possessed the highest finite sample breakdown point, and the influence functions are bounded with respect to outliers in either the response or the covariate domain.

Although Theorem 2 requires that the penalty has the form p_λnj (|β_j|) = λ_njg(|β_j|), where g(·) is a strictly increasing and unbounded function in [0, ∞]. We conjecture that the breakdown point result also holds for bounded penalties. Intuitively, we may use the one-step or k-step local linear approximation (LLA) proposed by Zou and Li (2008), where $p_{{\lambda }_{\mathit{\text{nj}}}}(|{\beta }_j|)\approx p_{{\lambda }_{\mathit{\text{nj}}}}(|{\beta }_j^{(0)}|)+p_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\beta }_j^{(0)}|)(|{\beta }_j|-|{\beta }_j^{(0)}|),\text{ for }{\beta }_j\approx {\beta }_j^{(0)}$. LLA provides a reasonable approximation in the sense that it posses the ascent property of the MM algorithm (Hunter and Lange, 2004), and yields the best convex majorization. Furthermore, the one-step LLA enjoys the oracle property. For the case where all $p_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\beta }_j^{(0)}|)>0$, Theorem 2 is applicable to LLA. For penalties where the derivative equals zero for some j (e.g., SCAD), the LLA can be implemented by using Algorithm 2 as suggested in Section 4 of Zou and Li (2008).

How to select both γ_n and regularization parameters λ_nj in a data-driven way is a difficult problem, since selection of γ_n depends on the choice of λ_nj and an estimate of β. Although the data-adaptive methods such as cross-validation can be applied, it could cause huge computation and may not satisfy condition (C2) of Remark 1. To implement our proposed ESL-LASSO, we consider a relative simple approach. We first choose regularization parameters λ_nj via a simple BIC criterion, and then proposed a data-driven approach to selecting the tuning parameter γ_n. We demonstrate the advantages of our methodology via simulation study and application. According to our simulation studies, the performance of our ESL-LASSO implementation is comparable to the oracle procedure irrespective of the presence and the mechanisms of outliers. We measure the performance by the model error, positive selection rate, and the non-causal selection rate. In the presence of outliers (regardless of the mechanisms), LAD-LASSO and CQR-LASSO perform poorly in terms of the non-causal selection rate.

After re-analyzing the Boston Housing Price Dataset and the Plasma Beta-Carotene Level Dataset, we find that the results and interpretation can be quite different with different methods. Although we do not know the real model from which the real data were generated, our simulation results suggest that a plausible cause of the discrepancies among ESL-LASSO, CQR-LASSO and LAD-LASSO is that there are outliers in the datasets. We refer to Harrison and Rubinfeld (1978) on the identification of influential points for these datasets. In short, our proposed ESL-LASSO is expected to produce a more reliable model without the need to identifying the specific influential points.

APPENDIX

Proof of Theorem 1 (i). Let ξ_n = n^−1/2 + a_n. We first prove that for any given ε > 0, there exists a large constant C such that

$$P\{\underset{\Vert \mathbf{u}\Vert =C}{\text{sup}}{\ell }_n({\mathit{\beta }}_0+{\xi }_n\mathbf{u})<{\ell }_n({\mathit{\beta }}_0)\}\ge 1-\epsilon ,$$ (A.1)

where u is d-dimensional vector such that ‖u‖ = C. Then, we prove that there exists a local maximizer β̂_n such that ‖β̂_n − β₀‖ = O_p(ξ_n). Let

$$D_n(\mathit{\beta },\gamma )={\displaystyle \sum _{i=1}^n}\text{exp }\{-{(Y_i-{\mathbf{x}}_i^T\mathit{\beta })}^2/\gamma \}\frac{2(Y_i-{\mathbf{x}}_i^T\mathit{\beta })}{\gamma }{\mathbf{x}}_i.$$

Since p_λnj (0) = 0 for j = 1, ⋯, d and γ_n − γ₀ = o_p(1), by Taylor’s expansion, we have

$${\ell }_n({\mathit{\beta }}_0+{\xi }_n\mathbf{u})-{\ell }_n({\mathit{\beta }}_0)\le {\xi }_n{D}_n{({\mathit{\beta }}_0,{\gamma }_n)}^T\mathbf{u}-\frac{1}{2}{\mathbf{u}}^T[-I({\mathit{\beta }}_0,{\gamma }_n)]\mathbf{u}n{\xi }_n^2\{1+o_p(1)\}-{\displaystyle \sum _{j=1}^s}[n{\xi }_n{p}_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\beta }_{0j}|)\text{sign}({\beta }_{0j})u_j+n{\xi }_n^2{p}_{{\lambda }_{\mathit{\text{nj}}}}^{″}(|{\beta }_{0j}|)u_j^2\{1+o(1)\}]={\xi }_n{\{D_n({\mathit{\beta }}_0,{\gamma }_0)+o_p(\sqrt{n})\}}^T\mathbf{u}-\frac{1}{2}{\mathbf{u}}^T[-I({\mathit{\beta }}_0,{\gamma }_0)+o(1)]\mathbf{u}n{\xi }_n^2\{1+o_p(1)\}-{\displaystyle \sum _{j=1}^s}[n{\xi }_n{p}_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\beta }_{0j}|)\text{sign}({\beta }_{0j})u_j+n{\xi }_n^2{p}_{{\lambda }_{\mathit{\text{nj}}}}^{″}(|{\beta }_{0j}|)u_j^2\{1+o(1)\}].$$ (A.2)

Note that n^−1/2D_n(β₀, γ₀) = O_p(1). Therefore, the order of the first term on the right side is equal to $O_p(n^{1/2}{\xi }_n)=O_p(n{\xi }_n^2)$ in the last equation of (A.2). By choosing a sufficiently large C, the second term dominates the first term uniformly in ‖u‖ = C. Meanwhile, the third term in (A.2) is bounded by

$$\sqrt{s}n{\xi }_n{a}_n\Vert \mathbf{u}\Vert +n{\xi }_n^2{b}_n{\Vert \mathbf{u}\Vert }^2.$$

Since b_n = o_p(1), the third term is also dominated by the second term of (A.2). Therefore, (A.1) holds by choosing a sufficiently large C. The proof of Theorem 1 (i) is completed.

Lemma 1 Assume that the penalty function satisfies (2.3). If $\sqrt{n}({\gamma }_n-{\gamma }_0)=o_p(1)$ for some γ₀ > 0, b_n = o_p(1), $\sqrt{n}{a}_n=o_p(1),\text{ and }1/{\text{min}}_{s+1\le j\le d}(\sqrt{n}{\lambda }_{\mathit{\text{nj}}})=o_p(1)$, then with probability 1, for any given β satisfying ‖β − β₀‖ = O_p(n^−1/2) and any constant C,

$${\ell }_n({\mathit{\beta }}_1,0)=\underset{\Vert {\mathit{\beta }}_2\Vert \le {\mathit{\text{Cn}}}^{-1/2}}{\text{max}}{\ell }_n({\mathit{\beta }}_1,{\mathit{\beta }}_2).$$

Proof of Lemma 1. We will show that with probability 1, for any β₁ satisfying β₁ − β₀₁ = O_p(n^−1/2), and for some small ε_n = Cn^−1/2 and j = s + 1, ⋯, d, we have ∂ℓ_n (β) /∂β_j < 0, for 0 < β_j < ε_n, and ∂ℓ_n (β) /∂β_j > 0, for −ε_n < β_j < 0. Let

$$Q_n(\mathit{\beta },\gamma )={\displaystyle \sum _{i=1}^n}\text{exp}\{-{(Y_i-{\mathbf{x}}_i^T\mathit{\beta })}^2/\gamma \}.$$ (5.3)

By Taylor’s expansion, we have

$$\frac{\partial {\ell }_n(\mathit{\beta })}{\partial {\beta }_j}=\frac{\partial Q_n(\mathit{\beta },{\gamma }_n)}{\partial {\beta }_j}-{\mathit{\text{np}}}_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\beta }_j|)\text{sign}({\beta }_j)=\frac{\partial Q_n({\mathit{\beta }}_0,{\gamma }_n)}{\partial {\beta }_j}+{\displaystyle \sum _{l=1}^p}\frac{{\partial }^2{Q}_n({\mathit{\beta }}_0,{\gamma }_n)}{\partial {\beta }_j\partial {\beta }_l}({\beta }_l-{\beta }_{l0})+{\displaystyle \sum _{l=1}^p}{\displaystyle \sum _{k=1}^p}\frac{{\partial }^3{Q}_n({\beta }^{\divideontimes },{\gamma }_n)}{\partial {\beta }_j\partial {\beta }_l\partial {\beta }_k}({\beta }_l-{\beta }_{l0})({\beta }_k-{\beta }_{k0})-{\mathit{\text{np}}}_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\beta }_j|)\text{sign}({\beta }_j),$$

where β^⋇ lies between β and β₀. Note that

$$n^{-1}\frac{\partial Q_n({\mathit{\beta }}_0,{\gamma }_0)}{\partial {\beta }_j}=O_p(n^{-1/2}),$$

and

$$n^{-1}\frac{{\partial }^2{Q}_n({\mathit{\beta }}_0,{\gamma }_0)}{\partial {\beta }_j\partial {\beta }_l}=E\left\{\frac{{\partial }^2{Q}_n({\mathit{\beta }}_0)}{\partial {\beta }_j\partial {\beta }_l}\right\}+o_p(1).$$

Since b_n = o_p(1) and $\sqrt{n}{a}_n=o_p(1)$, we obtain β − β₀ = O_p(n^−1/2). By $\sqrt{n}({\gamma }_n-{\gamma }_0)=o_p(1)$, we have

$$\frac{\partial {\ell }_n(\mathit{\beta })}{\partial {\beta }_j}=n{\lambda }_{\mathit{\text{nj}}}\{-{\lambda }_{\mathit{\text{nj}}}^{-1}{p}_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\beta }_j|)\text{sign}({\beta }_j)+O_p(n^{-1/2}/{\lambda }_{\mathit{\text{nj}}})\}.$$

Since $1/{\text{min}}_{s+1\le j\le d}(\sqrt{n}{\lambda }_{\mathit{\text{nj}}})=o_p(1),\text{and}{\text{lim}}_{n\to \infty }\text{inf }{\text{lim}}_{t\to 0+}\text{inf}\{{\text{min}}_{s+1\le j\le d}{p}_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|t|)/{\lambda }_{\mathit{\text{nj}}}\}>0$ with probability 1, the sign of the derivative is completely determined by that of β_j. This completes the proof of Lemma 1.

Proof of Theorem 1 (ii). Part (a) holds by Lemma 1. We have showed that there exists a root-n consistent local maximizer of ℓ_n{(β₁, 0)}, satisfying that

$$\frac{\partial {\ell }_n\{({\mathit{\beta ̂}}_{n1},0)\}}{\partial {\beta }_j}=0,\text{for }j=1,\cdots ,s.$$ (5.4)

Since β̂_n1 is a consistent estimator, we have

$$\frac{\partial Q_n\{({\mathit{\beta ̂}}_{n1},0),{\gamma }_n\}}{\partial {\beta }_j}-n{p}_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\mathrm{\beta ̂}}_j|)\text{sign}({\mathrm{\beta ̂}}_j)=\frac{\partial Q_n({\mathit{\beta }}_0,{\gamma }_n)}{\partial {\beta }_j}+{\displaystyle \sum _{l=1}^s}\{\frac{{\partial }^2{Q}_n({\mathit{\beta }}_0,{\gamma }_n)}{\partial {\beta }_j\partial {\beta }_l}+o_p(1)\}({\mathrm{\beta ̂}}_l-{\beta }_{01})-n[p_{{\lambda }_{\mathit{\text{nj}}}}^{\prime }(|{\beta }_{0j}|)\text{sign}({\beta }_{0j})+\{p_{{\lambda }_{\mathit{\text{nj}}}}^{″}(|{\beta }_{0j}|)+o_p(1)\}({\mathrm{\beta ̂}}_j-{\beta }_{0j})],$$

where Q_n (β, γ) is defined in (5.3). Since $\sqrt{n}({\gamma }_n-{\gamma }_0)=o_p(1)$, the proof of part (b) is completed by Slutsky Lemma and the central limit theorem.

Lemma 2 Let D_n = {D₁, ⋯, D_n} be any sample of size n, D_m = {D₁, ⋯, D_m} be a contaminating sample of size m, and $a_{\mathit{\text{nm}}}={\text{max}}_{\mathit{\beta }\in {ℝ}^d}\#\{i:m+1\le i\le n\text{ and }{\mathbf{x}}_i^T\mathit{\beta }=0\}/(n-m)$. Assume

$$a_{\mathit{\text{nm}}}<0.5,\epsilon <(1-2a_{\mathit{\text{nm}}})/(2-2a_{\mathit{\text{nm}}})\mathit{\text{ and }}\zeta ({\gamma }_n)<(1-\epsilon )(2-2a_{\mathit{\text{nm}}}).$$

For the weighted vector λ = (λ_n1, ⋯, λ_nd), if

$$0<\underset{\{j:1\le j\le d\}}{\text{min}}{\lambda }_{\mathit{\text{nj}}}<+\infty ,$$

there exists a C such that m/n ≤ ε implies

$$\underset{\Vert \mathit{\beta }\Vert \ge C}{\text{inf}}\{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\varphi }_{{\gamma }_n}\{r_i(\mathit{\beta })\}+{\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\beta }_j|)\}>\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\varphi }_{{\gamma }_n}\{r_i({\mathit{\beta ̌}}_n)\}+{\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\mathrm{\beta ̌}}_{\mathit{\text{nj}}}|),$$ (5.5)

where $r_i(\mathit{\beta })=Y_i-{\mathbf{x}}_i^T\mathit{\beta }$, β̌_n is an initial estimator of β and ϕ_γ(t) = 1 − exp(−t²/γ).

Proof of Lemma 2. By definition of a_nm, we have

$$\#\{i:m+1\le i\le n\text{ and }|{\mathbf{x}}_i^T\mathit{\beta }|>0\}/(n-m)\ge 1-a_{\mathit{\text{nm}}},$$

for all β. Since ε < (1 − 2a_nm)/(2 − 2a_nm) and ζ(γ_n) < (1 − ε)(2 − 2a_nm), there exist a_n1 > a_nm and a_n2 > a_nm such that ε < (1 − 2a_n1)/(2 − 2a_n1) and ζ(γ_n) < (1 − ε)(2−2a_n2).

Take $a_n^{*}=\text{min}\{a_{n1},a_{n2}\}>a_{\mathit{\text{nm}}}$, we have

$$\epsilon <(1-2a_n^{*})/(2-2a_n^{*})\text{ and }\zeta ({\gamma }_n)<(1-\epsilon )(2-2a_n^{*}).$$

Since $a_n^{*}>a_{\mathit{\text{nm}}}$, by using a compacity argument (Yohai (1987)), we can find δ > 0 such that

$$\underset{\Vert \mathit{\beta }\Vert =1}{\text{inf}}\#\{i:m+1\le i\le n\text{ and }|{\mathbf{x}}_i^T\mathit{\beta }|>\delta \}/(n-m)\ge 1-a_n^{*}.$$

Since $1-\epsilon >1/(2-2a_n^{*})$, we can find η such that $(1-\epsilon )(1-a_n^{*})>1-\eta >1/2$. Take Δ which satisfies

$$1<1+\mathrm{\Delta }<\text{min}\{\frac{(1-\epsilon )(2-2a_n^{*})}{\zeta ({\gamma }_n)},\frac{(1-\epsilon )(1-a_n^{*})}{1-\eta }\},$$

and take $a_0=\frac{(1-\eta )\zeta ({\gamma }_n)(1+\mathrm{\Delta })}{(1-\epsilon )(2-2a_n^{*})}$. We then have a₀ < min{1 − η, ζ(γ_n)/2}. Then m/n ≤ ε implies

$$a_0(n-m)/n\ge (1-\epsilon )a_0>(1-\eta )\zeta ({\gamma }_n)/(2-2a_n^{*}).$$

Because ϕ_γn(t) is a continuous, bounded, and even function, there exists a k₂ ≥ 0 such that ϕ_γn(k₂) = a₀/(1 − ζ). Let C₁ ≥ (k₂ + max_m+1≤i≤n |Y_i|)/δ. Then m/n ≤ ε implies

$$\underset{\Vert \mathit{\beta }\Vert \ge C_1}{\text{inf}}{\displaystyle \sum _{i=1}^n}{\varphi }_{{\gamma }_n}\{r_i(\mathit{\beta })\}\ge \underset{\Vert \mathit{\beta }\Vert =1}{\text{inf}}{\displaystyle \sum _{i\in A}}{\varphi }_{{\gamma }_n}(|Y_i|-C_1|{\mathbf{x}}_i^T\mathit{\beta }|)\ge (n-m)(1-a_n^{*}){\varphi }_{{\gamma }_n}(k_2)=(n-m)(1-a_n^{*})a_0/(1-\eta )>n\zeta ({\gamma }_n)/2\ge {\displaystyle \sum _{i=1}^n}{\varphi }_{{\gamma }_n}\{r_i({\mathit{\beta ̌}}_n)\},$$ (5.6)

where $A=\{i:m+1\le i\le n\text{ and }|{\mathbf{x}}_i^T\mathit{\beta }|>\delta \}$.

Let $C_2=\sqrt{p}{q}^{-1}\{{\displaystyle {\sum }_{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\mathrm{\beta ̌}}_j|)/(\text{min}\{{\lambda }_{\mathit{\text{ni}}}\})\}$. Take C = max{C₁, C₂}. We have

$$\underset{\Vert \mathit{\beta }\Vert \ge C}{\text{inf}}\{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\varphi }_{{\gamma }_n}\{r_i(\mathit{\beta })\}+{\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\beta }_j|)\}\ge \underset{\Vert \mathit{\beta }\Vert \ge C}{\text{inf}}\{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\varphi }_{{\gamma }_n}\{r_i(\mathit{\beta })\}\}+\underset{\Vert \mathit{\beta }\Vert \ge C}{\text{inf}}\{{\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\beta }_j|)\}\ge \underset{\Vert \mathit{\beta }\Vert \ge C_1}{\text{inf}}\{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\varphi }_{{\gamma }_n}\{r_i(\mathit{\beta })\}\}+\underset{\Vert \mathit{\beta }\Vert \ge C_2}{\text{inf}}\{{\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\beta }_j|)\}.$$

By (5.6), we only need to deal with the second term. Note that ‖β‖ ≥ C₂ implies that there exists an element β_j of β such that $|{\beta }_j|\ge C_2/\sqrt{p}$ for some j. Hence,

$$\underset{\Vert \mathit{\beta }\Vert \ge C_2}{\text{inf}}\{{\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\beta }_j|)\}\ge {\lambda }_{\mathit{\text{nj}}}g(|{\beta }_j|)\ge {\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\mathrm{\beta ̌}}_{\mathit{\text{nj}}}|).$$

Proof of Theorem 2. For a contaminated sample D_n, and m/n ≤ ε, according to Lemma 2, if ‖β̂_n‖ ≥ C, we have

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\varphi }_{{\gamma }_n}\{r_i({\mathit{\beta ̂}}_n)\}+{\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\mathrm{\beta ̂}}_{\mathit{\text{nj}}}|)>\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\varphi }_{{\gamma }_n}\{r_i({\mathit{\beta ̌}}_n)\}+{\displaystyle \sum _{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\mathrm{\beta ̌}}_{\mathit{\text{nj}}}|).$$

This is a contradiction to the fact that β̂_n minimizes $\{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n}{\varphi }_{{\mathrm{\gamma }}_n}\{r_i(\mathit{\beta })\}+{\displaystyle {\sum }_{j=1}^d}{\lambda }_{\mathit{\text{nj}}}g(|{\beta }_j|)\}$ for β ∈ ℝ^d. Therefore, we have

$$\mathit{\text{BP}}({\mathit{\beta ̂}}_n;{\mathbf{D}}_{n-m},{\gamma }_n)\ge \text{min}\{\mathit{\text{BP}}({\mathit{\beta ̌}}_n;{\mathbf{D}}_{n-m}),(1-2a_{\mathit{\text{nm}}})/(2-2a_{\mathit{\text{nm}}}),1-\frac{\zeta ({\gamma }_n)}{2-2a_{\mathit{\text{nm}}}}\}.$$

Proof of Theorem 3. Note that

$$(1-\epsilon ){\displaystyle \int }\left[\text{exp}\right\{-{(y-{\mathbf{x}}^T{\mathit{\beta }}_{\epsilon }^{*})}^2/{\gamma }_0\left\}\right(\frac{2}{{\gamma }_0}(y-{\mathbf{x}}^T{\mathit{\beta }}_{\epsilon }^{*})\left)\mathbf{x}\right]\mathit{\text{dF}}(\mathbf{x},y)+\epsilon \text{ exp }\{-{(y_0-{\mathbf{x}}_0^T{\mathit{\beta }}_{\epsilon }^{*})}^2/{\gamma }_0\}(\frac{2}{{\gamma }_0}(y_0-{\mathbf{x}}_0^T{\mathit{\beta }}_{\epsilon }^{*})){\mathbf{x}}_0-{\nu }_1(\epsilon )=0,$$ (5.7)

where ${\nu }_1(\epsilon )={(p_{{\lambda }_{01}}^{\prime }(|{\beta }_{\epsilon 1}|)\text{sign}({\beta }_{\epsilon 1}),\cdots ,p_{{\lambda }_{0d}}^{\prime }(|{\beta }_{\epsilon d}|)\text{sign}({\beta }_{\epsilon d}))}^T$.

Let $r_0=y_0-{\mathbf{x}}_0^T{\mathit{\beta }}_0^{*}$. Differentiating with respect to ε in both sides of (5.7) and letting ε → 0, we obtain

$${\displaystyle \int }[\text{exp}\{-{(y-{\mathbf{x}}^T{\mathit{\beta }}_{\epsilon }^{*})}^2/{\gamma }_0\}(\frac{-4{(y-{\mathbf{x}}^T{\mathit{\beta }}_{\epsilon }^{*})}^2}{{\gamma }_0^2})\frac{\partial }{\partial \epsilon }(y-{\mathbf{x}}^T{\mathit{\beta }}_{\epsilon }^{*})\mathbf{x}+\text{exp}\{-{(y-{\mathbf{x}}^T{\mathit{\beta }}_{\epsilon }^{*})}^2/{\gamma }_0\}\frac{\partial }{\partial \epsilon }(\frac{2(y-{\mathbf{x}}^T{\mathit{\beta }}_{\epsilon }^{*})}{{\gamma }_0}\left)\mathbf{x}\right]{\mathit{\text{dF}}(\mathbf{x},y)|}_{\epsilon =0}-\frac{\partial {\nu }_1(\epsilon )}{\partial \epsilon }=-\frac{\text{exp}\{-r_0^2/{\gamma }_0\}2r_0{x}_0}{{\gamma }_0}-{\nu }_2,$$ (5.8)

where ${\nu }_2={(p_{{\lambda }_{01}}^{\prime }(|{\beta }_{01}^{*}|)\text{sign}({\beta }_{01}^{*}),\cdots ,p_{{\lambda }_{0d}}^{\prime }(|{\beta }_{0d}^{*}|)\text{sign}({\beta }_{0d}^{*}))}^T$. By using (5.7) and (5.8), it can be shown that

$$(\frac{2A({\gamma }_0)}{{\gamma }_0}-B_1)[\mathit{\text{IF}}\{({\mathbf{x}}_0,y_0),{\mathit{\beta }}_0^{*}\}]=-\frac{\text{exp}\{-r_0^2/{\gamma }_0\}2r_0{x}_0}{{\gamma }_0}-{\nu }_2,$$ (5.9)

where

$$A(\gamma )={\displaystyle \int }{\mathbf{\text{xx}}}^T\text{ exp}\{-{(y-{\mathbf{x}}^T{\mathit{\beta }}_0^{*})}^2/\gamma \}(\frac{2{(y-{\mathbf{x}}^T{\mathit{\beta }}_0^{*})}^2}{\gamma }-1)\mathit{\text{dF}}(\mathbf{x},y),$$

$$B_1=\text{diag}\{p_{{\lambda }_{01}}^{″}(|{\beta }_{01}^{*}|)+p_{{\lambda }_{01}}^{\prime }(|{\beta }_{01}^{*}|)\delta ({\beta }_{01}^{*}),\cdots ,p_{{\lambda }_{0d}}^{″}(|{\beta }_{0d}^{*}|)+p_{{\lambda }_{0d}}^{\prime }(|{\beta }_{0d}^{*}|)\delta ({\beta }_{0d}^{*})\},$$

with

$$\delta (x)=\{\begin{array}{cc}+\infty \hfill & \text{if }x=0\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$

This completes the proof of Theorem 3.

Proof of Corollary 1. Since β̃_n is a root-n consistent estimator and τ̂_nj = log(n)/n, we obtain

$$\underset{1\le j\le s}{\text{max}}(\sqrt{n}{\mathrm{\tau ̂}}_{\mathit{\text{nj}}}/|{\mathrm{\beta ̃}}_{\mathit{\text{nj}}}|)=o_p(1),\text{and }1/\underset{s+1\le j\le d}{\text{min}}(\sqrt{n}{\mathrm{\tau ̂}}_{\mathit{\text{nj}}}/|{\mathrm{\beta ̃}}_{\mathit{\text{nj}}}|)=o_p(1),$$ (5.10)

which satisfies the conditions of oracle property in Theorem 1. This completes the proof of Corollary 1.