Abstract
Despite rapid advances in the field of stem/progenitor cells through experimental studies, relevant modeling approaches have not progressed with a similar pace. Various models have focused on particular aspects of stem cell physiology including gene regulatory networks, gene expression noise and signaling cascades activated by exogenous factors. However, the self-renewal and differentiation of stem cells is driven by the coordinated regulation of events at the subcellular, intercellular and milieu levels. Such events also span multiple time domains from the fast molecular reactions governing gene expression to the slower cell cycle and division. Thus, the development of multiscale computational frameworks for stem cell populations is highly desirable. Multiscale models are expected to aid the design of efficient differentiation strategies and bioprocesses for the generation of therapeutically useful stem cell progeny. Yet, challenges in making these models tractable and pairing those to sufficient experimental data prevent their wide adoption by the stem cell community. Here, we review modeling approaches reported for stem cell populations and associated hurdles.
Keywords: Stem cells, self-renewal, differentiation, multiscale model, stochastic model, deterministic model, population balance model
Introduction
Recent advances in stem cell biology and engineering have sparked hope that stem cell-based therapeutics will be soon available for maladies such as Parkinson, diabetes, and heart diseases. Human pluripotent stem cells (hPSCs) encompassing blastocyst-derived embryonic stem cells (hESCs) and induced pluripotent stem cells (hiPSCs) exhibit prolonged self-renewal and the potential to differentiate to all somatic cell types [1-3]. Therefore, hPSCs hold tremendous prospects for use in regenerative medicine and as tools for gaining deeper insights in developmental biology. Such prospects have fueled efforts to establish high-efficiency differentiation methods for the generation of progeny such as neural cells, hepatocytes, cardiomyocytes and pancreatic islet cells. The results are encouraging as remarkable successes have been noted on this front.
Yet, the development of quantitative frameworks is lagging for describing stem cell populations and predicting their behavior in a variety of environments with stimuli for self-renewal/differentiation (e.g. growth factors, extracellular matrix molecules) and/or other cell types (e.g. progenitor cells). Computational models linking the physiological state of stem cells to their niche is essential not only for identifying appropriate cultivation conditions for efficient propagation and commitment into functional progeny but also for the design, optimization and robust control of bioprocesses intended for the production of stem cell therapeutics. In this review, we summarize reports on different modeling approaches applied to stem cell systems. Furthermore, findings from several studies and the vistas they offer on stem cell self-renewal and differentiation are discussed. Finally, challenges are presented laying ahead for the development of computational frameworks, which will facilitate bringing stem cells closer to clinical reality.
Attributes of stem cells and computational modeling
Stem cells share common properties with other cell types (e.g. proliferation, death, cell cycle phases etc.) but also exhibit unique characteristics, which should be considered during the construction of a mathematical model. Unlike most phenotypically stable cell types, stem cells have the propensity to exit self-renewal and adopt multiple cell fates, depending on several factors including the presence of exogenous differentiation agents and cell-cell and/or cell-niche signals. The result is the emergence of inhomogeneous populations. Even self-renewing stem cells in vivo or in vitro exhibit variable levels of pluripotency markers such as POU5F1 (Oct4), SSEA-1, SSEA-3, NANOG and Stella [4-9]. The biological ramifications of heterogeneity, which may also be attributed to stochastic processes such as the expression of genes modulating cell specification, is still the subject of intense research efforts. From a modeling perspective, the prediction of stem cell responses should be considered in conjunction with the different cell subpopulations (e.g. undifferentiated and committed progenies) present and their respective ratios. Stem cells are also metastable undergoing dynamic fluctuations between particular states dictated by their environment. This calls for temporally dependent rather than time-invariant models.
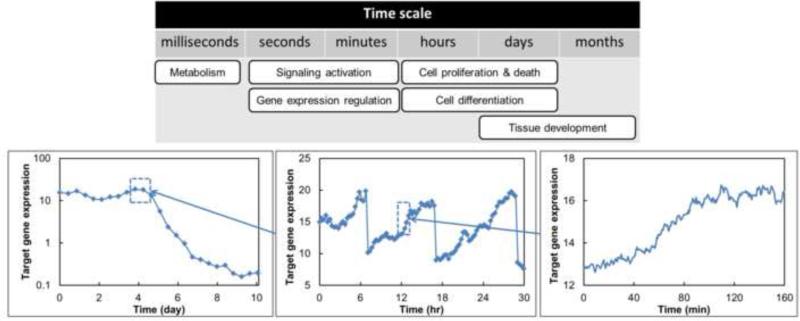
Interestingly, stem cell population events transpire at multiple spatiotemporal levels lending themselves to multiscale modeling. Processes at the subcellular (e.g. regulation of pluripotent/differentiation marker expression, signaling pathways), intercellular (e.g. secretion/degradation of extracellular soluble and insoluble (matrix) factors) and population-wide levels (e.g. cross-talk among subpopulations with different phenotypes) should be viewed simultaneously as they are innate to the stem cell niche and major determinants of stem cell fate decisions. Such processes occur over distinctly different time scales (Figure 1). For instance, DNA transcription/translation through the action of transcription factors (e.g. Nanog, Oct4) happens in seconds to minutes (if not faster) whereas cells divide every 10-30 hours (e.g. the doubling time td for hESCs is 24-36 hours). Thus, modeling modalities capable of coping with multiple scales are essential for quantitative description of stem cell populations.
Figure 1.
Stem cell processes span multiple time scales. Lineage commitment and reprogramming events are observed at longer intervals (days), for instance, as indicated by the increase/decrease of a target gene (lower left graph). Cell division and signal-regulated responses are normally observed in hours to minutes. Stochastic gene expression and associated protein translation can be resolved from relevant profiles spanning seconds to minutes.
Deterministic and stochastic approaches for stem cell systems
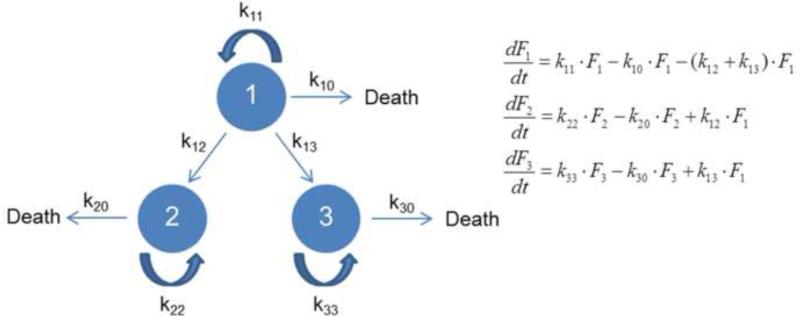
Stem cell models are broadly categorized as deterministic, stochastic, and hybrid. Deterministic models are largely based on the notion that stem cells exhibit a deterministic behavior given their response to differentiation stimuli in a dose-dependent manner. For instance, graded nodal/activin signaling promotes three distinct cell fate decisions in mouse ESCs [10]. Endogenous signaling is permissive to the maintenance of pluripotency whereas an increase or decrease in signaling leads to the induction of mesendoderm or trophoectoderm fates, respectively. In deterministic theorizations of fate selection, the experimentally observed randomness and heterogeneity of cell ensembles is attributed largely to fluctuations in the culture or tissue environment and the non-synchronous nature of the population. Deterministic models are generally more tractable from the standpoint of numerical computations than stochastic or even hybrid models. In many instances, systems of ordinary (ODEs) or partial differential equations (PDEs) –especially time-dependent– form the basis of deterministic frameworks for stem cells. In turn, the whole population or single cells always trace the same trajectory for a given set of initial/boundary conditions. A simple model is shown in Figure 2 with stem cells divided into three subpopulations: 1) Self-renewing cells, 2) cells undergoing apoptosis, and 3) differentiating cells. Cells in each pool proliferate and die according to first-order kinetics. The set of differential equations can be easily modified or extended to include distinct kinetics and constraints. Because the results portray the whole population rather than individual stem cells, traditional methods of cell analysis are suitable for experiments coupled to this class of models.
Figure 2.
A deterministic representation of stem cell activities. Each circle represents a subpopulation of a specific cell type (‘1’, ‘2’ or ‘3’). Cells within each circle can proliferate and die with kinetic parameters kii and ki0, respectively. Additionally, type ‘1’ cells can transition (e.g. differentiate) to cells of type ‘2’ or ‘3’ with kinetic parameters k12 and k13. The ODE system is also shown with Fi being the number (or fraction) of ith type cells.
In deterministic models, the population outcome is typically attributed to a variable of the physiological state vector of the cell influenced by selected environmental stimuli. Wang et al. [11] modeled the commitment of human mesenchymal progenitor cells as dependent on the accumulation of an (unspecified) intracellular ‘lineage factor’ (e.g. transcription factor(s), signaling or epigenetic events). The cells exhibit an ‘all-or-none’ response to BMP2 undergoing osteogenic or myogenic differentiation. The temporal change in the concentration of the ‘lineage factor’ was linked to the BMP2 concentration via an ODE. The equation featured a positive-feedback loop with Hill type kinetics generating bistability. Upon parameter estimation, the model correlated well with experimental data. Such approaches provide testable insights on how the outcome of stem cell differentiation varies with changes in environmental stimuli but reveal less about the molecular participants in the underlying differentiation programs.
Chang et al. [12] also observed a bistable expression pattern of stem cell antigen-1 (Sca-1; also known as Ly6a) in mouse HSCs. The presence of Sca-1high and Sca-1low cells was demonstrated to be only a one-dimensional projection of transcriptome-wide heterogeneity. The interaction between Sca-1low and Sca-1high populations was described by an ODE model taking into account the proliferation and transition kinetics between the two states. A bimodal distribution of HSCs based on Sca-1 expression was shown although the molecular programs engaged in the generation and maintenance of the observed heterogeneity in Sca-1 expression remain to be elucidated.
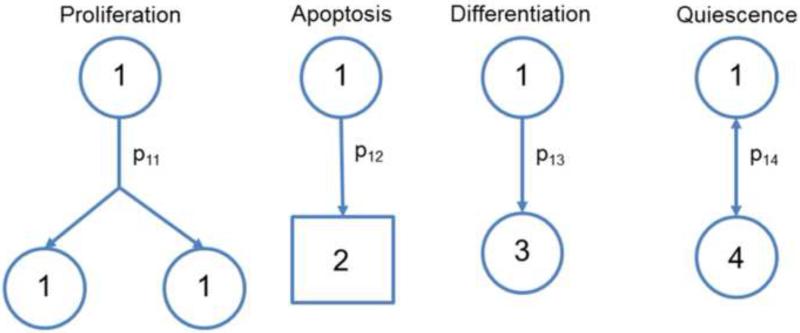
In contrast to deterministic models, stochastic approaches depict events such as differentiation and proliferation by probability functions (Figure 3) [13]. In their pioneering work, Till et al. [14] described a stochastic model for the proliferation of spleen colony-forming cells (referred to as ‘colony-forming units’ or CFUs). The populations analyzed were considered a mixture of a small number of new colony-forming cells (‘birth’ or self-renewal) and a larger fraction of cells without colony-forming capacity (‘death’ or differentiation). The ensemble of cells forming spleen colonies was determined experimentally and was found to follow a gamma distribution indicating that a random birth-and-death model is suitable to describe the population. Monte Carlo (MC) calculations carried out with a constant generation time and fixed probabilities for birth and death yielded results, which were in good agreement with the experimental observations, further justifying the selection of the model and associated assumptions. This study was the first to illustrate the decision of stem cells to self-renew or differentiate as a stochastic process.
Figure 3.
Stochastic model for stem cells. Possible fate decisions are shown for a stem cell “1” including proliferation (‘1’), apoptosis (‘2’), differentiation (to cell type ‘3’) and quiescence (‘4’). Each event has an associated probability (p1i) with a constraint that .
Subsequent studies particularly on hematopoietic stem cells (HSCs) [15-17] also supported the stochasticity in cell fate determination. Roeder and colleagues [18] described a single cell-based stochastic model for HSCs. The model coordinates of each HSC comprised its cycling status and its affinity to reside in each of two growth environments: One supporting nonproliferative cells and the other hosting proliferative cells. The study considered only symmetric cell duplication but stochasticity arose from the modeling of the transition between the two environments by transition intensities dependent on the affinity and cell numbers in the system. Differentiation was considered but not to a particular cell type. A lineage propensity variable was added to the model later [19] and conversion of cells to a particular type was dictated by randomly upregulating one lineage propensity at the expense of the others. Case studies included the comparative differentiation of paired daughter cells, lineage contribution of single differentiating cells and lineage specification in differentiating HSC cultures. The simulation results were compared with published experimental data. The commitment of stem cells along different lineages was proposed by the model to be a competing process between priming and the dominance of one lineage under the governance of environmental stimuli.
Models of signaling and gene expression networks in stem cells
Induction of stem cell specification by extracellular factors depends on the activation of intracellular pathways. Modeling of signal transduction provides insights of how stem cells respond to soluble stimuli (Table 1). These models typically consist of ODE systems depicting ligand binding to receptors, and the action of downstream secondary messengers as a series of chemical reactions. For example, a model was developed for mESC self-renewal in response to LIF and its analog hyper-interleukin-6 (HIL-6). HIL-6 is a fusion of human IL-6 and a truncated soluble IL-6 receptor and is active at 102-103-fold lower concentrations than regular IL-6 and its receptor [20]. The model considered the interactions of LIF and HIL-6 with the gp130 surface receptor complex [21] and predicted that LIF supports mESC self-renewal better than HIL-6 at the same concentration (e.g. 500 pM) due to the difference in the stoichiometry for ligand binding to the receptor. In agreement with this model, the fractions of SSEA-1+/E-cadherin+ mESCs and the mean alkaline phosphatase activity were higher in cells treated with LIF than those treated with the same concentration of HIL-6. In a subsequent study [22], the model was extended covering the entire Janus kinase/signal transducer and activator of transcription-3 (Jak/Stat3) pathway from the interaction of the gp130 receptor with LIF to the activation of Stat3 and its target SOCS3 (suppressor of cytokine signaling). Apart from global sensitivity analysis for quantifying the relative effect of model parameters on Jak/Stat3 activation, the inability of cells to respond to LIF (desensitization) was tested by manipulating the ligand stimulation frequency. SOCS3, nuclear export of Stat3 and receptor turnover were among the principal determinants controlling desensitization. Such models are useful for designing strategies for stem cell cultivation by adjusting ligand concentration based on signaling kinetics. It will be interesting if similar frameworks can be used to deconvolve synergistic effects from multiple factors (e.g. bFGF and Nodal in hESCs). More details regarding the mathematical models for signal transduction networks can be found elsewhere (e.g. [23,24]).
Table 1.
Summary of major stem cell modeling approaches surveyed, the insights they provide and their pros and cons.
| Modeling approach | Insights gained on: | Pros and cons |
|---|---|---|
| Ranges of ligand concentration and duration of stem cell exposure to trigger a particular response (e.g. self-renewal or differentiation). | Pros: Numerical treatment is typically straightforward (systems of ODEs). | |
| Signal transduction network (typically single-cell) models | Identifying network intermediates exerting more/less control over stem cell response(s) to given signals. | Cons: Require extensions of single-cell model to reflect population behavior. |
| Deconvolving synergistic effects from the action of multiple factors. | ||
| Interactions among key genes influencing stem cell fate decisions. Kinetics of gene expression related to stem cell phenotype adoption. |
Pros: Multiple approaches are available (e.g. Boolean, Bayesian, ODEs etc.) for GRN analysis. | |
| Pertinent numerical methods are typically well-defined. | ||
| Gene regulatory network (typically single-cell) models | Stochastic gene expression can be described. | |
| Cons: Require extension of single-cell model to reflect population-level behavior. | ||
| Source of stem cell heterogeneity is limited to noise in gene expression. | ||
| Effects of variability in gene expression and other subcellular processes (e.g. signaling, metabolism etc.) on stem cell population diversity. | Pros: Applicable numerical methods are straightforward to implement. | |
| Cell ensemble models | Linking adjustable bioprocess variables (e.g. factor and/or nutrient concentration) to property profiles of the population. | High-dimensional state vectors can be accommodated. GRNs can be directly included. |
| Multiple scales can be modeled (typically with steady-state assumptions). | ||
| Cons: Incorporation of cell division, differentiation and apoptosis is demanding. | ||
| Population balance models | How processes at different scales (e.g. fluctuating gene expression, stochastic partitioning of cellular material at mitosis, etc.) synergize to bring about a particular property distribution on the stem cell population. | Pros: Multiple scales can be accommodated. Allow incorporation of GRNs with noise (stochastic PBEs). |
| Describing stem cell population heterogeneity. Linking adjustable bioprocess variables to desirable state vector distributions. |
Cons: Achieving numerical solutions is not trivial and computational complexity increases with the state vector dimensionality. | |
| Single-cell functions (especially agent-dependent) for differentiation, death and growth under different states (e.g. self-renewing or committed) are challenging to obtain. | ||
In addition to signaling networks, gene regulatory networks (GRNs) operating in stem cells have garnered increased attention. GRNs have been modeled in various contexts by implementing different approaches including ODEs, stochastic differential equations (SDEs), Boolean and Bayesian networks. Among the GRNs reported to influence stem cell fate decision, those involving the pluripotency transcription factors Nanog, Oct4 and Sox2 have been studied extensively. Chickramane et al. [25] described this GRN via an ODE system featuring several feedback loops. The loops give rise to a bistable (on/off) switch depending on environmental signals. When the GRN is ‘on’, self-renewal but not differentiation genes are expressed and vice versa. Interactions were included between this GRN and Cdx2 and GATA-6 to describe stem cell commitment to the trophectoderm (high Cdx-2 and GATA-6 levels) and endoderm lineages (high Oct4 and GATA-6 levels) [26].
Trott et al. [27] examined the expression of eight genes involved in embryonic stem cell pluripotency to create single-cell level GRNs. Heterogeneity was noted in the expression of these genes, particularly Nanog and Fgf5, a differentiated cell marker. Each of these genes is associated with specific regulatory subnetworks indicating that the co-emergence of Nanoghigh/Fgf5low, Nanoglow/Fgf5high and Nanoglow/Fgf5low cells is potentially due to variations in active transcription factors and access to the target DNA regions. These findings support the view of GRNs as pivotal players in determining distinct fate trajectories for individual stem cells within populations.
Frameworks linking self-renewal and differentiation states in stem cells can serve as platforms for devising efficient methods for either reprogramming differentiated cells to a stem cell state or guiding stem cells toward particular phenotypes. Bistable distributions and switches between states result not only from feedback loops but also from noisy processes as evidenced by SDE models of Nanog GRNs [28,29]. Construction of such models was motivated by the bimodal distribution reported for mESCs engineered to express the green fluorescent protein (GFP) from the Nanog locus [5].
Cell ensemble models
Most GRN or signal transduction models refer to single cells and their solution is generalized to the whole population assuming complete homogeneity and no cross-talk among cells. Integrating individual stem cell responses to the population scale may be achieved through cell ensemble modeling, originally applied to bacteria and yeast systems [30,31]. Single-cell models comprising ODE (or SDE) systems depicting cellular activities such as metabolism, intracellular signaling and gene expression are repeated for each cell in the ensemble. Coupling between single cells may be through common effectors such as extracellular growth factors or nutrients. Each equation set might differ in its initial conditions and/or parameters. All equations are solved concurrently advancing the population profile in the time domain. The model output can be contrasted against experimental data for the cell population. Glauche et al. [29] simulated the Sox2-Oct4-Nanog network operating in a stem cell based on an ODE for the Oct4-Sox2 complex and a SDE (both time-depended) for Nanog. This equation set was solved simultaneously for a virtual ensemble of 5,000 cells generating a temporal evolution of the population distribution of Nanog. Another study [32] describing the clonal evolution of 1,000 mESCs and their differentiated progeny was simulated by coupling model results to cell numbers and Oct4+ fractions. The differentiation status of each cell was examined at the end of cell cycle based on two criteria: The (probabilistically distributed) number of LIF signaling complexes compared to a self-renewal threshold, and the level of Oct4 expression compared to 50% of that of undifferentiated cells. Apoptosis was also considered as a possible outcome. Heterogeneity was introduced by randomly setting the initial condition for each cell and stochastically assigning LIF receptor numbers to newborn cells after division. Although the model considered stem cell fate decision dependent both on fast molecular activities such as Oct4 expression and over several cell-cycle times, LIF signaling was assumed to immediately achieve steady-state and remain constant until the next decision-making point. Though cell ensemble models are straightforward to set up and computationally efficient, incorporation of cellular-level activities and detailed GRNs is still lacking. Inclusion of stem cell differentiation, division and death, which happen in a timescale of hours to days, will increase the complexity of cell ensemble models but at the benefit of enhanced prediction potential.
Population balance equation models
Population balance equation (PBE) models are inherently multiscale and have been applied to diverse systems [33]. In cellular populations, these integro-differential equations link attributes (e.g. levels of DNA, RNA, particular proteins etc.) of the physiological state vector of individual cells to the population profile [34-36].
A PBE model was used to simulate mesenchymal stem cell differentiation [37]. The rate of differentiation was linked to the concentration of extracellular growth factors inducing commitment via Michaelis-Menten kinetics with the growth factor being the ‘substrate’. The cell PBE was coupled to growth factor material balances. Model parameters were obtained from studies unrelated to stem cells but this work illustrated that PBEs can be utilized for gaining a better understanding of the effects of single-cell commitment kinetics and the temporal profiles of differentiation agents on the overall population. Hoffmann et al. [38] also employed a PBE model of stem cell differentiation. The state vector comprised a single variable representing the differentiation status of promyelocytic precursor cells and conforming to a Langevin equation. This work showed that the dynamics of stem cell and progenitor populations can be effectively driven by state-specific noise but practical methods for modulating noise in stem cells are still elusive.
PBE models are also amenable to the embedding of GRNs operating in stem cells and their differentiated progeny. Although GRN models can reveal the dynamics of phenotype change for single stem cells exposed to particular signals, predictions at the cell population level are challenging due to the intrinsic heterogeneity of stem cell ensembles. The formulation of PBE models combined with GRN models may resolve this issue by linking stem cell GRNs to major cellular events such as division and lineage specification. We reported the development of a multi-scale stochastic PBE model for describing and predicting the Nanog expression dynamics in self-renewing hESCs [39]. In conjunction with experiments, the constructed model provided insights on how cell division and gene expression noise influence the distribution of the Nanog protein. PBE models integrating GRNs present challenges in large part due to the lack of suitable methods for accurate quantitative measurements of GRN activity in real-time. Yet, such multiscale frameworks hold great promise as tools for establishing more efficient differentiation methods. Moreover, PBE models have been used for defining control strategies for bioreactors [40] indicating their potential for the development and optimization of bioprocesses for the production of stem cell progeny for clinical use.
The adoption of PBE models has been limited mainly due to the difficulties associated with their numerical solution. The computational requirements increase concomitantly with the dimensionality of the state vector. Numerical procedures for solving PBEs are based on traditional finite discretization schemes [41,42], multi-level discretization [43] and MC methods of stochastic simulation algorithms [44-46] facilitated by the increasingly available computational power. PBE modeling of stem cells is also hindered by the lack of known single-cell functions for processes such as agent-dependent lineage commitment and division of self-renewing/differentiating cells. Flow cytometry can be used to measure the distributions of cell properties such as DNA and protein content or cell size but require highly specific antibodies and obtaining data with adequate time resolution is practically limited. This may be addressed with the development of sophisticated microfluidic platforms for real-time acquisition of multiparametric data at single-cell resolution from stem cell populations [47].
Conclusions
Quantitative models of stem cell populations offer advantages in the analysis and prediction of stem cell activities in complex systems. Various mathematical approaches have been employed –especially over the past decade– with each one providing distinct insights (as summarized in Table 1). Signal transduction and GRN models can assist with defining ranges of factor concentrations and duration of treatment promoting stem cell self-renewal or lineage-specific differentiation. Quantification of the impact of subcellular processes such as gene expression and signaling on the population level is afforded by multiscale ensemble and PBE models. As such, these models are ideal for driving the design, optimization and control of bioprocesses for the generation of clinically useful stem cell derivatives.
We expect that the development of computational frameworks will be accelerated as these become integral of future advances in the fields of stem cell biology and engineering. Obviously, efforts should also be directed toward interweaving stem cell models with state-of-the-art methods, which yield abundant information with increasing temporal resolution at the gene (genomics) and protein (proteomics) levels. The interconnected nature of possible fates requires the dynamic examination of functions of multiple stem cell genes and factors in the context of multi-lineage rather than single-lineage differentiation and models can help to address germane fundamental questions including: Which mechanisms ensure the transduction of signals and corresponding response(s) in stem cells with precision despite fluctuations in gene transcription and translation? What is the contribution of noise from different processes on the differentiation outcome? Can this noise be regulated to promote particular phenotype change dynamics? How the heterogeneity observed in stem cell populations modulate or possibly facilitate fate determination in different milieus? Despite significant challenges remaining in model development and implementation, multiscale modeling will play a pivotal role in moving from empirically developed differentiation methods to rationally and systematically designed high-efficiency strategies for the generation of stem cell therapeutics.
Highlights.
A summary is given of major modeling approaches for stem cell populations.
Relevant frameworks are broadly classified as stochastic, deterministic and hybrid.
Models have been reported for stem cell gene networks and signaling cascades.
Multiscale models are highly desirable for the analysis of stem cell populations.
Acknowledgements
Funding support has been provided by the National Institutes of Health (NHLBI, R01HL103709) and the New York Stem Cell Science Trust (NYSTEM, contract C024355) to EST. This work was performed in part at the University at Buffalo's Center for Computational Research.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Jincheng Wu, Graduate Student, 1015 Furnas Hall, Chemical and Biological Engineering, State University of New York at Buffalo, Buffalo, NY, 14260, USA
Mahboubeh Rahmati Rostami, Graduate Student, 1015 Furnas Hall, Chemical and Biological Engineering, State University of New York at Buffalo, Buffalo, NY, 14260, USA
Emmanuel S. Tzanakakis, Associate Professor, 907 Furnas Hall, Chemical and Biological Engineering, State University of New York, Buffalo, NY, 14260, USA
REFERENCES
- 1.Evans MJ, Kaufman MH. Establishment in culture of pluripotential cells from mouse embryos. Nature. 1981;292:154–156. doi: 10.1038/292154a0. [DOI] [PubMed] [Google Scholar]
- 2.Martin GR. Isolation of a pluripotent cell line from early mouse embryos cultured in medium conditioned by teratocarcinoma stem cells. Proc Natl Acad Sci U S A. 1981;78:7634–7638. doi: 10.1073/pnas.78.12.7634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Smith AG. Embryo-derived stem cells: of mice and men. Annu Rev Cell Dev Biol. 2001;17:435–462. doi: 10.1146/annurev.cellbio.17.1.435. [DOI] [PubMed] [Google Scholar]
- 4•.Chazaud C, Yamanaka Y, Pawson T, Rossant J. Early lineage segregation between epiblast and primitive endoderm in mouse blastocysts through the Grb2-MAPK pathway. Dev Cell. 2006;10:615–624. doi: 10.1016/j.devcel.2006.02.020. [An elegant study showing that the early inner cell mass is not homogeneous but exhibits a rather ‘salt and pepper’ pattern with respect to the expression of genes such as Nanog and Gata6.] [DOI] [PubMed] [Google Scholar]
- 5.Chambers I, Silva J, Colby D, Nichols J, Nijmeijer B, Robertson M, Vrana J, Jones K, Grotewold L, Smith A. Nanog safeguards pluripotency and mediates germline development. Nature. 2007;450:1230–1234. doi: 10.1038/nature06403. [DOI] [PubMed] [Google Scholar]
- 6•.Stewart MH, Bosse M, Chadwick K, Menendez P, Bendall SC, Bhatia M. Clonal isolation of hESCs reveals heterogeneity within the pluripotent stem cell compartment. Nat Methods. 2006;3:807–815. doi: 10.1038/nmeth939. [Based on the expression of stage-specific embryonic antigen-3 (SSEA-3), the authors show that subpopulations of (SSEA-3+ and SSEA-3-) cultured hESCs exist within colonies of undifferentiated hESCs. The SSEA-3+ and SSEA-3- hESCs exhibit distinct cell-cycle attributes, clonogenic capacity and expression of transcription factors.] [DOI] [PubMed] [Google Scholar]
- 7.Enver T, Soneji S, Joshi C, Brown J, Iborra F, Orntoft T, Thykjaer T, Maltby E, Smith K, Abu Dawud R, et al. Cellular differentiation hierarchies in normal and culture-adapted human embryonic stem cells. Hum Mol Genet. 2005;14:3129–3140. doi: 10.1093/hmg/ddi345. [DOI] [PubMed] [Google Scholar]
- 8.Toyooka Y, Shimosato D, Murakami K, Takahashi K, Niwa H. Identification and characterization of subpopulations in undifferentiated ES cell culture. Development. 2008;135:909–918. doi: 10.1242/dev.017400. [DOI] [PubMed] [Google Scholar]
- 9.Hayashi K, Lopes SM, Tang F, Surani MA. Dynamic equilibrium and heterogeneity of mouse pluripotent stem cells with distinct functional and epigenetic states. Cell Stem Cell. 2008;3:391–401. doi: 10.1016/j.stem.2008.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lee KL, Lim SK, Orlov YL, Yit le Y, Yang H, Ang LT, Poellinger L, Lim B. Graded Nodal/Activin signaling titrates conversion of quantitative phospho-Smad2 levels into qualitative embryonic stem cell fate decisions. PLoS Genet. 2011;7:e1002130. doi: 10.1371/journal.pgen.1002130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang L, Walker BL, Iannaccone S, Bhatt D, Kennedy PJ, Tse WT. Bistable switches control memory and plasticity in cellular differentiation. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:6638–6643. doi: 10.1073/pnas.0806137106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12••.Chang HH, Hemberg M, Barahona M, Ingber DE, Huang S. Transcriptome-wide noise controls lineage choice in mammalian progenitor cells. Nature. 2008;453:544–547. doi: 10.1038/nature06965. [Subpopulations of mouse hematopoietic progenitor cells with extremely low or high levels of Sca-1 exhibit distinct trancriptomes but reconstitute the Sca-1 distribution of parental cells after over a week in culture. This Sca-1 heterogeneity is not due to gene expression noise but reflects metastable states of a slowly fluctuating transcriptome.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13•.Sun Z, Komarova NL. Stochastic modeling of stem-cell dynamics with control. Math Biosci. 2012;240:231–240. doi: 10.1016/j.mbs.2012.08.004. [A view of stem cell proliferation and differentiation dynamics with different types of self-renewal regulation. The probability of differentiation is taken as fixed, or dependent on the total stem cell number as a linear, hyperbolic or Hill-type function. Unlike the constant and linear models, the nonlinear models resulted in robust behavior of stem cells especially for high Hill coefficients.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Till JE, McCulloch EA, Siminovitch L. A Stochastic Model of Stem Cell Proliferation, Based on the Growth of Spleen Colony-Forming Cells. Proc Natl Acad Sci U S A. 1964;51:29–36. doi: 10.1073/pnas.51.1.29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nakahata T, Ogawa M. Hemopoietic colony-forming cells in umbilical cord blood with extensive capability to generate mono- and multipotential hemopoietic progenitors. J Clin Invest. 1982;70:1324–1328. doi: 10.1172/JCI110734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ogawa M. Differentiation and proliferation of hematopoietic stem cells. Blood. 1993;81:2844–2853. [PubMed] [Google Scholar]
- 17•.Marr C, Strasser M, Schwarzfischer M, Schroeder T, Theis FJ. Multi-scale modeling of GMP differentiation based on single-cell genealogies. FEBS J. 2012;279:3488–3500. doi: 10.1111/j.1742-4658.2012.08664.x. [This is a good example of stochastic modeling of a GRN linked to the differentiation of granulocyte-monocyte progenitors (GMPs). The results were compared with single-cell time-lapse microscopy data. A GRN-based molecular toggle switch determined the adoption of a granulocyte or monocyte fate by GMPs, unlike a branching process model. Parameters, which were inferred via Bayesian methods, pointed to multiple timescales for GMP differentiation stemming from differing decay rates of the antagonistic transcription factors for granulocytic and monocytic differentiation.] [DOI] [PubMed] [Google Scholar]
- 18.Roeder I, Loeffler M. A novel dynamic model of hematopoietic stem cell organization based on the concept of within-tissue plasticity. Experimental Hematology. 2002;30:853–861. doi: 10.1016/s0301-472x(02)00832-9. [DOI] [PubMed] [Google Scholar]
- 19••.Glauche I, Cross M, Loeffler M, Roeder I. Lineage specification of hematopoietic stem cells: mathematical modeling and biological implications. Stem Cells. 2007;25:1791–1799. doi: 10.1634/stemcells.2007-0025. [A model is depicted incorporating intrinsic lineage specification dynamics for single stem cells transitioning stochastically between two signaling contexts. In comparison with experimental data, the authors simulate lineage contribution of single differentiating cells and within the progeny of two first-generation daughter cells. The results demonstrate a correlation between stem cell self-renewal and lineage specification.] [DOI] [PubMed] [Google Scholar]
- 20.Fischer M, Goldschmitt J, Peschel C, Brakenhoff JP, Kallen KJ, Wollmer A, Grotzinger J, Rose-John S. I. A bioactive designer cytokine for human hematopoietic progenitor cell expansion. Nat Biotechnol. 1997;15:142–145. doi: 10.1038/nbt0297-142. [DOI] [PubMed] [Google Scholar]
- 21.Viswanathan S, Benatar T, Rose-John S, Lauffenburger DA, Zandstra PW. Ligand/receptor signaling threshold (LIST) model accounts for gp130-mediated embryonic stem cell self-renewal responses to LIF and HIL-6. Stem Cells. 2002;20:119–138. doi: 10.1634/stemcells.20-2-119. [DOI] [PubMed] [Google Scholar]
- 22.Mahdavi A, Davey RE, Bhola P, Yin T, Zandstra PW. Sensitivity analysis of intracellular signaling pathway kinetics predicts targets for stem cell fate control. Plos Computational Biology. 2007;3:1257–1267. doi: 10.1371/journal.pcbi.0030130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Aldridge BB, Burke JM, Lauffenburger DA, Sorger PK. Physicochemical modelling of cell signalling pathways. Nature Cell Biology. 2006;8:1195–1203. doi: 10.1038/ncb1497. [DOI] [PubMed] [Google Scholar]
- 24.Klipp E, Liebermeister W, Wierling C, Kowald A, Lehrach H, Herwig R. Systems Biology. Wiley-VCH; 2009. [Google Scholar]
- 25.Chickarmane V, Troein C, Nuber UA, Sauro HM, Peterson C. Transcriptional dynamics of the embryonic stem cell switch. Plos Computational Biology. 2006;2:e123. doi: 10.1371/journal.pcbi.0020123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26•.Chickarmane V, Peterson C. A computational model for understanding stem cell, trophectoderm and endoderm lineage determination. PLoS One. 2008;3:e3478. doi: 10.1371/journal.pone.0003478. [An ODE system was constructed based on ChIP-on-chip and microarray data to simulate a GRN involving the pluripotency factors Sox2, Oct4 and Nanog, and the differentiation genes Gata6, Cdx2 and Gcnf. The model links gene expression dynamics to differentiation decisions for adopting pertinent fates.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27•.Trott J, Hayashi K, Surani A, Babu MM, Martinez-Arias A. Dissecting ensemble networks in ES cell populations reveals micro-heterogeneity underlying pluripotency. Mol Biosyst. 2012;8:744–752. doi: 10.1039/c1mb05398a. [The authors observed the presence of Nanoghigh/Fgf5low, Nanoglow/Fgf5high and Nanoglow/Fgf5low mouse embryonic stem cells (mESCs) in the same population of 83 cells. Expression of each gene was linked to a particular ‘co-expression network’. The emergence of mESC subpopulations was attributed to the differential activity of these subnetworks. The findings underline the role of the distinct transcriptional state of each ESC within an ensemble and highlight the importance of single cell analysis and GRNs when studying stem cell systems.] [DOI] [PubMed] [Google Scholar]
- 28.Kalmar T, Lim C, Hayward P, Munoz-Descalzo S, Nichols J, Garcia-Ojalvo J, Martinez Arias A. Regulated fluctuations in nanog expression mediate cell fate decisions in embryonic stem cells. Plos Biology. 2009;7:e1000149. doi: 10.1371/journal.pbio.1000149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Glauche I, Herberg M, Roeder I. Nanog variability and pluripotency regulation of embryonic stem cells--insights from a mathematical model analysis. PLoS ONE. 2010;5:e11238. doi: 10.1371/journal.pone.0011238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dano S, Hynne F, De Monte S, d'Ovidio F, Sorensen PG, Westerhoff H. Synchronization of glycolytic oscillations in a yeast cell population. Faraday Discussions. 2001;120:261–276. doi: 10.1039/b103238k. [DOI] [PubMed] [Google Scholar]
- 31.Henson MA, Muller D, Reuss M. Cell population modelling of yeast glycolytic oscillations. Biochemical Journal. 2002;368:433–446. doi: 10.1042/BJ20021051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Viswanathan S, Davey RE, Cheng D, Raghu RC, Lauffenburger DA, Zandstra PW. Clonal evolution of stem and differentiated cells can be predicted by integrating cell-intrinsic and -extrinsic parameters. Biotechnol Appl Biochem. 2005;42:119–131. doi: 10.1042/BA20040207. [DOI] [PubMed] [Google Scholar]
- 33.Ramkrishna D. Population Balances: Theory and Applications to Particulate Systems in Engineering. Academic Press; 2000. [Google Scholar]
- 34.Eakman JM, Fredrickson AG, Tsuchiya HH. Statistics and dynamics of microbial cell populations. Chem. Eng. Prog. Symp. Ser. 1966;62:37–49. [Google Scholar]
- 35.Fredrickson AG, Ramkrishna D, Tsuchiya HM. Statistics and dynamics of procaryotic cell populations. Mathematical Biosciences. 1967;1:327–374. [Google Scholar]
- 36.Nielsen LK, Bender JG, Miller WM, Papoutsakis ET. Population balance model of in vivo neutrophil formation following bone marrow rescue therapy. Cytotechnology. 1998;28:157–162. doi: 10.1023/A:1008098118491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pisu M, Concas A, Cao G. A novel simulation model for stem cells differentiation. Journal of Biotechnology. 2007;130:171–182. doi: 10.1016/j.jbiotec.2007.02.028. [DOI] [PubMed] [Google Scholar]
- 38••.Hoffmann M, Chang HH, Huang S, Ingber DE, Loeffler M, Galle J. Noise-driven stem cell and progenitor population dynamics. PLoS One. 2008;3:e2922. doi: 10.1371/journal.pone.0002922. [Excellent article based on PBE formalism to describe stem cell and progenitor population dynamics as a probabilistic process arising from cell proliferation and fluctuations in the state of differentiation (modeled by a Langevin equation). Model results concur with experimental data on cultures of promyelocytic precursor cells.] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wu J, Tzanakakis ES. Contribution of Stochastic Partitioning at Human Embryonic Stem Cell Division to NANOG Heterogeneity. PLoS One. 2012;7:e50715. doi: 10.1371/journal.pone.0050715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mantzaris NV, Daoutidis P. Cell population balance modeling and control in continuous bioreactors. Journal of Process Control. 2004;14:775–784. [Google Scholar]
- 41.Mantzaris NV, Daoutidis P, Srienc F. Numerical solution of multi-variable cell population balance models: I. Finite difference methods. Computers & Chemical Engineering. 2001;25:1411–1440. [Google Scholar]
- 42.Mantzaris NV, Daoutidis P, Srienc F. Numerical solution of multi-variable cell population balance models. III. Finite element methods. Computers & Chemical Engineering. 2001;25:1463–1481. [Google Scholar]
- 43.Pinto MA, Immanuel CD, Doyle FJ. A feasible solution technique for higher-dimensional population balance models. Computers & Chemical Engineering. 2007;31:1242–1256. [Google Scholar]
- 44.Gillespie DT. General Method for Numerically Simulating Stochastic Time Evolution of Coupled Chemical-Reactions. Journal of Computational Physics. 1976;22:403–434. [Google Scholar]
- 45.Gillespie DT. Approximate accelerated stochastic simulation of chemically reacting systems. Journal of Chemical Physics. 2001;115:1716–1733. [Google Scholar]
- 46.Salis H, Kaznessis Y. Accurate hybrid stochastic simulation of a system of coupled chemical or biochemical reactions. Journal of Chemical Physics. 2005;122 doi: 10.1063/1.1835951. [DOI] [PubMed] [Google Scholar]
- 47••.Ranga A, Lutolf MP. High-throughput approaches for the analysis of extrinsic regulators of stem cell fate. Curr Opin Cell Biol. 2012;24:236–244. doi: 10.1016/j.ceb.2012.01.006. [A thorough review of new technologies for probing stem cell niche signaling in a high-throughput fashion. Both 2D and 3D systems such as cellular microarrays, microfluidics and dynamically tunable biomaterials are discussed along with pertinent experimental designs and systems biology analysis of resulting data.] [DOI] [PubMed] [Google Scholar]