Super resolution for common probes and common microscopes

Abstract

A sophisticated analysis approach based on the concept of fluorophore localization provides dynamic super-resolution data of GFP-labeled live cells using a common, arc lamp–based wide-field fluorescence microscope.

One class of methods for achieving fluorescence super-resolution is based around finding the positions of fluorescent molecules that label the cellular structure of interest^1–3. In this approach, positions can be determined precisely and accurately using fluorescent probes that can be photoactivated, photoconverted or photoswitched to generate single images with emitter densities of only about one active fluorophore per diffraction-limited area. Many images—each containing stochastic subsets of active fluorophores—are collected and analyzed to attain the spatial sampling required for a super-resolution image. One drawback of this approach is that the active density of fluorophores in each frame must be kept low, forcing long imaging times and requiring the use of probes that can be manipulated to a low single-frame density. Now Cox et al.⁴ describe a new approach to modeling such datasets using a Bayesian analysis that can work with fluorophore densities as high as those found when using conventional labeling and imaging.

In their analysis, called Bayesian blinking and bleaching (3B) analysis, they model the entire time series as a set of blinking and bleaching fluorophores; the analysis is weakly constrained by prior information about the blinking and bleaching characteristics of the fluorophore, which can be estimated from separate experiments. The result is that a few seconds of data collection using a typical lamp-based wide-field fluorescence microscope can yield an image with resolution approaching 50 nanometers.

Recently, several methods have been described to analyze images containing multiple emitters in a diffraction-limited area by fitting with multiple fluorophore models^5–7. The aim of these approaches is to find the single best estimates of fluorophore positions (point estimates). But as the density of emitters becomes high, these approaches fail because many different models of fluorophore location, parameterized with different numbers of fluorophores and intensities, may fit the data almost equally as well.

In another recently described approach⁸, the difference images of subsequent frames are used to identify bleaching and blinking events and to localize fluorophores. When conventional fluorophores are used, however, many fluorophores may need to be bleached to improve the signal-to-background ratio to an acceptable value.

In the 3B approach, the entire time series is globally analyzed, and a fluorophore location probability map is generated by making a weighted average over all possible models; the set of models includes varying numbers of emitters, emitter locations and fluorophore temporal dynamics. The probability map calculation takes into account the prior information about the blinking and bleaching of the fluorophore as well as how well the models fit the data.

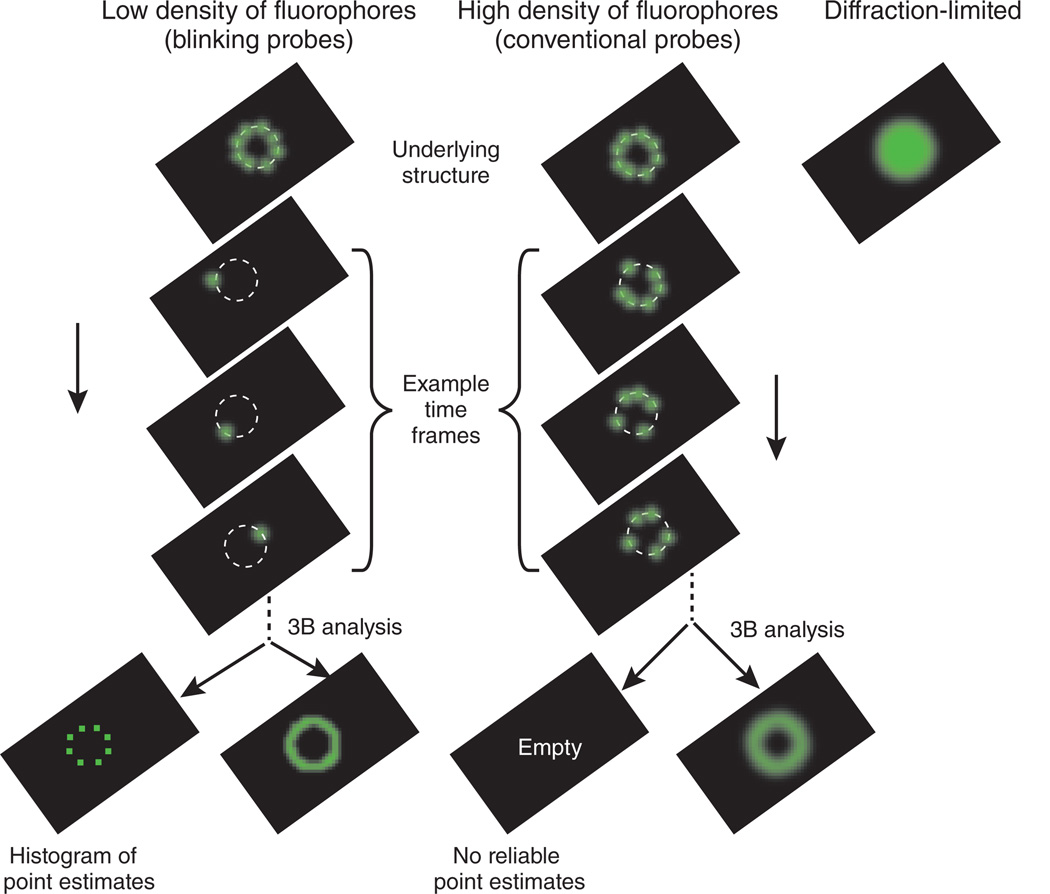
As illustrated in Figure 1, for data with a low density of fluorophores, the 3B analysis is similar to the point-estimate analysis. However, the 3B analysis averages over the possible bleaching and blinking models to give a spatial probability of fluorophore locations. In the case of high-density fluorophores, the point estimate fails because many models with different numbers of fluorophores or different fluorophores locations may fit the data nearly equally well (Fig. 1). Here is where the 3B analysis comes into its own. In the 3B approach, an average of all models is taken, so that the ambiguity in the models simply results in a more distributed range of possible fluorophore locations and shows up in the probability maps as what appears to be a region with worse resolution. Longer imaging times allow for better location estimates, so that imaging time can be traded for spatial resolution.

Figure 1.

The 3B analysis extends single-molecule super-resolution analysis to the high fluorophore densities found when using conventional fluorophores such as GFP.

The 3B analysis provides exciting new possibilities for super-resolution imaging with simple optical setups and probes that are neither photoactivatable nor photoswitchable, but there are a few caveats. The images generated with the 3B analysis must be interpreted with care. Fluorescence microscopy images taken from confocal and wide-field setups are understood by the viewer as an underlying structure that is blurred out homogeneously with the microscope point-spread function. This intuition cannot be directly applied to interpreting the 3B probability maps. Structure in the probability map indicates both sample structure and the ambiguity in the modeling of the data. Some structures, such as thin, linear structures may have anisotropic ambiguity, with the result that the effective resolution across the probability map image can be heterogeneous. The 3B approach shifts the complexity of super-resolution from the optical setup onto the postprocessing analysis. Adequately sampling from the set of all possible models is a demanding computational task, and analyzing datasets requires several hours per square micrometer of data analyzed, although the conventional images are immediately available.

Despite a few minor caveats, the ability to achieve super-resolution images of dynamic structures in living cells with simple optical setups makes the 3B method a powerful new tool for cellular imaging.