Transducer and base compliance alter the in situ 6 dof force measured from muscle during an isometric contraction in a multi-joint limb

Abstract

Although musculoskeletal models are commonly used, validating the muscle actions predicted by such models is often difficult. In situ isometric measurements are a possible solution. The base of the skeleton is immobilized and the endpoint of the limb is rigidly attached to a 6-axis force transducer. Individual muscles are stimulated and the resulting forces and moments recorded. Such analyses generally assume idealized conditions. In this study we have developed an analysis taking into account the compliances due to imperfect fixation of the skeleton, imperfect attachment of the force transducer, and extra degrees of freedom (dof) in the joints that sometimes become necessary in fixed end contractions. We use simulations of the rat hindlimb to illustrate the consequences of such compliances. We show that when the limb is overconstrained, i.e. when there are fewer dof within the limb than are restrained by the skeletal fixation, the compliances of the skeletal fixation and of the transducer attachment can significantly affect measured forces and moments. When the limb dofs and restrained dofs are matched, however, the measured forces and moments are independent of these compliances. We also show that this framework can be used to model limb dofs, so that rather than simply omitting dofs in which a limb does not move (e.g. abduction at the knee), the limited motion of the limb in these dofs can be more realistically modeled as a very low compliance. Finally, we discuss the practical implications of these results to experimental measurements of muscle actions.

INTRODUCTION

Understanding muscle actions is critical to understanding biological motor control. One common way of characterizing muscle action is to measure forces and moments produced on the limb. In such experiments, the limb is rigidly attached to a force transducer. The muscle is then stimulated directly or, in cadaveric studies, the proximal tendon loaded. The measured forces, and sometimes, moments are then used to characterize muscle action, as has been done in frogs (Loeb et al. 2000), cats (Lawrence and Nichols 1999; Lawrence et al. 1993), and human digits (Lee et al. 2008; Pearlman et al. 2004; Towles et al. 2004; Valero-Cuevas et al. 2000).

We performed this type of experiment in the rat hindlimb (Yeo et al. 2011). We immobilized the pelvis and attached the limb to a 6-axis force transducer. Individual muscles were stimulated and the resulting forces and moments recorded to characterize muscle actions. In these experiments a simple model suggested the limb was overconstrained: the transducer restricted movement in 6 dofs while the limb could move in 5 dofs. However, we found that even in this situation standard biomechanical analyses could explain the data well. The fit between experiment and model improved further when one dof at the transducer was released.

In this study we examine these issues further, clarifying how muscle actions can be characterized experimentally. We develop analyses incorporating common experimental conditions including imperfect skeletal fixation, non-trivial compliances in the force transducer attachment, and additional joint dofs, and show how these conditions affect measurements.

METHODS

Analysis of force transmission by individual muscles

We assume bones are rigid bodies and are linked by idealized joints where the input for each dof uniquely determines limb position (Delp and Loan 1995; Winter 1984). See Murray et al. (1994) for a comprehensive robotic treatment and see Valero-Cuevas et al. (2009) for a discussion of idealized joints.

Following common usage we define “endpoint” as a reference frame on the distal bone at which a force/torque transducer is attached, and we will abbreviate its position and orientation as “position.” Endpoint position, X, has 3 translational (x, y, z) and 3 rotational (rx, ry, rz) dimensions. Hence the dimension of the generalized forces is n ≤ 6 (see below). Generalized force is also commonly referred to as wrench (Firmani et al. 2008). Leg configuration is described by m generalized angles, θ (mx1). At a given configuration θ, changes in endpoint position and joint angles can be related by the Jacobian matrix (nxm)

$$\text{d}\mathbf{X}=\mathbf{J}\text{d}\mathbf{\theta }.$$ (1)

Jacobians also translate between endpoint force, F and joint torques, τ (mx1):

$$\mathbf{\tau }={\mathbf{J}}^{\text{T}}\mathbf{F}.$$ (2)

In this manuscript if any dof in F is always zero, either because it is not restrained by the transducer or because the limb cannot move in this direction, then this dof is removed from F and X and the corresponding row of J eliminated. Hence F and X are nx1, where n is 6 or less.

Analyses of muscle actions generally assume perfect skeletal fixation, rigid force transducer attachment, and rigid skeleton and joints. Such assumptions, however, are never practically achieved as there is always some internal skeletal flexibility and compliance in transducers. Moreover, even the number of limb dofs is an idealization: a dof in which a limb cannot move might be described with very small compliance. The importance of these issues has previously been recognized in robotics (Pai and Leu 1991). These considerations suggest that our analysis should incorporate the role of compliances.

We first consider compliances due to passive structures. These include compliances of ligaments, fascia, and other soft tissues. Passive muscle force can be included here or with the muscle torque term introduced later (Eq. 6). Extra joint dofs, those not needed during movement but necessary in isometric contractions, are added with corresponding stiffnesses in S_p. The compliance of the imperfectly immobilized skeletal base is also included here (see below). We assume that these elastic properties are linear for small limb movements and can be represented by the diagonal stiffness matrix, S_p. Assuming no resting torque, the torque due to compliances is related to joint movement by:

$${\mathbf{\tau }}_{\text{passive}}=-{\mathbf{S}}_{\text{p}}\text{d}\mathbf{\theta }$$ (3)

In order to consider base compliance, we can add dofs at the limb origin with corresponding stiffnesses, allowing base movement in response to muscle torques. Perfect base fixation occurs when these stiffnesses are infinite. Note that including these dofs increases the number of joint dofs and hence size of the Jacobian and S_p.

The other source of compliance is the attachment between the limb and force transducer. This includes transducer properties and properties of the skeletal coupling. If we assume that these stiffnesses can be described as linear springs, and they are not stretched at the starting position, then they can be represented with diagonal stiffness matrix S_t, where:

$$\mathbf{F}=-{\mathbf{S}}_{\text{t}}\text{d}\mathbf{X}$$ (4)

These endpoint forces can be translated to joint torques according to equation (4):

$${\mathbf{\tau }}_{\text{transducer}}={\mathbf{J}}^{\text{T}}\mathbf{F}$$ (5)

Muscle contraction produces torques, τ_muscle, around the joints it spans (Delp and Loan 1995). Muscle force can be related to joint torques using the muscle Jacobian, giving how small changes in muscle length are related to small changes in joint angles.

Because of the base and transducer compliances, muscle contraction will cause small skeletal movement (dθ_b). This movement will continue until the muscle torques are equal and opposite to torques generated by the compliances. Once the limb has reached this equilibrium, the net torque must be 0:

$${\mathbf{\tau }}_{\text{muscle}}+{\mathbf{\tau }}_{\text{passive}}+{\mathbf{\tau }}_{\text{transducer}}=0$$ (6)

Provided movements are small, the Jacobian and muscle torque remain constant. Substituting (3) and (5) into (6) gives:

$${\mathbf{\tau }}_{\text{muscle}}-{\mathbf{S}}_{\text{p}}\text{d}{\mathbf{\theta }}_{\text{b}}-{\mathbf{J}}^{\text{T}}{\mathbf{S}}_{\text{t}}\mathbf{J}\text{d}{\mathbf{\theta }}_{\text{b}}=0$$ (7)

Solving for dθ_b:

$$\text{d}{\mathbf{\theta }}_{\text{b}}={({\mathbf{J}}^{\text{T}}{\mathbf{S}}_{\text{t}}\mathbf{J}+{\mathbf{S}}_{\text{p}})}^{-1}{\mathbf{\tau }}_{\text{muscle}}$$ (8)

This is the joint angle displacement necessary to achieve equilibrium between the muscle torques and torques due to compliances. Once dθ_b is known, the endpoint force measured by the transducer can be calculated:

$$\mathbf{F}=-{\mathbf{S}}_{\text{t}}\mathbf{J}\text{d}{\mathbf{\theta }}_{\text{b}}$$ (9)

Substituting in the expression of dθ_b from (8):

$$\mathbf{F}=-{\mathbf{S}}_{\text{t}}\mathbf{J}{({\mathbf{J}}^{\text{T}}{\mathbf{S}}_{\text{t}}\mathbf{J}+{\mathbf{S}}_{\text{p}})}^{-1}{\mathbf{\tau }}_{\text{muscle}}$$ (10)

Equation 10 gives the measured endpoint force during a muscle contraction when transducer, base, and passive joint compliances are accounted for. Importantly, in this derivation there is no redundancy in solving for the measured endpoint forces since the matrix expression within parentheses in Equation 10 is square, even if the Jacobian is not square or full rank. The passive stiffnesses in S_t and S_p resolve these redundancies, giving a unique solution.

This well-posed solution is in contrast to analyses which do not account for compliances. In those analyses, Equation 2 is used to find endpoint forces due to the muscle torques:

$$\mathbf{F}={({\text{J}}^{\text{T}})}^{-1}{\mathbf{\tau }}_{\text{muscle}}$$ (11)

However, this inverse is only well defined when J^T is full rank and invertible. If multiple solutions are possible the Moore-Penrose pseudoinverse finds the solution with the minimum distance from the origin, but this pseudoinverse is a mathematical convenience and is not necessarily mechanically correct. The derivation above (Eq. 10), by incorporating compliances, captures the experimental situation in which muscle actions are measured.

Simulation based on the rat hindlimb

To illustrate the role of compliances in measuring muscle actions, we develop a rat hindlimb simulation based on our previous work (Yeo et al. 2011). We simulate the actions of gracilis posticus (GP) at a single leg configuration (Figure 1). Other positions and muscles were studied with qualitatively similar results.

Figure 1.

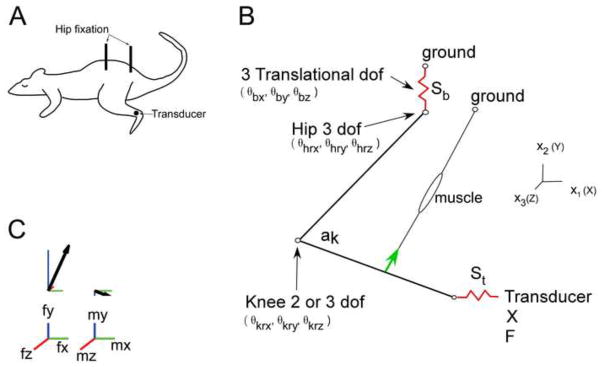
Schematic representation of the rat hindlimb. Part A) Rat experimental preparation. Metal posts are screwed and glued into the pelvis and connected to ground providing a very stiff fixation (S_b). A 6 dof transducer is screwed and glued into the distal end of the tibia and connected to ground. The compliance of the fixation and the compliance of the transducer is modeled as S_t. The attachment is designed so one dof can be released (rotation around z). Part B) Depicts the position of the left leg, the gracilis posticus (GP) muscle, and the joints angles. The base compliance acts in three translational directions between the hip and ground. The transducer compliance acts in 3 translational and 3 rotational directions between the ankle and the force transducer. The coordinate system is defined such that when all joint angles are zero the leg is assumed to extend behind the rat, with both the femur and tibia lying along the x-axis. Tibial movement relative to the femur is described by three angles: θ_krx, θ_kry, and θ_krz, and are applied by rotation around x, then y, and then z axes. Femur movement relative to the hip is described by three angles θ_hrx, θ_hry, and θ_hrz which are also applied by rotation around x, y, and then z axes. All simulation results shown here use the same joint angles: (θ_hrx=0, θ_hry=0, θ_hrx=− 110, θ_krx=0, θ_kry=0 (if used), θ_krz=105 degrees). We used segment lengths of 31mm for the femur and 41mm for the tibia. The origin and insertion of GP was taken from Johnson et al, (2008), with origin on the hip (world coordinates, x=.01267, y=−.010403, z=−.00478m) and an insertion on the tibia (tibia coordinates of x=.0156, y=−.00452, and z=−.00378m). Peak muscle force was 2.3 N (Yeo et al. 2011). Part C) Example of how the generalized 6 dof force at the ankle is displayed. The 3 dimensional force vector is plotted separately from the 3 dimensional moment vector. The projection of the vector on the x, y, and z axis is shown in green, blue, and red respectively.

In most analyses we considered the hindlimb to have 5 dofs. The hip was modeled as a ball and socket joint (3 rotational dofs). The knee was modeled as a universal joint with dofs in flexion/extension and external/internal rotation. Both joints had a fixed center of rotation. The omitted dof was knee movement in adduction/abduction for which the limb has minimal motion. In one analysis we attempted to model this restriction as a high stiffness. In that case we considered the limb to have 6 degrees of freedom (ball joint at hip and knee) but included a high stiffness along the abduction/adduction dof in the S_p matrix.

Base compliance was modeled by adding three translational movements at the hip and associated compliances (Figure 1). Thus, when base compliance was considered, the hip had an additional 3 dof increasing the size of τ, J, and S_p in equations 6–10.

In all simulations, we only allowed cases with endpoint movement less than 0.1% of leg length and angle movement less than 0.01 radians. This condition guaranteed that the simulations did not produce unrealistic movements and that our assumption of a constant Jacobian was appropriate.

RESULTS

Equation 10 describes the general relationship between endpoint generalized forces and internal joint torques when accounting for compliances. To illustrate the potential consequences of these compliances, we describe the results of special cases derived from this general relationship.

Perfect skeletal fixation, vary compliance at the force transducer attachment

In this case we include only compliance at the force transducer attachment (i.e. perfect skeletal fixation), and so Equation 10 becomes:

$$\mathbf{F}=-{\mathbf{S}}_{\text{t}}\mathbf{J}{({\mathbf{J}}^{\text{T}}{\mathbf{S}}_{\text{t}}\mathbf{J})}^{-1}{\mathbf{\tau }}_{\text{muscle}}$$ (12)

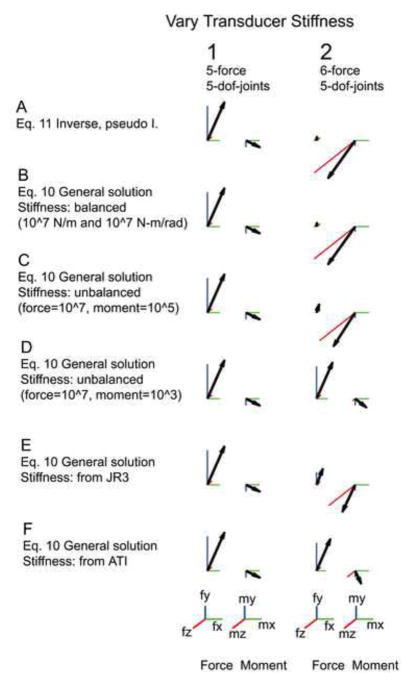
In the second column of Figure 2, we show the effects of varying the attachment compliance when all 6 endpoint dofs are constrained and there are 5 dofs within the limb. When the moment stiffness is small (row D), the transducer attachment acts as a ball joint, allowing rotation but not translation and therefore only small moments are measured at the transducer. With increased rotational stiffness (row B), the moments measured by the transducer become larger. Essentially, as the stiffnesses along particular dofs are increased, they become more important in restraining movement of the limb and therefore measure larger signals. Note also that because of the different units along translational and rotational dofs, it is difficult to determine ‘equivalent’ stiffnesses across all dofs (Murray et al. 1994). Figure 2 E and F shows the generalized force varies even when considering realistic compliances from commercial transducers. In conclusion, varying the attachment compliance significantly altered the measured forces and moments in this overconstrained case.

Figure 2.

Transducer compliance alters the measured forces and moments in the overconstrained condition. In this figure there is no compliance at the base and no passive joint stiffness (S_p=0). The leg and muscle configuration is defined in Fig 1 and is identical in all 12 generalized forces depicted. The scale bar for force is 0.3 N in all directions and for moments 0.01 N-m in all directions. Column 1 shows the released z axis (5-force) condition. Column 2 shows the overconstrained (6-force) condition. Row A shows force computed with a simple inverse (Eq. 11) or pseudo inverse (Eq. 15). Rows B to F show force computed with the derived Eq. 10. Row B shows a balanced compliance (all diagonal terms of the matrix S_t are equal). The forces in this row are identical to row A. Rows C and D show the forces resulting from decreased stiffness of the moments, 0.01 and 0.0001 respectively. Rows E and F show forces resulting from attachment to a JR3 transducer respectively. The last two rows were included to show that even if the fixation of the limb is perfect, actual transducer stiffness will affect the measured force. We did not measure the compliance of the attachment to the transducer. ( JR3, Model 67M25A, 22 Harter Ave, Woodland CA 95776, S_t diagonal [0.519, 0.519, 5.279 N/m, 0.0054, 0.0054, 0.0015 N-m/rad]; ATI mini 40, ATI Industrial Automation, Pinnacle Park, 1031 Goodworth Drive; Apex, NC 27539, S_t diagonal [11, 11, 20*10⁶ Nm, 2.8, 2.8, 4.0*10³ N-m/rad])

We also considered the effects of varying attachment compliance when one endpoint dof (rotation along the mediolateral axis, (Yeo et al. 2011) is released. In this situation, the dofs in the limb are matched with the dofs restrained by the transducer attachment. Considering Equation 12, in this case J is square and S_t is diagonal and therefore both are invertible. We can therefore evaluate the inverse of the terms within the parentheses by finding the inverse of each separate term:

$$\mathbf{F}=-{\mathbf{S}}_{\text{t}}\mathbf{J}({\mathbf{J}}^{-1}{{\mathbf{S}}_{\text{t}}}^{-1}{\mathbf{J}}^{-\text{T}}){\mathbf{\tau }}_{\text{muscle}}$$ (13)

which gives:

$$\mathbf{F}=-({\mathbf{J}}^{-\text{T}}){\mathbf{\tau }}_{\text{muscle}.}$$ (14)

Thus, when the number of limb dofs are matched to the number of constrained dofs, the transducer attachment compliance has no effect. As indicated by Equation 14, we can apply standard techniques of translating between forces/moments and torques using Jacobians.

Figure 2, column 1 confirms this analysis, showing that endpoint forces and moments are not affected by transducer compliance. Note that the forces and moments measured in this case can differ from those measured when the limb was overconstrained (Figure 2, column 2). However, there are some ranges of attachment compliances for which the two sets of forces and moments were very similar, particularly when the rotational stiffnesses at the attachment were less than translation stiffness (Figure 2D, F).

Finally, consider the overconstrained case with isotropic attachment compliances (S_t with all equal diagonal terms). In this case, we can factor out S_t in Equation 13:

$$\mathbf{F}=-\mathbf{J}{({\mathbf{J}}^{\text{T}}\mathbf{J})}^{-1}{\mathbf{\tau }}_{\text{muscle}}$$ (15)

This equation is the Moore-Penrose pseudoinverse. This pseudoinverse is therefore mechanically appropriate when the skeleton is perfectly fixed and the transducer attachment compliance is isotropic. Comparison of the forces and moments using this pseudoinverse (Figure 2A, column 2) to those in Figure 2B, column 2 in which a transducer attachment with an isotropic compliance is simulated confirms this result. When the Moore-Penrose solution is used without consideration of the transducer compliances, this is tantamount to arbitrarily selecting one of many solutions to equations 2.

Effect of varying the compliance of the skeletal fixation

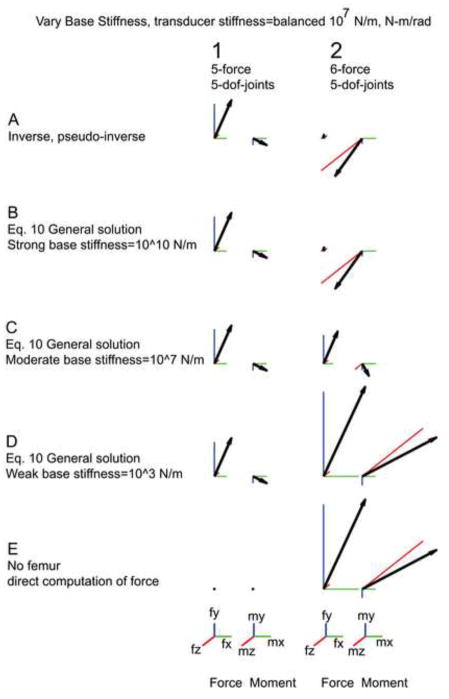
We next considered the effect of introducing compliance at the base of the skeleton in addition to including the transducer attachment compliance (see description surrounding Eq. 3). In our simulation, this compliance corresponds to imperfect hip fixation. In the rat hindlimb example the imperfectly fixated pelvis acts like a spring and is modeled as 3 translational compliances. Rotational compliances are redundant due to the hip ball joint (see Figure 1).

Varying the base stiffness caused the forces and moments to vary considerably when the limb was overconstrained. When the base stiffness was high (Figure 3B, column 2), the measured forces were similar to those calculated using the Moore-Penrose pseudoinverse, consistent with the previous results assuming infinite base stiffness. When the base stiffness was reduced, however, the endpoint forces and moments were significantly altered (Figure 3B, C, D, column 2). Consider the case where the base compliance is much less than the attachment compliance (Figure 3D, column 2). In the rat hindlimb, this means that the muscle contraction will mainly cause hip movement, with much less tibia movement since the tibia is secured by the transducer. This hip movement is accomplished by knee rotation and the femur consequently becomes irrelevant for force transmission as confirmed in simulations in which the femur was completely removed (Figure 3D, column 2).

Figure 3.

Base compliance alters the measured force in the over constrained case. The scale bar for force is 0.3 N in all directions and for moments 0.01 N-m in all directions. A balanced transducer compliance is used throughout this figure (diagonal terms of S_t are 10⁷). Column 1 shows generalized forces measured with matched force constraints and joint dofs. Column 2 shows forces from the overconstrained case. Row A shows results from the inverse and pseudoinverse. This is identical to Row A in Fig. 2. Row B depicts forces using a high base stiffness. As the base becomes less stiff larger force and torques are measured. See B, C, and D. Row E shows the force and moment calculated with the femur removed, that is, the tibia is assumed to be attached to the force transducer but there is no reaction force from the femur at the knee. Force from the muscle is pulling directly on the tibia. Note that column 2, D and E, are identical—if the base becomes compliant enough the tibia is completely constrained by the force transducer—no force is transmitted through the femur.

We also simulated the effects of varying base stiffness when the number of dofs were matched. As seen in Figure 3, column 1, in this situation variations of base stiffness did not alter the measured endpoint forces and moments.

Modeling dofs as joint stiffnesses

In each of the above simulations, we assumed that there were 5 dofs in the leg. However, in reality the rat knee can move slightly in the omitted abduction/adduction direction. We examined whether we could simulate this omitted dof by considering the knee to have 3 dofs (a ball joint) but with a very high stiffness along abduction/adduction. This simulation allows some movement in dofs which are usually simply omitted from analyses. Note, however, that introducing this dof potentially creates a redundant limb, since femur rotation has no effect on the tibia in this situation: although the Jacobian is apparently square (6 dofs at the endpoint, 6 dofs within the limb), it is actually only rank 5 because of this redundancy. As discussed above, Eq. 10 is only solvable by including passive joint stiffness. Fig 4A shows that with isotropic transducer compliance (Fig 4A) the results are identical to previous simulations (Fig 2B column 2) in which the abduction/adduction dof was simply omitted. In particular, note that the measured forces are altered when either transducer (Figure 4B) or base (Figure 4C) compliances are altered. Thus, the analysis developed in this study provides a natural description of biological joints, considering omitted dofs around joints to be simply directions of movement with a high stiffness.

Figure 4.

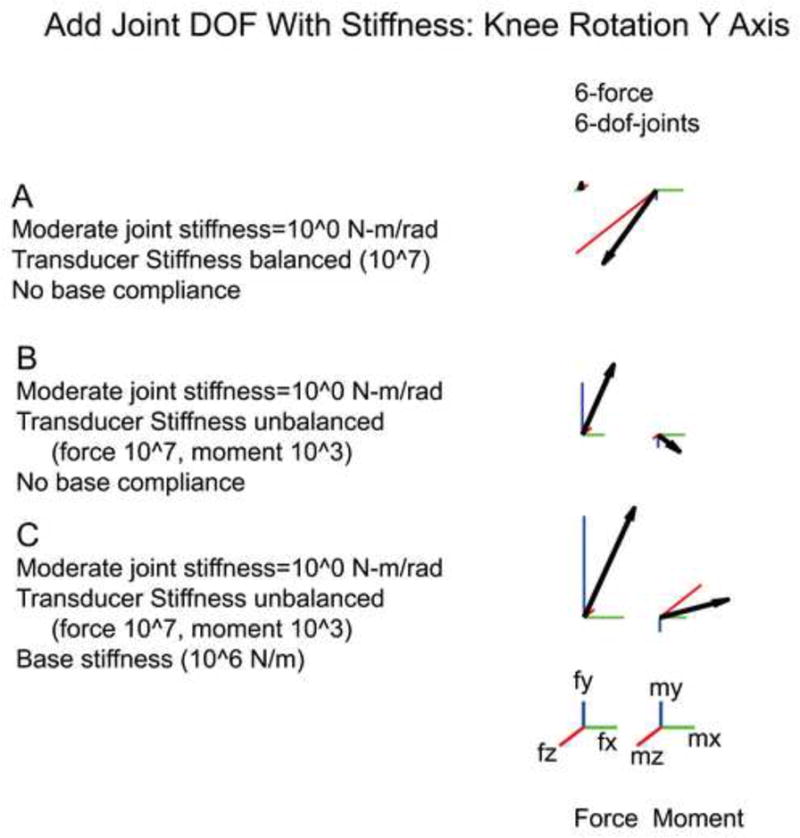
Added joint dofs with accompanying passive stiffness. Knee abduction/adduction (θ_kry) is added to the knee joint. Eq. 10 is solvable provided a passive stiffness (here, 1 N-m/rad) is added to S_p around θ_kry. Generalized force is once again dependant on transducer stiffness. Compare A and B with a transducer stiffness of: A) a balanced 10⁷ N/m and N-m/rad; and B) an unbalanced 10⁷ N/m and 10³ N-m/rad. Base compliance also alters the force and shown by the moderate mbase stiffness depicted in C.

DISCUSSION

We have developed an analysis accounting for compliances observed in experiments assessing muscle actions. We show that care is needed when performing such experiments as these compliances can potentially alter the forces and moments attributed to muscle actions. In particular, we show that when the limb is overconstrained, the compliances of the skeletal fixation and transducer attachment can alter measured forces.

Importantly, when the restrained dofs were matched to the limb dofs, these compliances have no effect and standard Jacobian analyses can be performed. Thus, one main conclusion of this study is that, when possible, the restrained dofs should be matched to limb dofs. Note that if there are fewer restrained dofs than internal dofs, the limb is underconstrained and there will then be internal movement of the limb in response to muscle contraction. This movement will continue until the limb reaches equilibrium, determined by the muscle action and limb compliances, as analyzed by Mussa-Ivaldi and Hogan (1991). The present study can be seen as extending the results of that previous work to consider the case when the limb is overconstrained rather than underconstrained: in both cases, limb compliances play a critical role.

It is important to note that it is not sufficient to match the number of dofs in the limb with the number that are restrained. Consider the example in Fig. 4. Here the knee had 3 dof and the hip 3 dof. In this case rotation of the femur is possible no matter how many dof are restrained at the ankle. Hence the Jacobian has rank 5 even though the number of dofs is apparently matched. In this case there is internal limb motion that cannot be restrained at the endpoint. In this situation, the limb is underconstrained and a unique solution can only obtained by adding stiffness across the additional knee dof.

In overconstrained situations, the dof that is released must be carefully selected to prevent self-movement of the limb. This can be examined by considering the Jacobian with an additional joint added to represent the released dof. This will add a column to the Jacobian and increase the dimension of dθ (eq. 1). If the new Jacobian is rank deficient, then the release will allow self-motion. In the rat hindlimb example (Fig.1) release of the axis of rotation around either the line from the ankle to the knee or from the ankle to the hip will allow self-motion. Analysis of the expanded Jacobian shows the release of any dof allowing rotation along a line passing through the ankle contained in the plane defined by those two axes will allow the limb to move. Hence, the axis released must have a component that is orthogonal to this plane in order to prevent self-motion. Release of the z-axis satisfies this constraint. Provided self-movement does not occur, any translational or rotational dof can be released. Obviously, this will alter the generalized force measured, but will not affect the computed internal torques at the joints.

Our analysis helps explain the results observed in the rat hindlimb. It is likely that because of the stiffness of the transducer that we were using (Figure 2F) and its skeletal attachment, we were working in a situation in which transducer attachment compliance had little effect. Note that the ‘unbalanced’ stiffness considered in Figure 2F can also be achieved by scaling the force and moments differentially. For instance, for the rat hindlimb it is natural to use N/cm for the translational stiffness and N-cm/rad for the rotational stiffnesses (Yeo et al. 2011). Consistent with this possibility, in our experiments we found that releasing a dof only minimally affected the measured forces and moments. It is important to point out that although the measured endpoint forces and moments could vary considerably depending on compliances due to the transducer or due to the skeletal fixation, the joint torques exerted by the muscle were identical in each case. Compliances only changed how these joint torques appeared at the endpoint. Thus, one simple suggestion of the present work is that muscle actions should be analyzed not in terms of endpoint forces and moments but in terms of torques around internal dofs. Compliances can then be ignored until it becomes necessary to predict interactions between the limb and environment. However, this equivalence of joint torques in these simulations required that we know the true Jacobian of the system. Whether this equivalence will hold when approximate Jacobians are used (as in real limbs) is not clear.

Finally, our analyses suggest a potential alternate approach to modeling dofs within a limb. Usually, a dof is considered to be binary: movement along a dof is either permitted or is excluded. In real limbs, however, dofs are determined by the ligaments and other soft tissues which have some non zero compliance. For instance, knee abduction/adduction in the rat has considerably lower compliance than knee flexion/extension. The framework presented here can account for such non-zero compliances within limbs and therefore handle situations where movement along particular dof might be only partially permissible. Of course, measuring such compliances is difficult and including them significantly complicates development of musculoskeletal models. It will be interesting to extend the present work by measuring these compliances and examining their potential role in motor production.