A heterogeneous human tissue mimicking phantom for RF heating and MRI thermal monitoring verification

Abstract

This paper describes a heterogeneous phantom that mimics a human thigh with a deep seated tumor, for the purpose of studying the performance of radiofrequency (RF) heating equipment and non-invasive temperature monitoring with magnetic resonance imaging (MRI). The heterogeneous cylindrical phantom was constructed with an outer fat layer surrounding an inner core of phantom material mimicking muscle, tumor and marrow-filled bone. The component materials were formulated to have dielectric and thermal properties similar to human tissues. The dielectric properties of the tissue-mimicking phantom materials were measured with a microwave vector network analyzer and impedance probe over the frequency range of 80 – 500 MHz and at temperatures of 24°C, 37°C, and 45°C. The specific heat values of the component materials were measured using a differential scanning calorimeter over the temperature range of 15 – 55°C. The thermal conductivity value was obtained from fitting the curves obtained from one-dimensional heat transfer measurement. The phantom was used to verify the operation of a cylindrical 4-antenna annular phased array extremity applicator (140 MHz), by examining the proton resonance frequency shift (PRFS) thermal imaging patterns for various magnitude/phase settings (including settings to focus heating in tumor). For muscle and tumor materials, MR imaging was also used to measure T1/T2* values (1.5 Tesla) and to obtain the slope of the PRFS phase change vs. temperature change curve. The dielectric and thermal properties of the phantom materials were in close agreement to well-accepted published results for human tissues. The phantom was able to successfully demonstrate satisfactory operation of the tested heating equipment. The MRI-measured thermal distributions matched the expected patterns for various magnitude/phase settings of the applicator, allowing the phantom to be used as a quality assurance tool. Importantly, the material formulations for the various tissue types may be used to construct customized phantoms that are tailored for different anatomical sites.

1 Introduction

Hyperthermia used as an adjuvant to other established treatment modalities, such as radiotherapy and chemotherapy, has demonstrated tremendous potential in cancer therapy (Seegenschmiedt et al 1996, Field et al 1990, Dewhirst et al 2003, Corry and Dewhirst 2005, van der Zee and van Rhoon 2006, Sneed et al 2010, Issels et al 2010). The clinical application of hyperthermia requires innovation and improvement in heating applicators, which, in turn, requires testing and validation (quality assurance) to ensure that the applicators function as desired. Quality assurance (QA) is also required to ensure that the heating pattern predicted by the treatment planning software matches reality. For thermal treatment of deep-seated tumors, current electromagnetic (EM) heating equipment includes commercially available applicators (BSD Medical Corporation, Salt Lake City, Utah, USA) as well as applicators developed and used at individual institutions (Lee et al 1992, Wu et al 2006, Paulides et al 2007, Stauffer et al 2010). Characterization of these EM heating devices have used an LED matrix (Schneider et al 1991), lamp phantom (Wust et al 1994), electric field measurement inside a liquid phantom by scanning electric-probe (Schneider et al 1995, Wust et al 1995), or a Schottky-diode sheet system contained within a split, solid, homogeneous phantom (Kaatee et al 1999, Fatehi et al 2008). Of late, non-invasive magnetic resonance (MR) thermometry (De Porter 1995a, De Porter et al 1995b, Ishihara et al 1995, MacFall et al 1996) has also shown great promise for use in quality assurance. Simultaneous heating and thermal imaging using hybrid systems integrating EM hyperthermia equipment and the MR scanner were realized by decoupling the signals from the two systems (MacFall et al 1996, Gellermann et al 2005, 2006).

Phantoms that closely mimic the physical properties of human tissues play an important role in testing and evaluating these heating devices and various treatment schemes (Lagendijk and Nilsson 1985, Kato H et al 1986, Marchal et al 1989, Gross EJ et al 1990, Surowiec et al 1992, Wust et al 1998, Madsen et al 1998, Stauffer et al 2003, Kato H et al 2004, Madsen et al 2006). To the best of our knowledge, the phantoms currently being utilized for the purpose of QA are generally simple homogeneous objects that do not accurately mimic the dielectric and thermal properties of human tissue. Therefore, interaction between the electromagnetic waves and human tissues, and thermal response of these tissues to the EM power deposition, which are essential in hyperthermia treatment planning, can not be realistically investigated. Furthermore, for MR thermometry, the temperature sensitivity of the tissue mimicking phantom materials needs to be characterized to accurately quantify temperature changes with the progression of heating.

In this work, we present a methodology for fabricating a human tissue mimicking heterogeneous phantom simulating the anatomy as well as dielectric and thermal properties of a human thigh with fat, muscle and deep seated tumor. To enable MR thermal monitoring, the proton resonance frequency phase sensitivity to temperature of the two high-water-content phantom materials (tumor and muscle) was characterized. For treatment planning verification, the heterogeneous phantom was scanned using Computed Tomography (CT), segmented, loaded within the applicator model for EM simulation, and post-processed to optimize the maximum power deposition in the “tumor” target. Experiments were performed to obtain the thermal patterns with some typical antenna magnitude/phase settings, and to verify the optimization of the maximum power deposition in the tumor.

2 Material and methods

2.1 Tissue-mimicking phantom materials

The materials used in the heterogeneous tissue-mimicking (TM) phantom were made following a modification of the procedure described in Lazebnik et al. (Lazebnik et al 2005). The materials were based on oil-in-gelatin dispersions, with different oil volume percentages for the purpose of simulating dielectric properties of various human tissues, such as high-water-content muscle and tumor, and low-water-content fat and bone marrow. In Lazebnik et al. (Lazebnik et al 2005) a set of TM phantom samples with varying percentages of oil were measured over a wide frequency range of 500 MHz to 20 GHz, and good agreement between the dielectric properties of these materials and four-pole Cole-Cole models for the corresponding human tissues (Gabriel et al 1996) was obtained. Another feature of these phantom materials is their long-term stability, which is essential for constructing a complex heterogeneous phantom for serial studies.

The phantom developed here was designed to not only simulate the dielectric properties, but also the thermal and magnetic resonance (MR) properties of human tissues. Consequently, pure vegetable oil (Canola oil) was used instead of a mixture of kerosene and vegetable oil (Lazebnik et al 2005), since kerosene would have thermal and MR properties that differ from human fat. The dielectric, thermal, and MR properties of vegetable oil are close to that of fat in the human body. We also found that in order to simulate the dielectric properties of human tissues over a frequency range below 500 MHz, which includes the operation frequency ranges of most hyperthermia applicators, it was necessary to tune the saline concentration in the aqueous gelatin to adjust conductivity of the oil-in-gelatin dispersions. In the work by Lazebnik et al. (Lazebnik et al 2005), conductivity of the phantom materials was adjusted via the oil composition, over the frequency range of 0.5 GHz to 20 GHz. At high frequencies, the conductivity of water increases greatly. Thus both the permittivity and conductivity can be adjusted by the oil composition in such phantoms.

The composition of the phantom materials are briefly summarized in Table 1. An aqueous gelatin solution was produced by mixing 225 bloom gelatin (225 bloom bakers gelatin, Gelatin Innovations Inc. Schiller Park, IL) in saline water, which was then combined with oil and a surfactant (liquid Ultra Ivory®, Procter and Gamble Co., Cincinnati, OH). The surfactant acts as an emulsifier, decreasing the surface tension between the oil and water, allowing for a homogenous mixture to be made. The conductivity of the material is mainly dependent on the saline concentration, while the permittivity is related to the oil volume percentage in the oil-in-gelatin dispersion. According to the measurement of dielectric properties of human tissues from 50 MHz to 900 MHz (Joines et al 1994), both conductivity and relative permittivity were generally larger in malignant tissues than in normal tissues of the same type at all frequencies. Therefore, a higher saline concentration and lower oil volume percentage was used in the tumor-equivalent material than in muscle-equivalent material. It should also be noted that the fat material and the bone marrow material had the same composition, since their dielectric properties are very similar (at 100 MHz, permittivity and conductivity are as follows: fat 5.9, 0.037 S/m, bone marrow 6.2, 0.024 S/m, and at 433 MHz: fat 5.6, 0.042 S/m, bone marrow 5.7, 0.030) (Gabriel et al 1996).

Table 1.

Compositions of tissue-mimicking phantom materials

Material type	Oil-in-gelatin dispersions		Saline concentration g / 1000 ml DI water at room temperature
	Volume % aqueous gelatin	Volume % oil
Tumor	95	5	7.5
Muscle	90	10	6.0
Fat (bone marrow)	15	85	0.24

2.2 Dielectric property measurement

Dielectric properties of these tissue-mimicking phantom materials were measured over a frequency range of 80 to 500 MHz with a high-temperature impedance probe (Model 85070C, HP/Agilent Corp, Santa Clara CA) in conjunction with a microwave vector network analyzer (Model E5071C, Agilent Corp, Santa Clara CA). The measurements were performed on the material samples at room temperature (approximately 24°C). To evaluate uniformity of the sample, measurements were taken on the top and the bottom flat surfaces of the samples and on each surface, and three measurements were taken at different positions. The results were averaged and compared with the dielectric properties of human biological tissues parameterized using the four pole Cole-Cole model (Gabriel et al 1996).

The dielectric properties were also measured at 37°C (normal human body temperature) and 45°C (typically close to the upper temperature limit in a hyperthermia treatment). The sample was uniformly heated in a water bath monitored using fiberoptic temperature sensors (Lumasense, Santa Clara, CA) and a readout instrument (Model 3100), Luxtron Corp. Santa Clara CA). The measurements were used to estimate the temperature dependence of the dielectric properties.

2.3 Thermal properties measurement

The specific heat of each phantom material was measured using a differential scanning calorimeter (Model Diamond DSC, PerkinElmer Instruments, Shelton, CT). Before the measurement, the Diamond DSC was programmed with an Isothermal-Scan- Isothermal procedure (isothermal 3 minutes, increase temperature by 10°C at a rate of 2°C/minute, and isothermal 3 minutes), which was repeated over the temperature range from 15°C to 55°C. The specific heat was measured during each isothermal period. To ensure accuracy of the measurements, a water sample was first measured and compared against reported water specific heat values over the temperature range of interest, and then a single measurement for each phantom material was performed.

The thermal conductivity of each phantom material was obtained from transient temperature measurements. The transient temperatures at various positions along the axis of a cylindrically shaped phantom sample were fitted to a one-dimensional heat transfer equation. The heat transfer equation comprised of known parameters (specific heat, density, etc.) as well as the unknown thermal conductivity, which was optimized to best fit the measurements. Details regarding the experimental setup, the heat equation and methods used are given in the Appendix.

2.4 MR temperature calibration and T1/T2* measurement

Phase sensitive proton resonance frequency shift (PRFS) (De Porter 1995a, De Porter et al 1995b, Ishihara et al 1995, MacFall et al 1996) images were taken in the MR system (1.5 Tesla, Signa, GE medical System, Milwaukee, WI), with fiberoptic measurements for comparison. Three solidified phantom material samples (aqueous gelatin material, tumor-equivalent material, and muscle-equivalent material) were prepared. The samples were immersed in ice until their temperatures equilibrated at 0°C and then placed inside the head coil of the MR system. As the sample temperatures increased to reach the ambient room temperature, PRFS images corresponding to the measurement plane were taken at 1 minute intervals (PRFS imaging protocol: 2D axial spoiled-gradient echo sequence with TR=38.5ms, TE=20ms, Flip angle=30°, BW=15.6 kHz, FOV = 30 cm, 128x128, and NEX=4.0). Four oil references placed at four corners surrounding the samples were used to correct for magnetic field drift (Wyatt et al 2009). A linear calibration fit was generated between the PRFS phase change (with respect to the baseline image) and temperature rise for aqueous gelatin, tumor and muscle materials.

T1/T2* values for the fat, muscle and tumor phantom materials were also measured at 1.5 Tesla. The fat (bone marrow) phantom (85% oil in oil-in-gelatin dispersion) and two high-water-content phantoms, i.e. the 5% oil tumor phantom and the 10% oil muscle phantom were placed inside a container full of deionized (DI) water to minimize field inhomogeneities from air. Imaging was performed on a 1.5T GE Signa Excite (1.5 Tesla, Signa, GE medical System, Milwaukee, WI). A coronal slice along the center of the phantoms was imaged using the spoiled gradient echo (SPGR) sequence to determine the T1/T2* values. T1 weighted images were acquired at the following TR values: [50,100,150,200,250,300,400,500,750,1000,2000,3000] with all times in ms. Other parameters included FA=90 degrees TE = 7.5, FOV=30cm, 128x128 matrix, and NEX=1. T2* weighted images were acquired at the following TE values: [7.5, 12.0, 16.5, 21.0, 25.5, 30.0, 34.5, 43.5, 52.6, 61.6, 70.6, 79.6, 88.6, 97.6, 115.6, 138.1, 160.7] with all times in ms. Other parameters were TR=180ms, FA=30, FOV=30cm, 128x128 matrix, and NEX=1. The TR and TE images were fit for M₀,T1 and T2* respectively using a nonlinear Levenberg Marquardt fitting algorithm in Matlab (The Mathworks, Inc., Natick, MA) and a monoexponential fit.

2.5 Heterogeneous phantom construction

The phantom was constructed as follows. Tumor equivalent material was poured into a small cylindrically shaped container (diameter = 50 mm, height = 70 mm) and allowed to solidify. Bone marrow material was poured and solidified within a hollow sterilized beef bone (Sterilized Beef Bone, Pacific Coast Distribution Inc. Phoenix, AZ) that simulated human leg bone cortex. The tumor and filled bone were then placed in a plastic cylindrical container (diameter = 100 mm, height = 230 mm) and muscle phantom material was poured to fill the remaining portion of the container. After complete solidification of the muscle material, the outer plastic container was cut and removed, and the inner cylindrical cast was inserted into a larger PVC cylinder (diameter 120 mm, height 230 mm) containing un-solidified fat-equivalent material. The previously cast cylinder was approximately centered in the PVC container, allowing the fat-equivalent material to rise and fill the outer gap. When making the phantom, the bone cortex and the muscle were wrapped with thin plastic films to prevent interaction and osmosis. Four catheters for temperature measurement were inserted parallel to the long axis of the phantom, one through tumor material, one inside the bone marrow material, and the other two in the muscle material.

A challenging issue in constructing the phantom was the removal of air bubbles, especially for the fat-equivalent mixture (oil/gelatin volume ratio of 85/15) that was much more viscous and tended to trap air bubbles. A strong vacuum, in combination with agitation, was used to dislodge and remove the bubbles. Following this, formaldehyde was gently stirred into the mixture (approximately 1 ml per 100 ml of water in the mixture) to raise the melting point of the gelatin matrix to above 100°C by chemical cross-linking of the gelatin molecules.

2.6 Phantom heating simulation

The phantom was CT-scanned (GE Healthcare, Milwaukee, WI) with a slice thickness of 3 mm and the different tissue types were segmented in the Eclipse treatment planning system (Varian Medical Systems, Inc., Palo Alto, CA). The segmented geometry was exported and gridded in the finite-element program HFSS (Ansoft Corporate, Pittsburgh, PA), which simulated phantom heating at 140 MHz in the fourantenna mini-annular phased applicator (MAPA) used for extremity hyperthermia. To compare against phantom heating measurements, the following simulations were performed: (1) relative specific absorption rate (SAR) pattern within the phantom given the antenna magnitude and phase settings in Table 2; (2) SAR pattern to optimize delivery of the radiofrequency (RF) power into the tumor material (Das et al 1999a,b), which is the basis for real-time feedback control algorithm implementation (Cheng et al 2009, Stakhursky et al 2009) in hyperthermia clinic.

Table 2.

The magnitude/phase settings applied to MAPA for representative heating

	Antenna 1	Antenna 2	Antenna 3	Antenna 4
Setting 1	30 W (−40°)	30 W ( 0°)	30 W ( 40°)	30 W ( 0°)
Setting 2	30 W ( 60°)	30 W ( 0°)	30 W (−60°)	30 W ( 0°)
Setting 3	30 W ( 0°)	30 W (−40°)	30 W ( 0°)	30 W ( 40°)
Setting 4	30 W ( 0°)	30 W ( 60°)	30 W ( 0°)	30 W (−60°)
Setting 5	30 W ( 0°)	14 W (−30°)	5 W (−90°)	23 W (−10°)

2.7 RF heating experiments: representative heating patterns and optimized heating

Heating experiments were performed in a hybrid hyperthermia/MRI system retrofitted to allow simultaneous imaging and heating within the magnet (Stakhursky et al 2009). The phantom loaded MAPA applicator was placed inside the head coil of the MR system (Signa HDX, GE Medical Systems, Milwaukee, WI) and heated using four heating settings with equal power but with phase variations on the opposite antennas (setting 1–4), and simulation computed optimized tumor heating setting (setting 5) of Table 2. These settings were sequentially applied to the MAPA system, with each magnitude and phase setting applied for 6 minutes. A central 0.5 cm thick axial slice through the phantom was imaged with a 2D axial SPGR (spoiled-gradient echo) sequence with TR=38.5ms, TE=20ms, Flip angle=30°, BW=15.6 kHz, FOV=30 cm, 256x256, and NEX=4.0. Images were acquired at time intervals of 2 minutes during the heating process.

3 Results and discussion

3.1 Phantom material dielectric properties

Figures 1(a) and (b) show the relative permittivity (${\epsilon }_r^{\text{'}}$) and conductivity (σ), respectively, of tumor, muscle, and fat phantom materials over the frequency range of 80 – 500 MHz at room temperature (approximately 24 °C). The permittivity of the phantom material decreases when the volume percentage of the aqueous gelatin in the gelatin-oil mixture decreases, and the conductivity decreases with the decrease of the saline concentration of the water used to make the aqueous gelatin solution. For comparison, four pole Cole-Cole measurements for muscle and fat (Gabriel et al 1996) are also plotted, showing good agreement. The mean and standard deviation of six measurements of relative permittivity and conductivity of each phantom material are tabulated in Table 3 for three frequencies that are typical of RF hyperthermia (100, 140, and 433 MHz).

Figure 1.

Measured dielectric properties for various phantom materials at room temperature, along with the dielectric properties of the corresponding human tissues described by Cole-Cole model (Gabriel et al 1996). (a) Relative permittivity, and (b) conductivity.

Table 3.

Measured permittivity and conductivity for the phantom materials at 100 MHz, 140 MHz, and 433 MHz.

Frequency	Tumor		Muscle		Fat
	${\epsilon }_r^{\text{'}}$	σ	${\epsilon }_r^{\text{'}}$	σ	${\epsilon }_r^{\text{'}}$	σ
100 MHz	69.38±1.94	0.844±0.032	61.47±1.70	0.641±0.026	7.66±0.79	0.019±0.005
140 MHz	67.07±1.82	0.862±0.031	59.76±1.66	0.657±0.027	7.36±0.78	0.021±0.005
433 MHz	61.52±1.69	0.969±0.035	55.30±1.74	0.759±0.032	6.78±0.73	0.034±0.006

Figures 2(a) and (b) show measured dielectric properties of the phantom materials at three different temperatures: 24°C (room temperature), 37°C (normal human body temperature), and 45°C (approximately the upper temperature limit in hyperthermia treatments). The uncertainties of the measurement at each temperature are almost the same for each phantom material over the whole frequency range. In general, the permittivity and the conductivity of each phantom material increases as the temperature rises. Calculated temperature coefficients (written in a form of Δε/ε and Δσ/σ, % per °C) for phantom materials at 100 MHz, 140 MHz, and 433 MHz are summarized in Table 4. These values are reasonable considering the ranges in the previously published temperature-dependent dielectric properties of biological tissues summarized in Lazebnik et al. (Lazebnik et al 2006). The typical variations for biological tissues in the microwave regime are Δε/ε: from -0.3-2 % per °C, and Δσ/σ: from 1–2 % per °C (Schwan et al 1980, Stauffer et al 2003).

Figure 2.

Measured dielectric properties for various phantom materials at 24°C (solid lines), 37 °C (dotted lines), and 45 °C (dot dash lines): (a) Relative permittivity, and (b) conductivity.

Table 4.

The calculated temperature coefficients (% per °C) for the phantom materials

Frequency	Tumor		Muscle		Fat
	Δε/ε	Δσ/σ	Δε/ε	Δσ/σ	Δε/ε	Δσ/σ
100 MHz	0.2	2.0	0.4	1.9	1.3	5.0
140 MHz	0.2	1.9	0.4	1.8	1.3	4.6
433 MHz	0.2	1.9	0.4	1.6	1.3	3.1

3.2 Phantom material thermal properties

The measured specific heat values for the phantom materials over the temperature range of 15°C to 55°C are shown in figure 3. Before each measurement, a water sample was measured and the measured specific heat value for the water was within 4.18 ± 0.05 J/(g·K) (the specific heat of water is 4.18 J/(g·K) over the temperature range of interest. It can be seen that the specific heat for the high-water-content tumor material and muscle material is larger than that of the low-water-content fat and bone cortical materials. This is because water has a larger specific heat than vegetable oil (4.19 J/(g·K) versus 1.67 J/(g·K)). The measured specific heat values for the phantom materials agree well with those of in vivo human tissues (Giering et al 1996) summarized in Table 5. Another important property of the specific heat of the phantom materials is that it changes very little (about 0.2 J/(g·K)), over the temperature range of 15°C to 55°C, which is the temperature range of interest for hyperthermia.

Figure 3.

Measured specific heat of various phantom materials over the temperature range from 15°C to 55°C.

Table 5.

Specific heat of human tissues and tissue mimicking phantom materials

	Human tissue specific heat at 37 °C in J/(g·K) (Giering et al 1996)	Phantom materials specific heat at 37 °C in J/(g·K)
Tumor	3.51–3.80	3.71
Muscle	3.55	3.48
Fat	2.22–2.43	2.17
Bone cortex	1.3	1.24

The thermal conductivity values for the phantom materials obtained from the transient heat transfer measurements are summarized in Table 6. For comparison, the thermal conductivities for human tissues (Hatfield et al 1951, Valvano et al 1985) are also listed in the table. The data for human tumors was obtained from human colon cancer (Valvano et al 1985). From the comparison, it can be seen that the thermal conductivity values for phantom materials are close to those for human tissues.

Table 6.

Thermal conductivity of human tissues and tissue mimicking phantom materials

	Human tissue thermal conductivity in W / (m·K) (Hatfield et al 1951, Valvano et al 1985)	Phantom materials thermal conductivity in W/(m·K)
Tumor	0.545	0.49
Muscle	0.385	0.42
Fat	0.204	0.20

3.3 Phantom material PRFS phase change versus temperature change, T1/T2* values and phantom MR image

The MR magnitude image of the phantom materials and the oil references used for the PFRS measurement is shown in figure 4(a). There was susceptibility in the central region due to the small air gaps between the containers, but the image phases in these regions were not used. The temperature of the samples was increased from approximately 5°C to 14°C during the MR scanning. Over this temperature range, the MR phase change versus temperature change curves for the aqueous gelatin, the muscle phantom material and the tumor phantom material are shown in figure 4(b). For comparison, the curve for deionized water from the theoretical model is also plotted. The curves of the aqueous gelatin and muscle phantom material almost overlap with that of water, while the curve of the tumor phantom material deviates slightly from that of water. On the selected ROIs (7x7 pixels) close to the catheters, the derived chemical shift values (slope of the curve) are 0.0104 ppm / °C and 0.0108 ppm / °C for muscle and tumor materials, and the corresponding standard deviation values are 0.0003 ppm / °C and 0.0002 ppm / °C, respectively. By contrast, and the value for the reference, i.e. deionized water is 0.01 ppm / °C (Hindman 1966, Ishihara et al 1995, Peters et al 1998).

Figure 4.

Measured PRFS phase change versus temperature change for various phantom materials (dashed lines), and calculated reference curve for deionized water (solid line).

The T1/T2* values for each phantom material from the measurements on several small homogenous phantoms are summarized in Table 7. These values are also compared with those of human tissues (Bottomley et al 1987, Duewell et al 1995, Akber et al 1996, Kato et al 2005). In most cases, the low-water-content phantom material (fat and bone marrow) and the high-water-content phantom materials (tumor and muscle) have T1/T2* values similar to human tissues (T1/T2). It should be noted that T2* relaxation is measured with gradient echo scans, which are typically used for thermometry sequences, and the T1/T2* results are from monoexponential fits of the combined water/fat signal. The adjusted coefficient of multiple determination (or adjusted R2) (Carballido-Gamio et al 2010) for T1/T2*, summarized in Table 8, are all greater than 0.94, suggesting an overall good fit for all these phantom materials.

Table 7.

T1/T2* values for phantom materials and human tissues at 1.5 Tesla

Phantom material	Oil-in-gelatin dispersions	T1 (ms)	T2* (ms)	Human tissue	T1 (ms)	T2 (ms)
Fat (bone marrow)	85% oil	198	37.3	Fat	310	47
Tumor	5% oil	1034.7	113.1	Misc. Tumor	1083	87
Muscle	10% oil	1084.9	64.5	Muscle	797–1206	31–47

Table 8.

Adjusted R² for T1/T2*

Phantom material	Adjusted R2
	T1	T2*
Fat (bone marrow)	0.998	0.945
Tumor	0.998	0.973
Muscle	0.998	0.997

A magnitude MR image of the heterogeneous phantom central cross-section is shown in figure 5. All components of the phantom, i.e., tumor material, bone cortex, bone marrow material, muscle material, and the outer fat material are easily visualized. Locations of catheters in the muscle and tumor materials are indicated in the figures along with the oil references used to correct for magnetic field drift. MR images in other cross-sections of the phantom were of good quality, demonstrating that the phantom component materials were consistently made and contained no air bubbles.

Figure 5.

MR image (magnitude) of the heterogeneous phantom for a cross-section near its center. Phantom components are shown in (a). Four pairs of oil references and catheters are shown in (b).

3.4 Phantom heating experiment and MR thermometry

In the heating experiments, D2O was filled between antennas and phantom as D2O has similar electrical and thermal properties to regular deionized water, but has no MR signal regardless of temperature or movement, thereby increasing contrast with respect to background and avoiding motion artifacts. Four representative simulated heating patterns and the simulated optimized heating pattern are shown in figure 6, using the RF system magnitude/phase settings described in Section 2.7. For comparison, the measured MR thermal images are also shown. The MR measured heating patterns demonstrate a high signal-to-noise ratio. The measured MR thermal image corresponding to the optimized setting demonstrates well focused heating in the tumor, as predicted by the simulation.

Figure 6.

The four representative heating patterns (from (a) to (d)) and tumor-optimized pattern (e) obtained from the five magnitude/phase settings listed in Table 2. In all these figures, left and right patterns are the simulated and measured heating patterns, respectively. Location of the “tumor” in upper left of phantom is indicated in white. Positions of the four antennas on the plexiglass shell of the applicator are also denoted.

4 Conclusions

The fabricated human thigh phantom is composed of tissue mimicking materials that accurately model both EM and thermal properties of fat, muscle, tumor, bone and bone marrow tissues. The chemical shift values for muscle- and tumor-equivalent phantom materials were also measured for the purpose of PRFS-based MR thermal imaging. The materials used in this phantom may be easily used to fabricate phantoms mimicking other body sites. The data demonstrate that such phantoms are a valuable tool for verification and quality assurance of heating equipment and MRI thermal monitoring, prior to clinical implementation.

Appendix

The one dimensional (1D) heat equation is

$$\frac{\partial u}{\partial t}-\alpha \frac{{\partial }^{2}u}{\partial x^2}=0$$ (1)

Where u(x, t) is the spatially and temporally dependent temperature, and α is the thermal diffusivity (unit:m² / s), $\alpha =\frac{k}{\rho c}$, where k is the thermal conductivity (unit: W / (m·K)), ρ is the density of the sample (unit: kg / m³), and c is the specific heat of the sample (unit: J / (kg·K)).

For the experimental configuration, the boundary and initial conditions are

$$\frac{\partial u}{\partial x}{|}_{x=0}=0u|{}_{x=L}=0u|{}_{t=0}=T_i$$ (2)

The solution is

$$u(x,t)=\sum _{n=0}^{\infty }{B}_n\text{cos}\left(\frac{2n+1}{2L}\pi x\right)e^{-\alpha {\left(\frac{2n+1}{2L}\right)}^{2}t}$$ (3)

Where$B_n=\frac{4T_i}{(2n+1)\pi }{(-1)}^n.$

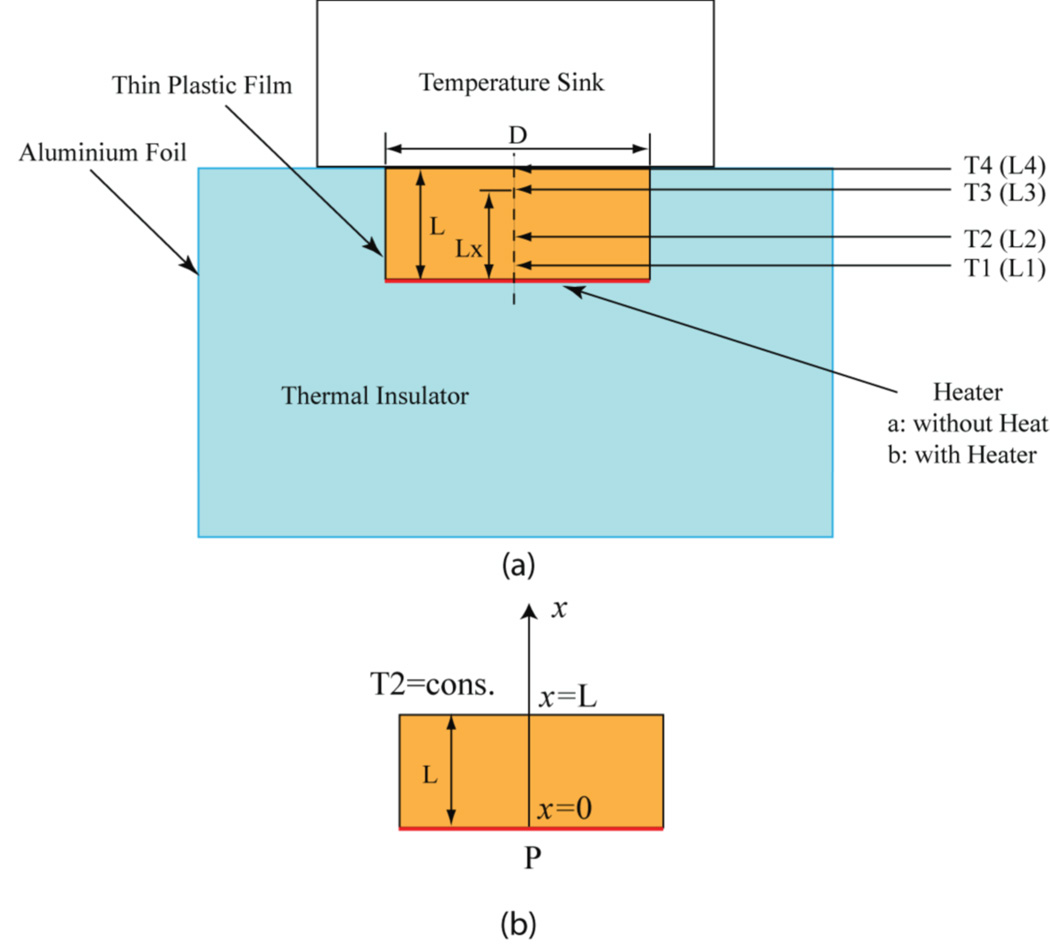
The experimental setup for transient heat transfer measurement is illustrated in figure 7. A cylindrical phantom sample with a diameter of D=50 mm and a height of L=21 mm was placed within an opening in a styrofoam block, which served as a thermal insulator for the bottom and sides of the sample. A metallic temperature sink containing a mixture of water and ice was placed on top of the sample. The sink was maintained at a constant temperature of 0°C. The transient temperature gradient induced in the sample was measured at 4 locations along the cylindrical axis (as shown in the figure; probe T4 monitored the sink temperature) and used to fit the 1D heat equation to compute thermal conductivity.

Figure 7.

(a) Schematic of experimental setup for the thermal conductivity measurement of the phantom materials. (b) One-dimensional (1D) model for the measurement. Dimensions: D=50 cm, L=21 cm, L1=2.5 mm, L2=8 mm, L3=17 mm, and L4=21 mm (L1–L4 are typical values in the measurement and may change for each measurement of the sample).

For tumor phantom material, the measured transient temperature and the corresponding analytical curves with the thermal conductivity k = 0.49 W / (m·K) are shown in figure 8. There is excellent agreement between the measurements and fitted curves for T1, T2, and T3 over the whole temporal range.

Figure 8.

The measured transient temperature and the corresponding analytical curves for tumor phantom material.