Modeling Plasmodium vivax : relapses, treatment, seasonality, and G6PD deficiency

Abstract

Plasmodium vivax (P. vivax) is one of the most important human malaria species that is geographically widely endemic and causes social and economic burden globally. However, its consequences have long been neglected and underestimated as it has been mistakenly considered a benign and inconsequential malaria species as compared to Plasmodium falciparum. One of the important differences between P. falciparum and P. vivax is the formation of P. vivax latent-stage parasites (hypnozoites) that can cause relapses after a course of treatment. In this work, mathematical modeling is employed to investigate how patterns of an incubation period and relapses of P. vivax, variation in treatment, and seasonal abundance of mosquitoes influence the number of humans infected with P. vivax and the mean age at infection of humans in tropical and temperate regions. The model predicts that: (i) the number of humans infected with P. vivax may increase when an incubation period of parasites in humans and a latent period of hypnozoites decreases; (ii) without primaquine, the only licensed drug to prevent relapses, P. vivax may be highly prevalent; (iii) the mean age at infection of humans may increase when a latent period of hypnozoites increases; (iv) the number of infectious humans may peak at a few months before the middle of each dry season and the number of hypnozoite carriers may peak at nearly the middle of each dry season. In addition, glucose-6-phosphate-dehydrogenase (G6PD) deficiency, which is the most common enzyme defect in humans that may provide some protection against P. vivax infection and severity, is taken into account to study its impact on the number of humans infected with P. vivax. Modeling results indicate that the increased number of infected humans may result from a combination of a larger proportion of humans with G6PD deficiency in the population, a lesser protection of G6PD deficiency to P. vivax infection, and a shorter latent period of hypnozoites.

1 Introduction

Malaria is a major public health problem in many parts of the world. Two of the most important human malaria parasites are Plasmodium vivax and Plasmodium falciparum. Although P. vivax is responsible for fewer deaths than P. falciparum and often referred as a benign tertian malaria, its clinical symptoms are not genuinely benign; patients face repeated episodes of high fever, convulsions, thrombocytopenia, and severe anaemia. As it has been mistakenly understood as benign and inconsequential, its burden has been underestimated. In fact, P. vivax is endemic in many parts of the world, including South and Southeast Asia, the Middle East, North Africa, the Western Pacific and South America (Mendis et al., 2001). Due to its wide geographical distribution, 2.85 billion people are at risk of infection, resulting in 132–391 million clinical cases per year (Price et al., 2007; Guerra et al., 2009).

One of the important features that distinguish P. vivax from P. falciparum is the formation of latent-stage parasites (hypnozoites) in a human liver that can remain dormant for weeks, months, or years during less optimal transmission periods before initiating subsequent blood-stage infections called relapses. Patterns and frequency of relapses are different between tropical and temperate strains of P. vivax; tropical strains are characterized by an early primary attack followed by multiple relapses with short latent periods (5–10 weeks), whereas temperate strains show fewer relapses with longer time intervals (5–10 months) (Craig and Kain, 1996). The primary attack normally occurs within 10–20 days after exposure to P. vivax sporozoites via a bite of an infectious mosquito. However, it has been demonstrated that an incubation period has a propensity to be prolonged in the temperate zones and may take approximately 27 days or even as long as 48 weeks (Shute et al., 1977; Nishiura et al., 2007; Price et al., 2007).

Chloroquine (CQ) and primaquine (PQ) have been used as the first line therapies for P. vivax infections in most endemic countries except where P. vivax is resistant to CQ. CQ is blood schizontocide that targets asexual blood-stage parasites while PQ is the only licensed drug for preventing relapses and neutralizing sexual gametocytes (consequently reducing transmission to mosquitoes) (Baird, 2009). However, PQ is an oxidative anti-malarial that can cause haemolytic anemia and hence is dangerous in persons who have glucose-6-phosphate dehydrogenase (G6PD) deficiency. Without PQ therapy, the risk of having relapses ranges from 5% to 80%, depending on a geographic location (Baird and Hoffman, 2004). Likewise, tafenoquine, an 8 aminoquinoline with a much longer half-life than PQ and currently in clinical trials, has the toxicity to G6PD-deficient individuals (Kitchener et al., 2007; Chattopadhyay et al., 2010).

G6PD deficiency is the most common enzyme defect that is present in more than 400 million people worldwide (Cappellini and Fiorelli, 2008). It is highly prevalent in Africa, Asia, Mediterranean, and the middle east in which P. vivax is endemic. More than 140 mutations of the G6PD gene have been described and the frequency of those variants differs among human populations (Cappellini and Fiorelli, 2008). Because of the wide geographical distribution of G6PD deficiency, it has been led to the hypothesis that this trait may confer protection against malaria infection. A recent study in Thailand showed that a common G6PD deficiency variant in Southeast Asia, the G6PD Mahidol, is associated with reduction of P. vivax parasite density (Louicharoen et al., 2009). Another recent study of Mediterranean variants of G6PD deficiency in Pakistan demonstrated a stronger protection of G6PD deficiency against P. vivax infection (Leslie et al., 2010). The findings suggest differences among variants.

Due to the latent-stage parasites, elimination of P. vivax is very challenging in comparison to P. falciparum. As well as the use of anti-malarial drugs, one of the effective means is to control mosquitoes. In tropical regions, seasonal rainfall can elevate the abundance of mosquitoes by increasing the availability of breeding sites and warmer weather can also increase rates of parasite transmission (Altizer et al., 2006). Based on these factors, for instance, it is important to understand the ecology of these vectors in association with the prevalence of P. vivax in designing effective control strategies.

Research has focussed on P. falciparum due to its lethality in Africa and the erroneous perception that P. vivax is benign. Mathematical models have been widely used in providing quantitative predictions and evaluating interventions. Many have been used to investigate the quantitative epidemiology of P. falciparum (Chamchod and Britton (2011); Childs and Boots (2010); White et al. (2009); Filipe et al. (2007); Smith et al. (2005), for instance). However, mathematical models developed particularly for studying P. vivax are still scant at both population and cell levels (De Zoysa et al., 1991; Kammanee et al., 2001; Ishikawa et al., 2003; Nah et al., 2010; Aguas et al., 2012).

De Zoysa et al. (1991) constructed a mathematical model to study levels of naturally-acquired transmission-blocking immunity in humans. They found that just slightly above the threshold for transmission, the effect of transmission-blocking immunity is very significant. Kammanee et al. (2001) developed a mathematical model for P. vivax transmission with relapse and studied steady states and the basic reproductive number. Ishikawa et al. (2003) proposed a mathematical model to study the impact of mass drug administration and vector control on the dynamics of P. vivax in the Solomon Islands. Their model was adjusted from the quantitative model for P. falciparum in the Africa Savannah by Dietz et al. (1974). They found that for P. vivax to remain below 1% for a long period of time, mass drug action should be accompanied by effective mosquito control. Nah et al. (2010) developed a mathematical model in which humans with short and long-term incubation periods of P. vivax are explicitly separated, and domestic animals act as diluting hosts (hosts that support mosquito feeding but not P. vivax parasite multiplication) that reduce a proportion of mosquito bites in humans. They found that the use of animals to mitigate mosquito bites on humans determines whether a basic reproduction becomes bigger than an outbreak threshold. A mathematical model for P.vivax transmission that includes latency classes and artemisinin-based therapy (ACT) was developed and compared to P. falciparum in a recent study by Aguas et al. (2012). Their study for example predicted that ACT combined with a hypnozoite killing drug would eliminate both species but P. vivax elimination may show instability.

Because of the complex biology of P. vivax that makes it difficult to predict the effect of control, transmission levels, and disease burden, detailed mathematical models needed to improve the understandings about this parasite (Mueller et al., 2009). Here, we construct a simple mathematical model that takes a latent stage of hypnozoites into account to study how incubation period and relapse patterns, the use of anti-malaria therapy, and the abundance of mosquitoes during a wet season, are associated with the endemic level of P. vivax in a human population. As the emergence of the P. vivax population from hypnozoites may differ from populations that cause the acute episode (Imwong et al., 2007; Chen et al., 2007), our baseline model allows new exposure of hypnozoite carriers with either the same strain of P. vivax in the primary infection or other different strains, that has not been included in previous modeling studies. In addition, the presence of humans with G6PD deficiency and the possible protection against P. vivax infection is incorporated into the baseline model to investigate how a proportion of persons with G6PD deficiency in humans and a level of protection against P. vivax infection affect the number of humans infected with P. vivax.

2 Methods

2.1 The baseline model for P. vivax transmission

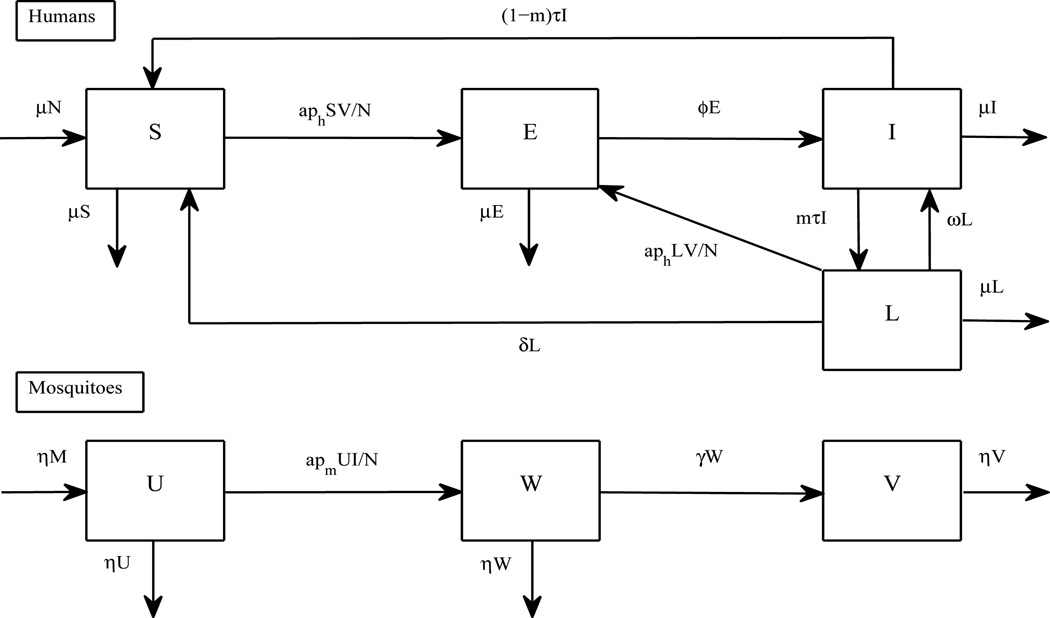
A model presented below describes the transmission dynamics of P. vivax by taking relapses into account (see a flow diagram in Figure 1 and parameter values in Table 1). It is based on a framework for vector-borne diseases with humans as hosts and mosquitoes as vectors. Humans are divided into four groups: susceptible (S), exposed (E), infectious (I), and latent (L). Note that exposed humans are persons who are infected but not yet active for P. vivax transmission. In a primary attack, uninucleate sporozoites either proceed to develop many thousands of merozoites within infected hepatocytes or remain as dormant hypnozoites for a long period of time before causing another attack of parasitaemia (Krotoski, 1985). Hence, we here define an individual in a latent stage of P. vivax (L) as a human who carries hypnozoites after the primary infection and anti-malarial therapy. Female Anopheles mosquitoes are divided into three groups: susceptible (U), exposed (W), and infectious (V).

Figure 1.

A flow chart to investigate the transmission dynamics of P. vivax. The diagram shows inflows and outflows of humans who are susceptible (S), exposed (E), infectious (I), and carrying hypnozoites (L), and mosquitoes that are susceptible (U), exposed (W), and infectious (V).

Table 1.

Lists of parameters for P. vivax transmission

Description	Symbol	Sample value	References
The total size of human population	N	50000	estimated
(per 40000 km2)(5 persons/km2)
Birth and death rate of humans (year−1)	μ	1/70	estimated
The total size of mosquito population	M	qN
The number of mosquitoes per individual	q	1.5	[1]
Biting rate (year−1)	a	245	[2]
Probability of successful infection in humans	ph	0.1	[1]
Incubation period in humans (year)	1/ϕ
-Tropical zones		15/365	[3]
-Temperate zones		27/365	[4]
Average time of carrying hypnozoites (year)	1/δ	1	[3]
Average time of a complete course of treatments (year)	1/τ	14/365	[5]
Average time from a primary attack to a relapse (year)	1/ω		[6]
-Tropical zones		60/365
-Temperate zones		150/365
Probability of carrying hypnozoites after a complete course of treatments	m		[7]
-without primaquine (tropically)		0.63
-with primaquine (tropically)		0.18
-without primaquine (globally)		0.68
-with primaquine (globally)		0.13
Birth and death rate of mosquitoes (year−1)	η	365/20	[9]
Probability of successful infection in mosquitoes (estimated to be less than P. falciparum)	pm	0.07	estimated
Incubation period in mosquitoes (year)	1/γ	9/365	[9]

Estimation of p_m. P. vivax is responsible for 50% of malaria cases in South and Southeast Asia with the prevalence ranging from 1% to 6% of the population (Price et al., 2007). By fixing m = 0.18, ϕ = 365/15, ω = 365/60 and other parameters according to Table 1, estimating p_m = 0.07 in the model leads to the prevalence of P. vivax around 2.25% of the human population. In this work, 0.07 is chosen as an estimation of the probability of mosquito infection upon biting an infectious human.

References. [1]= (Gupta and Day, 1994), [2]=(Filipe et al., 2007), [3]=(Cogswell, 1992), [4]=(Nishiura et al., 2007), [5]=(Naing et al., 2010), [6]=(Craig and Kain, 1996), [7]=(Baird and Hoffman, 2004), [8]=(Anderson and May, 1991), and [9]=(Ishikawa et al., 2003).

Model assumptions and justification

To construct the model, we make the following assumptions:

• 1Humans are born susceptible at rate of μN (where their average lifespan is 1μ) and the total number of humans (N) is constant. Humans infected with P. vivax malaria rarely die from the parasite (Mueller et al., 2009) and therefore we assume that the disease-related death rate is zero.
• 2Each mosquito bites at a constant rate (a) distributed uniformly among ruminants within an area (Keeling and Rohani, 2007). Hence, transmission is frequency-dependent with respect to a human population and the rate at which a particular human is bitten by a particular mosquito is a/N. Sporozoites of P. vivax enter each host through a bite of an infectious mosquito with a probability of p_h. A mosquito is exposed to P. vivax by ingesting gametocytes from an infectious human during its blood meal with a probability of p_m. Therefore, susceptible humans and hypnozoite carriers become exposed to P. vivax at rate ap_hSV/N and ap_hLV/N, respectively. Mosquitoes become exposed to P. vivax parasites at rate ap_mUI/N.
• 3Exposed humans become infectious at rate of ϕ where 1/ϕ is an average incubation period of P. vivax in humans.
• 4Partially acquired immunity to P. vivax needs repeated infections, wanes with time, and only prevents immune individuals to clinical symptoms (Doolan et al., 2009; Mueller et al., 2009). It is also strain-specific (Doolan et al., 2009; Cole-Tobian et al., 2009). As sterilizing immunity against infection is never fully acquired, asymptomatic carrier status (individuals remain infected, with gametocytes infectious to mosquitoes) is the rule among adults (Doolan et al., 2009). Moreover, because transmission of P. vivax is low to moderate in most regions where it is prevalent, repeated infections may be infrequent and hence people from all ages are at risk of infection (Joshi et al., 2008). Consequently, we assume that there is no acquired immunity in our model. Based on this assumption and the same sample values of parameters, the prevalence of P. vivax in this study may be higher than other preceding works that assumed protective immunity against P. vivax infections.
• 5It is assumed that all infectious persons are treated at rate of τ, where 1/τ is a duration of anti-malarial therapy. Because administration of anti-malarial drugs has less effect on overall transmission of P. vivax compared to P. falciparum and P. vivax can effectively transmit at low parasite densities (White, 2008), for simplicity, we assume that during the anti-malarial therapy infectious persons can still transmit the disease. After completing a course of treatment, infectious persons either become susceptible with a probability of 1−m or enter a latent stage when the treatment and their immune system fail to eliminate hypnozoites with a probability of m.
• 6Relapses occur at rate of ω, where 1/ω is the average time that hypnozoites remain dormant in hepatocytes before an onset of relapse.
• 7We assume that clearance of hypnozoites occurring at rate of δ is due to the lifespan of hepatic parenchymall cells which is less than a year (1/δ) although relapses may occasionally occur after more than a year (Cogswell, 1992).
• 8Mosquitoes are recruited into the susceptible compartment at rate of B. For simplicity, we assume that B equals η M, where 1/η is the average lifespan of mosquitoes, so that the total number of mosquitoes (M) remains constant.
• 9Exposed mosquitoes become infectious at rate of γ, where 1/γ is an average incubation period of P. vivax in mosquitoes. Once infected, mosquitoes remain infected for life.

These assumptions lead to the following model:

$$Ṡ=\mu N+\delta L+(1-m)\tau I-a{p}_{h}SV/N-\mu S,Ė=a{p}_h(S+L)V/N-(\mu +\varphi )E,İ=\varphi E+\omega L-(\mu +\tau )I,\mathrm{L̇}=m\tau I-a{p}_{h}LV/N-(\mu +\omega +\delta )L,\mathrm{U̇}=B-a{p}_{m}UI/N-\eta U,Ẇ=a{p}_{m}UI/N-(\eta +\gamma )W,\mathrm{V̇}=\gamma W-\eta V.$$ (1)

2.2 The P. vivax model with G6PD deficiency

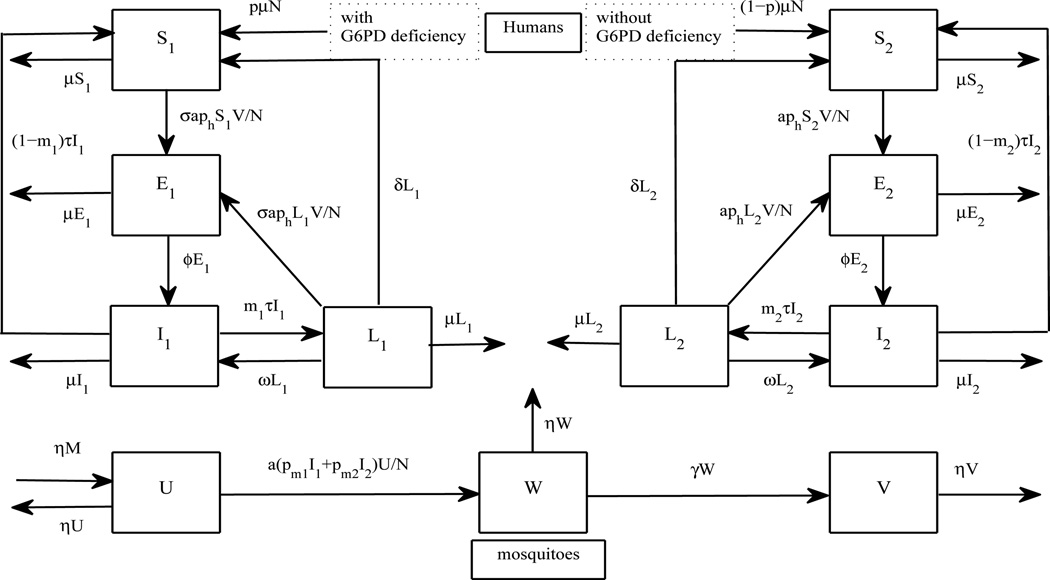
To consider G6PD deficiency in the model, humans are now separated into two subgroups: persons with and without G6PD deficiency (with subscripts 1 and 2, respectively). Each group is subdivided into four compartments in a similar way to the baseline model. Although certain variants of G6PD deficiency may be associated with the reduction of parasite density in humans that consequently helps to reduce severity of P. vivax symptoms, we do not consider this type of protection in this work (but the model presented below can be adjusted to consider it via the reduction of probability of successful infection). Here, we investigate how the presence of the stronger protection that prevents P. vivax infection (Leslie et al., 2010) influences P. vivax cases among humans. To construct the model, we make additional assumptions from the baseline model as follows:

• 10As G6PD deficiency is a hereditary genetic defect, we assume that persons are recruited into the G6PD deficiency group with a probability of p and the G6PD-normal group with a probability of 1 − p.
• 11We assume that G6PD deficiency helps reduce the probability of infection when individuals are challenged by P. vivax. Hence, susceptibility in individuals with G6PD deficiency is reduced by a factor σ, where 0 ≤ σ ≤ 1. If sigma=1, there is no additional protection to P. vivax from having G6PD deficiency. If sigma=0, there is a full protection to P. vivax and no infection and transmission occurs in individuals with G6PD deficiency. We define strong protection for σ toward 0 and weak protection for σ toward 1.
• 12It is assumed that G6PD testing is available and PQ is not given to individuals with G6PD deficiency so that PQ can be beneficially prescribed to individuals without G6PD deficiency to reduce relapses and haemolytic anemia can be prevented in individuals with G6PD deficiency.

A flow diagram is depicted in Figure 2 and parameter values can be found in Table 1. The system of equations can be described as follows:

$${Ṡ}_1=p\mu N+\delta L_1+(1-m_1)\tau I_1-\sigma a{p}_h{S}_{1}V/N-\mu S_1,{Ė}_1=\sigma a{p}_h(S_1+L_1)V/N-(\mu +\varphi )E_1,{İ}_1=\varphi E_1+\omega {\mathrm{L̇}}_1-(\mu +\tau )I_1,L_1=m_1\tau I_1-\sigma a{p}_h{L}_{1}V/N-(\mu +\omega +\delta )L_1,{Ṡ}_2=(1-p)\mu N+\delta L_2+(1-m_2)\tau I_2-a{p}_h{S}_{2}V/N-\mu S_2,{Ė}_2=a{p}_h(S_2+L_2)V/N-(\mu +\varphi )E_2,{İ}_2=\varphi E_2+\omega L_2-(\mu +\tau )I_2,{\mathrm{L̇}}_2=m_2\tau I_2-a{p}_h{L}_{2}V/N-(\mu +\omega +\delta )L_2,\mathrm{U̇}=\eta M-a{p}_{m1}U{I}_1/N-a{p}_{m2}U{I}_2/N-\eta U,Ẇ=a{p}_{m1}U{I}_1/N+a{p}_{m2}U{I}_2/N-(\eta +\gamma )W,\mathrm{V̇}=\gamma W-\eta V.$$ (2)

Figure 2.

A flow chart to investigate the transmission dynamics of P. vivax when G6PD deficiency is taken into account. Humans are separated into two main categories: with and without G6PD deficiency (with subscripts 1 and 2, respectively). Each category is subdivided according to disease statuses of P. vivax in humans.

2.3 Model simulations

In this study, numerical model simulations are used for investigating the impact of an incubation period of P. vivax in humans, a latent period of hypnozoites, variation in treatment, and the use of treatment for killing hypnozoites on the number of P. vivax cases in humans and the host’s mean age at infection. When seasonality of mosquito abundance is considered, relations between the number of humans infected with P. vivax in humans, peaks of mosquito abundance, a latent period of hypnozoites, and an incubation period of P. vivax in humans are investigated. By taking G6PD deficiency in humans into account, simulations for the extended model are created to study how protection against P. vivax infection in persons with G6PD deficiency and a proportion of humans with this trait in the human population influence the number of humans infected with P. vivax.

3 Analysis

3.1 Steady states

The baseline model has two steady states:

1. a disease-free steady state

   $$P^0=(S,E,I,L,U,W,V)=(N,0,0,0,M,0,0),$$
2. a disease-present steady state

   $$P^{*}=(S,E,I,L,U,W,V)=(S^{*},E^{*},I^{*},L^{*},U^{*},W^{*},V^{*}),$$

if there exists I* corresponding to the following equation:

$$C_2{I}^{*2}+C_{1}I*+C_0=0$$

with

$$C_0=(\mu +\tau )(\mu +Õ)(\mu +\omega +\delta ){\eta }^2{(\eta +\gamma )}^2{N}^3-Õ(\mu +\omega +\delta )\eta (\eta +\gamma )\gamma a^2{p}_h{p}_{m}M{N}^3-\omega m\tau (\mu +Õ){\eta }^2{(\eta +\gamma )}^2{N}^3,C_1=(\mu +\tau )(\mu +Õ)\eta (\eta +\gamma )\gamma a^2{p}_h{p}_{m}MN+2(\mu +\omega +\delta )(\mu +Õ)\eta {(\eta +\gamma )}^{2}a{p}_m{N}^2+(\mu +\omega +\delta )\eta (\eta +\gamma )\gamma a^2{p}_h{p}_{m}M{N}^2]-Õ\gamma a^2{p}_h{p}_{m}M[\gamma a^2{p}_h{p}_{m}MN+(\mu +\omega +\delta )(\eta +\gamma )a{p}_m{N}^2-(\mu +\omega +\gamma )\eta (\eta +\gamma )N^2]-\omega m\tau (\eta +\gamma )N[(\mu +Õ)\eta (\eta +\gamma )a{p}_h{p}_{m}MN+(\mu +Õ)\eta (\eta +\gamma )a{p}_{m}N,C_2=(\mu +\tau )[(\mu +Õ)(\eta +\gamma )a{p}_m+\gamma a^2{p}_h{p}_{m}M][(\mu +\omega +\delta )(\eta +\gamma )a{p}_{m}N+\gamma a^2{p}_h{p}_{m}M]+Õ\gamma a^2{p}_h{p}_{m}M[\gamma a^2{p}_h{p}_{m}M+(\mu +\omega +\delta )(\eta +\gamma )a{p}_{m}N]-\omega m\tau (\eta +\gamma )N[(\mu +Õ)(\eta +\gamma )a^2{p}_m^2+\gamma a^3{p}_h{p}_m^{2}M],$$

and

$$E^{*}=\frac{\gamma a^2{p}_h{p}_{m}M{I}^{*}(N-I^{*})}{(\mu +Õ)(\eta +\gamma )(\eta N+a{p}_m{I}^{*}+\gamma a^2{p}_h{p}_{m}M{I}^{*}},L^{*}=\frac{m\tau (\eta +\gamma )I^{*}N(\eta N+a{p}_m{I}^{*})}{\gamma a^2{p}_h{p}_{m}M{I}^{*}+(\mu +\omega +\delta )(\eta +\gamma )N(\eta N+a{p}_m{I}^{*})},S^{*}=N-E^{*}-I^{*}-L^{*},W^{*}=\frac{\eta a{p}_m{I}^{*}M}{(\eta +\gamma )(\eta N+a{p}_m{I}^{*})},V^{*}=\frac{\gamma a{p}_{m}M{I}^{*}}{(\eta +\gamma )(\eta M+a{p}_m{I}^{*})},U^{*}=M-W^{*}-V^{*}.$$

Note that the P. vivax model with G6PD deficiency (2) has four steady states which are not explicitly presented here:

• P⁰: the disease-free steady state:

  $$(S_1,E_1,I_1,L_1,S_2,E_2,I_2,L_2,U,W,V)=(pN,0,0,0,(1-p)N,0,0,0,M,0,0)$$
• P¹: the steady state with endemicity of P. vivax only in a human population with G6PD deficiency:

  $$(S_1,E_1,I_1,L_1,S_2,E_2,I_2,L_2,U,W,V)=(S_1^1,E_1^1,I_1^1,L_1^1,(1-p)N,0,0,0,U^1,W^1,V^1)$$
• P²: the steady state with endemicity of P. vivax only in a human population without G6PD deficiency:

  $$(S_1,E_1,I_1,L_1,S_2,E_2,I_2,L_2,U,W,V)=(pN,0,0,0,S_2^2,E_2^2,I_2^2,L_2^2,U^2,W^2,V^2)$$
• P*: the steady state with endemicity of P. vivax in both human populations (with and without G6PD deficiency)

  $$(S_1,E_1,I_1,L_1,S_2,E_2,I_2,L_2,U,W,V)=(S_1^{*},E_1^{*},I_1^{*},L_1^{*},S_2^{*},E_2^{*},I_2^{*},L_2^{*},U^{*},W^{*},V^{*}).$$

3.2 The basic reproductive number

The basic reproductive number (R₀) is a useful quantity to potentially determine whether a disease can spread through a population and is defined as the expected number of secondary infections resulting from an introduction of a single infected individual into a completely susceptible population. If R₀ < 1, a few infected individuals introduced into a disease-free population fail to replace themselves and hence the disease will not spread (Brauer et al., 2008). On the other hand, if R₀> 1, the number of infected individuals will increase with each generation and consequently the disease will spread.

To calculate the basic reproductive number of (1), we use a method of the next-generation matrix where the element (i, j) of the matrix represents the expected number of new infections of type i caused by an (infected) individual of type j (Diekmann and Heesterbeek, 2000; Diekmann et al., 2010). There are five types of infections in the baseline model: E, I, L, W, and V. Hence, the next generation matrix is

$$K=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{a{p}_h}{\eta }\hfill \\ \hfill \frac{\varphi }{\mu +\varphi }\hfill & \hfill 0\hfill & \hfill \frac{\omega }{\mu +\omega +\delta }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{m\tau }{\mu +\gamma }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{a{p}_{m}q}{\mu +\tau }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\gamma }{\eta +\gamma }\hfill & \hfill 0\hfill \end{array}\right],$$

where q = M/N. The basic reproductive number of (1) is then the maximum eigenvalue of the K matrix (Diekmann and Heesterbeek, 2000; Diekmann et al., 2010) and is given by:

$$R_0=\sqrt{\frac{1}{2}(\frac{m\tau }{(\mu +\tau )}\frac{\omega }{\mu +\omega +\delta }+\sqrt{{\left(\frac{m\tau }{(\mu +\tau )}\frac{\omega }{\mu +\omega +\delta }\right)}^2+4\frac{\varphi }{(\mu +\varphi )}\frac{a^2{p}_h{p}_{m}q\gamma }{(\mu +\varphi )(\mu +\tau )\eta (\eta +\gamma )}})}.$$

Therefore, the basic reproductive number depends on infectiousness durations in humans and mosquitoes, incubation periods of malaria parasites in humans and mosquitoes, the average time from a primary attack to a relapse, the probability of carrying hypnozoites after a course of treatment, a mosquito:human ratio, and a biting rate of mosquitoes, for instance. However, when incubation of malaria parasites in both humans and mosquitoes is not considered or the E and W compartments are removed, and transmission directly brings exposed hosts to the I compartment (so that İ = ap_h(S + L)V/N + ωL − (μ + τ)I) and exposed vectors to the V compartment (so that V̇ = ap_mUI/N − ηI), by the similar method, the basic reproductive number is in a simple form as follows:

$$R_0=\sqrt{\frac{m\tau }{(\mu +\tau )}\frac{\omega }{\mu +\omega +\delta }+\frac{a^2{p}_h{p}_{m}q}{(\mu +\tau )\eta }}.$$

This term is a square root of two components that relate to infections caused by transmission between humans and mosquitoes, and relapses from infectious hosts who do not die and become hypnozoite carriers.

When G6PD deficiency is taken into account, separating types of infections from both groups of humans (with and without G6PD deficiency) in the calculation of the basic reproductive number of (2) (E₁, I₁, L₁,E₂, I₂,L₂,W, and V) leads to the characteristic polynomial of order 8 of the next-generation matrix. Consequently, it is not possible to find an explicit maximum solution of the characteristic equation or the basic reproductive number. However, when similar types of infections from both groups of humans are added together (E = E₁ + E₂, I = I₁ + I₂, L = L₁ + L₂,W, V) and the probability that an individual has or has no G6PD deficiency (p and 1 − p, respectively) is considered, it is possible to find an explicit form of the basic reproductive number of (2) and the next-generation matrix is described by:

$$K=\left[\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{p\sigma a{p}_h}{\eta }+\frac{(1-p)a{p}_h}{\eta }\hfill \\ \hfill \frac{\varphi }{\mu +\varphi }\hfill & \hfill 0\hfill & \hfill \frac{\omega }{\mu +\omega +\delta }\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{m\tau }{\mu +\gamma }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{pa{p}_{m1}q}{\mu +\tau }+\frac{(1-p)a{p}_{m2}q}{\mu +\tau }\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\gamma }{\eta +\gamma }\hfill & \hfill 0\hfill \end{array}\right],$$

Therefore, when the protection from having G6PD deficiency is considered, the basic reproductive number is

$$R_0=\sqrt{\frac{1}{2}(\frac{m\tau }{(\mu +\tau )}\frac{\omega }{\mu +\omega +\delta }+\sqrt{{\left(\frac{m\tau }{(\mu +\tau )}\frac{\omega }{\mu +\omega +\delta }\right)}^2+4\frac{\varphi }{(\mu +\varphi )}\frac{\gamma }{(\mu +\varphi )\eta (\eta +\gamma )}{\gamma }_1{\gamma }_2})},$$

with $r_1=(\frac{p\sigma a{p}_h}{\eta }+\frac{(1-p)a{p}_h}{\eta })$ and $r_2=(\frac{pa{p}_{m1}}{(\mu +\tau )}+\frac{(1-p)a{p}_{m2}}{(\mu +\tau )}).$. Clearly, the probability that an individual has G6PD deficiency (p) and a level of protection against P. vivax infection (σ) are associated with the basic reproductive number and the persistence of P. vivax. When incubation of malaria parasites in both humans and mosquitoes is not considered or the E₁, E₂, and W compartments are removed, and transmission directly brings exposed hosts to the I₁ and I₂ compartments (so that İ₁ = σap_h(S₁ + L₁)V/N + ωL₁ − (μ + τ)I₁ and İ₂ = ap_h(S₂ + L₂)V/N + ωL₂ − (μ + τ)I₂) and exposed vectors to the V compartment (so that V̇ = ap_m1UI₁/N + ap_m2UI₂/N − ηI), by the similar way of calculating the basic reproductive number and by further assuming that p_m1 = p_m2 = p_m, the basic reproductive number is in a simple formula as follows:

$$R_0=\sqrt{\frac{m\tau }{(\mu +\tau )}\frac{\omega }{(\mu +\omega +\delta )}+\frac{p\sigma a^2{p}_h{p}_{m}q}{(\mu +\tau )\eta }+\frac{(1-p)a^2{p}_h{p}_{m}q}{(\mu +\tau )\eta }}.$$

Note that this term is comprised of three components; the first term is associated with infections from relapses; and the second and third terms are associated with infections from transmission between mosquitoes and humans with G6PD deficiency and without G6PD 14 deficiency, respectively.

4 Results

4.1 The baseline model for P. vivax transmission

Patterns of incubation periods and relapses

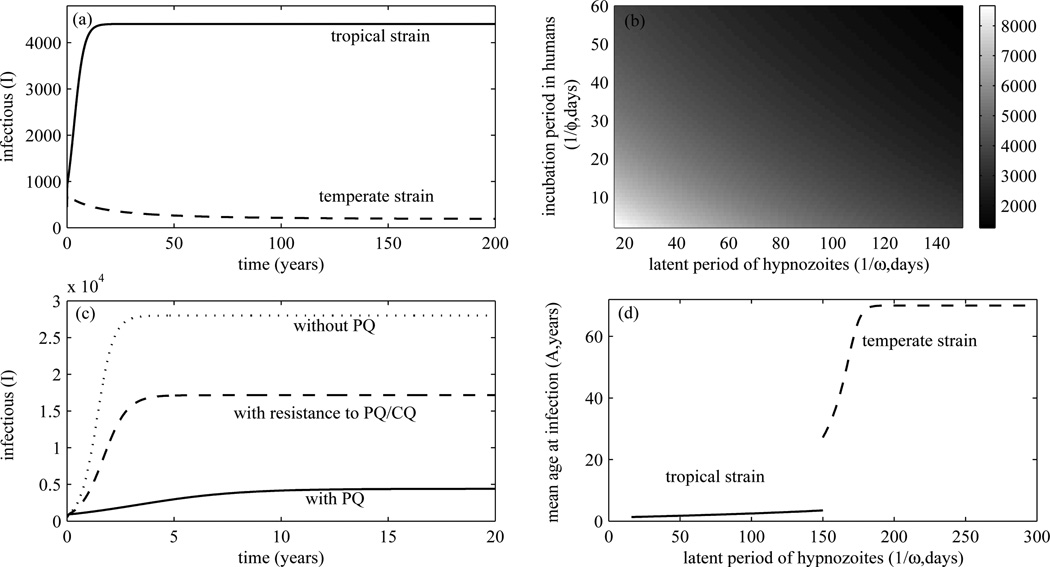
Tropical strains of P. vivax are distinguished from temperate strains by an early primary attack and a short latent period of hypnozoites (Craig and Kain, 1996). In Figure 3(a), it is more likely that a tropical strain of P. vivax leads to the higher number of infectious patients than a temperate strain. Figure 3(b) shows that the shorter the incubation period of malaria parasites in humans and the latent period of hypnozoites, the higher the number of humans infected with P. vivax. This finding results in a general conclusion that the of P. vivax cases in tropical regions may be higher than temperate regions.

Figure 3.

(a) shows the number of infectious humans in tropical and temperate regions over time. (b) shows the higher number of infectious humans when the incubation period of parasites and the latent period of hypnozoites become short. The number of infectious humans over time with the use of PQ and its resistance in tropical regions is shown in (c) (m = 0.3, p_m = 0.08 for resistance to PQ/CQ)(see Table 1 for other parameters). PQ and CQ help reduce P. vivax cases. (d) shows the mean age at infection of the human population in tropical and temperate regions. The mean age at infection is extended when the latent period of hypnozoites becomes longer.

Primaquine (PQ)

We here investigate the impact of the use of PQ therapy in tropical regions. Without PQ therapy, persons in an endemic area are at risk of having relapses ranging from 5% to 80%. For example, in Thailand, 63% of infected persons in an endemic area may have relapses without PQ therapy, whereas 18% of them may have relapses when PQ is prescribed (Baird and Hoffman, 2004). Figure 3(c) shows that without PQ therapy the endemic number of P. vivax cases may reach 56% of the human population in an endemic area while it approaches 8.8% of the human population if PQ treatment is administered. Resistance to PQ and CQ of P. vivax is still elusive (Baird, 2009). However, if resistance to PQ leads to a higher probability of infectious patients to become hypnozoite carriers (0.18 ≤ m ≤ 0. 63 for tropical strains and 0.13 ≤ m≤ 0.68 globally) and resistance to CQ leads to a higher probability of mosquito infection upon biting an infectious human (p_m is increased as infectious individuals with CQ resistance may have higher levels of parasitaemia) for example, it may lead to the higher number of humans infected with P. vivax in the endemic area than when the resistance is absent (also see Figure 3(c)). Moreover, because PQ can cause a life-threatening haemolytic anaemia in patients with G6PD deficiency so that it cannot be prescribed if G6PD testing is not available, this may lead to a higher rate of relapse that consequently results in the higher number of humans infected with P. vivax among humans in the endemic area.

Mean age at infection

The mean age at infection or the mean time that a human remains susceptible to P.vivax (Keeling and Rohani, 2007) can be estimated by the following formula:

$$A=\frac{1}{a{p}_{h}V*/N+\mu },$$

where V* is the endemic prevalence of infectious mosquitoes. It can be derived from the RHS of the first equation of (1) for Ṡ. Figure 3(d) shows the host’s mean age at infection when a latent period of hypnozoites varies. For tropical strains of P. vivax that have short incubation periods and short latent periods of hypnozoites, the mean age at infection is approximately less than four years (with 1/ϕ = 15 days, m = 0.13, and 1/ω ≤ 150 days). In contrast, temperate strains that have longer incubation periods and longer latent periods of hypnozoites, the mean age at infection is lengthened and ranges from 30–70 years (with 1/ϕ = 27 days, m = 0.13, and 1/ω ≥150 days). Hence, persons living in the P. vivax endemic areas in tropical regions are more likely to become infected at earlier ages than the temperate regions as the mean age at infection increases when a latent period of hypnozoites increases.

Seasonality

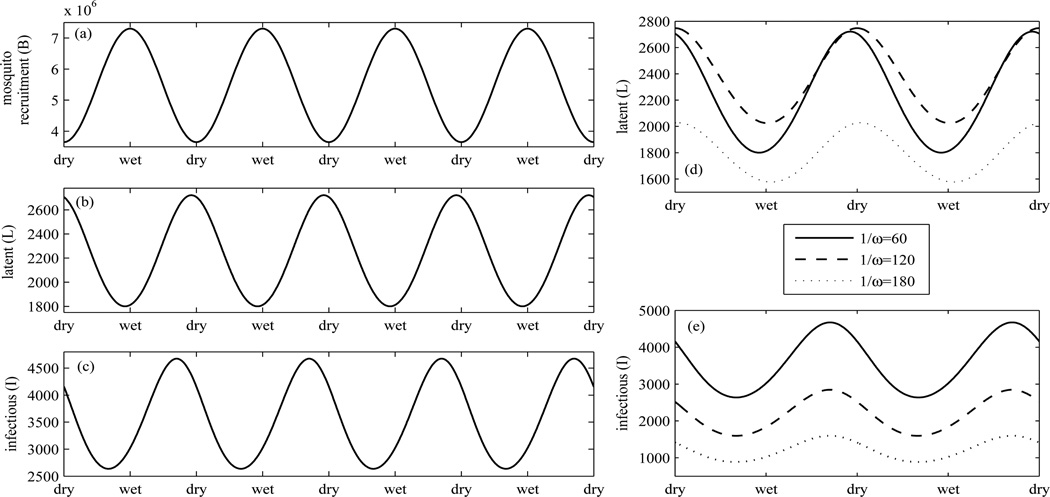
Mosquito abundance is greatly influenced by rainfall. We investigate this impact on the number of P. vivax cases (long-term behaviors) particularly in tropical regions by assuming that the recruitment rate of mosquitoes is highest at the middle of every wet season and lowest at the middle of every dry season and can be expressed as a sinusoidal function of the recruitment rate of mosquitoes as follows:

$$B=B_0(1-B_1\text{cos}2\pi t),$$

with B_min = ηM_min = ηq_minN, B_max = ηM_max = ηq_maxN (q_min = 1, q_max = 2), B₁ = (B_max/B_min − 1)/(B_max/B_min + 1), and B₀ = B_max/(1 + B₁), B_min = ηM_min = ηq_minN (see 16 Figure 4(a)). The number of diseased individuals is time-periodic with a peak of the number of hypnozoite carriers at nearly the middle of each dry season and a peak of the number of infectious persons at a few months after the beginning of each dry season (see Figure 4(b)–(c)). Consequently, infectious humans who transmit P. vivax to mosquitoes may be highly prevalent during a few months before the end of a wet season until a few months after the middle of a dry season. Hence, the follow-up of patients who carry hypnozoites after antimalarial therapy may be efficiently done during a dry season. These findings may be useful to help design control strategies in an attempt to reduce the prevalence and incidence of P. vivax. Furthermore, we investigate how a latent period of hypnoziotes affects the number of hynozoite carriers and infectious persons. Figure 4(d) shows that an intermediate latent period may lead to the higher number of hypnozoite carriers and there may be delay of a peak when the latent period of hyponozoites increases. However, the longer latent period of hypnozoites does not seem to delay but instead reduce a peak of the number of infectious humans (see Figure 4(e)).

Figure 4.

(a)–(c) show the recruitment rate of mosquitoes, the number of hypnozoite carriers, and the number of infectious humans, respectively, according to the seasonal abundance of mosquitoes. The abundance of mosquitoes plays a crucial role on the number of P. vivax cases. The impact of the latent period of hypnozoites on the number of hypnozoite carriers and the number of infectious humans over seasons is demonstrated in (d)–(e).

4.2 The P. vivax model with G6PD deficiency

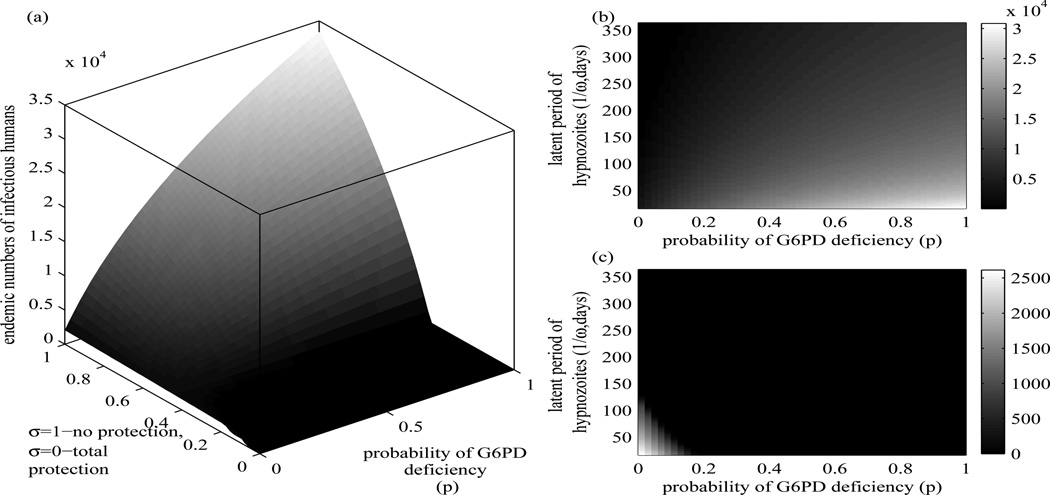
Figure 5(a) shows that the number humans infected with P.vivax increases when a proportion of humans with G6PD deficiency in a human population increases and a level of protection against P vivax infection decreases. In Figure 5(b), with weak protection against infection with P. vivax in persons with G6PD deficiency (σ is toward 1), the number of infectious humans increases according to the larger proportion of humans with G6PD deficiency and the shorter latent period of hypnozoites. In Figure 5(c), in case the G6PD deficiency variants in individuals give strong protection against P. vivax infection (σ is toward 0), the number of infectious humans increases according to the fewer number of humans with G6PD deficiency and the shorter latent period of hypnozoites. Consequently, the number of humans infected with P. vivax may be high in areas that the variants of P. vivax with short latent periods of hypnozoites are endemic and larger numbers of persons with G6PD deficiency variants that do not give protection or give less protection against P. vivax infection (σ is toward 1) live. In case G6PD deficiency gives strong protection against P. vivax infection (σ is toward 0), the larger the proportion of humans with G6PD deficiency, the less the number of P. vivax cases in the areas. Hence, P. vivax might go extinct or remain endemic in a very low level in some areas where G6PD deficiency variants give strong protection against P. vivax infection.

Figure 5.

The endemic number of infectious humans varies in relation to: (a) the level of protection and the probability of having G6PD deficiency, (b) the latent period of hypnozoites and the probability of having G6PD deficiency with weak protection (σ = 0.7), (c) similar to (b) but with strong protection (σ = 0. 3). All of the probability of having G6PD deficiency, the level of protection, and the latent period of hyponozoites are important factors in determining the endemic level of P. vivax.

5 Conclusions and discussion

The Ross-Macdonald model is a simplified structure that is often used in modeling vectorborne diseases especially with P. falciparum malaria (Macdonald, 1957). However, P. vivax has different features from P. falciparum. One of them is the ability to relapse from latentstage parasites that remain dormant for weeks, months, or years after a course of treatment. In this work, a baseline model for P. vivax was developed by including relapses and the possibility of reinfection of hypnozoite carriers in an attempt to understand how patterns of relapses of hypnozoites and incubation periods of parasites in tropical and temperate regions influence the number of infected humans and transmission dynamics of P. vivax, and the mean age at infection of the human population. Furthermore, the baseline model was extended in order to investigate how protection against P. vivax infection in persons with G6PD deficiency affects the number of infected humans in endemic areas.

The baseline model suggests that the number of humans infected with P. vivax may increase according to a shorter incubation period of parasites in humans and a shorter latent period of hypnozoites. Hence, it is possible that the number of P. vivax cases in tropical regions is higher than temperate regions as tropical variants of P. vivax tend to have shorter incubation periods and latent periods of hypnozoites. This model prediction corresponds to the national statistics reported by the World Health Organization in 1999 that the greatest burden of P. vivax occurred in South and East Asia (Price et al., 2007). Without treatment, individuals may stay infectious longer (a smaller τ) and may be more likely infectious to mosquitoes (a larger p_m). Consequently, this may lead to the higher number of humans infected with P. vivax as compared to having treatment. Hence, the number of humans infected with P. vivax in this study that assumed all infectious individuals treated may be lower than by assuming that all infectious individuals are untreated or only some of them are treated.

The model results suggest that a shorter incubation period of malaria parasites in humans and a shorter latent period of hynozoites may reduce the mean age at infection so that humans in tropical regions may be at risk of getting infected with P. vivax at earlier ages (or becoming reinfected in a shorter period) than temperate regions. For P. falciparum, persons with no clinical immunity in the hyperendemic malaria zones may experience one to five clinical attacks per year (Greenwood et al., 1991; Gupta and Day, 1994). For P. vivax, based on the mean age at infection formula in this study, it predicts that for tropical strains with two months as a latent period of hypnozoites (for instance) and with the use of PQ to prevent relapses, susceptible persons may experience clinical attacks in two years. Persons who carry hypnozoites of P. vivax may experience clinical attacks in a shorter period due to relapses or reinfections with different strains of P. vivax. Note that all infected persons are assumed to be treated and some parameters used in this study are assumed to be smaller than P. falciparum and cause a low level of prevalence, so the basic reproductive number used in this study might be rather small and the mean age at infection might be slightly high for a hyperendemic area.

The abundance of Anopheles mosquitoes can be driven by the amount of rainfall (Altizer et al., 2006). As many of Anopheles mosquitoes breed in small pools of clean water, droughts may limit the number of their breeding sites, and consequently decrease the mosquito population and transmission of malaria parasites (Gage et al., 2008). One of the previous crosssectional studies in Vanuatu has suggested that P. falciparum is predominant in the long wet season and P. vivax in the dry season (Maitland et al., 1996). Here, by incorporating seasonal forcing of mosquitoes into the model, in such a way that the number of mosquitoes is highest at the middle of every wet season and lowest at the middle of every dry season, the model predicts that the number of infectious humans peaks at a few months after the beginning of each dry season, and the number of hypnozoite carriers peaks at nearly the middle of each dry season. This finding is parallel with the previous empirical finding for P. vivax. Both may help to identify time periods for controlling P. vivax in humans and mosquitoes effectively.

PQ is the only licensed drug to prevent relapses. Without PQ, it may lead to a higher rate of relapse and consequently the higher number of P. vivax cases. PQ may cause a life-threatening haemolytic anemia in patients with G6PD deficiency so that it is not recommended and cannot be prescribed if G6PD testing is not available in areas that P. vivax is endemic. However, some variants of G6PD deficiency may provide partial protection against malaria infection that the presence of P. vivax infected patients with G6PD deficiency is less than the general population (Leslie et al., 2010). By taking into account the presence of G6PD deficiency in humans, its possible protection against P.vivax infection, and its consequence when primaquine cannot be administered, the model predicts that P. vivax is highly prevalent when (i) protection of G6PD deficiency variants to P. vivax infection is weak (σ → 1), (ii) a proportion of persons with G6PD deficiency in the human population is high (p → 1), and (iii) a latent period of hypnozoites is short. This finding supports previous empirical findings in Pakistan (Leslie et al., 2010) and provides important insights in understanding transmission dynamics and the number of P. vivax cases in areas that individuals with G6PD deficiency are present. With a global effort to eliminate malaria, mass drug administration with PQ could be a powerful strategy if it can be implemented safely and effectively and information on G6PD deficiency may be vital. (Kuwahata et al., 2010). Hence, further investigations are needed and it may be useful to extend this work to investigate how the distribution of G6PD deficiency variants and the levels and types of protection conferred by different G6PD variants influence the transmission dynamics of P. vivax. This study may also support some similar findings that suggest the rarity of P. vivax malaria in western or central continental Africa where the majority of the human population (95%–99%) has the Duffy-negative antigen (Miller et al., 1976) in that very strong protection against P. vivax infection and a high proportion of individuals who have the protection in the population may lead to a very low-level of the prevalence or even the absence of P. vivax in the areas. Note that individuals who do not express Duffy antigens (encoded by Fy gene) on their red blood cells are classified as Duffy negative. As the Duffy antigen acts as a receptor for P. vivax, Duffy-negative people may be resistant to P. vivax infection (Miller et al., 1976). However, some recent studies suggest that some Duffy-negative individuals can be infected by P. vivax parasites (Culleton et al., 2008, 2009; Mendes et al., 2011).

All in all, we believe that this work is primarily useful in identifying the important variables in determining the number of P. vivax cases, and making predictions for the population-level effects relating to different patterns of relapses and incubation periods of malaria parasites, variation of therapies, seasonality, G6PD deficiency and its possible protection against P. vivax infection. The challenge remains to consider other types of protection in persons with G6PD deficiency, asymptomatic infection, and coexistence of P. vivax with P. falciparum.

Highlights.

>Mathematical modeling is employed to investigate the transmission dynamics of P. vivax. >The mean age at infection and seasonality are also considered. >Incubation periods of parasites and hypnozoites are important predictors. > The proportion of humans with G6PD deficiency is also a predictor.