A Family-Based Probabilistic Method for Capturing De Novo Mutations from High-Throughput Short-Read Sequencing Data

Abstract

Recent advances in high-throughput DNA sequencing technologies and associated statistical analyses have enabled in-depth analysis of whole-genome sequences. As this technology is applied to a growing number of individual human genomes, entire families are now being sequenced. Information contained within the pedigree of a sequenced family can be leveraged when inferring the donors' genotypes. The presence of a de novo mutation within the pedigree is indicated by a violation of Mendelian inheritance laws. Here, we present a method for probabilistically inferring genotypes across a pedigree using high-throughput sequencing data and producing the posterior probability of de novo mutation at each genomic site examined. This framework can be used to disentangle the effects of germline and somatic mutational processes and to simultaneously estimate the effect of sequencing error and the initial genetic variation in the population from which the founders of the pedigree arise. This approach is examined in detail through simulations and areas for method improvement are noted. By applying this method to data from members of a well-defined nuclear family with accurate pedigree information, the stage is set to make the most direct estimates of the human mutation rate to date.

1 Introduction

As the characterization of genetic variation is a primary goal of genetics, an important aspect of that pursuit is studying the mutational origin of DNA sequence variants and quantifying the rate at which they occur. Motivation for understanding the nature of spontaneous, de novo, mutation is especially high in human medical genetics where they can contribute to disease and disease susceptibility (Awadalla et al., 2010, Marshall et al., 2009, Sayed et al., 2009, Vissers et al., 2009). Attempts to measure mutation rates in humans fall into two broad categories: direct methods (Roach et al., 2010, Xue et al., 2009) that estimate the number of mutations that have occurred in a known number of generations and indirect methods (Kondrashov, 2003, Lynch, 2010) that infer mutation rates from levels of genetic variation within or between species. These previous estimates represent an average across multiple generations.

With high throughput sequencing, a new type of approach has become feasible: identification of de novo mutations from whole-genome sequence data in human pedigrees. A simple approach is to independently call consensus genotypes on each family member and subsequently compare them to identify apparently new alleles present in the offspring. However, high throughput sequencing data can suffer from high error rates (due to base calling, alignment errors, low coverage, and other factors) leading to unavoidable uncertainty in genotype assignments across loci and individuals (Nielsen et al., 2011). Furthermore, genotype calling will typically lead to under-calling of heterozygous genotypes. Missing heterozygous sites in a child will contribute to false-negative mutational calls while an undetected heterozygous parent can lead to false positives (Figure 1).

Figure 1.

Under-calling heterozygous genotypes affects de novo detection at a given site. In the top panel, the mother’s genotype is called AA by the sample-independent approach since the binomial probability of sampling once the C allele among 20 reads if the mother is heterozygote is very small. (Nielsen et al., 2011, suggest calling a site homozygous if the minor allele is less than 20%, a rule which we adopt for these examples.) When the family data is considered jointly, identifying a C in the child increases the probability of the AC genotype for the mother, leading to a low probability of de novo mutation at this site. (It is much more likely that the mother’s chromosomes were sampled unevenly, ≈10⁻⁵, than that there is an actual mutation at the site, ≈10⁻⁸.) In the bottom panel, the child’s genotype is called AA. However, given an error rate and the parental coverage, the probability of a de novo mutation at this site is high. The de novo mutation probabilities were computed using the method described here with the following parameters: θ = 0.001, ε = 0.005, μ = μ_s = 2 × 10⁻⁸. (See section 2.1 for a description of these parameters.)

In order to make the most accurate genotyping calls possible, we present here a novel approach leveraging a probabilistic framework that uses the relatedness between the individuals to simultaneously infer genotypes at each site, taking full advantage of the information within the pedigree. This approach aims to identify candidate de novo mutations starting from read-level data and to produce direct estimate of the spontaneous mutation rate, as well as other important parameters such as the error rate of the sequencing technology and the population mutation rate for the population from which the samples were drawn.

The method described below will have substantial impact on studies interrogating partial or whole genome analyses aimed at asking which mutations contribute to sporadic disease or cancer and determining the genomic and population distribution of mutations and their characteristics (e.g. base composition, transitions/transversions, etc.). Until the development of this method, no other model-based approach has existed.

In a companion study (Conrad et al., 2011), we have applied our method to the “Pilot 2” dataset generated by the 1000 genomes project (Durbin et al., 2010). The Pilot 2 dataset consists of two father-mother-daughter trios sequenced to a post-mapping coverage greater than 22×. Conrad et al. (2011) used two other methods, including the traditional, family-independent method mentioned above, facilitating the comparison of these methods on human data.

This article is organized as follows. First, we introduce the model developed to produce a joint probability for the entire pedigree at each site and present the computational methods used, namely an EM algorithm to estimate the model parameters and a tree-peeling algorithm (Felsenstein, 1981) to recursively calculate the model probability. We then report on simulations conducted to assess the performance of the method. Finally, we conclude by discussing the principal assumptions currently made and the main biological applications of the method.

2 Probabilistic Inference of De Novo Mutations

2.1 Model Overview

A probabilistic model was constructed to account for the uncertainty and error in the process of de novo mutation discovery. The data used by our model falls into two categories. The observed data, R, consists of aligned sequence reads from each individual. The observed data derives from the hidden data, H, which is comprised of the actual parental and offspring genotypes, the pattern of inheritance, somatic and germline mutation events, how the chromosomes are sampled by the sequencing reads, and any sequencing error events. While R is observed as the product of sequencing reactions and genome assembly, H is not directly observed and must be inferred to estimate de novo mutations.

In order to simplify the biology, we assume that sites are independent, and thus the probability of all of our data is simply the product of the probabilities of each site:

$$P(R,H|\mathrm{\Theta })=\prod _{x=1}^{N_s}P(R_x,H_x|\mathrm{\Theta })$$ (1)

where R_x and H_x are the observed and hidden data associated with site x, N_s is the total number of sites, and Θ contains the parameters of the model:

θ	the per-site, population diversity parameter; θ = 4Neμ
μ	the per-site, per-generation germline mutation rate
μs	the per-site somatic mutation rate
ε	the per-site sequencing error rate

Treating each site independently allows us to parallelize our implementation and speed up analysis on modern computing clusters.

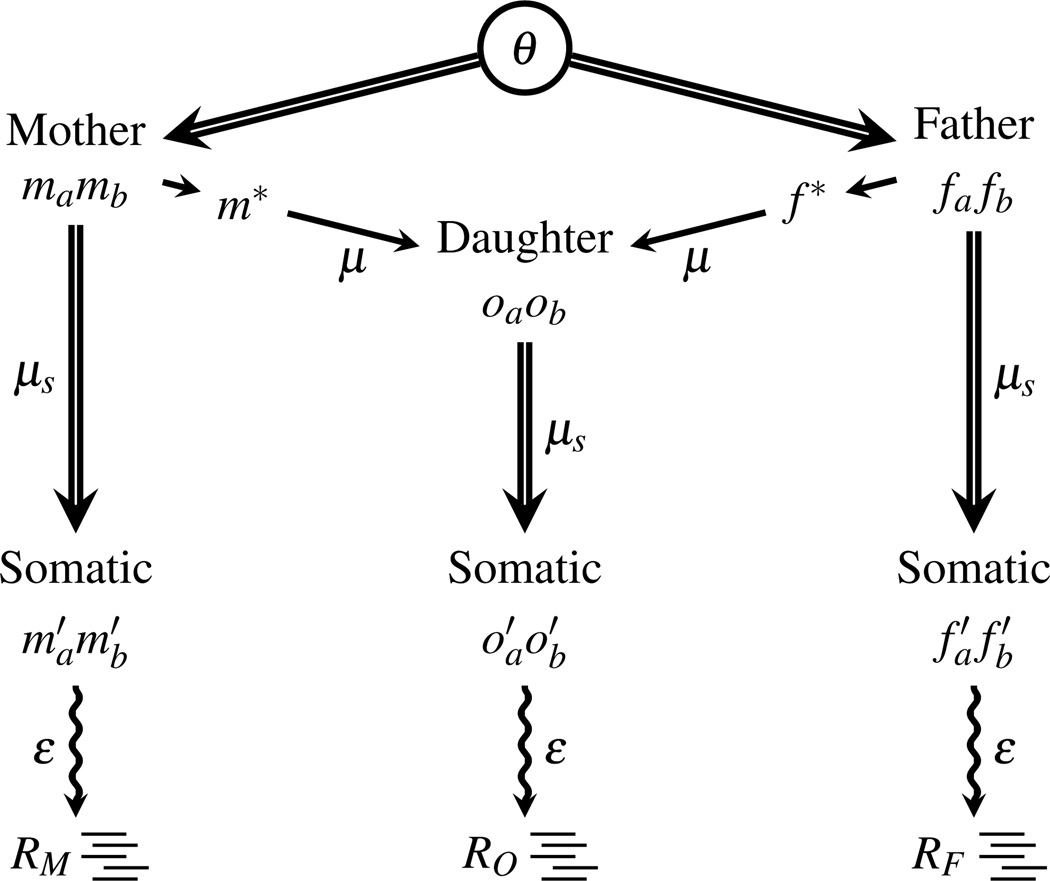
Our model is a generative model because it describes the process by which the observed data is generated from the hidden data. For a single family, including two parents and one offspring (hereafter referred to as a “trio”), the pedigree structure of the model is depicted in Figure 2. For simplicity, we will drop the site-specific subscript for the rest of the paper in our equations.

1. Starting from the root of the pedigree, the parental genotypes m = m_am_b and f = f_af_b are sampled from a population at equilibrium. These four nucleotides are the founders of the pedigree and form the zygotic genotypes of the two parents. The distribution of these alleles is calculated in a coalescent framework utilizing θ and allowing for at most two mutations on the coalescent genealogy. This allows the model to include sites with three segregating alleles, which is necessary with doing whole genome studies.

2. From this sample of nucleotides, one is transferred from each parent to the offspring, m^* and f^*, with the possibility of germ-line mutation at rate μ, to form the daughter’s zygotic genotype o = o_ao_b. The allele from chromosome a in the offspring is arbitrarily labeled as the allele inherited from the mother after possible mutation.

3. The original zygotic genotypes for each individual are independently passed through a somatic cell lineage to the tissue sampled for sequencing and somatic mutations accumulate at the per-nucleotide rate of μ_s to form the three somatic genotypes m′, f′, and o′.

4. The genotypes are sampled by sequencing with an error rate of ε per base, producing the observed data R = {R_M, R_F, R_O}. Each read samples a chromosome at random. There are N_RM reads sampled from the mother at this site, N_RF reads from the father, and N_RO from the daughter, so R is fully partitioned into R_Z = {R_Z1, R_Z2, …,R_ZNRZ} with the four possible nucleotide bases R_Zk ∈ {A,C,G,T} and Z ∈ {M,F,O}.

Figure 2.

Trio model for a single site. Nucleotide bases from the sequencing reads aligning to the site of interest (R = {R_M, R_F, R_O}) are the observed data. Neither individual genotypes nor their transmission pattern are observed; they are the hidden data. Double lines denote the transmission/sampling of diploid genotypes, while single lines haploid genotypes. The parental zygotic genotypes (m = m_am_b and f = f_a f_b) are sampled from a common population and are the founding alleles of the pedigree. Wavy lines denote where sequencing takes place. The parameters in the model have been placed in proximity to the branches that they affect.

2.2 Probability of the Observed Data

The probability of the full data at a single site is calculated based on the pedigree in Figure 2. The full data contains the identity of each genotype-node in the pedigree and the nature of the genetic transmission between nodes. The probability can therefore be calculated as the product of many transmission probabilities.

$$P=(R,H|\mathrm{\Theta })=P(m,f|\theta )\times P(o|m,f,\mu )\times P(o\prime |o,{\mu }_s)\times P(R_o|o\prime ,\epsilon )\times P(m\prime |m,{\mu }_s)\times P(R_M|m\prime ,\epsilon )\times P(f\prime |f,{\mu }_s)\times P(R_F|f\prime ,\epsilon )$$ (2)

The probability of the observed data is calculated by marginalizing over the hidden data:

$$P(R|\mathrm{\Theta })=\sum _{H}P(R,H|\mathrm{\Theta })$$ (3)

2.2.1 Population Model

The population model describes the probabilities when two genotypes of the parents are sampled from the same population. This probability is derived using coalescent theory (Kingman, 1982) under the finite sites model of mutation (Yang, 1996). The nucleotides m_a, m_b, f_a, and f_b are the founder alleles of the pedigree and constitute a sample from a finite, randomly-mating population, with effective size of N_e. Mutations are allowed to occur continuously along the genealogical tree connecting the four sampled nucleotides, back to their most recent common ancestor. Assuming that the population mutation rate θ is small, the probability that three or more mutations occurred in a single genealogy is negligible. Therefore the following allele spectra are possible:

4-0-0	all alleles are the same
3-1-0	two allele states, with the minor allele occurring once
2-2-0	two allele states, with the minor allele occurring twice
2-1-1	three allele states

While SNPs are nearly always modeled using two allele states, tri-allelic SNPs are more common than de novo mutations, and thus by modeling them we reduce false positives.

In general, the distribution of genotype patterns is given by the integration of the probability of mutations occurring over the length of the genealogical tree and summing the results across all groupings of mutations that can produce the possible allele spectrum (see Appendix). In addition, when calculating the probability of each parental genotype sample, the possible specific nucleotide used (assuming all are equal in frequency) and the possible order in which they occur must also be considered. The probabilities for the different allele spectra are given below:

$$P(4-0-0|\theta )=\frac{1}{4}(\frac{6}{6+11\theta }+\frac{19.7{\theta }^2}{(6+22\theta )(6+11\theta )})P(3-1-0|\theta )=\frac{1}{12\times 4}(\frac{48.7\theta }{36+132\theta }+\frac{37.7{\theta }^2}{(6+22\theta )(6+11\theta )})P(2-2-0|\theta )=\frac{1}{12\times 3}(\frac{17.3\theta }{36+132\theta }+\frac{22.3{\theta }^2}{(6+22\theta )(6+11\theta )})P(2-1-1|\theta )=\frac{1}{24\times 6}\left(\frac{41.3{\theta }^2}{(6+22\theta )(6+11\theta )}\right)$$ (4)

See Appendix for equations with higher precision.

2.2.2 Mutations and Error Models

We assume that mutations and sequencing errors happen via a homogeneous Poisson process, in which all four nucleotides are equally likely and exchangeable (i.e. the Jukes and Cantor, 1969, substitution model). While this model is oversimplified for genomic data, it reduces the amount of calculations that our implementation needs to preform because sites with the same pattern of allele counts will have the same probability. For example, the probability of 4 As and 2 Ts is the same as 2 As and 4 Ts. A single probability function is used to develop all mutation and error models:

$$P(i|j,u)=\frac{1}{4}(1-e^{-4u/3})+\mathrm{I}(i=j)e^{-4u/3}$$ (5)

where i and j are specific nucleotides, u is the mutation or error rate, and I is an indicator function that is 1 if i = j and 0 otherwise.

Somatic mutation

The somatic mutation model is the product of two mutation models, one for each nucleotide of the diploid genotype:

$$P(x\prime |x,{\mu }_s)=P(x_a^{\prime }|x_a,{\mu }_s)\times P(x_b^{\prime }|x_b,{\mu }_s)$$

Germline mutation

The germline mutation model is similar in form to the somatic mutation model, but adds the complicating factor of selecting the alleles inherited from the parents to the offspring zygote. To simplify computation, the possible inheritance patterns are marginalized out in this model:

$$P(o|m,f,\mu )=\sum _{m^{*},f^{*}}P(o_a|m^{*},\mu )P(o_b|f^{*},\mu )P(m^{*}|m)P(f^{*}|f)=\{\begin{array}{cc}\frac{1}{4}+\frac{3}{4}{e}^{-4\mu /3}\hfill & \text{if}{o}_a=m_a=m_b\hfill \\ \frac{1}{4}+\frac{1}{4}{e}^{-4\mu /3}\hfill & \text{if}{o}_a=m_a\ne m_b\text{or}{o}_a=m_b\ne m_a\hfill \\ \frac{1}{4}-\frac{1}{4}{e}^{-4\mu /3}\hfill & \text{if}{o}_a\ne m_a\text{and}{o}_a\ne m_b\hfill \end{array}\times \{\begin{array}{cc}\frac{1}{4}+\frac{3}{4}{e}^{-4\mu /3}\hfill & \text{if}{o}_b=f_a=f_b\hfill \\ \frac{1}{4}+\frac{1}{4}{e}^{-4\mu /3}\hfill & \text{if}{o}_b=f_a\ne f_b\text{or}{o}_b=f_b\ne f_a\hfill \\ \frac{1}{4}-\frac{1}{4}{e}^{-4\mu /3}\hfill & \text{if}{o}_b\ne f_a\text{and}{o}_b\ne f_b\hfill \end{array}$$

The cases correspond to whether parental genotype is homozygous or heterozygous and whether the child’s allele matches one of the parental alleles.

Sequencing error

The sequencing error model includes the basic mutation model at its core and calculates the joint probability for all N reads for one individual, x, at a site. An additional element to this model is the probability, p, that chromosome a of genotype x′ is sampled by a read.

$$P(R|x\prime ,\epsilon )=\prod _{k=1}^N[pP(R_k|x_a^{\prime },\epsilon )+(1-p)P(R_k|x_b^{\prime },\epsilon )]$$ (6)

When x′ is homozygous, $x_a\prime =x_b\prime$ and Equation 6 simplifies to

$$P(R|x\prime ,\epsilon )={(\frac{1}{4}+\frac{3}{4}{e}^{-4\epsilon /3})}^{{\sum }_k\mathrm{I}(R_k=x_a\prime )}\times {(\frac{1}{4}-\frac{1}{4}{e}^{-4\epsilon /3})}^{{\sum }_k\mathrm{I}(R_k\ne x_a\prime )}$$ (7)

When x′ is heterozygous, $x_a\prime \ne x_b\prime$ and Equation 6 simplifies to

$$P(R|x\prime ,\epsilon )={(\frac{1}{4}+[p-\frac{1}{4}\left]e^{-4\epsilon /3}\right)}^{{\sum }_k\mathrm{I}(R_k=x_a\prime )}\times {(\frac{1}{4}+[\frac{3}{4}-p\left]e^{-4\epsilon /3}\right)}^{{\sum }_k\mathrm{I}(R_k=x_b\prime )}\times {(\frac{1}{4}-\frac{1}{4}{e}^{-4\epsilon /3})}^{{\sum }_k\mathrm{I}(R_k\ne x_a\prime )\mathrm{I}(R_k\ne x_b\prime )}$$ (8)

Assuming that each chromosome is sampled equally, p = 0.5 and Equation 8 reduces to

$$P(R|x\prime ,\epsilon )={(\frac{1}{4}+\frac{1}{4}{e}^{-4\epsilon /3})}^{{\sum }_k\mathrm{I}(R_k=x_a\prime )+\mathrm{I}(R_k=x_b\prime )}\times {(\frac{1}{4}-\frac{1}{4}{e}^{-4\epsilon /3})}^{{\sum }_k\mathrm{I}(R_k\ne x_a\prime )\mathrm{I}(R_k\ne x_b\prime )}$$

2.3 Estimation of Model Parameters

The existence of hidden data makes estimating model parameters non-trivial. Some techniques like imputation (Li et al., 2009) infer the likely state of the hidden data, Ĥ, and then estimate parameters based on this estimation through maximum likelihood of the inferred full data:

$$\mathrm{\Theta ̂}=\underset{\mathrm{\Theta }}{\text{arg max}}P(R,Ĥ|\mathrm{\Theta })$$

Unfortunately, imputation does not produce maximum likelihoods that depend only on the real data, and the quality of these estimates may depend highly on the quality of the inferred Ĥ. During mutational analysis, imputation is expected to produced biased results as sites that may have a low probability of mutation always get resolved as having no mutation.

The proper solution is to estimate parameters from the marginal probability of the real data:

$$\mathrm{\Theta ̂}=\underset{\mathrm{\Theta }}{\text{arg max}}P(R|\mathrm{\Theta })=\underset{\mathrm{\Theta }}{\text{arg max}}\sum _{H}P(R,H|\mathrm{\Theta })$$

However, the summation makes finding a closed-form solution difficult. Luckily this can be solved iteratively using the expectation-maximization algorithm (EM; Dempster et al., 1977). EM can calculate true maximum-likelihood estimators (MLE) when there is hidden data. From an initial guess, Θ₀, the iteration is guaranteed to converge to a local MLE for the marginal probability. The E-step calculates a function, Q(Θ|Θ_;n), where

$$Q(\mathrm{\Theta }|{\mathrm{\Theta }}_n)=\sum _{H}P(R|H,{\mathrm{\Theta }}_n)\text{ln}P(R,H|\mathrm{\Theta })$$

and the M-step maximizes this function with respect to Θ, giving the next estimate of Θ:

$${\mathrm{\Theta }}_{n+1}=\underset{\mathrm{\Theta }}{\text{arg max}}Q(\mathrm{\Theta }|{\mathrm{\Theta }}_n)$$ (9)

The advantage of using EM to estimate parameters is that we simply need to determine the sufficient statistics for the full data, in order to find the MLE for the observed data. We can also directly estimate the variance of the MLEs (Louis, 1982), avoiding time-consuming techniques like bootstrapping.

2.3.1 Expectation Step

During the E-step, we calculate the expected values of several sufficient statistics for a site using the tree peeling algorithm (Felsenstein, 1981). Specifically, the statistics are

S400	the probability the parental zygotic alleles have the spectrum 4-0-0
S310	the probability the parental zygotic alleles have the spectrum 3-1-0
S220	the probability the parental zygotic alleles have the spectrum 2-2-0
S211	the probability the parental zygotic alleles have the spectrum 2-1-1
SM	the number of nucleotide mismatches between m* and oa
SF	the number of nucleotide mismatches between f* and ob
SSom	the number of nucleotide mismatches between all x and x′
SHom	the number of nucleotide matches between a somatic homozygous genotype and its sequencing reads
SHet	the number of nucleotide matches between a somatic heterozygous genotype and its sequencing reads
SE	the number of nucleotide mismatches between a somatic genotype and its sequencing reads.

The read coverage of somatic homozygous and heterozygous genotypes are summarized by S_Hom and S_Het. S_Som and S_E represent the total number of somatic mutations and of sequencing errors, respectively, in the pedigree. S_M and S_F represent the number of germline mutations from parental lineages.

We can efficiently calculate the expected sufficient statistics by “peeling” the family pedigree from the sequencing reads down to the zygotic genotypes of the parents. We consider the individual genotypes as nodes and the inheritance relationships as branches.

Let S_T (R_j, Y_j) be the statistic of type T calculated for node Y_j and its descendants, terminating with observed data R_j. Let S_T (R_j, X → Y_j) be the statistic due to the X → Y_j branch. The statistic for node X is calculated via a double sum over all the states of its immediate descendants, Y_j:

$$S_T(R,X)=\sum _j\left[\frac{{\sum }_{Y_j}P(Y_j|X)P(R_j|Y_j)\times [S_T(R_j,Y_j)+S_T(R_j,X\to Y_j)]}{{\sum }_{Y_j}P(Y_j|X)P(R_j|Y_j)}\right]$$

while

$$P(R|X)=\prod _j\sum _{Y_j}P(Y_j|X)P(R_j|Y_j)$$

And at the root of the tree/pedigree, the expected sufficient statistic is calculated as follows

$${\mathrm{S̄}}_T=\mathrm{E}(S_T)=\frac{{\sum }_X{S}_T(R,X)\times P(R|X)P(X)}{{\sum }_{X}P(R|X)P(X)}$$

while

$$P(R)=\sum _{X}P(R|X)P(X)$$ (10)

where here X represents a founder allele state. Note that we have dropped Θ from these equations for simplicity. See Appendix for further description of the tree peeling algorithm.

2.3.2 Maximization Step

By solving Equation (9), we calculated the equations needed for the M-step. Let ${\mathrm{S̃}}_T={\sum }_{s=1}^{N_s}{\mathrm{S̄}}_{T,s}$ be the sum of an expected sufficient statistic over the N_s independent sites. These sums are used to update the parameters of our model, using the equations below:

$$\mathrm{\mu ̂}=-\frac{3}{4}\text{log}[1-\frac{4}{3}\frac{{\mathrm{S̃}}_M+{\mathrm{S̃}}_F}{N_s}]{\mathrm{\mu ̂}}_s=-\frac{3}{4}\text{log}[1-\frac{4}{3}\frac{{\mathrm{S̃}}_{\mathit{\text{Som}}}}{N_s}]\mathrm{\epsilon ̂}=-\frac{3}{4}\text{log}[1-\frac{1}{3}\frac{3{\mathrm{S̃}}_{\mathit{\text{Hom}}}+2{\mathrm{S̃}}_{\mathit{\text{Het}}}+5{\mathrm{S̃}}_E-\sqrt{9{\mathrm{S̃}}_{\mathit{\text{Hom}}}^2+{(2{\mathrm{S̃}}_{\mathit{\text{Het}}}-{\mathrm{S̃}}_E)}^2+6{\mathrm{S̃}}_{\mathit{\text{Hom}}}(2{\mathrm{S̃}}_{\mathit{\text{Het}}}+{\mathrm{S̃}}_E)}}{{\mathrm{S̃}}_{\mathit{\text{Hom}}}+{\mathrm{S̃}}_{\mathit{\text{Het}}}+{\mathrm{S̃}}_E}]$$

In order to find the maximum likelihood estimate θ̂, we have to solve the following equation for θ:

$$\frac{d}{d\theta }[{\mathrm{S̃}}_{400}\text{log}P(4-0-0|\theta )+{\mathrm{S̃}}_{310}\text{log}P(3-1-0|\theta )+{\mathrm{S̃}}_{220}\text{log}P(2-2-0|\theta )+{\mathrm{S̃}}_{211}\text{log}P(2-1-1|\theta )]=0$$ (11)

The solution is equivalent to the positive root of a fifth order polynomial with coefficients defined by a 6 × 1 vector, V = M × S̃ (starting at power 0). S̃ = {S̃₄₀₀, S̃₃₁₀, S̃₂₂₀, S̃₂₁₁} is the 4 × 1 vector of sufficient statistics, and M is the 6×4 matrix given in Appendix A.3. Each element of M corresponds to a coefficient in the polynomial that is the numerator of the derivative in Equation 11, e.g. the top left element corresponds the the coefficient of the S̃₄₀₀θ⁰ term.

2.4 Probability of Mutation and Detection of De Novo Mutations

In order to detect sites that might contain a de novo mutation, we calculate the posterior probability of at least one de novo mutation at each site. This probability, δ, is used to rank sites and identify those most likely to have a mutation event. Because there are fewer possible pedigrees that contain no mutations, the probability of at least one mutation over the entire pedigree is calculated as one minus the probability of no mutations. Let ∅ denote the event of no mutation.

$$\delta =P(\mathit{\text{de novo}}\text{mutation}|R,\mathrm{\Theta })=1-P(\varnothing |R,\mathrm{\Theta })=1-\frac{P(\varnothing ,R|\mathrm{\Theta })}{P(R|\mathrm{\Theta })}=1-\frac{{\sum }_{H}P(\varnothing |R,H,\mathrm{\Theta })P(R,H|\mathrm{\Theta })}{{\sum }_{H}P(R,H|\mathrm{\Theta })}$$ (12)

The probability of the observed data, P(R|Θ), is calculated recursively via Equation (10), and P(∅, R|Θ) is calculated similarly via tree-peeling:

$$P(\varnothing ,R|\mathrm{\Theta })=\sum _X[P(X|\mathrm{\Theta })\times \prod _j\sum _{Y_j}I(Y_j=X)P(Y_j|X,\mathrm{\Theta })P(\varnothing ,R_j|Y_j,\mathrm{\Theta })]$$

where X represents a node in the pedigree and Y_j its descendant nodes. This algorithm depends on parameters which can either be estimated directly from the data via EM or supplied by expert knowledge. Note that this algorithm can be adjusted to only measure mutations on certain parts of the pedigree, such as germline mutations.

2.5 Model Extension to Larger Pedigrees

Our model is extendable to more complex families by changing the structure of the pedigree. First, it can allow for a second somatic sampling of a parent. This simple modification is often used to validate candidate de novo mutations. Here, we have to consider that the most recent common ancestor cell within the parental somatic tissue is not likely to be the zygote, allowing for the possibility of shared somatic mutations between the two somatic samples. This modification adds another instance of somatic and error models to Equation (2) and an extra sum over the possible somatic genotypes to Equation (3).

A second possible extension is the inclusion of multiple offspring zygotes, representing multiple full-siblings within the nuclear family. In accordance with Mendelian inheritance laws, each zygote is formed independently of the others. Incorporating multiple zygotes into the model amounts to multiplying the results of multiple sums over the possible offspring zygote genotypes, each with an included somatic and germline mutation components.

A third possible extension is the inclusion of monozygotic twins. Multiple offspring from a single zygote are represented identically to multiple somatic samplings from a single individual, except that the most recent common ancestor cell to the monozygotic offspring samples is by definition within the germline, and therefore they are assumed to share no somatic mutations.

3 Simulations

Simulation studies were carried out to investigate the performance of the method when applied to high throughput sequencing data. We first examined the effects that various read structures have upon the inference of the model at a single site. Second, we considered the model performance using a trio pedigree, where the distinction between somatic and germline status of a spontaneous mutation cannot be made. Finally, we simulated a pedigree with monozygotic twins to evaluate the power of the method to estimate the germline mutation rate without the confounding effects of somatic mutations.

3.1 Single-Site Simulations

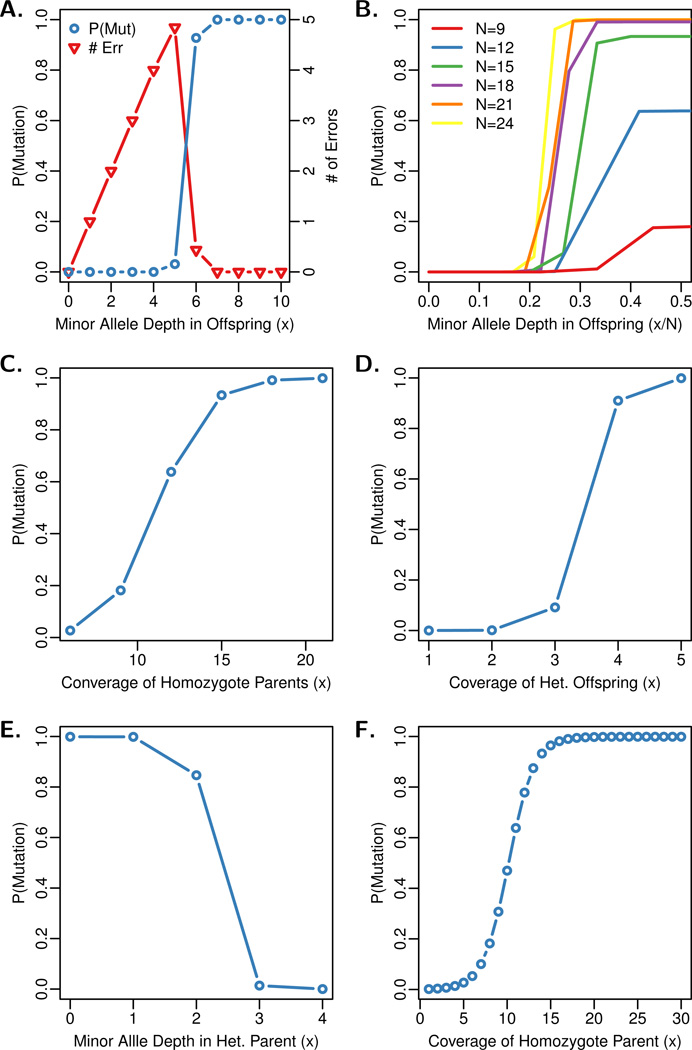
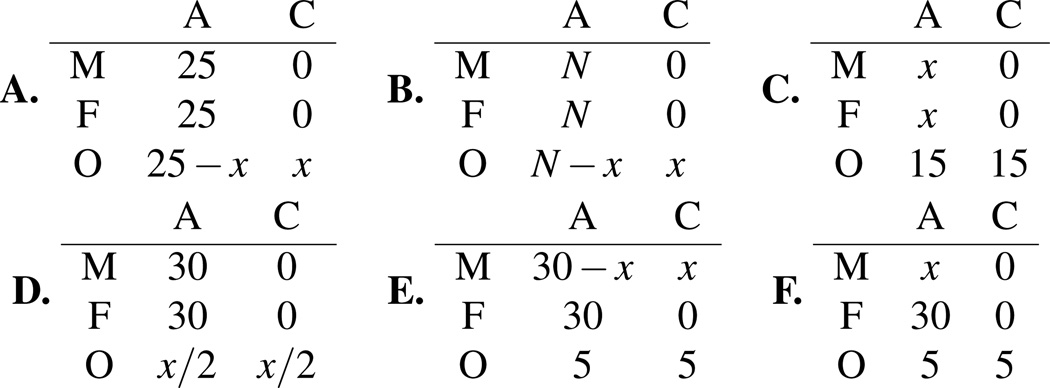
To illustrate the performance of the model, it is useful to examine the data points at which the inference transitions from predicting sequencing errors to predicting a mutation event. These transition points will depend on the model parameters used, including mutation and error rates. The posterior probability of mutation was inferred for a range of read structures across the family, described in Figure 3.

Figure 3.

Transition points in model inferences. (A) transition from error to de novo mutation, (B) effect of depth on error-mutation transition, (C) effect of low parent depth, (D) effect of low offspring depth, (E) transition from de novo mutation to inherited allele, (F) transition from de novo mutation to inferred inheritance. The parameter values used are θ = 0.001, ε = 0.01, μ = 2 × 10⁻⁷, μ_s = 0.0. The read structures are given in the tables; each row represents the read data taken for a family member, with the offspring data (O) as the bottom row, and the columns represent the number of reads observed for each allele. ‘G’ and ‘T’ read counts are always 0.

In short-read sequencing, reads are typically aligned back to a reference genome, and the data at a site in the reference consists of the nucleotide calls that align to that site. The number of reads that align to a site is known as the “coverage” or “depth” of that site. Multiple errors stacking on a single allele in an offspring may arise from sequencing errors or misalignment of short-sequencing reads to a reference genome. When both parents are homozygous, a de novo mutation may be inferred. This will depend on both the number of error-containing reads and the overall depth observed at the site (Figures 3A and B); the required ratio of minor-to-total allele depth for calling a mutation decreases as the depth increases. The model is largely affected by the binomial probability of observing a single chromosome a limited number of times relative to the number of samples taken. With coverage levels lower than 15×, the model is unable to conclusively call a mutation.

The effect of low parental read depths is shown in Figure 3C, where each structure tested has a clear signal of heterozygosity in the child, with 15 reads observed of both alleles. In order to be confident in the call of a mutation, both parents appear to require a read depth of at least 15 in the non-mutant allele. Much less coverage (~8×) is needed in the offspring, provided that both parents are clear homozygotes and the two offspring alleles are equally sampled by the sequencing reads (Figure 3D).

Lastly, we evaluated the transition from predicting a mutation to inferring the inheritance of a minor allele, when heterozygosity is established in the offspring. In Figure 3E this transition happens as mutant alleles stack in the parent. In Figure 3F this transition occurs more slowly, as the depth of the parental major allele decreases. The minimum depth of a parental allele proves to be one of the key factors in locating mutations in our simulation studies.

3.2 Simulations of Trio Pedigree Data

Resequencing of a trio was simulated to test the ability of our algorithm to estimate the parameters of our model and discern the location of actual de novo events. Simulations were based on the human chromosome 10 primary reference assembly (NCBI reference sequence NC 000010 from release hg18). It was downloaded in FASTA format, and all lines containing an ambiguous nucleotide were removed. This resulted in a 131,623,297 bp reference for the simulations.

Two diploid parental genomes were created from the reference, allowing up to three segregating alleles per site, with configurations in proportions expected from coalescent theory with θ = 0.001 (see Section 2.2.1). These parental genomes were used to generate a diploid offspring genome, allowing for germline mutations at rate μ = 10⁻⁶ (in order to detect something on this chromosome). Somatic mutations were not included since they are indistinguishable from germline mutations in a trio design. Sequencing reads of 35 bases each were generated from the diploid genomes of all three individuals, inserting sequencing error events at the per-base rate of ε = 0.01007. The reads, generated at different coverage levels, were aligned back to the reference using the BWA program (Li and Durbin, 2009). Finally, the EM algorithm (Section 2.3) was used to estimate the parameters from the aligned data, and, using the resulting parameter estimates, a list of candidate de novo mutation sites was generated.

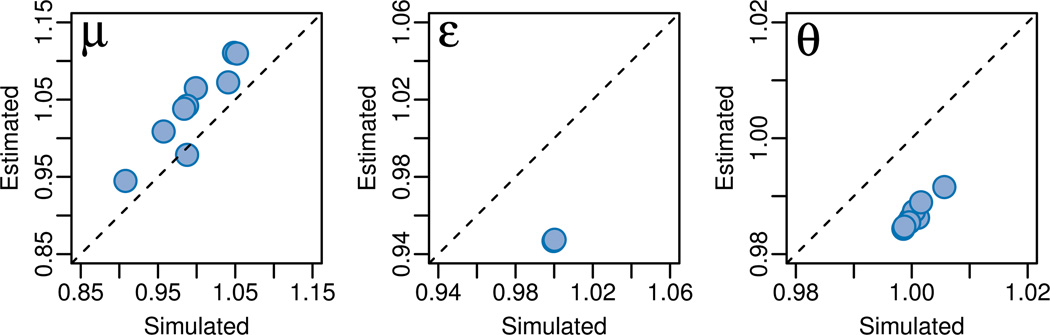
Ten replicates were done at the 20× coverage level to evaluate the spread of our parameter estimates around the true value (Figure 4). All three parameters were recovered close to their true value. The estimated mutation rate (calculated from the observable data) was consistently higher than the simulated rate (calculated from the full data) but varied with the simulated rate around the value of simulation parameter. The sequencing error rate and population mutation rate were consistently under-estimated. These biases are potentially the result of alignment error; reads that differ from the reference sequence are penalized and may not align back to any region of the reference. Thus less data supports errors and segregating variation, decreasing the estimates. In addition, repetitive segments that align back to the same location can appear to be mutations.

Figure 4.

Rate estimates from repeated trio simulations. Ten simulation replicates of trios with 20× coverage were generated. Parameters were estimated for each replicate. ‘Simulated’ rates were calculated from the full data, and ‘estimated’ rates from the observable data. Simulated rates only differ from simulation parameters due to the stochastic nature of the simulations. Both sets are plotted relative to the simulation parameters: μ = 10⁻⁶, ε = 0.01007, and θ = 0.001.

We next investigated the effect different levels of sequencing coverage had on the ability of EM to estimate model parameters (Table 1). Reads from a single simulated family set were produced at coverage levels of 10×, 20×, and 30×. Unsurprisingly, the estimates get progressively closer to the simulated rate as the coverage increases. To test the role which alignment error is playing in the simulations, the reads were re-aligned without error to the original reference, producing “control” sets of simulated data at the three coverage levels. Without alignment-error, the mutation rate goes from being over estimated to becoming underestimated. (There is an associated slight increase in θ, not shown due to rounding.) However, the estimates get closer to the simulated rate (9.84 × 10⁻⁷) as coverage increases. Clearly, a source of uncertainty remains even with perfectly aligned data because of the random sampling of the chromosomes by sequencing reads. This effect will be mitigated by increased coverage, as evidenced by these simulations: at 30×, the under-estimate bias is less than 0.5% of the simulated rate. The biases in the other parameter estimates are virtually eliminated by removal of alignment error, even at 10× coverage.

Table 1.

Parameter estimation results. A single family was simulated, and three independent sets of reads were created, one for each coverage level 10×, 20×, and 30×. The reads simulated from each set were aligned with or without error (ctrl) on the reference.

	True			Estimated Rate
	Rate	10×	20×	30×	10×-Ctrl	20×-Ctrl	30×-Ctrl
μ	1.00×10−6	1.22×10−6	1.06×10−6	1.04×10−6	9.01×10−7	9.70×10−7	9.79×10−7
ε	1.01×10−2	9.53×10−3	9.54×10−3	9.54×10−3	1.01×10−2	1.01×10−2	1.01×10−2
θ	1.00×10−3	9.78×10−4	9.89×10−4	9.92×10−4	1.00×10−3	1.00×10−3	1.00×10−3

Our method predicts a mutation by ranking every site examined by the probability of a mutation event, δ, as calculated in Equation 12 given the read data at the site and the estimated parameter rates. One can set a cutoff for δ and consider every site above that threshold a candidate for further investigation. In this application, our model acts as a binary classifier, assigning the data at a site to one of two groups: mutant site or non-mutant site. To test the utility of δ as a classifier, we produced receiver operating characteristic (ROC) curves based on every simulation performed. One useful metric of a ROC curve is the area under the curve (AUC); the ideal classifier will have an AUC of 1.0 and an uninformative classifier 0.5. Figure 5 shows the ROC curve derived from the simulated data. At 20× coverage, the method performs well, with an AUC of 0.9825. At 10× coverage, even after removing alignment error, it is difficult to accurately call heterozygote genotypes, leading to low performance. Therefore, it is better to increase coverage than increase alignment accuracy. However, at high coverage (30×), having perfect alignments creates a perfect predictor in our method, given the AUC of 1.0000.

Figure 5.

Trio Simulation ROC curves. For each simulated set, the corresponding ROC curve and AUC value are presented based on all calls with δ ≥ 0.01. The parameter values used in simulations are θ = 0.001, ε = 0.01, μ = 1 × 10⁻⁶, and μ_s = 0.0. The dashed line shown along the diagonal represents the expected ROC curve for a random, un-useful classifier. A perfect classifier goes straight up then straight across. The “-Ctrl” results are for simulations in which all reads are perfectly aligned back to the reference genome.

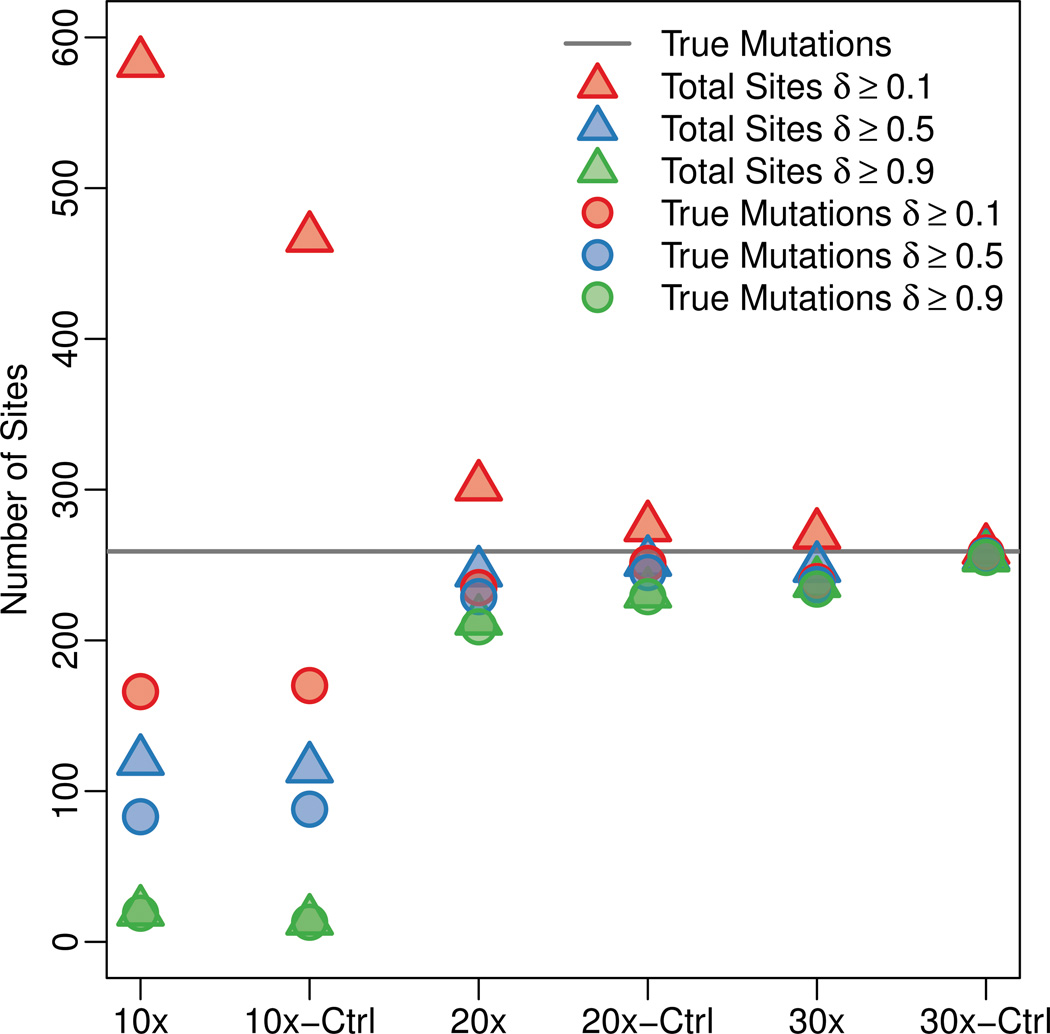
Figure 6 presents the number of true mutations predicted (true positives) at three different threshold values of δ, relative to the total number of predicted sites and of true mutant sites. In general, a threshold of 0.9 has very few false positive calls but also a higher false negative rate. Conversely, a threshold of 0.1 grants many more false positives but fewer false negatives. If the validation cost of any given candidate site is low, it may be more desirable to use a lower threshold to capture more true mutations at the expense of capturing non-mutant sites. However, at low coverage (10×) the proportion of true positive predicted is small, even at a threshold of 0.1. Finally, improving alignment quality reduces the number of false positive at all coverage levels. Again, eliminating alignment error at the 30× level creates a situation in which the method performs very well.

Figure 6.

De novo mutations predictions from trio simulations. 259 sites contained de novo mutations in the simulations (gray line). The total number of mutation calls at three different levels of δ are given by the triangles for each simulation. The circles indicate the amount of true positives for each δ threshold. The distances between triangles and circles represent the amount of false positives, and the distances between the circles and gray line gives the number of false negatives. The “-Ctrl” columns contain results for simulations in which all reads are perfectly aligned back to the reference genome.

3.3 Simulations of Quartet Pedigree Data

Following a procedure similar to that used in the trio simulation study, the performance of the de novo mutation discovery and rate estimation method was evaluated using a slightly more complicated but also more informative pedigree. A family with monozygotic twins provides an opportunity for simultaneous estimation of the germline mutation rate without the confounding effects of somatic mutations. When both offspring carry the same mutant allele that is unobserved in either parent, it is likely due to a germline mutation in one of the parents. Conversly, when a genotype is differentially called between monozygotic twins, a somatic mutation must have occurred.

We simulated a monozygotic-twin pedigree with a somatic rate (μ_s) several times higher than the germline rate (μ) and evaluated the ability of the estimation method to specifically call one event or the other. This situation is biologically relevant because within the span of one generation, depending on the ages of the donor individuals, many more somatic cell divisions have taken place than germline divisions, increasing the chances for mutation. Five replicate simulations were done following the same procedure as the trio simulation studies, with a germline mutation rate of 5 × 10⁻⁷ and a somatic mutation rate of 2.5 × 10⁻⁶. The somatic rate was neither consistently under-estimated nor over-estimated but varied with the simulated rate, as expected. The germline rate estimate, however, was consistently overestimated as with the trio simulations. Both the error rate estimates and population mutation rate estimates were recovered with the same accuracy as seen in the trio simulations, suggesting that extension to a larger pedigree had no effect on the ability to estimate these rates.

4 Discussion

The approach described here makes use of the relatedness of individuals and produces posterior probabilities of pedigrees at each site to facilitate correctly determining the family members’ genotypes. The utility of this methodology is two-fold; every genomic site investigated is ranked according to a posterior probability of carrying a de novo mutation, and a direct estimate is produced of the model parameters: the mutation rates, the sequencing error rate, and the initial genetic variation in the population from which the parents arise. By having good estimates of these rates, performing scans for actual spontaneous mutations will be made easier.

From the simulation results, both the parameter estimation and mutation prediction functionalities of this method were shown to produce accurate results, particularly at high coverage levels and with minimal alignment error. Furthermore, the method is able to distinguish germline from somatic mutations in an automated manner when applied to data from an appropriate pedigree. However, at low coverage levels (~10×), the method has particular trouble distinguishing true heterozygous sites from those affected by sequencing or alignment error. With the current state of high throughput sequencing, where high error rates and reference-based alignments are the norm, making incorrect inferences about de novo mutations are unavoidable at low coverage. Furthermore, when designing mutation discovery experiments, it is more advantageous to have high sequencing depth in parents to be certain of their genotypes than to have deep sequencing in the offspring at the expense of parental coverage.

Throughout the description of the model, four efficiency-based assumptions were made for simplicity and may easily be relaxed. First, we assume equal sampling of heterozygous alleles (p = 0.5, Section 2.2.2) because it is expected that either chromosome is equally likely to be sequenced. However, with some high-throughput sequencing technologies, particularly those relying on reference-based alignment, a bias towards observing reads matching the reference allele has been shown to exist (Durbin et al., 2010). Second, equal substitution rates between different nucleotide types were assumed, but the substitution model (Equation 5) can be changed to a better description of sequence evolution, such as the Kimura or HKY models (Kimura, 1980, Hasegawa, Kishino, and Yano, 1985), sacrificing computational efficiency. Thrid, the model currently assumes a constant mutation rate along the sequence. However, it is well understood that different areas of the human genome are evolving at different rates, so it may be desirable to estimate local mutation rates. Finally, we assumed that sites were independent of each other because it is computationally efficient, and currently we do not model context-dependent mutations, like CpG islands. We have specified one parameter, μ, for all genomic contexts. As a method of identifying de novo candidates, this is adequate but is suboptimal for estimating the patterns of mutation rates. We intend to explore handling context-dependent mutation in a future revision of this model.

While it is straightforward to adapt our model for context-dependent mutation, adapting it to respect haplotype structure is more cumbersome and less beneficial. Assuming that we had perfect phase information, then for each putative de novo we would know the parental chromosome of origin. The algorithm would then only need to consider the reads that came from that chromosome to determine if the variant in the child was a de novo mutation or inherited from the parent. However, this phase information will likely only be helpful in decreasing false positives in a few rare cases, such as when one chromosome is under-sequenced or when the parent is heterozygous, and would not decrease the number of false negatives. Thus, the potential advantages do not out weigh the algorithmic complexity required to use phased data.

Within the model, incorporating base quality and mapping quality information may improve the ability to distinguish errors from true sampling of novel alleles. Transitioning the fundamental data structure from a discrete count of observed alleles to continuous weighted average based upon these qualities is a possible solution. Extending the model to other forms of genetic variation would make the method more biologically and medically relevant as knowledge of the role that structural variants and indels play in human disease phenotypes gains increasing interest. Doing so would require including data from multiple sites compressed into a single data structure from which detection of Mendelian error can be done in an automated fashion.

The finite sites model is used since de novo mutations are considered a possibility even at sites with two alleles already segregating in the population. Biologically, such sites could be quite informative as hyper-mutable sites. In addition through investigations of real data, many sites are found to contain three parental alleles, a phenomena that has also been described in other human data sets (Hodgkinson and Eyre-Walker, 2010). Properly dealing with rare cases such as these is essential when working with whole-genome human sequence data.

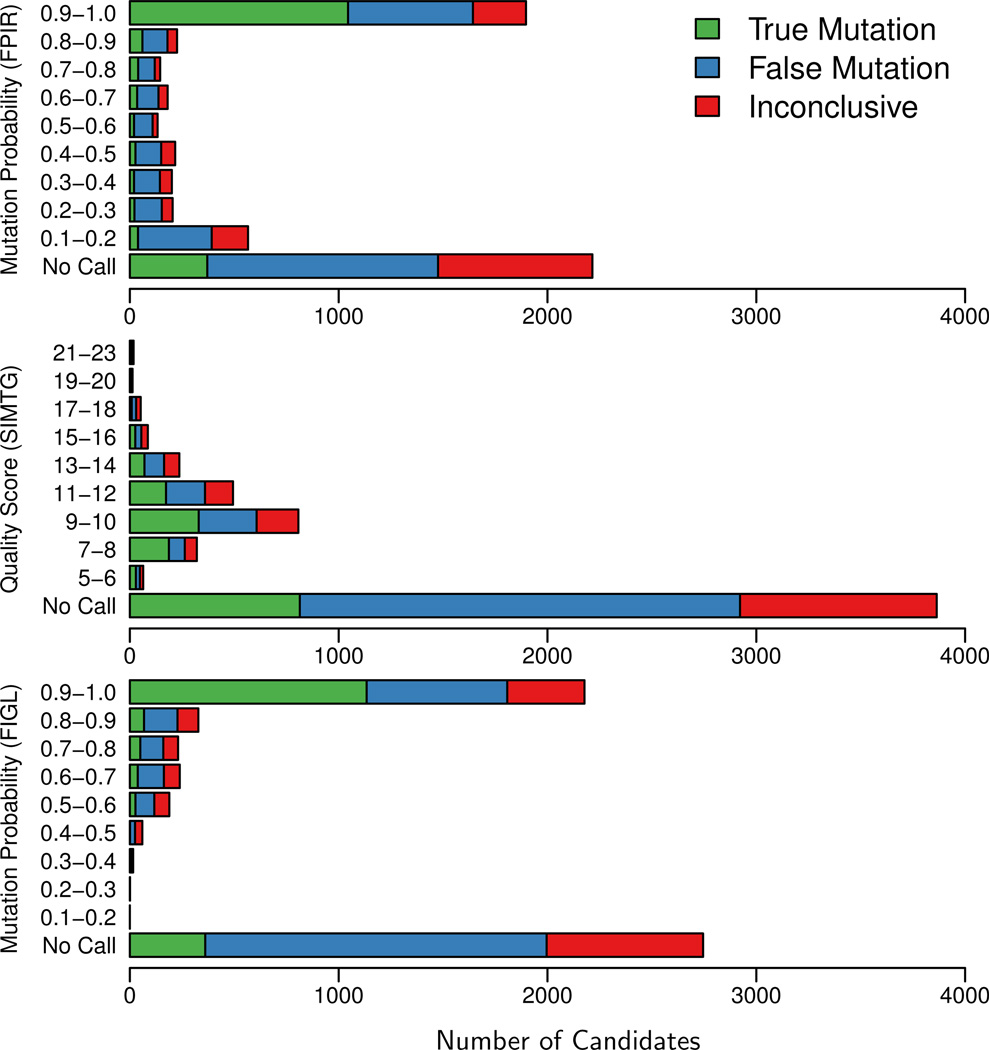
Conrad et al. (2011) analyzed the genomes of two trios using the probabilistic algorithm presented here (referred to as FPIR in their paper) and two other methods: a sample-independent approach (referred to as SIMTG and similar to Figure 1) and a likelihood-based method that uses the base error probabilities attached to each mapped read but does not sum over all possible patterns consistent with de novo mutation (referred to as FIGL). Their results provide a comparison of our method to two others using real data (Figure 7).

Figure 7.

Validation results stratified by de novo calling algorithm. Three methods were used to produce candidate sites of de novo mutation in two families (Conrad et al., 2011, Durbin et al., 2010). These candidates were then experimentally validated and classified as either “true mutations” (germline, somatic, or cell-line), “false mutations” (inherited genetic variation or no variation at all), or “inconclusive”. Sites not reported by a method but reported by another method appear in the No Call bar. FPIR corresponds to the method described in this paper. Modified from Conrad et al. (2011).

Although the trio design is uninformative for disentangling somatic and germline mutations, experimental validation has become cost effective enough for assaying many more candidate mutation sites than would be expected by current estimations of the expected mutation rate. This allows for locus-specific verification of predicted de novo events. In larger family designs, the framework we present here can be used to disentangle the effects of the mutational processes, which will make accurate germline mutation rate estimates possible without the extra commitment of resources to experimentally validate putative de novo mutations. Furthermore, the analysis of larger sibships is required to understand fully the effects of sex and parental age on the human mutation rate.

A Appendix

A.1 Probability of Allele Spectra

Coalescent theory can be use to derive the probability of a sample of four nucleotides. Under the coalescent, there are two possible trees connecting the four sampled chromosomes drawn from a finite, randomly-mating population, with effective size of N_e (Figure A.1). Mutations are allowed to occur continuously along the genealogical tree.

Figure A.1.

Possible genealogical trees for a sample of four alleles from a single population. The times of coalescent events, t_i, are expessed in 2N_e generations, where N_e is the effective population size. Type I occurs twice as often as Type II.

Under the finite sites model (Yang, 1996), the joint distribution of the times of coalescent events t₁, t₂, and t₃ is f (t₁, t₂, t₃) = 18e^{−t₁ − 2t₂ − 3t₃}. The total length of the genealogy is τ = 2(t₁ − t₂) + 3(t₂−t₃) + 4t₃ and its distribution is given by $f(\tau )=\frac{3}{2}{e}^{-\tau /2}{(1-e^{-\tau /2})}^2$. If u is the true mutation rate per-site-per-generation and θ = 4Nu, then the rate of mutation in 2N_e generations is θ/2. The probability no mutation will occur in a tree of length τ is e^−τθ/2, and the probability of no mutations in the genealogy of the four samples is constructed by integrating over the length of the tree:

$$p_0={\int }_0^{\infty }{e}^{-\tau \theta /2}\times \frac{3}{2}{e}^{-\tau /2}{(1-e^{-\tau /2})}^{2}d\tau \approx \frac{6}{6+11\theta }$$

In general, the probability of k mutations is

$$p_k=3{\theta }^k(\frac{1}{{(1+\theta )}^{k+1}}-\frac{2}{{(2+\theta )}^{k+1}}+\frac{1}{{(3+\theta )}^{k+1}})$$

From this equation, the probability of a single mutation is

$$p_1=\frac{6\theta (11+12\theta +3{\theta }^2)}{{(1+\theta )}^2{(2+\theta )}^2{(3+\theta )}^2}\approx \frac{66\theta }{36+132\theta }$$

Assuming that θ is small enough so that the probability of three mutations occurring in a single genealogy is negligible, the probability of 2 mutations is

$$p_2\approx (1-p_0-p_1)\approx \frac{121{\theta }^2}{(6+22\theta )(6+11\theta )}$$

Depending on when mutations happen and the type of genealogy, a site may have 1, 2, or 3 alleles segregating, and there are 4 possible allele spectra: 4-0-0, 3-1-0, 2-2-0, and 2-1-1. To simplify the calculation of the allele spectra, we unroot Type 1 and Type 2 genealogies, producing the standard four-sample unrooted tree (Figure A.1). For Type 1, a = t₃, b = t₃, c = t₂, d = 2t₁ − t₂, and e = t₂ − t₃. For Type 2, a = t₃, b = t₃, c = t₂, d = t₂, and e = 2t₁ − t₂ − t₃.

We consider first P(4 − 0 − 0). This allele spectrum of four copies of the same allele can occur when k = 2 and the mutations occur on the same branch with the second resetting the first. This happens 1/3 of the time under the assumption of homogenous mutations.

$$P(4-0-0|k=2)=\frac{1}{3}{\int }_0^{\infty }{\int }_0^{t_1}{\int }_0^{t_2}\frac{a^2+b^2+c^2+d^2+e^2}{{\tau }^2}f(t_1,t_2,t_3)d{t}_{3}d{t}_{2}d{t}_{1}P(4-0-0|k=2,\text{Type}\mathrm{I})=0.16698203195293615P(4-0-0|k=2,\text{Type}\mathrm{I}\mathrm{I})=0.15395300164642536$$

This spectrum can also occur when k = 0, and the full probability for the 4-0-0 spectrum is

$$P(4-0-0|\theta )=p_0+p_2\times [\frac{2}{3}P(4-0-0|k=2,\text{Type}\mathrm{I})+\frac{1}{3}P(4-0-0|k=2,\text{Type}\mathrm{I}\mathrm{I})]=\frac{6}{6+11\theta }+\frac{121{\theta }^2\times 0.1626390218507659}{(6+22\theta )(6+11\theta )}$$

where the results for Type I and Type II trees are weighted by their frequency.

The 3-1-0 spectrum occurs with a single mutation on any terminal branch (a to d) and with two mutations where both occur on a terminal branch without the second resetting the first or where one occurs on the internal branch and the second on an external branch while resetting the first.

$$P(3-1-0|k=1)={\int }_0^{\infty }{\int }_0^{t_1}{\int }_0^{t_2}\frac{a+b+c+d}{\tau }f(t_1,t_2,t_3)d{t}_{3}d{t}_{2}d{t}_{1}P(3-1-0|k=1,\text{Type}\mathrm{I})=0.9013877054843336P(3-1-0|k=1,\text{Type}\mathrm{I}\mathrm{I})=0.412352359168542P(3-1-0|k=2)=\frac{2}{3}{\int }_0^{\infty }{\int }_0^{t_1}{\int }_0^{t_2}\frac{a^2+b^2+c^2+d^2}{{\tau }^2}f(t_1,t_2,t_3)d{t}_{3}d{t}_{2}d{t}_1+\frac{1}{3}{\int }_0^{\infty }{\int }_0^{t_1}{\int }_0^{t_2}\frac{2e(\tau -e)}{{\tau }^2}f(t_1,t_2,t_3)d{t}_{3}d{t}_{2}d{t}_{1}P(3-1-0|k=2,\text{Type}\mathrm{I})=0.37904056583820833P(3-1-0|k=2,\text{Type}\mathrm{I}\mathrm{I})=0.1768080666255894$$

The full probability for the 3-1-0 spectrum is

$$P(3-1-0|\theta )=p_1\times P(3-1-0|k=1)+p_2\times P(3-1-0|k=2)=\frac{66\theta \times 0.7383759233790697}{36+132\theta }+\frac{121{\theta }^2\times 0.3116297327673353}{(6+22\theta )(6+11\theta )}$$

The 2-1-1 spectrum occurs only when two mutations occur on different branches and the second mutation does not reset the first.

$$P(2-1-1|k=2)=\frac{2}{3}{\int }_0^{\infty }{\int }_0^{t_1}{\int }_0^{t_2}(1-\frac{a^2+b^2+c^2+d^2+e^2}{{\tau }^2})f(t_1,t_2,t_3)d{t}_{3}d{t}_{2}d{t}_{1}P(2-1-1|k=2,\text{Type}\mathrm{I})=0.3327026036110817P(2-1-1|k=2,\text{Type}\mathrm{I}\mathrm{I})=0.3587606049731652$$

The full probability for the 2-1-1 spectrum is

$$P(2-1-1|\theta )=p_2\times P(2-1-1|k=2)=\frac{121{\theta }^2\times 0.3413886040651095}{(6+22\theta )(6+11\theta )}$$

Finally, the 2-2-0 spectrum occurs in all other cases: when one mutation occurs on the internal branch e, two mutations occur on e as long as the second does not reset the first, and when two identical mutations occur on two separate tips. The integrals for this spectrum are

$$P(2-2-0|k=1)={\int }_0^{\infty }{\int }_0^{t_1}{\int }_0^{t_2}\frac{e}{\tau }f(t_1,t_2,t_3)d{t}_{3}d{t}_{2}d{t}_{1}P(2-2-0|k=1,\text{Type}\mathrm{I})=0.09861225545086329P(2-2-0|k=1,\text{Type}\mathrm{I}\mathrm{I})=0.5876475173837374$$

$$P(2-2-0|k=2)=\frac{2}{3}{\int }_0^{\infty }{\int }_0^{t_1}{\int }_0^{t_2}\frac{e^2}{{\tau }^2}f(t_1,t_2,t_3)d{t}_{3}d{t}_{2}d{t}_1+\frac{1}{3}{\int }_0^{\infty }{\int }_0^{t_1}{\int }_0^{t_2}\frac{{(\tau -e)}^2-(a^2+b^2+c^2+d^2)}{{\tau }^2}f(t_1,t_2,t_3)d{t}_{3}d{t}_{2}d{t}_{1}P(2-2-0|k=2,\text{Type}\mathrm{I})=0.12127479467444843P(2-2-0|k=2,\text{Type}\mathrm{I}\mathrm{I})=0.31047829272367844$$

and the full probability is

$$P(2-2-0|\theta )=p_1\times P(2-2-0|k=1)+p_2\times P(2-2-0|k=2)=\frac{66\theta \times 0.26162400942848796}{36+132\theta }+\frac{121{\theta }^2\times 0.1843426273575251}{(6+22\theta )(6+11\theta )}$$

These probabilities are for unordered and untagged samples (tagged here refers to the specific nucleotides at each site). To get the full probabilities of the four-allele samples, we have to consider the number of possible tags and orders. Assuming that each nucleotide is equally likely, we have:

$$P(m_a,m_b,f_a,f_b|\theta )=P(\mathrm{\Phi }(m_a,m_b,f_a,f_b)|\theta )P_0(\mathrm{\Phi }(m_a,m_b,f_a,f_b))$$

where Φ (m_a, m_b, f_a, f_b) is the allele pattern from the data, and

$$P_0(4-0-0)=\frac{1}{4},P_0(3-1-0)=\frac{1}{12}\times \frac{1}{4},P_0(2-2-0)=\frac{1}{12}\times \frac{1}{3},P_0(2-1-1)=\frac{1}{24}\times \frac{1}{6}.$$

Note: the trio simulation results used an earlier version of the parental spectra model that differs slightly from what is outlined here. However, the stochastic nature of the simulations swamps the small differences between them.

A.2 Computation of Summary Statistics

The values of the summary statistics are determined by the genotype comparisons between a parent node X and child node Y, as described in the tree-peeling algorithm. Let S_T (R, X → Y) denote the contribution of the comparison between X and Y to a particular summary statistic. Beginning at the tips of the pedigree tree, at branches between somatic genotypes and sequencing reads, the summary statistics are calculated as

$$S_{\mathit{\text{Hom}}}(R_Z,Y\to R_Z)=I(Y_a=Y_b)\sum _{k=1}^{N_{RZ}}I(R_{Zk}=Y_a)S_{\mathit{\text{Het}}}(R_Z,Y\to R_Z)=I(Y_a\ne Y_b)\sum _{k=1}^{N_{RZ}}I(R_{Zk}=Y_a)+I(R_{Zk}=Y_b)S_E(R_Z,Y\to R_Z)=\sum _{k=1}^{N_{RZ}}I(R_{Zk}\ne Y_a)\times I(R_{Zk}\ne Y_b)$$

Moving to the somatic nodes, where X ∈ {m, f, o} and Y ∈ {m′, f′, o′}, the summary statistic describing somatic mutation events is calculated:

$$S_{\mathit{\text{Som}}}(R_Z,X\to Y)=I(X_a\ne Y_a)+I(X_b\ne Y_b)$$

On branches containing the transmission of parental alleles to the offspring zygote, X ∈ {m^*, f^*} and Y ∈ {o}, the summary statistic for germline mutation is calculated:

$$S_M(R_O,X\to Y)=I(X\ne Y_a)S_F(R_O,X\to Y)=I(X\ne Y_b)$$

At the root of the family, the four parent-allele spectra summaries are the probabilities from Equation 4.

A.3 Maximum Likelihood Estimation of θ

θ̂ is found as the positive root of a fifth order polynomial with coefficients defined by a 6 × 1 vector, V = M × S̃ (starting at power 0). S̃ = {S̃₄₀₀, S̃₃₁₀, S̃₂₂₀, S̃₂₁₁} is the 4 × 1 vector of sufficient statistics, and M is the 6 × 4 matrix given below.

$$M=\left[\begin{array}{cccc}0.0\hfill & 0.03486619657215915\hfill & 0.034866196572159135\hfill & 0.06973239314431828\hfill \\ -0.06392136038229179\hfill & 0.4063834312180521\hfill & 0.4452843194121218\hfill & 0.8447710620767139\hfill \\ -0.7948489929849523\hfill & 1.7896006938115314\hfill & 2.146192168923839\hfill & 3.8349977752357396\hfill \\ -3.7071570372902434\hfill & 3.5976773523251344\hfill & 4.664944098515855\hfill & 7.820707741673811\hfill \\ -7.660475993112385\hfill & 2.9698289148990122\hfill & 4.045621742438051\hfill & 6.382800832064958\hfill \\ -5.889366459562289\hfill & 0.3816993140208244\hfill & 0.5246479467550001\hfill & 0.8181818181818182\hfill \end{array}\right]$$