Behavioral Landscapes and Change in Behavioral Landscapes: A Multiple Time-Scale Density Distribution Approach

Abstract

In developmental arenas, it is well accepted that multiple observations are needed to obtain a robust characterization of individuals’ behavioral tendencies across time and context. In this paper, we fuse core ideas from the study of lifespan development with intraindividual variability based approaches to personality and methods used to characterize the topography of geographic landscapes. We generalize the notion of density distributions into bivariate and multivariate space and draw parallels between the resulting behavioral landscapes and geographic landscapes. We illustrate through an empirical example how multiple time-scale study designs, measures of intraindividual variability, and methods borrowed from geography can be used to describe both an individual’s behavioral landscape and changes in the behavioral landscape.

Notions of personality have progressed beyond the idea that people are well characterized by five or more scores obtained on a single occasion. In developmental arenas it is well accepted that multiple observations are needed to obtain a robust characterization of individuals’ behavioral tendencies (including action, cognition, emotion, physiology, etc.) across time and context. The current paper presents a novel fusion of methods from behavioral science and geography to extend the notions of personality as density distributions (Fleeson, 2001) and behavioral signatures (Mischel & Shoda, 1995) towards personality as behavioral landscapes. Specifically, we draw parallels between behavioral landscapes represented by multivariate density distributions and geographic landscapes that might be seen in the real, physical world – mountains, hills, plains. Integrating core ideas from the study of intraindividual variability (Nesselroade, 1991) and lifespan development (Baltes, Lindenberger, & Staudinger, 2006) we illustrate how 3-dimensional visualizations of multivariate repeated measures data (e.g., from diary and ecological momentary assessment studies) can be described analytically, and how those descriptions may be used to characterize both the topography of individuals’ behavioral landscape and how those behavioral landscapes change over time.

Personality as Density Distributions

The person-situation debate in personality (Kenrick & Funder, 1988) could be characterized as a clash between the person-view, that a person will act similarly much of the time because behavior is determined in large part by a person’s traits, and the situation-view, that a person will behave differently on different occasions because behavior is determined in large part by the immediate situation. These two points of view have been reconciled in a number of ways using repeated measures data. For instance, when multiple observations of an individual’s behavior are available, it is possible to collect them into an ensemble of scores and use the intraindividual variability in observed behavior to model both person-specific and situation-specific aspects of behavior (Nesselroade, 1988). Making use of the precision afforded by mathematics, a combined perspective can be written as

$$X_t={\mu }_x+x_t,$$

where X_t, the repeated measures of an individual’s behavior obtained at times t, are modeled as a combination of the individual’s behavioral tendency, μ_x = trait and situation-specific deviations from that tendency, x_t = state. Simplistically, the intraindividual mean, μ_x, is a measure of a person-level characteristic. Interindividual differences in this characteristic are noted by inclusion of an i subscript, noting that each individual’s ensemble of scores may have a different central tendency, μ_xi.

Abstracting from this simple trait+state model of behavior (the foundation of classical test theory; Lord & Novick, 1968), the density-distributions approach to personality (Fleeson, 2001) suggests that the “leftover” state variance is itself an aspect of personality. That is, the range of states a person can exhibit or experience is also a trait. Some individuals may behave in a relatively consistent manner in many situations (x_t scores are very similar across occasions), while others’ behavior may vary more dramatically from situation to situation (x_t scores are very different across occasions). Formally, the range of an individual’s behavior can be quantified as the intraindividual variability of the x_t scores, σ²_x. The density distributions approach acknowledges that individuals may differ in both μ_xi and σ²_xi and, as indicated by the inclusion of the i subscript, uses both parameters as measures of between-person differences in personality. The density-distributions approach to personality typically uses measures of intraindividual mean (iMean) and intraindividual standard deviation (iSD) as descriptors of person-level personality characteristics. For illustration, the univariate density distributions for repeated measures data for two hypothetical persons are shown in the upper panels of Figure 1 along with the corresponding iMeans and iSDs.

Figure 1.

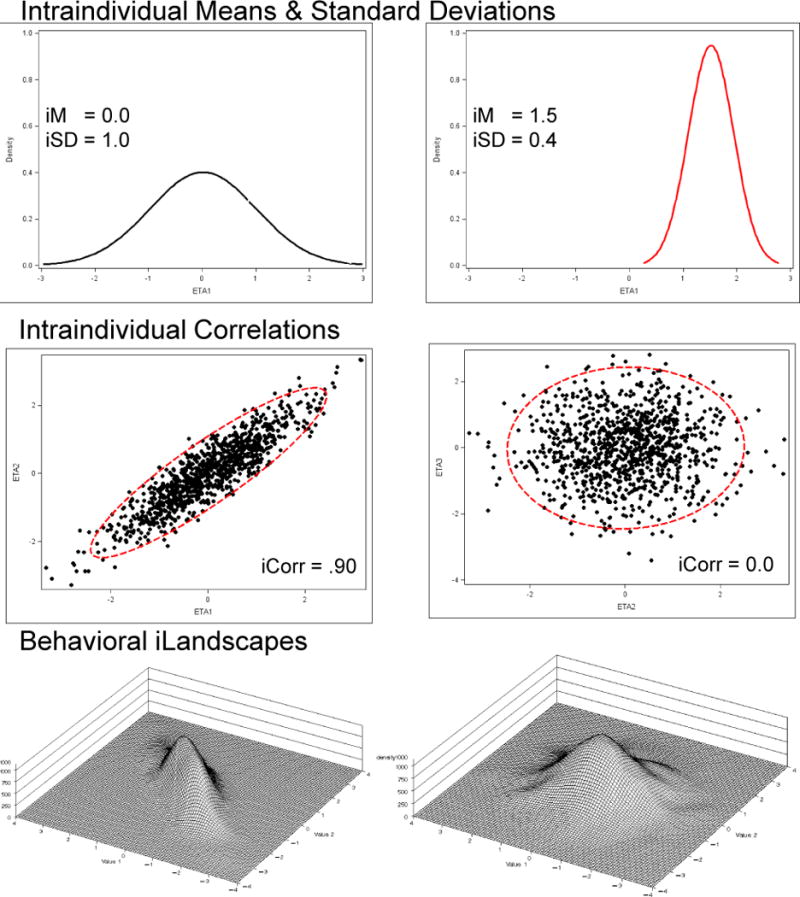
Simulated univariate and bivariate density distributions of intensive repeated measures obtained from an individual are described in upper panel using intraindividual means (iMean) and intraindividual standard deviations (iSD), in middle panel using intraindividual correlations (iCorr), and in lower panel as behavioral landscapes (iLandscape).

Placed within a lifespan developmental framework, the density distributions approach can be used to examine age differences or changes in density distributions by examining between-person differences in iMeans and iSDs. For example, Noftle and Fleeson (2010) examined how individuals within different periods of the life span (young, middle-aged, older adults) differed in trait-relevant behavior averages (iMean) and variabilities (iSD) in daily life. Similar to the hypothetical differences depicted in the upper row of Figure 1, they found some initial evidence that, compared to young adults (left panel, black distribution), middle-aged and older adults exhibited higher average levels and lower variabilities (right panel, red distribution) in agreeableness- and emotional stability-related behaviors.

Personality as Bivariate Associations

Extension from constructs based on univariate intraindividual variation to constructs based on intraindividual covariation is straightforward. Two variables are used to define a bivariate space in which the observed data are located, as seen in the middle panels of Figure 1. The extent of association between the two variables is described (a) visually by the oblong or circular nature of the oval covering the area in which the observations are located and (b) quantitatively by the intraindividual correlation (iCorr) or an intraindividual regression (iReg). The measure of association is then tethered to a specific trait-like construct. For example, Carstensen and colleagues (2011) have used the intraindividual correlation between repeated measures of positive and negative affect to describe poignancy, an individual’s potential for experiencing mixed emotions. Others have referred to the same operationalization as affective polarity (Ram et al., 2012) or emotional complexity (e.g., Ong & Bergeman, 2004; Ready, Akerstedt & Mroczek, 2012). All of these constructs are considered as person-level “traits” that are fixed over the short-term (however see e.g., Zautra et al., 2005), but that may also develop over the long-term as individuals mature and/or transition through life events.

In the behavioral signatures approach to personality, individuals’ potential or likelihood of behaving in particular ways in particular situation is described by if-then contingencies (Mischel & Shoda, 1995). For example, if person i is in situation S = 1, then he or she exhibits behavioral response R = 10; if in situation S = 100 then behavior R = 50. In this approach, if-then traits are operationalized using the pattern or strength of relation between situational features (S) and behavior (R) within a bivariate within-person time-series data. That is, an individual’s if-then contingency is quantified by a person-specific regression parameter, β_i from a model such as

$$R_t={\beta }_i{S}_t,$$

where R_t are the repeated measures of person i’s behavior at times t and S_t are the correspondent repeated measures of the situations the person was in. With its i subscript, the regression parameter is explicitly defined as a characteristic of the person and could be re-labeled P_i = β_i to make literal the interactionist perspective. Importantly, P_i, is a “latent” trait (time-invariant) score that is inferred from the observed S-R relations. Differences in if-then contingencies are quantified as between-person differences in the regression parameters, and straightforwardly tested by collecting the person-specific regressions within a multilevel modeling framework (see Bolger & Romero-Canyas, 2007). For example, Brose, Scheibe and Schmiedek (2012) examined age-related differences in the within-person association between daily stressors (S) and negative affect (R). Younger adults had stronger if-then contingencies than older adults (in part because of differences in stressor heterogeneity). From a birds-eye perspective, a younger individual would tend to look more like the middle-left panel of Figure 1 (strong correlation/regression), and older individuals more like the middle-right panel (no correlation).

Personality as Landscapes

The (univariate) density distributions and (bivariate) behavioral signatures approaches are all part of a “bottom-up approach to personality in which theorists start with the actual differences as they exist between individuals’ behaviors (including actions, cognitions, motivations, and emotions) and infer the personalities that produced those differences” (Fleeson & Noftle, 2008, p. 1358). Methodologically, these approaches acknowledge and measure the within-person variation or covariation in individuals’ behavior and use descriptive statistics (mean, standard deviation, correlation) to operationalize a wide variety of trait-like constructs that we have elsewhere labeled dynamic characteristics (see Ram & Gerstorf, 2009). Although the accompanying visualizations are usually drawn in 2-d, they are occasionally rendered in 3-d, as shown in the bottom panels of Figure 1, where the scatter-plots from the middle panels are now shown as bivariate density distributions. In these 3-d distributions, individuals’ behavior “resides” within the hills. Visualized this way, we can immediately see similarities between the density distributions and the natural world – mountains, hills, and plains, and may be reminded of the many theoretical perspectives that describe behavioral and developmental landscapes (e.g., Hooker, 2002; Waddington, 1957).

It is important to note that the univariate and bivariate density distributions depicted in Figure 1 are “clean” univariate and bivariate normal (Gaussian) distributions. They were simulated to conform to idealistic statistical assumptions. However, our experience with real data suggests that the observed distributions rarely look so symmetric and smooth. Rather they are filled with extra hills, sharp spires, and flat zones (as will be seen later). Intrigued by the notion that the visualizations of real data are pictures of behavioral landscapes, we explored if and how methods from geography might be used to generalize the interpretation of personality of multivariate density distributions that change and/or remain stable over macro time.

Geographic landforms come in all shapes and have implications for the types of ecosystems that can develop there (Bailey, 1996). In addition to land use characteristics (e.g., rural, urban) surface geometry is also sometimes used to differentiate various mesoecosystems and landscape mosaics (Botequilha Leitao, Miller, Ahern, & McGarigal, 2006). In particular, Hammond (1954) developed a system for differentiating landform classes into the categories listed in Table 1, which include both general (e.g., plains, tablelands) and more specific categories (e.g., irregular plains, open high hills). His classification was based on visual analysis of a local window (9.7 km × 9.7 km) that was moved without overlap across a 1:250 000-scale topographic contour map (Hammond, 1964). Specifically, the relative amount of gently sloping land (< 8%), local relief (meters), and generalized profile (where and how much of the gently sloping land is located in the valley bottoms or uplands) is combined using the codes in Table 2 to classify quadrangles delineated within the subject landscape into landform types. With the move to computer assisted, raster-based Geographic Information Systems (GIS) processing of satellite images such classification systems have been automated (Gallant, Brown, & Hoffer, 2005; Riley, DeGloria, & Elliot, 1999), greatly facilitating generation of landform maps, investigation of regional land use patterns, and management of environmental resources (Botequilha Leitao et al., 2006). In an attempt to generalize the density distribution approach to personality, map behavior in multivariate space, and investigate both between-person differences and within-persons changes in complex behavioral profiles, we consider how this approach to describing geographic landscapes might be applied to investigation of individuals’ behavioral landscapes.

Table 1.

Hammond (1954, 1964) Landform Classes

Plains
A1	Flat plains
A2	Smooth Plains
B1	Irregular plains, slight relief
B2	Irregular plains
Tablelands
B3c,d	Tablelands, moderate relief
B4c,d	Tablelands, considerable relief
B5c,d	Tablelands, high relief
B6c,d	Tablelands, very high relief
Plains with Hills or Mountains
A3a,b	Plains with hills
B3a,b	Plains with hills
B4a,b	Plains with high hills
B5a,b	Plains with low mountains
B6a,b	Plains with high mountains
Open Hills and Mountains
C2	Open low hills
C3	Open hills
C4	Open high hills
C5	Open low mountains
C6	Open high mountains
Hills and Mountains
D3	Hills
D4	High hills
D5	Low mountains
D6	High mountains

Table 2.

Hammond (1954, 1964) Landform Classification Rules

Slope Character (% local area gently sloping)	Local Relief (meters)	Profile Type (location of gently sloping area)
A. >80%	1. 0–30	a. > 75% in lowland
B. 50–80%	2. 30–91	b. 50–75% in lowland
C. 20–50%	3. 91–152	c. 25–50% in lowland
D. <20%	4. 152–305	d. <25% in lowland
	5. 305–914
	6. > 914

Note: Column categories are hierarchic, from left (most general) to right (finest). Gently sloping defined as < 8% grade. Lowland defined as below the median elevation of the area. Categories from each column are combined to identify the landform classes listed in Table 1.

Multiple Time-Scale Study Design

The density distributions approach to personality, and more generally, the study of intraindividual variability, is facilitated by intensive repeated measurement of individuals’ behavior at relatively fast, “micro”, time scales (e.g., hours, days). Advances in technology have facilitated researchers’ use of diary, ecological momentary assessment (EMA), ambulatory, and other experience sampling study designs (Mehl & Connor, 2012). The intensive longitudinal data obtained in these studies are being used in a wide variety of ways to measure the dynamic characteristics and processes that drive individuals’ moment-to-moment behavior (see Ram & Gerstorf, 2009).

In complement, the study of personality change, and more generally, the study of intraindvidual change, is facilitated by repeated measurement of individuals’ behavior at relatively slow, “macro” time scales (e.g., years, decades). Longitudinal panel designs are often used to describe how individuals grow, maintain stability and decline (see Hertzog & Nesselroade, 2003). The repeated measures data obtained in these studies are being used in a wide variety of ways to describe the trajectories individuals follow as they develop, age, and transition through life events (see Ram, Gerstorf, Fauth, Malmberg & Zarit, 2010).

Combining “micro-time” research designs with more “macro-time” designs for examining intraindividual change, researchers can examine questions about the development of individuals’ personality. Nesselroade (1991) suggested making use of a measurement-burst design that involves measuring individuals on multiple time scales. At the micro-time scale, observations are obtained from one or more individuals at closely spaced intervals (e.g., hours, days) – a “burst” of measurement. These intensive data are used to characterize individuals’ behavioral tendencies – density distributions and behavioral landscapes. At the macro-time scale, these same individuals are measured again at a wider interval (e.g., months, years), each time providing another “burst” of information – another density distribution. Thus, the multi-time-scale repeated measures design combines the benefits of short-term longitudinal studies and the study of behavioral tendencies with the benefits of long-term longitudinal studies and the study of development.

The Present Study

To illustrate how methods used in geography can be used to describe behavioral landscapes and how they transform over time, we collected EMA data from a sample of individuals from the local community across multiple bursts along with information about the life events they experienced during the 18 month study period. Patterns of emotional behavior captured through the intensive repeated measures within a burst (3-weeks) were described using kernel density methods and visualized as behavioral landscapes. Typical descriptive statistics as well as algorithms from geography were used to classify the landscapes into types and to describe if and how individuals’ landscapes changed over macro time (4-month intervals) as they did or did not transition through major life events.

The study of both individuals’ behavioral landscapes and changes in behavioral landscapes was facilitated by a multiple-time-scale study design wherein multiple reports of behavior were obtained over a relatively short span of micro time (e.g., 3 weeks of EMA) during multiple “bursts” of measurement obtained at more widely spaced intervals of macro time (4-months). Repeated measures obtained within-burst provide for observation of individuals’ behavioral tendencies. Comparison across bursts provides for observation of individual-level change in those tendencies.

Method

Participants and Procedure

Participants in this study were 4 persons selected (see below) from a larger longitudinal study on aging, health, and interpersonal behavior. After being recruited into the study and explained the intensive nature of the assessments, participants completed three 21-day “measurement bursts” (micro-time) spaced at about 4-month intervals (macro-time). During each 21-day burst, individuals reported about their interpersonal interactions as they went about their daily lives, and provided end-of-day reports about their feelings, thoughts, and behaviors. As well, prior to and after each 21-day burst, individuals completed a web-based battery of personality, health, and life-event questionnaires. Participants were compensated $500 for completing the entire protocol.

Measures

Our main interest was in exploring if and how 3-d landscape visualizations of multivariate repeated measures data (P-data) could be described analytically using methods adapted from geography. Concentrating here on illustration and extension of topography classification towards the density-distribution approach to personality we selected a few measures and a few persons from the larger set of multiple-time-scale repeated measures.

Life events

As a measure of the extent of (‘developmental’) change that individuals experienced between bursts (~4 month intervals), we used a set of items assessing the occurrence of major life events (adapted from Holmes & Rahe, 1967; Sarason, Johnson, & Siegel, 1978). Prior to each burst, participants were asked “Since your last visit [or, at the first visit, “In the last 6 months”], did you experience any of the following and, if so, how much did it affect you?” followed by a list of 12 events that included: a change in relationship status, death of a loved one, serious illness or injury, change in living conditions, etc. Responses on a 0 = did not experience, 1 = not affected, 2 = a little bit, 3 = somewhat, 4 = a lot, were summed to a total score where higher scores indicated that an individual recently experienced and/or was strongly affected by major life events. To explore the viability of a topographic approach to assessing changes in behavioral landscapes, we selected 2 persons who exhibited the least absolute change in life events across the three repeated measures (Δ = 0 and 0 = stable persons; i.e., experienced no such events during the entire study period) and 2 persons who exhibited the greatest absolute change (Δ = 23 and 20 = change persons).

Positive and negative affect

We describe person-specific density distributions in emotional aspects of behavior. Our choice of these two particular variables was driven by our familiarity and previous work operationalizing emotional variability and emotional polarity/poignancy constructs (e.g., Carstensen et al., 2011; Ram et al., 2011, 2012). These constructs and variables are among the ‘white rats’ we have been using to test out various methods. However, as will be discussed later, any ensemble of two repeated measures variables can be used.

In each end-of-day report, participants indicated the degree to which they felt a variety of affective states, “Today I felt _______” using a “touch-point continuum” (slider-type interface) that was digitally coded on a 0 (not at all) to 100 (strongly) scale. Items included adjectives for 10 pleasant feelings (enthusiastic, happy, alert, proud, excited, calm, peaceful, satisfied, content, relaxed), and 9 unpleasant feelings (nervous, embarrassed, upset, tense, sluggish, sad, bored, depressed, disappointed; Kuppens et al., 2007). For each participant on each day, responses for the two sets of items were averaged separately to obtain daily measures of positive affect (PA = x) and negative affect (NA = y).

Data Analysis

Within-person changes in affect across bursts were examined using descriptions of the repeated measures of PA and NA from each burst as univariate density distributions, bivariate density distributions, and topographic landscapes.

Univariate: Intraindividual Mean and Variance

Each individuals’ daily measures of PA and NA during each burst were collected into ensembles and described as separate univariate distributions using standard calculations for the intraindividual mean (iMean),

$${\mu }_{\text{xi}}=\frac{1}{T}{{\displaystyle \sum }}^{}_{t=1}^T{x}_{\text{ti}}$$

and intraindividual standard deviation (iSD),

$${\sigma }_{\text{xi}}=\sqrt{{\sigma }_{\text{xi}}^2}=\sqrt{\frac{1}{T-1}{\displaystyle \sum }_{t=1}^T{\left(x_{\text{ti}}-{\mu }_{\text{xi}}\right)}^2}$$

where x_ti are the repeated measures of positive affect for person i on t = 1 to T occasions. Correspondent equations with y_ti were used to describe the intraindividual distributions of NA.

Bivariate: Intraindividual Correlation

Considering the daily measures of PA and NA as a bivariate ensemble, we additionally described the bivariate distribution using standard calculations for the intraindividual correlation (iCorr),

$$r_{\text{xyi}}=\frac{1}{T-1}{\displaystyle \sum }_{t=1}^T\left(\frac{x_{\text{ti}}-{\mu }_{\text{xi}}}{{\sigma }_{\text{xi}}}\right)\left(\frac{y_{ti}-{\mu }_{\text{yi}}}{{\sigma }_{\text{yi}}}\right)$$

where μ_xi, μ_yi, σ_xi, and σ_yi are obtained as noted above.

Landscapes: Landform Classification

Taking an explicitly geographic perspective, we also examined the topography of the bivariate density distributions. We describe the approach in some detail because, to our knowledge, this is the first time the technique has been used in psychological research.

Our first task was to obtain the bivariate emotional landscape for each individual for each burst. A bivariate nonparametric kernel density surface – basically a histogram in 3-d was estimated with a binning width multiplier of 0.7 (which controls the width of the histogram bins, and was selected after viewing the resulting landscapes and choosing those that most closely matched the look of true landscapes). Thus we obtain a grid-like surface where the height/elevation indicates the proportion of observations that have each specific x, y score combination (i.e., 0,1; 1,1; 2,1 … 100,98; 100,99; 100,100) – like the bottom panels of Figure 1.

Our next task was to describe the topography of the resulting surface. To do so, we automated and adapted Hammond’s (1954, 1964) rule-based landform classification method based on the local area’s slope character, local relief and profile type. Generally, we followed the automation procedures implemented by Gallant, Brown and Hoffer (2005). However, a few adaptations were necessary. Because our data were psychological dimensions rather than physical dimensions, we needed to consider various ways that our densities could be converted from proportions (frequencies) into an elevation metric (e.g., meters). After trying a few options, we settled on a method wherein we rescaled the maximum density in each individual’s bivariate density distribution so that it corresponded to the base-to-peak elevation of the world’s large rock spires, such as those of the Paine del Torres at the southern end of Argentina (~1,000 m). Automated classification according to Hammond’s rules then proceeded with only slight adaptations.

Slope character

The slope for each cell (x, y combination) in the j = 101 × k = 101 (because the PA and NA response scales ranged from 0 to 100) grid of elevations was calculated as the slope of a plane fit to the elevations of each cell, Z_j,k, in the 3 × 3 neighborhood surrounding cell. Specifically, calculations of the third-order finite difference weighted by the reciprocal of distance were,

$$\begin{array}{c}\text{slope}\%=100\cdot \sqrt{E{W}^2+N{S}^2},\text{where}\\ EW=\left[\right(Z_{j+1,k+1}+2Z_{j+1,k}+Z_{j+1,k-1})-(Z_{j-1,k+1}+Z_{j-1,k}+Z_{j-1,k-1}\left)\right]\\ NS=\left[\right(Z_{j+1,k+1}+2Z_{j,k+1}+Z_{j-1,k+1})-(Z_{j+1,k-1}+2Z_{j,k-1}+Z_{j+1,k-1}\left)\right]/8\end{array}/8,\text{and}$$

(which also follows the implementation in ARC GIS, a commonly used geographic information systems software, and in R by the slopeasp() function within the landsat library). Note that, because the 3 × 3 neighborhood is incomplete for cells along the edges of the grid, the resulting slope matrix contains only 99 × 99 = 9801 total cells. Then, the slope values for each cell were categorized as “gentle slope” if < 8%, and the number of gently sloping cells counted. Finally, the percentage of gently sloping area (100*# gently sloping cells/total cells) was classified into four categories (A, B, C, D) based on the Hammond rules in the first column of Table 2.

Local relief

Local relief is usually quantified as the difference in elevation between the lowest and highest cells. However, because our landscapes always had minimums at or very near zero and maximums of 1000m, we instead simply used the median elevation as a general indicator of relief. The midlevel elevation value was classified into four categories (1, 2, 3, 4) based on the original Hammond rules shown in the second column Table 2.

Profile type

To obtain profile types, we first calculated the proportion of gently sloping (< 8% slope) lands that were below the midlevel elevation (which in all of our landscapes was 500 m). These percentages were then classified into four categories (a, b, c, d) based on the Hammond rules in the third column of Table 2.

These three aspects of each individual’s emotional landscape at each burst designated the Hammond landform class, as shown in Table 1 (e.g., irregular plains, open low hills).

Changes in iMean, iSD, iCorr, iReg and iLandscape

Our final task was to examine if and how the quantifications and classifications of individuals’ behavioral landscapes (kernel density distributions) changed across the three bursts of measurement. Taking a person-specific (bottom-up) approach here, between-person comparisons were made only after the person-specific changes had been obtained. Given the small sample, we simply summarized the differences and similarities through qualitative description of the individual-level quantifications and classifications, keeping in mind the differences/similarities we expected might coincide with the differences in how these four individuals’ lives changed across the 18 months of study.

Results

Univariate, bivariate, and topographic descriptions of the PA and NA density distributions obtained for each of the three bursts for each person are given in Table 3. Correspondent visual representations are shown in Figures 2 and 3.

Table 3.

Descriptions of Four Individuals’ Univariate and Bivariate Density Distributions using iMean, iSD, iCorr, and iLandscape Procedures

	Stable Persons						Change Persons
	Person #1			Person #2			Person #3			Person #4
	Burst 1	Burst 2	Burst 3	Burst 1	Burst 2	Burst 3	Burst 1	Burst 2	Burst 3	Burst 1	Burst 2	Burst 3
Life Events Total	3	3	3	0	0	0	32	22	9	22	2	5
iMeanPA	54.81	55.59	56.15	65.44	61.66	61.64	21.67	38.28	54.59	45.89	40.82	37.72
iSDPA	7.63	7.6	8.5	5.58	5.49	7.63	10.69	14.09	11.74	16.41	14.28	6.89
iMeanNA	34.49	24.92	28.49	26.33	29.61	29.39	44.04	26.76	9.98	28.36	29.24	25.37
iSDNA	14.18	11.6	10.71	6.35	6.99	5.32	18.10	12.12	6.91	19.22	14.09	15.23
iCorrPANA	−.49	−.28	−.61	−.46	−.62	−.84	−.58	−.88	−.36	−.68	−.40	−.38
iLandscape	B2	B2	B2	A1	A1	A1	C3	B3b	B2	C3	C3	B2
Classification	Irregular Plains	Irregular plains	Irregular plains	Flat plains	Flat plains	Flat plains	Open Hills	Plains with hills	Irregular plains	Open hills	Open hills	Irregular plains
Slope Character	62.70%	72.29%	68.74%	86.61%	85.31%	87.12%	48.15%	55.54%	74.14%	25.59%	40.40%	65.45%
Local Relief	73.06	55.3	57.17	19.75	16.48	10.31	138.19	94.66	40.74	131.03	94.18	49.1
Profile Type	66.98%	75.52%	72.18%	87.86%	85.99%	87.54%	55.56%	60.88%	76.35%	28.20%	42.91%	67.91%

Note: PA = positive affect, NA = negative affect, iMean, iSD (standard deviation), iCorr (correlation) calculated using standard procedures as indicated in text. iLandscape classification derived using adaptation of Hammond (1954, 1964) classification rules as described in text. Stable Persons and Change Persons selected based on extent of burst-to-burst change in Life Events scores.

Figure 2. Stable persons.

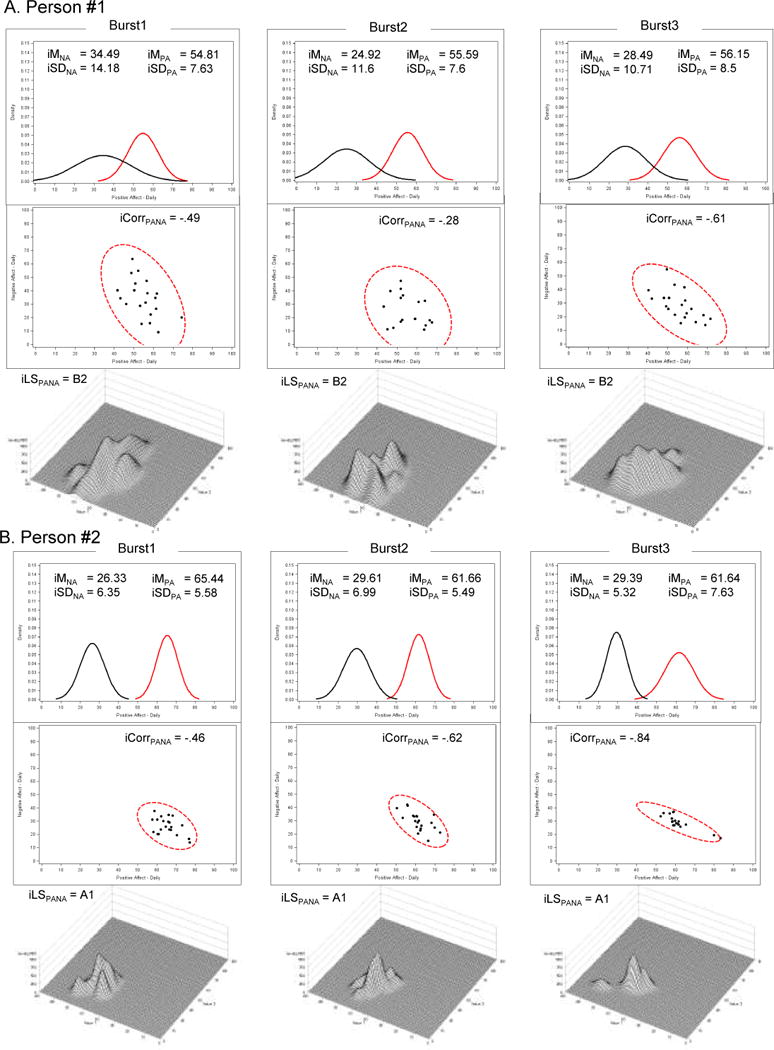
Univariate and bivariate density distributions of emotional behavior during three 21-day bursts of measurement (positive affect = PA and negative affect = NA) of two individuals who exhibited no change in life events during 18 months of study time. Top panel: Univariate representations described by iMean and iSD. Middle panel: 2-d bivariate representations described by iCorr. Bottom panel: 3-d bivariate representations described by classification of iLandscapes into Hammond (1954, 1964) landform classes. The descriptions highlight these two individuals’ stability across bursts.

Figure 3. Change persons.

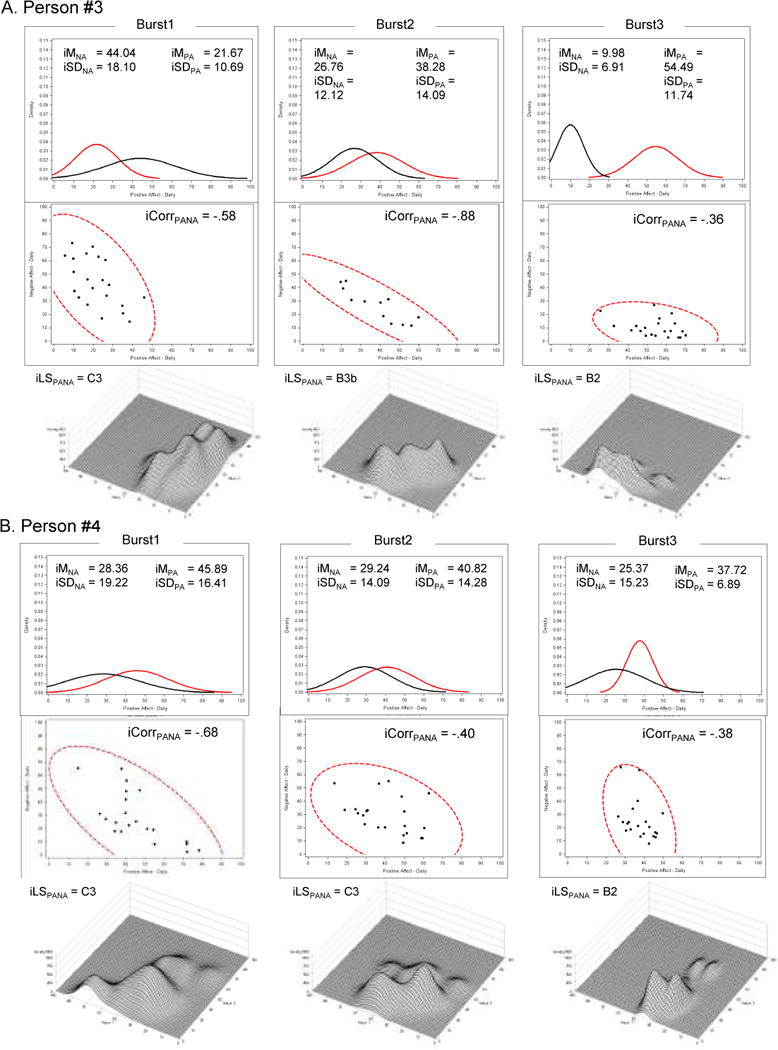
Univariate and bivariate density distributions of emotional behavior during three 21-day bursts of measurement (positive affect = PA and negative affect = NA) of two individuals who exhibited substantial change in life events during 18 months of study time. Top panel: Univariate representations described by iMean and iSD. Middle panel: 2-d bivariate representations described by iCorr. Bottom panel: 3-d bivariate representations described by classification of iLandscapes into Hammond (1954, 1964) landform classes. The descriptions highlight how these two individuals’ behavioral landscapes changed across bursts.

Stable Persons

As can be seen in the top row of Table 3, Person #1and #2′s life events scores remained stable across the study at 3 and 0, respectively. This stability was also reflected in the univariate density distributions. For both individuals, the iMeans of PA and NA stayed within a 5 point range across the three bursts and the iSDs stayed within a 2 point range across bursts. The stability of these distributions is evident in the top panels in Figure 2A and 2B where the locations and shapes of the PA and NA distributions are very consistent across bursts. The similarity of the density distributions across bursts could be interpreted as reflecting stability in these two individuals’ positivity, negativity, and (positive and negative) emotional variability. The bivariate correlations were somewhat consistent across bursts. Person# 1′s iCorrs ranged between r_PANA = −.61 to −.28 in raw correlation units, and Person #2′s iCorrs ranged between r_PANA = −.84 to −0.46, all in the expected direction, but, as seen in the 95% confidence ovals in the middle panels of Figure 2A and 2B, changing some from burst-to-burst. Stability was also reflected in the continuity of behavioral landscapes across bursts. Person #1′s and #2′s landscapes were consistently classified as type B2 (irregular plains) and A1 (flat plains), respectively.

Change Persons

In stark contrast to Persons #1 and #2′s stability, changes in Persons #3 and #4′s life circumstances are clearly evident in the Life Events scores in the top row of Table 3. For Person #3 changes were evident in the intraindividual means (30+ range for both iMean_PA and iMean_NA), in one aspect of the intraindividual variance (10+ range in iSD_NA), and perhaps in the intaindividual correlation, iCorrs ranged between r_PANA = −.88 to −.36. These changes can be seen readily in the top and middle panels of Figure 3A. Most striking, though, was that the behavioral landscape transformed from C3 (open hills) to B3b (plains with hills) to B2 (irregular plains) – as seen in the lower panel of Figure 3A the landscape flattened out. For Person #4 changes were not so evident in the intraindividual means (less than 10 point range for both iMean_PA and iMean_NA), although one aspect of the intraindividual variance did show some change (almost 10 point range in iSD_PA), as seen in the top panel of Figure 3B. As with all the other participants the intaindividual correlation exhibited some change across bursts, iCorrs ranged between r_PANA = −.68 to −.38. However, as seen in the lower panel of Figure 3B, the most striking change was in the transformation of the behavioral landscape, from C3 (open hills in bursts 1 and 2) to B2 (irregular plains) – again, a flattening of the landscape accompanied the drop in life events.

Discussion

In this paper, we attempted fusion of ideas from the study of lifespan development with intraindividual variability based approaches to personality and methods used to characterize the topography of geographic landscapes. The density distribution approach to personality has promoted the use of repeated measures data, like those obtained in daily diary and EMA designs to describe and quantify individuals’ typical behaviors and the potential range of behaviors exhibited across multiple situations and/or occasions (Fleeson, 2001). Across domains (e.g., emotion, cognition, motivation), this intraindividual variability based approach has promoted consideration of a wide set of dynamically-oriented constructs (e.g., stability, inconsistency, flexibility, lability) as viable descriptors of individuals’ personal characteristics (see Ram & Gerstorf, 2009). Generalizing from description of univariate density distributions to description of bivariate descriptions extends the possibilities and has promoted development and use of additional trait-like constructs (e.g., stress reactivity, Almeida, 2005; poignancy, Carstensen et al, 2011).

Behavioral Landscapes

Described in mathematical detail above, the operationalizations of the constructs are based on calculation of person-specific iMean, iSD, or iCorr (or iReg), standard descriptive statistics of time-series data based on assumptions that the repeated measures obtained from each individual are independent and identical draws from a normal (Gaussian) distribution (for additional implications of the iid assumptions, see Ram & Gerstorf, 2009). Our experiences with empirical density distributions suggested that the means, standard deviations, and correlations were not able to capture some interesting features of the data. In particular, the bivariate density distributions often look more like real geographic landscapes than like the single, symmetric hills in our (Gaussian-based) simulations. The real world (and real world data) is ‘rougher’ than the utopian worlds of simulated data in which methods are often developed. Thus, we began searching for methods to describe and quantify individuals’ traits using empirical iLandscapes. As illustrated in our example, the Hammond (1954, 1964) landform classification rules used to describe geographic landscapes can be adapted for description of behavioral landscapes.

In this initial exploration of viability of the methods, we used emotion data from a multi-time scale study design to capture both stability and change in emotional landscapes that proceeded in conjunction with changes (or stability) in life events. The Hammond (1954, 1964) classifications provided access to between-person differences within a burst (e.g., Burst 1 landscapes included A1, B2, and C3 forms), and access to within-person stability (Persons #1 and #2) and change (Persons #3 and #4) across bursts. Taking a person-specific approach, we purposively analyzed data from a very small set of “extreme” cases (with respect to life event change), and found some basic evidence that points towards an emerging hypothesis that higher life events scores for a given period contribute to the formation of hills and mountains in individuals’ emotional landscapes. These additional lumps in the distribution can be interpreted as emergence of additional “classes” of behavior. That is, the life events push individuals into previously unvisited spaces (recall that individuals “reside” in the hills) and affording additional levels and combinations of behavior. Although we remain cautious, the potential interpretability of the results suggests that the methods developed in geography can indeed be used to operationalize and investigate new behavioral science research questions.

Given intensive, multivariate repeated measures from a large sample of individuals we can investigate how interindividual differences are related to behavioral landscapes. For example, we might hypothesize that the emotional landscapes of individuals higher in neuroticism are characterized by more hills and mountains than their lower neuroticism peers. Given multiple bursts of data from the same individual, we can examine how his or her behavioral landscape changes with age – “the sharp bends in streams and the high, jagged mountain ranges, over time, becoming gently curving, wider rivers, and rounded, green hills” (Hooker, 2002, p. 329) – where some behavioral combinations get eliminated (or emerge) with development. With the automated version of the Hammond classification algorithm we have developed here (adapting Gallant et al., 2005), it is possible to describe iLandscapes for large samples of persons or bursts quickly and efficiently and then to examine them as both predictors of consequential outcomes (e.g., health, longevity, interpersonal functioning, family outcomes, career development) and consequential outcomes that are associated with genetic factors, early child variables, and/or environmental circumstances, etc. The possibilities are endless for using this new kind of personality variable on both the right and left hand sides of predictive equations. Needed is simply some focused thinking about the specific psychological constructs the iLandscapes represent, the specific meaning of between-person differences and within-person changes in those constructs, and how those differences and changes may relate to other aspects of human behavior.

Bivariate Density Landscapes

We described person-specific density distributions in emotional aspects of behavior using repeated measures of PA and NA. However, any 2-variable set will work, provided that the quantifications (iMean, iSD, iCorr, iLandscape) are tethered to theoretically meaningful constructs (Ram & Gerstorf, 2009). Many other bivariate spaces are well formulated and could be examined in a similar way (e.g., agency/communion, valence/arousal, approach/avoidance, goal engagement/disengagement, physical activity/inactivity). For example, public health researchers might apply these techniques to characterize behavioral profiles in individuals’ physical activity volume (movement with energy expenditure) and sedentary behavior (sitting/reclining with minimal energy expenditure; Owen, Healy, Matthews, & Dunstan, 2010). The behavioral landscape for an “active couch potato” (e.g., a person who gets physical activity by bicycling to and from work but sits at a desk most of the day) looks substantially different than either ideal high-activity/low-sedentary or compromised low-activity/low-sedentary (e.g., lots of standing without much movement) landscapes. To the extent that individuals’ behavioral landscapes differ, tailored interventions may be needed to effectively erode unhealthy landscapes and form healthy landscapes.

Trivariate Association Landscapes

As a generalized measure of net-intraindividual variability, the Hammond (1954, 1964) classification method demonstrated here can and should be generalized to 3-variable spaces. For example, rather than using density distributions where frequency/proportion of observations provides the vertical values, we could use three observed variables for the x, y, and z axes (e.g., valence, activation, dominance; Russell & Mehrabian, 1977). Then the landscape method can be considered as a map of the solution to a linear regression with two predictors (e.g., z_ti = β₀ + β₁x_ti + β₂y_ti + β₃x_tiy_ti) that defines a plane that bisects the 3 dimensional space. Of course, the surfaces (“planes”) defined by the raw trivariate data are likely rougher and more irregular – and may in many cases be described as the surface structure of high or very high relief tablelands (e.g., B5c, B6d). Methodologically, we see good potential for using the landform classification methods to examine between-person differences and within-person changes in trivariate concepts – and like how these fit with other landform descriptors (e.g., terrain ruggedness index; Riley, Degloria, Elliot, 1999). Although some additional theoretical work will be needed, we are confident that it is possible to formulate trait-like constructs that are truly operationalized as trivariate response surfaces – a worthy goal that can stretch personality theory in new directions.

Data Considerations

Our articulation of behavioral landscapes was both facilitated and constrained by the relatively continuous 0-100 response scale (see discussion in Ram et al., 2012). The continuous scale provides the opportunity for a wide variety of irregular shapes to emerge (while categorical variables only provide for a limited number of possible profiles), but also the chance that there are large, flat plains in the landscapes (e.g., A1 type) driven by the fact that density is relative to the total number of responses. In future applications, researchers should explore how to optimize the number of response scale options, the extent of smoothing needed in the kernel density estimation, and if and how to engage person-level and/or group-level standardization (e.g., conversion from raw metrics to z-scores).

The method introduced here fits in the space between the univariate density distributions (Fleeson, 2001), where repeated measures from many individuals are used to examine between-person differences in iMeans and iSDs, and a P-technique approach (Cattell, Cattell, & Rhymer, 1947) where the common factor model is applied to relatively long, many variable time series obtained from a single individual using relatively few latent variables (see Brose & Ram, 2012 for step-by-step implementation). Our initial experience here suggests that the iLandscape approach does not require as much data as a P-technique analysis. It is meant for low-dimensional time series (only 2 or 3 variables), and, as we demonstrated, can be applied to relatively short time series (e.g., 21 daily observations). Thus, it may be particularly useful in situations where a study design’s occasions/variables tradeoff resulted in a small number of items that each operationalize a distinct construct or piece of a 2 or 3-dimensional space – the approach used in many diary and EMA designs.

Conclusion

In developmental (and even personality) science, there is substantial movement towards use of intensive longitudinal, diary, and ecological momentary assessment designs to collect time-series data (Laursen, Little & Card, 2012; Ram, Lindenberger & Blanchard-Fields, 2009). Mobile technologies are becoming more and more ubiquitous, and facilitating the acquisition of high density repeated measures within on-going longitudinal studies (Mehl & Conner, 2012). The main goal of this paper has been to extend our ability to deliberately tether theoretico-methodological frameworks being used in geographic topography to the theoretical conceptions and time-series type data being collected in the study of development. There may soon be tremendous opportunities and need for methods that capture the richness of iLandscapes and afford the possibility to examine between-person differences and within-person changes in those landscapes. We have sought to refine and expand the methodological vernacular by explicitly making use of taxonomies developed in the study of geographic topography, and hopefully provoke a tsunami of new theoretical concepts in the study of human development.