Influences of Crowded Cellular Environments on Protein Folding, Binding, and Oligomerization: Biological Consequences and Potentials of Atomistic Modeling

Abstract

Recent experiments inside cells and in cytomimetic conditions have demonstrated that the crowded environments found therein can significantly reshape the energy landscapes of individual protein molecules and their oligomers. The resulting shifts in populations of conformational and oligomeric states have numerous biological consequences, including on the efficiency of replication and transcription, the development of aggregation-related diseases, and the efficacy of small-molecule drugs. Some of the effects of crowding can be anticipated from hard-particle theoretical models, but the in vitro and in vivo measurements indicate that these effects are often subtle and complex. These observations, coupled with recent computational studies at the atomistic level, suggest that the latter detailed modeling may be required to yield a quantitative understanding on the influences of the crowded cellular environments.

Motivation and scope

It is now widely recognized that the crowded conditions found in cellular environments can significantly impact the equilibria and kinetics of biochemical processes such as protein folding, binding, and oligomerization. Pioneering work by Minton [1], Kornberg [2], Ellis [3], and others as well as many recent studies have contributed to this recognition. As more and more researchers pay attention to and start to study the effects of crowded conditions, questions of general interest include: What has been established by studies of crowding? How best can we advance the quantitative understanding on the influences of the crowded cellular environments? This review presents a personal view on these and related questions.

A few studies have presented dramatic effects of macromolecular crowding. In Arthur Kornberg’s lab, many failed attempts finally led to success in replicating the oriC plasmid in a cell-free condition, upon including a high concentration of polyethylene glycol (PEG) in the incubation mixture [4]. As Kornberg [2] lucidly explained later, “the PEG gel occupies most of the aqueous volume and excludes a small volume into which large molecules are crowded. This concentration is essential when several proteins are needed in the consecutive steps of a pathway.” Hence Kornberg made “Thou Shalt Correct for Extract Dilution with Molecular Crowding” one of his ten commandments as he reflected on his studies of DNA replication.

More recently several labs observed that crowding agents such as PEG, Ficoll, and dextran drastically increased the aggregation rates of α-synuclein [5, 6] and apolipoprotein C-II [7], and enabled the efficient assembly of the HIV-1 capsid protein [8] and the alignment of FtzZ filaments into ribbons [9]. Red blood cells contain high concentrations (~320 g/l) of hemoglobin, and such a level of crowding is an essential condition for sickle hemoglobin (HbS) polymerization and sickle cell anemia [10]. A 20% reduction in the HbS concentration could reduce the rate of homogeneous nucleation of HbS into polymers by as much as 10¹⁰fold. Fetal hemoglobin (HbF) is unable to polymerize and replacement of HbS by HbF presents a potential therapy for sickle cell anemia. Ironically, as the HbF replacement essentially preserves the crowding effects, a 20% HbS-to-HbF replacement results in only a 10³-fold reduction in the rate of homogeneous nucleation, which would render HbF replacement an ineffective therapy.

In contrast to the foregoing studies, the effects of crowding found in many other studies are modest. For example, a number of papers [11–16] reported small increases, of the order of 1–2 k_BT (k_B: Boltzmann constant; T: absolute temperature), in protein folding stability by crowding agents. Similar results were found for the effects of crowding agents on the binding stability of protein-protein heterodimers [17, 18]. Two issues then arise: Can the dramatic effects of crowding observed in some studies be reconciled with the subtle effects found in other studies? Do these subtle effects of crowding nevertheless have biological significance?

Statistical thermodynamics provides a conceptual framework for addressing these issues and for a fundamental understanding of how crowding affects various biochemical processes. In principle, the equilibrium properties of these processes are determined by the energies of interactions within and between the “reactant” molecules and between the reactant molecules and bystander molecules such as crowders; kinetic properties requires in addition information on the dynamics of the reactant molecules in the solvent environment [19]. In practice, until recently, calculations of the effects of crowding on thermodynamic and kinetic properties were only possibly using simple models based on a hard-particle representation of reactant and crowder molecules, with excluded-volume interactions playing a dominant role [20, 21]. Molecular simulations have now opened a powerful way to model the effects of crowding, and promise to enable quantitative predictions on the influences of the crowded cellular environments.

The following sections present a critical assessment of some recent studies of biochemical processes in cells and in crowded solutions, with an eye toward answering the two questions posed in the opening paragraph. I mostly limit to studies that appeared in the last four years. Earlier studies are covered in several reviews [22–26], and some are already mentioned in the preceding paragraphs. In addition, the focus is on equilibrium properties; effects of crowding on kinetic properties are assessed elsewhere [19, 21, 23, 27–30]. Experimental studies, divided into three sections, are followed by computational studies in a single section.

Protein folding

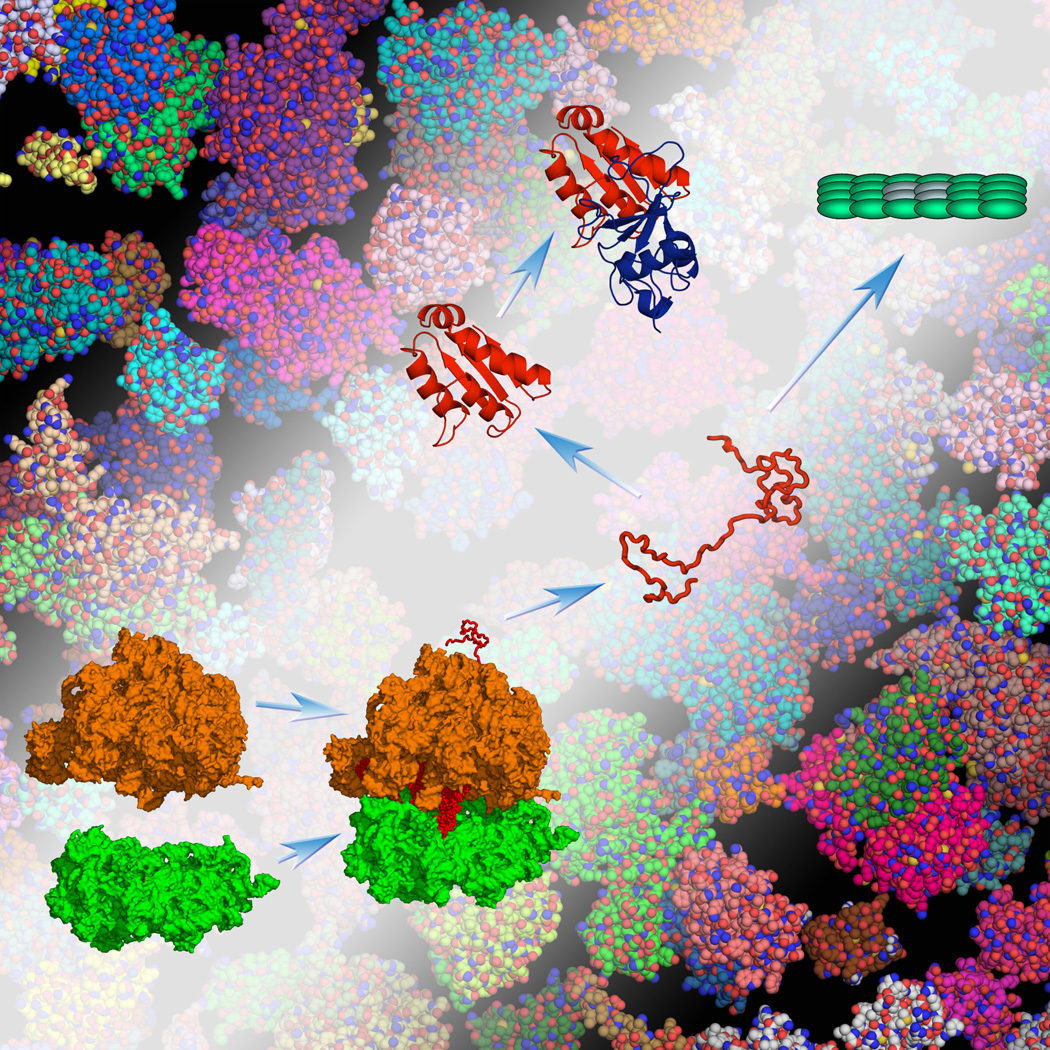
Upon synthesis, most, not all, proteins fold into defined 3-dimensional structures before gaining biological functions (Figure 1). Some others exist as unstructured in one functional state and structured in another (e.g., when bound to a biological target). Extending other studies [11–14, 16], the Pielak lab has assessed how crowded cytomimetic conditions affect the folding stability of proteins [15, 31–34]. These recent studies are notable both for the experimental technique used and for their findings, presenting additional subtleties and complexities of the effects of crowding. The technique is NMR-detected amide proton exchange, which probes residue-level local stability, i.e., the stability of individual residues to withstand opening up for hydrogen/deuterium exchange [35]. Opening of the residues with the highest local stability involves global unfolding; hence the highest local stability corresponds to the global folding stability.

Fig. 1.

Inside cells biochemical processes occur in crowded environments. The depicted processes include the binding of the large and small subunits of the ribosome, the folding of a nascent protein, its binding to another protein, and aggregation. The crowded conditions can significantly change the relative stability among the various species.

Regarding the influence of macromolecular crowding on global folding stability, Pielak and co-workers concluded: (1) Two polymer crowders, poly(vinylpyrrolidone) (PVP) and Ficoll, resulted in modest stabilization of chymotrypsin inhibitor 2 (CI2), in line with other studies [11–14, 16], but two protein crowders, lysozyme and bovine serum albumin (BSA), resulted in mild destabilization; (2) The temperature dependence of the stabilizing effect of Ficoll indicated enthalpy, not entropy, as the dominant component, contrary to expectations based on consideration of excluded-volume interactions alone; (3) Temperaturedependent data for the effects of PVP, Ficoll, lysozyme, and BSA on the stability of ubiquitin again suggest a dominant enthalpic component.

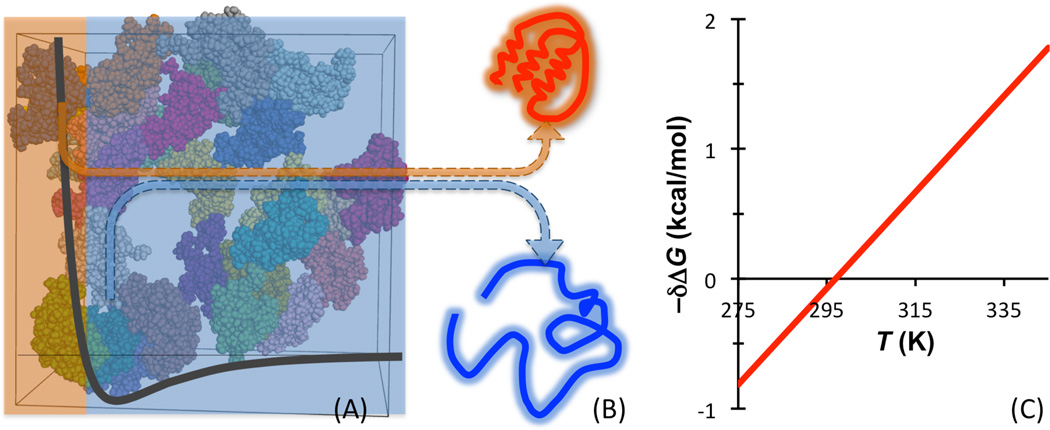
These conclusions cast serious doubt on the conceptual framework for understanding the effects of macromolecular crowding on protein folding stability. Recently, the published data of the Pielak lab were re-analyzed, with an emphasis for a unified mechanism of action for all macromolecular crowders [36]. It was recognized that all intermolecular interactions consist of hard-core repulsion and longer-ranged (mostly) attraction (Figure 2a). The hardcore repulsion between a protein molecule and the crowder molecules leads to an entropic component that favors the folded state of the protein, whereas the longer-ranged attraction leads to an enthalpic component that favors the unfolded state (Figure 2b). Because in the folding free energy the entropic component is weighted by the temperature, the net effect of macromolecular crowding is destabilizing at lower temperatures but becomes stabilizing at higher temperatures (Figure 2c). This predicted general trend is exactly what was observed for both polymer crowders and protein crowders on the folding stability of ubiquitin [33].

Fig. 2.

Illustration of the effects of macromolecular crowding on protein folding stability. (A) The interactions between a protein and surrounding crowder molecules consist of hard-core repulsion and longer-ranged attraction. (B) The hard-core repulsion leads to an entropic component that favors the folded state of the protein, whereas the longer-ranged attraction leads to an enthalpic component that favors the unfolded state. (C) The net effect of macromolecular crowding has a crossover temperature, where δΔG = 0.

According to the general trend just noted, for a given protein, every macromolecular crowder is predicted to have a crossover temperature at which the net effect of crowding changes from destabilizing to stabilizing. Hence the experimental temperature plays an important role in determining the sign (and magnitude) of the crowding effect. In line with this expectation, the stabilizing effects of PVP and Ficoll on CI2 were measured at a higher temperature, 37 °C, whereas the destabilizing effects of lysozyme and BSA were measured at a lower temperature, 20 °C. The prediction is that PVP and Ficoll will destabilize CI2 at lower temperatures whereas lysozyme and BSA will stabilize CI2 at higher temperatures. While this prediction on CI2 has yet to be tested, the Gruebele lab has now published results for the increased folding stability of λ_6–85 by a protein crowder (subL) [37] and of phosphoglycerate kinase inside cells [38], both at high temperatures.

While the existence of a crossover temperature is predicted to be universal, its exact value of course depends on the size, shape, and chemical nature of the crowders. It is possible that common polymer crowding agents such as Ficoll and dextran may exert weaker soft attraction than protein crowders toward test proteins. Pielak and co-workers measured the effects of polymer and protein crowders on the translational and rotational diffusion and the NMR relaxation of CI2 [39]. The results are consistent with the protein crowders exerting stronger soft attraction toward CI2. Stronger soft attraction will produce a larger enthalpic component favoring the unfolded state of the test protein, leading to a higher crossover temperature (assuming the entropic component is fixed).

NMR-detected amide proton exchange yields information not only on the global folding stability but also on the local stability against opening up. The latter information can potentially be a rich source for understanding how crowding affects local conformational sampling. Theories and computations have yet to make quantitative predictions that can be directly tested by experiments, so this source is still under-exploited.

The effects of crowding on protein folding stability revealed by all the in vitro and in vivo studies seem modest. Nevertheless these effects can have significant biological consequences. For example, a 2k_BT increase in folding stability will change a marginally stable protein from 75% unfolded into 75% folded. Searches for such cases have been carried out. A recent in-cell NMR study on a destabilized mutant of protein L did not find evidence of folding in E. coli [40]. This could mean that the effect of the cellular environment was too modest under the experimental conditions; it may also be possible that conformational exchange makes it difficult for a folded population to be detected by in-cell NMR spectroscopy. An earlier in vitro study [11] along the same line is instructive. With increasing concentrations of dextran, the unfolding free energy of a destabilized variant of ribonuclease T1 became less and less negative, extrapolating to a 22% folded population at 400 g/l dextran. At this crowder concentration, the fluorescence spectrum of the protein still resembled largely that of the unfolded state and little that of the folded state; nevertheless the protein gained 16% of the expected enzymatic activity of the folded state. Finally the prediction that temperature plays an important role in determining the net effect of crowding leads one to conclude that crowding effects make greater contributions to the in vivo folding stability of proteins in thermophilic organisms [36].

Conformational change of intrinsically disordered proteins

Some proteins, or fragments thereof, are thought to exist in the unfolded state and participate in cellular functions. A notable example is α-synuclein, a presynaptic protein linked to Parkinson’s disease and whose normal functions putatively include regulation of neurotransmitter release, in particular acting as a chaperone for SNARE-complex assembly in presynaptic terminals [41]. The classification of α-synuclein and others as “intrinsically disordered proteins” (IDPs) is usually based on conformational probes in dilute solution [42–47]. The conformational flexibility and the propensity to oligomerize and aggregate and to bind with different partner proteins and biological membranes make IDPs particularly susceptible to the effects of crowding under cellular conditions. For α-synuclein, recent studies have uncovered evidence that inside cells it exists as a stable α-helical tetramer [48] or as a dynamic tetramer with high α-helix content [49]. Other studies [50, 51], however, continue to suggest that native α-synuclein is an unfolded monomer. N-terminal acetylation, a posttranslational modification in eukaryotic cells, could contribute to the difference in conformational and oligomeric states [52].

In dilute solution of α-synuclein, raising temperature induces helix formation [45] and expansion in size [53], as indicated by circular dichroism, ¹H-¹⁵N heteronuclear single quantum coherence (HSQC) spectra, and pulse field gradient measurement of hydrodynamic radius. The expansion and helix formation are suppressed by 300 g/l of BSA and in the Escherichia coli periplasm [54], as shown by in vitro and in-cell NMR spectroscopy. Compaction under crowding has also been observed for other IDPs, including the N protein of bacteriophage λ (crowded by bovine pancreatic trypsin inhibitor (BPTI) and observed by small-angle neutron scattering) [55] and p21^Cip1 (crowded by dextran and observed by fluorescence correlation spectroscopy) [56]. Similarly, compression of the polymer PEG by Ficoll as a crowding agent has been observed [57], suggesting excluded-volume interactions as a common cause for the contraction in size. Reinforcing this contention, it was reported that Ficoll resulted in compaction of the unfolded state of a globular protein (as assessed by iodide quenching of tryptophan fluorescence and extent of cysteine modification with PEG-maleimide) [58] and an increase in the population of a more closed conformation in the folded state of phosphoglycerate kinase (indicated by decreased donor-to-acceptor fluorescence ratio) [59]. The increase in closed population is even more pronounced inside cells [38, 60].

Some IDPs gain structures upon binding a biological target. An example is FlgM, a ~10 kD transcriptional regulator involved in the ordered synthesis of proteins for bacterial flagellar assembly [61]. It binds to σ²⁸, the flagellar σ subunit of the RNA polymerase holoenzyme, thus occluding the catalytic core. Once the transmembrane flagellar base is assembled, FlgM is released through its lumen, allowing σ²⁸ to bind the RNA polymerase catalytic core and initiate late gene expression for completion of flagellar assembly. In dilute solution, FlgM is mostly unfolded, with transient helix formation in the C-terminal half [62, 63]. Upon binding the three-domain σ²⁸, FlgM adopts an extended configuration on the σ²⁸ surface, with two C-terminal helices interacting with the third σ²⁸ domain and a middle helix interacting with the first σ²⁸ domain [64]. The Pielak lab [65] has reported HSQC spectra showing that, in the presence of 400 g/l BSA or when overexpressed in E. coli, the C-terminal half gains structure, reminiscent of the situation with binding σ²⁸ [62]. Given that the helices of σ²⁸-bound FlgM are well separated and have few tertiary contacts, it is doubtful that the structure induced by crowding is the same as that formed on the σ²⁸ surface. However, it is entirely possible that, relative to the conformational ensemble in dilute solution, the conformational ensemble under crowding is more similar to the bound structure and has higher affinity for σ²⁸. Retaining conformational flexibility inside the cell may actually be beneficial, since FlgM has to be secreted when its inhibitory activity is no longer needed.

More generally, the crowded conditions in cellular environments could alter the relative stability of IDPs among different conformational and homo- and hetero-oligomeric states (Figure 3). As noted above, crowding agents like Ficoll and dextran were found to drastically increase the aggregation rates of α-synuclein [5, 6], presumably by stabilizing oligomers that nucleate the aggregation process. The tendency of IDPs to form homo- and hetero-oligomers, especially under crowding, can potentially be harmful to cells [66]. Perhaps as a defense mechanism, the expression levels of IDPs are lower relative to those of structured proteins, through increased degradation and decreased translation rate [67]. Oligomerizationrelated processes are further discussed next.

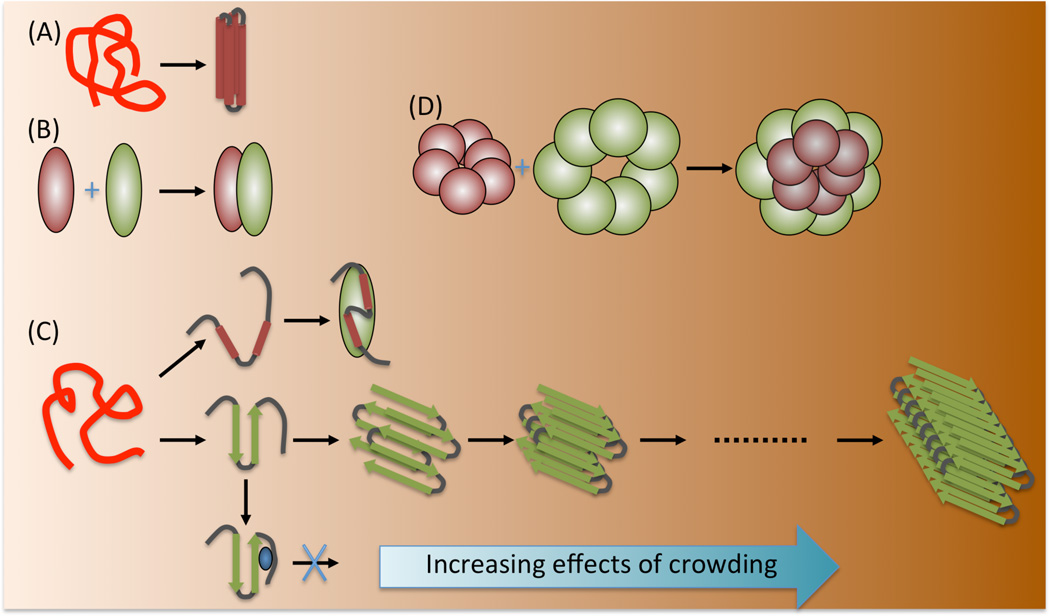
Fig. 3.

Varying magnitudes of the effects of macromolecular crowding on different biochemical processes. The effects are expected to be modest for (A) folding stability and (B) binding stability of single-domain proteins, (C) conformational changes of an IDP and its binding to a structured partner, and the binding of a small-molecule drug to a protein monomer, but dramatic for (D) the binding of multimeric proteins, (C) oligomerization, and aggregation.

Binding, oligomerization, and aggregation

The modest effects of macromolecular crowding on protein folding stability commented above is in line with similarly modest effects on the binding stability of heterodimers formed by single-domain proteins [17, 18]. A 1–2 k_BT increase in binding stability corresponds to a ~5-fold increase in binding affinity. While it is difficult to directly ascertain whether such an increase has any biological significance, one can infer a positive answer based on biological consequences of mutations that cause similar changes in binding affinities. For example, in vivo assays have identified a number of FlgM mutants as defective in inhibiting σ²⁸ [62]. These mutants were confirmed to be significantly less effective in suppressing in vitro transcription, and yet their binding affinities for σ²⁸ were reduced by only 4–10 fold [68].

Theories [20, 69] predict that, under the same crowding condition, the effects of crowding on binding stability increase when the sizes of the two reactant species increase, as in the cases of multi-domain or multimeric proteins (Figure 3). In the binding of the large and small subunits to form an intact ribosome (Figure 1) and the subsequent formation of a ribosome dimer, even a low concentration, 60 g/l, of dextran and Ficoll, resulted in ~10-fold increases in the two binding constants [70]. Similarly, 75 g/l of PEG 12K resulted in a 55-fold increase in the binding affinity between the trimeric gene 45 protein and the gene 44/62 protein complex (the latter having a 4:1 stoichiometry) [71], which are part of the DNA replication complex of bacteriophage T4. Jarvis et al. [71] further observed that PEG also significantly enhanced the stability of the replication complex formed on single-stranded DNA, such that a primer is extended much longer than in the absence of PEG. Echoing the words of Kornberg [2], Jarvis et al. noted that, given the µM cellular concentrations of T4 replication proteins, the ~µM dissociation constant between gene 45 and gene 44/62 proteins measured in dilute solution would be much too weak for holding the replication complex together on a template DNA strand for extended replication.

Yi et al. [72] recently studied the effects of dextran, Ficoll, and PEG on the binding affinity of two multimeric proteins, superoxide dismutase and catalase, at a range of temperatures. They found that the stabilizing effects of the crowding agents diminished when the temperature was lowered. This temperature dependence is very similar to that for crowding effects on protein folding stability noted above (Figure 2c) [36], and was indeed accorded a similar explanation, i.e., by invoking the balance of entropic and enthalpic components that favor the bound and unbound states, respectively.

It has also been recognized that the stabilization due to crowding is nonspecific, in that it is applicable to every binding step, regardless of the identities of the reactants [18]. Therefore, the stabilizing effects are cumulative when forming a higher oligomer (Figure 3) [18, 20, 73]: each addition of a monomer is accompanied by an increase in stability due to crowding. This cumulative nature can lead to substantial stabilization of the oligomer. Such stabilization could explain the drastic increases in protein aggregation rates by crowding agents [5–7], if the aggregations are nucleated, i.e., rate-limited by the formation of appropriately-sized oligomers. Recently, dextran 70K at 200 g/l was found to induce the formation of prion protein oligomers with high β-sheet content [74], which putatively are the infectious agents for prion diseases [75]. These results suggest that the crowded environments inside cells play a critical role in the development of protein-aggregation related diseases.

Many structured proteins form oligomers with defined sizes, and effects of crowding on the stability of some of them have been studied. As expected, stabilization much greater than that for dimers formed by single-domain proteins is observed. For example, using magnetic relaxation dispersion, Snoussi and Halle [76] found a 17000-fold increase in the association constant for BPTI decamer by 230 g/l of dextran 10K. Similarly, Aguilar et al. [77], based on tryptophan fluorescence, found that 300 g/l Ficoll resulted in a 300-fold increase in the association constant for heptamer formation by mitochondrial cochaperonin protein 10.

The significant stabilizing effects of crowding on protein oligomers suggest that many proteins that are identified as monomeric based on dilute-solution assays may actually be oligomeric inside cells. The α-synuclein tetramer recently found inside cells [48, 49] could be such an example, though as mentioned above the native oligomeric state is still controversial.

The increase in the effects of crowding with increasing physical or oligomeric sizes of reactant species potentially leads to an important downside: small-molecule drugs that are effective in blocking the formation of large complexes or high oligomers in dilute solution may lose their efficacy under crowded conditions. That is because crowding disproportionately stabilizes the higher oligomer over the competing complex formed by the drug molecule and the monomer (Figure 3). This expectation is borne out by a recent study on the inhibition of the assembly of the HIV-1 capsid protein by a capsid protein fragment or a short peptide [78]. In dilution solution, both inhibitors were found to be effective in slowing down the assembly and reducing the total assembled mass. Both Ficoll and dextran were found to speed up the assembly in the absence of inhibitors [8]. In the presence of either inhibitor, the two crowding agents were still able to speed up the assembly and nearly maintain the total assembled mass. In other words, the inhibitors lost their efficacy in the presence of the crowding agents.

Toward quantitative predictions: theoretical, coarse-grained, and atomistic modeling

In a number of the experimental studies reviewed above [7, 10, 12, 16, 57, 70, 72, 76], comparison was made to theoretical models based on representing reactant and crowder molecules as hard convex particles. Although these models often give qualitatively correct trends, the adjustable parameters in these models, such as on the shapes and sizes of the molecules, erode their predictive power. Recently molecular simulations have opened the possibility of making quantitative predictions and subjecting these predictions to direct interrogation by experiments.

To calculate the effects of crowding on the thermodynamic properties of biochemical processes, one can emulate what is done experimentally and simulates the reactant proteins along a biochemical process, both in the absence of crowders and in the presence of crowders [79–82] (horizontal paths in Figure 4a). The advantage of this direct simulation approach is that one can visualize how interactions with crowders reshape the energy landscapes of the reactant molecules. However, because one has to sample rare transitions between stable states along the biochemical process in order to calculate free energy differences, and has to do so in the presence of a large number of crowder molecules (Figure 4b), the direct simulation approach inherently carries a formidable computational cost.

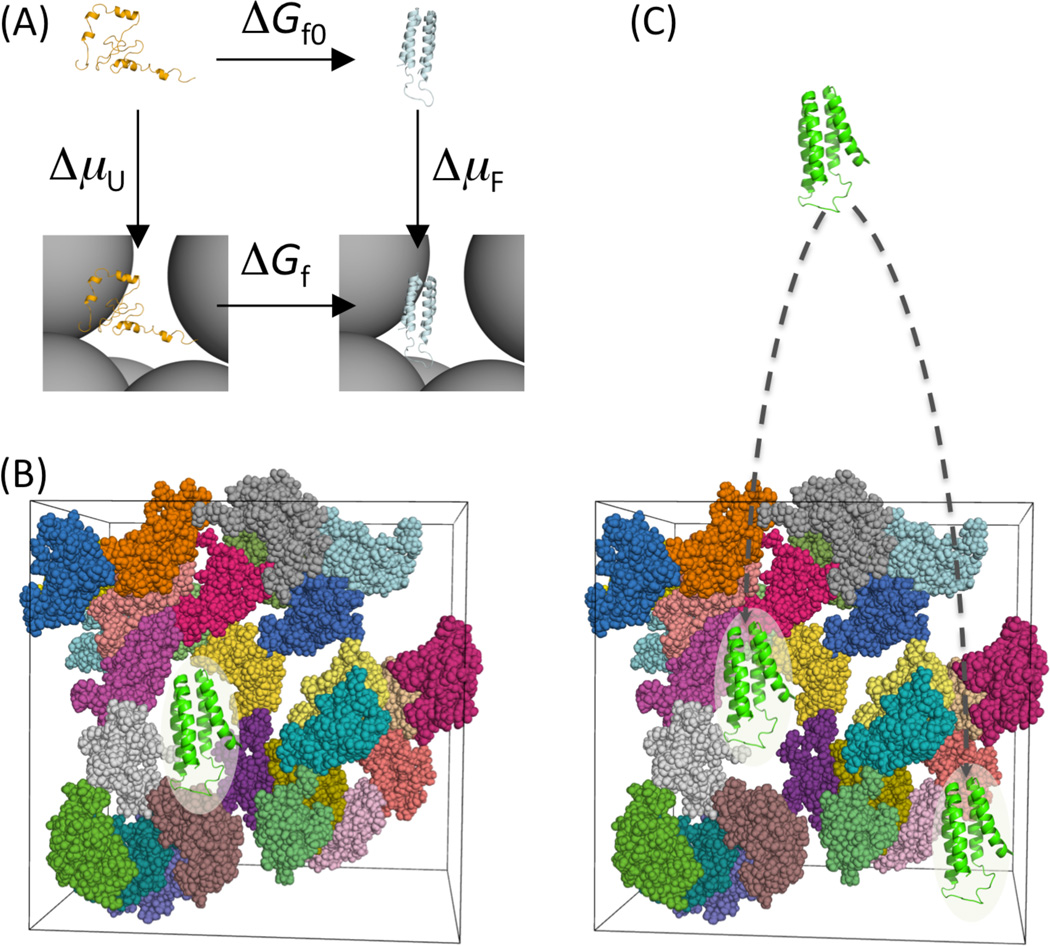
Fig. 4.

Two different approaches for modeling biochemical processes under crowding. (A) The direct simulation approach follows the horizontal paths whereas the postprocessing approach follows the vertical paths, illustrated on the folding process of a protein. The same free energy difference δΔG, here representing the effect of crowding on the folding free energy, is obtained by following either the horizontal paths (δΔG = ΔG_f −ΔG_f0) or the vertical paths (δΔG = Δμ_F − Δμ_U). (b) In the direct simulation approach, one follows the folding transition in the presence of crowders. Here the protein is shown in a folded conformation. (c) In the postprocessing approach, one simulates only the folded state and the unfolded state, not their inter-conversion, and does so in the absence of crowders [73]. To calculate Δμ_F, folded conformations are fictitiously inserted into the crowders. An analogous calculation yields Δμ_U.

The alternative approach is to follow the vertical paths in Figure 4a [73, 83, 84]. That is, one simulates just the stable states in dilute solution and then calculates the free energies of transferring these stable-state conformational ensembles to crowded solution (Figure 4c). In this “postprocessing” approach, one circumvents the need for sampling rare transitions between stable states. However, one does have to take the additional step of calculating the transfer free energies. Since the horizontal paths and vertical paths form a closed thermodynamic cycle, both approaches yield δΔG, the effect of crowding on the free energy difference between the reactant and product states.

To reduce the formidable computational cost of the direct simulation approach, it has only been implemented by representing the reactant protein molecules at the coarse-grained level, e.g., one bead per residue. This representation potentially limits the predictive power of the direct simulation approach, and so far it has mostly been used for calculating qualitative trends. The first such simulation study was by Cheung et al. [79], who calculated the folding stability and kinetics of the 34-residue WW domain in the presence of purely repulsive spherical crowders. Conformational sampling was helped with the replica exchange method. At a crowder volume fraction (Φ) of 0.25, the melting temperature was predicted to increase by as much as 24 °C. In a similar study, Mittal and Best [82] calculated the effects of crowding on the folding free energy surfaces of three small proteins. The reaction coordinate was the fraction of native contacts, and the free energy surfaces were obtained by combining the replica exchange method with umbrella sampling. Also using direct simulation, Minh et al. [80] studied the effects of crowding on the flap opening equilibrium of the HIV-1 protease dimer. This opening motion is essential for substrate and inhibitor binding. They found that repulsive crowders decreased the flap open population.

Recently Feig and Sugita [85] carried out all-atom explicit solvent molecular dynamics simulations of CI2 in the presence of either lysozyme or BSA as crowders. These simulations were motivated by the experiments of Miklos et al. [32], who, as noted above, found that the protein crowders decreased the local stability of many of the monitored CI2 residues. Interestingly, the residues showing decreased local stability largely overlapped with residues showing increased conformational fluctuations in the simulations in the presence of the protein crowders. It should be noted that the experiments of Miklos et al. present measurements on the equilibria between the folded state and the locally or globally unfolded state, whereas the simulations of Feig and Sugita probe nanosecond conformational fluctuations in the folded state.

The postprocessing approach uses only crowder-free simulations of proteins in their reactant and product states. Therefore the proteins can be represented at the all-atom level and the simulations done in explicit solvent. The atomistic representation makes it possible to make quantitative predictions on the effects of crowding. The additional step to calculate the transfer free energy (Δμ) of the reactant proteins requires a separate simulation of the crowder molecules to generate a configurational ensemble for the crowder solution. The latter simulation can be expensive, but needs to be done only once and then can be used over and over for different reactant proteins in various states.

To calculate Δμ, one fictitiously inserts each protein conformation into the crowder solution (Figure 4c). If the effective interaction energy between a reactant protein and the crowders is U(X, R, Ω), where X, R, and Ω represent the conformation, position, and orientation, respectively, of the protein, then

$$\text{exp}(-\mathrm{\Delta }\mu /k_{\mathrm{B}}T)=<\text{exp}[-U(\mathbf{X},\mathbf{R},\mathbf{\Omega })/k_{\mathrm{B}}T]{>}_0$$ (1)

where < ⋯ >₀ means averaging over the conformation, position, and orientation of the protein and over the configuration of the crowders. Both a numerical algorithm [73] and a theoretical formula [69] have been developed for calculating Δμ. The theoretical formula, validated by the numerical algorithm, speeds up the Δμ calculations considerably and is essential for cases where the numerical algorithm becomes impractical, such as when the reactant molecules are very large. Notably, the theoretical formula enabled the Δμ calculations for the binding of the large and small subunits of the ribosome [69]. In these calculations, the reactant molecules are represented at the all-atom level.

The postprocessing approach yields the transfer free energy by reweighting the protein conformations, sampled in the absence of crowders, according to the would-be protein-crowder interaction energy. The important conformational region will likely be shifted by the crowders. The postprocessing calculation would be exact if the conformational space of the protein is exhaustively sampled so as to cover the important conformational region in the presence of crowders. For both the flap open population of the HIV-1 dimer [83] and the free energy surfaces of three small proteins [86], the results of the postprocessing approach predicted from the crowder-free simulations were found to agree well with those calculated from the direct simulation approach in the presence of crowders [80, 82].

In several studies, postprocessing predictions have been interrogated by experimental results. In the first such study [73], a modest increase in the folding stability of a four-helix bundle protein by 85 g/l PEG 20K [13] was reproduced when the folded and unfolded states were represented atomistically while the crowder was modeled simplistically as a 20 Å sphere. A subsequent study [87], with the folding transition state represented atomistically, also yielded the experimentally observed small effects of crowding on the folding and unfolding rates. Similarly, modest increases in the binding stability of the ε and θ subunits of E. coli DNA polymerase III by dextran of various molecular weights and Ficoll70 were quantitatively rationalized with atomistic representation of the proteins [18]. Using the postprocessing approach, Johansen et al. [55] was able to explain the compaction of the N protein of bacteriophage λ when crowded by BPTI. While in these applications of the postprocessing approach the crowders were modeled as repulsive spheres, a major step forward was taken by McGuffee and Elcock [84], who represented protein crowders at the coarse-grained level with compositions and concentrations mimicking those of the E. coli cytoplasm, and included repulsive as well as attractive interactions with the reactant proteins.

Conclusion and outlook

Various in vitro and in vivo studies have now demonstrated effects of crowding that range from modest to drastic. On the modest side are protein folding stability and binding stability of single-domain proteins. On the drastic side are the efficiency of replication and transcription, the rates of protein aggregations linked to Parkinson’s and other diseases, and the efficacy of small-molecule drugs. Regardless of magnitudes of the effects, the biological consequences of crowding in all these cases are important.

Two emerging trends will significantly contribute to the progress of our understanding on the influences of the crowded cellular environments. The first is the convergence of in vitro and in vivo observations on the effects of crowding. For example, the Pielak lab has observed similar compaction or structure formation inside cells and when crowded by BSA [54, 65]. Likewise the Gruebele lab has observed similar increases in the closed population of a folded protein inside cells [38, 60] and when crowded by Ficoll [59]. These convergent observations strengthen the confidence in our understanding on the nature of the cellular environments and in our ability to make inferences on biochemical processes inside cells based on experiments under cytomimetic conditions.

The second emerging trend is the convergence of experimental and computational studies on the same reactant proteins under the same crowding conditions. In this regard, the postprocessing approach, with the ability to represent reactant proteins and crowders at the atomistic level, will have a significant role to play. Unlike the previous generation of theoretical models based on a hard-particle representation, the new computational approach potentially holds truly predictive power, because the parameters of intermolecular interactions, once set, should be applicable to all reactant proteins and all crowders. There is hope that computations will be able to capture the subtle and complex effects observed in recent experiments, and the integration of the two will bring us toward a quantitative understanding on the influences of the crowded cellular environments.

ABBREVIATIONS

BPTI

bovine pancreatic trypsin inhibitor

BSA

bovine serum albumin

CI2

chymotrypsin inhibitor 2

HbF

fetal hemoglobin

HbS

sickle hemoglobin

HSQC

¹H-¹⁵N heteronuclear single quantum coherence

IDP

intrinsically disordered protein

PEG

polyethylene glycol

PVP

poly(vinylpyrrolidone)