Simple liquid models with corrected dielectric constants

Abstract

Molecular simulations often use explicit-solvent models. Sometimes explicit-solvent models can give inaccurate values for basic liquid properties, such as the density, heat capacity, and permittivity, as well as inaccurate values for molecular transfer free energies. Such errors have motivated the development of more complex solvents, such as polarizable models. We describe an alternative here. We give new fixed-charge models of solvents for molecular simulations – water, carbon tetrachloride, chloroform and dichloromethane. Normally, such solvent models are parameterized to agree with experimental values of the neat liquid density and enthalpy of vaporization. Here, in addition to those properties, our parameters are chosen to give the correct dielectric constant. We find that these new parameterizations also happen to give better values for other properties, such as the self-diffusion coefficient. We believe that parameterizing fixed-charge solvent models to fit experimental dielectric constants may provide better and more efficient ways to treat solvents in computer simulations.

1 Introduction

In molecular simulations, solvents such as water are often represented by explicit models such as TIP3P or SPC.^1,2 Many of these explicit-solvent models were originally developed and parameterized a few decades ago. They were parameterized to agree with experimental data such as the density and enthalpy of vaporization of the neat liquid, key quantities that are readily available from accurate experiments. However, such molecular solvent models don’t typically predict the correct experimental value of the dielectric constant.^3–7 This is unfortunate because molecular simulations are so commonly used to treat the solvation of polar and charged molecules, for which it is essential that the solvent respond properly to electrostatic fields. Reproducing the dielectric constant is especially critical in low-dielectric solvents like chloroform or cyclohexane. While solvents with dielectric constants of 80 and 60 can give solvation free energies of a charge within 1% of one another, solvents with dielectric constants of 2 and 1.5 will give solvation free energies that are more than 50% different.

When current solvent models fail to reproduce the dielectric constant, it is often concluded that improvement can only be achieved by resorting to more complicated geometries or additional interactions, such as those present in expensive polarizable or quantum chemical models.^5,6,8–15 We take a different approach here. Here, we develop classical fixed-charge molecular solvent models for water, CCl₄, CHCl₃, and CH₂Cl₂, but we parameterize them based on experimental dielectric constants, in addition to the solvent density and enthalpy of vaporization. We find that our newly parameterized solvent models capture some additional experimental properties at least as well as previous models, in addition to getting the dielectric constant correct. The benefit of re-parametrized fixed-charge models is that it allows for much more efficient simulations than those involving polarizable or QM forcefields.

We develop molecular models of carbon tetrachloride (ε(0) = 2.2 at 298.15 K and 1 atm), chloroform (ε(0) = 4.7), dichloromethane (ε(0) = 8.9), and water (ε(0) = 78.4). Our choice of which solvents to model was based on wanting a wide range of dielectric constants and wanting no more than two primary atom types. The latter is so that we can test our parameterization methodology for incorporating experimental dielectric constant information without the extra complexity or additional parameters that would be needed for multi-atom-type solvents.

2 Methods

2.1 Building initial molecular structures

For the chloromethanes, we start with the gas-phase geometry, and for water we used both the gas-phase geometry as in TIP3P water¹ and the simplified tetrahedral geometry of SPC water.² As chloroform and dichloromethane contain three atom types, we chose to work with united-atomvariants to simplify the liquids to two atom-types, and compare how well an optimized united-atom model reproduces experimental quantities relative to an existing all-atom model.

To start the model optimization process, we first need an initial set of parameters. These include Lennard-Jones (LJ) σ_LJ and ∊_LJ parameters for each atom-type, as well as an initial distribution of partial charges. For each of these, we chose experimentally derived or simple values. As the σ_LJ parameter corresponds to an atom size, we chose the Bondi radii as the initial LJ radius, or σ_LJ/2.¹⁶ For united-atom sites in CH₂Cl₂ and CHCl₃, we calculated the initial van der Waals volume of the all-atom versions of these molecules using a mutual overlapping spheres procedure.¹⁷ We then placed the united-atom (UA) site at the center-of-mass of the carbon and hydrogen atoms and scaled the size of this UA site until the new volume of the molecule was equal to the all-atom van der Waals volume (see Fig. 1). As these molecules consist of only two atom-types, we distributed charges evenly amongst like atoms in accordance with the experimentally determined gas-phase molecular dipole moments. Finally, there are several avenues that one could take for assigning ∊_LJ parameters for atom-types. The ∊_LJ parameter corresponds to an atom’s dispersion attraction, and one could assign relative depths based on polarizability, electronegativity, or even the number of valence electrons.¹⁸ We have opted for the simpler route of assigning the same ∊_LJ value to all atom-types.

Figure 1.

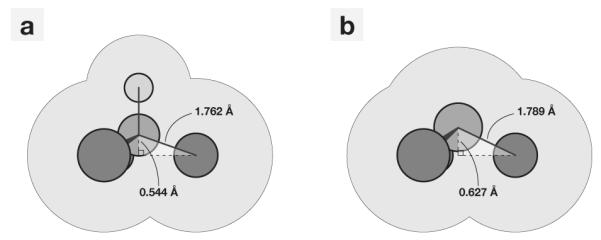
The (a) initial gas-phase geometry representation of chloroform and (b) the resulting united atom representation.

2.2 Optimization procedure

The typical route for developing molecular models for liquid simulations is to focus on matching the density, enthalpy of vaporization (ΔH_vap), and possibly another property like the self-diffusion coefficient or liquid structure.^{1–3,6,7,10,19–21} Here we aim for agreement also with the dielectric constant, in addition to the experimental density and ΔH_vap. To show how these molecular models can be made to agree with these experimental quantities, we uniformly scaled the σ_LJ values, charge magnitudes, and ∊_LJ values and calculated how the properties changed. An example illustrating how scaling of these parameters affects these properties is shown in Fig. 2. Starting from the constructed united-atom CH₂Cl₂ model, it is apparent that both the density (ρ) and dielectric constant (ε(0)) are sharply dependent upon the size of the molecule. However, when the chargemagnitudes (q) are uniformly scaled, the dielectric constant is effected to a much greater degree than the density. Finally, ∊_LJ changes primarily affect the ΔH_vap mostly independent of the other properties. This gives a prescription for sequential optimization of the model parameters for fitting to the experimental properties of interest.

1. Fit ρ by uniformly scaling all the σ_LJ values

2. Fit ε(0) by uniformly scaling all the q values

3. Fit ΔH_vap by uniformly scaling all the ∊_LJ values

Figure 2.

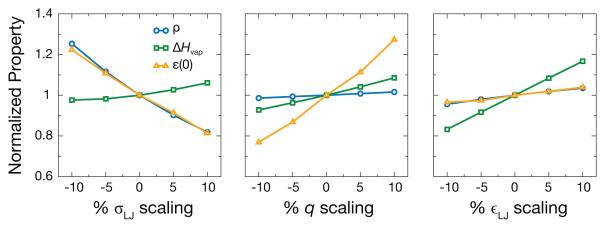
The variation of the normalized density (ρ), enthalpy of vaporization (ΔH_vap), and dielectric constant (ε(0)) of CH₂Cl₂ as a function of uniform parameter variation. As the LJ σ_LJ (left) is scaled, both ρ and ε(0) sharply vary. When the charge magnitude (middle) and LJ ∊_LJ (right) are scaled, only ε(0) and only ΔH_vap sharply vary respectively.

Each step of this optimization process involves a linear fitting procedure in the specific parameter space of interest. For example, the initial process of fitting the density involves an initial simulation with the starting set of parameters and a check to see if it is greater or less than the target value. If the liquid is too dense, the σ_LJ values are all increased by 5% to expand the system, and the density is recomputed after another simulation. We then linearly interpolate to find the σ_LJ scaling that corresponds to the target density. Since the relations between properties and parameters are not strictly linear, multiple interpolation steps using the current and previous step information are often needed to fit a given parameter. Typically, we see convergence on a given property to a specified tolerance within 2 to 4 interpolation steps.

It is apparent in Fig. 2 that the liquid properties are not exclusively dependent upon single model parameters – changing one of the parameters will have some effect on all of the properties. This means that this sequence needs to be iterated to focus in on the optimal set of experimental properties. The amount of iteration depends on the degree to which the parameters are correlated with the properties and the width of the specified tolerances. Table 1 lists the target properties for all the liquids and fitting tolerance for each. For the chloromethanes, convergence was typically achieved within 2 or 3 iterations. Water properties tended to be more correlated to the model parameters, so 5 or more iterations were not uncommon.

Table 1.

Experimental properties at 298 K and 1 atm²² and fitting tolerances for the investigated liquids.

	ρ	tolerance	Δ H vap	tolerance	ε(0)	tolerance
	(kg/m3)		(kJ/mol)
CCl4	1587	±2	32.45	±0.5	2.23	±0.15
CHCl3	1473	±2	31.30	±0.5	4.71	±0.15
CH2Cl2	1317	±2	28.82	±0.5	8.93	±0.15
H2O	997	±2	43.99	±0.5	78.4	±1.5

Solutions found by this optimization procedure are not necessarily unique, particularly given that there is an allowed tolerance window for each property. Despite this, multiple optimizations involving different initial dipole moments all ended with similar final parameters.

2.3 CCl₄ poses a challenge

CCl₄ poses an interesting challenge for our present approach. CCl₄ is tetrahedral and symmetric. It has no dipole moment in the gas-phase. Without a dipole moment, a rigid fixed-charge liquid model will have a dielectric constant ε(0) close to 1. Yet, CCl₄ has a dielectric response (ε(0) > 2). It and other non-polar liquids have apparent dipolar character in the liquid state.²³ This situation has motivated the recent development of polarizable models for CCl₄ and for other low-dielectric liquids.^14,15 In order to retain the advantages of fixed-charge force fields, our approach here instead is to include a permanent dipole in the model. Such a dipole moment will likely be different than an experimentally measured dipole moment for CCl₄ as it will incorporate the polarizable contributions to the permittivity.

There are different ways to incorporate a dipole in CCl₄. We explored all the possibilities for distributing the positive and negative partial charges of a dipole throughout the atoms in a molecule having this symmetry. All models successfully fit the experimental data and exhibited identical experimental properties that were not part of the fitting procedure. In the interest of simplicity, we only discuss two of the models, illustrated in Fig. 3. In these models, the dipole is either localized along one of the C-Cl bonds or distributed across three of them. All plotted data below is from the simpler localized model (Fig. 3a).

Figure 3.

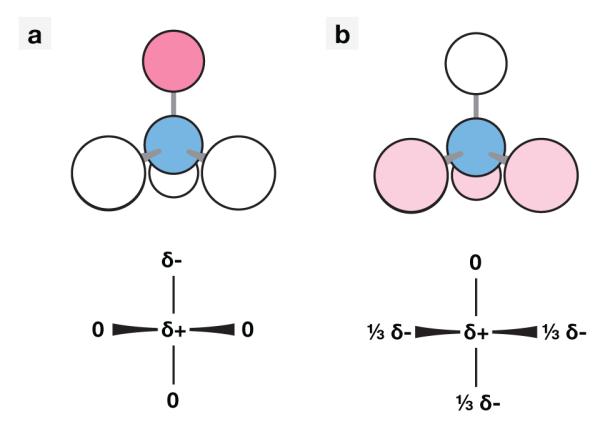
The (a) localized and (b) distributed dipole models for CCl₄. The localized model places the positive charge on the carbon atom and the negative on a single chlorine, while the distributed model splits the negative charge over three of the chlorine atoms.

2.4 Simulation details

All molecular dynamics calculations were performed using version 4.5.5 of the GROMACS molecular dynamics package.^24,25 The leap-frog algorithm with time steps of 4 fs for chloromethane and 2 fs for water simulations were used to integrate the equations of motion. The chloromethane models were held rigid using the SHAKE algorithm,²⁶ while the water models were held rigid using the SETTLE algorithm.²⁷ The isothermal-isobaric ensemble (NPT) using the Nose-Hoover thermostat and the Parrinello-Rahman barostat was used in both the optimization and temperature dependent property simulations. Dynamical properties were also computed from these simulations, and these properties were independently verified with sets of microcanonical (NVE) ensemble simulations. Long-range electrostatics were handled using the smooth version of the particle mesh Ewald (PME) method²⁸ under tin-foil boundary conditions with a grid spacing of 0.12, a PME order of 4, an Ewald parameter energy tolerance of 10⁻⁵, and a real-space cutoff of 15Å for chloromethane and 12Å for water simulations. The Lennard-Jones (LJ) interactions were switched off from 10 to 12Å for the chloromethane and 8 to 10Å for water simulations, and energy and pressure tail corrections were included in all cases. As seen by others,^29,30 the longer LJ cutoff is necessary to achieve converged system densities. Lorentz-Berthelot mixing rules were used to compute mixed-LJ interactions between differing atom types.

Optimization simulations involved rhombic dodecahedral boxes of 325 molecules for chloromethane simulations and cubic boxes of 650 molecules for water simulations. All of these simulations were carried out at 298.15 K and 1 atm. Run-time lengths ranged from 1 ns for density and ΔH_vap optimization to 10 ns for ε(0) optimization. System size effects were investigated with the final parameter sets by calculating properties for systems with four times the number of atoms with increasingly larger interaction cutoff radii, and property results were identical within error to those from these smaller systems. The calculated final properties are averages from five independent10 ns simulations, and standard errors are reported for these averages. For the water models, we also extended the 298.15 K simulations out to 50 ns to test the convergence of ε(0). All calculated properties for water at 298.15 K come from these longer simulations.

2.5 Calculation of liquid properties

With proper sampling of the given ensemble, thermodynamic and dynamic properties can be computed from fluctuations over the course of the simulation. In addition to the density, the following properties were calculated for all the optimized models.

2.5.1 Enthalpy of vaporization

The enthalpy of vaporization is traditionally computed from the difference between the enthalpy of an ideal gas and the liquid state,

$$\Delta H_{\mathrm{vap}}\left(T\right)=H{\left(T\right)}_{\text{ideal}}-H{\left(T\right)}_{\mathrm{liq}}=-\langle E_{\mathrm{liq}}\rangle ∕N+\mathit{RT},$$ (1)

where E_liq is the total intermolecular energy of the system of N molecules, R is the ideal gas constant, and T is the temperature. Others have noted that more detailed estimations of ΔH_vap can be determined by including non-classical and non-ideal gas corrections.⁶ We decided to use the traditional approximation as it corresponds to the heat required to vaporize these non-polarizable models in simulations, though including such corrections could lead to improved agreement with experimental properties.

2.5.2 Static dielectric constant

For non-polarizable liquids, ε(0) can be calculated from fluctuations of the total system dipole moment (M) according to,

$$\epsilon \left(0\right)=1+\frac{4\pi }{3k_{\mathrm{B}}T\langle V\rangle }\left(\langle M^2\rangle -\langle M^2\rangle \right),$$ (2)

where k_B is the Boltzmann constant and V is the total system volume.³¹ One difficulty in calculating ε(0) is that it is accumulated as a running average and will typically not converge over subnanosecond simulations. We needed to perform 10 ns simulations in order to obtain consistent estimates of ε(0) for all liquids.

2.5.3 C_p, κ_T, and α_p

As an additional test of thermodynamic quantities for the resulting models, we computed the isobaric heat capacity (C_p), the isothermal compressibility (κ_T), and the thermal expansion coefficient (α_p). These were calculated using the following fluctuation formulae from NPT simulations,

$$C_p={\left(\frac{\partial H}{\partial T}\right)}_{N,P}=\frac{\langle H^2\rangle -{\langle H\rangle }^2}{{Nk}_{\mathrm{B}}{T}^2}+3R,$$ (3)

$${\kappa }_T=-\frac{1}{V}{\left(\frac{\partial V}{\partial P}\right)}_{N,T}=\frac{\langle V^2\rangle -{\langle V\rangle }^2}{k_{\mathrm{B}}T\langle V\rangle },$$ (4)

$${\alpha }_p=\frac{1}{V}{\left(\frac{\partial V}{\partial T}\right)}_{N,P}=\frac{\langle \mathit{VH}\rangle -\langle V\rangle \langle H\rangle }{k_{\mathrm{B}}{T}^2\langle V\rangle }.$$ (5)

2.5.4 Self-diffusion coefficient

The self-diffusion coefficient was calculated for all the models alongside the above thermodynamic quantities. D was calculated from a regression fit to the linear region (0.5–6 ns) of a plot of the Einstein relation,³²

$$D=\underset{t\to \infty }{\lim }\frac{\langle {\mid {\mathbf{r}}_i\left(t\right)-{\mathbf{r}}_i\left(0\right)\mid }^2\rangle }{6t},$$ (6)

where r_i (t) is the position of the center of mass of molecule i at time t. Dynamical quantities are typically calculated from NVE simulations in order to avoid perturbations introduced by thermostats and barostats. We calculated D for all models from NVE simulations near 298.15 K and 1 atm, and found that they were identical to the NPT simulations used for the above thermodynamic quantities. This indicated that the thermostat and barostat coupling was weak enough to not significantly perturb the dynamics. We report D results from the NPT simulations for simplicity.

2.5.5 Structural analysis

Finally, we calculated radial distribution functions between various atom types for comparisons with other models and experimental scattering data. These distribution functions were calculated by binning separation distances (r_ij) between atoms of type A and B via

$${\mathsf{g}}_{\mathit{AB}}\left(r\right)=\frac{1}{N_A\langle \rho B\rangle }\sum _{i∊A}^{N_A}\sum _{j∊B}^{N_B}\frac{\delta (r_{ij}-r)}{4\pi r^2},$$ (7)

where ρ_B is the bulk system density of atom type B.

3 Results and Discussion

Table 2 gives the values of our parameters for the non-polar solvents we modeled. And, Table 3 compares the properties we calculate from our models compared to all-atom RESP models from Fox & Kollman³⁰ and to experiments. The models from the present work are labelled with DC, to indicate that they are ‘dielectric corrected’. The Fox models are flexible all-atom models – they allow harmonic bond stretching and angle bending motions – that are derived from the AMBER force field.³³ The values reported here differ considerably from those published (specifically the self-diffusion constant). This difference comes from the expanded sampling in these simulations that provide a better estimate of the actual thermodynamic and dynamic properties of the models.

Table 2.

Model parameters for CCl₄-DC with a localized dipole (L), CCl₄-DC with a distributed dipole (D), CHCl₃-DC, and CH₂Cl₂-DC

Model	Atom-type	Constraint	d (Å)	q (e−)	σ (Å)	ε (kJ/mol)
CCl4-DC (L)	C			0.14780	4.06640	0.587072
	CL			−0.14780 & 0	4.18602	0.587072
		C–CL	1.7670
		CL–CL	2.8855
CCl4-DC (D)	C			0.22542	4.06830	0.585791
	CL			−0.07514 & 0	4.18796	0.585791
		C–CL	1.7670
		CL–CL	2.8855
CHCl3-DC	UA			0.55179	3.73400	1.078200
	CL			−0.18393	3.58871	1.078200
		UA–CL	1.7894
		CL–CL	2.9028
CH2Cl2-DC	UA			0.40440	3.71813	1.281890
	CL			−0.20220	3.53079	1.281890
		UA–CL	1.8215
		CL–CL	2.9344

Table 3.

Liquid properties for chloromethanes calculated at 298.15 K and 1 atm with standard error of the last digit in parentheses

Liquid	Model	ρ (kg/m3)	ΔHvap (kJ/mol)	ε(0)	Cp (J/mol·K)	κT (105 atm−1)	αp (106 K−1)	D (10−9 m2/s)	μ (D)
CCl4	CCl4-DC (L)	1588.7 (1)	32.392 (3)	2.202 (6)	154 (2)	134 (2)	213 (4)	1.24 (2)	1.26
	CCl4-DC (D)	1588.77 (7)	32.406 (1)	2.112 (8)	156 (2)	137 (2)	219 (4)	1.26 (3)	1.23
	Fox	1626.6 (5)	34.51 (1)	1.0302 (2)	120 (1)	102 (3)	126 (3)	1.73 (3)	0.23
	Expt	1587a	32.43a	2.228a	130.7a	111b	116b	1.4c
CHCl3	CHCl3-DC	1471.16 (7)	31.222 (4)	4.77 (3)	85 (1)	78 (2)	116 (2)	1.48 (3)	1.66
	Fox	1476.7 (2)	30.119 (6)	4.39 (1)	118 (1)	121 (4)	244 (5)	2.74 (8)	1.40
	Expt	1473a	31.28a	4.711a	114.2a	106b	123b	2.3d, 2.5e
CH2Cl2	CH2Cl2-DC	1316.34 (1)	28.740 (1)	8.8 (1)	92.3 (8)	98 (1)	159 (2)	2.13 (2)	2.10
	Fox	1265.9 (4)	25.95 (1)	8.65 (3)	118 (1)	158 (1)	180 (2)	4.11 (5)	2.01
	Expt	1317a	28.82a	8.93a	101.2a	104a	139a	3.3 (2) f

^aReference 22

^bInterpolated to 298.15 K from data in Reference 22

^cReference 34

^dReference 35

^eReference 36

^fReference 37

All the DC models shown in Table 3 are converged on the experimental density, ΔH_vap, and dielectric constant to within the previously stated tolerances. The dielectric constant was the slow step in the fitting process. Fig. 4 shows the running average of the ε(0) values, over the course of 10 ns of molecular dynamics. The lines are average traces over five simulations, and the shaded region shows the standard deviation of these averages. While the dielectric constant of CCl₄ levels quickly and the deviations are barely visible, the CH₂Cl₂ trace shows the difficulty in fitting when considering liquids with higher dielectric constants. At the end of the 10 ns, the standard deviation is still roughly ±0.2 dielectric units, very close to the size of our tolerance window for convergence. To fit the dielectric to a tighter window, we would need proportionally longer simulation times. If we wanted to work with a material with a larger dielectric constant, we would either need a looser ε(0) convergence criterion or longer simulation lengths.

Figure 4.

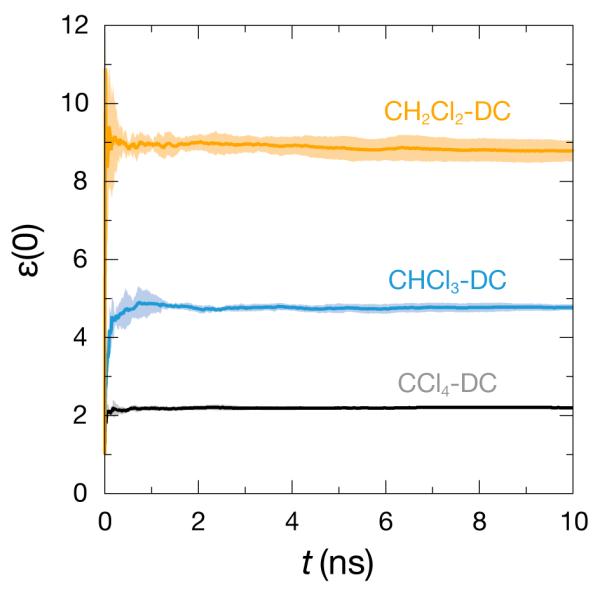
The static dielectric constant for the DC chloromethane models over the course of 10 ns of molecular dynamics at 298.15 K and 1 atm. The lines are averages of five simulations, and the shaded regions show the standard deviation of these averages.

3.1 Adding a dipole improves the permittivity of CCl₄

In Table 3, there is a noticeable trend of increasing dipole moment with increasing ε(0) from CCl₄ down to CH₂Cl₂. This trend has been recognized in the past,^5,21,38 and it simply follows that the greater the partial charges, the greater the screening ability of the liquid. This results holds true for the flexible all-atom models as well, as they have lower average dipole moments than the analogous DC models and consistently under-predict the dielectric constant. In the case of CCl₄, the embedded dipole actually allows the DC models to express a ε(0) in line with experiment. Both the thermodynamic and dynamic properties are nearly identical for the localized and distributed CCl₄ models, as are the dipole moments for the two models. These results indicate that the geometry of the charge distribution that makes the dipole moment is less important than the magnitude.

As the CCl₄-DC models are fit to experimental density, ΔH_vap, and ε(0) quantities, it is not surprising that they reproduce these quantities better than the all atom model. The Fox & Kollman model captured a small fraction of the permittivity as it is flexible and has a small dipole moment in the liquid phase. While the diffusivity relative to experiment for CCl₄-DC is improved over the flexible model, the α_p for the CCl₄-DC models is considerably degraded. Embedding a dipole had the effect of increasing the σ_LJ values on the atoms, and this makes the volume of the liquid more sensitive to temperature changes. This results in the liquid having a less tightly structured first solvation shell than the flexible Fox & Kollman model (see Supporting Information) and a possibly less accurate fit to neutron scattering experiments.³⁹

3.2 United-atom chloromethanes behave similarly to all-atom models

In addition to corrected dielectric versions of these liquids, we were interested in united-atom variants of CHCl₃ and CH₂Cl₂ that could work as a more efficient mimic of a detailed all-atom model. The results in Table 3 indicate this to be the case. Not surprisingly, the DC models fit well the experimental data to which they were matched. More interesting, however, is the observation that these new models do well at reproducing other thermodynamic properties of the real liquid that were not part of the parameterization exercise, often better than the more detailed Fox & Kollman models. While structural comparisons between united-atom and all-atom models are inexact, a qualitative radial distribution function comparison indicates that both CHCl₃-DC and CH₂Cl₂-DC are more structured than the flexible all-atom Fox & Kollman models (see Supporting Information). This is likely due to the enhanced dipole moments of the dielectric corrected models, resulting in stronger pair interactions and larger ΔH_vap values. These results indicate that even with a less complex model geometry, correcting for the dielectric has additional advantages.

3.3 The DC chloromethane models capture some of the temperature dependence of ε(0)

These DC models, like other liquid models, are fit to one temperature. We tested how well our DC models capture the temperature dependence of the dielectric constant, in 5 K increments within the available range of experimental data for ε(0); see Fig. 5. At the fitting temperature of 298.15 K, all the models match with experiments. All the models have the correct sign of the slope: ε(0) decreases with increasing temperature. At low temperatures, the CH₂Cl₂ and CHCl₃ models deviate from the experimental ε(0) values, while the CCl₄-DC model results (localized dipole model shown in Fig. 5) are quantitative across the entire available range.

Figure 5.

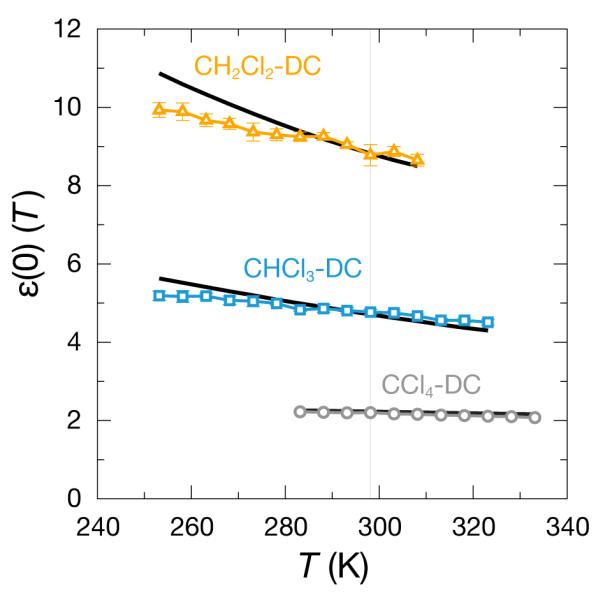
The temperature dependence of ε(0) for the DC chloromethane models compared with experimental data.²² The black lines are the experimental curves for each liquid shown.

3.4 Applying the dielectric correction to water models

We were interested to see if we could improve upon current water models, by correcting their dielectric constants in the manner described above. We considered two water models: TIP3P (ε(0) > 90) and SPC (ε(0) < 70).⁴⁰

The atom sites in TIP3P are arranged in the experimental gas-phase geometry, and from a property standpoint, the density is less than experiment and ε(0) is greater than experiment. We would therefore expect both the σ parameter and charge magnitudes to decrease in order to align with experiment. Indeed these changes occur; however, the intermediate models rapidly crystallize into face-centered cubic lattices. We tested multiple starting states (larger and smaller σ and q values), and this crystallization was repeatable in all cases. Weakening the electrostatic interaction in TIP3P to match the experimental ε(0) eliminates its ability to effectively hydrogen-bond. This observation appears to agree with findings showing alteration of the bond-angle of SPC/E below 105° (the bond-angle of TIP3P is 104.5) and above 115° causes a breakdown in the liquid properties.^41,42 This also corresponds to how other researchers have been successful in modifying the TIP4P model to better reproduce liquid and phase behavior properties.^6,7 By having the negative partial charge offset from the Lennard-Jones site center, TIP4P models are effectively more tetrahedral than the gas-phase geometry suggests.

The atom sites in SPC are perfectly tetrahedral, and the dielectric correction procedure was able to converge on a liquid-state model. The resulting parameters for SPC/DC are listed in Table 4. In addition to this SPC geometry based model, we show the resulting parameters for a tetrahedral model that has O–H bond lengths equal to the experimental gas-phase value (also the TIP3P value). We refer to this model as H₂O-DC, and it is a hybrid water model that probes both how SPC would respond to having bond-lengths in better agreement with experiment and how TIP3P would respond with a more tetrahedral geometry. Properties at 298.15 K and 1 atm are listed in Table 5 alongside those for SPC, SPC/E, and experiment.

Table 4.

Model parameters for SPC/DC and H₂O-DC

Model	Atom-type	Constraint	d (Å)	q (e−)	σ (Å)	ε (kJ/mol)
SPC/DC	O			−0.87362	3.15767	0.822882
	H			0.43681	0.00000	0.000000
		O–H	1.00000
		H–H	1.63299
H2O-DC	O			−0.90990	3.18400	0.593000
	H			0.45495	0.00000	0.000000
		O–H	0.95800
		H–H	1.56441

Table 5.

Liquid properties for water calculated at 298.15 K and 1 atm with standard error of the last digit in parentheses

Model	ρ (kg/m3)	DHvap (kJ/mol)	ε(0)	Cp (J/mol·K)	κT (105 atm−1)	αp (106 K−1)	D (10−9 m2/s)	μ (D)
SPC	978.41 (3)	36.820 (1)	65.6 (2)	82.9 (3)	53.7 (5)	71.5 (7)	3.99 (1)	2.27
SPC/E	999.53 (2)	41.905 (1)	71.1 (1)	86.3 (2)	46.1 (2)	49.1 (4)	2.46 (1)	2.35
SPC/DC	998.69 (2)	43.993 (1)	78.3 (6)	83.2 (3)	43.7 (3)	48.8 (9)	2.48 (1)	2.42
H2O-DC	997.55 (2)	43.366 (1)	78.7 (6)	87.8 (2)	45.0 (2)	44.8 (4)	2.17 (1)	2.42
Expt	997.5a	43.99a	78.36a	75.3a	45.84a	25.6a	2.299b

^aReference 22

^bReference 43

3.5 Optimized SPC resembles models with lower dielectric constants

When the SPC/E water model was originally developed, the authors recognized the need for an added extended polarization interaction to the SPC model.¹⁹ They incorporated this effect by uniformly increasing the charge magnitude on the atom sites, keeping all other model parameters the same. This changed the dipole moment from 2.27 D to 2.35 D and subsequently improved most of the structural, thermodynamic, and dynamic properties. This increase in the dipole moment is the maximum possible without increasing the density of the liquid above 1 g/cm³. One point of note shown in Table 5 is the increase in ε(0) from 66 to 71. To bring the SPC model ε(0) up to the experimental value, the charge magnitudes need to be scaled up further, and the other model parameters (namely σ and ∊) will need to be simultaneously adjusted to compensate for the increasing density. The resulting SPC/DC model parameters shown in Table 4 do exactly this. The oxygen site charge increases from 0.82 to 0.8476 to 0.87362 for SPC, SPC/E, and SPC/DC respectively, and the LJ parameters are modified to accommodate this additional charge. Fig. 6 shows the convergence of ε(0) over the course of 50 ns of molecular dynamics. These traces further emphasize the difficulty in converging on a specific ε(0) when working with high dielectric liquids. The standard deviation spread for SPC/DC has reached the ±1.5 dielectric unit tolerance by 10 ns, though the dielectric optimization process would likely be more efficient using longer simulations for more accurate intermediate assessments of ε(0).

Figure 6.

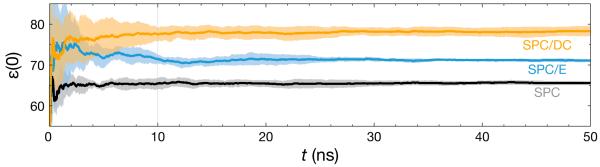
The static dielectric constant for SPC (black line), SPC/E (blue line), and SPC/DC (gold line) over the course of 50 ns of molecular dynamics at 298.15 K and 1 atm. The lines are averages of five simulations, and the shaded regions show the standard deviation of these averages. The plots show that the models have difficulty converging ε(0) on time-scales less than 10 ns, the length of simulations in our dielectric correction procedure. Longer simulations would likely aid in optimization processes set to converge on a high ε(0).

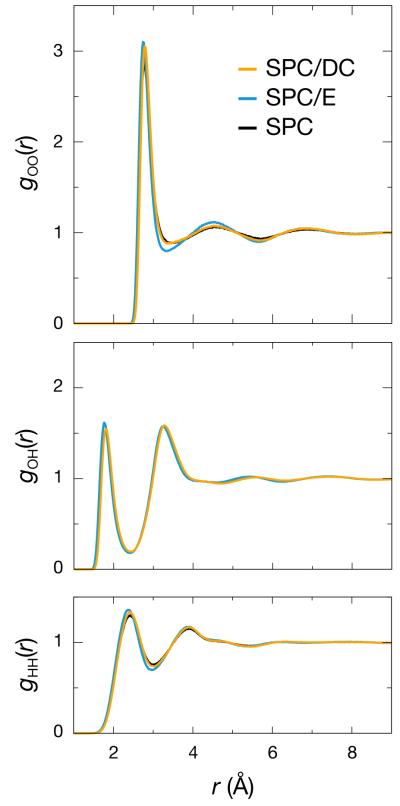
Table 5 shows that our dielectric correction leads to minor improvements of agreement with experiments for most of the thermodynamic and dynamic quantities, compared to SPC/E. Fig. 7 shows that the g_OO(r), g_OH(r), and g_HH(r) for these three water models are nearly superimposable. The SPC and SPC/DC g(r) curves fall right on top of one another in all three plots, while the SPC/E curves are more peaked and have a slightly more ordered second-shell. This is likely a degradationin the overall liquid structure as the SPC/E model has been shown to be a better fit to neutron and x-ray scattering data.^44–46

Figure 7.

The oxygen-oxygen (top), oxygen-hydrogen (middle), and hydrogen-hydrogen (bottom) radial distribution functions for SPC, SPC/E, and SPC/DC. The SPC and SPC/DC curves overlap tightly in all the plots with the only deviations being slightly enhanced peaking in the g_OO(r) and g_HH(r).

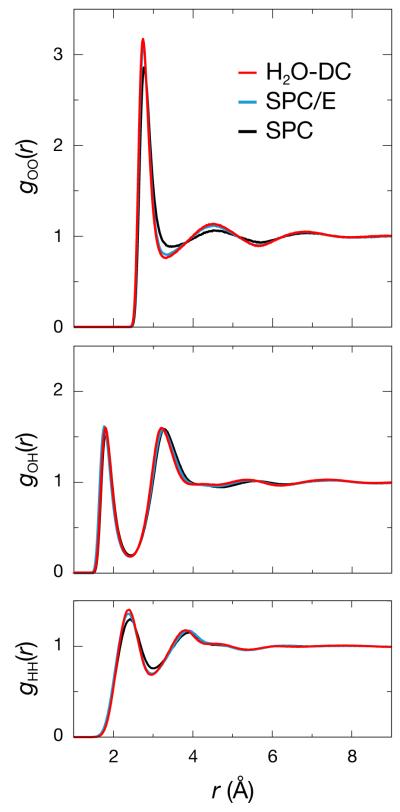
One possible consideration in matching experimental structural data is the geometry of the particular model. For the SPC models, the OH bond-length was simplified to 1 Å, while experimental structural data recommends a value closer to 0.958 Å. 47 Taking this geometry consideration into account, we developed and optimized a tetrahedral model with these OH bond-lengths that we call H₂O-DC. While this model has a less converged ΔH_vap than SPC/DC, it shows further improvements in most of the other liquid properties. By using shorter OH bond-lengths, we expect and observe some changes in the liquid structure. Fig. 8 shows the same sequence of radial distribution functions as Fig. 7, only with H₂O-DC in place of SPC/DC. H₂O-DC is slightly more structured beyond the first solvation shell than SPC/E in all of the curves. This structuring is more in line with scattering data,^44–46,48 making it a potentially truer representation of the real liquid. It should be noted that the first solvation shell for SPC/E type models is typically more peaked than the curves derived from model fits to this experimental scattering data, and this could likely be optimized by using a softer function for the van der Waals potential and/or decreasing the strength of the direct pair-interaction energy.

Figure 8.

The oxygen-oxygen (top), oxygen-hydrogen (middle), and hydrogen-hydrogen (bottom) radial distribution functions for SPC, SPC/E, and H₂O-DC. The H₂O-DC model is even more structured than SPC/E, making it a potentially better fit to experimental scattering data.

3.6 DC water models reproduce temperature dependent properties

We looked at the maximum in density as a function of temperature, T_max for these water models. This is experimentally observed at 277 K. Additional interaction sites have been added to some water models to capture this behavior.^6,10 SPC/E also has a T_max, though it is located around 235 K, well below the experimental melting point.⁴⁹

Fig. 9 compares the predicted density-maximum temperatures from various models, spanning the supercooled-liquid and liquid phases. Here, the T_max for SPC/E is at 247 K. Our computation of this differs from past estimates, likely because the uses of the Ewald summation and LJ pressure correction were not as common when the original estimates were made.⁴⁹ As noted in past studies,⁵² the SPC model does not exhibit a T_max in the temperature range shown, and interestingly, SPC/DC shows a density maximum (calculated from the sign crossover in α_p seen in the supplementary materials) at 239 K, near the edge of the simulated temperature range. Thus, by adopting a liquid structure similar to SPC, this model shows a degradation in the T_max relative to SPC/E. The more structured H₂O-DC has a T_max at 255 K, closer to experiment than SPC/E. This result indicates that it may be possible to optimize a rigid, 3-site water model through geometry distortions and interaction energy scaling to simultaneously reproduce both the ε(0) and T_max.

Figure 9.

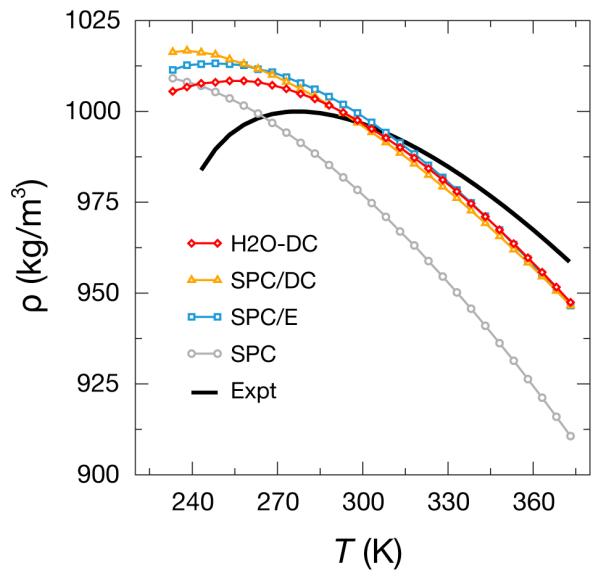
The density of the studied water models as a function of temperature. These fully tetrahedral water models all exhibit a density maximum at a lower temperature than real water,^50,51 though geometric differences between the models indicate a route to correct this flaw.

Fig. 10 shows the temperature dependence of ε(0). The DC models reproduce the experimental ε(0) at the optimization temperature and the correct trend of decreasing ε(0) with increasing temperature, but not the slope quantitatively. All these models have the same slope, so correcting the dielectric constant at one temperature simply results in a vertical shift of the trend. More complex water models with different interaction site geometries have been shown to better capture the experimental slope,^6,21 so it may be useful in the future to couple changing molecular geometries with the present approach for correcting the dielectrics.

Figure 10.

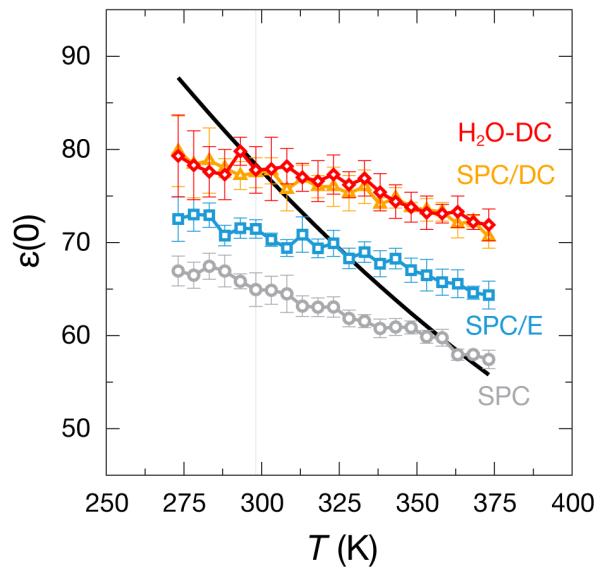
The ε(0) as a function of temperature for the labeled water models alongside experiment²² (black line). All models capture the trend of decreasing ε(0) with increasing temperature, though they all fail to reproduce the experimental slope of this trend.

4 Conclusions

We have developed here parameters for solvents carbon tetrachloride, a united-atom chloroform, a united-atom dichloromethane, and water for molecular simulations in fixed-charge force fields. The usual approach to development is to choose parameters that cause the molecular simulations of the pure solvent to agree with experiments on the solvent density and enthalpy of vaporization. What’s novel here is that our parameters are chosen so that the simulations also give the correct experimental dielectric constants. We find that our models also generally give better agreement with other properties, such as the self-diffusion constant. For water, there is some subtlety. When TIP3P is made to have the correct dielectric constant, it loses the appropriate level of water-water hydrogen bonding. However, when SPC is made to have the correct dielectric constant, it also has improved thermodynamic and dynamic properties. The present work indicates that the present approach to parameterizing fixed-charge solvent models for molecular simulations can improve the properties of those solvents relative to older parameterizations. And, this approach may circumvent the need, at least in some cases, to resort to more expensive polarizable or quantum mechanical solvent models.