Abstract
Antibodies are under development to treat a variety of cancers, such as lymphomas, colon, and breast cancer. A major limitation to greater efficacy for this class of drugs is poor distribution in vivo. Localization of antibodies occurs slowly, often in insufficient therapeutic amounts, and distributes heterogeneously throughout the tumor. While the microdistribution around individual vessels is important for many therapies, the total amount of antibody localized in the tumor is paramount for many applications such as imaging, determining the therapeutic index with antibody drug conjugates, and dosing in radioimmunotherapy. With imaging and pretargeted therapeutic strategies, the time course of uptake is critical in determining when to take an image or deliver a secondary reagent. We present here a simple mechanistic model of antibody uptake and retention that captures the major rates that determine the time course of antibody concentration within a tumor including dose, affinity, plasma clearance, target expression, internalization, permeability, and vascularization. Since many of the parameters are known or can be estimated in vitro, this model can approximate the time course of antibody concentration in tumors to aid in experimental design, data interpretation, and strategies to improve localization.
Keywords: tumor targeting, permeability, antibody localization, tumor retention
1. INTRODUCTION
Antibody therapies for cancer have been developed because of their ability to specifically target tumor cells that have up-regulated, altered, or inappropriately expressed antigens on their surface. This specific binding provides an advantage over traditional chemotherapeutics by enabling antibodies to accumulate in neoplastic tissue while largely sparing normal tissue. However, the large size of these molecules and rapid binding in tumor tissue, combined with the abnormal physiology of tumors, causes slow, heterogeneous uptake (Jain, 1999). The antibody dose in the tumor is often insufficient to mediate a significant therapeutic response, and poor microdistribution leaves many cells with little to no treatment.
The distribution of antibodies in tumors is a complex, erratic process. Vascularized tumors have a network of poorly formed vessels throughout a highly disorganized, heterogeneous cluster of tumor and multiple stromal cell types (Dvorak, 1986). Due to several biological mediators secreted locally, the tumor blood vessels are often much more permeable than normal capillaries, and, with a lack of efficient lymphatic drainage, this leads to elevated interstitial pressure and elimination of the normal pressure gradients between the tissue and vessel (Boucher et al., 1990). With the loss of pressure across the capillary wall, these vessels are susceptible to collapse from the growth and solid stress of the surrounding cancerous tissue, causing areas of low vessel density and necrosis (Boucher & Jain, 1992). The disrupted pressure gradients and malformed, tortuous paths of vessels (Ahlstrom et al., 1988) interfere with blood flow patterns, causing temporary cessation and even reversal of flow direction. Poor blood flow and avascular regions give rise to hypoxia, making some areas more resistant to radiation and chemotherapeutics (Vaupel et al., 2001). Once antibodies exit the blood vessel, they face a variety of other transport barriers. The lack of convection means these macromolecular drugs rely primarily on diffusion to extravasate and move through the tissue. Within the tumor interstitium, variations in extracellular matrix and cell density cause heterogeneous diffusion (Jain, 1999). Rapid binding to antigen immobilizes these drugs almost immediately, causing perivascular localization, and differences in local antigen density further vary the local concentration even in regions that are efficiently targeted (Aquino et al., 2004).
Given the stochastic development of the vasculature and complexity of targeting in tumors, modeling the uptake is an unwieldy task. Significant intra- and inter-tumor variability, even more so in the clinic (Scott et al., 2005) than in animal models, can further complicate modeling attempts. Despite these complexities, simplified models can still provide a basic understanding of the most important parameters for designing experiments, interpreting data, and developing strategies to improve targeting (Bertuzzi et al., 2008; Fujimori et al., 1989). These models are equally useful in determining which assumptions have not been met when tumor uptake is significantly different than anticipated, and whether these differences can be exploited.
The purpose of developing this model is to create a mechanistic description of total antibody uptake in a tumor based on the dominant principles controlling localization. We have previously developed a simplified model of transport in micrometastases and around individual blood vessels in solid tumors (Thurber et al., 2008a; Thurber et al., 2007). These models showed that the ratio of extravasation of antibodies from the blood vessels to the rate at which they diffuse within the tissue (Biot number) is very low (< 0.01 for most targeting molecules). We show here that this results in the total uptake from the vessels being almost independent from the microscopic distribution. This reduction in dimensionality allows a compartmental model to describe the total antibody in the tumor, even though the tumor is not well-mixed (i.e. not homogeneous). The result is a simple analytical model that clearly delineates the major factors controlling tumor uptake and can be used by non-modeling researchers to estimate the time course of antibody uptake in solid tumors. Ideally this will be used in conjunction with experiments to further our understanding and develop improvements in targeting.
2. METHODS
This model describes the total amount of antibody in the tumor tissue, which includes unbound antibody in the interstitium and antibody bound to its target. While the local concentration of these two pools will vary considerably throughout the tumor, it is often the total amount of antibody that is measured in practice. This includes both studies using excised tumors where the total amount of activity is measured from a radiolabeled antibody and imaging experiments where the local concentration is estimated from signal originating in the tumor. In this paper, [Ab]total is used for the sum of the free antibody in the tumor interstitium, noted as [Ab]free, and antibody bound to antigen, [Ab]bound.
2.1. Binding
The relative amounts of bound and free antibody depend on the antibody dissociation constant (Kd), antigen concentration [Ag], and available volume fraction in the tumor, ε (the interstitial space divided by the total tumor volume, required because antibodies diffuse through the interstitial space). Because antibody binding occurs quickly, on the order of seconds, a local equilibrium is often reached in the tissue (Thurber et al., 2008a). Since internalization occurs on a slower time scale (minutes to hours), it is assumed this does not affect the local equilibrium. It is also assumed in the current model that the tumor is not saturated, therefore the concentration of antigen in the tumor is greater than the concentration of antibody ([Ab]total<[Ag]). Since tumor saturation requires a large dose, for example hundreds of micrograms in mice (Blumenthal et al., 1991; Fenwick et al., 1989; Ong & Mattes, 1989; Thurber & Weissleder, 2010) and hundreds of milligrams for humans (Schroff et al., 1987), this assumption is typically valid in practice. With these two assumptions, the fraction of bound and free antibody can be defined as:
| 1. |
| 2. |
and
| 3. |
where Kd is the dissociation constant, [Ag] is the antigen concentration in the tumor tissue, and ε is void fraction.
Following systemic administration, antibody enters a tumor either from the vasculature (extravasation) or the outer tumor surface from the surrounding tissue (surface uptake). Due to slow diffusion of macromolecules in tissue, uptake from the surface is negligible in tumors larger than a couple millimeters in size (Thurber & Weissleder, 2010) (supplemental). Once in the tumor interstitium, it binds, dissociates, and is internalized by cells. Signal is lost from the tumor in much the same way, either by diffusion back into the vasculature, out through the tumor surface, or by degradation within the cells. During degradation, the label may behave differently than the antibody, either diffusing out of the tumor or being retained in the cells (Press et al., 1996). The processes leading to antibody movement between the plasma, normal tissues, tumor interstitium, and bound complexes are illustrated schematically in Figure 1a.
Figure 1.
Diagram of the Compartmental Model and Krogh Cylinder Simulations. A) Arrows indicate transport between compartments. The dotted line surrounds the two-compartment model for normal tissue. B) Diagram of the Krogh cylinder model with the equations and boundary conditions within the tissue.
2.2. - Vascular Transport
One of the most important results stemming from the analysis of transport around individual vessels is that antibody extravasation across the vasculature is the slowest and therefore rate-limiting step due to the low permeability of the vasculature (Thurber et al., 2008a). Previous analysis of antibody transport shows that the rate of binding is faster than the rate of diffusion (Graff & Wittrup, 2003), resulting in the perivascular distribution of antibodies due to immediate binding before they can diffuse throughout the tissue. However, both binding and diffusion are faster than extravasation. The Biot number, which is the ratio of the rate of extravasation from the blood to the rate of interstitial diffusion, is very small (~0.01) (Thurber et al., 2007). The Biot number is defined as:
where P is the permeability coefficient for antibody across the tumor capillary wall, Rcap is the capillary radius in the tumor, and D is the diffusion coefficient.
The low Biot number results in the amount of antibody entering the tumor being independent of binding and diffusion within the tissue, since both of these processes are faster than the rate-limiting extravasation step. Therefore, only extravasation has a major impact on the total antibody uptake and loss, even though the distribution of antibodies and antigen is heterogeneous. It is not assumed that the distribution is uniform, but rather that the heterogeneity of the distribution does not significantly affect the average signal within the tumor. This principle of scaling resistances in series is often used in engineering to reduce the dimensions of a problem, and in this case, it allows going from the three dimensional representation of antibody distribution in the tumor to a “zero dimensional” (i.e. ignoring the spatial distribution of vessels in the tumor) compartment (Deen, 1998).
Discounting the heterogeneous distribution, the transport of antibodies across the tumor vasculature can be described as:
where d[Ab]total/dt is the change in total antibody concentration in the tumor over time from the vessels, RKrogh is the average radius of tissue surrounding each blood vessel, [Ab]plasma is the plasma concentration of antibody, and [Ab]free is the free antibody concentration in the tumor. The surface area to volume ratio (S/V) for a Krogh cylinder is incorporated into the permeability surface area product in the vascular transport term.
2.3. Internalization and Degradation
High affinity antibodies are often lost from the surface of tumor cells by internalization and degradation (Mattes et al., 1994; Thurber et al., 2008a). This typically occurs when the antibody is bound to a target that gets internalized, therefore it only affects antibody/target complexes. Increased affinity results in a larger bound fraction and greater internalization and degradation as recently shown with a series of HER2 antibodies (Rudnick et al., 2011). The loss of signal from internalization and degradation is the rate constant, ke, multiplied by the concentration of bound antibody, [Ab]bound.
The above terms describe the rate at which antibody enters and exits the tumor as a whole. Combining these yields the time course of antibody in the tumor:
| 4. |
| 5. |
Using the definitions of bound and free antibody, the total antibody concentration in the tumor changes according to:
| 6. |
The first term on the right hand side of the equation describes the movement of antibody between the plasma and the tumor. 2PRcap/RKrogh2 is the permeability surface area product per tumor volume (sometimes represented as PS/V). The second term describes internalization and degradation within the tumor. This is based on the internalization rate of the bound antibody-antigen complex and the clearance rate of degraded labels from the tumor.
3. RESULTS
3.1. Model Solution
The plasma clearance of antibodies and their fragments is often well described by a biexponential decay (Fujimori et al., 1989; Sung & Vanosdol, 1995). Implicit in this assumption is that the dose is large enough that free antigen in the blood and uptake in the tumor and normal tissues do not significantly affect the clearance (although this can sometimes be the case, resulting in target mediated drug disposition or TMDD (Lammerts van Bueren et al., 2006)). With the assumption of no TMDD, the model can be solved to give an analytical expression for the antibody concentration in tumor as a function of time:
| 7. |
where:
| 8. |
and:
| 9. |
The plasma clearance is represented with a biexponential clearance, where kα is the redistribution rate constant, kβ is the clearance phase rate constant, A is the fraction of alpha phase clearance, and B is the fraction of beta phase clearance. While this expression is somewhat long, it is nevertheless an analytical solution to the time course within the tumor. Furthermore, this solution can be significantly simplified for many parameter regimes as discussed below.
Because antibody uptake in tumors is often expressed as a percentage of the injected dose per gram of tumor mass, it is useful to define the localization in these terms.
| 10. |
where the plasma volume is in mL, and the tissue density is ~1 g/mL for a tumor. Since the concentration is the pertinent parameter for uptake, a dose diluted in a larger plasma volume gives a much lower %ID/g, which is a measure of the efficiency of uptake. This results in a three order of magnitude lower %ID/g for humans (~3 L plasma volume) than mice (~2 mL).
3.2. Validation of model assumptions
Several assumptions were made in simplifying the model, most notably ignoring spatial heterogeneities due to the low Biot number. To ensure that this assumption does not significantly alter the model results, predictions were compared to a more complex numerical model that does not make this assumption.
The simplification of ignoring spatial heterogeneity was addressed by comparing compartmental model predictions to a numerical Krogh cylinder model (Figure 1 b) that predicts antibody levels around individual vessels. Figure 2a shows the difference in plasma and interstitial antibody concentrations as a function of the Biot number using the Krogh cylinder model (Thurber et al., 2007). If vessels are situated very close to each other in the tumor, the local interstitial concentration will be elevated due to the proximity of the sources, reducing the diffusive gradient for antibody entering the tumor. However, with a very low Biot number, on the order of 0.01 for antibodies and antibody fragments, this interstitial concentration will remain insignificant compared to the plasma concentration, such that the extravasation rate into the tumor will be unaffected. (The bound antibody concentration may be very high surrounding the vessels due to binding in this area, but the amount of free antibody in the tissue prior to saturation is low for tight binders.) Similarly, areas of high vascular density will be targeted quickly, but antibody will then diffuse to adjacent regions to bind new antigen without significantly affecting the extravasation rate in the saturated area. With a Biot number of ~0.01, antibody can diffuse large distances (hundreds of microns or more, supplemental) depending on the vessel density, reducing the effect of regional differences in antigen expression. Despite the heterogeneity in vessel distribution, with areas of closely spaced vessels adjacent to avascular regions (Baish et al., 2011), the average tumor uptake of these macromolecules is not dependent on this spacing, despite the large effect on microscopic distribution. This demonstrates that interactions between vessels have little effect on uptake, so the influence of the heterogeneous antibody localization around a single vessel was analyzed next. If both the antibody concentration between vessels and distribution around a single vessel do not influence uptake, then the spatial distribution of antibody will have negligible impact on the amount of antibody entering the tumor tissue. Using a numerical simulation of the binding, diffusion, and internalization of antibody in a Krogh-like cylinder (Thurber et al., 2007), the total antibody within the cylinder (Figure 2b) was compared to the concentration predicted by the current compartmental model. For low Biot number (~0.01), the Krogh cylinder simulation results in a similar concentration as the compartmental model that ignores spatial heterogeneity, yielding a ratio of one. This demonstrates that with a low Biot number, the spatial heterogeneity has little impact on the total tumor uptake.
Figure 2.

Low Biot Number Justifies Compartmental Model
Effects of Vessel and Tissue Heterogeneity. The ratio of unbound interstitial antibody versus the plasma concentration is shown for a range of Biot numbers (A). A comparison between the current compartmental model and a spatially distributed Krogh cylinder numerical simulation is shown with varying values of the Biot number (B).
For comparison, vascular permeability is not limiting for oxygen and small molecules (Thurber & Weissleder, 2011). The concentration of oxygen just outside the blood vessel is very close to that in the blood (Torres et al., 1994), indicating a large Biot number (Tabata et al., 1997). Instead, oxygen transport is primarily limited by blood flow to the tumor and diffusion within the tumor tissue. Poor blood flow can result in a lack of oxygen transport to certain regions causing transient/acute hypoxia. Other regions of the tumor are located very far away from the blood vessel, and diffusion is too slow to keep up with metabolism in the tissue, giving rise to chronic hypoxia (Dewhirst et al., 1996).
Figure 3 shows the comparison between the simplified compartmental model and the spatially dependent Krogh cylinder numerical solutions. The left side graphs show the predicted time course for a typical IgG, and those on the right are for a single chain variable fragment of an antibody (scFv). Notice the difference in time scales on the x-axis (and magnitude of the y-axis). Both a high affinity binder and non-specific antibody are simulated. These non-specific antibodies display localization based on the enhanced permeability and retention (EPR) effect shown in gray lines. Transport across the blood vessel wall is very slow, and once the molecule is in the tumor interstitium, clearance back to the blood is also very slow. As expected from the small Biot number, ignoring spatial heterogeneities within the tumor causes little deviation between the spatially dependent numerical simulation and the lumped parameter compartmental model. The graphs on the bottom show the deviation of the compartmental model from the numerical simulations when the assumption of a subsaturating dose is violated. Antibody that enters the tumor after saturation has no free antigen to bind, so it behaves in general as a non-binding antibody. When this subsaturating dose assumption is not valid, the compartmental model over-predicts the uptake, since it still assumes antibody that enters the tumor will bind antigen. The numerical simulations show two periods of decline, the first being the rapid loss of unbound antibody, due to intravasation, that has no unoccupied sites to bind, and the second period where bound antibody is cleared from the tumor. The subsaturating dose assumption must be checked especially in tumors with low or down-regulated antigen density since these will become saturated more easily.
Figure 3.
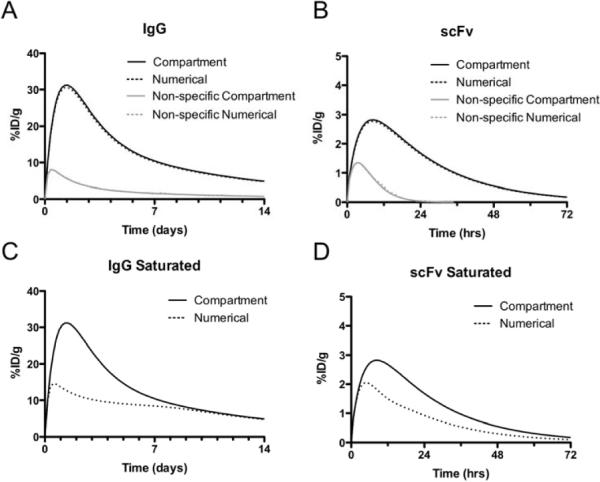
Time profiles for specific and non-specific scFv and IgG in mouse
Time profiles for specific and non-specific IgGs (A, C) and scFvs (B, D) under subsaturating (A, B) and saturating (C, D) conditions in mice. Profiles are shown for the spatially distributed Krogh cylinder numerical simulation (dotted lines) and the current compartmental model (solid lines).
3.3. Model Simplifications and Maximum Uptake
The expression in equation 7 captures the time dependent concentration in tumors with varying properties and antibodies with different affinities. However, scenarios are often encountered when not all the factors are significant, and the model can be simplified to more clearly show which factors are controlling uptake.
Simplifications can be made based on affinity. The fraction of bound antibody is based on the ratio between the antigen concentration and antibody affinity. With interstitial antigen concentrations typically in the low micromolar range, antibodies with Kd values less than 100 nM (Kd ⪡ [Ag]/ε) will have similar uptake values, although their spatial distribution within the tumor may vary (Rudnick et al., 2011). These antibodies will be cleared primarily due to internalization, so intravasation can be ignored. This yields the simplified version for a high affinity antibody:
| 11. |
and
| 12. |
For comparison, the model for a non-binding antibody can also be simplified. Here, Kd ⪢ [Ag]/ε.
| 13. |
and
| 14. |
where:
| 15. |
Even these non-binding molecules will accumulate to some extent within the tumor. While the uptake of these antibodies in the tumor interstitium is slow (but higher than normal tissue) due to the transport across the vascular wall, the loss of antibody is equally slow. Once the plasma clearance drops below the interstitial concentration, antibodies wash out of the tissue slowly due to equally poor permeability going from the interstitium to the plasma, resulting in non-specific retention.
Antibodies are typically cleared from the plasma in a biexponential fashion as it redistributes in different tissues and is cleared by various organs (Fujimori et al., 1989; Sung & Vanosdol, 1995). Because of this biexponential behavior, it is not possible to find an analytical expression for the maximum tissue concentration. However, in practice, the redistribution phase is often ignored and drug clearance is assumed to follow a single exponential decay (Katzung, 2004). While this simplification overlooks the distinct redistribution and clearance phases, it is useful in obtaining a simple expression for the time of maximum uptake. This is a very important question for imaging and pretargeting strategies, where investigators need to know when the highest level of antibody has reached the tumor. Given this approximation of kβ for the overall clearance rate, the time of maximum uptake occurs at:
| 16. |
Note that for a high affinity antibody, Ω is simply the internalization rate, ke, for the antibody. Looking at this term for the time of maximum uptake, if either plasma clearance or tumor loss occurs rapidly, the time of maximum uptake will occur quickly. This is typical for scFvs with fast plasma clearance, and to a lesser extent, anti-HER2 antibodies that have an internalization rate of several hours. However, if both the clearance and internalization rates are very slow, the maximum uptake will occur after an extended incubation period. This is typical for slowly clearing IgGs that target gradually internalized antigens, such as A33 (Ackerman et al., 2008b). Here, the maximum uptake may not occur for several days (Carrasquillo et al., 2011).
The time of maximum uptake can be used to determine the maximum concentration in the tumor. Entering this value in the expression for antibody concentration in the tumor:
| 17. |
The first term in square brackets indicates the maximum amount of antibody that can be taken up into the tumor prior to clearance from the plasma. The second square bracket expression adjusts the maximum uptake by taking into account loss from the tumor. This value ranges from 0 to 1 depending on the ratio of antibody loss from the tumor (Ω) to clearance from the plasma (kβ). It approaches the maximum value of 1 when loss from the tumor is much less than the clearance rate and approaches 0 when antibody is lost faster than it can be taken up (i.e. Ω ⪢ kβ). For a high affinity antibody:
| 18. |
3.4. Model Validation
This model provides a time course of antibody localization given certain fundamental parameters of tumors. Many of these parameters have been measured previously, as shown in table 1, so the model predictions can be tested against published experimental data. While the comparisons with the Krogh cylinder simulations above show the current model does not neglect the spatial heterogeneity of antibody uptake in tumors, this section compares predictions with published in vivo experimental data.
Table 1.
List of Symbols and Parameter Values
| Symbol | Parameter | Typical Value | Ref. | Note | Measured* | |
|---|---|---|---|---|---|---|
| [Ab]plasma,0 | Dose, initial plasma concentration | Varies | 10 ug IgG dose in mouse = ~30 nM | In vivo (mice, human) |
||
| Rcap | Average tumor capillary radius | 8μm (5–15 μm) |
(Hilmas & Gillette, 1974; Jain, 1999) | Rcap and RKrogh define the blood vessel surface area to tumor volume ratio. Necrosis lowers the surface area of blood vessels for targeting. |
In vivo (mice) |
|
| RKrogh | Average radius of tissue surrounding tumor capillary |
75 μm (20–150+ μm) |
(Baish et al., 1996; Krogh, 1919) | In vivo (mice) |
||
| Kd | Antibody dissociation constant | 10−12 – 10−6 M | (Schier et al., 1996) | IgGs are often 1–10 nM | In vitro | |
| D | Antibody diffusion coefficient | IgG ~ 14 μm2/s (5–50 μm2/s) |
(Berk et al., 1997; Brown et al., 2004; Thurber et al., 2008b; Thurber & Wittrup, 2008) | Dependent on molecule size | In vitro, In vivo (mice), Ex vivo (human) |
|
| P | Tumor capillary permeability | IgG ~ 3×10−9 m/s (1–150×l0−9 m/s) |
(Dreher et al., 2006; Yuan et al., 1995) | Rate limiting step in uptake Dependent on molecule size |
In vivo (mice) |
|
| [Ag] | Tumor antigen concentration | 100 nM – 1 μM | (Ballangrud et al., 2004; Berk et al., 1997; Thurber & Wittrup, 2008) | Depends on Ag/cell and cell packing density | In vitro, In vivo (mice) |
|
| ε | Tumor void fraction | IgG ~ 0.1–0.3 (0.05 – 0.5) |
(Krol et al., 1999; Thurber & Wittrup, 2008) | Dependent on molecule size, cell packing | In vitro, in vivo (mice) |
|
| ke | Internalization/ degradation rate |
2×10−4 – 2×10–6 s−1 |
(Ackerman et al., 2008a; Austin et al., 2004; Mattes et al., 1994; Schmidt et al.) | Related to properties of target | In vitro | |
| A, B, kα, kβ | Clearance parameters | minutes to weeks see ref. |
(Thurber et al., 2007) | Dependent on size, charge, FcRn interactions, etc. | In vivo (mice, human) |
|
| Vplasma | Plasma volume | ~2 mL mouse ~3 L human |
(Green, 1966; Kaliss & Pressman, 1950; Katzung, 2004; Yang et al., 1978) | Species/weight dependent | In vivo (mice, human) |
|
| t | Time | NA | NA | Critical for imaging/pretargeting protocols | ||
| Bi | Biot number | lgG ~ 0.01 | (Thurber et al., 2007) |
|
||
| Ω | Total tumor clearance rate constant | 10−4 – 10−6 s−1 | Dominated by fastest loss rate |
This column indicates whether the values have been measured in vivo or in vitro. The in vivo measurements were further classified as to whether they were in humans or mice.
3.4.1. Uptake
Other compartmental models have been developed that describe the uptake and loss of antibody in tumors. Many of these models allow antibody in the plasma to directly bind antigen in the tumor, by-passing the critical extravasation step to the tumor interstitium. Comparisons with models of this form are not very fruitful since the fit rate constants do not match the physical processes incorporated in the current model. However, several models have been published that are similar enough to make comparisons. Sung et al. used a similar model to fit rate parameters between compartments for an immunotoxin, although these rates were assumed to be completely convective, and degradation within the tumor was ignored (Sung et al., 1990). Baxter et al. used a comparable model for the tumor compartment in their physiology based pharmacokinetic model, although transport to and from the tumor was assumed to be both diffusive and convective in nature (Baxter et al., 1994). Finally, Ferl et al. have used compartmental models to analyze the uptake of both IgGs (Ferl et al., 2005) and scFv-Fc (Ferl et al., 2006) molecules. Because the loss terms in these models can come from several mechanisms (e.g. intravasation and internalization), it is most straightforward to compare rates of uptake from the plasma. Table 2 compares the uptake rate predicted in this compartmental model to the rates that were fitted from experimental data in these papers. In all cases, the rates are comparable with the current model, indicating the mechanistic model is consistent with these data.
Table 2.
Comparison of Current Model with Extravasation Rates from Compartmental Models Using Fitted Data.
| Model | Extravasation Rate (day−1) | Molecule |
|---|---|---|
| Sung et al. 1990(Sung et al., 1990) | 0.187 | IgG-immunotoxin |
| Baxter et al. 1994(Baxter et al., 1994) | 0.191 | IgG |
| Ferl et al. 2005(Ferl et al., 2005) | 0.730 | IgG |
| Current | 0.737 | IgG |
| Ferl et al. 2006(Ferl et al., 2006) | 0.888 | scFv-Fc |
3.4.2. Affinity
To determine if the relationship between uptake and affinity predicted by the model agrees with experimental data, model predictions were compared to published in vivo data from a series of HER-2 binding scFvs (Adams et al., 2001). The model inputs (found in supplementary data) were the same as used in a previously described microscopic analysis of antibody distribution surrounding tumor capillaries (Thurber et al., 2007) with two exceptions. The surface area to volume ratio of the vasculature was changed to an average value (Graff et al., 2000; Jackson et al., 1999), since it is the average value over the whole tumor that will determine uptake. This differs from the conservative estimates typically used in our microscopic model to ensure targeting of all cells (Thurber et al., 2007). The second difference in parameters is the loss rate of antibody signal from the tumor. For the microscopic analysis, the internalization rate of the antigen determines the distribution of antibody surrounding the vessel. However, after degradation, the radioactive iodine tag remains in the cell for a certain period of time. Since the experimental setup cannot distinguish between intact and degraded antibody, the loss of signal due to cellular clearance is determined by the slowest rate between antibody internalization and label clearance (supplemental). Previous investigations determined that the loss of this isotope occurs with a roughly 15 hour half-life, suggesting that it is the pertinent parameter in this case (Mattes et al., 1994; Press et al., 1996).
The top two panels in figure 4 show the experimental results on the left and the model prediction on the right. All data points and model results were taken at 24 hours. Using only literature estimates of the various parameters in the model, the shape and order of magnitude of uptake agree roughly with the experimental results. As the affinity decreased (Kd increased) to values similar to the antigen concentration, more antibody remained unbound and could diffuse out of the tumor. Loss of the high affinity antibodies from the tumor occurred as bound molecules were internalized and the degraded iodine labels cleared from the tumor.
Figure 4.
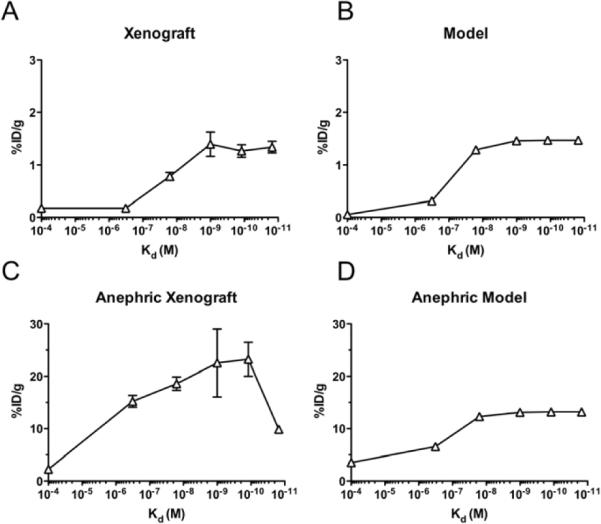
Effects of Affinity and Clearance on HER2 Binding scFvs. Experimental data from Adams and colleagues (Adams et al., 2001) with anti-ER2 scFvs in normal (A) and anephric (C) mice. Model predictions for both cases (B and D) are shown on the right. The control antibody was modeled as a 100 μM Kd binder.
3.4.3. Clearance
In the same paper (Adams et al., 2001), the authors performed a second experiment where the kidneys were removed in order to eliminate rapid renal clearance. This was simulated in the compartmental model by setting the beta phase clearance rate to zero (and reducing the fraction of redistribution to take into account rapid clearance by the kidneys). Essentially, the antibody distributes between the plasma and normal tissue, but then remains at that level until cleared by non-renal processes. Using the same parameters in Figure 4B except for the single change in plasma clearance, the model predicts roughly the same level of uptake by reducing renal clearance as was found by experiment. Notice that the y-axis limit is increased by an order of magnitude. Interestingly, the final experimental point actually decreases - potentially due to faster degradation and loss of the signal as seen with an IgG variant (Rudnick et al., 2011).
3.4.4. Time Course
A second model comparison was chosen that differs considerably from the above experiment to see if the model could be generalized to other cases. Whereas the previous experiment was a HER-2 binding scFv analyzed after 24 hours, Shockley et al. analyzed the time course of uptake of four different monoclonal antibodies that target two different melanoma antigens using two different cell lines with varying antigen densities (Shockley et al., 1992). All the model parameters and references used for these experiments can be found in the supplementary data.
The top panel of figure 5 shows the experimental uptake time course in a SK-MEL-2 cell line on the left and the model predictions on the right. All parameters were estimated from the literature, with no values fit to the experimental results, to rigorously test whether the model captures the fundamental rates present in tumor targeting. The LMW-MAA binding 436 IgG, HMW-MAA binding 9.2.27 IgG, and non-specific B72.3 IgG all have %ID/g and time courses similar to those predicted by the model. However, the HMW-MAA binding IND1 IgG is predicted to accumulate at a relatively higher level compared to the other antibodies than found experimentally. Moving to the lower panels, the experimental results in the M21 cell line are given on the left with model predictions on the right. Here, the relative values are in reasonable agreement with the model predictions. The more accurate model prediction for the IND1 antibody in this second cell line raises the question of the difference between the two cell lines, and this mechanistic model can be used to determine potential causes of the discrepancy. The antigen density on the surface of the SK-MEL-2 cell line is 4 times lower than the M21 cell line, and Tang et al. have demonstrated that even for antibodies with apparent sub-nanomolar affinity, the antibody may have reduced affinity for cells with a low antigen density on the surface (Tang et al., 2007). The authors assumed that the affinity of IND1 on the surface of SK-MEL-2 cells was equivalent to that on the surface of M21 cells, as used in the model, but the low antigen copy number on the surface of SK-MEL-2 cells may have caused a higher proportion of IND1 antibody to be lost from the tumor.
Figure 5.

Comparison to IgG Uptake – Melanoma Xenografts
Time Course of Four Different Anti-Melanoma IgGs in Small Xenografts. Experimental data from Shockely and colleagues (Shockley et al., 1992) is shown for four different antibodies in SK-MEL-2 xenografts (A) and M21 xenografts (C). Using parameter values from the literature, the model predictions for these two cell lines are given for the SK-MEL-2 (B) and M21 (D) xenografts.
The decrease in signal at later time points occurs faster than predicted by internalization. In a later paper, the authors examined the form of localized antibody in the tumor and found a significant fraction was attached to shed antigen (Lin et al., 1994). Although this shed complex may diffuse and intravasate slower than a free antibody, it is not anchored into the cell and can leave the tumor faster, increasing the rate of antibody loss. This effect from shed antigen can be detrimental to therapies requiring internalization (Zhang et al, 2007).
3.4.5. Clinical Application
Because this compartmental model is based on specific mechanisms, the results can be extended from mice to humans by changing the relevant parameters (such as plasma clearance and dose, supplemental). Model predictions for uptake of an anti-A33 IgG in humans were compared to a phase I clinical trial in which 12 patients received varying doses of humanized monoclonal antibody A33 (Scott et al., 2005). Values and references for all the model inputs can be found in the supplemental data. While data in the clinic varies widely, the average value for all 12 patients was 0.005 %ID/g and ranged from 0.0021 to 0.011 %ID/g. After 7 days, the compartmental model predicts 0.0167 %ID/g in the tumor, in reasonable agreement with the clinical data (also taken at 7 days). Tumor histology images and the authors' discussion of the clinical data indicate some tumors contained extensive necrosis, which would lower the functional blood vessel surface area and the model predictions of uptake. A more recent study using PET imaging with the same antibody resulted in 0.010 %ID/g as measured by PET or 0.017 %ID/g in the biopsy samples (Carrasquillo et al., 2011), in even closer agreement with the compartmental model prediction. Given the difficulty in obtaining biopsies in clinical samples, these results demonstrate the utility of the model for understanding the distribution in humans. It can also be used to scale experiments from mice to humans without the need for data from multiple species and allometric scaling, providing a powerful tool for understanding and predicting uptake in the clinic.
3.5. Sensitivity
The sensitivity of the model output to variations in model parameters is important, both in understanding the impact of input values, in which case more care may be taken with measurements, as well as the impact on the output when changing a particular parameter. Kinetic models are often generated by combining multiple kinetic components, simulating the outcome, and afterwards testing the variables to see which are important. The reductionist and scaling approach used in developing this model works in reverse. Many of the insensitive parameters were eliminated from the model during development. For example, the surface area of functional vessels (S/V), and therefore the vascularization, is very important, but the velocity of blood flowing through the vessels does not have a major impact due to the extremely slow rate of extravasation and lack of depletion along the length of the vessel (supplemental). This analysis of tumor blood flow found that the antibody localization is insensitive to this parameter, and as a result, tumor blood flow does not appear in the final equation.
The sensitivity of the maximum antibody uptake in a tumor is defined as:
| 19. |
where k is the parameter of interest. Looking at equation 17, it can be shown that the sensitivity to antibody dose is one, the exponent of the parameter. For the Krogh cylinder radius, the sensitivity is −2. The results are not as straightforward for other parameters, such as plasma clearance, affinity, and internalization. Here, the sensitivity depends on the base case chosen for analysis. For example, if the Kd is much less than the antigen concentration, the results become relatively insensitive to the affinity as seen in Figure 4 at high affinity where the curve levels off. In the summation terms of the model, one parameter becomes vanishingly small relative to the other parameter in the sum, making it insensitive to the smaller parameter. Similarly, if the internalization rate is much slower than plasma clearance, the uptake is only impacted by the plasma clearance with a sensitivity of −1 as shown in equation 18. The opposite is true if ke ⪢ kβ. The sensitivity is ~0 for kβ and −1 for ke. While the model provides a very basic look at factors determining uptake in tumors, the trends, trade-offs, and impact of all the relevant parameters in these complicated animal experiments become increasingly clear with this type of mathematical approach.
4. DISCUSSION
4.1. Model Development
This paper presents a simple, predictive method for simulating the uptake and retention of antibodies in tumor tissue. Unlike many other compartmental models, all of the model rates are physical processes and parameters that can be measured with independent experiments, providing insight into which mechanisms will improve targeting. The parameters that determine uptake can be measured in vitro (antibody affinity, antigen density, internalization rate, etc.) or estimated from the literature (permeability, clearance, etc.) (Schmidt & Wittrup, 2009). The utility of this model stems from 1) the analytical form which clearly indicates dominant factors that dictate uptake and trends based on affinity, clearance, internalization, etc. 2) the ability to quickly obtain an order of magnitude estimate of the time course of antibody uptake even for non-modelers, and 3) the capability of extending these results from mouse to man since the processes are based on measurable physical mechanisms and not fit from animal data. For example, while some parameters change from mouse to humans (e.g. clearance, plasma volume), others do not (e.g. affinity, radioisotope decay rates).
Targeting of systemically delivered antibody involves four major steps: 1) blood flow to the tumor, 2) transport across the capillary wall, 3) diffusion through the tissue, and 4) binding/metabolism (Thurber & Weissleder, 2011). Of these four steps, extravasation of macromolecules is by far the slowest process. Binding occurs on the order of seconds, diffusion takes minutes, and extravasation takes hours (Thurber et al., 2008a). Blood flow to the tumor was not discussed in depth, but it is faster than transcapillary extravasation (Butler et al., 1975), so the plasma concentration is not significantly depleted of macromolecules before exiting the tumor (Heijn et al., 1999). In three of the models cited in table 2 (Baxter et al., 1994; Ferl et al., 2006; Ferl et al., 2005), the blood flow to the tumor was treated explicitly, and this rate was ~100 to 1000 times faster than the rate of extravasation. It is important to note that blood flow, like many properties in a tumor, is heterogeneous, and certain regions may be limited by flow. However, from a design perspective, it is important to consider the typical values encountered in a tumor to optimize targeting, since tailoring an agent only for rare conditions will miss the majority of the tumor.
One of the reasons this reductionist model, which admittedly does not capture all the complex details of tumor targeting, is able to provide reasonable estimates of targeting levels with such a simple form is because extravasation is so much slower than the other steps; very few antibodies exit the tumor vasculature to reach the tumor interstitium. This concept is often underappreciated, since the perivascular binding of antibodies in the tumor can mask the low levels of unbound antibody and give the appearance of a large free concentration outside the blood. It is more obvious for non-binding macromolecules, where the concentration in the blood is much higher at early times after injection (before the interstitium has equilibrated and the plasma level drops), indicating poor extravasation (Dreher et al., 2006). With both of these situations, the exchange rate between the plasma and tissue, often referred to as Ktrans, is equal to the permeability surface area product (Tofts et al., 1999).
The compartmental analysis explicitly ignores spatial variations surrounding each vessel in order to examine the time course of total tumor uptake. The microscale distribution around vessels, which has been analyzed previously (Thurber et al., 2007), does not provide estimates for the total uptake within a tumor, a critical value for imaging and certain therapies. The reductionist model was therefore extended to whole tumor uptake. For whole animal/clinical imaging, the resolution of the instruments is typically too low to visualize heterogeneity on the 100 micron length scale, therefore it is the time course of whole tumor uptake that is important. With some therapies, for example Yttrium-90 radioimmunotherapy, the range of the low LET (linear energy transfer) radiation is several millimeters (Koppe et al., 2005). This `smooths out' any heterogeneity on the 100 micron length scale, rendering it less important. It is vital to keep in mind, however, that for many therapies, such as those utilizing immunotoxins or Fc effector functions, the microdistribution should be taken into consideration. For example, `cold' doses of antibody lacking a radioisotope or toxin conjugate are often given prior to the therapeutic antibody to quickly saturate easily accessible antigen in the plasma and normal tissues (Hernandez & Knox, 2004). This compartmental analysis presented here only indicates the average concentration of the total antibody (cold and conjugated antibody) in the tumor, whereas a microscopic analysis shows this cold dose may help the antibody conjugate penetrate deeper into the tumor to target more cells, as shown with fluorescent (Ackerman et al., 2008c) and radiolabeled (Blumenthal et al., 1991) antibodies.
4.2. Model Utilization
The effect of some properties on overall uptake, such as antibody charge that influences clearance, permeability, and diffusion (Dellian et al., 2000; Lambert et al., 2004) or local biological mediators such as the blood-brain barrier (Hobbs et al., 1998), can be assessed by altering the relevant parameters in the model. Since uptake is an explicit function of time, the results can be paired with radioactive decay to optimize imaging protocols (Williams et al., 1995) and targeting agents that utilize clearing agents (Williams et al., 2000). Without the need for computer simulations, the compartmental model and analytical solution can be used by non-modelers to help in experimental design, interpretation of in vivo data, and strategies to improve targeting by rapidly generating concentration time profiles for varying input parameters.
Although the geometry (spacing and orientation of vessels) does not have a large impact on total tumor uptake, the vessel surface area to tumor volume ratio is a major determinant of average localization. The S/V typically ranges from 20–200/cm in xenografts (data not shown), with clinical measurements falling in the same range (Barth et al., 1997; Kamijo et al., 2001). While the variability in this parameter will not affect the predicted trends, the value can affect absolute levels even more than antigen density in many cases(Thurber & Weissleder, 2010). However, this ten-fold variability is often less than the orders of magnitude difference in antigen internalization rates, plasma clearance rates, and number of antigens per cell, so it still provides a reasonable range in predicted values(Schmidt & Wittrup, 2009). Conservative estimates can be used to ensure saturation if this is required for imaging or therapy.
This compartmental model describes the major mechanisms determining antibody uptake in tumors. Since most antibodies have dissociation rates well below the antigen concentration in the tumor, the profile is determined by equation 12. Notice this equation does not contain the antigen concentration, indicating uptake is relatively independent of expression level at subsaturating doses as seen experimentally (Thurber & Weissleder, 2010). Approximating the clearance using a single exponential, the maximum uptake is given by equation 18. Examining this expression yields the major factors that determine uptake and potential ways of improving localization. One of the most straightforward ways of increasing the tumor concentration is to increase the dose. Maximum tumor uptake is proportional to initial dose prior to saturation, as demonstrated by a constant %ID/g until all antigen is bound (Koppe et al., 2003; Kranenborg et al., 1998; Liu et al., 2005; Sharkey et al., 2003). Uptake is also increased by lowering the clearance rate, increasing permeability, or increasing the vascular density (2Rcap/RKrogh2). These parameters may be enhanced by debulking the tumor through traditional chemotherapy and/or radiation, allowing previously collapsed, non-functional vessels to transport blood (Hilmas & Gillette, 1974). Finally, targeting antigens with longer surface persistence will increase the maximum uptake in the tumor by lowering the amount lost by internalization.
There are trade-offs in varying many of these parameters. For example, a larger dose will drive greater tumor localization, but increased uptake in normal tissues may make this unfeasible due to increased background in imaging and toxicity with therapeutics. The size of the targeting molecule often has opposing effects, since larger molecules persist in the blood for longer times (Wu & Senter, 2005) but extravasate across the vasculature more slowly (Dreher et al., 2006). While choosing a slowly internalizing antigen will increase retention, this will decrease efficacy for immunotoxins that must be internalized (Pirie et al., 2011; Wenning & Murphy, 1999). The ideal properties will vary depending on the application (e.g. imaging or therapy) and design (e.g. radioisotope, therapeutic mechanism), making this simple model a useful tool during agent development. In fact, this modeling approach has been used to analyze the uptake of molecules from less than 10 kDa to nanoparticles, showing excellent agreement with experimental data and utility in the design of a wide range of agents (Schmidt & Wittrup, 2009).
In conclusion, certain fundamental physiological principles determine the overall time course of the pharmacokinetic distribution of antibodies in tumors. The slow extravasation of macromolecules results in the low uptake seen in tumors, causing failure with many treatments and making the development of imaging agents more challenging by lowering tumor to background ratios. A simple, mechanistic model was developed and quantitatively compared to numerical simulations of a Krogh cylinder model that describes spatial heterogeneity in the tumor. The current model adequately captures many of the factors that determine total tumor uptake in these simulations. Predictions based on independently measured parameters also compare favorably to quantitative in vivo experiments. Since these parameters are known or can be obtained from the literature, this simple model can give a rough estimate of the time course in order to aid with experimental design, data interpretation, and strategies to improve uptake.
Supplementary Material
Highlights
-
-
We develop a predictive and mechanistic model of antibody uptake in tumors
-
-
Simulations demonstrate that heterogeneous distribution does not affect total uptake in tumors
-
-
Simple analytical expressions predict the localization time course
-
-
Predictions are consistent with multiple preclinical and clinical studies
Acknowledgments
This work was funded by CA101830 and a Ludwig Fellowship to GMT. Helpful comments on the manuscript were provided by Mike Schmidt and John Rhoden.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ackerman M, Chalouni C, Schmidt M, Raman V, Ritter G, Old L, Mellman I, Wittrup K. A33 antigen displays persistent surface expression. Cancer Immunology, Immunotherapy. 2008a doi: 10.1007/s00262-007-0433-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ackerman ME, Chalouni C, Schmidt MM, Raman VV, Ritter G, Old LJ, Mellman I, Wittrup KD. A33 antigen displays persistent surface expression. Cancer Immunology Immunotherapy. 2008b;57(7):1017–1027. doi: 10.1007/s00262-007-0433-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ackerman ME, Pawlowski D, Wittrup KD. Effect of antigen turnover rate and expression level on antibody penetration into tumor spheroids. Molecular Cancer Therapeutics. 2008c;7(7):2233–2240. doi: 10.1158/1535-7163.MCT-08-0067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adams G, Schier R, McCall A, Simmons H, Horak E, Alpaugh K, Marks J, Weiner L. High Affinity Restricts the Localization and Tumor Penetration of Single-Chain Fv Antibody Molecules. Cancer Research. 2001;61:4750–4755. [PubMed] [Google Scholar]
- Ahlstrom H, Christofferson R, Lorelius L. Vascularization of the continuous human colonic cancer cell line LS 174 T deposited subcutaneously in nude rats. APMIS. 1988;96:701–710. doi: 10.1111/j.1699-0463.1988.tb00933.x. [DOI] [PubMed] [Google Scholar]
- Aquino A, Formica V, Prete SP, Correale PP, Massara MC, Turriziani M, De Vecchis L, Bonmassar E. Drug-induced increase of carcinoembryonic antigen expression in cancer cells. Pharmacological Research. 2004;49(5):383–396. doi: 10.1016/j.phrs.2003.12.007. [DOI] [PubMed] [Google Scholar]
- Austin CD, De Maziere AM, Pisacane PI, van Dijk SM, Eigenbrot C, Sliwkowski MX, Klumperman J, Scheller RH. Endocytosis and sorting of ErbB2 and the site of action of cancer therapeutics trastuzumab and geldanamycin. Mol Biol Cell. 2004;15(12):5268–82. doi: 10.1091/mbc.E04-07-0591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baish JW, Gazit Y, Berk DA, Nozue M, Baxter LT, Jain RK. Role of tumor vascular architecture in nutrient and drug delivery: an invasion percolation-based network model. Microvasc Res. 1996;51(3):327–46. doi: 10.1006/mvre.1996.0031. [DOI] [PubMed] [Google Scholar]
- Baish JW, Stylianopoulos T, Lanning RM, Kamoun WS, Fukumura D, Munn LL, Jain RK. Scaling rules for diffusive drug delivery in tumor and normal tissues. Proceedings of the National Academy of Sciences of the United States of America. 2011;108(5):1799–1803. doi: 10.1073/pnas.1018154108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballangrud AM, Yang WH, Palm S, Enmon R, Borchardt PE, Pellegrini VA, McDevitt MR, Scheinberg DA, Sgouros G. Alpha-particle emitting atomic generator (actinium-225)-labeled trastuzumab (herceptin) targeting of breast cancer spheroids: Efficacy versus HER2/neu expression. Clinical Cancer Research. 2004;10(13):4489–4497. doi: 10.1158/1078-0432.CCR-03-0800. [DOI] [PubMed] [Google Scholar]
- Barth PJ, GhafouriSanati H, Kohler HH, Bittinger A, Riedmiller H. Histological determinants of the vascular surface in prostatic carcinoma. Urological Research. 1997;25(5):303–308. doi: 10.1007/BF01294655. [DOI] [PubMed] [Google Scholar]
- Baxter L, Zhu H, Mackensen D, Jain RK. Physiologically Based Pharmacokinetic Model for Specific and Nonspecific Monoclonal Antibodies and Fragments in Normal Tissues and Human Tumor Xenografts in Nude Mice. Cancer Research. 1994;54:1517–1528. [PubMed] [Google Scholar]
- Berk DA, Yuan F, Leunig M, Jain RK. Direct in vivo measurement of targeted binding in a human tumor xenograft. Proc Natl Acad Sci U S A. 1997;94(5):1785–90. doi: 10.1073/pnas.94.5.1785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertuzzi A, Fasano A, Gandolfi A, Sinisgalli C. Tumour Cords and Their Response to Anticancer Agents. In: Bellomo N, Chaplain M, DeAngelis E, editors. Selected Topics in Cancer Modeling: Genesis, Evolution, Immune Competition, and Therapy. Birkhauser Boston; USA: 2008. 675 Massachusetts Ave, Cambridge, Ma 02139-2333. [Google Scholar]
- Blumenthal RD, Fand I, Sharkey RM, Boerman OC, Kashi R, Goldenberg DM. The Effect of Antibody Protein Dose on the Uniformity of Tumor Distribution of Radioantibodies - an Autoradiographic Study. Cancer Immunology Immunotherapy. 1991;33(6):351–358. doi: 10.1007/BF01741594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boucher Y, Baxter LT, Jain RK. Interstitial Pressure-Gradients in Tissue-Isolated and Subcutaneous Tumors - Implications for Therapy. Cancer Research. 1990;50(15):4478–4484. [PubMed] [Google Scholar]
- Boucher Y, Jain RK. Microvascular Pressure Is the Principal Driving Force for Interstitial Hypertension in Solid Tumors: Implications for Vascular Collapse. Cancer Research. 1992;52:5110–5114. [PubMed] [Google Scholar]
- Brown EB, Boucher Y, Nasser S, Jain RK. Measurement of macromolecular diffusion coefficients in human tumors. Microvasc Res. 2004;67(3):231–6. doi: 10.1016/j.mvr.2004.02.001. [DOI] [PubMed] [Google Scholar]
- Butler TP, Grantham FH, Gullino PM. Bulk Transfer of Fluid in Interstitial Comparment of Mammmary-Tumors. Cancer Research. 1975;35(11):3084–3088. [PubMed] [Google Scholar]
- Carrasquillo JA, Pandit-Taskar N, O'Donoghue JA, Humm JL, Zanzonico P, Smith-Jones PM, Divgi CR, Pryma DA, Ruan ST, Kemeny NE, Fong YM, Wong D, Jaggi JS, Scheinberg DA, Gonen M, Panageas KS, Ritter G, Jungbluth AA, Old LJ, Larson SM. (124)I-huA33 Antibody PET of Colorectal Cancer. Journal of Nuclear Medicine. 2011;52(8):1173–1180. doi: 10.2967/jnumed.110.086165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deen W. Analysis of Transport Phenomena. Oxford University Press; 1998. [Google Scholar]
- Dellian M, Yuan F, Trubetskoy VS, Torchilin VP, Jain RK. Vascular permeability in a human tumour xenograft: molecular charge dependence. British Journal of Cancer. 2000;82(9):1513–1518. doi: 10.1054/bjoc.1999.1171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dewhirst MW, Kimura H, Rehmus SWE, Braun RD, Papahadjopoulos D, Hong K, Secomb TW. Microvascular studies on the origins of perfusion-limited hypoxia. British Journal of Cancer. 1996;74:S247–S251. [PMC free article] [PubMed] [Google Scholar]
- Dreher MR, Liu WG, Michelich CR, Dewhirst MW, Yuan F, Chilkoti A. Tumor vascular permeability, accumulation, and penetration of macromolecular drug carriers. Journal of the National Cancer Institute. 2006;98(5):335–344. doi: 10.1093/jnci/djj070. [DOI] [PubMed] [Google Scholar]
- Dvorak H. Tumors: Wounds That Do Not Heal: Similarities between Tumor Stroma Generation and Wound Healing. The New England Journal of Medicine. 1986;315(26):1650–1659. doi: 10.1056/NEJM198612253152606. [DOI] [PubMed] [Google Scholar]
- Fenwick J, Philpott G, Connett J. Biodistribution and histological localization of anti-human colon cancer monoclonal antibody (MAb) 1A3: the influence of administered MAb dose on tumor uptake. International Journal of Cancer. 1989;44:1017–1027. doi: 10.1002/ijc.2910440614. [DOI] [PubMed] [Google Scholar]
- Ferl GZ, Kenanova V, Wu AM, DiStefano JJ. A two-tiered physiologically based model for dually labeled single-chain Fv-Fc antibody fragments. 2006;5(6):1550–1558. doi: 10.1158/1535-7163.MCT-06-0072. [DOI] [PubMed] [Google Scholar]
- Ferl GZ, Wu AM, DiStefano JJ. A predictive model of therapeutic monoclonal antibody dynamics and regulation by the neonatal fc receptor (FcRn) Annals of Biomedical Engineering. 2005;33(11):1640–1652. doi: 10.1007/s10439-005-7410-3. [DOI] [PubMed] [Google Scholar]
- Fujimori K, Covell D, Fletcher J, Weinstein J. Modeling Analysis of the Global and Microscopic Distribution of Immunoglobulin G, F(ab')2, and Fab in Tumors. Cancer Research. 1989;49:5656–5663. [PubMed] [Google Scholar]
- Graff BA, Bjornaes I, Rofstad EK. Macromolecule uptake in human melanoma xenografts. relationships to blood supply, vascular density, microvessel permeability and extracellular volume fraction. Eur J Cancer. 2000;36(11):1433–40. doi: 10.1016/s0959-8049(00)00120-9. [DOI] [PubMed] [Google Scholar]
- Graff CP, Wittrup KD. Theoretical analysis of antibody targeting of tumor spheroids: importance of dosage for penetration, and affinity for retention. Cancer Res. 2003;63(6):1288–96. [PubMed] [Google Scholar]
- Green E. Biology of the Laboratory Mouse. Dover Publications & The Jackson Laboratory; New York: 1966. [Google Scholar]
- Heijn M, Roberge S, Jain RK. Cellular membrane permeability of anthracyclines does not correlate with their delivery in a tissue-isolated tumor. 1999;59(17):4458–4463. [PubMed] [Google Scholar]
- Hernandez M, Knox S. Radiobiology of radioimmunotherapy: targeting CD20 B-cell antigen in non-Hodgkin's lymphoma. International Journal of Radiation Oncology Biology Physics. 2004;59(5):1274–1287. doi: 10.1016/j.ijrobp.2004.02.065. [DOI] [PubMed] [Google Scholar]
- Hilmas D, Gillette E. Morphometric Analyses of the Microvasculature of Tumors During Growth and After X-Irradiation. Cancer. 1974;33:103–110. doi: 10.1002/1097-0142(197401)33:1<103::aid-cncr2820330116>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- Hobbs S, Monsky W, Yuan F, Roberts W, Griffith L, Torchilin V, Jain RK. Regulation of transport pathways in tumor vessels: Role of tumor type and microenvironment. Proceedings of the National Academy of Science, USA. 1998;95:4607–4612. doi: 10.1073/pnas.95.8.4607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson TL, Lubkin SR, Siemers NO, Kerr DE, Senter PD, Murray JD. Mathematical and experimental analysis of localization of anti-tumour antibody-enzyme conjugates. British Journal of Cancer. 1999;80(11):1747–1753. doi: 10.1038/sj.bjc.6690592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain RK. Transport of Molecules, Particles, and Cells in Solid Tumors. Annual Reviews in Biomedical Engineering. 1999;01:241–263. doi: 10.1146/annurev.bioeng.1.1.241. [DOI] [PubMed] [Google Scholar]
- Kaliss N, Pressman D. Plasma and blood volumes of mouse organs as determined with radioactive iodoproteins. Proceedings of the Society for Experimental Biology and Medicine. 1950;75:16–20. doi: 10.3181/00379727-75-18083. [DOI] [PubMed] [Google Scholar]
- Kamijo T, Yokose T, Hasebe T, Yonou H, Hayashi R, Ebihara S, Ochiai A. Image analysis of microvessel surface area predicts radiosensitivity in early-stage laryngeal carcinoma treated with radiotherapy. Clinical Cancer Research. 2001;7(9):2809–2814. [PubMed] [Google Scholar]
- Katzung B, editor. Basic and Clinical Pharmacology. 9 edit Lange Medical Books; McGraw-Hill Companies; New York: 2004. [Google Scholar]
- Koppe E, Soede AC, Pels W, Oyen WJG, Goldenberg DM, Bleichrodt RP, Boerman OC. Experimental radioimmunotherapy of small peritoneal metastases of colorectal origin. International Journal of Cancer. 2003;106(6):965–972. doi: 10.1002/ijc.11304. [DOI] [PubMed] [Google Scholar]
- Koppe MJ, Bleichrodt RP, Oyen WJG, Boerman OC. Radioimmunotherapy and colorectal cancer. British Journal of Surgery. 2005;92(3):264–276. doi: 10.1002/bjs.4936. [DOI] [PubMed] [Google Scholar]
- Kranenborg M, Boerman OC, Oosterwijk-Wakka JC, De Weijert MCA, Corstens FHM, Oosrterwijk E. Two-step radio-immunotargeting of renal-cell carcinoma xenografts in nude mice with anti-renal-cell-carcinoma X anti-DTPA bispecific monoclonal antibodies. International Journal of Cancer. 1998;75(1):74–80. doi: 10.1002/(sici)1097-0215(19980105)75:1<74::aid-ijc12>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- Krogh A. The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. Journal of Physiology. 1919;52(6):409–415. doi: 10.1113/jphysiol.1919.sp001839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krol A, Maresca J, Dewhirst MW, Yuan F. Available volume fraction of macromolecules in the extravascular space of a fibrosarcoma: implications for drug delivery. Cancer Res. 1999;59(16):4136–41. [PubMed] [Google Scholar]
- Lambert B, Cybulla M, Weiner S, Van De Wiele C, Ham H, Dierckx R, Otte A. Renal Toxicity after Radionuclide Therapy. Radiation Research. 2004;161:607–611. doi: 10.1667/rr3105. [DOI] [PubMed] [Google Scholar]
- Lammerts van Bueren JJ, Bleeker WK, Bogh HO, Houtkamp M, Schuurman J, van de Winkel JG, Parren PW. Effect of target dynamics on pharmacokinetics of a novel therapeutic antibody against the epidermal growth factor receptor: implications for the mechanisms of action. Cancer Res. 2006;66(15):7630–8. doi: 10.1158/0008-5472.CAN-05-4010. [DOI] [PubMed] [Google Scholar]
- Lin K, Nagy JA, Xu HH, Shockley TR, Yarmush ML, Dvorak HF. Compartmental Distribution of Tumor-Specific Monoclonal-Antibodies in Human-Melanoma Xenografts. Cancer Research. 1994;54(8):2269–2277. [PubMed] [Google Scholar]
- Liu GZ, He J, Dou SP, Gupta S, Rusckowski M, Hnatowich DJ. Further investigations of morpholino pretargeting in mice - establishing quantitative relations in tumor. European Journal of Nuclear Medicine and Molecular Imaging. 2005;32(9):1115–1123. doi: 10.1007/s00259-005-1853-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattes MJ, Griffiths G, Diril H, Goldenberg D, Ong G, Shih L. Processing of Antibody-Radioisotope Conjugates after Binding to the Surface of Tumor Cells. Cancer. 1994;73:787–793. doi: 10.1002/1097-0142(19940201)73:3+<787::aid-cncr2820731307>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- Ong G, Mattes MJ. Penetration and Binding of Antibodies in Experimental Human Solid Tumors Grown in Mice. Cancer Research. 1989;49:4264–4273. [PubMed] [Google Scholar]
- Pirie CM, Hackel BJ, Rosenblum MG, Wittrup KD. Convergent Potency of Internalized Gelonin Immunotoxins across Varied Cell Lines, Antigens, and Targeting Moieties. Journal of Biological Chemistry. 2011;286(6):4165–4172. doi: 10.1074/jbc.M110.186973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press OW, Shan D, HowellClark J, Eary J, Appelbaum FR, Matthews D, King DJ, Haines AMR, Hamann P, Hinman L, Shochat D, Bernstein ID. Comparative metabolism and retention of iodine-125, yttrium-90, and indium-111 radioimmunoconjugates by cancer cells. Cancer Research. 1996;56(9):2123–2129. [PubMed] [Google Scholar]
- Rudnick SI, Lou JL, Shaller CC, Tang Y, Klein-Szanto AJP, Weiner LM, Marks JD, Adams GP. Influence of Affinity and Antigen Internalization on the Uptake and Penetration of Anti-HER2 Antibodies in Solid Tumors. Cancer Research. 2011;71(6):2250–2259. doi: 10.1158/0008-5472.CAN-10-2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schier R, McCall A, Adams GP, Marshall KW, Merritt H, Yim M, Crawford RS, Weiner LM, Marks C, Marks JD. Isolation of picomolar affinity Anti-c-erbB-2 single-chain Fv by molecular evolution of the complementarity determining regions in the center of the antibody binding site. Journal of Molecular Biology. 1996;263(4):551–567. doi: 10.1006/jmbi.1996.0598. [DOI] [PubMed] [Google Scholar]
- Schmidt MM, Thurber GM, Wittrup KD. Kinetics of Anti-Carcinoembryonic Antigen (CEA) Antibody Internalization: Effects of Affinity, Bivalency, and Stability. Cancer Immunology and Immunotherapy. doi: 10.1007/s00262-008-0518-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt MM, Wittrup KD. A modeling analysis of the effects of molecular size and binding affinity on tumor targeting. Molecular Cancer Therapeutics. 2009;8(10):2861. doi: 10.1158/1535-7163.MCT-09-0195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroff R, Morgan A, Woodhouse C, Abrams P, Farrell M, Carpenter B, Oldham R, Foon K. Monoclonal Antibody Therapy in Malignant Melanoma: Factors Effecting In Vivo Localization. Journal of Biological Response Modifiers. 1987;6:457–472. [PubMed] [Google Scholar]
- Scott AM, Lee FT, Jones R, Hopkins W, MacGregor D, Cebon JS, Hannah A, Chong G, U P, Papenfuss A, Rigopoulos A, Sturrock S, Murphy R, Wirth V, Murone C, Smyth FE, Knight S, Welt S, Ritter G, Richards E, Nice EC, Burgess AW, Old LJ. A phase I trial of humanized monoclonal antibody A33 in patients with colorectal carcinoma: Biodistribution, pharmacokinetics, and quantitative tumor uptake. Clinical Cancer Research. 2005;11(13):4810–4817. doi: 10.1158/1078-0432.CCR-04-2329. [DOI] [PubMed] [Google Scholar]
- Sharkey RM, Karacay H, Richel H, McBride WJ, Rossi EA, Chang K, Yeldell D, Griffiths GL, Hansen HJ, Goldenberg DM. Optimizing bispecific antibody pretargeting for use in radioimmunotherapy. Clinical Cancer Research. 2003;9(10):3897S–3913S. [PubMed] [Google Scholar]
- Shockley TR, Lin K, Sung C, Nagy JA, Tompkins RG, Dedrick RL, Dvorak HF, Yarmush ML. A Quantitative-Analysis of Tumor Specific Monoclonal-Antibody Uptake by Human-Melanoma Xenografts - Effects of Antibody Immunological Properties and Tumor-Antigen Expression Levels. Cancer Research. 1992;52(2):357–366. [PubMed] [Google Scholar]
- Sung C, Vanosdol WW. Pharmacokinetic Comparison of Direct Antibody Targeting with Pretargeting Protocols Based on Streptavidin-Biotin Binding. Journal of Nuclear Medicine. 1995;36(5):867–876. [PubMed] [Google Scholar]
- Sung C, Youle RJ, Dedrick RL. Pharmacokinetic Analysis of Immunotoxin Uptake in Solid Tumors - Role of Plasma Kinetics, Capillary-Permeability, and Binding. Cancer Research. 1990;50(22):7382–7392. [PubMed] [Google Scholar]
- Tabata Y, Kawai T, Murakami Y, Ikada Y. Electric charge influence of dextran derivatives on their tumor accumulation after intravenous injection. 1997;4(3):213–221. [Google Scholar]
- Tang Y, Lou J, Alpaugh RK, Robinson MK, Marks JD, Weiner LM. Regulation of antibody-dependent cellular cytotoxicity by IgG intrinsic and apparent affinity for target antigen. 2007;179(5):2815–2823. doi: 10.4049/jimmunol.179.5.2815. [DOI] [PubMed] [Google Scholar]
- Thurber G, Schmidt M, Wittrup KD. Factors determining antibody distribution in tumors. Trends in Pharmacological Sciences. 2008a;29(2):57–61. doi: 10.1016/j.tips.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thurber GM, Schmidt MM, Wittrup KD. Antibody tumor penetration: transport opposed by systemic and antigen-mediated clearance. Advanced Drug Delivery Reviews. 2008b doi: 10.1016/j.addr.2008.04.012. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thurber GM, Weissleder R. Quantitating Antibody Uptake In Vivo: Conditional Dependence on Antigen Expression Levels. Molecular Imaging and Biology. 2010 doi: 10.1007/s11307-010-0397-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thurber GM, Weissleder R. A Systems Approach for Tumor Pharmacokinetics. PLoS ONE. 2011;6(9) doi: 10.1371/journal.pone.0024696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thurber GM, Wittrup KD. Quantitative spatiotemporal analysis of antibody fragment diffusion and endocytic consumption in tumor spheroids. Cancer Research. 2008;68:3334–3341. doi: 10.1158/0008-5472.CAN-07-3018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thurber GM, Zajic SC, Wittrup KD. Theoretic criteria for antibody penetration into solid tumors and micrometastases. J Nucl Med. 2007;48(6):995–9. doi: 10.2967/jnumed.106.037069. [DOI] [PubMed] [Google Scholar]
- Tofts PS, Brix G, Buckley DL, Evelhoch JL, Henderson E, Knopp M, Larsson HBW, Lee TY, Mayr NA, Parker GJM, Port RE, Taylor J, Weisskoff RM. Estimating kinetic parameters from dynamic contrast-enhanced T-1-weighted MRI of a diffusable tracer: Standardized quantities and symbols. Journal of Magnetic Resonance Imaging. 1999;10(3):223–232. doi: 10.1002/(sici)1522-2586(199909)10:3<223::aid-jmri2>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- Torres IP, Leunig M, Yuan F, Intaglietta M, Jain RK. Noninvasive Measurement of Microvascular and Interstitial Oxygen Profiles in a Human Tumor in Scid Mice. 1994;91(6):2081–2085. doi: 10.1073/pnas.91.6.2081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaupel P, Thews O, Hoeckel M. Treatment resistance of solid tumors - Role of hypoxia and anemia. Medical Oncology. 2001;18(4):243–259. doi: 10.1385/MO:18:4:243. [DOI] [PubMed] [Google Scholar]
- Wenning LA, Murphy RM. Coupled cellular trafficking and diffusional limitations in delivery of immunotoxins to multicell tumor spheroids. Biotechnol Bioeng. 1999;62(5):562–75. [PubMed] [Google Scholar]
- Williams LE, Liu A, Wu AM, OdomMaryon T, Chai A, Raubitschek AA, Wong JYC. Figures of merit (FOMs) for imaging and therapy using monoclonal antibodies. Medical Physics. 1995;22(12):2025–2027. doi: 10.1118/1.597646. [DOI] [PubMed] [Google Scholar]
- Williams LE, Liu A, Wu AM, Yazaki PJ, Yamauchi DM, Lopatin G, Raubitschek AA, Wong JYC. Truncation of blood curves to enhance imaging and therapy with monoclonal antibodies. Medical Physics. 2000;27(5):988–994. doi: 10.1118/1.598963. [DOI] [PubMed] [Google Scholar]
- Wu AM, Senter PD. Arming antibodies: prospects and challenges for immunoconjugates. Nature Biotechnology. 2005;23(9):1137–1146. doi: 10.1038/nbt1141. [DOI] [PubMed] [Google Scholar]
- Yang SSL, Nickoloff EL, McIntyre PA, Maddrey WC, Mikesell HH, Scheffel U, Kasecamp W, Macallister NP. Tc-99m Human-Serum Albumin - Suitable Agent for Plasma-Volume Measurements in Man. Journal of Nuclear Medicine. 1978;19(7):804–807. [PubMed] [Google Scholar]
- Yuan F, Dellian M, Fukumura D, Leunig M, Berk D, Torchilin V, Jain RK. Vascular Permeability in a Human Tumor Xenograft: Molecular Size Dependence and Cutoff Size. Cancer Research. 1995;55:3752–3756. [PubMed] [Google Scholar]
- Zhang YJ, Xiang LM, Hassan R, Pastan I. Immunotoxin and Taxol synergy results from a decrease in shed mesothelin levels in the extracellular space of tumors. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(43):17099–17104. doi: 10.1073/pnas.0708101104. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.



