Challenges and approaches in modern biometry and IOL calculation

Abstract

The introduction of new intraocular lenses (IOLs), industry marketing to the public and patient expectations has warranted increased accuracy of IOL power calculations. Toric IOLs, multifocal IOLs, aspheric IOLs, phakic lenses, accommodative lenses, cases of refractive lens exchange and eyes that have undergone previous refractive surgery all require improved clinical measurements and IOL prediction formulas. Hence, measurement techniques and IOL calculation formulas are essential factors that affect the refractive outcome.

Measurement with ultrasound has been the historic standard for measurement of ocular parameters for IOL calculation. However the introduction of optical biometry using partial coherence interferometry (PCI) has steadily established itself as the new standard. Additionally, modern optical instruments such as Scheimpflug cameras and optical coherence tomographers are being used to determine corneal power that was normally the purview of manual keratometry and topography.

A number of methods are available to determine the IOL power including the empirical, analytical, numerical or combined methods. Ray tracing techniques or paraxial approximation by matrix methods or classical analytical ‘IOL formulas’ are actively used in for the prediction of IOL power. There is no universal formula for all cases – phakic and pseudophakic cases require different approaches, as do short eyes, long eyes, astigmatic eyes or post-refractive surgery eyes. Invariably, IOLs are characterized by different methods and lens constants, which require individual optimization. This review describes the current methods for biometry and IOL calculation.

Introduction

After nearly 60 years of intraocular lens (IOL) implantation, this procedure is the most frequent and most successful surgical intervention in modern medicine. Every year, more than 11 million eyes undergo IOL implantation worldwide. In the majority of patients, functional postoperative vision is easily regained. The success and safety of this procedure are due to continuous advances in surgical technique and measurement methods.

However, new challenges have emerged due to the recent introduction of ‘premium lenses’, such as torics, multifocals, aspheric, phakic and accommodative IOLs. Premium lenses allow the patient to reach their intended visual performance only if there is reliable accuracy of the postoperative outcome. Good predictability is mandatory for any refractive procedure and post-refractive surgery eyes. Hence, the precision of clinical measurements and the accuracy of IOL calculations become significant factors in achieving satisfactory postoperative refractive outcomes. This review describes the current methods of ocular biometry, IOL calculation formulae and addresses new challenges and solutions for normal eyes and challenging cases.

Measurement techniques to determine ocular parameters

Measurement of ocular distances

The first A-scan echogram was taken by Mundt and Hughes in 1956.¹⁷ Since these initial measurements, ultrasound remained the clinically accepted method to determine ocular distances for more than half a century. The introduction of partial coherence interferometry (PCI) in optical biometers has steadily replaced ophthalmic echography as the clinical standard for ocular biometry. For example, surveys of the American Society for Cataract and Refractive Surgery (ASCRS) members from 1998 to 2009 show that applanation ultrasound was consistently the dominant biometry method for quite some time, yet it fell below 10% by 2009 (Fig. 1). By 2009, the use of optical biometry increased up to 80% among ASCRS members (Fig. 1). Interestingly, immersion ultrasound experienced an increase to nearly 20% in 2005 and subsequently decreased to just below 15% in the following years (Fig. 1).

Figure 1.

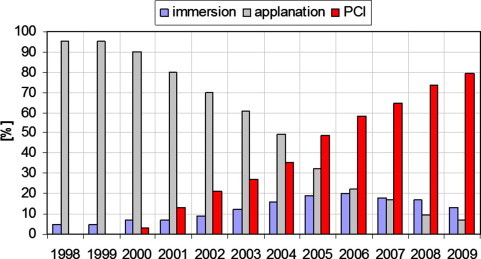
Usage of different biometry techniques in the USA. Immersion: immersion ultrasound; applanation: contact ultrasound; PCI: optical biometry (IOLMaster). Data for 1998–2003.¹² Data for 2004.¹³ Data for 2005.¹⁶ Data for 2006–2009.¹⁴

These surveys clearly indicate that the current method of choice is optical biometry. Since the commercial availability of the IOLMaster (Zeiss AG, Jena, Germany) in autumn 1999, thousands of units have been installed in clinics worldwide making this optical biometer the de-facto clinical standard. In common vernacular, optical biometry is virtually synonymous with the IOLMaster. Approximately two years ago, Haag-Streit introduced a competitive optical biometer, the Lenstar LS 900 (Haag-Streit AG, Koeniz, Switzerland) (identical to the Biograph by Alcon). Although the hardware of the Lenstar differs from the two-beam principle of the IOLMaster, the measurement principle is also based on the principle of partially coherent light. Measurements with the Lenstar are slightly more technically demanding, requiring more time than the IOLMaster. However the Lenstar measures all the ocular segments that biometrists are familiar with from ultrasonography.

A number of comparative studies of the IOLMaster and the Lenstar have been published in English peer reviewed literature (e.g. Refs. 2,9,10. Generally, these studies show no differences in the axial length measurements between the two instruments. However, significant differences have been reported in the measurement of anterior chamber depth and in some cases, the keratometry.^2,9,10 Similar results were obtained from our research [unpublished data].

The IOLMaster 500, the current model offered by Zeiss, represents the 3rd generation unit. Recently the OA 1000 optical biometer was introduced by the Tomey Corporation (Nagoya, Japan). The OA 1000 allows the measurements of axial length, anterior chamber depth (ACD) and corneal thickness. Our initial experience with the OA 1000 in the laboratory indicates that the axial length measurements are directly comparable to the Zeiss IOLMaster, yet the ACD measurements differ between both instruments. Based on published data and our experience, the axial length from the three instruments (IOLMaster, Lenstar LS 900 and OA 1000) is interchangeable, but the ACD measurements and keratometry differ.

An overview of the currently available PCI based optical biometry instruments is presented in Table 1. For comparison we have included the ACMaster (Zeiss AG, Jena, Germany) which is an instrument similar to the IOLMaster yet designed for anterior segment measurements. Unfortunately, production of the ACMaster has been recently discontinued.

Table 1.

Currently available optical biometers utilizing partially coherent light.

	Zeiss IOLMaster	Zeiss ACMaster⁎	Haag-Streit Lenstar LS 900	Tomey OA 1000
Corneal radii	x		x
Axial length	x		x	x
Anterior chamber depth	x	x	x	x
Lens thickness		x	x
Corneal thickness		x	x	x
Retinal thickness	(x)		x
White-to-White	x	x	x
Pupillometry	x		x
Visual axis	x	x	x

^⁎Recently discontinued by manufacturer.

Determination of corneal power

Manual or automated keratometers (ophthalmometers) and corneal topographers have been traditionally used to determine corneal power. There is no instrument which can measure refractive power directly. The curvature of the anterior corneal surface is extrapolated from the corneal radius and translated into power using a keratometric index. Keratometric indices are based on models of corneal geometry, especially the correlation between the anterior and posterior corneal radii. Keratometric indices differ from manufacturer to manufacturer. For example, Zeiss favors a value of 1.332, while 1.3375 is commonly used in the US. Using the indices above, the difference in corneal power for the same patient (and corneal radius) between two keratometers will be approximately 0.8 D.

The keratometer index can be problematic during (K-index problem) IOL calculations (Fig. 2). To avoid problems inherent to the keratometric index, the Haigis IOL calculation formula requires corneal radii of curvature in millimetres. However, all ‘American formulas’ (Holladay-1, Holladay-2, HofferQ, SRK II, SRK/T) require keratometry in diopters and assume that the keratometer was set to 1.3375. If the keratometry readings stem from an instrument with the Zeiss calibration (1.332), then a systematic error of nearly 1 D would occur during IOL calculation.

Figure 2.

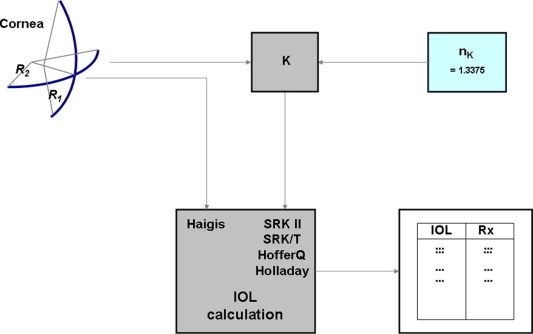
Intraocular lens calculation and keratometer index: the ‘American formulas’ expect K-readings in [diopters] and assume that the keratometer was set to an index of 1.3375; the Haigis formula requires corneal radii of curvature in [mm] for intraocular lens calculation.

The anterior corneal radius is easily accessible for measurement, however the posterior corneal radius could only be measured with the incorporation of modern optical methods such as dynamic Scheimpflug and slit imaging techniques, optical coherence tomography and other methods. Imaging devices for the anterior segment (e.g. Orbscan, Pentacam, Galilei, Sirius, several optical coherence tomographers) enable reproducible measurement of the posterior corneal radius. These instruments display the contours of the anterior and posterior corneal surfaces allowing the derivation of the anterior and posterior apical radii of curvature. Incorporating this data into suitable formulas using Gaussian optics allows the calculation of the corneal power (total power or back vertex power) without resorting to keratometer indices.

Recent studies indicate that the outcomes of corneal power calculation with these new techniques are unsatisfactory. Shammas et al.²³ found that the keratometry values from a Scheimpflug camera did not improve accuracy over auto-keratometer values for routine IOL power calculations. Similarly, Lam¹⁵ reported smaller mean absolute errors after IOL implantation using automated keratometry values compared to Scheimpflug based keratometry. We observed significant differences in total corneal power after myopic LASIK between Pentacam-based values and the results derived from the refractive history method.⁷ Furthermore, we found higher absolute prediction errors for keratometry with the Pentacam (OCULUS Optikgeräte GmbH, Wetzlar, Germany) than with the IOLMaster during IOL calculations for normal eyes [unpublished data].

Calculation procedures for IOL power

A variety of methods are available to determine the necessary IOL power for a given patient including empirical, analytical, numerical or combined procedures. The optical system ‘eye + spectacle glasses’ may be treated by exact ray tracing or as a paraxial approximation, using matrix optics or vergences, considering thick or thin lenses. However it is the classic analytical ‘IOL formulas’ based on Gaussian optics that remain the most popular. For example, these formulas are used for clinical IOL calculation in more than 98% of all cases reported in a recent survey¹⁴ of the ASCRS members (ASCRS, 2008).

All these formulas are based on the same optical approximation – paraxial thin lens optics – they differ in the number and type of variables necessary to derive a value for IOL power. All formulae require axial length and corneal power (or corneal radius) as basic input parameters. Some require additional parameters such as (phakic) anterior chamber depth or lens thickness. Essentially, these factors are required to predict effective lens position. Table 2 presents an overview of the different input parameters of some popular IOL power formulas. Table 2 includes the Olsen formula²⁰ with 5 variables and the Holladay-2 formula with 7 variables. The latter formula – unlike the other ones – has never been published and is only available as part of a software package (Holladay IOL Consultant (HIC), www.hicsoap.com).

Table 2.

Differences between classic IOL formulas: overview of the input variables required by each formula.

	Haigis	HofferQ	Holladay-1	Holladay-2	SRK/T	SRK II	Olsen
K	x⁎	x	x	x	x	x	x
AL	x	x	x	x	x	x	x
ACD	x			x			x
LT				x			x
W-t-W				x			x
Age				x
Rxpre				x

K: corneal power, AL: axial length, ACD: (phakic) anterior chamber depth, LT: thickness of phakic lens, W-t-W: White-to-White diameter, Rxpre: preoperative refraction.

^⁎The Haigis formula requires radii of curvatures in [mm] instead of corneal powers in [D].

Classic ray tracing does not play a role in the clinical IOL calculation with a number of reports finding similar results between ray tracing and the classic IOL formulas.^4,18,11 Ray tracing, however, may be of interest in special cases and certainly continues to be of importance in science, research and development.

Challenging eyes

There is no ‘one-size-fits-all’ or universal formula for all cases of phakic and pseudophakic eyes. The same is true for short and long eyes, for astigmatic eyes or eyes after refractive surgery.

Astigmatic eyes

An IOL calculation for an astigmatic eye can be performed by calculating the steep and the flat meridians separately. However, this can be problematic when the surgeon orders the toric lens from the manufacturer, as there is no current standard accepted by the International Standards Organization (ISO) governing the labeling of toric IOLs. However, an ISO standard will be published in the near future. Astigmatic lenses are characterized not only in the traditional manner by sphere, cylinder and axis, but also by a combination of spherical equivalent with cylinder and axis. For example, an eye that requires 20.0 D in the steep meridian and 23.0 D in the flat meridian then the power notations sph 20.0 cyl 3.0 and sph 21.5 cyl 3.0 describe the same toric IOL. In such cases we recommend the use of the manufacturer’s proprietary IOL calculation software (online via a website or offline via a program CD), which usually offers additional information beyond the power calculation itself.

Short and long eyes

It is well-known that the prediction errors of popular IOL formulas are characterized by their dependence on different axial lengths.⁵ The Haigis, HofferQ and Holladay-2 formulas perform very well for short eyes. For long eyes Haigis, Holladay-1 and Holladay-2⁸ are more appropriate. SRK I is considered outdated and SRK II should not be used for short eyes.

Weak plus or minus lenses, which are required for extremely long eyes, should be characterized by different lens constants. High power lenses for extremely short eyes are custom-made and it is advisable to determine the power calculation in close cooperation with the IOL manufacturer.

Phakic IOLs

The IOL power calculation for phakic eyes is usually less critical than for aphakic eyes. Although precise measurements of the axial length are mandatory for aphakic eyes, it is not required for the calculation of phakic IOLs. Additionally, an accurate preoperative refraction is critical as the correction is implanted inside the eye.

We recommend the use of the manufacturers’ software for the calculation of phakic lenses. In addition to the IOL calculation, these programs offer other valuable information such as the critical distance between the lens and corneal endothelium or warnings for shallow anterior chamber depth.

Eyes that have undergone refractive surgery

In the case of post-refractive surgery eyes, one formula cannot address all cases. The problem of IOL calculation in eyes that have undergone laser vision correction (LVC) can be distilled down to the size of the optical zone, the measurement instruments used and the IOL formulas applied.⁶ Consequently, specific corrections are necessary for these factors. Additionally these factors depend on time, since treatment modalities as well as clinical measurement instruments change with time. Optical zones, for example, have become larger over time thus reducing the error in keratometry due to small optical zones. Therefore, newer formulas for eyes that have undergone previous laser vision correction are likely on the horizon.

Numerous publications on this topic are present in peer reviewed literature. The published methods for IOL calculation after refractive surgery may be roughly classified based on whether historical patient data are necessary for IOL calculation or whether current measurements suffice. The latter are clinically the most relevant cases, as historical patient data are often not available.

Formulas that do not require historical data include the R-factor method by Rosa and coworkers,²¹ the no-history method by Shammas and Shammas,²² the BESSt formula by Borasio et al.¹ based on the Pentacam and the Haigis-L formula⁶ for the IOLMaster, for which current results will be presented in the following section.

A practical overview of today’s IOL calculation methods for eyes after refractive surgery can be downloaded for free in a spreadsheet (Hoffer–Savini Tool) from Dr. Kenneth J. Hoffer’s website (www.eyelab.com). This spreadsheet is programed with virtually all algorithms that have been currently published. The ASCRS website (www.ascrs.org) is also helpful, offering free online-use of their Post-Refractive Surgery IOL Calculator. This calculator provides a variety of published calculation algorithms for eyes after refractive surgery.

The largest number of clinical cases analyzed to date seems to be from our laboratory. At present we are analyzing 278 post-refractive eyes (partially published⁶) that have undergone IOL implantation. Prior to LVC, 222 eyes were myopic and 56 were hyperopic. The myopic eyes received 35 different types of IOLs implanted by 64 surgeons worldwide; the hyperopic eyes received 13 different types of IOLs implanted by 15 different surgeons. All patients underwent IOLMaster biometry (axial length and ACD) and keratometry. IOL calculation was performed using the Haigis-L formula (included in the IOLMaster software version 4 onwards). Most cases were calculated prospectively.

The mean arithmetic prediction errors were −0.08 ± 0.71 D for the myopic eyes and −0.06 ± 0.77 D for the hyperopic eyes; the respective medians of the absolute prediction errors were 0.37 D and 0.40 D. The percentage predicted to be within ±2 D, ±1 D and ±0.5 D were 98.6%, 82.9% and 59.9% for the myopic eyes respectively and 96.4%, 82.1% and 58.9% for the hyperopic eyes respectively.

For normal eyes, Gale et al.³ proposed a “benchmark standard of 85% of patients achieving a final spherical equivalent within 1 D of the predicted and 55% of patients within 0.5 D should be adopted”. Based on Gale et al.’s³ recommendation, our results for post-refractive surgery cases show that the latter exceed the 55% benchmark for the ±0.5 D group and closely approached the 85% benchmark for the ±1 D group. Hence, the outcomes for challenging eyes are nearly equivalent to those postulated for normal eyes.

Minimizing errors

The accuracy of the preoperative prediction of postoperative refraction is limited by systematic and random errors. Measurement errors spread according to the Gaussian error propagation law. Currently, mean absolute errors of typically 0.4–0.5 D can be achieved under optimized conditions.¹⁹ In individual cases, errors as low as 0.25–0.3 D have been reported.⁸

Using optical biometry and optimized IOL constants, a typical mean arithmetic prediction error (ME) of 0.0 ± 0.5 D is achievable. Without IOL constant optimization to mitigate or eliminate systematic errors, a 1.0 ± 0.5 D ME may result indicating a hyperopic shift of 1 D. With these values it is possible to calculate the percentage of correct refraction predictions within certain limits using the mathematical properties of the Gaussian error function (Table 3). Table 3 indicates that lens constant optimization provides greater benefit as the tolerance of the prediction becomes more stringent. For example, the percentage of correct predictions within ±1 D nearly doubled and the percentage within ±0.5 D more than quadrupled by optimization, while the predictions within ±2 D were mildly affected. These results reinforce the value of optimization of IOL constants.

Table 3.

Typical percentages of correct refraction predictions for state-of-the-art measurement equipment with and without optimization of intraocular lens constants, calculated from the mathematical properties of the Gaussian error function.

	Good surgeon, state-of-the-art measurement techniques, without lens constant optimization	Good surgeon, state-of-the-art measurement techniques, with lens constant optimization
Mean arithmetic error (ME) [D]	ME = 1.0 ± 0.5	ME = 0.0 ± 0.5
Correct refr. predictions within ± 2.0 D [%]	97.73	99.99
Correct refr. Predictions within ± 1.0 D [%]	50.01	95.45
Correct refr. Predictions within ± 0.5 D [%]	15.74	68.27

Refr. denotes refraction.

Summary

With state of the art technology and modern IOL calculation formulas, excellent refractive outcomes can be achieved after IOL implantation in challenging eyes, that approach the benchmarks postulated for normal eyes.