Inter-subject alignment of human cortical anatomy using functional connectivity

Abstract

Inter-subject alignment of functional MRI (fMRI) data is necessary for group analyses. The standard approach to this problem matches anatomical features of the brain, such as major anatomical landmarks or cortical curvature. Precise alignment of functional cortical topographies, however, cannot be derived using only anatomical features.

We propose a new inter-subject registration algorithm that aligns intra-subject patterns of functional connectivity across subjects. We derive functional connectivity patterns by correlating fMRI BOLD time-series, measured during movie viewing, between spatially remote cortical regions. We validate our technique extensively on real fMRI experimental data and compare our method to two state-of-the-art inter-subject registration algorithms. By cross-validating our method on independent datasets, we show that the derived alignment generalizes well to other experimental paradigms.

1. Introduction

Group analysis of fMRI data requires deriving a spatial correspondence across a set of subjects, i.e., the data must be aligned, or registered, into a common coordinate space, sometimes referred to as spatial normalization (Gholipour 2007). Inter-subject registration enables one to identify “equivalent” brain locations across a population. Most current approaches derive an anatomical equivalence by matching anatomically-defined features. For example, Talairach normalization (Talairach and Tournoux 1988) performs piecewise-affine alignment to a template based on the location of major anatomical landmarks, including the anterior commissure (AC) and the posterior commissure (PC). More advanced techniques utilize higher-resolution features and employ non-rigid transformation models to better account for inter-subject variability, such as free-form deformations (Rueckert et al. 1999) or diffeomorphic demons (Vercauteren et al. 2007). Alternatively, surface-based techniques explicitly model the topology of the cortical surface and match cortical features, such as local cortical convexity (Fischl 1999; Yeo et al. 2010), which afford alignment of major sulci and gyri. Although current techniques can provide highly accurate anatomical alignment, functional variability of anatomically corresponding areas across subjects has been widely reported (Watson 1993; Tootell 1995). For example, the location of the visual motion area, MT, can vary by more than 2cm (Watson 1993; Tootell 1995). As a result, it is common to spatially smooth the fMRI data from each subject prior to a group analysis, but this has the adverse effect of blurring both cortical boundaries between areas and functional topographies within areas.

We decided to develop alignment methods that are based on measures of local brain function, rather than anatomy (Sabuncu, Singer et al. 2010; Conroy et al. 2009; Haxby et al. 2011). The algorithms of Sabuncu, Singer et al. (2010) – function time-series alignment (FTSA) – and Haxby et al. (2011) – hyperalignment – derive inter-subject functional correspondence by maximizing the inter-subject correlation of fMRI time-series elicited while watching a movie (Hasson et al. 2004; Bartels and Zeki, 2004). FTSA achieves this correspondence with a rubber-sheet warping of cortex that preserves cortical topography. Hyperalignment, by contrast, aligns functional data into a common, high-dimensional space. However, FTSA and hyperalignment are effective only for cortical structures that produce a similar time-locked response to the same stimulus across subjects. Such cross-subject synchrony is found in the extrinsic system, where cortical response is reliably time-locked to the audiovisual stimulus (Hasson 2004, 2009), but is less evident in many prefrontal regions, which are believed to be involved in higher-level cognitive tasks, such as planning and decision-making, and in the so-called default-mode (Grecius et al. 2003; Raichle et al. 2001; Vincent et al. 2006) or intrinsic (Golland et al. 2007a) system. In a repeated movie-viewing experiment (Golland 2007a), in which subjects were shown the same movie segment in two different sessions, the response elicited in the intrinsic system was not even reproducible within each subject. Consistent with these results, the improvement of alignment of function using FTSA (Sabuncu, Singer et al. 2010) was restricted mostly to the extrinsic system, including visual and auditory areas of the occipital, temporal, and parietal lobes.

In an effort to learn a functional correspondence that is valid across a greater expanse of cortex, we seek to extract features that localize function beyond the extrinsic system. To this end, we developed a new algorithm, functional connectivity alignment (FCA), which matches intra-subject patterns of cortical functional connectivity. Here, functional connectivity refers to intra-subject temporal synchrony of functional response between remote regions of the brain (Friston 1994; Horwitz 2003), which is estimated by correlating the functional time-series between pairs of cortical nodes within a subject. Thus, at a high level, FCA is distinct from FTSA (Sabuncu, Singer et al. 2010) in that there is no direct comparison of functional time-series response across subjects. Rather, comparisons are made based on the similarity of patterns of interactions between functional loci.

A number of recent studies motivate our approach. In particular, Golland et al. (2007a) found that the intrinsic system forms a functionally-connected network that is spatially disjoint from the extrinsic system. These results were subsequently replicated in a purely unsupervised approach, in which k-means clustering was used to divide the brain into two distinct cortical networks (Golland et al. 2008). The exploratory technique identified remarkably similar networks to the extrinsic and intrinsic system that were also consistent across subjects.

Other studies have further validated the use of functional connectivity for functional localization. Golland et al. (2007b) further subdivided the intrinsic and extrinsic systems into more specific cortical networks using an unsupervised hierarchical clustering approach. Driven by within-subject similarity of fMRI response during movie viewing, the clustering was able to identify visual and motor areas within the extrinsic system, while also subdividing the intrinsic system into 2 distinct spatially coherent networks that were consistent across subjects. Others (Cohen et al. 2008; Yeo et al. 2011) have analyzed resting state functional connectivity to segment functional areas of cortex (Cohen et al. 2008) and identify networks of areas, including default-mode networks (Yeo et al. 2011). In this vein, independent component analysis (ICA) is quickly becoming a popular technique for identifying these networks. For example, applying spatial ICA to resting state data has been shown to identify spatially consistent cortical networks across subjects that correspond to functional networks, such as visual and sensory-motor cortical areas (Beckmann et al. 2005). There is also the potential for identifying temporal relationships between functional networks identified by ICA, termed functional network connectivity (FNC) (Jafri et al. 2008; Calhoun et al. 2008). FNC has been used to identify network differences between schizophrenic and control populations (Jafri et al. 2008).

We compute functional connectivity between pairs of cortical nodes rather than between larger anatomical regions of interest. Thus, for each cortical node we calculate a vector of connectivities with all other cortical nodes. The alignment is driven by an objective that seeks to minimize the difference between functional connectivity vectors of corresponding cortical nodes across subjects. We do so by learning a dense-deformation field on the cortex of each subject that is regularized to preserve cortical topology (Fischl 1999; Sabuncu, Singer et al. 2010).

We apply FCA to real experimental fMRI datasets. We offer a detailed comparison with the anatomical registration technique of (Fischl 1999) based on matching cortical curvature patterns, and to FTSA (Sabuncu, Singer et al. 2010), which aligns by maximizing the inter-subject correlation of fMRI time-series.

2. Methods

2.1 Data acquisition

Subjects

Ten healthy young subjects (5 men, mean age = 23 yrs) participated in two fMRI studies (a movie stimulus and a face and object stimulus). All subjects gave written informed consent.

fMRI image acquisition

Blood oxygen level dependent (BOLD) images were obtained with echo-planar imaging using a Siemens Allegra head-only 3T scanner (Siemens, Erlangen, Germany) and head coil.

Movie stimulus

In the first fMRI study, subjects watched Raiders of the Lost Ark in two sessions. Subjects watched the first 55:03 of the movie and after a short break, during which subjects were taken out of the scanner, the second 55:30 of the movie was shown. Subjects were instructed to simply watch and listen to the movie and pay attention. The movie was projected with an LCD monitor onto a rear projection screen that the subject could view through a mirror. The soundtrack for the movie was played though headphones using an air conduction system.

For the movie stimulus, whole brain volumes of 48 3mm thick sagittal images (TR = 3000, TE = 30 ms, Flip angle = 90, 64 × 64 matrix, FOV = 192 mm × 192 mm) were acquired continuously through each half of the movie (1101 volumes for part 1, 1112 volumes for part 2).

Face and object stimulus

In the second fMRI study, subjects viewed static pictures of four categories of faces (human female, human male, monkeys, and dogs) and three categories of objects (houses, chairs, and shoes) in a block design experiment. Images were presented for 500 ms with 2000 ms inter-stimulus intervals. During each block, sixteen images from one category were shown, and subjects performed a one-back repetition detection task. Repetitions were different pictures of the same face or object. Blocks were separated by 12 s blank intervals. One block of each stimulus category was presented in each of eight runs.

For the face and object study, partial brain volumes were acquired, consisting of 32 3 mm thick axial images (TR = 2000, TE = 30 ms, Flip angle = 90, 64 × 64 matrix, FOV = 192 mm × 192 mm) that included all of the occipital and temporal lobes and all but the most dorsal parts of the frontal and parietal lobes. 192 volumes were obtained in each of eight runs.

Structural MRI image acquisition

High-resolution T1-weighted images of the entire brain were obtained in each imaging session (MPRAGE, TR = 2500 ms, TE = 4.3 ms, flip angle = 8°, 256 × 256 matrix, FOV = 256 mm × 256 mm, 172 1 mm thick sagittal images). Additional T1-weighted MPRAGE images were available for some subjects from unrelated experimental sessions.

2.2 fMRI data preprocessing

Movie fMRI data

Preprocessing of the movie fMRI data began with correcting between-scan head movements (3dVolreg in AFNI, Cox, http://afni.nimh.nih.gov), then reducing extreme values (3dDespike in AFNI). Movement-related artifacts were further suppressed by regressing the time-series data against the motion parameters calculated in the motion-correction step (3dDeconvolve in AFNI). We then calculated the residuals around the model of movement-related signal changes. The data were then low- and high-pass filtered to remove temporal variation with frequencies higher than 0.1 Hz and lower than 0.00667 Hz (3dFourier in AFNI). High pass filtering removes low temporal frequency changes with periods longer than 150 s. Low pass filtering temporally smoothes fluctuations with frequencies higher than the hemodynamic response function. Global variations in signal were factored out by first calculating the mean whole brain intensity for each timepoint then regressing the time series against the whole brain means (3dmaskave then 3dDeconvolve in AFNI). The residuals around variation that correlated with whole brain means were used for the analysis of between-subject synchrony of neural activity. By removing the effect of global variation, the data reflects only local variation (Hasson et al. 2004). The data were not smoothed spatially.

Face and object fMRI data

Preprocessing of the visual categories fMRI data began with correcting between-scan head movements (3dVolreg in AFNI, Cox, http://afni.nimh.nih.gov), then reducing extreme values (3dDespike in AFNI). In the next step, we removed the mean, linear and quadratic drifts from each time series and further reduced movement-related artifacts by regressing the time-series data against the motion parameters that were calculated in the motion-correction step (3dDeconvolve in AFNI). We then calculated the residuals around the calculated model of signal changes that could be related to these factors.

We corrected for rigid-body registration errors between the fMRI datasets acquired from each subject by aligning the average brain volume of the motion-corrected EPI data from each movie session to that of the face/object study (3dTstat and 3dVolreg in AFNI). We then applied these transformations to the time-series data of the movie sessions (3drotate in AFNI).

2.3 Building a model of the cortical surface from the structural MRI

The process of creating a triangular mesh of each subject’s cortical surface was carried out using FreeSurfer (Fischl, http://surfer.nmr.mgh.harvard.edu). First, the structural T1-weighted MRI images for each subject were brought into alignment by an affine transformation and then averaged to produce a high-quality, low noise image. The resultant three-dimensional brain image was then registered to the Talairach atlas using affine transformations, intensity-normalized, and segmented into gray matter (cortical) and white matter (non-cortical) regions. Cortical regions were fit with a tessellated triangular mesh and inflated to a sphere, providing a simplified 2D (spherical) coordinate system. A secondary anatomical alignment step then registers the spherical model of cortex to a spherical atlas based on cortical curvature (Fischl). The meshes were re-sampled using standard numbering, uniformly on the sphere, at 2 mm resolution (MapIcosahedron in SUMA, Saad, http://afni.nimh.nih.gov/afni/suma.) The re-sampled meshes provide a common spherical grid for comparing cortex across subjects.

2.4 Placing fMRI data on the cortical surface

Since the volumetric fMRI data from each of the movie sessions were re-sampled into the coordinate system of the face/object study (see pre-processing), the fMRI data from all 3 experiments (both halves of the movie data and the face and object data) were placed on the cortical surface by first registering the structural image acquired during the face/object study that is aligned to the functional data to the high-resolution structural image used to derive the cortical surface model (3dvolreg in AFNI). Functional data recorded at locations falling on or between corresponding inner and outer (pial) cortical mesh nodes were then averaged and associated with that standard mesh node number (3dVol2Surf in SUMA). Hence, each node in the anatomically aligned cortical mesh (2mm resolution, 36002 nodes) is associated with a functional time-series.

2.5 Defining the extrinsic and intrinsic systems

In order to evaluate alignment improvement in the extrinsic and intrinsic systems, we developed regions of interest (ROI)’s for each of these systems. A cortical node was deemed in the extrinsic system if its average inter-subject time-series correlation exceeded a threshold (r > +0.1) under either of the functional registration algorithms. Basing the ROI criterion on the two functional registration algorithms rather than on the anatomical registration method lowers the risk that regions of the extrinsic system are mislabeled due to anatomical registration errors. Additionally, the inter-subject correlation criterion was estimated on the first half of the movie dataset, which also served as the training dataset for the functional registration techniques.

An ROI for the intrinsic system was constructed by identifying the cortical nodes whose functional time-series correlated (as computed on the training dataset) with either the temporoparietal junction (TPJ) or the medial prefrontal cortex (MPFC). To accomplish this, seed time-courses were developed for the TPJ and MPFC by averaging the functional time-series located within a disk of radius 6mm around the center of each region (Talairach coordinates of ROI centers: (−47, −61, 23) and (52, −53, 20) for left- and right-hemispheres of TPJ, respectively; (6, 53, 13) for MPFC (Gobbini et al. 2007)). A cortical node was included in the intrinsic system if its functional time-series correlation with any of the seed time-courses exceeded a threshold (r > +0.2). To ensure that the ROI’s for the extrinsic system and intrinsic system were disjoint, any cortical nodes that were selected by both systems were only included in the extrinsic system.

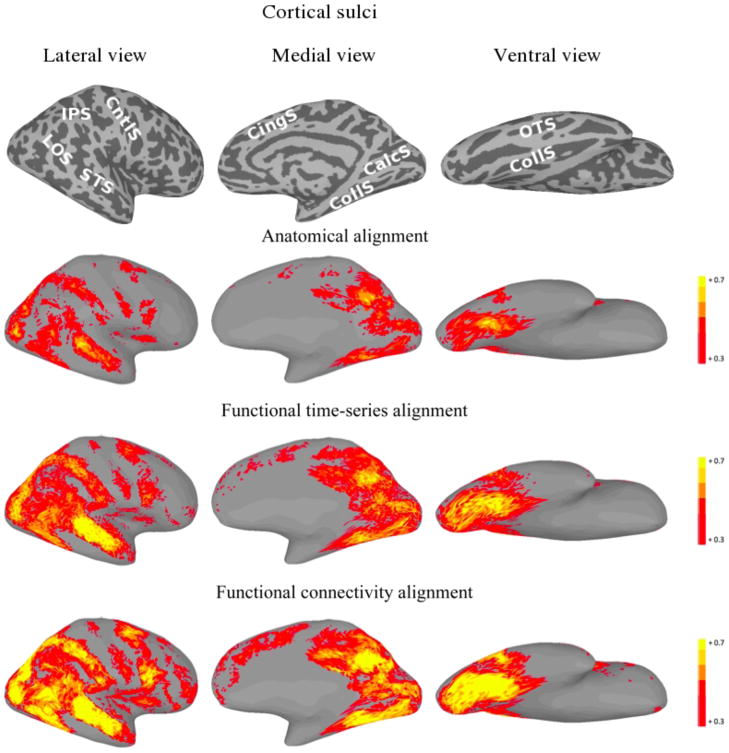
This method found 31,726 cortical nodes (approximately 44% of cortex) to be in the extrinsic system, covering much of posterior cortex, including occipital and ventral-temporal regions of cortex. In total, 13,711 cortical nodes (approximately 19% of cortex) were defined to be in the intrinsic system. Figure 1 shows surface plots of both the extrinsic and intrinsic systems.

Figure 1.

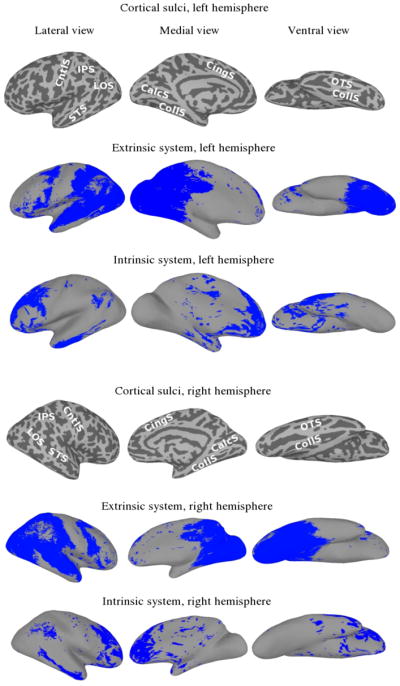
Extrinsic and intrinsic systems. For reference, images of the sulcal anatomy on the inflated cortical surfaces are provided (IPS—intraparietal sulcus; LOS—lateral occipital sulcus; STS—superior temporal sulcus; CntlS—central sulcus; CingS—cingulate sulcus; CalcS—calcarine sulcus; CollS—collateral sulcus; OTS—occipitotemporal sulcus).

2.6 Functional connectivity alignment: Approach

Since the purpose of this paper is to provide a detailed analysis of results of the functional connectivity algorithm, as well as a quantitative comparison with other existing registration techniques, only a brief summary of the algorithm is provided here. A more detailed description of the technical aspects of the algorithm is available in Conroy et al. (2009, 2010).

The registration is driven by an objective function that seeks to minimize differences between functional connectivity patterns across subjects. Conceptually, a functional connectivity vector is computed at each cortical node, which contains the correlation between the time-series at that node and the time-series of all other nodes in the surface model. This information can be summarized by a functional connectivity matrix C, whose (i,j)^th element contains the time-series correlation between nodes i and j. Given a matrix T whose i^th column contains the zero-meaned time-series from the i^th cortical node, C may be computed as:

$$C={DT}^{T}TD$$

where D is a diagonal matrix that standardizes the time-series to have unit norm.

Given two datasets – a reference with connectivity matrix C_R, and a floating dataset with connectivity matrix C_F, the goal is to impose a spatial transformation, denoted by g, on the floating dataset so as to match C_F to C_R. In this case, the reference corresponds to an average model derived from the population, while the floating dataset corresponds to a particular subject. Upon warping the floating subject by the transformation g, its connectivity matrix is altered, which we represent by C̃_F. For the moment, we set aside the specific parameterization of the transformation and how the connectivity matrix depends on g. The optimal transformation then minimizes the following alignment objective:

$$\widehat{g}=arg\underset{g}{min}{\Vert {\stackrel{\sim }{C}}_F-C_R\Vert }_F^2+\lambda Reg(g)$$

where ${\Vert C\Vert }_F^2={\displaystyle \sum _i}{\displaystyle \sum _j}{C}_{ij}^2$ denotes the Frobenius norm of a matrix, and the second term denotes a regularization on the warp field that serves to preserve the cortical topology. This alignment objective is fundamentally different from that used in the FTSA algorithm of (Sabuncu, Singer et al., 2010). Although both are derived from fMRI data, FTSA directly compares the time-series across subjects, while the FCA approach above compares patterns of functional connectivity as measured by within-subject correlations between pairs of cortical nodes.

In order to optimize the alignment objective, the dependence of the warped connectivity matrix C̃_F on the transformation g must be made explicit. Doing so requires specifying how the cortical time-series are warped: once we compute the warped time-series data matrix T̃_F, the warped connectivity matrix follows from above as ${\stackrel{\sim }{C}}_F=\stackrel{\sim }{D}{\stackrel{\sim }{T}}_F^T{\stackrel{\sim }{T}}_F\stackrel{\sim }{D}$. Our approach interpolates the time-series by a linear interpolation scheme with a spherical kernel. Specifically, let p₁,…, p_N denote the pre-warped spatial coordinates of the N cortical nodes, g(p₁),…,g(p_N) as their locations after warping, and let t₁,…, t_N be the original time-series data. Then the post-warp time-series of cortical node j is given by $\stackrel{\sim }{t_j}={\displaystyle \sum _i}{t}_i{\mathrm{\Phi }}_i(g(p_j))$, where Φ_i(g(p_j)) is a radial basis function that is a monotone decreasing function of the distance between p_i and g(p_j) (Conroy et al. 2009). By assembling these interpolation coefficients into a matrix A with A_ij = Φ_i(g(p_j)), we may compute the warped time-series data matrix as T̃_F = T_FA. Thus, the post-warp connectivity matrix is given by:

$${\stackrel{\sim }{C}}_F=\stackrel{\sim }{D}{A}^T{T}_F^T{T}_{F}A\stackrel{\sim }{D}$$

where, again, D̃ is a diagonal matrix that standardizes the time-series to unit norm.

Note that, at a spatial resolution of 2mm, the cortical surface model contains approximately 72,000 nodes across both hemispheres. As a result, computing the registration objective would require storage and computation of on the order of 72,000² connectivity values. Despite this, the algorithm is computationally and memory efficient by utilizing low-rank matrix factorizations. In fact, the alignment objective is computed without ever forming the large connectivity matrices. To illustrate, let $T_F=U_F{\mathrm{\sum }}_F{V}_F^T$ be a singular value decomposition of the time-series data matrix, where U_F and V_F are orthogonal matrices whose columns comprise the left- and right-singular vectors, and Σ_F is a diagonal matrix of positive singular values. Note that the number of columns in U_F and V_F is equal to the rank of T_F, which is limited to the number of temporal acquisitions in the experiment (usually much smaller than the number of cortical nodes). Given this decomposition, the post-warp connectivity matrix may be expressed as:

$${\stackrel{\sim }{C}}_F=(\stackrel{\sim }{D}{A}^T{V}_F){\mathrm{\sum }}_F^2(V_A^{T}A\stackrel{\sim }{D})$$

Thus, a low-rank representation for C̃_F is obtained by filtering the right singular vectors of T_F. In practice, we further reduce the rank of T_F and C̃_F by employing a principal components analysis (PCA) on T_F that preserves a certain percentage of the variance (usually around 95%). Given a similar low-rank representation for the reference connectivity matrix, $C_R=V_R{\mathrm{\sum }}_R^2{V}_R^T$, the alignment objective can be expressed in terms of linear algebraic operations on the low-dimensional Σ_F, V_F, Σ_R, V_R, instead of the high-dimensional connectivity matrices (Conroy et al., 2009).

The choice of transformation space over which the registration optimization is performed is very important, and depends on the type and variability present in the data. Correcting for inter-subject variability requires the use of highly nonlinear warping models (Ardekani et al. 2004; Bajcsy 2003). We follow the dense-deformation approach taken in (Fischl et al. 1999), and also pursued in (Sabuncu, Singer et al. 2010), in which each cortical node is allowed to move freely in two dimensions along the spherical model. However, although such nonlinear models are capable of correcting inter-subject variability locally, they also have the potential to over-fit due to the many degrees of freedom. As a result, the warping model is regularized by metric distortion and folding energy terms that preserve cortical topology. The metric distortion term penalizes warps that greatly stretch or compress the cortical surface, while the folding energy term ensures the final warp to be invertible by preventing folds (Fischl et al. 1999). This model was selected both due to its successful application to registration in the past (Fischl et al. 1999; Sabuncu, Singer et al. 2010), as well as to offer a consistent and fair comparison in the Results section.

A frequent problem in registration is that the optimization objective function is not convex, so that iterative solution methods, such as gradient descent, are only guaranteed to find a locally optimal solution. As a result, the initialization to our algorithm is an important choice. Similar to (Sabuncu, Singer et al., 2010), we find that the best results are obtained by initializing with an accurate anatomical alignment. Moreover, recent studies have shown that surface-based anatomical alignment techniques are capable of reducing variability of functional areas such as V1 (Fischl et al. 2008; Hinds et al. 2009; Yeo et al. 2010). We therefore initialize our algorithm from the anatomical alignment technique of Fischl et al. (1999). To further avoid local optima, we employ a multi-resolution strategy, in which the alignment is first performed at a lower (smoothed) spatial resolution, which is progressively refined at higher spatial resolutions until convergence.

As implemented in MATLAB, the algorithm requires about 20 minutes for each pairwise alignment on an Intel 3.8GHz Nehalem quad-core processor with 12GB RAM.

2.7 Validation testing

Cross-validation was used to compare the functional registration techniques with the anatomical registration technique in an unbiased way. We apply the derived warps to independent datasets. Unless stated otherwise, the first half of the movie dataset was used as training data for the functional registration techniques, with the second-half of the movie dataset and the face and object stimuli dataset used for evaluation of alignment results. This procedure allows us to test the ability of the functional correspondence to generalize to independent functional datasets.

We used nearest neighbor interpolation when applying the derived warps in order to prevent the comparison of results between anatomical alignment, functional time-series alignment, and functional connectivity alignment from bias due to the inherent smoothing that is incurred by other interpolation kernels

3. Results

We validate the FCA algorithm by application on real experimental fMRI datasets and compare it with the anatomy-based registration technique (Anat) of (Fischl et al. 1999), and the FTSA algorithm of (Sabuncu, Singer et al. 2010). Results for the functional registration algorithms are always calculated on an independent dataset from the one used to derive the correspondence. Unless specified otherwise, the first half of the movie data is used as training data for the functional alignment algorithms.

We used a number of metrics for evaluating and comparing the registration algorithms. They are briefly summarized here:

• Inter-subject correlation of time-series (ISC). This measure directly compares the similarity (Pearson correlation) of time-series across subjects, and is a useful measure of functional alignment in the extrinsic system of cortex, where cortical response is expected to be temporally synchronized with the experimental stimulus (Hasson 2004, 2009).

• Inter-subject correlation of functional connectivity vectors (FCC). This measure compares the similarity (Pearson correlation) of functional connectivity vectors for corresponding nodes across subjects and can be used to measure functional alignment in both the extrinsic and intrinsic systems of cortex.

• Between-subject classification of visual categories. Multivariate pattern (MVP) classification of brain states (Haxby et al. 2001, 2011; LaConte et al. 2005; Pereira et al. 2009; Norman et al. 2006; Haynes and Rees 2005; Kamitani and Tong 2005; Kay et al. 2008; Kriegeskorte et al. 2006; Mitchell et al. 2004,2009; Poldrack et al. 2010) attempts to decode the presented stimulus from the distributed pattern of cortical activity. The classification algorithm learns from a set of labeled data, in which the class of stimulus is known at each point in time, and the cortical response from each voxel is treated as a feature. In most cases, due to inter-subject variability in the fine structure of functional topographies, the data for each subject is classified based on a classifier model trained on that subject’s own data. An interesting validation technique for inter-subject alignment, first presented in (Haxby 2011), is to apply the classifier derived from the data of a group of aligned subjects to the data of a held-out subject, which has also been aligned to the group using an independent dataset. The cross-validation accuracy of the classifier on this held-out subject tests whether the inter-subject correspondence successfully aligns features that carry relevant information that discriminates among cognitive states.

• Across-stimulus alignment. While FTSA explicitly relies on temporal synchrony of the stimulus across subjects, the temporal dimension is removed in FCA. If functional connectivity maps are fairly stationary when averaged over a long time window of movie-viewing, then it should be possible to align one subject’s brain to another using the fMRI data from different segments of the movie. Otherwise, it may be that functional connectivity alignment is driven more by connectivity patterns that are non-stationary and highly stimulus-dependent. We test this directly by performing an across-stimulus alignment experiment, in which subjects are aligned across different windows of the movie viewing dataset.

3.1 Inter-subject correlation of time-series (whole brain)

Spatial maps of ISC were computed by calculating the mean correlation between the time-series of each subject and the mean time-series of the other nine subjects at corresponding cortical nodes. The ISC for each node is the average of all pairwise between-subject correlations. An ISC > 0.10 was considered significant. The mean ISC was computed by averaging ISC values over all cortical nodes.

For FTSA, the cross-validated improvement over anatomical alignment in mean ISC on the second-half of the movie dataset was 33% (from +0.0743 to +0.0985, p < 0.001), with a 39% increase in the number of significant ISCs (from 20,223 to 28,072). For FCA mean ISC on the second half of the movie dataset improved by 31% (from +0.0743 to +0.0973, p < 0.001), with a 36% increase in the number of significant inter-subject correlations (from 20,223 to 27,469). The increases in mean ISC under FTSA and FCA were not significantly different (p > 0.3)

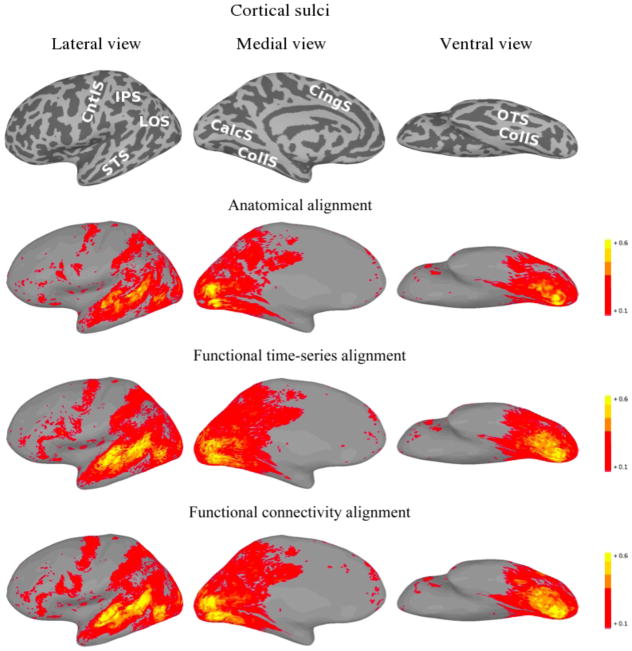
For each of the three alignment methods, Figures 2 and 3 present cortical surface plots of ISC on the second half of the movie datasets for the left and right hemispheres, respectively.

Figure 2.

Left hemisphere plots of average inter-subject time-series correlation for the second half of the movie under various alignments. For the function-based alignments, the first half of the movie session was used as the training set. The top images show the sulcal anatomy on the inflated cortical surfaces (IPS—intraparietal sulcus; LOS—lateral occipital sulcus; STS—superior temporal sulcus; CntlS—central sulcus; CingS—cingulate sulcus; CalcS—calcarine sulcus; CollS—collateral sulcus; OTS—occipitotemporal sulcus).

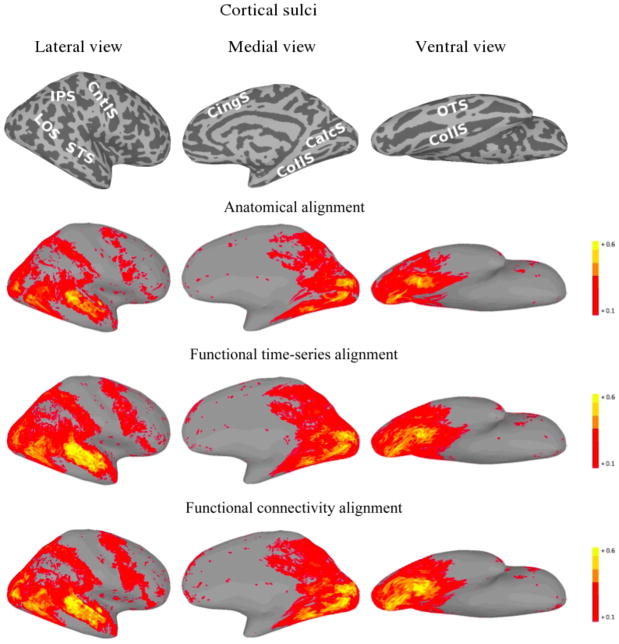
Figure 3.

Right hemisphere plots of average inter-subject time-series correlation for the second half of the movie under various alignments. For the function-based alignments, the first half of the movie was used as the training set. The top images show the sulcal anatomy on the inflated cortical surfaces (IPS—intraparietal sulcus; LOS—lateral occipital sulcus; STS—superior temporal sulcus; CntlS—central sulcus; CingS—cingulate sulcus; CalcS— calcarine sulcus; CollS—collateral sulcus; OTS—occipitotemporal sulcus).

3.2 Inter-subject correlation of time-series (extrinsic and intrinsic systems)

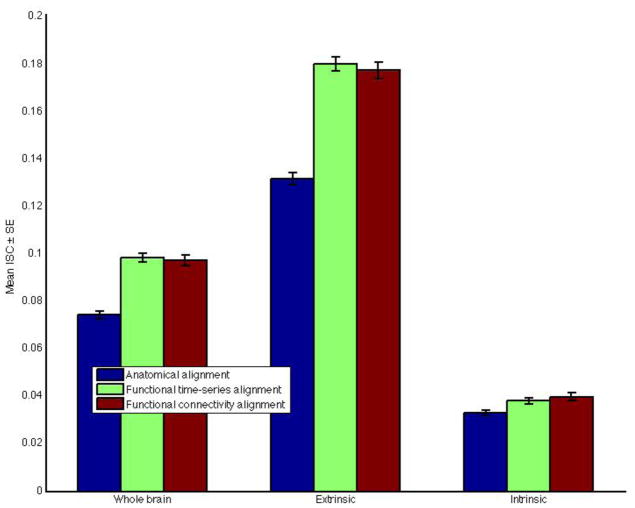
To differentiate the spatial extent of the improvement in ISC, we also calculated ISC results restricted to the extrinsic and intrinsic systems. Under FTSA, mean ISC in the extrinsic system increased by 37% (from +0.1316 to +0.1802, p < 0.001), while the mean improvement was 35% (from +0.1316 to 0.1775, p < 0.001) under FCA.

By contrast, mean ISC in the intrinsic system was substantially lower than in the extrinsic system (p < 0.001) but, nonetheless, increased significantly under both FTSA (15%, from +0.0330 to +0.0381, p < 0.001) and FCA, (20%, from +0.0330 to +0.0398, p < 0.001).

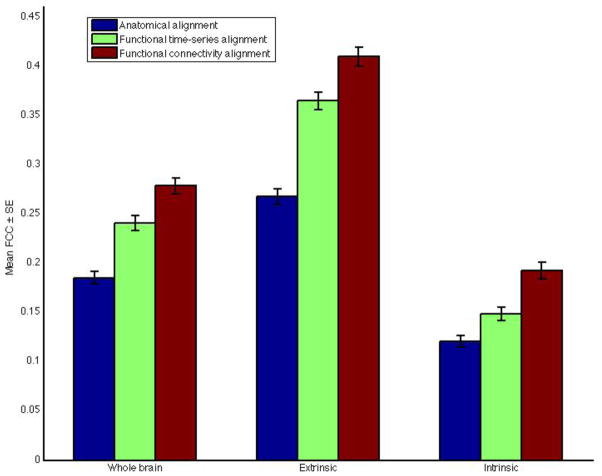
Mean ISC improvements under the three alignments restricted to the various brain systems are summarized in Figure 4.

Figure 4.

Inter-subject correlation of time-series results restricted to different brain systems and under various alignments.

3.3 Inter-subject correlation of functional connectivity vectors (FCC) (whole brain)

The fMRI time-series for each cortical node was correlated with those from all other cortical nodes within a subject, resulting in a functional connectivity vector for that node. For a given alignment method, spatial maps of FCC were computed by calculating the mean correlation between functional connectivity vectors of each subject and the mean functional connectivity vector of the other nine subjects at corresponding cortical nodes. FCC for each node is the average of all pairwise between-subject correlations. The mean FCC was computed by averaging the FCC values over all cortical nodes.

For FTSA, the cross-validated improvement over anatomical alignment in mean FCC on the second-half of the movie dataset was 30% (from +0.185 to +0.241, p < 0.001). For FCA, the cross-validated improvement over anatomical alignment in mean FCC was 51% (from +0.185 to +0.279, p < 0.001), which was a significantly greater increase than that for FTSA (p < 0.001).

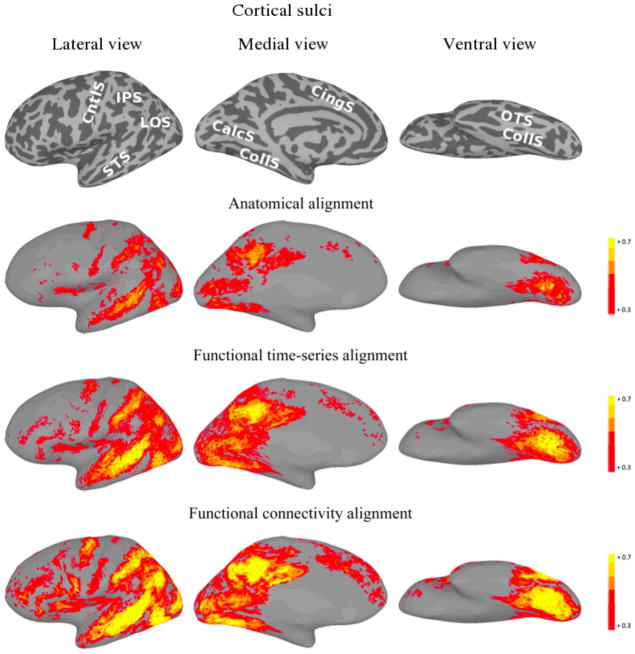
For each of the three alignment methods, Figures 5 and 6 present cortical surface plots of FCC on the second half of the movie datasets for the left and right hemispheres, respectively.

Figure 5.

Left hemisphere plots of average inter-subject functional connectivity vector correlation for the second half of the movie under various alignments. For the function-based alignments, the first half of the movie was used as the training set. The top images show the sulcal anatomy on the inflated cortical surfaces (IPS—intraparietal sulcus; LOS— lateral occipital sulcus; STS—superior temporal sulcus; CntlS—central sulcus; CingS— cingulate sulcus; CalcS—calcarine sulcus; CollS—collateral sulcus; OTS—occipitotemporal sulcus).

Figure 6.

Right hemisphere plots of average inter-subject functional connectivity vector correlation for the second half of the movie under various alignments. For the function-based alignments, the first half of the movie was used as the training set. The top images show the sulcal anatomy on the inflated cortical surfaces (IPS—intraparietal sulcus; LOS— lateral occipital sulcus; STS—superior temporal sulcus; CntlS—central sulcus; CingS— cingulate sulcus; CalcS—calcarine sulcus; CollS—collateral sulcus; OTS—occipitotemporal sulcus).

3.4 Inter-subject correlation of functional connectivity vectors (FCC) (extrinsic and intrinsic systems)

To differentiate the spatial extent of mean FCC improvement, as well as to evaluate alignment improvement in the intrinsic system, we computed cross-validated mean FCC confined to the extrinsic and intrinsic systems. Under FTSA, mean FCC in the extrinsic system increased by 36% (from +0.2680 to +0.3654, p < 0.001), while the mean improvement was significantly larger under FCA (53%, from +0.2680 to +0.4101, p < 0.001; significantly greater than under FTSA, p < 0.001)

While improvement in mean ISC in the intrinsic system was limited, FCA in particular produces a robust improvement in mean FCC. Under FTSA, mean FCC in the intrinsic system increased by 23% (from +0.121 to +0.149, p < 0.001), while under FCA, mean FCC increased by 59% (from +0.121 to +0.192, p < 0.001). In terms of percent increases over anatomic alignment, the advantage of FCA over FTSA was greater in the intrinsic system (36% ± 3%) than in the extrinsic system (17% ± 2%; p < 0.001).

Mean FCC improvements under the three alignments are summarized in Figure 7. Increases in between-subject FCC in the intrinsic system were prominent in medial and lateral prefrontal cortices (Figures 5 and 6).

Figure 7.

Inter-subject correlation of functional connectivity vector results restricted to different brain systems and under various alignments.

3.5 Between-subject classification of visual categories

Seven category classification on the face and object stimuli dataset was run using multi-class linear SVM, with features corresponding to the block-averaged cortical responses in ventral temporal (VT) cortex. Cortical nodes that were included in the analysis were located in VT cortex for at least 5 of the subjects. The classification analysis was run 2 different ways. First, in the within-subject condition, classifiers were built independently for each subject. The accuracy results were cross-validated in a leave-one-out fashion, averaged over all possible data folds, by training the classifier using all but one run and then testing on the left-out run. In the between-subject condition, the classifier for a particular subject was built using the pooled data from all of the other subjects. Again, leave-one-out cross-validation was employed, with the training data corresponding to all but one run from all but one subject, and accuracy was subsequently tested on the left-out subject and left-out run. The test run was left out of the training data to avoid any run-specific effects that could not be accounted for in the within-subject classification analysis. The between-subject classification was performed under each of the alignment conditions to compare how well the relevant features for a cognitive state were brought into register.

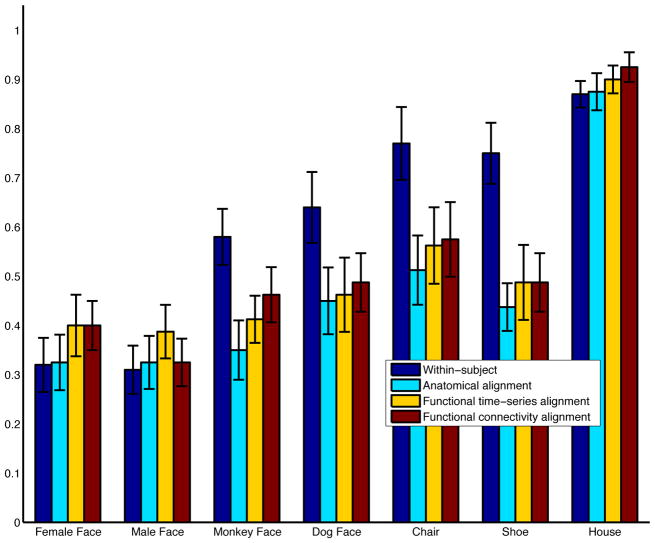
Category-specific classification accuracies (averaged over subjects) are provided in Figure 8, and the confusion matrices are depicted in Figure 9. Average between-subject cross-validation classifier accuracy improves from 0.468 under anatomical alignment, to 0.516 under FTSA (p = 0.07), and to 0.523 under FCA (p < 0.01). Classification accuracies after FTSA and FCA were not significantly different (p > 0.5). Category-specific accuracies under FTSA and FCA are higher than those under anatomical alignment for every category. This shows that the mean improvement in classification accuracy cannot be explained by a surge in classification of one particular category. Although these results are promising, the between-subject classification results under FTSA and FCA are still weaker than those derived independently for each individual (accuracy=0.597). The confusion matrix for within-subject classification is provided in Figure 9a.

Figure 8.

Category-specific between-subject classification accuracies under the various alignments. Within-subject classification accuracies are also included for reference.

Figure 9.

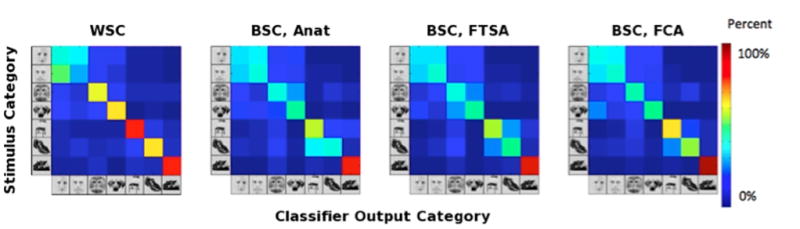
Confusion matrices (averaged over subjects) for 7-category classification. (a) Within-subject classification (WSC); (b) Between-subject classification, anatomical alignment (BSC, Anat); (c) Between-subject classification, FTSA (BSC, FTSA); (d) Between-subject classification, FCA (BSC, FCA).

3.6 Across-stimulus alignment

To test the ability of functional connectivity alignment to successfully register subjects across different stimulus conditions, we performed an across-stimulus alignment experiment. First, in a template generation phase, a leave-one-out template was developed for each subject, by aligning the remaining subjects together using functional connectivity alignment trained on the first 500 TR’s (TR’s 1–500, first 25 minutes) of the first half of the movie viewing experiment. The left-out subject was then aligned to the functionally aligned template in two ways:

1. Within-stimulus alignment: as in our standard approach, the same 500 TR’s of the left-out subject was used by the functional connectivity alignment algorithm to align the subject to the template.

2. Across-stimulus alignment: the last 500 TR’s of the first half of the movie experiment (TR’s 600–1100, last 25 minutes) of the left-out subject was used by functional connectivity alignment to align to the template. The separation of 100 TR’s (5 minutes) between the template data and the left-out subject data in the across-stimulus alignment case ensures that the two datasets are from distinct segments of the movie.

The generalization performance of the within-stimulus and across-stimulus alignments were then compared on the second half of the movie dataset. Specifically, for each subject k, the template warps learned from the first 500 TR’s were applied to the second-half of the movie dataset for the remaining nine other subjects. Then, the warps for subject k learned from the within-stimulus alignment and the across-stimulus alignment were applied to the second-half of the movie dataset for subject k. For the within-stimulus alignment case, cross-validated mean ISC increased, relative to anatomical alignment, from +0.074 to +0.0912, while the mean ISC increased from +0.074 to +0.0913 under the across-stimulus alignment. The strikingly similar results suggest that functional connectivity alignment matches stationary patterns of connectivity that are reproducible across different segments of the movie.

To further analyze the applicability of the across-stimulus alignment, we directly compared the warp derived from the across-stimulus alignment to the warp derived from the within-stimulus alignment for each subject. If the algorithm is indeed insensitive to having a common stimulus presentation across subjects, then the two alignments (within-stimulus and across-stimulus) should produce similar outcomes. To test this consistency, we computed two measures of similarity between the warps: (i) the angle between warp tangent vectors, and (ii) a normalized warp consistency measure. The first measure computes the angle between warp displacement vectors at corresponding locations and provides a measure of similarity in the directionality of the warps. The normalized consistency measure also takes the magnitude of the warps into account. Specifically, if g₁,g₂ are the warps produced by the within-stimulus and across-stimulus alignments, respectively, then the normalized consistency measure (WNC) is given by:

$$\mathit{WNC}=\frac{d(g_1(p_i),g_2(p_i))}{d(g_1(p_i),p_i)+d(g_2(p_i),p_i)}$$

where d is a distance function, and this is computed at all cortical node locations p₁,…,p_N. WNC is bounded to the range [0,1] and is equal to zero only if the warps are identical.

Figure 10 provides histogram distributions of the two warp similarity measures. For the angle θ between warp tangent vectors, the tight distribution centered near θ =0 suggests significant consistency in the warp direction between within-stimulus and across-stimulus alignment. In particular, 87% of the density for θ lies inside π/2, 67% inside π/4, and 44% inside π/8. The WNC distribution in Figure 10b has a mean of 0.38 (s.d.=0.6), with a peak at 0.2.

Figure 10.

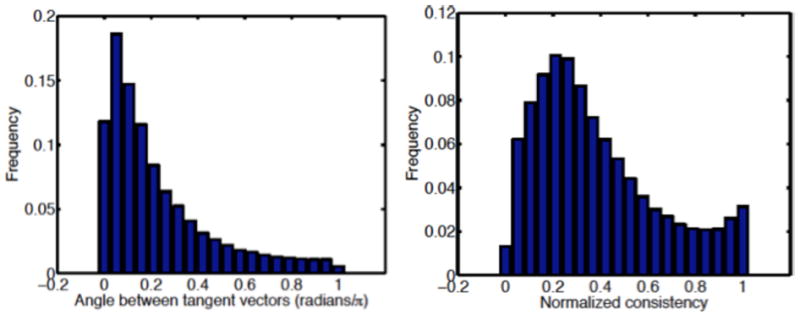
Warp consistency analysis between within-stimulus and across-stimulus alignments. (a) Angle between warp tangent vectors; and (b) Normalized warp consistency measure.

4. Discussion

FTSA and FCA are algorithms that warp cortical topographies to maximize the inter-subject correspondence of indices of local brain function. Whereas FTSA attempts to maximize the correspondence of local, time-varying responses during a task, FCA attempts to maximize the correspondence of functional connectivity vectors. The results presented here show that both algorithms are effective but FCA has distinct advantages over FTSA. FTSA and FCA produced equivalent increases in ISC of time-series, showing that the use of functional connectivity as the basis for alignment also effectively enhances between-subject temporal synchrony of local responses. FTSA and FCA also produced similar, significant improvements in MVP classification of responses to face and object categories, another indication that both find improved alignment of fine-scale topographies of responses to external stimuli. FCA, however, produced significantly larger increases in FCC than did FTSA in both the extrinsic and intrinsic systems. Better performance in the extrinsic system suggests that FCA enhances functional alignment for more than just response synchrony. The advantage of FCA was especially apparent in the functional alignment of the intrinsic system. Finally, FCA makes it possible to align functional topographies based on responses to different stimulus sequences (Section 3.6), whereas FTSA is effective only for aligning responses to identical stimulus sequences.

As expected, the improvement in ISC was limited mostly to posterior regions of cortex with some improvement also in premotor cortices. Increased ISC in posterior cortices reflects the role that these areas play in perception and their central role in the extrinsic system (Raichle et al. 2001; Golland Y et al. 2007, 2008). The increase in ISC in premotor cortices may reflect the role that these areas play in perception of actions (Hasson et al. 2004; Buccino et al. 2004; Montgomery et al. 2007). Although FCA does not explicitly attempt to maximize ISC, it does so effectively. FTSA does attempt to maximize ISC explicitly, and ISC increases in the training data under FTSA (70%) were greater than those under FCA (41%), but this advantage evaporated with generalization testing, indicating that FTSA was overfitting between-subject synchrony. FCA explicitly attempts to maximize FCC and does so more effectively than does FTSA. The enhanced performance of FCA in the extrinsic system, with respect to this validation measure, suggests that FCA is finding a better functional alignment in this system, even though it is not apparent in ISC. FCA did provide better alignment of the functionally-defined, category-selective parahippocampal place area (PPA) than did FTSA (see Supplemental Material).

The intrinsic system is defined as cortical areas whose activity does not show responses to external stimuli that are consistent across subjects or even within individual subjects with repetition of the same stimulus sequence (Raichle et al. 2001; Golland Y et al. 2007, 2008). In the resting state, activity in the default system correlates negatively with activity in the extrinsic system (Fox et al. 2005). During movie viewing, they are uncorrelated (Golland Y et al. 2007), but different regions in the default system are correlated with each other, suggesting that these areas are processing related types of information. Between-subject synchrony in intrinsic areas is enhanced for some stimuli that require more ‘mentalizing’ – understanding the mental states of others, and other evidence exists that these areas may be involved more in social cognition (Frith and Frith, 1999; Gobbini et al. 2007; Mitchell, 2009; Meyer et al. 2012). FCA was more effective than was FTSA at finding a better correspondence between functional topographies in the intrinsic system, an advantage that was especially apparent in medial prefrontal cortex. ISC was only marginally improved in the intrinsic system by both algorithms. FCC, on the other hand, showed large increases that were much larger under FCA than under FTSA. Although not tested here, this result suggests that FCA may be useful for functional alignment of areas that are involved in social cognition.

Currently, many investigations of human cortical organization based functional connectivity uses fMRI time-series collected while subjects are at rest (Biswal et al. 1995; Power et al. 2010; Yeo et al. 2011). A recent study, for example, proposed improving inter-subject registration by aligning two of the robust and reliable functional networks that may be identified by applying ICA on resting state data (Khullar et al. 2011). The resulting alignment generalized well to improving group statistics on a separate auditory oddball task. The FCA algorithm could be applied to such resting state data. We find that we need at least 30 minutes of movie data for good performance of FCA, and data sets with 30 minutes or more of resting state are rare. It would be of interest to test whether FCA performance with resting state data is equivalent to FCA on movie data.

Both FTSA and FCA significantly improved between-subject MVP classification, in which an individual’s responses are classified based on responses observed in other subjects’ brains. This result suggests that some aspects of the topographies of response that support MVP classification of responses to faces and objects can be aligned across subjects with preserved topology. Between-subject MVP classification after FTSA and FCA, however, was still markedly inferior to within-subject classification, suggesting that there are aspects to these topographies that are difficult to align while preserving topology. We have presented a different method for inter-subject alignment of fMRI data, ‘hyperalignment’, that does not preserve topology and showed that this method does afford between-subject MVP classification that is equivalent or even better than within-subject classification (Haxby et al. 2011). This result suggests that there may be fine-scale aspects of functional topographies that are not topologically consistent across brains.

5. Conclusion

We present here a new algorithm, FCA, for inter-subject alignment of functional cortical topographies measured with fMRI. FCA aligns topographies based on patterns of functional connectivity, by contrast with our previous algorithm, FTSA, which aligns topographies based on between-subject synchrony of local responses to a standard stimulus. Results show that FCA is equivalent to FTSA in some respects and superior in others. In particular, FCA provides a better alignment of functional topographies in the intrinsic system and, therefore, may be better for aligning data in studies of social cognition. Moreover, FCA tolerates variation in the stimulus sequence that is used to collect data upon which the alignment is based, allowing one to select different movies for different subjects, according to subject preferences or abilities.

Supplementary Material

01

Supplementary Figure 1: FFA and PPA subject overlap plots under various alignments.

Supplementary Figure 2: Inter-subject FFA overlap plots under various alignments.

Supplementary Figure 3: Inter-subject PPA overlap plots under various alignments.

Supplementary Figure 4: Histogram of within-subject warp displacements under functional connectivity alignment.

Supplementary Figure 5: Warp consistency analysis of functional connectivity alignment and functional time-series alignment, comparing the angle between warp tangent vectors when trained on the first and second half of the movie datasets.

Supplementary Figure 6: Warp consistency analysis of functional connectivity alignment (left) and functional time-series alignment (right), comparing the normalized warp consistency measure when trained on the first and second half of the movie datasets.

Supplementary Figure 7: Warp consistency analysis for the across-stimulus alignment experiment.