Abstract
Actively all-optical tunable plasmon-induced transparency in metamaterials paves the way for achieving ultrahigh-speed quantum information processing chips. Unfortunately, up to now, very small experimental progress has been made for all-optical tunable plasmon-induced transparency in metamaterials in the visible and near-infrared range because of small third-order optical nonlinearity of conventional materials. The achieved operating pump intensity was as high as several GW/cm2 order. Here, we report an ultralow-power and ultrafast all-optical tunable plasmon-induced transparency in metamaterials coated on polycrystalline indium-tin oxide layer at the optical communication range. Compared with previous reports, the threshold pump intensity is reduced by four orders of magnitude, while an ultrafast response time of picoseconds order is maintained. This work not only offers a way to constructing photonic materials with large nonlinearity and ultrafast response, but also opens up the possibility for realizing quantum solid chips and ultrafast integrated photonic devices based on metamaterials.
Metamaterial, an artificial microstructure material constructed by resonant subwavelength electromagnetic units arranged periodically in space, has enormous applications in the field of integrated photonic devices due to its freakish electromagnetic response properties, such as negative refractive index, and plasmon-induced transparency, i.e. plasmonic analogue of classical electromagnetically induced transparency1,2. Especially, tunable plasmon-induced transparency, the central wavelength of the transparency window varying with external parameters, in metamaterials has much flexible and important applications3. The basic idea is to directly adjust the structure parameters of metamaterials, which only reaches a passive tunability4,5,6,7,8. Actively tunable plasmon-induced transparency is more preferred in practice. However, up to now, few achievements have been made in actively tunable plasmon-induced transparency in metamaterials. In 2011, Kurter et al. and Wu et al. reported a thermally tunable plasmon-induced transparency in a metal-superconductor terahertz metamaterial9,10. The response time of thermally tuning method only reaches several seconds order. An ultrafast response time for actively tunable plasmon-induced transparency in metamaterials is possible to be achieved based on third-order nonlinear optical Kerr effect, which provides the perfect basis for the realization of ultrahigh-speed quantum information processing chips11. However, very limited experimental achievements have been made in all-optical tunable plasmon-induced transparency in metamaterials in the visible and near-infrared range. Moreover, the achieved operating pump intensity was as high as several GW/cm2 order because of small third-order optical nonlinearity of conventional nonlinear materials12. Though resonant excitation can be used to reduce the pump intensity, the response time will be slowed down seriously13. Recently, our group achieved all-optical tunable resonances in plasmonic nanostructures based on polycrystalline lithium niobate, having a pump intensity of the order of several MW/cm2 and an response time of the order of tens of picoseconds11,14. Therefore, to date, it is still a great challenge to realize an ultralow-power and ultrafast plasmon-induced transparency in metamaterials with a large tunability.
Here, we report a strategy to realize an ultralow pump intensity and ultrafast response time for all-optical tunable plasmon-induced transparency in metamaterials at the optical communication range. A metamaterial made of periodic arrays of square lattice of gold meta-molecules was coated on a high-conductivity polycrystalline indium-tin oxide (ITO) layer, which was adopted as the third-order nonlinear optical material. Owing to the strong quantum confinement effect provided by nanoscale crystal grains of polycrystalline ITO, the third-order optical nonlinearity of polycrystalline ITO layer is enhanced greatly11. Moreover, under excitation of a femtosecond pump laser with a wavelength at the optical communication range, the hot-electron injection from gold meta-molecules to polycrystalline ITO also offers a huge dedication to the nonlinearity enhancement of polycrystalline ITO15. Furthermore, the field reinforcement provided by plasmonic resonances also contributes to the nonlinearity enhancement of polycrystalline ITO14. Therefore, the polycrystalline ITO provides a very large third-order nonlinear susceptibility because of enormous nonlinearity enhancement associated with strong quantum confinement effect, hot-electron injection, and field reinforcement, which ensures an ultralow pump intensity of 0.1 MW/cm2 order. A large tunable range of 86 nm in the central wavelength of the transparency window was also realized. An ultrafast response time of 51 ps was maintained simultaneously due to the fast recombination process of carriers at lattice defects in nanoscale crystal grains of polycrystalline ITO. Compared with previous reports, the threshold pump intensity is reduced by four orders of magnitude, while an ultrafast response time of several picoseconds order and a large tuning range in the central wavelength of the transparency window is maintained. This work not only offers a way to constructing photonic materials with a large third-order optical nonlinearity and an ultrafast time response, simultaneously, but also opens up the possibility for realizing quantum solid chips and ultrafast integrated photonic devices based on metamaterials.
Results
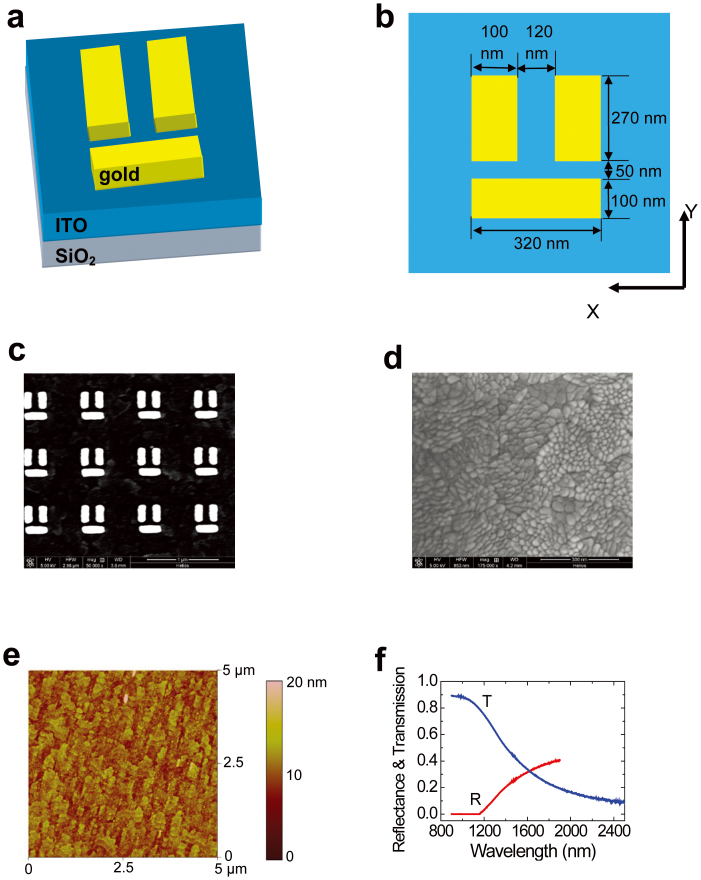
The metamaterial consisted of periodic arrays of square lattice of gold meta-molecules coated on a 180-nm-thick ITO layer with a high conductivity deposited on a SiO2 substrate. The sheet resistance was about 8 Ω/square for the high-conductivity ITO layer. A single meta-molecule was composed of two meta-atoms, i.e. a superradiant meta-atom and a subradiant meta-atom, as shown in Fig. 1(a). A single gold cuboid was used as the superradiant meta-atom, the length, width, and height of which were 320, 100, and 60 nm, respectively, as shown in Fig. 1(b). A pair of parallel gold cuboids formed the subradiant meta-atom, the length, width, and height of which were 270, 100, and 60 nm, respectively, as shown in Fig. 1(b). The separation between two parallel gold cuboids was 120 nm. The vertical gap between the superradiant meta-atom and the subradiant meta-atom was 50 nm. The perpendicular bisector of the superradiant meta-atom was just the symmetry axis of the subradiant meta-atom. The top-view small-scale scanning electron microscopy (SEM) image of the periodic arrays of square lattice of meta-molecules is shown in Fig. 1(c). The lattice constant was 800 nm. The patterned area was about 200 μm × 200 μm. The top-view small-scale SEM image of a 180-nm-thick ITO layer is shown in Fig. 1(d). It is very clear that the ITO layer took on the configuration of polycrystal, constructed from small crystal grains with an average diameter of about 50 nm. An atom force microscopy (AFM) system (Model MFP-3D, Asylum Company, USA) was used to measure the surface roughness of the ITO layer. The AFM image of a 180-nm-thick ITO layer is shown in Fig. 1(e). The surface roughness was less than 10 nm for the ITO layer. The AFM image also confirms the polycrystalline configuration of the ITO layer. To study the plasma frequency of polycrystalline ITO, we measured the transmission and reflectance spectra of a 180-nm-thick ITO layer by using a Fourier transform infrared spectrometer system (Model Magna-IR 750, Nicolet Company, USA) with a resolution of 25 nm, and the measured results are shown in Fig. 1(f). There was a cross point located at 1667 nm for the transmission and reflectance spectra. Howson et al. and Shanti et al. have pointed out that the plasma resonant frequency of ITO film could be estimated from the cross point of the transmission and reflectance spectra of ITO film according to the Drude theory16,17. The plasma resonant wavelength was estimated to be 1670 nm, which ensures the perfect dielectric response of the polycrystalline ITO when the measurement wavelength range is less than 1670 nm in our experiment.
Figure 1. Characterization of the metamaterial.
(a) Schematic structure (a) and top-view structure (b) of the meta-molecule. (c) Top-view small-scale SEM image of the metamaterial. (d) Top-view small-scale SEM image of a 180-nm-thick ITO film. (e) AFM image of a 180-nm-thick ITO film. (f) Measured reflectance and transmission spectrum of a 180-nm-thick ITO film.
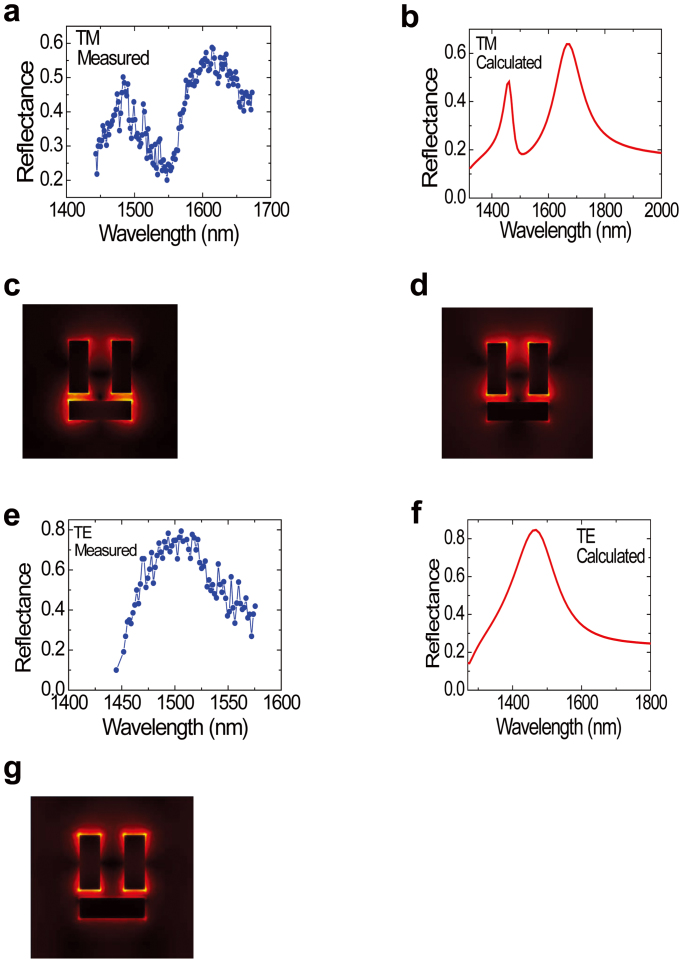
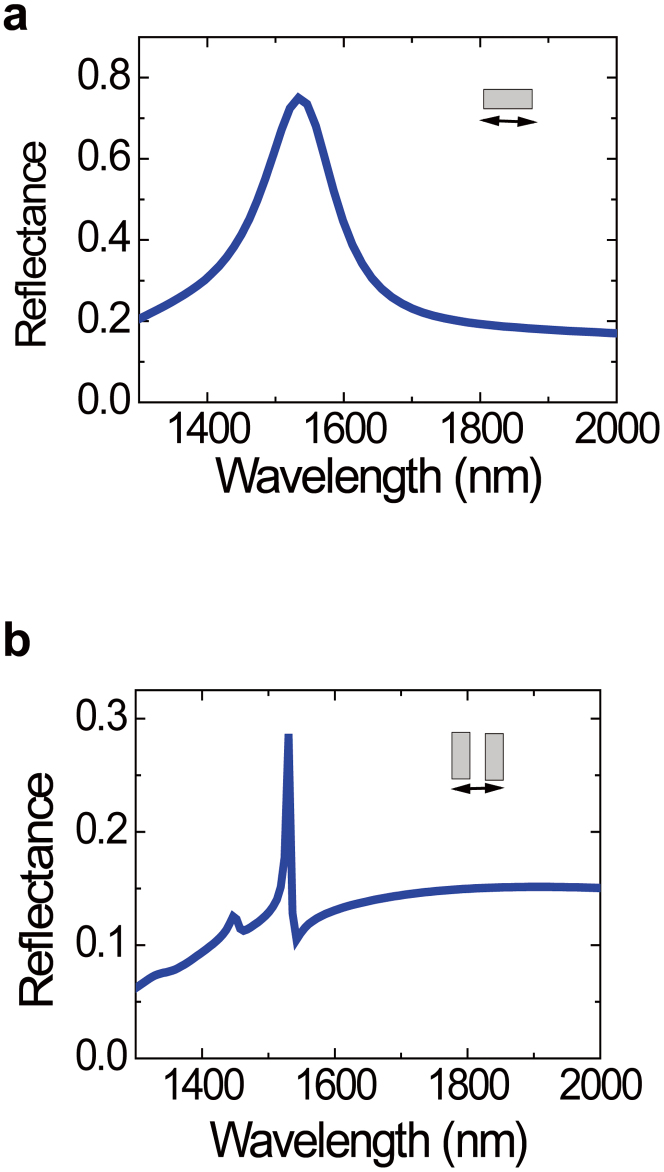
To study the linear reflectance properties of the metamaterial sample, we measured the linear reflectance spectrum of the metamaterial by using the femtosecond pump and probe method when the pump laser was switched off. A beam (with a pulse duration of 35 fs and a repetition rate of 1 kHz) from a femtosecond optical parameter amplifier system (model Opera Solo, Coherent Company, USA) was used as the light source. Limited by the tunable wavelength range of the laser system, we only measured the linear reflectance spectrum from 1450 to 1650 nm. The reflectance was normalized with respect to a pure 180-nm-thick polycrystalline ITO layer on SiO2 substrate, which is the standard method to study the reflectance properties of photonic metamaterials18. For the transverse-magnetic (TM) polarization incidence case, the electric-field vector of the incident laser was adjusted to be parallel to the upper surface of the ITO layer, while perpendicular to the gold cuboid pair, i.e. along X direction as shown in Fig. 1(b). The measured linear reflectance spectrum for the TM-polarized normal-incidence case is depicted in Fig. 2(a). A sharp and deep reflectance dip appeared near the center of the broad and strong reflectance band, which indicates the formation of plasmon-induced transparency. A single gold cuboid could function as an optical dipole antenna, which has a large scattering cross section and could strongly couple the energy of the incident TM light into the plasmonic resonance mode. So, a single gold cuboid forms the superradiant meta-atom. Zhang et al. have pointed out that a parallel gold-cuboid pair could provide antisymmetric plasmonic resonance mode, having counterpropagating currents on two gold cuboids, which could be considered as an artificial magnetic dipole in the optical frequency range19. It is very difficult for the direct electrical dipole coupling between the parallel gold-cuboid pair and the incident TM-polarized light, which forms the subradiant meta-atom2. The physical mechanism of the plasmon-induced transparency can be understood as following: the destructive interference coupling between two excitation pathways, i.e. the direct diploe excitation of the superradiant meta-atom by the incident TM-polarized light, and the excitation of the subradiant meta-atom by the superradiant meta-atom and coupling back to the superradiant meta-atom19. The central wavelength of the transparency window was located at 1547 nm, which was in qualitative agreement with the calculated results (Fig. 2(b)) by the finite element method20. The difference between the measured and calculated results originates from the discrepancy in the configuration and structural parameters of the fabricated sample and the simulation model. To confirm the measured results, we also calculated the electric-field distribution of the meta-molecule for the TM-polarizd incident light with a wavelength of 1460 nm (situated in one reflectance maximum) and 1550 nm (situated in the center of the reflectance dip), and the calculated results are shown in Fig. 2(c) and (d), respectively. For the incident 1460-nm TM-polarized light, the electric-field distribution was mainly confined around the end facets of the superradiant meta-atom and very weak electric-field distribution was in the subradiant meta-atom, as shown in Fig. 2(c), which indicates that the superradiant meta-atom is strongly excited by the incident 1460-nm TM-polarized light. While for the incident 1550-nm TM-polarized light, the electric-field distribution was mainly confined around the end facets of the subradiant meta-atom and very weak electric-field distribution was in the superradiant meta-atom, as shown in Fig. 2(d), which indicates that the subradiant meta-atom is excited by the superradiant meta-atom and the electric-field is coupled back and forth between two meta-atoms. Therefore, the plasmonic resonance of the superradiant meta-atom was suppressed and a narrow transparency window was formed in the broad plasmonic resonance mode of the superradiant meta-atom. This has been confirmed by the calculated results of Zhang et al19. For the transverse-electric (TE) polarization normal-incidence case, the electric-field vector of the incident laser was adjusted to be parallel to the upper surface of the ITO layer, also parallel to the gold cuboid pair, i.e. along Y direction, as shown in Fig. 1(b). The measured linear reflectance spectrum for the TE-polarized normal-incidence case is depicted in Fig. 2(e). There was only a broad reflectance band centered at 1510 nm, which is in qualitative agreement with the calculated ones by the finite element method, as shown in Fig. 2(f). The difference between the measured and calculated results originates from the discrepancy in the configuration and structural parameters of the fabricated sample and the simulation model. To study the physical origination, we calculated the electric-field distribution of the meta-molecule for the TE-polarized incident light with a wavelength of 1510 nm (situated in the reflectance maximum), and the calculated result is shown in Fig. 2(g). It is very clear that there is a symmetric electric-field distribution in the meta-molecule. For the TE polarization incidence case, the whole meta-molecule acts as a large dipole antenna strongly coupled with the free space incident light, which leads to a broad-band plasmonic resonance mode. To further confirm the measured results, we calculated the linear reflectance spectrum of the single superradiant and subradiant meta-atoms for the TM polarization incidence case by the finite element method, and the calculated results are shown in Fig. 3(a) and (b), respectively. The light is oblique incidence at an angle of 45° away from the vertical direction to efficiently excite the antisymmetric plasmonic resonance mode provided by the subradiant meta-atom. There was only one plasmonic resonance mode both for a single superradiant and subradiant meta-atoms for the TM polarization incidence case. The resonance wavelength of the plasmonic mode provide by the subradiant meta-atom, 1530 nm, was close to that of the superradiant meta-atom, 1550 nm. The quality factor and line width were 13.8 and 112 nm for the superradiant meta-atom, and 255 and 6 nm for the subradiant meta-atom, respectively. The quality factor of the plasmonic mode provided by the superradiant meta-atom was much less than that of the subradiant meta-atom. The reason lies in the larger radiant losses of the superradiant meta-atom. The peak reflectance of the subradiant meta-atom, 27%, was much less than that of the superradiant meta-atom, 79%, which indicates that the subradiant meta-atom is very difficult to be directly excited by the free-space incident TM light. These evidences confirm that the subradiant meta-atom provides a dark plasmonic resonance mode, while the superradiant meta-atom provides a bright plasmonic resonance mode. The spectral range was overlapped completely for the bright and dark modes. It is the destructive interference coupling between the bright and dark plasmonic resonances that forms the plasmon-induced transparency.
Figure 2.
Measured (a) and calculated (b) linear reflectance spectrum of the metamaterial for TM polarization incidence case. Calculated electric-field distribution of the meta-molecule for the TM-polarizd incident light with a wavelength of 1460 nm (c), and 1550 nm (d). Measured (e) and calculated (f) linear reflectance spectrum of the metamaterial for TE polarization incidence case. (g) Calculated electric-field distribution of the meta-molecule for the TE-polarizd incident light with a wavelength of 1510 nm.
Figure 3. Calculated linear reflectance spectrum of the superradiant atom (a) and the subradiant atom (b) for the TM polarization incidence case by the finite element method.
Insert shows the schematic structure of meta-atoms. Arrow shows the polarization direction of the incident light.
To study the all-optical tunability of the plasmon-induced transparency, we measured the reflectance changes of a 1550-nm (situated in the center of the transparency window) and 1500-nm (situated in one reflectance maximum) probe laser as a function of delay time between pump and probe pulses by using the femtosecond pump and probe method, and the measured results are shown in Fig. 4 (a) and (b), respectively. The femtosecond optical parameter amplifier system (model Opera Solo, Coherent Company, USA) with a pulse duration of 35 fs and a repetition rate of 1 kHz was used as light source. Both the pump and probe pulse were adjusted to be TM polarized. The intensity of the probe laser was attenuated to be less than 10 kW/cm2, so that the influences of the probe laser on the refractive index change of polycrystalline ITO can be neglected. As for the measurement of the signal curve for the 1550-nm probe laser, the intensity and the wavelength of the pump laser were 890 kW/cm2 and 1550 nm, respectively. The signal curve took on a triangular profile, i.e. a fast rise followed by a slow drop. The reflectance of the probe laser maintained the minimum value of 25% when the probe pulse was far away from the pump pulse in the time sequence. According to third-order nonlinear optical Kerr effect, the refractive index n of the polycrystalline ITO can be obtained by the relation21
Where 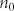 and
and 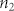 are linear and nonlinear refractive index of polycrystalline ITO,
are linear and nonlinear refractive index of polycrystalline ITO, 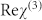 is the real part of the third-order nonlinear susceptibility of polycrystalline ITO,
is the real part of the third-order nonlinear susceptibility of polycrystalline ITO, 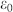 is the permittivity of the vacuum, c is the light velocity in the vacuum. Because polycrystalline ITO has a negative value of nonlinear refractive index
is the permittivity of the vacuum, c is the light velocity in the vacuum. Because polycrystalline ITO has a negative value of nonlinear refractive index 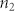 , the linear refractive index of polycrystalline ITO decreases under excitation of a pump laser22. Therefore, when the probe and pump pulses overlapped in the time sequence, the plasmonic resonance modes provided by the superradiant and subradiant meta-atoms shifted in the short-wavelength direction because of a decrease in the refractive index of the surrounding dielectric material23. Accordingly, the central wavelength of the transparency window also shifted in the short-wavelength direction. As a result, the reflectance of the 1550-nm probe laser increased under excitation of the pump laser. The maximum reflectance reached 60%. The threshold pump intensity was only 890 kW/cm2, which is reduced by four orders of magnitude compared with previously experimental reports12. The nanoscale crystal grains of polycrystalline ITO could provide enormous quantum confinement enhancing nonlinearity effect, which has been confirmed by our previous measurement11. Abb et al. have pointed out that for an ITO film coated with gold nanostructures under excitation of a femtosecond pump laser at the optical communication range, there was a remarkable hot-electron injection from gold nanostructures into ITO film, which tremendously enlarged the carriers density in ITO24. The hot-electron injection also contributed to the optical nonlinearity enhancement of polycrystalline ITO, which has been confirmed by the measurement of Traviss et al15. Furthermore, there was enormous electric-field distribution near the end factes of meta-molecules when the wavelength of the pump laser was near resonant with that of the plasmonic modes provided by the meta-molecues, as shown in Fig. 2(d). The field reinforcement also dedicated to the optical nonlinearity enhancement of polycrystalline ITO, which has been confirmed by our previous measurement14. Therefore, the polycrystalline ITO could provide a very large nonlinear refractive index due to strong nonlinearity enhancement associated with strong quantum confinement effect, hot-electron injection, and field reinforcement, which ensures an ultralow pump intensity of 0.1 MW/cm2 order. To confirm the measured results, we also calculated the reflectance spectrum of the metamaterial with different pump intensity of a 1550-nm light for the TM-polarized incidence case, and the calculated results are depicted in Fig. 4(c). It is very clear that the central wavelength of the transparency window shifted in the short-wavelength direction under excitation of a pump light. The reflectance at 1550 nm varied from 25% to 60% when the pump intensity increased from zero to 890 kW/cm2, which is in agreement with the measured result. The central wavelength of the transparency window changed from 1550 to 1464 nm when the pump intensity increased from zero to 890 kW/cm2, which implies that the central wavelength of the transparency window could be continuously tuned within a large range of 86 nm. As for the measurement of the signal curve for the 1500-nm probe laser, the intensity and the wavelength of the pump laser were 110 kW/cm2 and 1500 nm, respectively. The signal curve took on an inverse-triangular profile, i.e. a fast drop followed by a slow rise. The reflectance of the probe laser maintained the maximum value of 45% when the probe pulse was far away from the pump pulse in the time sequence. When the probe and pump pulses overlapped in the time sequence, the reflectance of the probe laser decreased. The minimum reflectance was 25% for the probe laser. This confirms that the transparency window shifts in the short-wavelength direction under excitation of a femtosecond pump laser at the optical communication range, and the negative value of nonlinear refractive index
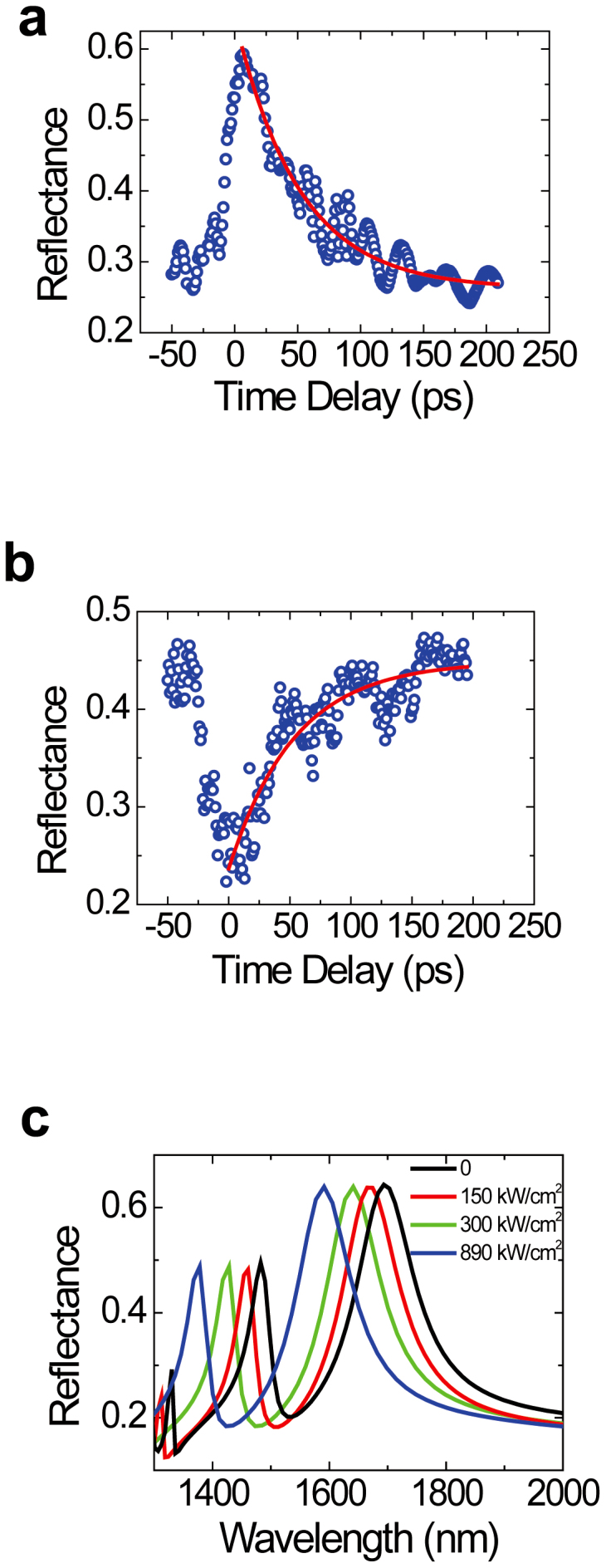
, the linear refractive index of polycrystalline ITO decreases under excitation of a pump laser22. Therefore, when the probe and pump pulses overlapped in the time sequence, the plasmonic resonance modes provided by the superradiant and subradiant meta-atoms shifted in the short-wavelength direction because of a decrease in the refractive index of the surrounding dielectric material23. Accordingly, the central wavelength of the transparency window also shifted in the short-wavelength direction. As a result, the reflectance of the 1550-nm probe laser increased under excitation of the pump laser. The maximum reflectance reached 60%. The threshold pump intensity was only 890 kW/cm2, which is reduced by four orders of magnitude compared with previously experimental reports12. The nanoscale crystal grains of polycrystalline ITO could provide enormous quantum confinement enhancing nonlinearity effect, which has been confirmed by our previous measurement11. Abb et al. have pointed out that for an ITO film coated with gold nanostructures under excitation of a femtosecond pump laser at the optical communication range, there was a remarkable hot-electron injection from gold nanostructures into ITO film, which tremendously enlarged the carriers density in ITO24. The hot-electron injection also contributed to the optical nonlinearity enhancement of polycrystalline ITO, which has been confirmed by the measurement of Traviss et al15. Furthermore, there was enormous electric-field distribution near the end factes of meta-molecules when the wavelength of the pump laser was near resonant with that of the plasmonic modes provided by the meta-molecues, as shown in Fig. 2(d). The field reinforcement also dedicated to the optical nonlinearity enhancement of polycrystalline ITO, which has been confirmed by our previous measurement14. Therefore, the polycrystalline ITO could provide a very large nonlinear refractive index due to strong nonlinearity enhancement associated with strong quantum confinement effect, hot-electron injection, and field reinforcement, which ensures an ultralow pump intensity of 0.1 MW/cm2 order. To confirm the measured results, we also calculated the reflectance spectrum of the metamaterial with different pump intensity of a 1550-nm light for the TM-polarized incidence case, and the calculated results are depicted in Fig. 4(c). It is very clear that the central wavelength of the transparency window shifted in the short-wavelength direction under excitation of a pump light. The reflectance at 1550 nm varied from 25% to 60% when the pump intensity increased from zero to 890 kW/cm2, which is in agreement with the measured result. The central wavelength of the transparency window changed from 1550 to 1464 nm when the pump intensity increased from zero to 890 kW/cm2, which implies that the central wavelength of the transparency window could be continuously tuned within a large range of 86 nm. As for the measurement of the signal curve for the 1500-nm probe laser, the intensity and the wavelength of the pump laser were 110 kW/cm2 and 1500 nm, respectively. The signal curve took on an inverse-triangular profile, i.e. a fast drop followed by a slow rise. The reflectance of the probe laser maintained the maximum value of 45% when the probe pulse was far away from the pump pulse in the time sequence. When the probe and pump pulses overlapped in the time sequence, the reflectance of the probe laser decreased. The minimum reflectance was 25% for the probe laser. This confirms that the transparency window shifts in the short-wavelength direction under excitation of a femtosecond pump laser at the optical communication range, and the negative value of nonlinear refractive index 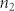 of the polycrystalline ITO. Zhang et al. pointed out that an optical-excitation-induced broadening and red-shift in the central wavelength of the plasmonic resonance mode provided by gold nanostructures will occur under excitation of a pump laser25. However, the plasmonic resonance mode is influenced enormously by the refractive index of ambient dielectric material. Under excitation of a femtosecond pump laser, the refractive index of polycrystalline ITO decreases, which makes the plasmonic resonance mode shift in the short-wavelength direction26. According to our calculation, the magnitude of the blue-shift was much larger than that of the red-shift. This is of great benefit for the formation of plasmon-induced transparency. So, influences of the optical nonlinearity of gold can be neglected.
of the polycrystalline ITO. Zhang et al. pointed out that an optical-excitation-induced broadening and red-shift in the central wavelength of the plasmonic resonance mode provided by gold nanostructures will occur under excitation of a pump laser25. However, the plasmonic resonance mode is influenced enormously by the refractive index of ambient dielectric material. Under excitation of a femtosecond pump laser, the refractive index of polycrystalline ITO decreases, which makes the plasmonic resonance mode shift in the short-wavelength direction26. According to our calculation, the magnitude of the blue-shift was much larger than that of the red-shift. This is of great benefit for the formation of plasmon-induced transparency. So, influences of the optical nonlinearity of gold can be neglected.
Figure 4.
Measured reflectance changes of a 1550 nm (a) and 1500 nm (b) probe laser as a function of delay time between pump and probe pulses. The red solid line is the exponential fit to the data. (c) Calculated reflectance spectrum of the metamaterial with different pump intensity by the finite element method.
The dynamical process of the reflectance changes in Fig. 4(a) and (b) indicates the time response properties of the all-optical tunable plasmon-induced transparency. Humphrey et al. pointed out that under excitation of a femtosecond pump laser at optical communication range, the time response properties of ITO was controlled by the relaxation dynamics of carriers in ITO22. The fast rise in Fig. 4(a) (and also the quick drop in Fig. 4(b)) is attributed to the formation of nonequilibrium electrons in gold and free carriers in polycrystalline ITO22,27. The red thick line in Fig. 4 (a) (and (b)) was exponentially fitted results of the drop (and rise) curve. The time constant was fitted to be 51 ps both for Fig. 4 (a) and (b). For gold nanostructures, the electron-electron scattering redistributes the energy in the conduction electrons with a characteristic time of less than 500 fs27. Subsequently, the energy is transferred to the lattice by electron-phonon interactions on a time scale of 2 to 3 ps28. Finally, the phonon-phonon interactions redistribute the energy with a characteristic time of 24 ps29. Abb et al. pointed out that the hot-electron injection from gold nanostructures to polycrystalline ITO responses on a time scale of subpicesecond order24. Losego et al. pointed out that there were a large number of lattice defects in crystal grains of polycrystalline ITO and fast recombination of carrier could occur at the lattice defect sites30. Therefore, it is the fast recombination of carrier at lattice defects in crystal grains of polystyrene ITO that determines the ultrafast response time of all-optical tunable plasmon-induced transparency.
Discussion
Abb et al. also pointed out that the hot-electron injection process may results in a fast local heating of ITO surrounding the gold meta-molecules, and relaxation dynamics of the carriers may be influenced seriously by the cooling of the heated area on a time scale of several hundreds of picoseconds24. In our experiment, we did not find remarkable effect of the cooling of the heated ITO area on the all-optical tunability. The reason may lies in the extremely weak pump intensity of 0.1 MW/cm2 order, and the low repetition rate of 1 kHz for the pump laser pulse.
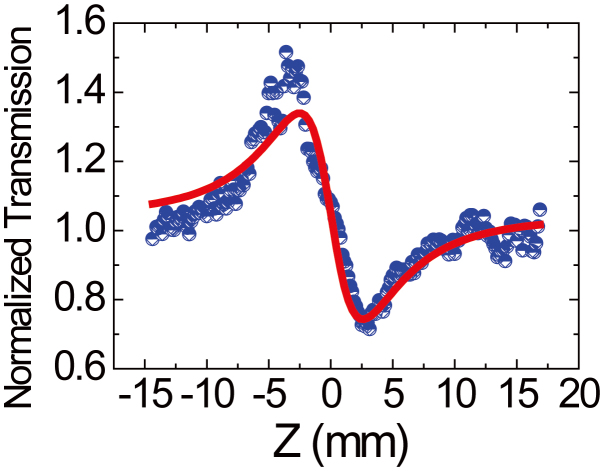
To further confirm the nonlinear response of polycrystalline ITO layer, we measured the nonlinear refractive index 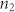 of a 180-nm-thick pure ITO film by using the close-aperture Z-scan method with a 35-fs, 1550-nm laser. The measured close-aperture Z scan curve is showed in Figure 5. The remarkable peak–valley profile of the curve implies the negative value of the nonlinear refractive index
of a 180-nm-thick pure ITO film by using the close-aperture Z-scan method with a 35-fs, 1550-nm laser. The measured close-aperture Z scan curve is showed in Figure 5. The remarkable peak–valley profile of the curve implies the negative value of the nonlinear refractive index 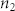 of the polycrystalline ITO at the optical communication range. The normalized transmission can be fitted to31
of the polycrystalline ITO at the optical communication range. The normalized transmission can be fitted to31
Where T is the normal transmittance, 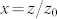 ,
,  is the longitudinal distance from the focal point,
is the longitudinal distance from the focal point, 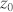 is the Rayleigh range of the laser beam, and
is the Rayleigh range of the laser beam, and 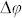 is the phase change. The nonlinear refractive index
is the phase change. The nonlinear refractive index 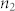 could be obtain from31
could be obtain from31
Where 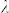 is the laser wavelength in vacuum,
is the laser wavelength in vacuum,  is the linear absorption index,
is the linear absorption index, 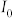 is the peak intensity of the laser beam, and L is the sample thickness. The non-linear refractive index was measured to −1.32 × 10−11 cm2/W for a pure polycrystalline ITO film, which is one order of magnitude larger than that of the single-crystal ITO film with a high conductivity at near-infrared range24. The real part of the third-order nonlinear susceptibility of polycrystalline ITO film, obtained based on equation (1), was 9.65 × 10−9 esu at the optical communication range. Bristow et al. have pointed out that the real part of the third-order nonlinear susceptibility of silicon was 9.36 × 10−12 esu at the optical communication range32. Therefore, the absolute value of the real part of the third-order susceptibility of polycrystalline ITO was three orders of magnitude larger than that of the conventional semiconductor material silicon. This confirms that the gold/polycrystalline ITO nanostructure possesses excellent third-order optical nonlinearity at the optical communication range. In our laboratory, we only had a 1 kHz amplified pulse laser system operating at the optical communication range. Although the 1 kHz amplified pulse laser system was less stable and more difficult to control the ultralow average power, about 1 nW, compared with the conventional 80 MHz pulse laser system, we had no choice but to use the 1 kHz amplified pulse laser system due to the limitation of the experimental conditions of our laboratory.
is the peak intensity of the laser beam, and L is the sample thickness. The non-linear refractive index was measured to −1.32 × 10−11 cm2/W for a pure polycrystalline ITO film, which is one order of magnitude larger than that of the single-crystal ITO film with a high conductivity at near-infrared range24. The real part of the third-order nonlinear susceptibility of polycrystalline ITO film, obtained based on equation (1), was 9.65 × 10−9 esu at the optical communication range. Bristow et al. have pointed out that the real part of the third-order nonlinear susceptibility of silicon was 9.36 × 10−12 esu at the optical communication range32. Therefore, the absolute value of the real part of the third-order susceptibility of polycrystalline ITO was three orders of magnitude larger than that of the conventional semiconductor material silicon. This confirms that the gold/polycrystalline ITO nanostructure possesses excellent third-order optical nonlinearity at the optical communication range. In our laboratory, we only had a 1 kHz amplified pulse laser system operating at the optical communication range. Although the 1 kHz amplified pulse laser system was less stable and more difficult to control the ultralow average power, about 1 nW, compared with the conventional 80 MHz pulse laser system, we had no choice but to use the 1 kHz amplified pulse laser system due to the limitation of the experimental conditions of our laboratory.
Figure 5. Measured closed-aperture Z-scan curve of a 180-nm-thick ITO film.
The red solid curve is the theoretical fit to the data.
In summary, we have realized an ultralow-power and ultrafast all-optical tunable plasmon-induced transparency in metamaterials at the optical communication range. Ultralow threshold pump intensity of 0.1 MW/cm2 order and ultrafast response time of 51 ps were reached simultaneously. A shift of 86 nm in the central wavelength of the transparency window was realized. Compared with previous reports, the threshold pump intensity is reduced by four orders of magnitude, while an ultrafast response time of several picoseconds order and a large tunability are maintained. This work not only offers a way to constructing photonic materials with a large third-order nonlinear susceptibility and an ultrafast time response, simultaneously, but also opens up the possibility for realizing quantum solid chips and ultrafast integrated photonic devices based on metamaterials.
Methods
Sample fabrication
High-conductivity ITO layer was deposited on SiO2 substrate by using radio frequency sputtering in an oxygen/argon plasma with a mixing ratio of 1:140 at a temperature of 500°C. The gold film was fabricated by using a laser molecular beam epitaxy (LMBE) growth system (Model LMBE 450, SKY Company, China). The beam (with a wavelength of 248 nm and a pulse repetition rate of 5 Hz) output from an excimer laser system (Model COMPexPro 205, Coherent Company, USA) was used as the excitation light source. The beam was focused onto a gold target mounted on a rotating holder, 15 mm away from the ITO film on SiO2 substrate. The typical energy density of the excitation laser was about 500 mJ/cm2. The growth rate measured by a film thickness/rate monitor was about 0.01 nm/pulse. The growth process was conducted under a pressure of 6.5 × 10−4 Pa for gold films. An electron-beam lithography system (Model Raith 150, Raith Company, Germany) was used to prepare the periodic patterns of the metamaterial.
Femtosecond pump and probe measurement setup
A beam (with a pulse duration of 35 fs and a repetition rate of 1 kHz) from a femtosecond optical parameter amplifier system (model Opera Solo, Coherent Company, USA) was split into two beams with a ratio of 10:1. The weak beam, used as the probe light, was incident normal to the upper-surface plane of the metamaterial with a spot size of about 100 μm. The strong beam, used as the pump light, was also incident on this upper-surface plane and focused with a spot size of about 200 μm. There was a small angle of 15° between the pump and probe light. The probe light was in the center of the pump light when propagating through the metamaterial sample. The probe light propagating through the metamaterial was detected using a fiber monochromator (Model NIR-512, Ocean Optics, USA) with a resolution of 0.74 nm, the output signal of which was collected and analyzed by a computer. A delay line was used to adjust the timing between the pump and probe pulses.
Closed-aperture Z-scan measurement setup
A 35 fs, 1550 nm laser beam from a femtosecond optical parameter amplifier system (model Opera Solo, Coherent Company, USA) with a repetition rate of 1 kHz was used as the light source. The experimental measurement setup was as detailed in Ref. 30.
Author Contributions
Q.G. proposed the idea. Y.Z. fabricated samples. Y.Z., X.H., Y.F. and H.Y. performed measurements. Y.Z., X.H., Y.F., H.Y. and Q.G. analyzed data and co-wrote the manuscript.
Acknowledgments
This work was supported by the National Basic Research Program of China under grant 2013CB328704, the National Natural Science Foundation of China under grants 11225417, 61077027, 11134001, 11121091, and 90921008, and the program for New Century Excellent Talents in University.
References
- Dominguez R. P., Abujetas D. R. & Gil J. A. S. Ultralow-loss isotropic optical negative-index metamaterial based on hybrid metal-semiconductor nanowires. Sci. Rep. 3, 1507 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y. H. et al. Magnetic plasmon resonance: underlying route to plasmonic electromagnetically induced transparency in metamaterials. Phys. Rev. B 82, 195112 (2010). [Google Scholar]
- Liu N. et al. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nat. Mater. 8, 758–762 (2009). [DOI] [PubMed] [Google Scholar]
- Liu X. J. et al. Electromagnetically inducd transparency in terahertz plasmonic metamaterials via dual excitation pathways of the dark mode. Appl. Phys. Lett. 100, 131101 (2012). [Google Scholar]
- Lukyanchuk B. et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 9, 707–715 (2010). [DOI] [PubMed] [Google Scholar]
- Liu N. et al. Three-dimensional plasmon rulers. Science 332, 1407–1410 (2011). [DOI] [PubMed] [Google Scholar]
- Tassin P., Zhang L., Koschny T., Economou E. N. & Soukoulis C. M. Low-loss metamaterials based on classical analogue of electromagnetically induced transparency. Phys. Rev. Lett. 102, 053901 (2009). [DOI] [PubMed] [Google Scholar]
- Papasimakis N., Fedotov V. A., Zheludev N. I. & Prosvirnin S. L. Metamaterial analog of electromagnetically induced transparency. Phys. Rev. Lett. 101, 253903 (2008). [DOI] [PubMed] [Google Scholar]
- Kurter C. et al. Classical analogue of electromagnetically induced transparency with a metal-superconductor hybrid metamaterials. Phys. Rev. Lett. 107, 043901 (2011). [DOI] [PubMed] [Google Scholar]
- Wu J. B. et al. Superconducting terahertz metamaterials mimicking electromagnetically induced transparency. Appl. Phys. Lett. 99, 161113 (2011). [Google Scholar]
- Chai Z. et al. Low-power and ultrafast all-optical tunable plasmon-induced transparency in plasmonic nanostructures. Appl. Phys. Lett. 102, 201119 (2013). [Google Scholar]
- Gu J. Q. et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nat. Commun. 3, 1151 (2012). [DOI] [PubMed] [Google Scholar]
- Hu X. Y., Jiang P., Ding C. Y., Yang H. & Gong Q. H. Picosecond and low-power all-optical switching based on an organic photonic-bandgap microcavity. Nat. Photonics 2, 185–189 (2008). [Google Scholar]
- Zhang F. et al. Ultrafast all-optical tunable Fano resonance in nonlinear metamaterials. Appl. Phys. Lett. 102, 181109 (2013). [Google Scholar]
- Traviss D., Bruck R., Mills B., Abb M. & Muskens O. L. Ultrafast plasmonics using transparent conductive oxide hybrids in the epsilon-near-zero regime. Appl. Phys. Lett. 102, 121112 (2013). [Google Scholar]
- Howson R. P., Ridge M. I. & Bishop C. A. Production of transparent electrically conducting films by ion plating. Thin Solid Films 80, 137–140 (1981). [Google Scholar]
- Shanti E., Dutta V., Banerjee A. & Chopra K. L. Electrical and optical properties of undoped and antimony-doped tin oxide films. J. Appl. Phys. 51, 6243–6251 (1980). [Google Scholar]
- Wu C. H. et al. Fano-resonant asymmetric metamaterials for ultrasensitive spectroscopy and identification of molecular monolayers. Nat. Mater. 11, 69–75 (2012). [DOI] [PubMed] [Google Scholar]
- Zhang S., Genov D. A., Wang Y., Liu M. & Zhang X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 101, 047401 (2008). [DOI] [PubMed] [Google Scholar]
- Fu Y. L. et al. All-optical logic gates based on nanoscale plasmonic slot waveguides. Nano Lett. 12, 5784–5790 (2012). [DOI] [PubMed] [Google Scholar]
- Boyd R. W. Nonlinear Optics (Academic Press Inc., San Diego, 1992). [Google Scholar]
- Humphrey J. L. & Kuciauskas D. Optical susceptibilities of supported indium tin oxide thin films. J. Appl. Phys. 100, 113123 (2006). [Google Scholar]
- Lapine M., Shadrivov I. & Kivshar Y. Wide-band negative permeability of nonlinear metamaterials. Sci. Rep. 2, 412 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abb M., Albella P., Aizpurua J. & Muskens O. L. All-optical control of a single plasmonic nanoantenna-ITO hybrid. Nano Lett. 11, 2457–2463 (2011). [DOI] [PubMed] [Google Scholar]
- Zhang X. P., Sun B. Q., Hodgkiss J. M. & Friend R. H. Tunable ultrafast optical switching via waveguided gold nanowires. Adv. Mater. 20, 4455–4459 (2008). [Google Scholar]
- Mulvaney P. Surface plasmon spectroscopy of nanosized metal particles. Langmuir 12, 788–800 (1996). [Google Scholar]
- Fatti N. D. et al. Nonequilibrium electron dynamics in noble metals. Phys. Rev. B 61, 16956–16966 (2000). [Google Scholar]
- Schoenlein R. W., Lin W. Z. & Fujimoto J. G. Femtosecond studies of nonequilibrium electronic processes in metals. Phys. Rev. Lett. 58, 1680–1683 (1987). [DOI] [PubMed] [Google Scholar]
- Sasai J. & Hirao K. Relaxation behavior of nonlinear optical response in borate glasses containing gold nanoparticles. J. Appl. Phys. 89, 4548–4553 (2001). [Google Scholar]
- Losego M. D. et al. Conductive oxide thin films model systems for understanding and controlling surface plasmon resonance. J. Appl. Phys. 106, 024903 (2009). [Google Scholar]
- Henari F. Z., Cazzini K., Akkari F. E. & Blau W. J. Beam waist changes in lithium niobate during Z-scan measurement. J. Appl. Phys. 78, 1373–1375 (1995). [Google Scholar]
- Bristow A. D., Rotenberg N. & Driel H. M. V. Two-photon absorption and Kerr coefficients of silicon for 850–2200 nm. Appl. Phys. Lett. 90, 191104 (2007). [Google Scholar]