Assessing smectic liquid-crystal continuum models for elastic bilayer deformations

Abstract

For four decades, since W. Helfrich’s pioneering study of smectic A liquid crystals in 1973, continuum elastic models (CEMs) have been employed as tools to understand the energetics of protein-induced lipid bilayer deformations. Among the assumptions underlying this use is that all relevant protein–lipid interactions can be included in the continuum representation of the protein–bilayer interactions through the physical parameters determined for protein-free bilayers and the choice of boundary conditions at the protein/bilayer interface. To better understand this assumption, we review the general structure of CEMs, examine how different choices of boundary conditions and physical moduli profiles alter the predicted bilayer thickness profiles around gramicidin A (gA) and mitochondrial voltage-dependent anion channels (VDAC), respectively, and compare these profiles with those obtained from all-atom molecular dynamics simulations. We find that the profiles differ qualitatively in the first lipid shell around the channels, indicating that the CEMs do not capture accurately the consequences of the protein-induced local changes in lipid bilayer dynamics. Therefore, one needs to be careful when interpreting the results of CEM-based analyses of lipid bilayer-membrane protein interactions.

1. Introduction

Membrane protein function is regulated by changes in the host lipid bilayer composition (Sandermann, 1978; McElhaney, 1989; Bienvenüe and Marie, 1994; Dowhan, 1997; Lee, 2004; Andersen and Koeppe, 2007; Marsh, 2008). This regulation arises because: first, membrane proteins are coupled to the lipid bilayer through hydrophobic (Singer and Nicolson, 1972) as well as more specific (Lee, 2011) interactions, which make the system respond so as to maximize the match between the protein’s hydrophobic transmembrane domain and the lipid bilayer hydrophobic core (Andersen and Koeppe, 2007); second, bilayer-spanning proteins perturb their surrounding bilayer (Marsh, 2008; Seelig et al., 1981), which incurs an energetic cost, the bilayer deformation energy (ΔG_def) (Mouritsen and Bloom, 1984; Huang, 1986); and third, membrane proteins occur in different conformations (Brown, 1994; Lundbaek et al., 2010) that in general will interact differently with the bilayer. The difference in bilayer deformation energy between two different protein conformations (I and II) becomes the bilayer contribution $(\Delta G_{\text{bilayer}}^{I\to \mathit{II}}=\Delta G_{\text{def}}^{\mathit{II}}-\Delta G_{\text{def}}^I)$ to the total free energy difference $\left(\Delta G_{\text{total}}^{I\to \mathit{II}}\right)$ for the conformational transition (Lundbaek et al., 2010):

$$\Delta G_{\text{total}}^{I\to \mathit{II}}=\Delta G_{\text{protein}}^{I\to \mathit{II}}+\Delta G_{\text{bilayer}}^{I\to \mathit{II}}$$ (1)

where $\Delta G_{\text{protein}}^{I\to \mathit{II}}$ denotes energetic contributions intrinsic to the protein (or contributions other than those due to the protein–bilayer interactions). The equilibrium distribution between different protein conformations (n_II/n_I) will vary with changes in $\Delta G_{\text{bilayer}}^{I\to \mathit{II}}$ associated with changes in lipid bilayer properties from, for example, lipid bilayer composition:

$$\frac{n_{\mathit{II}}}{n_I}=\exp \left[-\frac{\Delta G_{\text{total}}^{I\to \mathit{II}}}{k_{B}T}\right]=\exp \left[-\frac{\Delta G_{\text{protein}}^{I\to \mathit{II}}+\Delta G_{\text{bilayer}}^{I\to \mathit{II}}}{k_{B}T}\right]$$ (2)

where k_B is the Boltzmann constant and T is temperature in Kelvin.

To evaluate the role of the bilayer in membrane protein function, ΔG_def has been evaluated using continuum models of elastic bilayer deformations (Huang, 1986; Helfrich, 1973; Helfrich and Jakobsson, 1990; Aranda-Espinoza et al., 1996; Nielsen et al., 1998; Nielsen and Andersen, 2000; Partenskii and Jordan, 2002), which we denote as continuum elastic models (CEMs), as well as other models (Brown, 2008; Tang et al., 2006; Zimmerberg and Kozlov, 2006). In this review we evaluate CEMs based on the smectic liquid crystalline approximation (Huang, 1986), in which a cylindrical membrane protein with a hydrophobic length (l) is embedded in a lipid bilayer with an unperturbed hydrophobic thickness, d₀. In this model, ΔG_def caused by a protein inclusion has three contributions: compression-expansion (CE), due to changes in membrane thickness; splay-distortion (SD), due to deviations from the (approximately) parallel alignment of the acyl chains of the lipids; and surface tension (ST), due to changes in the surface area. We base our analysis on a cylindrically symmetrical bilayer from the protein center, in which ΔG_def can be expressed as:

$$\Delta G_{\text{def}}={\int }_{r_0}^{\infty }\mathit{dr}\cdot 2\pi r\cdot {\mathcal{L}}_{1\mathrm{D}}\left(r\right)\equiv {\int }_{r_0}^{\infty }\mathit{dr}\cdot {\mathcal{L}}_{1\mathrm{D}}^{\prime }\left(r\right)$$ (3)

with

$$\begin{array}{cc}\hfill {\mathcal{L}}_{1\mathrm{D}}\left(r\right)=& \Delta G_{\mathit{CE}}+\Delta G_{\mathit{SD}}+\Delta G_{\mathit{ST}}=\frac{2K_a}{{d_0}^2}{u}^2\left(r\right)\hfill \\ \hfill & +\frac{K_c}{2}{\left(\frac{d^{2}u\left(r\right)}{{\mathit{dr}}^2}+\frac{1}{r}\cdot \frac{\mathit{du}\left(r\right)}{\mathit{dr}}-c_0\right)}^2+\frac{\alpha }{2}{\mid \frac{\mathit{du}\left(r\right)}{\mathit{dr}}\mid }^2\hfill \end{array}$$ (4)

where r₀ is the distance from the protein center to a protein-lipid contact; u(r) the space-dependent deviation of the membrane from the unperturbed condition—the lipid adaption to the protein inclusion (u(r) = (d₀ − d(r))/2, where d(r) is the membrane thickness at distance r from the protein center); and c₀ the intrinsic monolayer curvature, K_a the compression modulus, K_c the bending (splay) modulus, and α the surface tension coefficient.

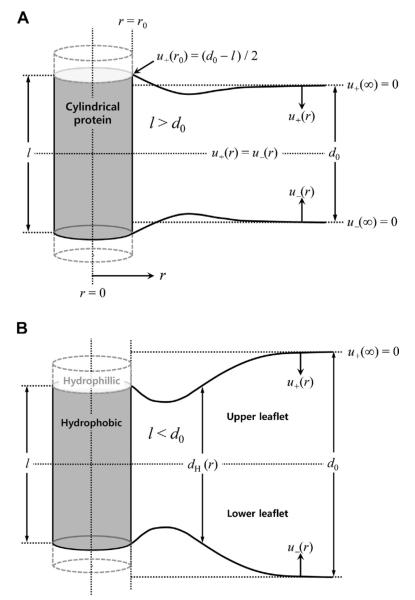
Fig. 1 sketches u(r) for the systems with positive (top) and negative (bottom) hydrophobic mismatches. Mathematically, ΔG_def is a functional of u(r). Because ΔG_def must be a minimum at equilibrium, there will be a u(r) profile that minimizes ΔG_def. Such a profile satisfies the Euler–Lagrange equation, which up to the second derivative of u(r) is written as:

$$\frac{\partial {\mathcal{L}}_{1D}^{\prime }\left(r\right)}{\partial u}-\frac{\partial }{\partial r}\left[\frac{\partial {\mathcal{L}}_{1D}^{\prime }\left(r\right)}{\partial (\partial u∕\partial r)}\right]+\frac{{\partial }^2}{\partial r^2}\left[\frac{\partial {\mathcal{L}}_{1D}^{\prime }\left(r\right)}{\partial ({\partial }^{2}u∕\partial r^2)}\right]=0$$ (5)

Fig. 1.

Bilayer deformation profiles upon inclusion of a cylindrically symmetric protein. (A) Positive hydrophobic mismatch (l > d₀) and (B) negative hydrophobic mismatch (l < d₀), where l represents the hydrophobic length of the transmembrane protein and d₀ represents that of the unperturbed lipid bilayer. The hydrophobic match condition is used at the protein-lipid contact (r = r₀) and the unperturbed membrane condition is assumed at r = r_∞. Also, symmetry of the upper and lower leaflets is assumed.

Hence, for a particular set of parameters, u(r) can be determined by solving Eq. (5) with boundary conditions specified by the endpoints of the integral in Eq. (3). This procedure is discussed further below.

The surface tension contribution to ΔG_def has been found to be negligible (Huang, 1986; Helfrich and Jakobsson, 1990). Neglecting the surface tension term, ΔG_def can be expressed as a biquadratic function of l − d₀ and c₀:

$$\Delta G_{\text{def}}=H_B{(l-d_0)}^2+H_X(l-d_0)c_0+H_C{c}_0^2$$ (6)

where the elastic spring coefficients, H_B, H_X, and H_C are functions of d₀, r₀, K_a, and K_c. Eq. (6) can be derived from Eq. (4) (cf. (Nielsen and Andersen, 2000; Lundbaek et al., 2005)), which allows explicit evaluation of the H coefficients and the bilayer thickness profile (u(r)). The biquadratic form of Eq. (6), however, applies more generally (Andersen and Koeppe, 2007; Rusinova et al., 2011) because ΔG_def can be expressed as a Maclaurin series in l − d₀ and c₀, where the first-order derivatives for reasons of symmetry are zero:

$$\begin{array}{cc}\hfill \Delta G_{\text{def}}(c_0,l-d_0)=& \Delta G_{\text{def}}(0,0)+H_B{(l-d_0)}^2\hfill \\ \hfill & +H_X(l-d_0)c_0+H_C{c}_0^2\hfill \end{array}$$ (7)

where ΔG_def(0, 0) denotes the energetic cost of embedding a protein of hydrophobic length d₀ (i.e., l = d₀) in a bilayer with c₀ = 0, including the loss of conformational entropy of the lipid acyl chains adjacent to the protein (Fattal and Ben-Shaul, 1993) and the H coefficients become phenomenological spring coefficients. The ΔG_def(0, 0) term is assumed to be zero in the conventional CEM, which leads to Eq. (6).

In general, assuming uniform bilayer moduli, Eq. (3) is solved by minimization and becomes:

$${\nabla }^{4}u\left(r\right)-\gamma {\nabla }^{2}u\left(r\right)+\beta u\left(r\right)=0$$ (8)

where γ = α/K_c and $\beta =4K_a∕K_c{d}_0^2$. The solution to Eq. 2 (8) requires four boundary conditions. Two are straightforward, because the protein-induced bilayer deformation should disappear far from the protein: u(r = ∞) = 0 and du/dr(r = ∞) = 0. The other two are not, though it usually is assumed that one of them is determined by the hydrophobic match condition at the protein/lipid boundary: u(r₀) = (l − d₀)/2 (Helfrich and Jakobsson, 1990; Nielsen et al., 1998). This assumption is likely to be valid in the case of proteins with a single transmembrane helix (Kim and Im, 2010), where there usually will be a well-defined transition between the helix’s hydrophobic and hydrophilic residues, but it may be problematic in the case of proteins with multiple transmembrane segments where the hydrophobic/hydrophilic transition in adjacent segments may not be aligned (Mondal et al., 2011). (The hydrophobic match condition also may be violated in the case of very large mismatches between the protein’s hydrophobic length and the hydrophobic thickness of the unperturbed bilayer, where there may be hydrophobic slippage (Lundbaek and Andersen, 1999).) The final boundary condition is the most problematic. In the simplest case, it is the slope (s) or the curvature (c) of the bilayer/solution interface at the protein/lipid boundary that minimizes ΔG_def (Helfrich and Jakobsson, 1990). But this so-called natural boundary condition (Lebedev, 1965) turns out to predict ΔG_def values that are inconsistent with experimental results (Huang, 1986; Helfrich and Jakobsson, 1990; Nielsen et al., 1998; Nielsen and Andersen, 2000; Goulian et al., 1998). Though this discrepancy might indicate a fundamental failure of CEMs, it more likely reflects that some feature of protein–lipid bilayer interactions is not incorporated in the description because it is possible to account satisfactorily for the experimental results if s (or c) is allowed to vary.

The CEM of protein-induced bilayer deformations has been tested using gramicidin A (gA) single-channel experiments, where the single-channel appearance rate (f) and lifetime (τ) was examined as a function of membrane tension σ (Goulian et al., 1998), and in experiments that determined how σ varies as a function of unperturbed bilayer thickness (d₀) (Lundbaek and Andersen, 1999). Neither the f – σ nor τ – σ relations (Goulian et al., 1998) nor the τ – d₀ relation (Lundbaek and Andersen, 1999) conform to predictions based on the CEM using uniform bulk bilayer elastic moduli and the value of s that minimizes ΔG_def (Eqs. (3) and (6)). The experimental results, however, could be fit by varying s at the channel/bilayer boundary, indicating that there are additional constraints on lipid packing such as the energetic cost of acyl chain tilt (Nielsen et al., 1998); the τ – d₀ relation could be fit by assuming s = 0. Alternatively, or in addition, the bilayer elastic moduli close to the channel may differ from (be larger than) the bulk moduli (Partenskii and Jordan, 2002). Either modification of the basic CEM would be compatible with the τ – d₀ results, but the former (constraining s to be 0) is difficult to reconcile with the observed effects of varying the spontaneous curvature (Nielsen and Andersen, 2000; Lundbaek et al., 1997; Andersen and Ingolfsson, 2010). These observations on the consequences of varying the modulus profile and boundary condition raise fundamental questions about the CEM. What is the proper boundary condition for the CEM? Where and in what conditions does the continuum assumption hold or break down? Can the CEM be applied to the region close to the protein/bilayer contact (e.g., the first shell of the lipids) or is it limited to some distance from the protein/lipid contact?

Protein–lipid interactions may be dominated by physical interactions near the contact because the relatively rigid protein may impose constraints on the acyl chain motions (similar to the rigidity imposed by cholesterol), and/or because more specific atomic details become more important. Hence, the choice of boundary condition for the CEM and the range of applicability of the CEM require validation from molecular-resolution experimental and computational investigations of protein–lipid interactions. In this review we use of all-atom molecular dynamics (MD) simulations to explore the lipid organization adjacent to bilayer-spanning proteins and compare the results from the CEM analyses with those obtained from the MD simulations. The MD simulations require large systems and long time scales to obtain well-converged membrane profiles, and the results are subject to the unavoidable limitations of the force fields. However, despite these limitations, all-atom MD simulations with carefully fine-tuned force fields (such as the CHARMM36 lipid force field (Klauda et al., 2010)) provide a valuable starting point for analysis which can be revisited when more accurate simulations are available. Membrane deformations also have been examined using coarse-grained (CG) models (Yoo and Cui, 2009) such as MARTINI (Marrink et al., 2007) which reduce computer requirements, but incur the risk that detailed features may be not be predicted accurately.

The following section provides additional historical background. We then compare the profiles obtained from the CEM using various boundary conditions and physical parameters with those from MD simulations of gA channels embedded in four different homogeneous lipid bilayers, and the voltage dependent anion channel (VDAC) in a heterogeneous lipid bilayer. We further explore the energetic consequences of protein-induced lipid bilayer perturbations to illustrate the usefulness and limitations of CEMs in protein-bilayer systems.

2. Historical background

The CEM was first explicitly applied to the deformation of lipid bilayers with cylindrical symmetry by Huang (Huang, 1986), using the mechanical theory developed for smectic A lipid crystals by W. Helfrich (Helfrich, 1973), which simplifies to a near-parallel structure in the continuum representation. In its original formulation, the model was assumed to be a symmetric lipid bilayer around the membrane center, and the included transmembrane protein also was assumed to have cylindrical symmetry and to be aligned normal to the unperturbed membrane surface (Fig. 1). The deformation profile u(r) usually is taken to be the distance from the ideal, non-perturbed position of the bilayer/solution interface to the actual position of the perturbed interface.

Huang evaluated the possible importance of the surface tension (ST) term, and concluded that it introduces only a small change (<3%) in the coefficient of the second term in Eq. (8). Ignoring this term leads to an analytic solution for the deformation profile. By analyzing the changes in gA channel lifetimes as a function of lipid bilayer thickness, Huang concluded that a “concave-then-convex” deformation profile (cf. Fig. 1B) that extended out to r ≈ 35A̋ provides for a suitable solution to match the gA channel lifetime in the negative hydrophobic mismatch condition. Helfrich and Jakobsson (Helfrich and Jakobsson, 1990) included the ST term in their analysis and solved the profile numerically. Their calculation confirmed that the ST term is negligible for thin membranes, but that it may become important in thicker membranes, such those containing solvent. Another analytic solution was derived by Aranda-Espinoza et al. (Aranda-Espinoza et al., 1996), where the extent of deformation region and ΔG_def were examined according to the slope boundary condition and moduli. Nielsen et al. (Nielsen et al., 1998; Nielsen and Andersen, 2000) further developed the theory by examining the effect of altering the boundary conditions at the protein/bilayer boundary (extending the analysis of Helfrich and Jakobsson). They examined the consequences of using two different boundary conditions, a free contact slope where the deformation energy is evaluated at the value of s that minimizes ΔG_def(s = s_min) and at a fixed slope (s = 0). They concluded that the s_min boundary condition underestimates ΔG_def about two-fold and that ΔG_def evaluated using the s = 0 boundary condition is in better agreement with experimental results.

The preceding studies all assumed the elastic moduli to be uniform throughout the system. This assumption was relaxed by Partenskii and Jordan (Partenskii and Jordan, 2002), who introduced space-dependent moduli variations (their model will be referred to as the PJ model). The possibility of space-dependent moduli had been raised earlier, but the PJ model was the first to examine the consequences of spatially varying moduli near the protein/bilayer boundary. This was important because even though the lipid bilayer elastic moduli have been determined for various bilayers (Nielsen and Andersen, 2000; Waheed and Edholm, 2009; Kucerka et al., 2005; Katsov et al., 2004; Chen and Rand, 1997), the presence of a protein is likely to alter the acyl chain dynamics in the vicinity of the relatively rigid protein (Fattal and Ben-Shaul, 1993). Because lipid molecules near the protein will be more constrained than in the bulk, the lipid will be stiffer which will tend to increase the elastic moduli. Assuming that the modulus profile, K(r), depends only on the radial distance r, Partenskii and Jordan expressed K(r) as:

$$K\left(r\right)=(K_0-K_{\text{bulk}})e^{-(r-r_0)∕\lambda }+K_{\text{bulk}}$$ (9)

where K₀ is the modulus at the protein/bilayer boundary, K_bulk the bulk modulus, and λ a characteristic length. Partenskii and Jordan first evaluated ΔG_def for K₀ = K_bulk and with either s = s_min or s = 0, and then varied K₀ to find the value that would make ΔG_def (evaluated at the s_min for that particular K(r) profile) equal to the ΔG_def at s = 0. They found that the modulus at the boundary should be approximately four-fold larger than the bulk value (Partenskii and Jordan, 2002) to change ΔG_def from the value estimated by Helfrich and Jakobsson (Helfrich and Jakobsson, 1990), ~4 k_BT, to a value consistent with experimental changes in single-channel lifetimes, 10 to 12 k_BT.

Choe et al. (Choe et al., 2008) suggested additional contributions to ΔG_def, such as electrostatic and non-polar contributions, and used a global minimization method to find the deformation profile. Such coupling, however, remains technically challenging. Zhou et al. (Zhou et al., 2010) introduced a formal coupling of the elastic and electrostatic interactions in a finite-element analysis of bilayer deformation, but this approach has not been extended to include membrane proteins.

Recently, Mondal et al. (Mondal et al., 2011) were able to relax the assumption of radial symmetry and extend the CEM to two-dimensional (2D) systems. They further were able to relax the assumption of strong hydrophobic coupling (with no exposure of hydrophobic and polar groups to each other). In this case, the energy-minimizing condition was determined iteratively using the curvature boundary condition at the protein/bilayer boundary.

The proper choice of boundary conditions at the protein/bilayer boundary remains to be determined. The s = s_min condition is the most widely used and the easiest to defend from a theoretical point of view, but yields poor agreement with the available experimental results. The s = 0 condition provides better agreement (assuming uniform elastic moduli), but is harder to justify theoretically. Moreover, the role of acyl chain tilt remains uncertain (Nielsen et al., 1998; Kuzmin et al., 2005). s probably should be somewhere between s = 0 and s = s_min in order to balance the need to minimize the deformation energy (in the conventional CEM) and the acyl chain packing constraints at the protein/bilayer boundary. However, one also needs to consider that the moduli on a priori grounds should vary as a function of distance from the protein. To resolve these questions and independently test the assumptions that underlie the development of CEMs of membrane protein–lipid bilayer interactions, it becomes important to compare the predictions from CEM-based descriptions with the results from all-atom MD simulations, which until recently has been impractical due to limitations in computational resources.

3. Comparison of deformation profiles from CEMs with all-atom MD simulations

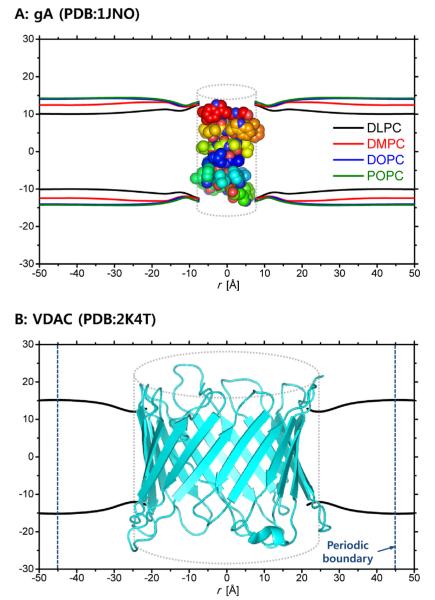
The MD-based bilayer deformation profiles to be described below were calculated using all-atom MD simulation trajectories of gA in four homogeneous lipid types (dilauroylphosphatidylcholine (DLPC), dimyristoylphosphatidylcholine (DMPC), dioleoylphosphatidylcholine (DOPC), and 1-palmitoyl-2-oleoyl-phosphatidylcholine (POPC)) (Kim et al., 2012) and VDAC in a mixed (heterogeneous) lipid bilayer containing dioleoylphosphatidylethanolamine (DOPE), dioleoylphosphatidylcholine (DOPC), and cholesterol (Rui et al., 2011). These systems are large (the number of atoms is up to ~70, 000) and were simulated for sufficiently long times to allow for calculation of reliable deformation profiles. For further details, please see METHODS in Kim et al. (Kim et al., 2012) and Rui et al. (Rui et al., 2011). The MD trajectories of the lipid molecules were converted into 2D membrane thickness profiles, tested for radial symmetry (in the case of the gA system (Kim et al., 2012)), and averaged to generate 1D thickness profiles. These profiles then were smoothed using a cubic B-spline in order to achieve numerical stability when calculating the derivatives of the profiles in Eqs. (4) and (8). Fig. 2 shows the smoothed MD profiles for gA and VDAC, and Table 1 lists the average lipid properties. The distance from the protein center to a protein-lipid contact (r₀) was 7.5A̋ (for gA) and 21.5A̋ (for VDAC), which was respectively used as the radius of the (cylindrical) protein in the CEM calculations.

Fig. 2.

The membrane (hydrophobic thickness) profiles obtained and smoothed from the MD simulations of (A) gA and (B) VDAC systems. The dotted cylinder represents the cylindrical approximation of the protein structure in the CEM and the radii are 7.5 A̋ (gA) and 21.5 A̋ (VDAC), respectively.

Table 1.

Smoothed membrane profiles based on a cubic B-spline function for gA and VDAC

Protein	Lipid type	d0 [Å]	l [Å]	∂u/∂r(r0) unitless	∂2u/∂r2(r0) [Å−1]	∂2u/∂r2(r∞)a [Å−1]
gA	DLPC	20.2	26.7	0.806	−0.067	−0.001
	DMPC	24.9	27.9	0.515	0.220	−0.003
	DOPC	28.1	28.0	0.458	0.256	0.003
	POPC	28.5	27.9	0.415	0.294	0.004
VDAC	Mixedb	30.4	25.7	0.559	−0.119	0.002

^a50 Å for gA and 45 Å for VDAC.

^bDOPE:DOPC:cholesterol = 40:40:1.

We compared various boundary conditions used in CEM calculations of ΔG_def to find the boundary condition that best reproduces the MD deformation profile. The boundary conditions examined were s₀ = 0 (Huang, 1986; Nielsen et al., 1998) and s₀ obtained from the MD profiles (s_MD). Following Helfrich and Jakobsson (Helfrich and Jakobsson, 1990), we also tested s₀ = s_min, which resulted in profiles that differed considerably from the MD profiles, and too small ΔG_def estimates. This case was not considered further. Table 2 summarizes information about the bulk elastic moduli from experiments and MD simulations. Given this information, and assuming that the MD-derived profiles fairly closely mirror the actual profiles, we calculated ΔG_def using (i) the uniform moduli in Table 2, (ii) the PJ space-dependent modulus model for all moduli, and (iii) the MD-derived area compressibility profile obtained from the gA simulations to describe the space-dependence of the other moduli. Fig. 3 shows the space-dependent modulus profiles we used.

Table 2.

Physical parameters used in the CEM calculation: K_a is the compression–expansion (area compressibility) modulus, K_c is the bending modulus, and α is the surface tension coefficient. K_a values are from experiments and our MD simulations.^a

Lipid type	Ka [10−11N/Å]	Kc [10−10N/Å]	α [10−13N/Å]
DLPC	2.34b/2.24a	5.5c	3.0d
DMPC	2.34b/2.38a	6.9c
DOPC	2.40d/2.11	3.6d
POPC	2.78e/1.97	8.5e
Mixedf	1.78g	6.6h	3.0

^afrom Kim et al., 2012.

^bfrom Waheed and Edholm, 2009.

^cfrom Kucerka et al., 2005.

^dfrom Nielsen and Andersen, 2000.

^efrom Olsen et al., 2009.

^fDOPE:DOPC:cholesterol = 40:40:1. The parameters are from the average of the DOPC and DOPE values.

^gfrom Katsov et al., 2004.

^hfrom Chen and Rand, 1997.

Fig. 3.

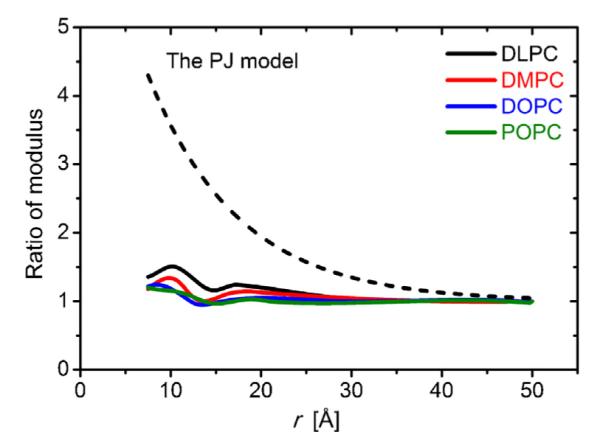
Space-dependent modulus profiles used for the gA system. We used three different choices of moduli: first, the uniform profile, which assumes that the bulk values apply throughout the system (not shown); second, the space-dependent modulus profile from Partenskii and Jordan (PJ) (Partenskii and Jordan, 2002); as well as four profiles determined from MD-based areal compressibility profiles.

3.1. Gramicidin A

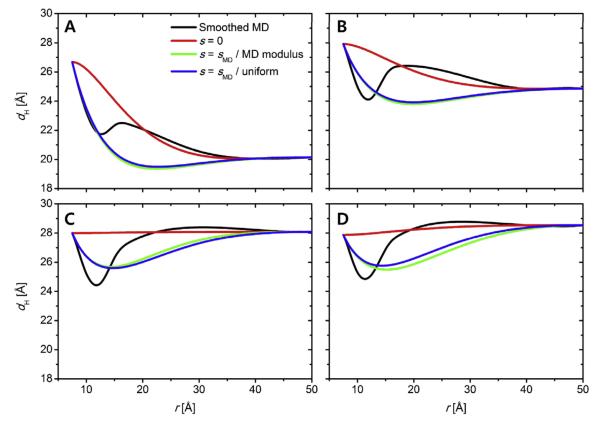
gA is a 15-amino acid peptide with an alternating l-d amino acid sequence that forms cation-selective transmembrane channels by transmembrane dimerization of single-stranded, right-handed β-helices with 6.3 residues/turn. The gA channels have been extensively used to test CEMs because the structure is known to be proximately cylindrical (PDB:1JNO (Townsley et al., 2001)).Figure 4 plots the thickness profiles (d_H) for the hydrophobic bilayer obtained from the MD simulations as well as the CEM profiles calculated using the three different boundary conditions and modulus models: (i) s₀ = 0 (red), (ii), s₀ = s_MD (green) with MD-based K(r) in Fig. 3, and (iii) s₀ = s_MD (blue) with K(r) = constant. The resulting ΔG_def and their components are listed in Table 3.

Fig. 4.

Comparison of the CEM-derived thickness profiles with the MD-derived profiles for the gA systems in membranes composed of (A) DLPC, (B), DMPC, (C) DOPC, and (D) POPC.

Table 3.

Calculated ΔG_def (in kcal/mol) for gA in four types of lipid membrane according to the boundary condition using (A) uniform moduli and (B) spatially varying moduli using the boundary condition from the MD profile. The values in the parentheses denote the contributions from the compression-expansion (CE), splay-distortion (SD), and surface tension (ST) terms

Lipid type	s0 =sMD	s0 =0
(A) Uniform modulus (experimental values)
DLPC	7.59 (2.25/5.13/0.21)	14.84 (9.45/5.28/0.11)
DMPC	4.19 (0.62/3.49/0.08)	2.72 (1.70/0.99/0.03)
DOPC	4.22 (1.11/3.05/0.06)	0.00 (0.00/0.00/0.00)
POPC	9.27 (2.74/6.47/0.06)	0.13 (0.08/0.05/0.0)
Lipid type	PJ	Area compressibility from MD
(B) Space-dependent modulus with s0 = sMD
DLPC	23.35 (8.85/13.66/0.85)	8.05 (2.38/5.42/0.25)
DMPC	11.97 (2.81/8.84/0.33)	4.42 (0.74/3.67/0.01)
DOPC	11.89 (4.16/7.49/0.24)	5.11 (1.38/3.66/0.06)
POPC	25.62 (9.88/15.53/0.21)	8.97 (2.66/6.24/0.07)

For consistency, the ΔG_def estimates are based on the hydrophobic length of the gA dimer that was deduced from the MD simulations. This length, 27–28 Å, is 5–6 Å longer than the length based on the gA structure and previous CEM analyses (Huang, 1986;Nielsen et al., 1998).

As expected, the CEM d_H profiles depend on the choice of boundary conditions, but none of the boundary conditions imposed at the protein-bilayer contact (r = r₀) reproduces the MD profiles. The s₀ = 0 profiles show the largest deviation from the MD profiles. Even though the boundary conditions were swept to search for the best-fit and energy-minimized conditions (data not shown) in addition to the plotted conditions, the CEM-derived profiles invariably show significant deviations from the MD-derived profiles. The non-monotonic (oscillating) behavior of the CEM solution was observed in earlier studies (Huang, 1986; Aranda-Espinoza et al., 1996; Nielsen et al., 1998), as illustrated schematically in Fig. 1, but the distances of the extrema in the CEM-derived profiles from the protein-bilayer contact are longer than those from MD simulations (Fig. 4). Moreover, regardless of hydrophobic mismatch condition (positive mismatch: DLPC, near match: DMPC, and negative mismatch: DOPC and POPC), all the MD profiles display minimum corresponding to the first lipid shell around the protein.

The various moduli profiles are reflected in different estimates for ΔG_def, as summarized in Table 3. Not surprisingly, ΔG_def is increased when evaluated using models in which the moduli increase near the protein, whether the increase is described by the PJ model or MD-based areal compressibility profiles. The common feature is that the splay-distortion (SD) term is the dominant contribution to ΔG_def. In the case of s₀ = s_MD, the ΔG_def estimates obtained using the uniform (experimental) moduli or the space-dependent MD-derived moduli are similar ranging from 4 to 9 kcal/mol (7–15 k_BT). The s₀ = 0 boundary condition resulted in the largest deviation from the MD-derived profile, and the energy values are inconsistent with the other observations. (For consistency among the different estimates, the gA channel’s hydrophobic length that was used in these estimates was based on the MD simulations, and 5 – 6A̋ longer than the length used in most other CEM models.) The PJ model also predicts large ΔG_def (about three-fold larger than those deduced using the uniform moduli profile), though the bilayer thickness profiles are similar (data not shown). This illustrates the importance of any modulus increased near the protein-lipid boundary.

3.2. Voltage dependent anion channel

VDAC is in the outer membrane of mitochondria, and plays an important role in cell metabolism by providing a selective pathway for the movement of anions and small metabolites between the cytosol and the mitochondrial intermembrane region (Hodge and Colombini, 1997). For the simulations, we used the NMR-derived human VDAC1 isoform (hVDAC1) structure (PDB:2K4T) (Hiller et al., 2008). The lipid bilayer profile around VDAC has zero gradient at r = 45 A̋ (corresponding to the periodic boundary in the MD simulations), and we took this point to represent the unperturbed bilayer (r_∞ = 45 A̋). The pure bulk bilayer was not realized in the MD simulations because of larger radius of VDAC as compared to gA; i.e., the distance between the nearest VDACs (between the primary system and its images) was about 90A̋ that was not sufficient for the membrane to reach its bulk condition. The vanishing boundary at r = 45 A̋ includes the areal density of VDAC, which is another energy component associated with inserting a protein into a lipid bilayer. The MD-derived membrane profiles were fitted by the CEMs using s_MD with uniform moduli and the PJ model (Fig. 5). As was the case for gA, any combination of boundary conditions failed to reproduce the MD profile. Again the transition from the protein-lipid to the bulk condition in the CEM profiles extends longer than in the MD profile. The resulting ΔG_def estimates are 73.43 kcal/mol (ΔG_CE = 12.48/ΔG_SD = 60.46/ΔG_ST = 0.48) with uniform moduli and 211.15 kcal/mol (44.06/165.60/1.49) with the PJ model. As was the case for the gA, the PJ model resulted in about three-fold larger ΔG_def values than those with the uniform moduli profile. In contrast to the gA cases, however, the change in the elastic moduli profile affected the membrane deformation profiles in the case of VDAC.

Fig. 5.

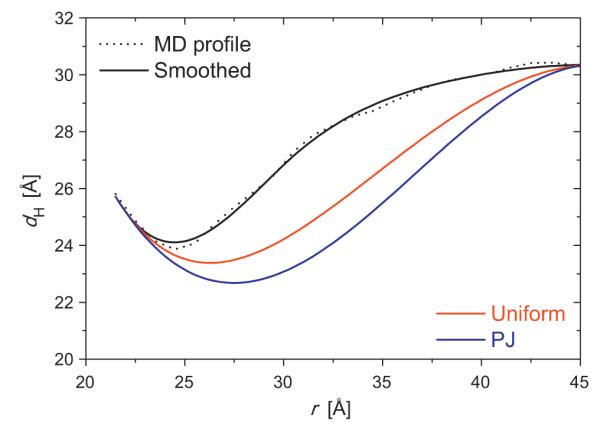
Comparison of the thickness profiles around VDAC from MD and CEM. The black lines are for the MD-derived profile (dotted) and its smoothed profile (solid). The boundary conditions for the CEMs were from the MD profiles (s₀ = s_MD) with uniform modulus (red) and the PJ model (blue). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Concluding discussion

CEMs have been used for more than 25 years to understand the energetics in protein-induced lipid bilayer deformations. The range of validity of the CEM calculations remains uncertain, however, because direct comparison with experiments or MD simulations have been hindered by insufficient experimental resolution (which still is true) and the computational demands for well-converged molecular simulations (where the resources are beginning to become available). Concerns about the applicability of CEMs arise because the protein–lipid bilayer interactions are simplified (choice of boundary condition and uncertainty about the spatial variation of the elastic moduli), which is known to impact on estimates of ΔG_def. To begin addressing these issues, we have reviewed the variations in the CEMs and compared predictions obtained using the CEMs with those from the all-atom MD simulations.

Both the gA and the VDAC systems show that the deformation in the first lipid shell around the protein is not fully described by the CEMs. The most noticeable difference between the MD- and the CEM-derived profiles is the extent of the oscillating region (Figs. 4 and 5). The length of the transition region is much shorter in MD than CEM, meaning that the protein–lipid interactions exert short-range effects on the membrane deformation. The continuum representation in the first lipid shell appears to be over-simplified, indicating that a different physical model will be needed to account for the deformation profile in the first lipid shell. Beyond the first lipid shell, the CEM seems to be in good agreement with the MD profiles. It is possible to improve the prediction of ΔG_def (relative to experimental values), but the effects on the deformation profile turn out to be modest, at least in the case of gA. In this context, it is important that, while bulk moduli are known for many different bilayers, there is little information about their space-dependent properties. We also note that, though the area compressibility (K_a) can be accurately estimated from MD simulations, the bending moduli (K_c) are more difficult to obtain.

Comparison of the CEM- and MD-derived results shows that protein–lipid interactions profoundly alter the conditions assumed in the development of the CEMs. This conclusion, though dependent on the force fields used in the MD simulations, is unlikely to change as more accurate simulations become available. More realistic consideration of global energetics probably would require that Eq. (3) includes explicitly any interactions between protein and lipid, as well as the residual exposure contribution identified by Mondal et al. (2011). This would be particularly important for the first lipid shell around the protein. The deformation profile should eventually be calculated by minimizing ΔG_def plus the other energy contributions—including electrostatics and non-polar energies—and the space-dependent behavior of the elastic moduli. Eventually, one probably would need to reformulate Eq. (3) to include asymmetric bilayer deformations, as well as possible redistribution of the membrane lipids within the perturbed bilayer, for more realistic analysis of membrane–protein interactions.