Dispersion of Response Times Reveals Cognitive Dynamics

Abstract

Trial to trial variation in word pronunciation times exhibits 1/f scaling. One explanation is that human performances are consequent on multiplicative interactions among interdependent processes – interaction dominant dynamics. This article describes simulated distributions of pronunciation times in a further test for multiplicative interactions and interdependence. Individual participant distributions of ≈1100 word pronunciation times are successfully mimicked for each participant in combinations of lognormal and power law behavior. Successful hazard function simulations generalize these results to establish interaction dominant dynamics, in contrast with component dominant dynamics, as a likely mechanism for cognitive activity.

Cognitive studies of response times almost always concern components of cognitive architecture. This article is not about cognitive architecture. Instead, it poses a complementary question: How do the essential processes of cognitive activities interact to give rise to cognitive performance? The shapes of response time distributions supply information about how a system’s processes interact. The response time data used to answer this question come from speeded naming of individual printed words. The characteristic shapes of pronunciation time distributions (and their hazard functions) reveal the kind of interactions generally in cognitive activity.

This is not a new idea, and a familiar precedent exists for the logical inferences that are required. Familiar Gaussian distributions also support conclusions about how components interact, without requiring first that one know the identities, or details, of interacting components. This logic is introduced next using the example of skilled target shooting. Ballistics research was historically very important in the discovery and characterization of Gaussian distributions. The explanation is somewhat tutorial, however, and readers who are familiar with how dispersion informs system theories and with the properties of lognormal and power law distributions could skip forward to the Cocktail Hypothesis.

Dispersion and Interactions among System Components

A skilled target shooter’s bullets form a familiar bell-shaped pattern around a bull’s-eye. Strikes mostly pile up close to the bull’s-eye. Moving further from the bull’s-eye, on any radius, fewer and fewer strikes are observed. This pattern of bullet strikes is distributed as a bivariate Gaussian distribution, a fact worked out in late 19^th and early 20^th century ballistics research. The Gaussian provides a relatively complete statistical description of how the bullet-strikes are distributed.

Theoretical conclusions about the idealized bivariate Gaussian distribution explain how separate components of the target-shooting system combine to distribute bullet strikes in the Gaussian pattern. The dispersion or variability around the bull’s-eye is the product of small accidental differences from shot to shot in the shape of the shell, the shell casing, and the amount of gun powder in the shell, plus other innumerable weak, idiosyncratic, independently acting factors or perturbations (Gnedenko & Khinchin, 1962). Each perturbation influences the trajectory of the projectile, if ever so slightly, on any given discharge of the weapon. All these independent causes of deviation add up to determine where the shooter’s bullet will strike, the measure of distance from the bull’s-eye.

Prior to this corroboration in ballistics, Laplace had worked out the relation between additive interactions and dispersion of measurements. Laplace reasoned that each measurement reflects the sum of many sources of deviation. This reasoning about dispersion of measurements allowed him to apply his central limit theorem. From that, he deduced that the overall distribution of measurements would appear in a bell-shape, a curve that had been recently described by Gauss, and prior to that, by De Moivre (Porter, 1986; Stigler, 1986; Tankard, 1984).

Laplace’s reasoning anchored Gauss’s curve in explicit assumptions about the system being measured and how components interact to yield dispersion in the bell shape. These abstract assumptions were justified empirically in the later application to ballistics. Ballistics research effectively proved that large numbers of perturbations sum-up their effects in ballistic trajectories to produce the Gaussian pattern (Klein, 1997). By the beginning of the 20^th century, the abstract Gaussian description was trusted to describe the dispersion of measurements of almost any system (Stigler, 1986).

Gaussian distributions come from systems whose behavioral outcomes are subject to vast arrays of relatively weak, additive, and independently acting perturbations. Weak interactions among causal components insure that perturbations affect components locally, individually, which allows effects to be localized in individual components. Weak interactions thus insure component dominant dynamics because the dynamics within components dominate interactions among components.

Given the inherent links between additivity and research methods to identify causal components (cf. Lewontin, 1974; Sternberg, 1969), the question of how components interact, arguably has priority over identifying components themselves. At least, one would want to establish first that components interact additively, before applying the general linear (additive) model to infer components in component effects. If components interact in some way other than additive, then scientists require research methods appropriate to the other kind of interaction – at least that is our contention (Riley & Turvey, 2002; Riley & Van Orden, 2005; Speelman & Kirshner, 2005; Van Orden, Kello, & Holden, in press; Van Orden, Pennington, & Stone, 2001).

Of course one could always mimic evidence of additive interactions in ways that do not truly entail weak additive interactions and component dominant dynamics, by artfully mimicking the Gaussian shape for example. No theoretical conclusion is ironclad. Consider, on the one hand, even strongly nonlinear and discontinuous trajectories can be mimicked in carefully chosen component behaviors, combined additively. On the other hand, linear behaviors are not rare, even for systems of strongly nonlinear equations, which can make the term nonlinear dynamics appear superficially like an oxymoron.

Still we accept assumptions that predominate empirically and provide simple yet comprehensive accounts, while we trust that scientific investigation, over the long term, will root out false assumptions. For example, the association between Gaussian patterns of dispersion and component dominant dynamics became so useful, so engrained, and so trusted, as to license the logical inverse of Laplace’s central limit theorem. Thus, when an empirical distribution appears Gaussian, then the system must be subject to vast arrays of relatively weak, independently acting perturbations because it produced a Gaussian distribution. The Gaussian inference trusts empirical patterns of dispersion to reveal intrinsic dynamics as component dominant dynamics.

A reliable Gaussian account includes trustworthy links between ideal description, empirical pattern, and intrinsic dynamics of the system in question — how the components of a system interact. The account moves beyond superficial description to become a reliable systems theory. Understandably, early social scientists like Galton and Pearson looked to this reliable theory for inspiration (Depew & Webber, 1997; Klein, 1997; Porter, 1986; Stigler, 1986). The crucial point for the present article is that we can know how processes interact without knowing what these processes are. The necessary information is found in the abstract shape of dispersion alone.

Multiplicative Interactions and Lognormal Dispersion

At the beginning of the 21^st century, other abstract distributions of measured values vie for scientists’ attention. Many physical, chemical, and biological laws rely on multiplicative operations, for instance, which yield a lognormal pattern of dispersion in measurements (Furusawa, Suzuki, Kashiwagi, Yomo, & Kaneko, 2005; Limpert, Stahel, & Abbt, 2001). We stay with the metaphor of ballistics to explain how multiplicative interactions deviate from the additive Gaussian pattern.

Imagine a slow motion film that tracks a bullet’s trajectory from the point it exits a rifle’s muzzle to its entry point at the target. At any point along its trajectory, the bullet’s location on the next frame of film, after the next interval of time, can be predicted by adding up the effects of all the independent perturbations that acted on the bullet, up to and including the present frame.

Sources of variation are independent of each other. Some push left, some right, some up, some down, and most push in oblique directions, but the overall effect is represented simply by their sum. Large deviations from the bull’s-eye are uncommon, for a skilled shooter at least, and a sufficient number of bullet strikes will yield the expected Gaussian pattern.

Imagine next a magic bullet for which sources of variation combine multiplicatively. This violates the Newtonian mechanics of bullets, of course, but we pretend that our magic bullet exists. Each change in the magic bullet’s trajectory is the product of the current trajectory and the force of the perturbation.

For magic bullets, sometimes multiplication has a corrective influence and shrinks the effects of previous perturbations, when the multiplier is greater than zero but less than one. Other times the multiplier amplifies previous perturbations and exaggerates the dispersion that they cause, when the multiplier is greater than one.

For magic bullets, corrective multiplicative interactions tend to concentrate bullets already close to the bull’s-eye, in a tighter distribution, while amplifier multiplications produce more extreme deviations away from the bull’s-eye. Multiplication erodes the middle range of deviation compared to addition. It produces a dispersion of bullets that is denser at its center and more stretched out at the extreme.

The result, in the limit, appears as a lognormal distribution. The name comes from the fact that a lognormal will reappear as a standard Gaussian or normal distribution, if its axis of measurement undergoes a logarithmic transformation. The transformation redistributes the variability to become once again a symmetric Gaussian distribution as a comparison of Figures 1A and 1B illustrates.

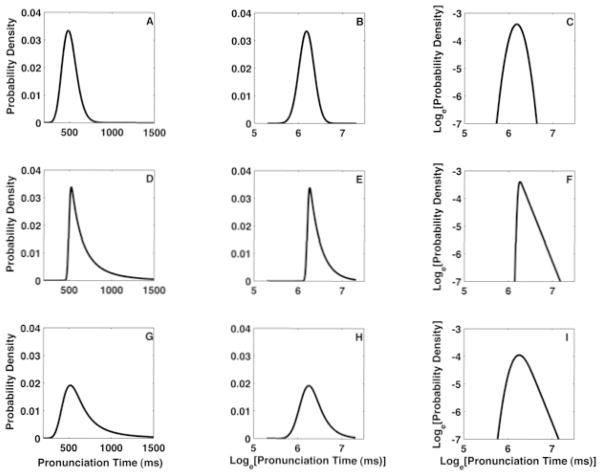
Figure 1.

Panel A illustrates an ideal lognormal probability density function, plotted on standard linear axes. The X-axis depicts response time and the Y-axis tracks the probability of observing a response time in any given interval of time. Panel B depicts the same density, now on log-linear axes, where it appears as a symmetric, standard Gaussian density. Panel C depicts the same density curve now plotted on double-logarithmic axes, where it appears as a downward turning parabola. Panel D depicts an ideal inverse power-law density on standard linear axes. Panel E depicts the same power-law density on log-linear axes. Notice that the power-law density maintains its extreme, slowly decaying tail distinct from a simple exponential-tailed density, which falls off linearly on log-linear scales. The power-law density falls off as a line on double-logarithmic axes, as in panel F, the characteristic footprint of a power-law scaling relation. The density in panel G depicts an idealized 50%-50% “cocktail” of the two density functions, on standard linear axes. Panel H depicts the same mixture density in log-linear domain, and it is depicted in the double-logarithmic domain on panel I. Depicting the probability density functions on the different scales helps to distinguish them from other potential ideal descriptions.

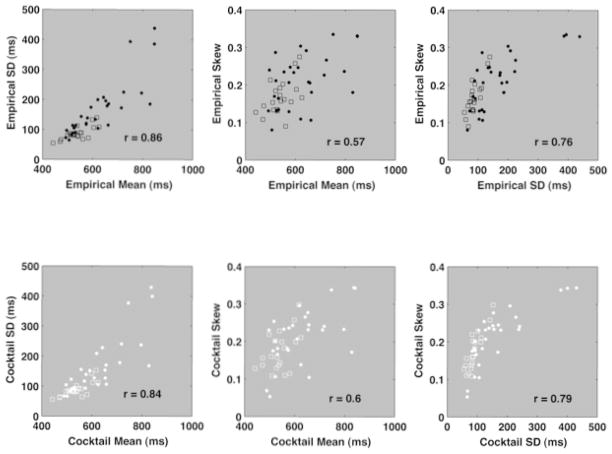
Gaussian and lognormal patterns are closely related. As such, they share the assumption that variation comes from perturbations of independent processes. Multiplication in the linear domain equals addition in the logarithmic domain. If vast arrays of independent perturbations interact as in a serial chain of multiplications, then event times such as response times will be log-normally distributed. Independent processes also imply that both distributions are additive, one on a linear scale and the other on a logarithmic scale.

Yet lognormal distributions are produced by multiplicative interactions, which also makes them cousins to multiplicative interdependent interactions. Multiplicative interdependent interactions produce power laws. As kin to power laws, systems that produce lognormal distributions illustrate a stable, special case of interdependence. Lognormal dispersion is found in multiplicative feedback systems for which the interacting processes are sufficiently constrained (Farmer, 1990). Sufficiently constrained interactions quickly stabilize solutions, minimizing the empirical consequences of feedback, and giving the impression of independent processes. Next, we discuss multiplicative feedback more generally and its consequences for dispersion of measurements.

Multiplicative Feedback Interactions and Power Law Dispersion

Aggregate event times of interdependent processes accumulate in lawful patterns called power laws. Specifically, in the aggregate, interdependent processes produce response times, or event times, in the pattern of an inverse power-law — a straight line on an X-axis of (log) magnitude and a Y-axis of (log) frequency of occurrence. For example, fast response times are relatively common and very slow response times are rare. If the pattern is a power law, however, then the frequency of occurrence of a particular response time will be directly related to its magnitude.

The probability of a particular event time equals beta times that event time raised to the power of negative alpha. Alpha is a scaling exponent that describes the rate of decay in the slow tail of the distribution. Beta is a scaling term; it moves the equation up and down on the Y-axis. (This is clearer in Equation 2 in which Equation 1 has been transformed by taking the logarithm of both sides.) The power law relation is represented in Equations 1 and 2.

$$\text{P}(\text{event}\text{time})=\beta \ast \text{event}{\text{time}}^{-\alpha }$$ (1)

$$log[\text{P}(\text{event}\text{time})]=-\alpha \ast log(\text{event}\text{time})+log(\beta )$$ (2)

Notice that Equation (2) is simply the equation for a line; the (log) probability of an event time equals negative alpha (slope) times the (log) event time itself plus a constant (log(beta)). The graph of an ideal inverse power-law is simply a line with a negative slope on double-logarithmic axes (see Figure 1F). The key term in these equations is alpha. Alpha is the exponent of the power law and describes the rate of decay in the skewed tail of the distribution.

Equation 1 will diverge as event times approach zero. Consequently, raw variables are often normalized to make beta intercept the Y-axis. Instead, in Figure 1, the graphic depiction of the power law appends a low-variability, lognormal front-end to “close up” the probability density. This allows the probability density function to be shifted off the Y-intercept, and to resemble standard probability density functions of response time.

The power law equations 1 and 2 describe possible patterns of dispersion in measurements. Recall that the dispersion of measurements in ballistics was due to a vast array of independent perturbations, of bullet casings, powder load, and so on. Interdependent interactions are likewise subject to vast arrays of perturbations, amplified in recurrent multiplicative interactions due to feedback. Feedback behavior is also lawful behavior in this case and the dispersion of (log) event times remains proportional to the magnitudes of the perturbations.

Many natural systems yield event magnitudes that obey inverse power-laws and power laws are associated with a wide array of organisms, biological processes, and collective social activities (Bak, 1996; Farmer & Geanakoplos, 2005; Jensen, 1998; Jones, 2002; Mitzenmacher, 2003; Philippe, 2000; West & Deering, 1995). Allometric laws are examples of power-law scaling in biology, although they are not statistical distributions like the topic of this article. Power law dispersion most like response time dispersion includes Zipf’s law, earthquake magnitudes, book and online music sales, and scientific citation rates (Anderson, 2006; Turvey & Moreno, 2006). These are all succinctly described as inverse power-law distributions.

Anderson (2006) and Newman (2005) include more examples of power law behavior. Newman (2005) and Clauset, Shalizi, and Newman (2007) are good sources for mathematical and statistical details of power-laws. The key to understanding power-law behavior is amplification via multiplicative feedback, to which we will return several times in this article.

The feedback interactions that produce power law behavior are called interaction dominant dynamics (Jensen, 1998). Feedback spreads the impact of perturbations among interacting components. Consequently, one can no longer perturb individual components to produce isolated effects. Multiplicative feedback creates stronger interactions among components and distributes perturbations throughout the network of components. It is this property of interaction dominant dynamics that promotes a global response to perturbations, in systems that organize their behavior in multiplicative feedback.

The Cocktail Hypothesis

The previous sections introduced power law and lognormal distributions. Cognitive dynamics are multiplicative if response time distributions entail either or both of these distributions. Cognitive dynamics are interdependent if response times are distributed as power laws. Multiplicative interdependent dynamics are interaction dominant dynamics, as noted in the previous paragraph.

Interaction dominant dynamics insure necessary flexibility in cognition and behavior (Warren, 2006). Flexibility is achieved when interaction dominant dynamics self-organize to stay near choice points, called critical points, which separate the available options for cognition and behavior, thus the technical term self-organized criticality (Van Orden et al., 2003a). Interaction dominant dynamics anticipated widely evident fractal 1/f scaling, found in trial series of response times and other data (Gilden, 2001; Kello, Anderson, Holden, & Van Orden, 2008; Kello, Beltz, Holden, & Van Orden, 2007; Riley & Turvey, 2002).

This article is not about 1/f scaling, however. The predictions tested here simply derive from the shared parent hypothesis, interaction dominant dynamics, which predicted fractal 1/f scaling. The shared parent strictly limits choices for possible distributions of response times. Most famously and straightforwardly it favors data distributed as an inverse power law relating the magnitude (X-axis) and likelihood (Y-axis) of data values (Bak, 1996).

Of course response times are not exclusively power laws, thus the hypothesis of lognormal behavior for the fast front end. Lognormal behavior is a motivated hypothesis due to its theoretical relation to power law behavior. The theoretical explanation can be found in West and Deering (1995), for example, who place power law and lognormal behavior on a continuum with Gaussian distributions (see also Montroll & Shlesinger, 1982).

The Gaussian, a signature of weak additive interactions among independent, random variables – component dominant dynamics – is at one end of the continuum. At the other extreme is the inverse power law, a signature of interdependent multiplicative interactions – interaction dominant dynamics. The lognormal stands between the two extremes because it combines independent, random variables with multiplicative interactions.

In our turn, we added one fact to the above: Power law behavior transitions to lognormal behavior if sufficient constraints accrue to mask superficial consequences of feedback. For example, this is observed in generic recurrent “neural” models in which available constraints include configurations of connection weights (Farmer, 1990). More generally, available constraints derive from history, context, the current status of mind and body, the task at hand, and their entailments – available aspects of mind, body and world that reduce or constrain the degrees of freedom for cognition and behavior (Hollis, Kloos, & Van Orden, 2008; Kugler & Turvey, 1987).

Notice how constraints naturally motivate new predictions about mixtures of power law and lognormal behaviors, and the direction of change in relative mixtures as interactions become more or less constrained, due to practice or rehearsal for example (cf. Wijnants, Bosman, Hasselman, Cox, & Van Orden, 2009), or aging, damage, and illness (cf. Colangelo, Holden, Buchanan, & Van Orden, 2004; Moreno, Buchanan, & Van Orden, 2002; Van Orden, 2007; West, 2006). Available constraints determine the mixture of power law and lognormal dispersion, which invites analyses that may reject either lognormal, power law, or the mixture of both in response time dispersion.

Figure 1 summarizes the ideal patterns of dispersion on linear, log-linear, and log-log axes (see caption). Figure 1 also illustrates a cocktail mix of power law and lognormal dispersion. Each pronunciation time is sampled from either a power law or a lognormal that in the aggregate makes a power-law/lognormal cocktail. We call this a cocktail because each word’s pronunciation time, like a liquid molecule in a cocktail, comes from separate power-law or lognormal bottles. In the subsequent cocktail, response times are mixed in proportions that pile up as a participant’s aggregate distribution. The proportion of power law behavior and the exponent of the power law are the key parameters of this hypothesis.

Like a cocktail, different collections of response times, from different participants, from different task conditions, from the same participant on different tasks, or from the same task on different occasions, can be a different mix of power law and lognormal behavior. The mix proportions can range from predominantly power law behavior to almost exclusively lognormal – lognormal straight up with a dash of power-law so to speak (compare Holden, 2002; Van Orden, Moreno, & Holden, 2003).

Notice that each response time could summarize deterministic, stochastic or random component contributions, or all of the above. The cocktail hypothesis generalizes across all these cases because we make no assumptions about the intrinsic dynamics of components, only about how they interact. The total event time combines all factors in multiplicative interactions yielding a response time that is either a power law or lognormal sample.

The Hazard Function Test

We now introduce a test for generality of the cocktail hypothesis. In the early chapters of Luce’s (1986) classic survey of response time studies, he underscored the importance of reconciling cognitive theory with the widely identified characteristic shapes of response time hazard functions. Hazard functions are mathematical transformations of probability density functions and their cumulative distributions. They portray information so that new questions can be asked about the probability of events. For instance, the hazard function portrait answers the question ‘What is the likelihood that an event will occur now given that it has not occurred so far?’ We describe more details of hazard functions later, but here we focus on how they function as a test of generality.

Three characteristic shapes are found for hazard functions across otherwise different laboratory tasks and manipulations. The three shapes emerge in single experiments designed to examine a single kind of performance, such as word pronunciation. A risk of paradox exists because the three shapes could indicate qualitatively different dynamics (Luce, 1986); such heterogeneity could require that analyses re-focus on details of intra-individual variation for instance (Molenaar, 2008).

Consequently, although hazard functions are typically ignored in response time studies, they are nonetheless sources of limiting constraints for theories of response time (Ashby, Tien, & Balakrishnan, 1993; Balakrishnan, & Ashby, 1992; Maddox, Ashby & Gottlob, 1998). Arguably, characteristic hazard functions offer critical linchpins between data and theory because they are so difficult to simulate with limited ad-hoc assumptions (Luce, 1986; Maddox et al., 1998; Van Zandt & Ratcliff, 1995).

It is this fact, that they are not easily mimicked, that makes hazard functions useful to test generality. For instance, all other things equal, to mimic the full shape of a probability density function is to provide a more complete account of response times, compared to accounts focused on summary statistics like means or standard deviations. In the same vein, to successfully mimic a hazard function also expands the inclusiveness, completeness, and generality of an account. Townsend (1990) used these facts to argue why the qualitative ordering of hazard functions is more diagnostic than an ordering of condition means or even probability density functions, for example.

Thus, in the present case, all other things equal, if mathematical transformations of simulated density functions yield the same hazard functions as their empirical counterparts, then the simulations have met a much greater challenge than density functions alone. Generality accrues in meeting this challenge because one can successfully mimic empirical density functions, for example, and still fail to mimic their derived hazard functions, but not vice versa. Consequently, in the existence proofs that follow, we fit individual participants’ density functions of word naming times and also fit participants’ hazard functions.

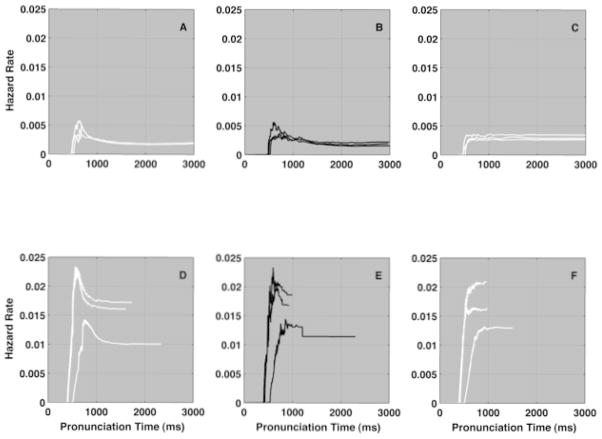
As the simulations will reveal, one easily recognizes in the cocktail simulations the characteristic hazard functions that other cognitive scientists have so carefully excavated. Luce (1986) and Maddox, et al. (1998) describe the three characteristic empirical hazard functions of response time distributions: Either the hazard function rises monotonically to an asymptote (compare Figure 2G), or it rises rapidly to a peak and then declines to an asymptote (Figure 2H), or it rises rapidly to a much higher peak and then falls off sharply (Figure 2I). This remarkably succinct characterization of response time outcomes in very many or all cognitive tasks is a basis for another kind of generality. A theory of response times that explains the three characteristic hazard functions generalizes to response times at large.

Figure 2.

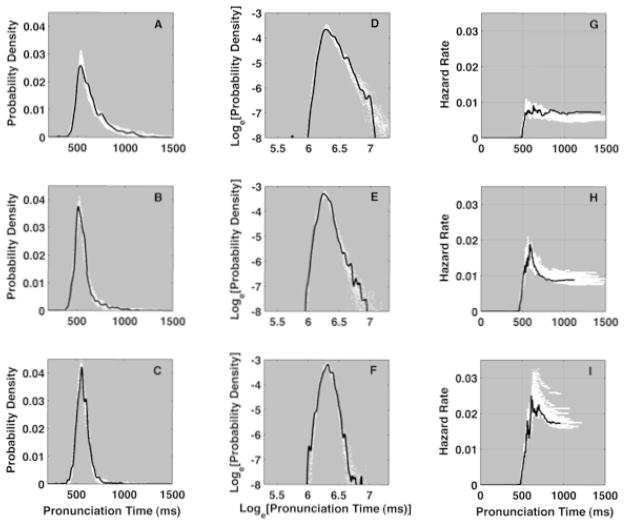
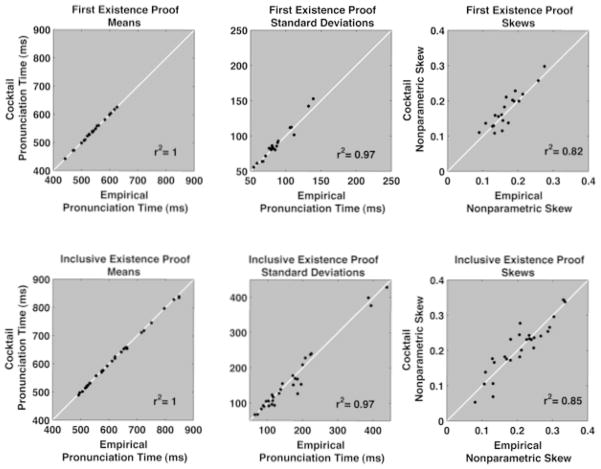
Three characteristic hazard functions found generally in response time data and the distributions of pronunciation times from which they were computed, on linear (A, B, C) and log-log (D, E, F) scales. Panels A, B, & C correspond to pronunciation times of three individual participants from the first existence proof. The heavy black line in each panel is the probability density of one participant’s pronunciation time distribution. The white points surrounding each black line, in each panel represents 22 simulation mixtures of ideal lognormal and inverse power-law distributions, using fixed parameters of synthetic distributions in a resampling or bootstrap technique (cf. Efron & Tibshirani, 1993). The boundaries established by the white clouds of the 22 simulated distributions circumscribe a 90% confidence interval around each empirical probability density and hazard function.

An Existence Proof Using Word Pronunciation Times

We begin with an existing data set of word pronunciation times (Thornton & Gilden, 2005; Van Orden, Holden, & Turvey, 2003a). A word pronunciation trial presents the participant with a single word that they pronounce aloud quickly. Pronunciation time is measured from when the word appears until the participant’s voice triggers a voice relay. The data come from a word pronunciation experiment in which 1100 pronunciation trials present four- and five-letter monosyllabic words in a unique random order, across trials, to each of 20 participants, one word per trial. Empirical power laws can only be distinguished in the slow extremes of rare response times and large samples of within-participant response times better fill out the slow extremes of a person’s response time distribution.

Simulations of Participant Probability Density Functions

Figures 2A, 2B, and 2C depict three individual participants’ pronunciation time, probability density functions. The smooth and continuous functions are products of a standard procedure of nonparametric, lognormal-kernel smoothing (Silverman, 1989; Van Zandt, 2000; a lognormal-kernel is equivalent to a Gaussian-kernel in the log-linear domain). Construction of density functions, including smoothing, was done after a logarithmic transformation of raw pronunciation times. The three figures illustrate the three categories of distributions that produce characteristic hazard function shapes. We explain more details of hazard functions after describing the methods used to simulate individual participants’ probability density functions.

Simulation Methods

Cocktail mixture simulations were conducted to capture each of the 20 shapes of empirical density curves from the 20 participants’ data reported in Van Orden et al. (2003a). Simulations mixed together synthetic samples from parent distributions of inverse power-law and lognormal pronunciation times. As the simulations demonstrate, the sample mixtures suffice to mimic participant data. Each choice of parameter values mimicked one participant’s pronunciation time distribution.

Data preparation

The criteria to select the data points to be simulated were conservatively inclusive. In a sample of the skilled word-naming literature, the most conservative criteria for exclusion were cutoffs less than 200 ms and greater than 1500 ms (cf. Balota, Cortese, Sergent-Marshall, Spieler, & Yap, 2004; Balota & Spieler, 1999; Spieler & Balota, 1997). We also included the small proportion of pronunciation times that resulted in errors because it did not change the outcome (M = 2.12%, SD = 1.48%). Inclusion of error response times is also conservative; we assume errors are produced by the same dynamics that produce correct pronunciations.

The total number of simulated response times, from a participant’s data set, equaled the total number of pronunciation times that were greater than or equal to 200 and less than or equal to 1500 ms. The maximum possible number was 1100. The actual number varied from participant to participant (M = 1094, SD = 8.76). The number of empirical observations on this interval determined the number of synthetic data points generated in the same interval on each replication of a simulation.

Parameters

The cocktail simulations included seven parameters: The mode Ω_PL and exponent α of the inverse power-law, the lognormal mode Ω_LN and standard deviation σ, the sample mixture proportions ρ_FLN and ρ_BLN that index relative proportions of lognormal behavior on each side of the lognormal mode, and ρ_PL that indexes the proportion of power-law behavior in the slow tail. Only two of the three proportion parameters were free to vary, since the relative proportions must sum to one. Thus six parameters were available to simulate individual patterns of dispersion across participants. By comparison, standard diffusion models that simulate decision time data collapsed across participants include at least seven parameters and up to nine have been used in some circumstances (Wagenmakers, 2008).

On log-response-time axes the mode Ω_LN of a parent lognormal is also its midpoint. The standard deviation σ controls relative width around this midpoint. The mode Ω_PL of the parent power-law is also its maximum probability and its starting point — i.e. the minimum or fastest response time on the X-axis at which power law behavior is inserted. On double logarithmic axes, the exponent parameter α indexes the rate of linear decay of the slow power-law tail. On linear axes, the slow tail of the distribution diminishes as the curve of power-law decay (e.g., compare Figure 1F with Figure 1D).

Choosing the mode parameters

Almost all parameter choices for synthetic parent distributions were equated with estimated parameters of participant’s empirical distributions. For example, in most cases the parent lognormal mode Ω_LN was equal to the estimate of the mode of the target empirical distribution with the following caveat: The mean, not the mode, is specified in equations that define the shape of a lognormal density. However, on log axes the mean and mode are equal in the statistical long run and the mode is relatively impervious to extreme values in the slow tail. Since the parameters of the lognormal densities were specified in the logarithmic domain, it was convenient to substitute the log of the empirical modes in these equations.

The value of the empirical mode was established using a bootstrap routine that repeatedly re-sampled and estimated the location of the empirical mode (Efron & Tibshirani, 1993). Thirteen of the twenty participant’s distributions were successfully approximated using lognormal mode parameters pulled directly from the mode statistics of the empirical distributions. Seven additional distributions required a slight adjustment of the statistical estimate of the mode to align the empirical and synthetic distributions.

Some empirical distributions appeared to be bi-modal, which can be accommodated by setting the faster-time mode equal to the lognormal mode Ω_LN and the slower-time mode equal to the power law mode Ω_PL. Thirteen of the 20 empirical distributions were bimodal; the average difference between modes was 29 ms. Apparent spurious bimodality was also present however (e.g., two modes very close to each other). Spurious versus real bimodality was judged from the hazard functions, where real bimodality has a more prominent effect. For seven participants’ simulations the power law mode Ω_PL and lognormal mode Ω_LN were equivalent.

Choosing the dispersion parameters

The seed estimate to find a standard deviation (σ) for the parent lognormal came from a conventional error-minimization fitting routine. The routine fits a lognormal curve to the fast front curve of the empirical distribution, up to and including the empirical mode. Past this point however the standard deviation parameter σ was adjusted by hand to improve the fit.

All synthetic pronunciation times less than or equal to an empirical distribution’s (fastest) mode (the Ω_LN parameter) were sampled exclusively from the lognormal parent. In every case, the proportion of synthetic lognormal data points was the same as the corresponding proportion of the participant’s data points, less than or equal to the empirical mode. The parameter ρ_FLN indicates the proportion of synthetic times less than or equal to the mode Ω_LN.

The parameter ρ_BLN equals the maximum proportion of synthetic lognormal times greater than Ω_LN. The actual proportion of synthetic lognormal times greater than Ω_LN depends on the tradeoff of lognormal and power law behavior in the slow end of the simulated distribution. The slow tails of distributions were hand fit using small adjustments to the two remaining free parameters—namely the exponent parameter α and the proportion ρ_PL of power law behavior in the slow tail mixture. Synthetic mixtures were eyeballed and adjusted using a program that allowed visual comparison of synthetic and empirical density and hazard functions. The program required that all parameters were set to some value in any and all adjustments.

Synthetic lognormal/power law mixture densities were realized in the following manner. First, both a lognormal and a power law density function, defined according to specific mode and dispersion parameters were generated and normalized to occupy unit area within the specified response time interval. The densities were then combined in the required proportions, on either side of the lognormal mode, according to a formula for generating mixture densities provided by Luce, (1986, pp. 274–275). The equation for a normalized power law density appears in Clauset, et al. (2007). The resulting cocktail density was then transformed to a cumulative distribution function. Following that, a rectangular unit-interval random number generator was used to produce the required number of synthetic samples from the inverse of the mixture distribution function.

Initially the power-law exponent parameter α was set to a relatively small “shallow” value. If initial attempts to mimic the empirical distribution failed across a range of mixture proportions then the exponent of the parent power-law was increased to a larger “steeper” value and another attempt was made. Trial-and-error fitting continued until an apparently optimal choice of parameters was reached to approximate the density (and hazard) function of a participant’s data. Table 1 lists the parameter values of the parent distributions for each participant’s simulated data.

Table 1.

Lists parameters of the parent lognormal and power-law distributions, and the proportion of power-law samples used in the simulations. The participant numbers were established by ordering each distribution in terms of the empirically estimated slope of the tail of the distribution. This explains why the participant numbers correspond to a close rank ordering of the α parameter. Participants numbered 1 and 2 were classified as power-law dominant; participants numbered 17 through 20 were classified as lognormal dominant. The remaining participants were classified as intermediate mixtures. The full collection of simulations can be viewed as an on-line supplement at http://www.csun.edu/~jgh62212/RTD.

Parameters used to generate synthetic distributions for the first existence proof.

Participant	Mo ΩLN	SD σ	Mo ΩPL	PL Tail α	F LN Prop ρFLN	B LN Prop ρBLN	PL Prop ρPL
1	6.25	0.1	6.27	6	0.311	0.019	0.670
2	6.256	0.095	6.256	5.5	0.241	0.000	0.759
3	6.32	0.11	6.46	7.75	0.370	0.397	0.233
4	6.123	0.085	6.24	8.5	0.315	0.405	0.280
5	6.2	0.09	6.21	7.5	0.355	0.045	0.600
6	6.37	0.11	6.37	8	0.379	0.001	0.620
7	6.254	0.11	6.4	8	0.474	0.446	0.080
8	6.1269	0.09	6.23	8.5	0.293	0.347	0.360
9	6.205	0.1	6.205	8.75	0.417	0.000	0.583
10	6.349	0.1	6.51	8	0.494	0.466	0.040
11	6.253	0.095	6.253	7.5	0.428	0.192	0.380
12	6.24	0.11	6.24	8.75	0.476	0.224	0.300
13	6.236	0.09	6.3	7.75	0.375	0.425	0.200
14	6.14	0.1	6.25	8.25	0.513	0.407	0.080
15	6.176	0.12	6.28	8.5	0.378	0.452	0.170
16	6.23	0.11	6.23	8.5	0.436	0.204	0.360
17	6.254	0.085	6.27	8.5	0.371	0.089	0.540
18	6.144	0.11	6.165	10	0.525	0.295	0.180
19	6.04	0.08	6.06	10	0.370	0.230	0.400
20	6.304	0.09	6.4	10	0.445	0.465	0.090
Mean:	6.22	0.1	6.28	8.21	0.398	0.255	0.346

Simulation Details

With parameter values in place, each individual’s pronunciation time distribution was simulated 22 times and one synthetic distribution was selected at random for a statistical contrast. The contrast was a two-sample Kolmogorov-Smirnov goodness-of-fit test with a Type I error rate of .05. Success was counted if the synthetic distribution captured the prominent features of the participant’s density functions and it passed the Kolmogorov-Smirnov test.

All 22 independent simulation outcomes are plotted in white, behind each participant’s black empirical curve (e.g. Figure 2). The boundaries that define the cloud of white points circumscribe statistical estimates of the 5^th and 95^th percentiles around each empirical probability density and hazard function (Efron & Tibshirani, 1993). Thus, the repeated replications of the synthetic distributions establish 90% confidence intervals around the empirical density and hazard functions. The fact that so few replications of the synthetic distributions so closely approximate the empirical curves makes plausible, in a statistical sense, that cocktail mixtures are reliable descriptions of the empirical patterns.

Shortly we discuss details of three categories of simulated distributions, power law dominant, intermediate mixtures, and lognormal dominant, right after we describe how we arrived at those category distinctions. First, a line was fit to the slow tail of each participant’s density, on log/log axes, beginning at the empirical mode. The slope of the line was then used to rank empirical distributions from most shallow to most steep. The distributions with the most shallow rank versus the most steep rank are what we eventually call power-law versus lognormal dominant distributions, respectively.

Of interest here is that the rank of distributions, according to estimates of unadulterated power law behavior (their slow tail exponents), also respected an ordering of the three characteristic hazard functions. Small unadulterated exponents corresponded to hazard functions that rose to relatively constant asymptotes and tended to lack prominent peaks. These required relatively higher proportions of power-law behavior drawn from distributions with smaller exponents.

By contrast, distributions with larger exponents corresponded to hazard functions that rapidly rose to a high peak, and tended to require low proportions of power law behavior, from parent power-laws with large exponents. The remaining distributions, between the two extremes, had hazard functions that rose to an intermediate peak, and declined to an asymptote. These intermediate cases combine the features of the extreme cases. Simulations drew intermediate proportions of power law behavior and/or drew from a power law distribution with an intermediate exponent.

Nonetheless, the relation between hazard function shape and cocktail parameters was neither isomorphic nor monotonic. This is due partly to the log scales. More extreme linear values are more compressed on log scales. Consequently a power law with a mode equaling 400 ms that decays with an exponent of 4 will cover a narrower range of linear values than a power law distribution with the same exponent and a 600 ms mode, for example.

If one could create comparable modes on the response time axis, however, then the three categories of hazard functions could be set on a continuum that ties together proportion of power law behavior and the magnitude of the power law exponent (α). However our goal was to simulate actual values of empirical distributions.

Except where noted, these same methods and criteria were applied in all simulations reported in this article. PDF files containing plots of all 20 simulations are available on-line at http://www.csun.edu/~jgh62212/RTD.

Simulation Results

Characteristic distributions

All participants’ data came from a common set of stimulus words. Nevertheless, different participants produced visibly distinct distributions as we illustrate in Figure 2. The obvious difference is in the relative skew of slow pronunciation-time tails (the fast lognormal front ends are pretty much the same shape). Figure 2A includes a dramatically stretched slow tail. Figure 2B also has a visible positive skew, but less dramatic than in Figure 2A, while the density depicted in Figure 2C is similar to the lognormal density in Figure 1A. The solid black curves in Figures 2D, 2E, and 2F illustrate the same three participant’s density functions, now plotted on double-logarithmic axes. In each plot the X-axis is the natural logarithm of pronunciation time and the Y-axis is the natural logarithm of the probability density. (Wavy oscillations in extreme tails are an artifact of the sparse observations in the extreme tail.)

Power law dominant

Figure 2A shows synthetic density functions plotted as white points behind the participant’s empirical density. Figure 2A is plotted on linear axes and Figure 2D is plotted on double-logarithmic axes. The white cloud of points represents the 22 synthetic density functions, one on top of the other, to depict a range of potential density functions that could arise from the particular 75.9% power-law mixture. This cloud of simulated density functions captures virtually every point along the curve of the empirical density function, so the empirical density could plausibly be a similar mixture.

For this participant, the proportion of power-law behavior was ρ_PL = 75.9% of 1094 simulated pronunciation times. The power-law mode was set at Ω_PL = 6.256 log units (521 ms), which corresponds to the first “hump” on the distribution’s tail; the inverse power-law exponent α = 5.5. The parent lognormal had a mode Ω_LN = 6.256 in natural logarithm units (521 ms) and a standard deviation σ = .095 log units (±50 ms; note that when transformed onto a linear scale, the SD resulting from a given σ depends on the value of Ω_LN and is not symmetric about the mean. We report an average of the linear SD’s that result from adding and subtracting one σ from a given Ω_LN mean). Of the 1094 synthetic trials, 24.1% were drawn exclusively from the fast end of a parent lognormal distribution, all were less than or equal to the lognormal mode. This particular case required no data points from the slow tail (slower than the mean/mode) of the lognormal distribution. The slow tail is apparently exclusively power law. The participants’ data were successfully mimicked in a ρ_FLN 24.1% + ρ_BLN 0% + ρ_PL 75.9% = 100% mix of lognormal and power law behavior.

Looking more closely at details, this participant’s density has a dramatically stretched slow tail seen in Figure 2A. On the linear axes of Figure 2A the slow tail begins its dramatic decline from the mode (≈531 ms) extending, at least, through the 1100 ms mark. When re-plotted on double logarithmic axes in Figure 2D, the previously stretched tail falls off approximately as a line. The slow tail in Figure 2D is apparently an inverse power-law spanning an interval of about 600 ms beyond the distribution’s mode, about 2.78 decades of response time. This density illustrates a category of density functions that we call hereafter power-law dominant. The solid black lines in Figures 2A and 2D depict one of only two power law dominant pronunciation time distributions present in the 20 participants’ data sets.

Intermediate mixtures

Figure 2B illustrates an intermediate mixture of power-law and lognormal distributions. Synthetic density functions are plotted as white points behind the participant’s empirical density (and on log-log axes in Figure 2E). The white cloud represents all 22 synthetic samples and again supplies a potential range of density functions that can arise from the particular ρ_PL = 38% inverse power-law mixture. The synthetic densities capture the participant’s density function so the participant’s data could plausibly be a similar mixture.

For this participant ρ_PL = 38% of 1096 data points were drawn in each of 22 simulations from the same power-law distribution. The exponent of the power-law α = 7.5, and the power-law mode Ω_PL = 6.253 log units (520 ms). The remaining 62% of the samples were taken from a lognormal parent with a mode Ω_LN = 6.253 log units, or 520 ms, and a standard deviation σ = .095 log units (±49 ms). 42.8% of synthetic and empirical data are less than or equal to the lognormal mode, which means 19.2% of data points came from the lognormal tail (ρ_FLN 42.8%, + ρ_BLN 19.2% + ρ_PL 38% = 100%).

Power-law behavior is much less pronounced in the slow tail of this participant’s density, compared to Figure 2D’s density. Yet the slow tail in Figure 2B still declines more or less linearly, on log axes, only at much faster rate. The more rapid decay of the stretched slow tail and the more symmetric shape are mimicked with an intermediate mix of power law and lognormal behavior. So we call such examples intermediate mixtures. Fourteen participants’ data sets were matched with intermediate mixtures.

Lognormal dominant

Figure 2C illustrates another 22 synthetic density functions plotted as white points behind a participant’s empirical density. This cloud depicts the potential range of density functions that can arise from the particular ρ_PL = 9% power-law mixture. Figure 2F portrays the empirical and simulated density functions on double-logarithmic axes. As before, the cloud of simulated density functions captures the shape of the empirical function so the participant’s data could be a similar mixture.

For this participant, the sample proportion of power-law behavior was only ρ = 9% of 1100 simulated pronunciation times. The power-law mode Ω_PL = 6.4 log units (602 ms) and the inverse power-law exponent α = 10. The parent lognormal had a mode Ω_LN = 6.304 in natural logarithm units (547 ms) and a standard deviation σ = .09 log units (±49 ms). The remaining 91% of the 1100 synthetic trials were drawn from the parent lognormal distribution of which 44.5% were less than or equal to the lognormal mode, leaving 46.5% of data points from the lognormal tail (ρ_FLN 44.5% + ρ_BLN 46.5% + ρ_PL 9% = 100%).

On double log axes, the third participant’s data resemble a symmetric, down-turned parabola depicted by the solid black curve in Figure 2C. This is also how idealized lognormal densities appear on double logarithmic axes (Figure 2C). Given the close resemblance, we called this third kind of density lognormal dominant. The solid black lines in Figures 2C and 2F represent one of four lognormal dominant distributions.

Simulations of Participant Hazard Functions

One simple arithmetic principle captures variation in pronunciation times, namely multiplicative interaction among random variables. Hypothetical cocktails of power law and lognormal behavior successfully mimicked the dispersion of each and every participant’s data. In each case, repeatedly replicated synthetic distributions establish 90% confidence intervals around the empirical density. These detailed matches between empirical and simulated probability density functions are encouraging but the hazard function test is more conservative.

Next we combine the discriminatory power of a hazard function analysis with nonparametric bootstrapping (Efron & Tibshiriani, 1993). The bootstrap procedure is based on re-sampling techniques to compute standard errors and conduct statistical tests using empirical distributions with unknown population distributions. We used the bootstrap procedure to transform hazard function simulations into a quantitative statistical test.

Hazard Functions

So what exactly is a hazard function? Hazard functions track the continuously changing likelihood of an event. For instance that a response will occur given that some time has passed and it has not already occurred. The empirical hazard function of response times estimates the probability that a response will occur in a given interval of time, provided that it has not already occurred (Chechile, 2003; Luce, 1986; Van Zandt & Ratcliff, 1995). It is calculated using the probability density and cumulative density functions of a participant’s response times.

Equation (3) is a formal definition in which t refers to the time that has passed without a response, on an increasing time axis; f(t) is the probability density as a function of time and F(t) is the cumulative distribution function as a function of time.

$$\text{h}(t)=\text{f}(t)÷[1-\text{F}(t)]$$ (3)

The hazard rate is represented graphically by plotting the successive time intervals against their associated probabilities. It is straightforward to compute a hazard function from a histogram, except the histogram method generally yields unstable hazard function estimates. This is especially true in the slow tail of the distribution where the hazard function tracks a ratio of two numbers that approach zero as they close in on the slow tail’s end.

The previous difficulty can never be fully eliminated but it can be minimized somewhat by using very large data sets and a random smoothing technique described by Miller and Singpurwalla (1977). The latter technique divides the time axis so that each time interval uses equal sample sizes. While other techniques exist, many previous studies also used this method and so our results compare with the existing literature.

Response time hazard functions commonly increase to a peak, decrease, and then level off to a more or less constant value. Peaked hazard functions have interesting and counterintuitive implications. For response times they mean that when a response does not occur within the time interval up to and including the peak, it becomes less likely to occur at points in the future. This shape is so widely observed that candidate theoretical distributions whose hazard functions cannot mimic this pattern are dismissed out of hand (see discussion in Balakrishnan & Ashby, 1992; Luce, 1986; but take note also of Van Zandt & Ratcliff, 1995).

Probability density functions can appear nearly identical, both statistically and to the naked eye, and yet are clearly different on the basis of their hazard functions (but not vice versa). Hazard functions are thus more diagnostic than density functions (Townsend 1990). On this basis, Luce (1986) rejected many classical and ad-hoc models of response time because they lack known qualitative features of empirical hazard functions — no need of more details, such as parameter estimation and density fitting.

Despite their utility, hazard functions remain mostly absent from the wide-ranging response time literature. Perhaps this is because no straightforward inferential statistical test is associated with differences in hazard functions. Instead, hazard functions are usually contrasted qualitatively, in terms of their relative ordering (Townsend, 1990) or with the help of statistical bootstrapping methods.

Characteristic Hazard Functions

So what do hazard functions of power-law and lognormal cocktails look like? They look like the three characteristic hazard functions previously identified by mathematical psychologists. The illustrated hazard functions are plotted on standard linear axes and may be readily compared to hazard functions that appear in the response time literature. Each participant’s set of 22 synthetic hazard functions was computed from the same 22 synthetic data sets used to generate the previously described synthetic density functions.

Power Law Dominant

Recall that the solid black lines in Figures 2A and 2D each represent an individual participant’s empirical, pronunciation time density function, on linear and double-logarithmic axes. Plots of 22 separate simulations of the participant’s density function are depicted together as clouds of white points. Cocktail simulations generate both probability density and hazard functions simultaneously.

The participant data portrayed in Figure 2A is one of two participants’ distributions that were power law dominant. The heavy black curve in Figure 2G represents the empirical hazard function of the same data, on standard linear axes. In each of the hazard function graphs, the X-axis indexes pronunciation time, in ms, and the Y-axis indexes the instantaneous hazard rate for the given interval of pronunciation time.

Hazard functions for a participant’s 22 simulations are depicted as white points plotted behind the participant’s hazard function, as in Figure 2G. The cloud of points supplies a 90% confidence interval and a visual sense of the range of hazard function shapes that emerge from repeated simulations using the same mixture of power law and lognormal behavior.

Notice that the synthetic hazard functions in this example match one class of characteristic hazard functions — hazard functions that rise to an asymptote and stay more or less constant past that point. Hazard functions that level off to constant values imply that the likelihood that a response will occur stays approximately constant into the future. Past a certain point, knowing how much time has elapsed supplies no additional information about the likelihood that a response will be observed. Power law dominant data also yield this hazard function shape and two of twenty participants’ hazard functions fit this description.

Intermediate Mixture

Figure 2H portrays hazard functions for another participant as white points plotted behind the empirical hazard function. The hazard functions of these synthetic densities all rise to a peak and decline to an asymptote past that point. Fourteen of the twenty empirical hazard functions rose to a noticeable peak, and then declined to an asymptote. All fourteen match the second and most prominent class of hazard functions described by Luce (1986) and Maddox, et al., (1998). Intermediate-mixture density functions yield these characteristic peaked hazard functions.

Lognormal Dominant

Four of the twenty participants produced hazard functions that rose quickly to a much higher peak and fell off sharply, which matches the third class of characteristic hazard functions. Lognormal dominant simulated data mimicked this class of hazard functions. The solid black line in Figure 2I portrays the hazard function of one participant’s data plotted in Figure 2C and the cloud of hazard functions in Figure 2I again illustrate the range of shapes that emerged from repeated simulations using the same mixture.

Discussion

The cocktail hypothesis yields a continuum of mixtures that encompass all three distinct hazard function categories. End points at the extreme ends of the continuum are simulations of lognormal dominant versus power-law dominant distributions. These extremes are most tightly constrained by the data. Intermediate mixtures are less constrained and likely support multiple parameterizations in some cases. Nonetheless, the intermediate cases do not require much beyond what is got from the extreme ends of the continuum. They are parsimonious with these two extremes.

Thus the account is anchored at the extremes in the choice of lognormal and power law behaviors, and the intermediate cases follow without additional assumptions. In each case, 22 replications of synthetic distributions establish 90% confidence intervals around the corresponding hazard function. Thus multiplicative interaction among random variables again captures participants’ dispersion, this time in the hazard functions of pronunciation times. Most important, synthetic mixtures of power law and lognormal behavior replicate the three generic shapes that Luce (1986) and Maddox, et al. (1998) highlight as generally characteristic of response time behavior.

The three generic hazard shapes are well documented in the response time literature, and occur in a wide variety of experimental contexts. On this basis, Maddox et al., (1998) speculated that the similarity of empirical hazard functions across experimental contexts suggests a common origin. We now propose the common origin to be multiplicative interactions. The sufficiency of the present mix of lognormal and inverse power-law behavior supports this proposal.

Notably, the motivation in evidence for multiplicative interactions is more reliable than the motivation for any specific cocktail model. The fixed parameters of each participant’s parent distributions were adopted as a simplifying assumption (cf. Van Zandt & Ratcliff, 1995). Thus these particular simulations establish that relatively constrained cocktails of multiplicative interactions are sufficient to capture salient empirical details of response time density and hazard functions, the same details that have frustrated previous modeling efforts.

A Second More Inclusive Existence Proof

To this point, we have conducted a conservative test of simulated response time densities, using hazard functions, to identify the kind of system dynamics that underlie cognitive response times. To the extent that power law behavior is diagnostic, system dynamics are interaction dominant dynamics. We next generalize this result to a new data set more broadly inclusive of variation in word naming performance.

This is one kind of model testing approach. The value of the test is simply that it compares the model’s capacity to mimic human performance in data that are more inclusive of the performance at issue (cf. Kirchner, Hooper, Kendall, Neal, & Leavesley, 1996). This kind of model testing is seen for instance when a connectionist model of word naming is tested on a larger or different word population. The second existence proof included a wider variety of words to further explore participant individual differences in dispersion of pronunciation times.

The second existence proof also includes another test of the cocktail hypothesis in a contrast with ex-Gaussian simulations of response time distributions. Ex-Gaussians resemble power-law/lognormal cocktails in that both convolve a distribution and a skewed slow-tail curve. The ex-Gaussian has been introduced several times in history and is known to closely mimic the details of response time probability density functions (Andrews & Heathcote, 2001; Balota & Spieler, 1999; Luce, 1986; Moreno, 2002; Ratcliff, 1979; Schmiedek, Oberauer, Wilhelm, Süß, & Wittmann, 2007; Schwarz, 2001).

Method

Participants

Thirty introductory psychology students participated in exchange for course credit.

Stimuli

1100 target words were selected at random from a 23,454-word corpus described in Stone, Vanhoy, and Van Orden (1997). They comprised 4 to 15 letter words (M = 6.53, SD = 2.07), ranging from 2 to 15 phonemes (M = 5.49, SD = 2.02), 1 to 5 syllables (M = 2.08, SD = 1.06), and ranging in frequency from 5 to 5146 per million (M = 70.2, SD = 295.16; Kuçera & Francis, 1967). By contrast, the 1100 targets in the initial existence proof were sampled from the more narrowly circumscribed corpus of Spieler and Balota (1997), which were 4 to 5 letter words (M = 4.45, SD = .5), with 3 to 5 phonemes (M = 3.59, SD = .61), all single syllable, ranging in frequency from 1 to 10,601 per million (M = 86.81, SD = 458.28; Kucera & Francis, 1967).

Procedure

A participant was presented with each of the 1100 target words, one per trial, in a random order. Each trial began with a fixation signal (+++) visible for 172 ms (12 raster refresh cycles) followed after 200 ms by the word to be named. Participants were instructed to pronounce the word aloud quickly and accurately into a microphone. Each word appeared in the center of a computer monitor controlled by DMASTR software running on a PC (Forster & Forster, 1996).

A word target remained on the screen for 200 ms, after its pronunciation tripped a voice key, but no longer than 972 ms from presentation. If no response was recorded, trials timed out after 10 s. The voice key was reliable to within 1 ms. The experimenter sat quietly, well behind the participant, and recorded pronunciation errors. Each response was followed by a fixed, 629 ms, inter-trial interval. Every participant completed 45 practice trials and then the 1100 experimental trials, which required about 45 minutes.

Results

Four analyses were conducted. The first analysis tested for fractal structure in the form of 1/f scaling in the pattern of variation of response times across response trials. The second tested whether the cocktail simulations adequately mimic the distributions of word pronunciation times, to replicate and extend the first existence proof. The third analysis compared parameters of the cocktail mixtures for the two existence proofs and descriptive parameters of empirical distributions and cocktail mixtures. And the fourth analysis contrasted the hazard functions of cocktail mixtures, ex-Gaussian mixtures, and empirical pronunciation times.

Fractal Scaling

The first analysis was conducted to test for 1/f scaling in each individual’s trial series of pronunciation times, to replicate Van Orden et al. (2003a) and Thornton and Gilden (2005). 1/f scaling in a trial ordered data series supplies independent converging evidence of multiplicative interactions and interaction dominant dynamics, a point we return to in the discussion (and see also Van Orden et al.). The rationale and details behind the procedures are described in Holden (2005).

We again included the small proportion of pronunciation times that resulted in errors because it did not change the outcome (M = 2.45%, SD = 1.84%). As a first step, all naming times shorter than 200 ms and longer than 3000 ms were eliminated from each series. After that, naming times that fell beyond ±3 SDs from the series mean were eliminated. More than 1024 data points remained after the censoring procedure and the initial observations were truncated so that each series was comprised of 1024 observations, with one exception. The exception required a larger 5000 ms truncation value to insure 1024 observations in the data series.

An initial 511-frequency power spectral density analysis was computed, and the power spectra were examined visually for consistency with the fractional Gaussian noise (fGn) model. Next, the spectral exponents of the power spectra were computed, using methods described in Holden (2005). Three different statistical analyses were conducted on the 29 remaining series (excluding participant 9, which did not pass the visual test for fractional Gaussian noise). Linear and quadratic trends were removed from the series, and the analyses were limited to scales equal to or below ¼ the size of the series to minimize the impact of the detrending procedure on the analyses (see Holden, 2005; Van Orden et al. 2003a; Van Orden, Holden, & Turvey, 2005).

The first analysis was a 127-frequency window-averaged spectral analysis. The mean overall spectral exponent for the 29 series that were straightforwardly consistent with the fractional Gaussian noise description was .21 (SD=.14). Twenty-seven of the thirty series displayed steeper spectral slopes than those of a randomly shuffled version of the same trial series — otherwise known as a surrogate trial series (Theiler, Eubank, Longtin, Galdrikian, & Farmer, 1992), p < .05 by a sign test.

The average fractal dimension, computed using the standardized dispersion statistic was 1.39 (SD = .06). The fractal dimension for white noise is 1.5. Twenty-eight of the 30 series yielded smaller fractal dimensions than their shuffled surrogate counterparts, p < .05 by a sign test. This outcome was in close agreement with an average fractal dimension of 1.40 (SD = .06) produced by the detrended fluctuation analysis (Peng, Havlin, Stanley, & Goldberger, 2007) in which 29 of the 30 series yielded smaller fractal dimensions than their surrogate counterparts, p < .05 by a sign test.

The outcomes of these fractal analyses replicate previous reports of fractal 1/f scaling in pronunciation time trial-series conducted under similar conditions. The average spectral exponent of the data in the first existence proof, reported in Van Orden et al. (2003a), was .29 (SD = .10) with an average fractal dimension of 1.40 (SD = .06). The reliable difference in average spectral exponents between the first and second existence proofs, t(47) = 2.20, p < .05, suggests that the heterogeneity of the inclusive targets tended, on average, to induce weaker patterns of fractal 1/f scaling. However, the average fractal dimensions were not reliably affected. The discrepancy may be due to the spectral analysis being more readily influenced by changes at the scale of individual trials (Holden, 2005).

As an additional check, we also computed an 8-point power spectrum, averaged across participants, as described in Thornton and Gilden (2005). For this analysis, we expanded the maximum response time to 5 sec, and included all 30 series in the analysis. We then used a simplex fitting routine to estimate the parameters of a mixture of 1/f noise and white noise that could yield the same 8-point power spectrum.

A simple sum of a normalized 1/f noise (M = 0, SD & Var = 1) with a spectral exponent of .61 and a zero-mean white noise with a variance of 1.29 yields a power spectrum very much like trial-series of pronunciation times (χ² (7) = .08, p >.05, see Thornton & Gilden, 2005, for details). The analysis produced almost the same parameters when re-run using only the series that met the visual 512-point spectral analysis, and passed all three of the above sign tests. Overall, the pronunciation trial-series display evidence of fractal scaling that is consistent with the earlier reports. Table 2 and 3 list the spectral exponents and fractal dimensions for the data series from the two existence proofs.

Table 2.

Spectral exponent and fractal dimension statistics that characterize the fractal scaling in the naming series are depicted for both analyses. The details of the SDA fractal dimension statistic are described in Holden, (2005), the details of the DFA fractal dimension statistic are described in Peng, Havlin, Stanley, and Goldberger (1995). Participant 1’s series contained many extreme observations, and a more liberal 5 second cutoff was required to recover at least 1024 observations for the fractal analyses. Participant 9 was eliminated from the analyses because visual inspection of the 512-frequency spectral plot revealed an inverted U-shaped spectrum.

Spectral slopes and fractal dimension statistics for the second existence proof.

Participant	Spectral Exponent	SDA Fractal Dimension	DFA Fractal Dimension
1	0.07	1.45	1.46
2	0.32	1.42	1.38
3	0.07	1.42	1.43
4	0.15	1.41	1.42
5	0.15	1.42	1.46
6	0.43	1.33	1.35
7	0.25	1.38	1.37
8	0.26	1.33	1.35
9	N/A	N/A	N/A
10	0.15	1.36	1.4
11	0.46	1.27	1.31
12	0.17	1.38	1.42
13	0.23	1.42	1.45
14	−0.05	1.47	1.48
15	0.16	1.44	1.39
16	0.04	1.44	1.44
17	0.24	1.36	1.42
18	0.14	1.43	1.42
19	0.56	1.25	1.22
20	0.11	1.46	1.49
21	0.1	1.4	1.42
22	0.39	1.35	1.34
23	0.32	1.37	1.35
24	0.42	1.27	1.25
25	0.09	1.42	1.42
26	0.32	1.36	1.4
27	0.06	1.48	1.43
28	0.33	1.39	1.42
29	0.11	1.38	1.41
30	0.19	1.34	1.38
Mean:	0.21	1.39	1.40
SD:	0.14	0.06	.06

Table 3.

Spectral slopes and fractal dimension statistics for the first existence proof. Note that the participants were numbered according to the value of the scaling exponent that characterized the decay in the slow tail of their response time distribution. This table supplies a different ordering of the same spectral and fractal dimension statistics that appear in Van Orden, Holden, and Turvey, (2003a, p. 342).

Spectral slopes and fractal dimension statistics for the first existence proof.

Participant	Spectral Exponent	SDA Fractal Dimension	DFA Fractal Dimension
1	0.4	1.34	1.31
2	0.21	1.41	1.46
3	0.28	1.44	1.47
4	0.25	1.42	1.42
5	0.14	1.43	1.45
6	0.22	1.51	1.47
7	0.4	1.33	1.31
8	0.28	1.35	1.39
9	0.41	1.41	1.37
10	0.35	1.35	1.33
11	0.2	1.52	1.5
12	0.49	1.3	1.26
13	0.38	1.33	1.32
14	0.19	1.4	1.41
15	0.27	1.4	1.41
16	0.22	1.45	1.45
17	0.4	1.33	1.31
18	0.16	1.47	1.47
19	0.22	1.37	1.4
20	0.29	1.4	1.41
Mean:	.29	1.40	1.40
SD:	.10	.06	.07

The contrast of spectral exponents suggests the more inclusive existence proof yielded a weaker pattern of fractal 1/f scaling. It is possible that relative presence of fractal 1/f scaling in a trial series trades-off with the relative dispersion in response time. All other things equal, wider dispersion of response time may yield more whitened patterns of fractal 1/f scaling. This finding is noteworthy because no statistically necessary relation exists between degree of dispersion and the presence of scaling behavior in trial series. However, the evidence at this point is merely suggestive, and we address this question more directly in separate studies.

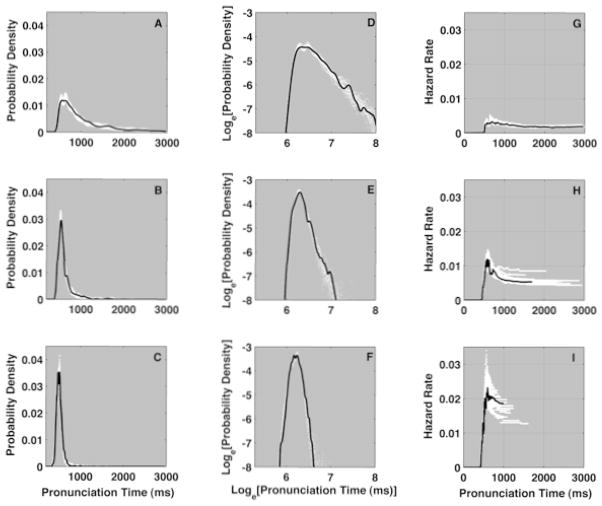
Cocktail Simulations

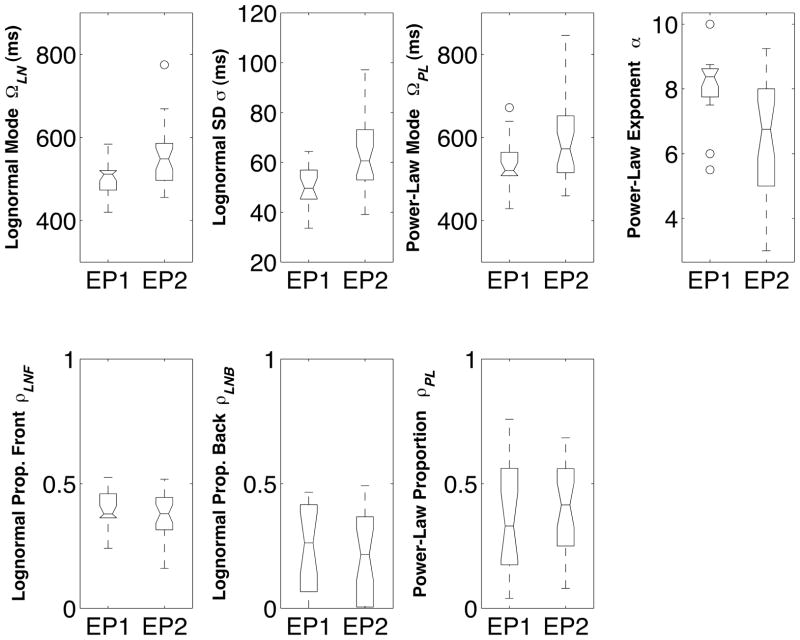
We used the statistical procedures described in the first existence proof to estimate initial parameters and simulate the pronunciation time distributions of each individual participant. As expected, this more inclusive heterogeneous set of words yielded a more heterogeneous set of pronunciation time distributions, compared to naming data in the first existence proof. For the cocktail simulations, overall, the power-law modes and the lognormal modes were shifted towards slower values.

Twenty-four of the 30 participants were successfully approximated using modes from the empirical distribution’s mode statistics. For the twenty bimodal participants’ data the average difference between the lognormal mode Ω_LN and the power law mode Ω_PL was 53 ms, an increase of 24 ms from the average difference for bimodal participants in the first existence proof.

Cocktail mixtures successfully mimic 29 of 30 density and hazard functions. The single failure came from participant 13. The front fast half of this participant’s density was well approximated by samples from a lognormal density, but a double logarithmic plot of the density revealed a slow tail that decayed faster than linear. This could mean, for example, that slow times are consistent with an exponential tail instead of a power-law tail.

However, the tail also contained multiple extreme observations that deviate from the otherwise exponential pattern, more in line with power-law behavior. Thus, for instance, the data could reflect a power-law, partially collapsed into a lognormal curve, as that pattern could also appear like the data from participant 13. Nonetheless, we counted this as a failure to disambiguate, one way or the other. Table 4 lists the parameter values of the parent distributions for each participant’s simulated data.

Table 4.

Lists cocktail parameters that approximate each of the 30 empirical density functions of the second existence proof. The participant numbers were established by ordering each distribution in terms of the empirically estimated slope of the tail of the distribution. This explains why the participant numbers approximate a rank ordering of the α parameter. Participants numbered 1, 2 and 3 were classified as power-law dominant; participants numbered 28, 29, and 30 were classified as lognormal dominant. The parameters reported for participant 13 represent a failure of the cocktail mixture, and were excluded from the summary statistics. The remaining participants were classified as intermediate mixtures. Plots of all the empirical and cocktail distributions and hazard functions can be viewed on-line at http://www.csun.edu/~jgh62212/RTD.

Parameters used to generate synthetic distributions in the second existence proof.

Participant	Mo ΩLN	SD σ	Mo ΩPL	PL Tail α	F LN Prop ρFLN	B LN Prop ρBLN	PL Prop ρPL
1	6.260	0.1	6.410	3	0.160	0.190	0.650
2	6.370	0.115	6.480	3.25	0.227	0.213	0.560
3	6.337	0.135	6.350	3	0.339	0.191	0.470
4	6.312	0.135	6.312	4.5	0.377	0.143	0.480
5	6.244	0.1	6.244	5	0.317	0.003	0.680
6	6.373	0.11	6.480	4.74	0.259	0.311	0.430
7	6.506	0.11	6.620	5	0.274	0.346	0.380
8	6.423	0.12	6.590	6.5	0.313	0.367	0.320
9	6.292	0.135	6.440	6	0.445	0.325	0.230
10	6.123	0.09	6.130	6.5	0.315	0.001	0.684
11	6.123	0.1	6.130	7.25	0.398	0.001	0.601
12	6.339	0.11	6.350	7.25	0.436	0.005	0.560
13	6.378	0.1	6.378	7.25	0.433	0.077	0.490
14	6.372	0.115	6.380	6.25	0.375	0.000	0.625
15	6.377	0.09	6.500	7.25	0.310	0.400	0.290
16	6.372	0.09	6.372	6.5	0.372	0.001	0.627
17	6.208	0.11	6.208	8.25	0.454	0.000	0.546
18	6.284	0.11	6.284	6	0.452	0.148	0.400
19	6.196	0.11	6.310	8	0.370	0.380	0.250
20	6.330	0.13	6.490	8.75	0.518	0.402	0.080
21	6.248	0.12	6.248	5	0.482	0.218	0.300
22	6.303	0.12	6.303	6	0.484	0.266	0.250
23	6.159	0.1	6.280	9	0.315	0.425	0.260
24	6.414	0.13	6.414	9	0.507	0.000	0.493
25	6.130	0.085	6.230	8.5	0.226	0.284	0.490
26	6.653	0.125	6.740	7	0.438	0.312	0.250
27	6.232	0.11	6.232	8	0.453	0.147	0.400
28	6.160	0.115	6.210	8.75	0.428	0.442	0.130
29	6.436	0.13	6.550	8	0.388	0.492	0.120
30	6.176	0.11	6.230	9.25	0.383	0.467	0.150
Mean:	6.30	0.11	6.35	6.60	0.373	0.223	0.404

Power-Law Dominant

Three of 30 empirical density functions displayed hazard functions consistent with power-law dominant behavior. Exponents of the parent power-law distributions ranged from 3 to 3.25 and the ρ_PL mixture proportions ranged from 65% to 47%. Lognormal modes ranged from 6.24 to 6.37 on a log scale, or 513 to 584 ms, with lognormal standard deviations set between .105 and .135 log units. These densities were best approximated by allowing the mode of the parent power-law distribution to fall slightly beyond the mode of the parent lognormal distribution, by .01 to .15 log units.

Figure 3A depicts the power-law dominant distribution of one participant. The sample proportion of power-law behavior was ρ_PL = 65% of 1029 simulated pronunciation times. The power-law mode was set at Ω_PL = 6.41 log units or 608 ms, and the inverse power-law exponent was α = 3. The remaining 35% of the 1029 synthetic trials were drawn from a parent lognormal distribution with a mode of Ω_LN = 6.26, or 523 ms and a standard deviation σ = .1 log units or 53 ms. Of this 35% of synthetic times, 16% were less than or equal to the lognormal mode, and 19% exceeded the lognormal mode (ρ_FLN 16% + ρ_BLN 19% + ρ_PL 65% = 100%).

Figure 3.

Three individual’s pronunciation time density functions from the second existence proof are depicted in the same format as Figure 2. Notice that the X-axes now extend out to 3 sec, twice that required for the distributions in the first existence proof. Panels A, B, and C depict the kernel-smoothed density functions on linear axes, the solid black line represents the empirical density and the white cloud of points plotted behind the participant’s empirical density represents the density functions of the corresponding 22 cocktail simulations. Panels D, E, and F depict the same densities as in panels A, B, and C, now on double-logarithmic axes. Panels G, H, and I depict the empirical hazard functions in black, and the 22 simulated hazard functions in white. The boundaries established by the 22 simulated distributions circumscribe 90% confidence intervals around each empirical probability density and hazard function.

Intermediate Mixture

Twenty-three of the 30 empirical hazard functions were simulated with intermediate mixtures of lognormal and inverse power-law behavior. Power law exponents ranged from 4.5 to 9 and the ρ_PL mixture proportions ranged from 68% to 8%. Lognormal modes ranged from 6.13 to 6.65 log ms with standard deviations that ranged from .085 to .135 log units. Fourteen of the 23 densities were best approximated if the mode of the parent power-law distribution was allowed to fall slightly beyond the mode of the parent lognormal by .008 to .17 log units.

Figure 3B illustrates the intermediate mix of one participant: ρ_PL = 40% of the 1097 data points drawn in each of 22 simulations from an inverse power-law distribution, the exponent of the power-law α = 6, and the power-law mode Ω_PL = 6.284 log units (536 ms). The remaining 60% of synthetic data were taken from a lognormal parent with a mode Ω_LN = 6.284 log units, or 536 ms, and a standard deviation σ = .11 log units or about 59 ms. Of the remaining 60% of the synthetic samples, 45.2% were less than or equal to the mode, and 14.8% exceeded the lognormal mode (ρ_FLN 45.2% + ρ_BLN 14.8% + ρ_PL 40% = 100%).

Lognormal Dominant

The remaining three empirical densities were lognormal dominant with less power-law behavior sampled from power laws entailing larger exponents. Power-law exponents ranged from 8 to 9.25, and lognormal mode parameters ranged from 6.16 to 6.463 with lognormal standard deviations of .1 to .13. Modes of power-law distributions fell just past modes of lognormals by .05 to .11 log units.

Figure 3C illustrates the lognormal dominant mix of one participant: ρ_PL = 15% of the 1098 data points drawn in each of 22 simulations, the exponent of the power-law was α = 8.5, and the power-law mode was Ω_PL = 6.24 log units. The remaining 85% of synthetic data came from a lognormal parent with a mode Ω_LN = 6.176 log units, or 481 ms, and a standard deviation σ = .105 log units or about 53 ms; 38.3% of synthetic and empirical data were less than or equal to the lognormal mode, leaving 46.7% of data points from the lognormal tail (ρ_FLN 38.3% + ρ_FLN 46.7% + ρ_PL 15% = 100%).

Parameter Contrasts

The two existence proofs used two different samples of word targets, the principal difference being longer and multi-syllable words in the present sample. With this in mind, we examined distributions of cocktail parameters from both sets of simulations. Figure 4 depicts seven boxplots to contrast the parameters required to mimic the two data sets.

Figure 4.

Individual boxplots contrast each parameter used to generate the cocktail mixture distributions between the two existence proofs. The EP1 label corresponds to data from the first existence proof and the EP2 label indicates the second existence proof. For these plots, the lognormal parameters and the power-law modes were converted to linear units of pronunciation time. Distributions of lognormal parameters and power-law modes from existence proof 1 were somewhat faster and less variable than those of the more inclusive existence proof 2. The proportion of lognormal behavior in the fast front ends of cocktail simulations was similar between existence proof 1 and 2, but the existence proof 2 data sets tended to require more power-law behavior in the slow tails.

The proportion of lognormal data in the front end of simulated distributions stayed most consistent across the two data sets. The inclusive naming study yielded a more heterogeneous distribution of lognormal modes (Ω_LN), however, focused on somewhat slower times. This same basic pattern held for the lognormal SD (σ) and the power-law mode (Ω_PL). Simulations of the inclusive word data tended to exchange samples from the back of the lognormal for more power-law samples, and often required shallower power-law tails (i.e., smaller α). Other things being equal, these differences imply increases in the dispersion of distributions associated with the inclusive targets, which underscores the importance of accounting for changes in dispersion in theoretical descriptions of word naming and other cognitive tasks (e.g, Andrews & Heathcote, 2001; Balota et al., 2004; Balota & Spieler, 1999; Heathcote, Popiel, & Mewhort, 1991; Schmiedek, et al., 2007; Wagenmakers & Brown, 2007; Yap, Balota, Tse, & Besner, 2008).

The scatter plots in Figure 5 illustrate how well the cocktail simulations recover summary statistics of pronunciation time distributions, means, standard deviations, and the positive pattern of skew. Summary statistics would not likely distinguish the cocktail mixtures from empirical data.

Figure 5.

The top three scatterplots compare the pronunciation times from the first existence proof to simulated times in three descriptive statistics: the mean, the standard deviation, and a nonparametric measure of skew ([M−Md]/SD). The bottom three panels illustrate the same comparison for the second existence proof (Participant 13 was excluded). The statistics for the simulated times were computed using an omnibus distribution that included all 22 cocktail mixtures. The successful cocktail mixtures reliably recover empirical means, standard deviations, and skews.

Cocktail mixtures also capture the linear correlation between means and standard deviations, which has long been recognized in response time data (e.g., Luce, 1986, pp. 64–66). In the most recent example, Wagenmakers and Brown (2007) examined the relation between a participant’s mean response time and standard deviation and found a clear pattern of linear correlation across a wide range of decision-based response time tasks. They speculated that the relationship is a law-like property of response time distributions. We conducted a parallel analysis.

The Wagenmakers and Brown (2007) analysis indexed condition means and SDs on a participant-by-participant basis. This analysis held participant, constant, to examine how different experimental conditions varied with relative task difficulty. By contrast, our analysis holds the task constant, to examine individual differences among participants. Thus, whereas they found that more difficult, slower conditions give more widely dispersed response times, we find that slower participants tend to produce wider dispersion.

Faust, Balota, Spieler, & Ferraro (1999) anticipated both previous outcomes in formal analyses of their Rate-Amount model, and they reported similar corroboration in data from Hale, Myerson, Faust and Fristoe (1995). Individual participants’ mean response times were positively correlated with their respective standard deviation, and condition means were positively correlated with standard deviations in the respective condition.

Both existence proofs also yielded reliable correlations between the mean and standard deviation, r(47) = .86, p < .05. A scatter plot of the data is presented in the upper left panel of Figure 6. Since word naming is not an explicit decision process, the correlation suggests a more general relationship than Wagenmakers and Brown’s speculation (that it applies primarily to decision based tasks). An identical analysis on the synthetic cocktail data yielded a nearly identical relationship between means and standard deviations, r(47) = .84, p < .05. A scatter plot of the relationship for the cocktail simulations is presented in the bottom left panel of Figure 6.

Figure 6.

The top three scatter plots depict correlations between mean and standard deviation, mean and skew, and the standard deviation and skew for the empirical pronunciation time distributions. The open square symbols represent participants from the first existence proof; the closed circular markers indicate participants from the second existence proof. Since it was an ambiguous case, participant 13’s data was excluded from this and all subsequent analyses. The white markers on the bottom three plots depict the same information for the cocktail simulation of each participant’s pronunciation time distribution. In addition to capturing a comparable magnitude of linear association between the variables, the cocktail mixtures capture additional details of the relationships. For example both empirical and cocktail mean-SD plots display a fanning pattern as a function of increases in both variables, and both empirical and cocktail SD-SK plots display evidence of a curvilinear relationship.

In addition, synthetic and empirical scatter plots display a similar pattern of fanning. In the parlance of linear regression, this trapezoidal fanning indicates heterogeneity of error variance. Thus, in addition to displaying the three characteristic hazard functions of response time, the cocktail mixtures also successfully replicate and extend the pervasive pattern of correlation between the mean and standard deviation in response time distributions (Andrews & Heathcote, 2001; Balota et al., 2004; Balota & Spieler, 1999; Faust, et al., 1999; Heathcote, et al., 1991; Holden, 2002; Van Orden, Moreno, & Holden, 2003; Schmiedek, et al., 2007).

Additional relationships are seen across the mean, standard deviation, and skew statistics. A reliable positive correlation exists between participants’ mean pronunciation time and a nonparametric estimate of skew, r(47) = .57, p < .05, and also between the standard deviation and skew, r(47) = .76, p < .05. The same correlations were present in the cocktail mixtures (M & SK: r(47) = .60, p < .05; SD & SK: r(48) = .79, p < .05). Notably, the positive skew of pronunciation time distributions implies that the mean, SD, and SK will not generally pass as statistically independent (a point made previously by Van Zandt, 2002).

Ex-Gaussian Contrast

Finally, we provide additional context for the generality of the cocktail simulations in a contrast with synthetic ex-Gaussian pronunciation time distributions. A mixture of samples from exponential and Gaussian distributions has long been known to closely approximate empirical response time distributions (e.g., Luce, 1986; Ratcliff, 1979). The word recognition literature includes the ex-Gaussian as a tool for describing the loci of manipulation effects of factors such as word frequency, consistency, and even task that influence the shape of response time distributions (Andrews & Heathcote, 2001; Balota et al., 2004; Balota & Spieler, 1999; Yap, et al., 2008).

We used the ex-Gaussian density function to perform maximum likelihood fits to our pronunciation time distributions (Van Zandt, 2000). The ex-Gaussian description supplied reasonable fits to the empirical pronunciation time distributions, despite our special effort to collect many more observations than a typical single-session pronunciation experiment. This was true even when contrasted with a simplified 3-parameter version of the cocktail that rendered it more comparable to the ex-Gaussian. The simple cocktail convolved a lognormal and inverse power law distribution using fixed 50%-50% proportions, and fixed the power law mode to the value of the lognormal mean. Only the 3 remaining parameters, the lognormal mean, SD, and power-law exponent were free to vary in our subsequent nonlinear least-squares fits to the empirical density functions. The ex-Gaussian and both versions of the cocktail mixtures were statistically indistinguishable at the level of the probability density.

As others have pointed out, model selection is not easy to decide on the basis of best fits to probability density functions. It is a different matter to fit both the probability density and the hazard function, however, and the following procedures allowed a contrast of hazard functions for the two kinds of synthetic hazard functions. In addition to the 22 cocktail mixture simulations, described earlier, we generated 22 synthetic ex-Gaussian distributions for each participant’s empirical distribution. Ex-Gaussian distributions were generated using samples from a synthetic Gaussian and exponential distribution, generated according to the parameters returned by the maximum likelihood parameter estimation routine.

Both sets of 22 synthetic distributions were collapsed into two respective omnibus distributions, comprising a maximum of 24,200 data points (less if there were fewer than 1100 observations in the empirical distribution). Following that, we computed hazard functions for each omnibus cocktail and ex-Gaussian synthetic distribution.

Panel B in Figure 7 depicts the three empirical power-law dominant hazard functions, from the inclusive word data, as three black lines. To their left, depicted as white lines in panel A, are the hazard functions of the omnibus cocktail mixtures that correspond to each empirical distribution depicted in panel B. The synthetic ex-Gaussian omnibus hazard functions for the same three empirical distributions appear as white lines in panel C.

Figure 7.

The center column, panel B and E, depicts apparently power-law dominant and lognormal dominant empirical hazard functions from the second existence proof. Each panel displays three different participants’ hazard functions as three black lines. In the left-most column, panels A and D, depict the omnibus hazard functions as three white lines for cocktail mixtures corresponding to empirical panels B and E. Similarly, in the right-most column, panels C and F, depict hazard functions of omnibus ex-Gaussian distributions corresponding to the empirical data sets in panels B and E. The figure makes clear that the shapes of cocktail hazard functions are more consistent with the empirical hazard functions than ex-Gaussian hazard functions.

These three plots clarify the power of the hazard function test. The ex-Gaussian hazard functions are qualitatively different from both the empirical and cocktail hazard functions for example. However, the empirical and cocktail hazard functions share many details in their shapes, they both include subtle peaks and both decay slowly to asymptotic values. By contrast, ex-Gaussian hazard functions simply rise to a constant asymptote.

Panels D, E and F, in Figure 7, are organized to depict the same triptych of contrasts for three lognormal dominant distributions from the inclusive naming task. The two empirical hazard functions with the highest peaks rise to a prominent peak, and fall off sharply past that point. The cocktail mixtures in panel D do a much better job of recovering this structure than the ex-Gaussian hazard functions in panel F.

The third empirical hazard function, with the lowest peak, presents an ambiguous case. It possesses a peak, but the peak is broader than those of the cocktail mixtures. The ex-Gaussian description, on the other hand does not seem quite peaked enough to capture its shape. This case illustrates that it is largely the properties of the slow tails of distributions that are decisive in discriminating the two frameworks. Lognormal dominant participants tend to produce tighter pronunciation time distributions with few extreme values and their hazard functions do not span very large time intervals.

Figure 8 depicts the same triptych of contrasts for distributions comprised of intermediate mixes of lognormal and power-law samples. Each panel in the center column of the figure depicts four empirical hazard functions from the inclusive naming study. The third row contains only three participant’s hazard functions because participant 13 was excluded as an ambiguous case. The left column of panels depicts the corresponding omnibus cocktail hazard functions; the right column depicts the corresponding omnibus ex-Gaussian hazard functions. In this figure one sees most clearly the failure of the ex-Gaussian description. It simply fails altogether to display peaks prominent in all the empirical hazard functions.

Figure 8.

The center column of panels depicts the apparently intermediate mixture, empirical hazard functions as black lines. Each panel presents four individual participant’s hazard functions from the second existence proof, except for the third row, which contains 3 hazard functions. The left-most column of panels depicts the omnibus hazard functions for cocktail mixtures corresponding to empirical distributions on the same row. The right-most column depicts hazard functions of corresponding omnibus ex-Gaussian distributions. The plots make clear that cocktail simulations better approximate empirical hazard functions and that ex-Gaussian hazard functions fail to display the prominent peaks that are present in both empirical and cocktail mixture hazard functions.

We have only reported simulation details of the ex-Gaussian contrast, but we also conducted extracurricular simulations of inverse-Gaussian, ex-Wald, and Weibull alternatives. In contrast to ex-Gaussian and cocktail simulations, the latter distributions all failed Kolmogorov-Smirnov tests and failed to mimic the hazard functions of data from both existence proofs.

We evaluated hazard functions by generating synthetic distributions based on maximum likelihood fits of the three alternative distributions. The resulting parameter sets supplied each distribution’s best approximation to the empirical distributions. We did this mainly because, given certain parameter sets, the inverse-Gaussian and ex-Wald can display peaked hazard functions. In fits of the present data, however, the inverse-Gaussian hazard functions generally failed to display peaks. Simulated hazard functions tended to rise too quickly, almost always overtaking the empirical hazard functions.

Weibull hazard functions usually rose monotonically, and too slowly, always undershooting the empirical hazard functions. Only the ex-Wald hazard functions fell in the neighborhood of the empirical hazard functions. Ex-Wald hazard functions rarely exhibited peaks however. They were qualitatively similar to ex-Gaussian hazard functions but typically failed to track the empirical hazard function as well as the ex-Gaussian. The results of the extracurricular simulations are not surprising, given that fits to the empirical density functions of the three alternative distributions were generally much poorer than those of the ex-Gaussian.

All these simulations, extracurricular and ex-Gaussian, speak to an obvious worry about whether cocktail mixtures might be too powerful. If power law/lognormal cocktails can fit any distribution, then successfully mimicking pronunciation time distributions is expected. Recall that ex-Gaussian simulations are essentially indistinguishable from the empirical distributions, and also from the cocktail mixtures, at least for probability density functions. This is why the ex-Gaussian is so popular. Once the hazard functions are examined, however, it is clear that the cocktail descriptions have subtle properties that successfully mimic the empirical hazard functions. Nonetheless, and this is the crux, those same properties render cocktail simulations unable to mimic ex-Gaussian hazard functions.

Figures 7 and 8 demonstrated that cocktail mixture hazard functions are usually poor descriptions of ex-Gaussian hazard functions. Thus the cocktail mixture scheme cannot fit every possible distribution or hazard function. Taking into account the extracurricular simulations, power law/lognormal cocktails fail to mimic best-fit density and hazard functions of three common model-distributions of response time, each tuned to the same empirical distributions as the cocktail mixtures.

Taken together, these four alternate distributions supply perhaps the most plausible empirical forms that a participant’s response time distribution could take, other than the cocktail scheme. They are all routinely used to model response time distributions. Nevertheless, the cocktail mixtures fail to represent them reliably. Thus, while the cocktail mixtures are flexible, they are also poised for falsification. Plausible data patterns exist, very similar to empirical response times that cocktail simulations fail to accommodate.

The most plausible of these is the ex-Gaussian. Repeatedly in the history of response time research, scientists have either embraced the ex-Gaussian description or pointed out its weaknesses. The ambivalence comes from the excellent fits to response time distributions versus the discrepancy between the analytic form of the ex-Gaussian hazard function and empirical hazard functions (e.g., Luce, 1986; Moreno, 2002; Van Zandt, 2003; Ashby, Tien, & Balakrishnan, 1993). To the discrepancy, we add that ex-Gaussian hazard functions tend to be too short, they contain too few synthetic data points in their slow tails; a failing that is more prominent in a contrast between exponential and power-law decay.

In conclusion, previous lines of argument that question the ex-Gaussian have been largely analytic in nature, derived from knowledge of the asymptotic behavior of idealized hazard functions. What has been missing is the promise of a motivated alternative that can pass the hazard function test. Interaction dominant dynamics predicts multiplicative interactions among component processes and power law behavior in the slow tails of response time distributions. Sufficiently constrained interaction dominant dynamics also predict lognormal behavior, as we have described. Cocktail combinations of power law and lognormal behavior pass the hazard function test.

Discussion

Employing a more inclusive and representative sample of the English language revealed a more heterogeneous collection of response time distributions, as indexed by the wider range of simulation parameters required to capture empirical distributions. Nonetheless, no new assumptions were required to accommodate the more inclusive dispersion of pronunciation times. Once again, different mixes of power law and lognormal data points accommodate individual differences in the pattern of dispersion.

In both existence proofs, power law and lognormal behavior sufficiently mimic the three characteristic hazard functions that distinguish individual participants. This success is most important. It guarantees generality beyond these particular existence proofs; the same hazard functions are found in most or all response time performances. This outcome further justifies the choice of word naming times as a test case. What we learn from the particulars of pronunciation time distributions tells us about general system properties of cognition.

We learn, for instance, that response time distributions vary qualitatively across participants, even in the same cognitive task. Thus, one must either posit different processes for the different participants or common processes that can change the quality of their dynamics. This has wide ranging implications for how to think about human performance, whether the goal is data analysis of a particular experiment or a comprehensive theory of cognitive activity.

One challenge yet remains to the reliability of cocktail simulations, however, which we fully discuss now. The possibility exists, at least in principle, that our fitting technique, with six parameters, is too flexible and simply exploits ad hoc statistical mimicking. This is a potential problem for any statistical description of any empirical pattern. As we noted earlier in this article, no theory has ironclad protection from this challenge. Any curve, including hazard functions, can be mimicked in many ways, and models with more parameters are more dubious than models with fewer parameters.

It is worth asking, for example, whether conclusions based on hazard function structures, such as peaks, are trustworthy. As one progresses further into the right tail of a hazard function, for instance, the statistical reliability of the hazard function tends to diminish. Events that unfold in the slow tails of response time distributions are always more sparsely sampled than events that unfold near the mode. Other statistical descriptions of response time are also affected by this limitation, not only hazard functions, and statistical tools exist that do a better job than others to compensate for these issues.

We addressed the previous concern with the following statistical tools. We chose kernel density estimation (Silverman, 1989; Van Zandt, 2000) and the Miller and Singpurwalla (1977) hazard function estimation routine. In addition, we combined the density and hazard estimation tools with bootstrapping procedures. Bootstrapping makes the inherent variability of the statistical tools visible by repeatedly resampling simulated distributions to evaluate them in the same manner as empirical distributions.

Bootstrapping yields visible confidence intervals across the estimated function, which supplies information about the reliability of the features of simulated distributions. For example, the synthetic cocktail mixtures typically preserved the peaks and other prominent features of empirical hazard functions. Also, reports of other researchers using different tasks buttress, or focus on, these features of hazard functions. The three characteristic hazard shapes were established in the literature at least as early as Luce’s (1986) monograph and they replicate across tasks and laboratories.

Laboratory methods were also chosen to enhance statistical reliability. We collected 1100 observations from each individual to greatly increase the resolution of our analyses, and used single laboratory sessions to minimize parameter variability across different sessions. Very important, all parameter estimation and distribution fitting was executed for individual participants to avoid known artifacts that result from collapsing across participants (e.g., Estes & Maddox, 2005).

Nevertheless all the previous safeguards to enhance reliability can fail to protect curve fitting from an infinite regress of possible fits. In that regard, Van Zandt and Ratcliff (1995) recommend strictly coherent theoretical motivation to justify the chosen description. They place a premium on principled, theoretically motivated, a priori choices when adopting statistical descriptions. Thus models must be grounded in reasonable theoretical assumptions, which can be tested with empirical patterns.

The cocktail simulations were strictly motivated by interaction dominant dynamics, which previously anticipated widely observed, fractal, 1/f scaling. Power law and lognormal distributions are both necessary consequences of multiplicative interactions, but neither of these choices is obvious outside of a theory based on interaction dominant dynamics. 1/f scaling by itself, for instance, does not strongly constrain the choice of event-time distribution. The default distribution of synthetic 1/f noise is the Gaussian distribution.

1/f scaling only entails interdependent processes and multiplicative interactions within a theory in which processes interact via interaction dominant dynamics, which of course also predicts inverse power-law dispersion (Bak, 1996; Jensen, 1998; Montroll & Shlesinger, 1982). The remaining challenge was to invent a reasonable scheme to combine power law and lognormal distributions. We chose the simplest scheme that we imagined. The six parameters of the cocktail mixtures come simply from locating both distributions within an interval on the response time axis and mixing them in varying proportions.

In sum, the cocktail hypothesis comes from the a priori hypothesis of interaction dominant dynamics, and cocktail simulations supply independent tests of this inclusive hypothesis (cf. Wagenmakers, Ferrell, & Ratcliff, 2005). Consequently, the cocktail hypothesis complies with Van Zandt and Ratcliff’s (1995) recommendations to minimize ad hoc statistical mimicking.

General Discussion

Our essential finding is that the synthetic cocktail mixtures, symptomatic of interdependence and multiplicative interaction, successfully mimic empirical pronunciation time probability density and hazard functions. Successful means simply that the cocktail descriptions were not contradicted statistically by any of the analyses we conducted. All other models that we examined were less successful.

Shapes of synthetic cocktail density functions were consistent with the shapes of empirical probability density functions over large portions of the response time interval, whether plotted on linear or double-logarithmic axes. The cocktail mixtures reliably produced cumulative distribution functions that passed a Kolmogorov-Smirnov test of equivalence. And the cocktail mixtures captured the qualitative features of individual participants’ hazard functions, including the three shapes that characterize most response time data documented in the literature.

The specific value of the power law exponent and the relative mixture proportions in cocktails simulate the transition from power law dominant to lognormal dominant densities. Empirical transitions presumably reflect tipping points or critical points of constraint that transition individual word pronunciations into tightly reinforced dynamics, in the broad sense of reinforced, and therein minimize the contingencies of feedback. This hypothesis marks constraints and the power-law/lognormal tradeoff to account for individual differences.

Cocktail mixtures also closely replicate the values of, and relationships among, empirical parameters such as mean, standard deviation, and skew. In sum, a working hypothesis grounded in the interaction dominant dynamics of feedback processes captures most of the empirical facts of individual participants’ pronunciation time distributions. We are not aware of a more inclusive or more general account of response time data.

Standard Cognitive Manipulations

But what of the vast library of standard mean-effects that resulted from standard cognitive manipulations? How do they make contact with the present success? Individual differences in background history, development, current status and context — in currently available constraints — were predicted to yield different mixes of two kinds of multiplicative functions. Systematic qualitative differences among the consequent hazard functions corroborated the prediction. Reliable qualitative differences in data from the same word-naming task, however, bring into question the logic of design or analysis that contrasts or equates descriptive statistics from different college students’ response times. Such contrasts are not ruled out by this finding, but it raises the bar for their justification. One way forward is to develop new statistical tools that are commensurate with qualitative variability changes and interaction dominant dynamics (e.g, Riley & Van Orden, 2005).

Also, we noted several times how, all other things equal, adequate accounting of distributions or densities supplies the more inclusive account. For instance, how can an account based on means alone anticipate correlations among means, SDs, and skew? Likewise, how can an account based on distributions alone anticipate the three characteristic hazard functions? More narrowly conceived empirical findings are not necessarily inconsistent with the present results, but they are weaker tests of models. Nonetheless, if researchers could expand the existing library, and re-examine all mean effects using contrasts among densities and hazard functions, it would greatly increase empirical power to constrain models and theories.

For example, standard manipulations usually test stimulus properties in performance, which define different word classes. A general basis of many word class distinctions is ambiguity. Ambiguity refers to the relative consistency of relations between spelling patterns and pronunciations, among other things, consider _ear in pear vs. near. Ambiguous spellings support more than one pronunciation, and ambiguous words are more slowly pronounced on average in a word naming task (Glushko, 1979).

Relatively more ambiguous words also disperse their pronunciation times more broadly, in harmony with the present account (Holden, 2002). Specifically, word items can be more or less infected by ambiguity, i.e. ambiguity can be restricted locally to a few letters or the whole word’s spelling can be ambiguous as in homographs such as tear and wind (Van Orden & Kloos, 2005, is a review). A close look at word class effects, using a systematic increase in pronunciation ambiguity (e.g., punt vs. pear vs. tear), sampling across participants, revealed progressively wider dispersion in the heavy slow tails of pronunciation time distributions.

The more all-embracing the infection of ambiguity the more prominent the power law behavior in the slow tail. Yet the fast leading edges of contrasted pronunciation distributions, up to the mode, were close to the same. The same pattern was found for ambiguity in a lexical decision task using patterns of pronunciation that support multiple spellings, such as cube vs. hone vs. hare (Holden, 2002; cf. Stone, Vanhoy, & Van Orden, 1997). In fact, the shapes of the response time distributions to different item classes in Holden (2002) appear consistent with the cocktail mixtures (however, the sample sizes were smaller than those reported here). We re-examined those distributions to determine whether different item classes yielded different hazard functions. Indeed, the item classes most infected by ambiguity yielded hazard functions most like the power law dominant mixtures, in both word naming and lexical decision. The item classes least infected with ambiguity yielded hazard functions most like the lognormal dominant mixtures. Qualitatively similar dispersion effects have been reported in other word recognition studies (e.g. Andrews & Heathcote, 2001; Balota et al., 2004).

Power law behavior was reported in other reading tasks as well. Schultz and Tabor (2005) reported power law behavior in sentence reading times. The extent of garden path ambiguity in sentence comprehension amplifies power law behavior in the slow heavy tails of reading time distributions. As in Holden (2002) the extent of power law behavior is determined by word or phrase ambiguity. These outcomes agree with the present studies, and the hypothesis that motivates the tradeoff between power law and lognormal behavior. All other things equal, relatively ambiguous stimuli produce power law behavior, and sufficiently unambiguous stimuli produce lognormal behavior. Unambiguous in our terms refers to available constraints sufficient to mask, or dampen down, the contingencies of feedback (cf. Gottlob, Goldinger, Stone, & Van Orden, 1999; Van Orden & Goldinger, 1994).

The success of the cocktail mixtures generalizes to response time data from other cognitive tasks as well (e.g., Ashby, Tien, & Balakrishnan, 1993; Balakrishnan, & Ashby, 1991; Luce, 1986; Maddox, Ashby, & Gottlob, 1998). Thus the manner in which cognitive manipulations impact the shape of response time distributions may likewise generalize and give a common account of contrasts between-items, and other factorial contrasts.

Constraint and Cognitive Performance

Historically, cognitive manipulations have been equated with cognitive components, as efficient causes, in causal chains that unfold within the brief interval of a response time. Causal configurations as constraints, however, refer to relations among processes and the coordination of their activities in nonlinear dynamics (Juarrero, 1999). Constraints refer to any aspect of history, context, the present status of mind and body, and task environment that limit or control the degrees of freedom for cognition and behavior.

Many standard “causal” manipulations can be reinterpreted as manipulations of available constraints. Consequently, one can generate predictions and manipulate the dispersion of response times. Other things being equal, manipulations that entail stronger competitions among contradictory sources of constraint, or that rely on a weaker arrays of constraints should display more widely dispersed behavior, the increasing presence of power law behavior.

The current existence proofs demonstrate the plausibility of constraints on performances organized via interaction dominant dynamics. From a cognitive perspective, supporting constraints change slowly, more slowly than the pace of trial performances, while they dispose the mind and body on each trial to receive and pronounce the stimulus word (Hollis et al., 2008; Van Orden et al., 2003a). The arrival of the stimulus further narrows degrees of freedom, to close the system and unfold the specific pronunciation response (Järvilehto, 1998).

From a physiological perspective, constraints on interaction dominant dynamics, within the trial, coordinate the fastest rhythms of the nervous system with the stimulus-perturbation of the environment “upward” through intermediate timescales of brain and body to the limiting timescale of performance, the timescale on which the stimulus word’s pronunciation unfolds (compare Buzsáki, 2006). Pre-stimulus preparation and coordination of embodied dynamics, across all the body’s timescales, guarantees the appropriate post-stimulus degrees of freedom for within-trial dynamics, on their very fast timescales (Gilden, 2001; Hollis et al., 2008).

Conclusions

Interaction dominant dynamics anticipated, previously, the widely evident 1/f scaling in trial series of response times. Presently, interaction dominant dynamics successfully predicts that aggregate response times disperse as power laws, due to interdependence among feedback processes. Interaction dominant dynamics as multiplicative feedback processes also predict power law behavior, as well as lognormal behavior. Power law and lognormal dispersion are symptomatic of multiplicative interactions among process on a hierarchy of timescales.

If mixtures of power law and lognormal distributions mimic empirical dispersion then empirical dispersion originates in a vast array of multiplicative interactions. This conclusion rests upon an inverse inference, similar to the classic inference trusted for Gaussian dispersion. Strictly speaking then, the success of the cocktail mixtures is not sufficient evidence of interaction dominant dynamics, success is simply a necessary consequence. That is what it means that we call cocktail simulations existence proofs. In this way, of course, the present support in evidence is like most evidence in science.

The complex emergence of on-line word naming performance, or any response behavior, presents daunting challenges without simplifying principles. In that regard, all sources of constraint combine via multiplicative interaction. Each trial performance is a temporary dynamical structure visible from “above” in the slower timescale patterns of scaling relations and from “below” in the faster timescale changes that dispersion portrays.

Still, coordination across all these timescales is necessary to perform a word pronunciation, so scaling relations, inverse power laws, and lognormal dispersion must imply complementary mechanisms. In fact it suffices to speak of one kind of mechanism, interaction dominant dynamics, which coordinates processes slower than and faster than the trial-pace of measurement. We draw this essential conclusion from the success of the present existence proofs.