Stability along with Extreme Variability in Core Genome Evolution

Abstract

The shape of the distribution of evolutionary distances between orthologous genes in pairs of closely related genomes is universal throughout the entire range of cellular life forms. The near invariance of this distribution across billions of years of evolution can be accounted for by the Universal Pace Maker (UPM) model of genome evolution that yields a significantly better fit to the phylogenetic data than the Molecular Clock (MC) model. Unlike the MC, the UPM model does not assume constant gene-specific evolutionary rates but rather postulates that, in each evolving lineage, the evolutionary rates of all genes change (approximately) in unison although the pacemakers of different lineages are not necessarily synchronized. Here, we dissect the nearly constant evolutionary rate distribution by comparing the genome-wide relative rates of evolution of individual genes in pairs or triplets of closely related genomes from diverse bacterial and archaeal taxa. We show that, although the gene-specific relative rate is an important feature of genome evolution that explains more than half of the variance of the evolutionary distances, the ranges of relative rate variability are extremely broad even for universal genes. Because of this high variance, the gene-specific rate is a poor predictor of the conservation rank for any gene in any particular lineage.

Introduction

The distribution of evolutionary distances between orthologous genes is one of the key universals of genome evolution. This distribution is approximately lognormal, spans a range of three to four order of magnitude and is nearly identical, up to a scaling factor, when estimated for pairs of closely related genomes from all three domains of cellular life (bacteria, archaea, and eukaryotes) (Grishin et al. 2000; Drummond and Wilke 2008; Wolf et al. 2009). Recently we have shown that the near invariance of this distribution across billions of years of evolution can be accounted for by the Universal Pace Maker (UPM) model of genome evolution (Snir et al. 2012). The UPM model yields a significantly better fit to the data than the classical Molecular Clock (MC) (Zuckerkandl 1987; Bromham and Penny 2003) in a comparison of thousands of gene-specific phylogenetic trees spanning the entire diversity of prokaryotes to the supertree of these organisms (Puigbo et al. 2009). Unlike the MC, the UPM model does not assume constant gene-specific evolutionary rates but rather postulates that, in each lineage, all genes in evolving genomes change their evolutionary rates (approximately) in unison although the pacemakers of different lineages are not necessarily synchronized.

The universal conservation of the distribution of the evolutionary rates of orthologous gene is manifest as the near constancy of its shape (normalized by evolutionary distance) (Grishin et al. 2000; Drummond and Wilke 2008; Wolf et al. 2009). However, this conservation of the rate distribution shape does not necessarily imply that the relative rates of the individual gene evolution, or put another way, the evolutionary conservation ranks of genes remain nearly constant throughout the course of the evolution of life. Simply put, the pertinent question is: Is it the case that the slowest evolving gene in, say, a particular clade of archaea also has the top conservation rank in all bacterial and archaeal clades? Our previous analysis indicates that the UPM of genome evolution, although a better fit to the data on the evolution of numerous genes than the MC, is strongly overdispersed (Snir et al. 2012). To expose the concrete basis of the overdispersion of the UPM, we sought to assess the variability of relative evolutionary rates of individual genes that are (nearly) universal among bacteria and archaea (Koonin 2003) by comparing their positions (ranks) in the rate distributions for multiple, diverse groups of closely related organisms. We show that, although the gene-specific relative rate is an important feature of genome evolution that explains more than half of the evolutionary distance variation, the ranges of relative rate variability are extremely broad even for universal genes.

Materials and Methods

Clade Selection

To select genome pairs at comparable distances, the following procedure was applied. First, a target ancestral node “depth” (defined as half of the distance between the organisms) was chosen. In the rooted binary tree of concatenated ribosomal proteins (Yutin et al. 2012), the depth of all internal nodes was calculated recursively from the leaves to the root as the mean length of all distances from the node to its descendant leaves. The node with the depth closest to the target depth was selected; one species was selected from each of the two subtrees descending from this node, such that the distance from this species to the selected node is closest to the target depth. The pair of species is recorded, and the selected node and all its descendants are removed from the tree. The procedure is repeated until no nodes are available at depths within 75–150% of the pair target depth.

In addition, a genome within 75–150% of the separately defined outgroup target depth was sought for each selected pair. If present, the triplet of genomes (the pair and the outgroup) was recorded.

Two sets of genome pairs were selected for the target depths of 0.03 and 0.075 (P1 and P2, respectively). Outgroup genomes were identified at target depths of 0.05 and 0.1 (T1 and T2, respectively) (see table 1; supplementary fig. S4 and data S1, Supplementary Material online).

Table 1.

Relative Evolutionary Rate and Conservation Rank Variation among Nearly Universal Genes of Bacteria and Archaea

	P1, T1	P2, T2
Bacterial clades (pairs, triplets)	48, 32	52, 43
Archaeal clades (pairs, triplets)	6, 3	5, 3
Mean standard deviation factor within 100 COGs	×1.84	×1.51
Mean standard deviation factor within 100 COGs expected from sampling fluctuation	×1.26	×1.16
	38% of total	37% of total
Spearman correlation between rate variation and COG profile length	−0.54	−0.36
Spearman correlation between rate variation and relative rate	−0.44	−0.59
Mean rank interquartile distance	0.19	0.16
Mean interquartile distance for genomic ranks of COGs with median evolution rates	0.26	0.25
Mean interquartile distance factor for sister branch ratios	×1.68	×1.61

Distances between Orthologs and Phylogenetic Analysis

Reciprocal BlastP (Altschul et al. 1997) searches (e-value threshold 0.01, no composition-based statistics adjustment) were performed between members of each pair or triplet of genomes. For the pairs, bidirectional best hits (BBHs) were recorded as a proxy for orthologs (Tatusov et al. 1997; Wolf and Koonin 2012); in the genome triplets, strict BBH triangles formed triplets of orthologs.

Alignments of putative ortholog pairs or triplets were produced using the MUSCLE alignment program (Edgar 2004). Distances between sequences were calculated using the FastTree program (Price et al. 2010) that produces log-corrected distances calculated with the BLOSUM45 amino acid similarity matrix. If the sequences of orthologs were exactly identical, they were assigned a distance of 0.5 divided by alignment length (Wolf et al. 2009). The same software (MUSCLE and FastTree) was used to reconstruct approximate maximum likelihood (ML) phylogenetic trees from multiple alignments of Clusters of Orthologous Group (COG) representatives that were used for Xenologous Gene Displacement (XGD) detection. The trees in the Newick format are available at ftp://ftp.ncbi.nih.gov/pub/wolf/_suppl/ratevar.

It should be noted that with so closely related species, the quality of pairwise alignments and therefore the accuracy of distance estimate is not expected to represent a problem. The most distant pair of sequences in the entire P1 set (YP_004138486 vs. YP_003007995, COG0221) has three indels within 175 amino acid protein sequence alignment and has a reported BlastP e-value of 4 × 10⁻²⁵ at 28% sequence identity. However, to test the robustness of the results to the potential inaccuracy of sequence alignments, we produced a variant of the P1 data set distances that were estimated only for alignments with ≥40% identity (set P1’). To test the robustness of the results to the distance calculation method, we produced a variant of the P1 data set distances that were estimated using the Protdist program of the PHYLIP package (Felsenstein 1996) with the Jones, Taylor, and Thorton evolutionary model and gamma-distributed site evolution rates with shape parameter of 1 (set P1”).

COG Assignments

Protein-coding sequences of the genomes in the selected clades were assigned to COGs (Tatusov et al. 2003) using PSI-BLAST (Altschul et al. 1997) searches with COG-derived Position-Specific Scoring Matrices. For the purpose of this analysis, both members of the BBH pair have to be assigned to the same COG and satisfy the following criteria: the COG profile footprint must cover at least 75% of the protein length and at least 75% of the COG profile length. When multiple BBH pairs from the same clade are assigned to the same COG, the pair with the shortest distance (Index Orthologs [Wolf et al. 2006]) is used for further analysis. Although theoretically comprehensive phylogenetic analysis yields the most accurate assignment of gene orthology, it presents substantial practical difficulty (Kristensen et al. 2011) However, several benchmarking studies have convincingly shown that the BBH represent an excellent orthology indicator (Altenhoff and Dessimoz 2009; Wolf and Koonin 2012; Gabaldon and Koonin 2013) allowing one to rely on the BBH/COG approach for most purposes, especially for highly conserved genes that typically do not have numerous paralogs as is the case for the sets of genes analyzed here.

For the P1 data set, 100 COGs (supplementary data S1, Supplementary Material online) are present in at least 36 of the 48 bacterial clades and at least five of the six archaeal clades. The 54 × 100 matrix of index ortholog distances contains 4,887 (90.5%) available values. The same set of 100 COGs is present in 5,230 of the 57 × 100 COG-clade combinations (91.8%) in the P2 data set (supplementary data S2, Supplementary Material online).

Least-Squares Solution

Equation (2) gives the least-squares estimate for the evolution rates associated with individual COGs and interspecies distances specific to analyzed clades. Under the assumption that the log of the deviation in equation (1) is distributed normally, these estimates provide also the ML estimates (supplementary text S1, Supplementary Material online). We used Sage (Stein and Joyner 2005) to find the exact solution. Because the rates and the distances are mutually confounded in equation (2), we arbitrarily assign the value of 1 to one of the relative rates (r₀), obtaining a unique solution.

Results

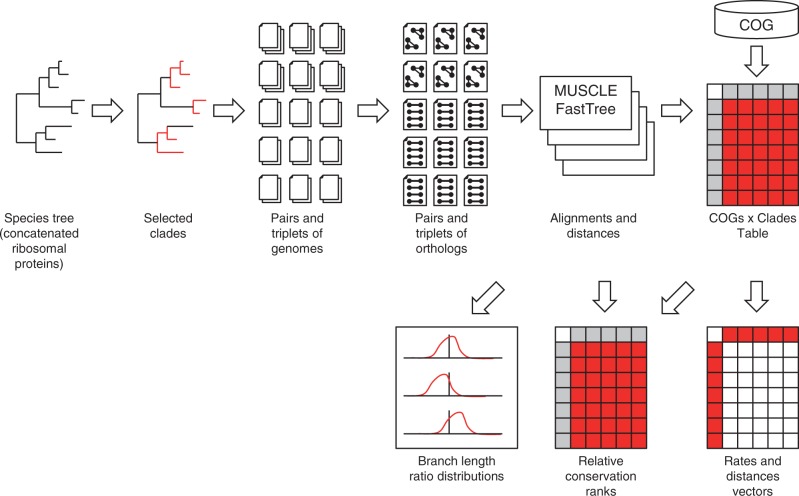
We compiled two data sets of nearly universal genes for pairs of prokaryotic genomes: P1 that included the most closely related of the analyzed genomes and P2 that consisted of more diverged genomes (see supplementary data S1, Supplementary Material online). Both data sets included 100 COGs [Tatusov et al. 1997, 2003]) (see supplementary data S1, Supplementary Material online), each represented in at least 36 of the 48 analyzed bacterial clades and in at least five of the six archaeal clades. In addition, we compiled the T1 and T2 data sets that represented triplets of orthologous genes from closely related genomes, that is, included an outgroup to those of the pairs in P1 and P2, respectively, for which it could be identified at an appropriate evolutionary depth (see Materials and Methods; fig. 1).

Fig. 1.—

Schematic of the comparative analysis of sets of closely related species of archaea and bacteria.

The evolutionary distances are not the same between clades because all pairs of genomes are selected at different depths (despite our efforts to confine them within a relatively narrow range) or between genes (COGs) because different genes generally evolve at different rates (supplementary fig. S1A, Supplementary Material online). To account for both sources of variation in the analysis of observed distances, we apply the following quantitative model:

(1)

where d_ij is the observed distance between the orthologs for COG i and clade j; r_i is the intrinsic evolution rate of family i; t_j is the distance (divergence time) separating the two genomes in clade j; and ε_ij is the deviation factor, such that <log ε> = 0. Vectors r and t are unknown but can be estimated from the data by minimizing the difference between the expected (r_i t_j) and observed (d_ij) distances across all COG-clade combinations. Minimizing

(2)

by differentiating over r and t yields the least-squares estimate for the COG-specific evolution rates and clade-specific distances. Under the assumption that log ε is distributed normally, the least-squares estimates for r and t are also the ML estimates. Normalizing the observed distances by corresponding r and t values reduces them to ε_ij, the distance deviation factors that are comparable across the COGs and the clades. Variance of ε is the measure of the relative evolutionary rate variation that is sought in this work. Conceptually, this rate variation model is equivalent to that under the UPM (Snir et al. 2012). Indeed, in our model, the existence of the single rate vector r and single distance vector t implies that the family-specific relative evolution rates are universal across clades, and the clade-specific distances are the same for all families. Unlike in the classical MC model (Zuckerkandl 1987; Bromham and Penny 2003), no ultrametric relationship between the tree branches leading to the sister genomes from their common ancestors is assumed; only the total distance between the compared genomes is relevant for this model.

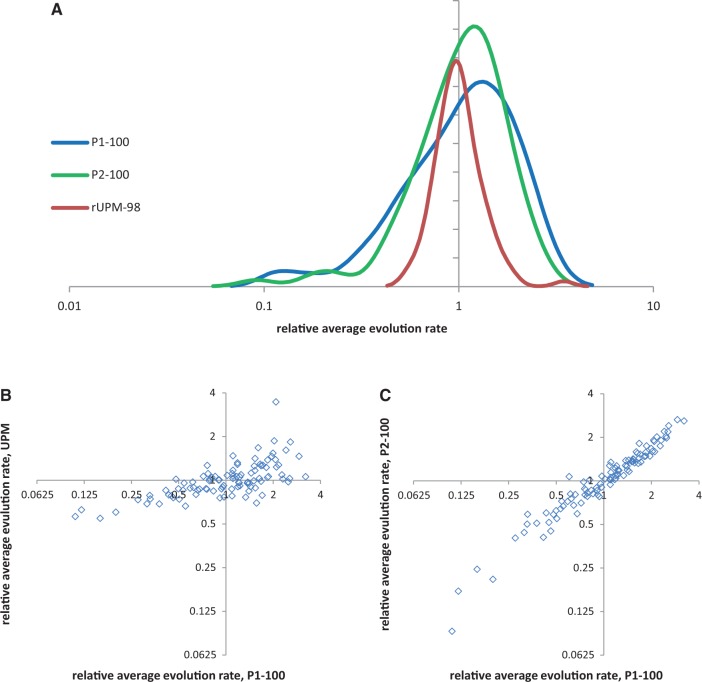
Solving equation (2) for minimum E², we calculated the COG-specific values of r and clade-specific values of t for the P1 and P2 data sets (supplementary data S2, Supplementary Material online). The 100 COG-specific relative evolution rates in both sets are almost perfectly correlated (Spearman rank correlation coefficient r_S = 0.97, P < 0.0001; fig. 2A) despite the fact that these rates are computed for different pairs of orthologs (although this correlation is expected to be high, we considered it important to explicitly calculate it to ascertain the robustness of the procedure). Among the 98 COGs that are shared between P1, P2, and the UPM analysis (Snir et al. 2012), relative evolutionary rates in both P1 and P2 are also significantly correlated with the UPM-derived rates (r_S = 0.69, P< 0.0001 for both; fig. 2B). The range of variation in relative rates for the P1 and P2 data sets is much wider than that in the data set used for the UPM analysis that spans much longer evolutionary distances (fig. 2C). Specifically, the distribution of short-term relative rates covers approximately two orders of magnitude compared to approximately one order of magnitude for the long-term (UPM) rates (fig. 2C). Given that the distribution of the long-term relative rates is truncated roughly symmetrically on the high and low ends, it appears unlikely that the difference in the distribution width is caused by artifacts of rate estimation. This finding supports our previous conclusion that short-term variation plays a major role in the extant distribution of evolutionary rates but tends to average out over longer evolutionary spans (Snir et al. 2012).

Fig. 2.—

Relative evolution rates. (A) Distributions of the short-term (obtained from distances in the P1 and P2 data sets) and long-term (obtained under the UPM model) relative evolutionary rates. (B) Correlation between short-term (P1) and long-term (UPM) evolutionary rates. (C) Correlation between short-term (P1 and P2) evolutionary rates.

The standard deviation of log ε_i* (eq. 1), σ_i, gives the variation of local relative evolutionary rates within a COG between the clades. This variation was in the range of 0.127–0.458 decimal log units (deviation factor of ×1.34 to ×2.87) for the P1 data set (mean deviation factor ×1.84, 0.266 decimal log units) (table 1). The P2 data set shows similar, albeit somewhat lower variation (mean deviation factor of ×1.51). Part of the variation of the evolutionary rates can be explained by fluctuations in finite samples. Distances between proteins are ultimately estimated by counting differences between aligned sequences. Given that the compared genes come from closely related organisms, such that in many cases the number of substitutions is small, one might expect a significant contribution from sampling error. Following the logic of the UPM analysis (Snir et al. 2012), we estimated the expected sampling error by assuming that mutations are generated by a Poisson process. Taking the observed distance multiplied by the alignment length as the expected effective number of substitutions and averaging the log of the mean deviation factor across the clades and the COGs, one can estimate the expected sampling error. For the P1 and P2 data sets, the fluctuations due to the finite number of observed substitutions are expected to produce variation of the distances with the mean deviation factors of ×1.26 and ×1.16, respectively, that is, 38% and 37% of the observed deviation factors (table 1). Thus, most of the variance is due to causes other than sampling error, that is, the short-term relative evolutionary rates show substantial overdispersion similar to the overdispersion of the MC (Takahata 1987; Cutler 2000; Wilke 2004; Bedford and Hartl 2008) and UPM models (Snir et al. 2012).

To test whether these results were robust to the effects of potentially unreliable alignments and to details of distance estimation procedures, we produced two additional derivatives of the P1 data set. The set P1’ consisted of ML evolutionary distances that were estimated only for alignments with ≥40% amino acid sequence identity. The set P1” included distances that were estimated using a different substitution model (see details in Materials and Methods and supplementary data S2, Supplementary Material online). Solutions for the r and t vectors were obtained for both P1’ and P1”. The results obtained with both variants showed a near-perfect match to the results for the original data set: The Pearson linear correlation coefficient between r vectors was 0.9998 (root mean square deviation [rmsd] is 0.0063 decimal log units, a factor of ×1.015) for P’ and 0.9986 (rmsd of 0.0161 decimal log units, a factor of ×1.038) for P”. The correlation coefficient between the t vectors was 0.9996 (rmsd of 0.0039 decimal log units, a factor of ×1.009) for P’ and 0.9827 (rmsd of 0.0775 decimal log units, a factor of ×1.195) for P”.

The effect of these variations on the rate variation estimates was also negligible. Compared with the mean deviation factor of ×1.84 (0.266 decimal log units) for the P1 set, exclusion of 7 of the 4,887 alignments with identity less than 40% from the set P1’ leads to the decrease of the mean deviation factor to ×1.83 (0.264 decimal log units). When distances were estimated using a different substitution model (set P1”), the mean deviation factor increased to ×1.87 (0.271 decimal log units).

Taken together, these results indicate that the extreme variation of the evolutionary rates of core prokaryotic genes detected in this work is a robust observation that is not due to artifacts of either alignment methods or of methods employed to estimate the evolutionary distances.

We further pursued the possible effects of statistical artifacts on the observed variance of the evolutionary rates. The gene-specific variation of relative evolutionary rates negatively, significantly, and independently correlates with the alignment length and with the COG-specific evolution rate itself (table 1). Shorter and slower-evolving proteins exhibit greater variation in relative evolutionary rates across the clades, consistent with the expected lower effective number of substitutions and suggesting that sampling fluctuations significantly contribute to the evolutionary rate variation for these genes. The estimated variation caused by sampling error positively and significantly correlates with the observed variation (r_S = 0.59 and r_S = 0.64 for P1 and P2 data sets, respectively; P< 0.0001 for both data sets) but was insufficient to fully explain the dependency of the variation of the evolutionary rate on the alignment length and the COG-specific evolution rate.

The observed wide range of local variation of the relative evolutionary rates might cast doubt on the very validity (in a sense, the very existence) of gene-specific relative evolution rates. However, analysis of variance shows that taking into account COG-specific evolution rates explains 55% and 64% of the clade-normalized distance variance in the P1 and P2 data sets, respectively; the reduction in variance is highly significant in both cases (P<< 1 × 10⁻¹⁰; supplementary fig. S1B, Supplementary Material online). Thus, at least within the set of nearly universal genes analyzed here, the intrinsic, gene-specific relative evolutionary rate is a key characteristic of a gene’s evolution that explains more than half of the variation of the observed rates. The rest of this variation is apparently caused by uncorrelated clade-specific fluctuations.

In the context of whole-genome comparison, distances between orthologs can simply be sorted within the clades and characterized by their conservation ranks that are normalized to the range of 0–1, the least conserved to the most conserved, to account for the different numbers of orthologous pairs. Then, the differences between clade depths become irrelevant and the normalized conservation ranks become directly comparable to each other. The median relative rank is negatively and near perfectly correlated with the relative evolution rate calculated from the distances (r_S = −0.99, P< 0.0001 for both P1 and P2 data sets; fig. 3A and B), and the ranks were strongly, positively correlated between P1 and P2 (fig. 3C). Also, as expected, 95 of the 100 COGs in P1 and 96 of the 100 COGs in P2 had a median relative rank >0.5, that is, nearly universal COGs also show the tendency to be highly conserved at the level of sequence evolution. This result is compatible with the previous observations on the negative correlation between a gene’s loss rate and sequence evolution rate that were obtained with unrelated data and using different methods (Krylov et al. 2003; Borenstein et al. 2007).

Fig. 3.—

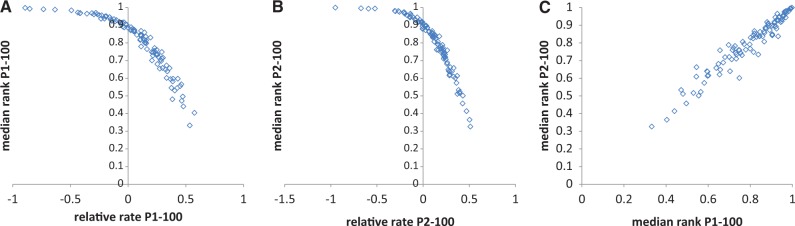
Relative conservation ranks and relative evolutionary rates. (A) Correlation between the relative evolutionary rates and the median conservation ranks (P1). (B) Correlation between the relative evolutionary rates and the median conservation ranks (P2). (C) Correlation between the median conservation ranks (P1 and P2).

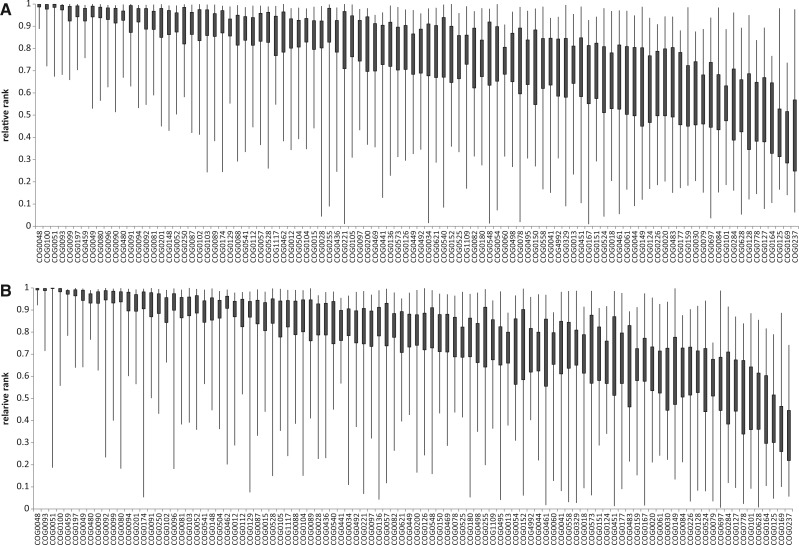
However, the conservation ranks within most of the COGs show unexpectedly high variation across the clades: In 80 of the 100 COGs in P1 and 85 of the 100 COGs in P2, the difference between the highest and the lowest ranks exceeds 0.5 (i.e., the ranks of these COGs span more than half of the total range; fig. 4, supplementary data S3 and fig. S1C, Supplementary Material online). Moreover, for many of the genes in both data sets, the variation spans nearly the entire range. For example, in the P1 data set, members of COG0221 (inorganic pyrophosphatase) in Chloroflexus aurantiacus J-10-fl and C. aggregans DSM 9485 form the second most conserved pair of orthologs out of 3,234 orthologous pairs (sequences YP_001636897 and YP_002462381 are identical). In contrast, members of this COG in Haemophilus influenzae F3047 and Aggregatibacter aphrophilus NJ8700 are ranked #1331 of the 1,345 orthologous gene pairs (normalized rank of 0.01); the alignment of the corresponding sequences YP_004138486 and YP_003007995 contains only 28% identical positions (we note parenthetically that even in this extreme case, the alignment contains only three indels over 175 positions and the corresponding Blast hit has an e-value of 4 × 10⁻²⁵ emphasizing that the alignment quality is not an issue in the present analysis). This dramatic case seems to result from XGD (Koonin et al. 2001; Koonin 2005) whereby evolutionary histories of apparent orthologs in closely related organisms involve different routes of horizontal gene transfer (supplementary fig. S2, Supplementary Material online). Similarly, COG0078 (ornithine carbamoyltransferase) includes a pair of orthologs from Pyrococcus abyssi GE5 and P. furiosus DSM 3638 (NP_126998 and NP_578323) that are 99% identical (rank #22 out of 1,506 pairs) and a pair from Anaplasma marginale str. St. Maries and A. centrale str. Israel (YP_154290 and YP_003328179) that are only 50% identical (rank 842 of 858 orthologous pairs). In this case, there is no sign of XGD, and the anomalously low similarity is probably due to the acceleration of evolution in the Anaplasmataceae lineage (supplementary fig. S3, Supplementary Material online). Large variations of normalized conservation ranks were observed for genes with diverse functions including some of the most conserved ones such as ribosomal proteins and other translation system components (table 2 and supplementary data S3, Supplementary Material online).

Fig. 4.—

Variation of the relative conservation ranks. (A) Set P1. (B) Set P2. The boxes show interquartile distances; the whiskers show the full range.

Table 2.

Examples of (Nearly) Universal Genes with Diverse Biological Functions and Varying Ranges of Conservation Ranks

COG	Max	q3	Med	q1	Min	Protein Name/Function
COG0048	1.000	0.999	0.993	0.987	0.888	Ribosomal protein S12
COG0099	1.000	0.989	0.967	0.924	0.658	Ribosomal protein S13
COG0092	0.996	0.980	0.962	0.887	0.546	Ribosomal protein S3
COG0096	0.996	0.982	0.961	0.931	0.625	Ribosomal protein S8
COG0250	0.999	0.985	0.936	0.820	0.581	Transcription antiterminator
COG0174	0.992	0.970	0.928	0.870	0.244	Glutamine synthetase
COG0057	0.992	0.958	0.904	0.832	0.365	Glyceraldehyde-3-phosphate dehydrogenase/erythrose-4-phosphate dehydrogenase
COG0504	0.983	0.927	0.880	0.806	0.392	CTP synthase (UTP-ammonia lyase)
COG0436	0.984	0.926	0.873	0.783	0.245	Aspartate/tyrosine/aromatic aminotransferase
COG0469	0.951	0.912	0.859	0.698	0.355	Pyruvate kinase
COG0548	0.979	0.919	0.834	0.634	0.012	Acetylglutamate kinase
COG0449	0.973	0.865	0.814	0.684	0.325	Glucosamine 6-phosphate synthetase; contains amidotransferase and phosphosugar isomerase domains
COG0152	1.000	0.900	0.779	0.647	0.358	Phosphoribosylaminoimidazole-succinocarboxamide (SAICAR) synthase
COG0495	0.969	0.838	0.748	0.637	0.305	Leucyl-tRNA synthetase
COG0524	0.981	0.808	0.748	0.511	0.043	Sugar kinases; ribokinase family
COG0329	0.996	0.845	0.700	0.581	0.090	Dihydrodipicolinate synthase/N-acetylneuraminate lyase
COG0149	0.988	0.803	0.657	0.450	0.120	Triosephosphate isomerase
COG0177	0.881	0.782	0.649	0.457	0.172	Predicted EndoIII-related endonuclease
COG0084	0.984	0.682	0.594	0.434	0.152	Mg-dependent DNase
COG0778	0.838	0.648	0.565	0.383	0.145	Nitroreductase

Note.—Highest, 3rd quartile; median, 1st quartile; and lowest relative conservation ranks are shown for selected COGs in the P1 set.

To quantitatively assess the contribution of XGD to the observed variance of the relative evolutionary rates, we reconstructed phylogenetic trees for all genes in the P1 set and examined the positions in these trees of the most distant pairs of orthologs that appear to be prime suspects for XGD (supplementary data S4, Supplementary Material online). Of the 100 families, in 16 these most distant pairs show signs of XGD, that is, the genes from these pairs belong to distant clades. In the remaining 84 cases, the genes from the most deviant pairs occupy the positions that are expected from the overall relatedness of the organisms. Thus, we conclude that the contribution of XGD to the observed variance of relative evolutionary rates is substantial but not dominant.

A more robust measure, interquartile distance, reveals comparatively moderate variability (fig. 4). This measure of variation does not show any dependence on the alignment length but tends to increase for genes with lower conservation ranks (probably because of the trivial fact that all the values are within the 0–1 range). For COGs with conservation ranks close to the genomic median (mean normalized rank between 0.4 and 0.6), the width of the interquartile band is 0.26 and 0.25 for P1 and P2, respectively (table 1 and fig. 4). In other words, for genes with mean evolution rates in the middle of the genomic distribution, we cannot predict the rank with precision better than within a quartile for half of the clades.

We used the T1 and T2 data sets of triplets of closely related genomes to estimate the variation of the sister branch length ratio. Under the MC model, the branches have the same length (1:1 ratio) because the divergence time from the common ancestor is obviously the same for both sister genomes. Under the UPM model, the ratio can deviate from 1 but should be the same for all orthologs in the sister genomes up to the sampling error and rate variation.

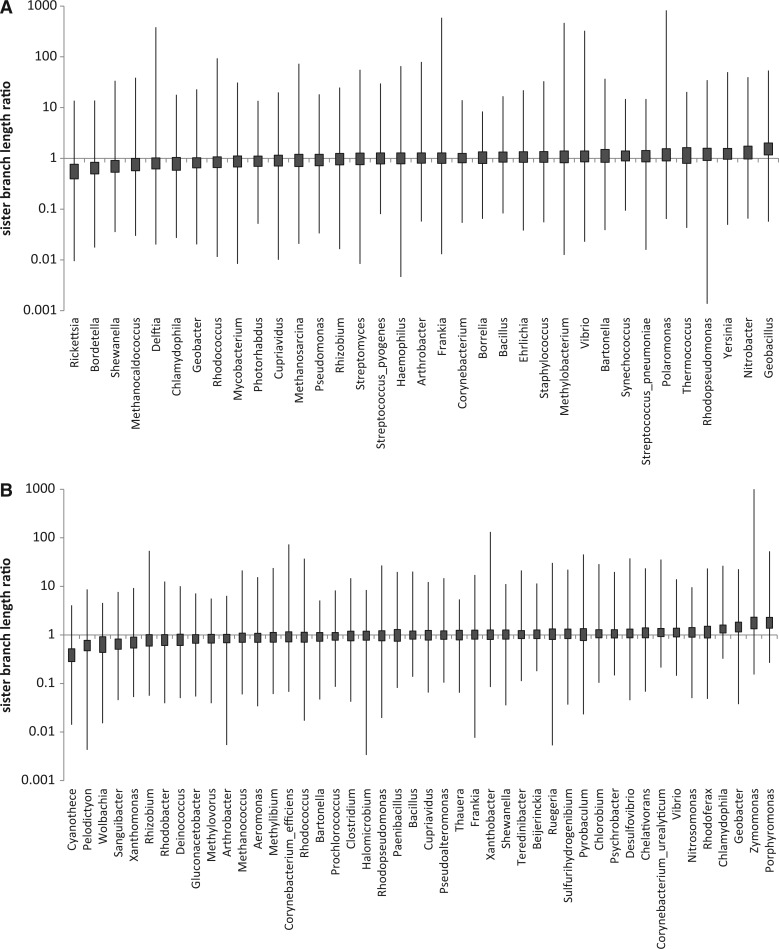
The observed ratios of the sister branch lengths show enormous variation between orthologs within the clade. The mean difference between the highest and the lowest ratios is greater than 3 orders of magnitude (a factor of ×1,640 for T1 and ×426 for T2; fig. 5; supplementary fig. S1D, Supplementary Material online). The interquartile distance factors are much smaller, ×1.68 and ×1.61, respectively (table 1). Despite such a wide range of variability, the median sister branch length ratio is highly robust and shows strong positive correlation with the branch length ratio in the tree of concatenated ribosomal proteins (r_S = 0.62 and r_S = 0.65, P< 0.0001 for T1 and T2, respectively). Thus, the contrast between the robustness of the median and the wide range of the extremes is even more pronounced for the ratio of sister branch lengths in close genome triplets than it is for relative conservation ranks in genome pairs.

Fig. 5.—

Variation of the ratio of sister branch lengths. (A) Set T1. (B) Set T2. The boxes show interquartile distances; the whiskers show the full range.

Discussion

The overdispersion of the MC that results from widespread and often substantial deviations from the constancy of gene-specific evolutionary rates within orthologous gene sets is a well-established phenomenon (Takahata 1987; Cutler 2000; Wilke 2004; Bedford and Hartl 2008; Bedford et al. 2008). Here, we examine the variability of the evolutionary process under a more general model, the UPM, that allows arbitrary deviations from the absolute gene-specific evolutionary rate (the MC) as long as the relative rates remain constant (Snir et al. 2012). Comparative analysis of the relative rates (or conservation ranks) of genes in multiple sets of taxonomically diverse groups of archaea and bacteria reveals substantial robustness of the gene-specific relative evolutionary rates. In this respect, the results of this study are compatible with the existing body of work on MC models (Kimura 1983; Zuckerkandl 1987; Bromham and Penny 2003) and more specifically support the UPM model (Snir et al. 2012). However, the observed robustness of the gene-specific rates is unexpectedly and at first glance paradoxically combined with extreme variability that, to the best of our knowledge, was not appreciated in previous work. Indeed, on the one hand, the assumption of constant gene-specific relative rates explains more than half of the observed variance, but on the other hand, this gene-specific rate is a poor predictor of the conservation rank of any gene in any particular lineage. Strikingly, for many genes, the conservation rank can be almost anywhere in the genome-wide distribution. The analysis described here involved pairs or triplets of closely related genomes and included stringent alignment quality control, so that it appears highly unlikely that the variability of the relative evolutionary rates is significantly affected by alignment artifacts. We further assessed the contributions of substitutions sampling error and showed that the observed variance greatly exceeds the variance that can be attributed to sampling. Although the observed variance of the relative evolutionary rates is unexpectedly large, the results reported here do not contradict the UPM model and so do not call for a new general model of gene evolution. On the contrary, a strong correlation was shown to exist between the short-term relative evolutionary rates measured here and the long-term rates derived from the UPM model (fig. 2B) indicating that overall the results are compatible with the UPM. The high variance of the relative gene-specific evolutionary rates reported here puts concrete information on the evolution of individual genes behind the overall overdispersion of the UPM that we have reported previously (Snir et al. 2012).

The unexpected shuffling of the conservation ranks in the genomic distribution is observed even among genes that are (almost) never lost during evolution and are known to be essential for the survival of model organisms such as translation system components. By building and examining the phylogenetic trees for all analyzed genes, we assessed the contribution of horizontal gene transfer, or more specifically, XGD to the observed dramatic variance of the relative rates of gene evolution. The results indicate that this contribution is important but still accounts only for a minority of the extreme deviations from the characteristic relative rates. Thus, the main causes of the variance of relative evolutionary rates remain enigmatic. Given that most of the analyzed genes encode proteins involved in universal cellular functions, such as translation, it seems unlikely that the variations are directly and primarily caused by differences in the life styles of the respective organisms. In agreement with this anticipation, analysis of the supplementary data S2, Supplementary Material online, failed to detect obvious differences in the relative evolutionary rate variation in thermophiles versus mesophiles or in parasites versus free-living organisms (not shown). Theoretical and empirical study of the causes of the deviations from the characteristic gene-specific relative rates could become an important direction in evolutionary genomics.

Supplementary Material

Supplementary data S1–S4, figures S1–S4, and text S1 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).