The length–tension curve in muscle depends on lattice spacing

Abstract

Classic interpretations of the striated muscle length–tension curve focus on how force varies with overlap of thin (actin) and thick (myosin) filaments. New models of sarcomere geometry and experiments with skinned synchronous insect flight muscle suggest that changes in the radial distance between the actin and myosin filaments, the filament lattice spacing, are responsible for between 20% and 50% of the change in force seen between sarcomere lengths of 1.4 and 3.4 µm. Thus, lattice spacing is a significant force regulator, increasing the slope of muscle's force–length dependence.

1. Introduction

For more than three centuries, physiologists have known that a contracting muscle maintains a constant volume [1]. Contraction under constant volume dictates that muscle must grow wider as it shortens, thus expanding radially. This, in turn, dictates that the distance (lattice spacing) between adjacent thick (myosin) and thin (actin) filaments must increase [2,3]. Historically, most attention paid to how the force of contraction changes with muscle length has ignored changes in lattice spacing, focusing instead on changes in filament overlap. Here, we demonstrate that changes in lattice spacing can play a little-recognized and critical role in determining the length–tension (LT) curve, a basic property of contracting muscle.

The LT curve of isometric muscle contraction provides key experimental support for the sliding-filament hypothesis [4]. The LT curve describes the maximum isometric force a muscle generates as sarcomere lengths vary. As muscle is stretched from extremely short to extremely long lengths, the force it generates increases over the ascending limb, peaks in the plateau region and decreases over the descending limb [5]. The rise and fall of force with sarcomere length is an indicator that the basic mechanism of force generation is myosin cross-bridge interaction with actin binding sites along the thin filament. Because the LT curve describes the behaviour of muscle across a wide range of lengths, the maintenance of a constant cell volume dictates that lattice spacing must change dramatically. This makes the LT curve an ideal mechanism to demonstrate whether and how changes in lattice spacing alter the force muscle generates.

Evidence that lattice spacing changes as sarcomere length changes comes from X-ray diffraction measurements and from the requirement that muscle remain at a constant volume (if only approximately) [2,3]. This isovolumetric assumption posits that the lattice volume of muscle is constant over the time scale of contractions, implying there is no bulk flow of fluids into or out of the myofibrils. Aside from the difficulty in removing fluid from a tightly packed lattice, the sarcolemma surrounding each fibre enforces a constant cell volume at the subsecond time scale. Although the fibre maintains a constant volume over a contraction, this constraint is slightly relaxed over longer durations [6].

For more than the last half century, most studies of the molecular machinery that generates force in muscles have relied on skinned muscle fibres, which have had their surrounding membranes removed or disrupted [4,7–9]. Unlike intact muscle, skinned muscle does not necessarily maintain a constant volume and so may or may not exhibit volume-associated radial expansion when shortening. Skinned fibres' lack of a well-regulated radial direction has led to conceptions of force–length dependence that are focused on variation in the direction of shortening [5].

Explanations of the LT curve based exclusively on processes in the axial direction are appealing, in part, because the known lengths and dimensions of the thick and thin filaments can predict the sarcomere lengths where the LT curve transitions between phases [5]. However, purely axial explanations are likely to be incomplete as the accompanying changes in lattice spacing affect the kinetics and forces of myosin heads [10–13]. An increase in lattice spacing implies that the unstrained location of a myosin head is farther from a potential binding site and that a head must diffuse over a greater distance to bind, as well as that the head will produce a different force vector upon binding [12,13]. The resulting changes in kinetics have been offered as explanations of, for example, changes in Ca²⁺ sensitivity [14,15]. This leads us to ask: how much of the force change on the ascending and descending limbs is caused by changes in lattice spacing?

Here, we test whether changes in lattice spacing regulate maximum force production across the LT curve. We use skinned fibre X-ray diffraction experiments to parametrize a multiple filament, spatially explicit model of the sarcomere that incorporates lattice spacing (figure 1a; electronic supplementary material, figure S1). We check our spatially explicit model against both new data and classic published data [4]. We demonstrate that changes in lattice spacing substantially increase the length dependence of force. Thus, the slope and shape of the LT curve is a product of both the axial and the radial geometry of contracting muscles (figure 1b).

Figure 1.

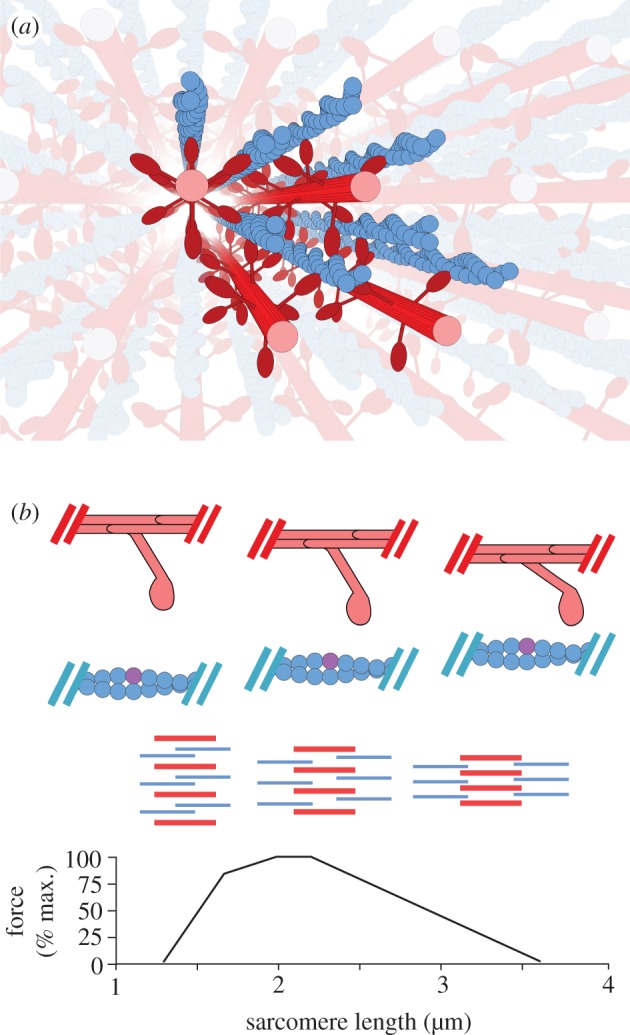
(a) A spatially explicit three-dimensional multifilament model of the sarcomere generates varying levels of force as lattice spacing varies across the length–tension (LT) curve. The multifilament model of the half-sarcomere uses eight thin filaments and four thick filaments, populated by two-dimensional cross-bridge models. Simulated filaments are depicted in bold colours, and mirrored versions of those filaments which are reached by passing through a boundary are shown in light colours. Toroidal boundary conditions simulate an infinite lattice of contractile filaments, which is sensitive to changes in radial spacing. (b) Filament overlap and lattice spacing changes across the LT curve. From bottom to top, the LT curve for vertebrate skeletal muscle, a diagram of the relative degree of overlap and lattice spacing in the sarcomere across the LT curve, and a cartoon depicting the relative locations of a single cross-bridge and the thin filament across the LT curve. In the filament schematic, the thick filaments are shown in red while the thin filaments are shown in blue. The thick filaments are radially compressed from left to right, as overlap with the thin filaments decreases and sarcomere length increases. In the single cross-bridge cartoon, the lattice spacing decreases as sarcomere length grows from left to right. An example binding site is shown in purple, demonstrating in the rightmost column the geometric restriction that accompanies highly compressed lattice spacings. (Online version in colour.)

2. Results

We first show that force generation under isovolumetric conditions in our spatially explicit model agrees with the experimental LT curve. We then isolate changes in sarcomere length and changes in lattice spacing, showing that neither is sufficient to produce an LT relationship with the levels and slopes of force change muscle displays. Changing only sarcomere length produces a shallow force–length relationship, reducing the force–length slope by 28–67% from isovolumetric conditions. The slope of the LT curve requires changes in both sarcomere length and lattice spacing. We confirm model predictions of lattice spacing's influence in skinned fibres by osmotically changing only lattice spacing, reproducing much of the force change expected from isovolumetric conditions.

(a). Theoretical and experimental isovolumetric length–tension curves agree

The force produced by our model under isovolumetric conditions closely matches published actively generated force levels for frog striated muscle (figure 2) [4]. As shown in figure 2a,d, the model produces 18–21% of its peak force for simulations at extreme sarcomere lengths of 1.4 or 3.4 µm, where isolated striated muscle fibres generate 25–30% of their peak forces. By linear regression, the ascending limbs of the isovolumetric model and isolated striated muscle fibres have respective slopes of 1.44 ± 0.07 and 1.57 ± 0.11, which are not significantly different (ANCOVA, p = 0.61; electronic supplementary material, figure S4). Likewise, there is no significant difference (ANCOVA, p = 0.52) between the slopes of the isovolumetric model (−0.72 ± 0.02) and the fibres (−0.74 ± 0.02) on the descending limb. These comparisons address only actively generated forces, as our model does not include passive-force-generating elements such as titin.

Figure 2.

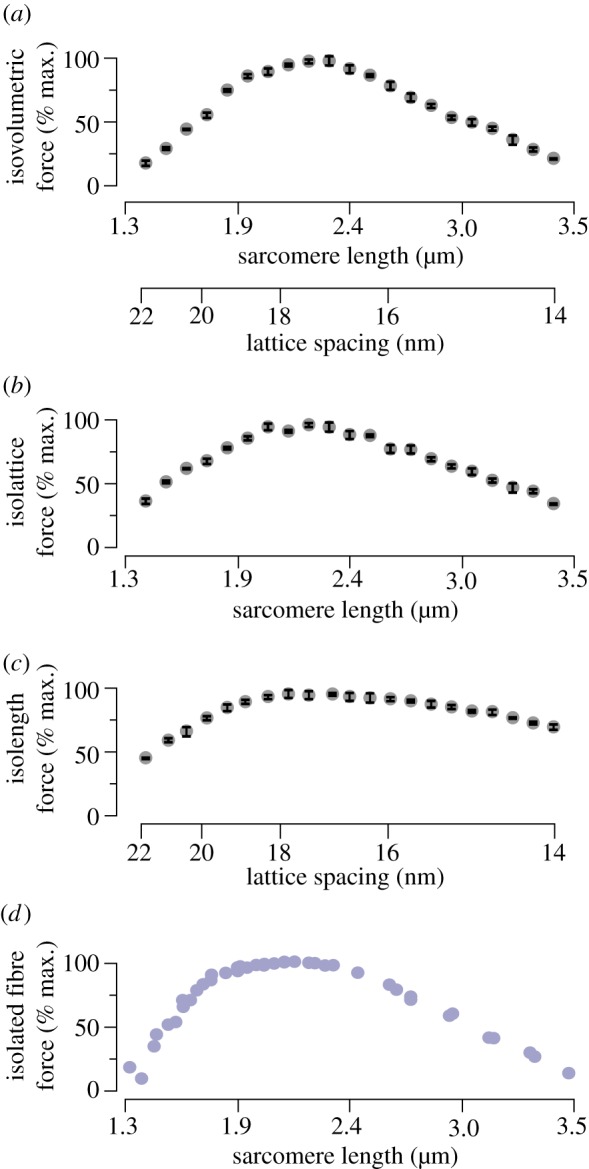
Isovolumetric, isolattice and isolength force curves compared with isolated fibre measurements. (a) The force generated along a simulated isovolumetric LT curve shows the classic three-region shape. To maintain a constant lattice volume, lattice spacing changes as the square root of (1 divided by sarcomere length). Force at extreme sarcomere lengths/lattice spacings is decreased by over 75% from its peak value. Error bars depict the standard deviation of the maximal force across all trials. (b) The simulated LT curve where only sarcomere length varies, and lattice spacing is held at 17.1 nm (corresponding to a d₁₀ lattice spacing of 36 nm), recreates more of the isovolumetric case's slope. Force decreases by over 50% at either extreme. (c) The simulated LT curve where only lattice spacing changes, and sarcomere length is fixed at 2.4 µm, shows a reduced slope. However, force decreases by more than 50% from its peak at larger lattice spacings (corresponding to short sarcomere lengths) and decreases by more than 25% at smaller lattice spacings (corresponding to long sarcomere lengths). (d) For comparison with the above, the maximum force developed by isolated frog striated muscle is presented, modified from Gordon et al. [4]. All sarcomere lengths and lattice spacings are chosen to reflect the range over which vertebrate striated muscle varies in isometric contractions along the length–tension (LT) curve [3]. (Online version in colour.)

Transitions between different phases of the LT curve occur at similar sarcomere lengths in both isolated fibres and our model. In both experimental data and model results, the steepest part of the ascending limb transitions into the start of the plateau region at sarcomere lengths 1.8 ± 0.1 µm and the descending limb begins at 2.3 ± 0.1 µm. In neither instance does the model disagree with the experimental results by more than the uncertainty in estimating the transitions between phases of the LT curve. Agreement between our computational results and the force generated by isolated fibres gives us confidence to use the force generated by our model under isovolumetric conditions as a basis to which we compare constant length and constant lattice spacing forces. These comparisons are shown for the LT curve in figure 2, and the relative dependence of force on both changes in lattice spacing and degree of overlap is shown for all parameters in figure 3.

Figure 3.

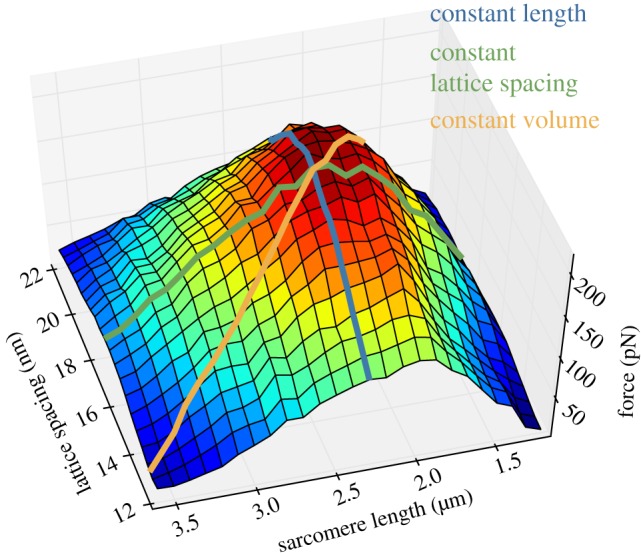
Force at all lattice spacings and sarcomere lengths. Both lattice spacing and sarcomere length tune force, as shown by the dependence of force on lattice spacing at all sarcomere lengths and on sarcomere length at all lattice spacings. An isovolumetric path through the parameters of lattice spacing and sarcomere length results in an LT curve of nearly maximal steepness. Peak force is seen at 17.5 nm lattice spacing and 2.3 µm sarcomere length. (Online version in colour.)

(b). Changing only overlap reproduces a shallower version of the isovolumetric  length–tension curve

When lattice spacing is held constant and only sarcomere length is changed, the classic LT curve is followed, but is less steep than predicted by an isovolumetric relation on the ascending and descending limbs (figure 2a,b; electronic supplementary material, figure S4). To isolate the effects of filament overlap on isometric maximum force, the model allows us to hold lattice spacing at a constant value, 17.1 nm in this case, while changing sarcomere length. In the case shown in figure 2b, changes in sarcomere length caused filament overlap and binding site availability to vary, but the lattice spacing remained fixed.

On the ascending limb, below sarcomere lengths of 1.8 µm, changing only length drops the force produced to 37.3% of the maximum value. This decrease occurs with a slope of 1.04 ± 0.08, significantly different from the slope of the isovolumetric case (figure 2a; electronic supplementary material, figure S4; ANCOVA, p < 0.01).

On the descending limb, as sarcomere length increases beyond 2.3 µm, the overlap of the thin filament and the myosin S1 decorated regions of the thick filament is reduced. As sarcomere length approaches 3.5 µm, the force drops to 35.2% of its peak, replicating 81% of the drop present under isovolumetric conditions. This decrease in force occurs with a slope of −0.55 ± 0.02, again significantly different from that of the isovolumetric case (ANCOVA, p < 0.01).

The force–length relationship seen when only sarcomere length is changed is a shallower version of that observed under simulated and experimental isovolumetric conditions. Without varying lattice spacing, the slope of the LT curve on both the ascending and descending limbs is not replicated.

(c). Changing only lattice spacing alters force similar to the isovolumetric length–tension curve

Changing only lattice spacing, while holding filament overlap constant, is sufficient to recapture much of the force change along the model's isovolumetric LT curve (figure 2a,c). Mirroring the above, we isolate the effects of lattice spacing on isometric maximum force by holding sarcomere length at a constant value, 2.3 µm in this case, while changing lattice spacing to the values present along an isovolumetric LT curve. This isolength curve allowed us to compare the effect of a change solely in lattice spacing with the effect of an equal change in lattice spacing produced by a length change under isovolumetric conditions.

As we move leftward from the peak force of the isolength curve, two trends are apparent: (i) the lattice spacing expands, causing the distance over which myosin heads must diffuse in order to bind and generate force to grow, and (ii) the force generated decreases (figure 2b; electronic supplementary material, figure S4). While the overlap and thus the number of myosin heads with an opposing thin filament remains constant, the force generated at the leftmost extreme drops to 47.1% of its peak value with a slope of 1.00 ± 0.05 where lattice spacing reaches 21.9 nm (see the electronic supplementary material, figure S3b for lattice spacing definitions). The combined shielding of binding sites and increased lattice spacing present under equivalent isovolumetric conditions produce a reduction to 17.6% of peak force with a significantly steeper slope of 1.44 ± 0.07. From this, we can say that changing only lattice spacing results in a shallower LT curve which still replicates more than 60% of the force change seen at shorter sarcomere lengths under isovolumetric conditions. Interestingly, there is no significant difference between the influence of lattice spacing and of overlap on the force produced over the ascending limb (see the electronic supplementary material, figure S4; ANCOVA, p = 0.70).

As we move rightward from the peak force of the isolength curve, two complementary trends are evident: (i) the lattice spacing decreases below its plateau-region value, confining the myosin heads to a smaller volume, and (ii) cross-bridges become less likely to form and generate force [13]. The force at 14.1 nm, the smallest lattice spacing, dips to 72.0% of the maximum force with a slope of −0.24 ± 0.02. With the equivalent isovolumetric drop over a slope of −0.72 ± 0.02 producing just 21.4% of the maximal force, lattice spacing change alone reproduces only 36% of the isovolumetric force drop, and is thus less influential to the right of the region of maximal force than is overlap. On the descending limb, changing only lattice spacing reproduces a significantly shallower force curve.

As when only overlap is changed, changing only lattice spacing fails to replicate the slope of the LT curve on both the ascending and descending limbs. Changing only overlap better predicts the force decrease at extreme lengths, although isolating either property more poorly predicts the experimentally observed LT curve than when both lattice spacing and sarcomere length change isovolumetrically.

(d). Lattice spacing tunes force at all overlaps and vice versa

Our results show that lattice spacing partially regulates the level of force produced at every sarcomere length and, conversely, sarcomere length partially regulates the level of force produced at every lattice spacing. This mutual dependence can be seen in the shape of figure 3, which is peaked rather than a section of a cylinder.

The interdependence of lattice spacing's and sarcomere length's influence on force can be seen, for example, by tracing the paths of the three cases examined in figure 2 across the force surface of figure 3. Constant length and constant lattice spacing traces are steepest when their respective fixed values are near those present at peak tension in the isovolumetric case. The increasingly reduced influence of lattice spacing as sarcomere lengths grow more extreme is demonstrated in the greatly reduced variation of force across all lattice spacings when sarcomere length is at its longest (on the leftmost section of figure 3). The steepest slope is only generated in the isovolumetric case where movement along the force surface is simultaneously descending two slopes: the slope of lattice spacing and the slope of sarcomere length. The isovolumetric case is thus steeper than if it was descending only one slope: the contributions of both changes in lattice spacing and changes in filament length are needed to produce the steepness of the isovolumetric LT curve.

(e). Decreasing lattice spacing reduces force on skinned fibres' descending limb

Insect flight muscle provides an outstanding model for skeletal muscle fibres in general. It offers a preparation that provides excellent X-ray diffraction signals while holding up well to stretching for investigating changes in sarcomere length across the LT curve. Skinned bundles of Manduca sexta flight muscle fibres stretched to a near maximal force producing sarcomere length of 4.0 ± 0.2 µm reproduce the LT relationship of the descending limb solely through osmotic compression of the filament lattice (figure 4b). Force decreases to 20% of its maximum value with a reduction in lattice spacing equivalent to that seen as vertebrate muscle lengthens from 2.3 to 3.4 µm. This is greater than the predicted constant-length force decrease in figure 2c. The variance in initial sarcomere lengths between 3.8 and 4.2 µm is not a significant factor; maximum force is independent of influence from this noise (Hoeffding's d-value −0.015, p = 0.72).

Figure 4.

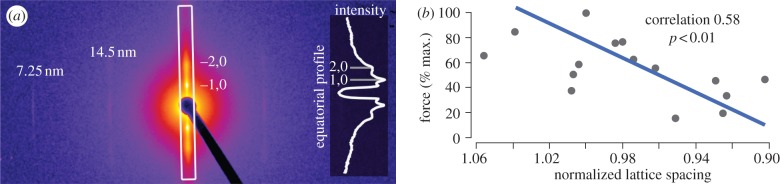
Normalized force of skinned fibres under osmotic compression. The force generated by skinned osmotically compressed fibres was measured using small-angle X-ray fibre diffraction, a sample image of which is shown. (a) Diffraction image of skinned Manduca sexta flight muscle bundle with largely vertical equatorial axis. The dark line and dark central circle are due to a backstop protecting the detector from direct exposure to the X-ray beam. The 1,0 and 2,0 equatorial diffraction peaks, along with the 14.5 nm and 7.25 nm meridional reflections, are labelled. The boxed intensity profile along the equator is inset. Lattice spacings were estimated from the separation of the 1,0 equatorial diffraction peaks as described by Irving [16]. (b) Maximum force produced through Ca²⁺ activation of fibres stretched to the descending limb decreases as lattice spacing is shrunk through osmotic compression. Lattice spacing is displayed as normalized to the lattice spacing on the initial post-skinning activation to control for variability between fibres. Lattice spacing is shown as decreasing from left to right to facilitate comparison with the descending limb of the LT curve as conventionally depicted in figure 2. (Online version in colour.)

3. Discussion

(a). Lattice spacing amplifies the length dependence of force

This study shows that lattice spacing has a substantial influence on the LT curve. While filament overlap has a greater effect on the force produced over the LT curve than does lattice spacing, changing lattice spacing significantly augments the effects of changes in length. Varying lattice spacing increases the steepness of the LT curve by altering myosin kinetics and the force generated by attached cross-bridges [12,13]. The slope of the LT curve would be 28% shallower on the ascending limb and 23% shallower on the descending limb without the effects of lattice spacing, and thus the effect of length changes would be commensurately reduced. Effects such as the Frank–Starling mechanism in cardiac muscle rely on a steep slope on the ascending limb to passively regulate the amount of force produced [17]. Without the effects of lattice spacing as an additional source of regulation, processes such as the Frank–Starling mechanism may not remain in a stable equilibrium.

(b). Lattice spacing dependence of force extends into the descending limb

It is interesting that the effects of lattice spacing extend into the descending limb, where, unlike with the large lattice spacings in the ascending limb, myosin heads are not required to bridge a large distance in order to bind and generate force. This is likely to be due to the geometric restrictions such small lattice spacings place on cross-bridge movement (figure 1b). The limited radial distance over which a myosin diffuses on the descending limb, which will be reduced as the thick and thin filaments approach each other, restricts the section of the opposing thin filament it can access [13]. These effects do not reduce force as quickly as does the change in lattice spacing along the ascending limb, in part because of the square root dependence of lattice spacing on sarcomere length. Lattice spacing changes less with a given length change at longer lengths than at shorter lengths [3,16]. The observed lattice spacing dependence of skinned M. sexta muscle over the descending limb confirms the lattice spacing–force relationship observed in our simulations (figures 2c and 4b).

(c). Simple geometry enhances the dependence of force on sarcomere length

The geometry of the thick–thin filament interaction is a regulator of force. Changes in the radial direction, such as those owing to altered lattice spacing, have significant effects that are similar in magnitude to those in the axial direction. Including these relatively simple geometries in our mathematical and conceptual models of sarcomeric force generation alters force predictions and provides a demonstration of the importance of geometry in force regulation.

The fact that lattice spacing changes over the LT curve has been known for some time, but its importance in generating the steep length dependence of force has not been previously demonstrated. Given the importance of the LT curve in both functional processes and as a diagnostic of the cross-bridge cycle, this study forms a new basis of interpretation for experiments and thinking about the mechanisms regulating contraction. In the end, we cannot properly understand the LT curve unless the three-dimensional geometry of the sarcomere is taken into account.

4. Models and methods

(a). Single myosin model

Our theoretical results are produced using a conceptually new model of the half-sarcomere (see the electronic supplementary material, figure S1a). This half-sarcomere is populated with two-spring models of the cross-bridge as described previously [13]. The two-spring cross-bridge generates force through a change in angle matched to myosin's lever arm mechanism. These cross-bridges are sensitive to changes in lattice spacing because they are modelled in two dimensions, rather than because of any explicit lattice-spacing-dependent terms. As in our prior work, lattice spacing is measured from the face of a thick filament to that of an opposing thin filament (see the electronic supplementary material, figure S3b) [13]. At resting lattice spacing, these cross-bridges' kinetics are derived from, and are compatible with, the kinetics of prior models [18,19]. The force produced by these cross-bridges also depends on the lattice spacing of the system as it affects the angle at which they attach, and thus the deviation of their constituent springs from their rest values.

(b). Multifilament model's geometry

A semi-infinite muscle lattice is created with toroidal boundary conditions as in prior work [19,20]. As shown in figure 1a and electronic supplementary material, figure S1b, when a cross-bridge passes through a boundary it wraps around to the other side of the model. A total of four thick and eight thin filaments suffice to create a semi-infinite lattice where no thick filament is attaching to a neighbouring thin filament from two directions (once directly and once across a boundary) and where the ratio of thick to thin filaments is the same as in skeletal muscle (figure 1a).

Each thick filament is populated by a 43 nm repeating pattern of cross-bridges [19,20]. Each repeating unit has three evenly spaced axial crowns of three cross-bridges each [19,20]. The cross-bridges in a crown are azimuthally distributed such that they are each separated by a 120° rotation about the long axis of the thick filament. Subsequent crowns within the 43 nm repeat are azimuthally offset by 60°, such that every cross-bridge faces a thin filament (figure 1a) [21].

The lattice of thick and thin filaments is a hexagonally packed array. Lattice spacing within the model is isotropic (i.e. the radial distance between thick and thin filaments is the same in all orientations). The lattice spacing is an input parameter to the model and can be controlled independently of sarcomere length. The other radial distances, such as myosin plane separation (d₁₀) and actin plane separation, are determined by lattice geometry.

Availability of binding sites is modulated by thin filament overlap. When adjacent thin filaments overlap they shield each other's binding sites, disallowing the formation of cross-bridges at those locations. This simulates shielding of binding sites, consistent with the classic understanding of reduced force on the ascending limb [4].

(c). Simulation details

A single 1 ms time-step in the model consists of allowing each myosin head to calculate the probability of a change in state, and then check that probability against a random number between zero and one taken from a uniform distribution. The force at a given myosin base can be calculated from the locations of the base, the locations of the adjacent bases and the actin location, if any, to which the myosin is attached (see the electronic supplementary material, figure S1c). After each myosin has switched or retained its state, the positions of each location along the thick and thin filaments are found such that the only locations experiencing a net force are those at the ends of the filaments. The sum of the force at the ends of each of the thick filaments is opposite and equal to the sum of the force at the ends of each of the thin filaments, and is the force output of the model. Repeating this process generates the force traces from which maximum force is determined (see the electronic supplementary material, figure S1d).

For each combination of lattice spacing and sarcomere length, the maximum isometric force was calculated by taking the mean of the force developed in each of 10 runs. The model was allowed to rise to a steady force level over 400 ms, or 400 time-steps at 1 ms resolution. The maximum force level was reached within the first quarter of the run for all parameter combinations, allowing the force of the run to be calculated as the mean of the instantaneous force at each of the last 50 time-steps. As the model lacks passive elements which span its length, the maximum force developed by the model in a given run is comparable with the classically maximum active tension displayed in figure 2d [4].

Model runs were carried out in parallel on a dynamically created cluster of spot-priced machine instances in Amazon's EC2 service (http://aws.amazon.com/ec2). Model runs were controlled with a first-in-first-out command queue hosted by Amazon's SQS (http://aws.amazon.com/sqs).

(d). Skinned moth flight muscle fibre bundles

Skinned-fibre experiments were carried out using the BioCAT beamline 18ID at the Advanced Photon Source, Argonne National Laboratory [22]. Fibres were harvested from subunits B and C of the dorsolongitudinal flight muscles of M. sexta [23]. The large fibres and well-ordered structure of Manduca flight muscle permit a strong diffraction pattern and stand up well to successive osmotic pressure changes. Manduca flight muscle also has a clear role in organismal movement and is easily available.

Individuals were selected fewer than 5 days post-eclosion, decapitated under cold anaesthesia and stored at 4°C for up to 3 days before their fibres were harvested. Fibres were harvested by bisecting the thoraces in the median plane and dissecting out fibre bundles in calcium-free relaxing solution [24]. The fibre bundles were skinned overnight in a 1% Triton relaxing solution before being washed and stored for up to 4 days at 4°C in relaxing solution.

(e). Apparatus

Skinned fibre bundles were mounted between two posts, the ends affixed with cyanoacrylate glue (see the electronic supplementary material, figure S2). The fibre was then lowered into a flow cell where the solution bathing the fibre could be changed by means of a multi-port programmable syringe pump (ML560C, Hamilton Company, Reno, NV). Fibres were mounted in pCa 9.0 relaxing solution and were activated by a two-step protocol. The pCa 9.0 solution was first replaced with an EGTA-free pre-activating solution before that was replaced with a pCa 4.0 activating solution. Activating solutions were made similar to those of Kreutziger et al. [24], with CaCl₂ added to a desired Ca²⁺ concentration, but omitting dithiothreitol, creatine kinase and 2,3-butanedione monoxime. Double washes at each solution swap ensured full exchange.

A dual-mode force lever (model 305B, Aurora Scientific, Ontario, Canada) both held fibre-length constant and monitored force developed by the fibre. This force lever was coupled to one of the posts to which the fibre was mounted, whereas the other post was rigidly held in place.

The flow cell was printed with ABS plastic on a dimension µPrint (Stratasys Inc., Eden Prairie, MN). Windows at the front and back of the flow-cell were covered with flat 2 mil Kapton sheets (McMaster-Carr, Atlanta, GA) to permit the X-ray beam to pass through the solution and fibre without scattering on the ABS. After passing through the fibre and exiting the flow cell, X-rays travelled through a further 2 m evacuated flight tube before being imaged (example shown in figure 4a) and used to measure the d₁₀ lattice spacings as in Irving [16] (see also [25]).

A diode laser mounted above the flow cell was used to measure the average sarcomere length in the region being imaged with X-ray diffraction. A flat Kapton window below the fibre permitted the laser to pass through the cell and a strip of Kapton laid on the solution above the fibre eliminated distortion from solution meniscus. The centre of the laser's primary diffraction line was found by eye, and initial sarcomere length was stretched to 4.0 ± 0.2 µm.

(f). Contraction

Activating, relaxing and pre-activating solutions were prepared with 0%, 2%, 4% and 6% dextran T500 by weight. All activations were carried out at 20°C. Prior to activation, fibre bundles were perfused with a pre-activating solution. Bundles were given 20 min to equilibrate to a new level of osmotic compression with each change in dextran concentration. The force of each activation was taken as the difference between the peak force and the mean of the pre- and post-contraction relaxed force levels.

(g). Analysis

Over the course of activations at 0% dextran, two randomly chosen values from 2%, 4% and 6% dextran, and a final contraction at 0 per cent rundown of the fibre bundles, were observed. This rundown was compensated for by normalization of force to the I_20/10 ratio. The I_20/10 ratio is a measure of the radial distribution of cross-bridge electron density and is frequently used as a measure of the level of cross-bridges associated with the thin filament [16,26]. This thus normalizes the force to the loss of functional cross-bridges that occurs over the course of multiple activations. Lattice spacing was normalized to the initial post-skinning lattice spacing to facilitate comparisons between skeletal and insect flight muscle.

Funding statement

Funding was provided by IOS-1022471 to T.L.D. and T.C.I., funds from the Joan and Richard Komen Endowed Chair to T.L.D., an NIH pre-doctoral training grant (no. T32 EB001650) to C.D.W., an Amazon Grant For Research to C.D.W., and an NHLBI Project grant (no. R01 HL65497) to M.R. who is an Established Investigator of the AHA. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript. Use of the BioCAT facility was supported by grants from the National Center for Research Resources (2P41RR008630-17) and the National Institute of General Medical Sciences (9 P41 GM103622-17) from the National Institutes of Health.