Prediction of fracture healing under axial loading, shear loading and bending is possible using distortional and dilatational strains as determining mechanical stimuli

Abstract

Numerical models of secondary fracture healing are based on mechanoregulatory algorithms that use distortional strain alone or in combination with either dilatational strain or fluid velocity as determining stimuli for tissue differentiation and development. Comparison of these algorithms has previously suggested that healing processes under torsional rotational loading can only be properly simulated by considering fluid velocity and deviatoric strain as the regulatory stimuli. We hypothesize that sufficient calibration on uncertain input parameters will enhance our existing model, which uses distortional and dilatational strains as determining stimuli, to properly simulate fracture healing under various loading conditions including also torsional rotation. Therefore, we minimized the difference between numerically simulated and experimentally measured courses of interfragmentary movements of two axial compressive cases and two shear load cases (torsional and translational) by varying several input parameter values within their predefined bounds. The calibrated model was then qualitatively evaluated on the ability to predict physiological changes of spatial and temporal tissue distributions, based on respective in vivo data. Finally, we corroborated the model on five additional axial compressive and one asymmetrical bending load case. We conclude that our model, using distortional and dilatational strains as determining stimuli, is able to simulate fracture-healing processes not only under axial compression and torsional rotation but also under translational shear and asymmetrical bending loading conditions.

1. Introduction

Numerical simulations are able to predict mechanobiological processes in the regions of secondary fracture healing. Numerous finite-element (FE) models have been developed to analyse local mechanical responses to varying loading conditions assuming either linear elastic or poroelastic material behaviour. Several models [1–5] are based on the tissue differentiation hypotheses proposed by Pauwels [6] which were refined by Carter et al. [7] and Claes & Heigele [8] using distortional strain and dilatational strain (which is directly related to hydrostatic pressure [5]) as the determining stimuli for tissue differentiation and development. By contrast, other models [9–15] use a linear combination of distortional strain and fluid velocity as determining stimulus, as characterized by the hypothesis of Prendergast et al. [16]. Furthermore, Garcia-Aznar et al. [17,18] use only the distortional strain as stimulus. Isaksson et al. compared these approaches and concluded that all algorithms were suitable to predict fracture-healing processes under axial loading [19], whereas the successful simulation of healing processes under torsional load required the combination of deviatoric strain and fluid velocity as regulatory stimulus [12].

All numerical models of fracture healing however depend on many input parameters with considerable degrees of uncertainty. The choice of tissue material properties, one of the most important steps in FE model development [20,21], represents particularly high variability [22]. Parameters defining the underlying tissue differentiation hypothesis (e.g. the correlation between strain magnitude and bone formation rate) are also highly uncertain because they are based on limited experimental data. Therefore, it is difficult to decide whether numerical simulation of fracture healing under torsional loading is only possible by including fluid velocity as regulatory stimulus or whether models using distortional and dilatational strains as regulatory stimuli only need calibration on their uncertain input parameters to predict the same results.

Our aim was to calibrate the fracture-healing algorithm previously developed by Simon et al. [5], which is based on the distortional and dilatational strains as regulatory stimuli, to be applicable to a greater range of different mechanical conditions, especially predicting fracture healing under axial compressive as well as under torsional rotational isolated loading. Furthermore, the model should also be able to predict healing processes under non-axially symmetric loading such as translational shear or bending.

Therefore, in a first step, we developed an optimization procedure to calibrate our model input parameters within acceptable and physiological ranges against several well-characterized in vivo experiments for axial compression [23], torsional rotation [24] and translational shear load cases [25] based on the mechanical responses (i.e. change in interfragmentary movement (IFM) over time). Subsequently, the ability of the calibrated model to predict physiological tissue distributions during the simulated healing process was also qualitatively evaluated. Finally, the ability of the calibrated model to predict healing processes under further loading conditions, such as different axial load cases [23] as well as fracture healing under asymmetrical bending [26], was checked.

We hypothesize that the resulting model regulated by local distortional and dilatational strains [4,5] will be able to predict the course of IFM and tissue distribution over the healing time of various healing situations under axial compression, torsional rotation, translational shear and bending loading conditions.

2. Methods

2.1. In vivo experiments

All in vivo data used for simulation in the present numerical study were taken from previously published experimental studies in sheep [23–25]. Thus, four different healing situations (case A, B, C and D) were defined as calibration targets. Cases A and B represent axial compressive load cases with different magnitudes of interfragmentary strain (IFS; i.e. case A as stable case with 11% IFS and case B as flexible case with 39% IFS) described in detail by Claes et al. [23]. Briefly, this experimental study compared the healing of a transverse osteotomy under different axial stabilities at the ovine metatarsus. An external fixator allowed a lower maximal IFM of 0.25 mm in case A, and a higher maximal IFM of 1.3 mm in case B. The gap size in the loaded situation was 2 mm for both cases. The gap sizes in the unloaded situations were 2.25 and 3.3 mm for cases A and B, respectively. The axial load of the metatarsus was assumed to be 1.1 × bodyweight (BW) according to Duda et al. [27]. With an average BW of 75 kg [23], the axial load for cases A and B was set to 840 N. Case C represents a torsional rotation load case performed by Bishop et al. [24]. Briefly, the sheep underwent a transverse tibial osteotomy that was fixed with an external fixator adjusted to a 2.4 mm fracture gap. Daily stimulation of 120 sinusoidal cycles of interfragmentary torsional rotation was applied with a maximum strain magnitude of 25 per cent corresponding to 7.2° rotation at a frequency of 0.5 Hz up to a load limit of 1670 N m² allowing IFS to decrease with increasing callus stiffness. In contrast to the shear load case occurring under torsional rotation, case D represents a translational shear load case performed by Augat et al. [25], where sheep underwent a transverse tibial osteotomy with a fracture gap adjusted to 3 mm. An axially rigid external fixator allowed a transverse sliding movement of 1.5 mm at the centre of the mid-diaphyseal osteotomy. The average body weight was 78 kg [25], which according to Heller et al. [28], results in maximal shear loads of approximately 200 N.

2.2. Numerical fracture-healing model

We used a previously published fracture-healing model which is described in detail elsewhere [4,5]. Briefly, this algorithm combines FE and fuzzy logic methods to simulate fracture-healing processes over time in an iterative loop. The three-dimensional geometries of idealized diaphyseal osteotomies and their healing regions in the ovine metatarsus (for cases A and B, geometry according to Claes & Heigele [8]) and tibia (for cases C and D, geometry according to Isaksson et al. [12]) were implemented and meshed in ANSYS (ANSYS Inc., Canonsburg, PA) using 10-node tetrahedral elements with linear elastic material properties. The respective fixation behaviour was separately implemented using a nonlinear force–displacement function. Additionally, the mechanical behaviour of the bone–fixator system as well as the load and boundary conditions were defined to represent the initial state for seven input variables. These were, two mechanical stimuli (distortional strain and dilatational strain derived from the strain tensor), three state variables of the element itself (local blood perfusion, cartilage and bone fractions) and two state variables of the adjacent elements (perfusion and bone fraction). Tissue composition (a mixture of three tissue types: woven bone, fibrocartilage and connective tissue), material properties and blood supply were assigned to each of the FEs. For the resulting Young's modulus E_j of each element j, the following rule of mixtures was used:

2.1

where E_conn, E_cart and E_bone are Young's moduli for connective tissue, cartilage and bone, respectively; c_cart and c_bone are the respective tissue fraction for cartilage and bone within one element; exp_cart and exp_bone are the exponents of the respective cartilage and bone fractions. These variables were subjected to the optimization procedure (cf. table 1).

Table 1.

Ranges and literature data for the 12 input parameters included in the step 1-calibration process. Asterisks denote parameters that are not included in the calibration.

parameter	literature review	bounds
		low	up
Young's modulus, Etiss in MPa
cortical bone*, Ecort	10 000a; 15 750b; 17 400c; 20 400d	15 750
woven bone, Ebone	6000e; 201f; 540–8300g; 4000h; 1381–2380i	500	9000
cartilage, Ecart	3.1j; 200k; 5–39l; 20–76m	5	50
connective tissue, Econn	0.99n; 1.9o; 3p;	0.5	3
Poisson's ratio, νtiss
cortical bone*, νcort	0.39c; 0.36d; 0.325q	0.325
woven bone, νbone	0.23r; 0.32s	0.26	0.39
cartilage, νcart	0.174t; 0.4u; 0.35v; 0.47w; 0.46x	0.26	0.49
connective tissue, νconn	0.4p; 0.167y	0.26	0.49
fuzzy thresholds, Δ.decthr in % between ‘decrease’ and ‘stay unchanged’ for change in
blood perfusion, Δ.decperf		−47.5	−2.5
bone concentration, Δ.decbone		−47.5	−2.5
cartilage concentration, Δ.deccart		−47.5	−2.5
fuzzy thresholds, Δ.incthr in % between ‘stay unchanged’ and ‘increase’ for change in
blood perfusion*, Δ.incperf		=−Δ.decperf
bone concentration*, Δ.incbone		=−Δ.decperf
cartilage concentration, Δ.inccart		2.5	47.5
exponent values in the rule of mixture, exptiss
woven bone, expbone		1	5
cartilage, expcart		1	5

^aHuman femoral metaphysis [29].

^bPoroelastic properties of human cortical bone [30].

^cHuman cortical bone [31].

^dBovine cortical bone [31].

^eAssumption for ovine stiff callus tissue [8].

^fIndentation modulus for rat callus woven bone [32].

^gPoroelastic properties of the human calcaneus [33].

^hApparent elastic modulus of ovine callus woven bone [34].

ⁱPreliminary results for ovine bony callus tissue [35].

^jIndentation modulus for rat callus chondroid tissue [32].

^kApparent elastic modulus of ovine callus fibrocartilage [34].

^lPreliminary results for ovine callus fibrocartilage [35].

^mHuman fibrocartilaginous callus tissue [36].

ⁿIndentation modulus for rat callus granulation tissue [32].

^oCanine fibrous tissue at bone–cement interfaces [37].

^pInitial connective tissue within ovine fracture callus [8].

^qPoroelastic properties [38].

^rHuman calcaneus [33].

^sBovine cancellous bone [39].

^tArticular cartilage after equilibrium [40], applied as linear elastic material properties in a computational model by Witt et al. [41].

^uCanine articular cartilage [42].

^vCartilaginous tissue in rabbit spinal fusion [43].

^wAssumptions for cartilaginous non-ossified callus tissue [44].

^xBovine articular cartilage [45].

^yApplied in a computational model using poroelastic material properties [14].

Subsequently, the local mechanical stimuli (dilatational and distortional strain components) are calculated in an iterative loop, which together with the current tissue composition and blood supply are used as input to a fuzzy logic controller (fuzzy logic toolbox in Matlab (v. 7.11, R2010b), The MathWorks Inc., Natick, MA). A set of 20 linguistic fuzzy logic rules [3,5] controls how the tissue composition and vascularization for each FE within the healing region changes depending on local mechanical and biological stimuli. The rules are partly based on the mechanoregulatory model proposed by Claes & Heigele [8] and represent intramembraneous ossification, chondrogenesis, endochondral ossification, revascularization and tissue destruction. In the present model, rules concerning the chondrogenesis process were modified for an improved representation of the tissue differentiation hypothesis of Claes & Heigele [8]. Modifications included the enlargement of the range from ±30 per cent in Simon et al. [5] to ±50 per cent and automatically adjustable thresholds between different membership functions of the three different fuzzy logic output variables (according to figure 1 and see below). With this iterative healing model, experimental healing situations under different isolated loading conditions, such as axial compression [23], torsional rotation [24], translational shear [25] and asymmetrical bending [26], were simulated. The respective in vivo mechanical and geometrical conditions (i.e. fracture gap size, initial IFM, fixator stiffness and loading magnitudes) were adopted from the respective experimental publications. The outcomes of the model were quantitatively (course of IFM over healing time) and qualitatively (course of tissue distribution over healing time) compared with the respective experimental data.

Figure 1.

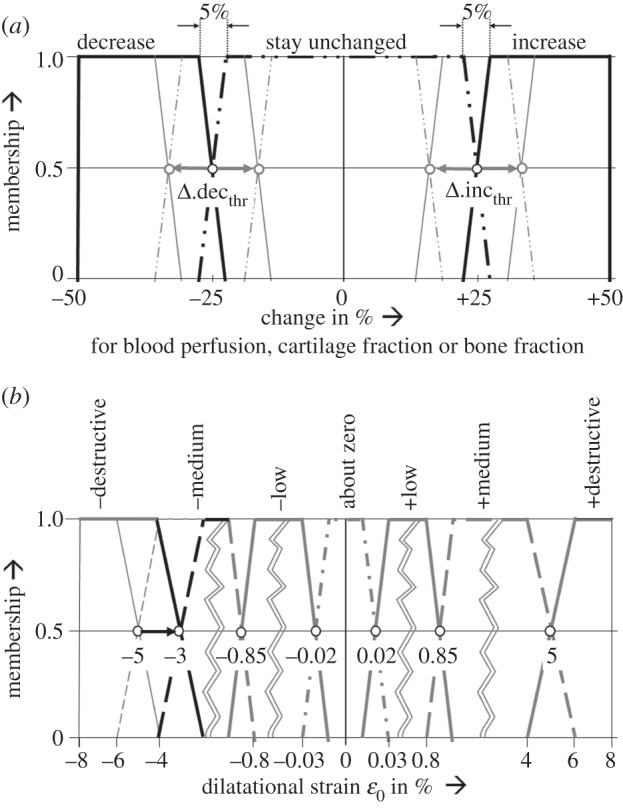
Membership functions as defined by Simon et al. [5]. (a) For the fuzzy logic output parameters change in blood perfusion, change in elements' cartilage and bone fractions. Values for the thresholds Δ.dec_thr, Δ.inc_thr between the single membership plateaus were subject to the optimization procedure. (b) For the dilatational strain in the underlying tissue differentiation hypothesis of Claes & Heigele [8], where the threshold of negative destructive dilatational strain was changed from −5% to −3% during the step 2-adjustment.

2.3. First step: model calibration on interfragmentary movements

A total of 12 model-specific general input parameters were considered for calibration purposes. Beneath them were six material parameters: Young's modulus (E_tiss) and Poisson's ratio (ν_tiss), each for woven bone (E_bone, ν_bone), cartilage (E_cart, ν_cart) and connective tissues (E_conn, ν_conn). Additionally, within the three fuzzy logic output variables, four membership function thresholds (between ‘decrease’ and ‘stay unchanged’, Δ.dec_thr, as well as between ‘stay unchanged’ and ‘increase’ Δ.inc_thr, for the change in blood perfusion (Δ.dec_perf, Δ.inc_perf) and the changes in elements' cartilage (Δ.dec_cart, Δ.inc_cart) and bone fraction (Δ.dec_bone, Δ.inc_bone); cf. Figure 1) were included and, excepting the change in cartilage fraction, positive and negative thresholds were varied symmetrically. Finally, two exponents of the rule of mixtures exp_tiss were subject to the calibration process (exp_bone, exp_cart; cf. equation (2.1)). The literature was reviewed to determine material parameter values that best represented the mechanical behaviour of the involved tissues. Because the reviewed data show large variability, the lower (lo) and upper (up) bounds of the parameter ranges were defined to largely cover these observed parameter uncertainties (table 1).

For calibration on mechanical data, an optimization procedure was performed to minimize the difference between simulated IFM and experimental IFM of the four load cases A, B, C and D by variation of the general input parameter values within their respective bounds (table 1). This led to a minimum value of the objective function (2.2), defined as the average relative quadratic deviations between measured mean IFM (u.EXP_i) and simulated IFM (u.FE_i) at the in vivo measurement time points i, scaled by the respective standard deviation. Each load case is normalized to the number of its respective time-points. Therefore, the objective was to minimize

2.2

with

2.3

subject to

2.4

and

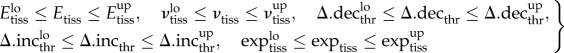2.5

where subscript ‘tiss’ stands for the different tissues connective tissue, cartilage and bone; and subscript ‘thr’ stands for the fuzzy thresholds of blood perfusion, bone and cartilage fractions. Cortical bone is much stiffer than the other materials, with well-established material properties, which were therefore excluded from the optimization process, according to Isaksson et al. [22]. All IFM and standard deviations were normalized to their initial in vivo values to allow comparability between the different cases.

The software package optiSLang (Dynardo GmbH, Weimar, Germany) was used to minimize the objective G by applying the particle swarm optimization (PSO) method [46–48]. Briefly, this nature-inspired stochastic optimization method creates a ‘population’ of individual designs (single sets of stochastically determined parameter values), equally spread out all over the parameter space. Each iteration creates a new ‘generation’ of the population by modifying the parameter values of the individual designs influenced by the ‘global best design’ (i.e. parameter set leading to the smallest objective value in the history of the whole population) and the ‘best design’ of its own history. A population of 32 individual designs was used for each generation. To define the start population, Latin hypercube sampling (LHS; [49]) was used to evenly distribute 150 designs over the design space, assuming uniform distribution for each parameter. Thirty-two designs with the smallest objective values were chosen as the start population for the following PSO process. The stop criteria were defined as reaching a maximum of 35 generations or no update of the global optimum for six generations, whichever came first [50].

2.4. Second step: model evaluation on tissue distribution

In the optimization process, the model was exclusively calibrated against mechanical data from the respective experiments using IFM as the quantitative indicator. To ensure a physiological prediction of the spatial tissue distribution over the healing time, the simulated courses of tissue developments were qualitatively evaluated based on histological data from the underlying experiments.

Unfortunately, the evaluation was rather limited, because histological data were available only for the eighth healing week for all investigated load cases and additionally for the fourth healing week for the torsional loading case. Therefore, we compared our simulated tissue distributions with generally accepted typical patterns for predominant axial loading [51] and predominant shear loading [52] for further corroboration. Vetter et al. [51] defined six different healing stages based on histological data after two, three, six and nine weeks. We compared our predictions of the axial load cases A and B to these stages, not regarding stage VI, because remodelling is not covered by our model. Fracture healing under translational shear with very large IFM was histologically investigated by Peters et al. [52] at two, three, six and nine weeks of healing. These findings were compared with the results of the simulated translational shear load case D.

For adjustment of the simulated courses of tissue distributions to the in vivo findings, a subsequent manual modification was performed on those simulation parameters that could not be included in the calibration process owing to their small impact on the IFM. In this analysis, we identified the threshold of negative destructive dilatational strain in the underlying tissue differentiation hypothesis [8] and changed it from −5 per cent to −3 per cent (figure 1b).

2.5. Third step: model corroboration on various loading conditions

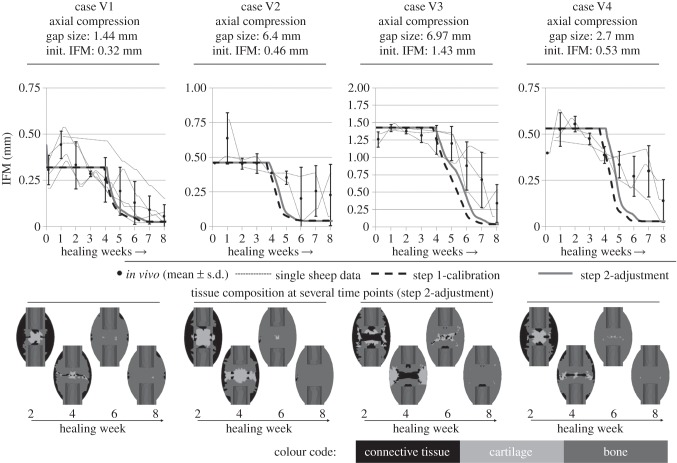
In addition to the four load cases included in the calibration process, five other well-documented in vivo groups with axial compressive load cases (V1–V5) taken from experiments of the group of Claes et al. [23,53] were simulated. To check the models' validity regarding the simulation of mechanical outcomes, simulated IFMs were compared with respective in vivo results. These experiments were performed according to load cases A and B, with variations of the gap sizes and initial IFMs, listed in figures 4 and 5.

Figure 4.

Predicted IFM courses using the parameter values of the step 1-calibration process (dashed black line) and from the step 2-adjustment (solid grey line), compared with the in vivo data for corroboration load cases V1 to V4 (mean ± s.d.) and single sheep data (small dashed lines). For the four load cases, the tissue compositions at several healing time points are shown.

Figure 5.

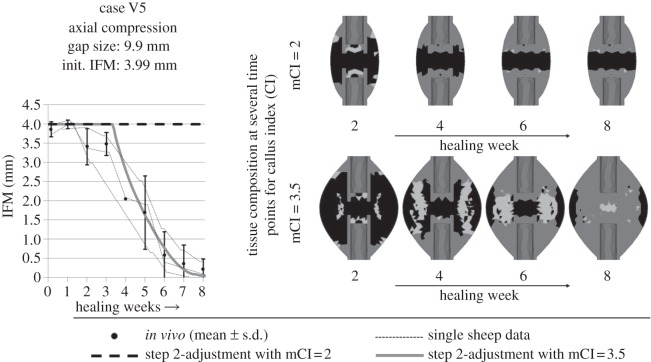
For an axial compressive load case with a large gap of 9.9 mm and additional large initial deformations of 3.99 mm IFM within the gap, the step 2-adjusted simulation showed a disagreement between the predicted (dashed black line) and in vivo (mean ± s.d. and single sheep data shown as small dashed lines) course of IFM over the healing time (left). The respective tissue composition is shown on the top right row. The respective maximal callus index (i.e. the relation between the outer diameter of the callus and the outer diameter of the cortex, mCI) was commonly set to 2. It was shown that this healing process would need more space for development of an adequate fracture callus. Therefore, applying a mCI 3.5 showed good accordance between simulated (grey solid line) and in vivo data for the IFM. The respective tissue composition is shown on the bottom right.

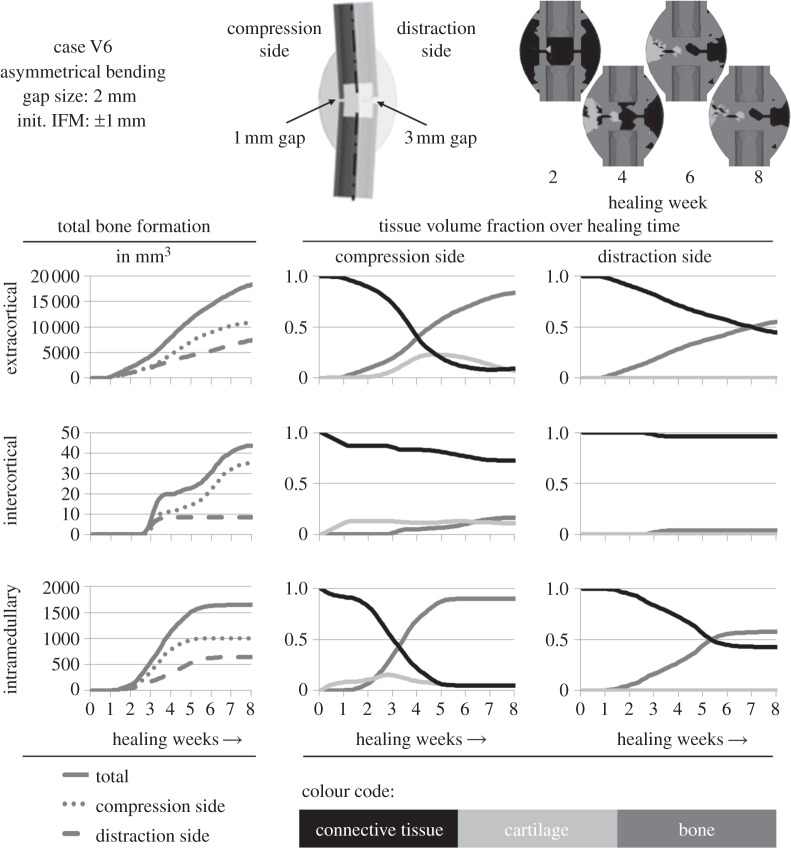
To examine the models' ability to be transferred to completely different loading situations, fracture healing under bending was also simulated. Thus, case V6 represents an asymmetrical bending load case performed by Hente et al. [26], who achieved active cyclic bending displacement using a unilateral external fixator over a 2 mm ovine tibial osteotomy. The resulting IFM was pure compression to a reduced gap size of 1 mm at one side and distraction to a widened gap of 3 mm at the other side of the fracture gap. An actuator generated a maximal bending moment of 22.5 Nm.

3. Results

3.1. First step: model calibration on interfragmentary movements

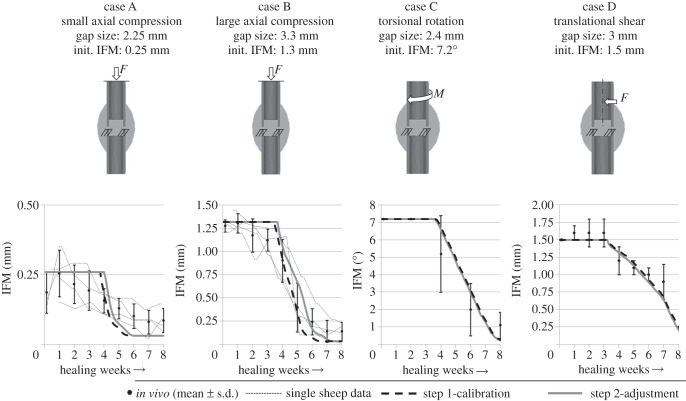
The 32 best designs from the LHS representing the initial population showed objective values of 2.59 to 6.16. The following optimization process converged after no update of the global optimum for six generations reaching a total of 29 generations (928 designs) and improved the objective value to 0.39 for the optimal design (no. 706) with the following calibrated material parameters: for woven bone, cartilage and connective tissue Young's moduli were 538, 28 and 1.4 MPa, respectively, and the Poisson's ratios were 0.33, 0.3 and 0.33, respectively. For blood perfusion, bone fraction and cartilage fraction, the fuzzy thresholds between ‘decrease’ and ‘stay unchanged’ were −22 per cent, −47.5 per cent and −28 per cent, respectively, and the threshold between ‘stay unchanged’ and ‘increase’ for cartilage fraction was 23 per cent. The exponents for the rule of mixtures were found to be 4.5 and 3.1 for bone and cartilage fractions, respectively. Figure 2 shows the simulated course of IFM of the calibrated design for the four in vivo load cases that were subject to the optimization process (dashed lines). For all four calibration load cases, the simulated course of IFM is in reasonable accordance with the respective in vivo data.

Figure 2.

Predicted IFM courses using the parameter values of the step 1-calibration process (dashed black line) and from the step 2-adjustment (solid grey line), compared with the in vivo data for the four calibration load cases (mean ± s.d.). Where available, data from the single sheep are also shown (small dashed lines).

3.2. Second step: model evaluation on tissue distribution

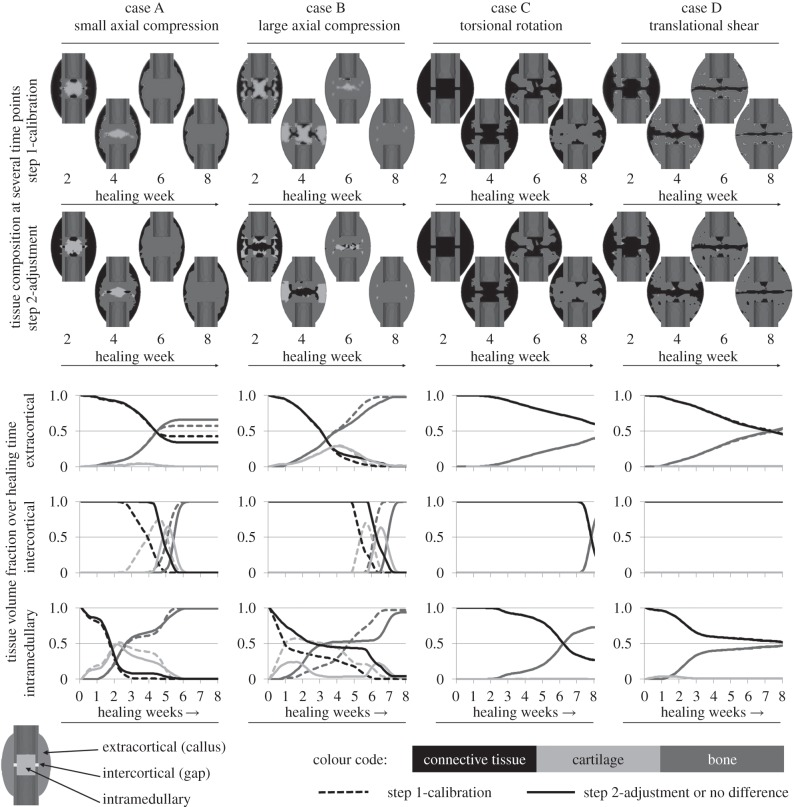
For both axial load cases, evaluation of the simulated change of tissue distribution over the healing time (figure 3, first two columns) revealed that according to the in vivo results of Vetter et al. [51] physiological patterns can be predicted as follows. Initial intramembranous bone formation was predicted periosteally but not in the gap. Subsequently, the bone propagates into the peripheral callus region where distinct cartilage is formed starting around week 2 (figure 3, first row of diagrams—dashed lines). Around week 3, this cartilage bridges between the two opposite sides of the callus and gives rise to endochondral ossification and thus, bony bridging in the extracortical region starting at week 4 for case A and around week 5 for case B. Later on, bone is also formed within the gap (figure 3, second row of diagrams, dashed lines) around week 5 for case A and around week 6 for case B. Endosteal bone formation starts slightly around week 2 for both cases and the callus is completely filled with bone at week 5 for case A and at week 7 for case B (figure 3, last row of diagrams, dashed lines). It is generally accepted that callus size increases with increasing IFM (i.e. decreasing fixation stiffness) [17,54–56]. Accordingly, a larger callus was formed in the flexible load case B, which is visible in the remaining connective tissue within the extracortical region of case A. In contrast to the in vivo findings, our model predicts large amounts of intramedullary cartilage for both cases at early healing time points. After adjusting the threshold of negative destructive dilatational strain (figure 1b), less intramedullary cartilage was predicted, especially for the large compression case B, whereas the small compression case A still showed amounts of intramedullary cartilage (figure 3, second row of callus sketches).

Figure 3.

Tissue distribution for the four calibration load cases. The first and second row of callus sketches show the tissue composition within the fracture calluses at several time points during the process of healing for the step 1-calibration and the step 2-adjustment, respectively. The diagrams show the change of volume fraction of each tissue over the healing time for three different callus regions: extracortical (top row), intercortical (centre row) and intramedullary (bottom row) according to the outline on the bottom left. Black colour represents connective tissue which is present in the callus in the beginning of the healing phase and turns into fibrous tissues in later phases. Light grey colour represents cartilaginous tissue developed prior to endochondral ossification and dark grey colour represents bony tissue (i.e. cortical bone, woven bone and calcified cartilage). Dashed lines indicate results for the step 1-calibration, solid lines for the step 2-adjustment or if no differences between both can be detected.

According to histological data for the torsional load case C, at four weeks, our results show woven bone formation extracortically and connective tissue within the gap zone (figure 3, third column). At week 8, bony bridging occurred extra- and intercortically likewise to the in vivo results, whereas bone formation was also predicted for the intramedullary callus. No cartilage developed at all, whereas in vivo data showed little cartilaginous tissue. As described in the respective radiographical analysis of Bishop et al. [24], our simulation of the torsional load case C predicts extracortical bone formation close to the cortical corners next to the gap starting around week 3. The effects of changing the threshold of negative destructive dilatational strain were negligible.

In consistent with the experimental findings for the translational shear load case D, we found less bone than in a comparable axial load case (according to case B) at week 8 (figure 3, fourth column). Fibrous tissue was dominant along the line where the callus joins from opposite sides of the osteotomy. The experimental findings of Peters et al. [52] for translational shear load cases with large IFM showed good accordance with simulated tissue distributions as follows. At week 2, we simulated bone formation on the periosteal cortical surface at some distance of the gap. This increases at week 3, whereas the gap is still filled with connective tissue and little bone formation occurs intramedullary. At week 6, the periosteal and intramedullary callus size is increased, fibrous tissue is predominant in the gap. At week 8 and later, bony bridging occurred basically extracortically and moved towards the gap, some intramedullary bridging started. Adjusting the threshold of negative destructive dilatational strain had negligible influences on the predicted healing patterns.

Furthermore, the step 2-adjustment of the model regarding a more physiological prediction of tissue distribution for the axial load cases had no or negligible influences on both, the predicted tissue distributions for torsional rotation as well as translational shear load cases (figure 3, second row, last two columns), and the simulated courses of IFM over the healing time for all load cases (figure 2).

3.3. Third step: model corroboration on various loading conditions

Corroboration of the calibrated fracture-healing simulation model was performed on five additional axial compressive load cases with regard to the mechanical responses using IFM as indicator as well as comparison of the change in spatial tissue composition over healing time (figures 4 and 5).

For load cases V1 to V3, our simulated change of IFM over the healing time is in good accordance with the in vivo data; however, a trend towards too fast healing predictions is visible. The step 2 adjustment was able to slightly correct this trend. The gradient of IFM decrease for load cases V2 and V4 is larger than mean in vivo courses. This leads to early healing time points which however are observed for single sheep in the case V2, whereas not for case V4.

Respective tissue compositions show typical patterns of secondary bone healing under axial compressive loading (figure 4) according to Vetter et al. [51]. However, in the cases with small IFM (V1, V2, V4), large amounts of intramedullary cartilage are formed, whereas for large IFM (case V3 and V5), this cartilage formation is not visible, according to respective in vivo results [34]. For the large gap size of 9.9 mm in combination with a large initial IFM of 3.99 mm in case V5, the calibrated design leads to a delayed healing or non-union (figure 5). Assuming that the given healing zone with a maximal callus index (mCI; i.e. the relation between the outer diameters of the healing zone and the cortical bone tube, which represents the possible maximal size of a callus) of 2 is too small for healing under these conditions (figure 5, upper right), a larger healing zone with mCI of 3.5 was applied. The resulting course of IFM showed good accordance with the in vivo data. Furthermore, the corresponding tissue composition develops as expected, with extracortical endochondral ossification and bony bridging around eight weeks. The effective callus index (i.e. relation between the outer diameters of the actual developed bone and the cortical bone tube) was approximately 2.7 (figure 5, bottom right).

For additional corroboration on other mechanical loading conditions, the adjusted design was used to simulate an asymmetrical bending load case performed by Hente et al. [26]. They documented only the amount of bone formation after six weeks of healing under active bending and detected significantly higher amounts of bone and callus formation on the compression side, as noted by Pauwels [6] before (figure 6, left column of diagrams). The simulation predicts development of cartilage followed by endochondral ossification on the compression side, whereas ossification on the distraction side was less and had intramembranous character exclusively starting from the periosteal periphery of the healing region (figure 6, centre and right column of diagrams and top right callus sketches). Bridging was predicted in the endosteal region of the compression side after six weeks of healing (figure 6, top right callus sketches), as described for the in vivo evaluation of Hente et al.

Figure 6.

An asymmetrical bending load case according to Hente et al. [26] was performed for validation reasons (outlined on the top centre), using the step 2-adjustment design. The simulated outcome regarding the tissue development in areas of different mechanical conditions were calculated. The in vivo data suggest a significantly higher amount of bone formation on the compression side [26], which basically can be recognized in the simulated data in the left column of diagrams. The percentage of different tissues in the respective areas can be seen in the centre column for the compression side and in the right column for the distraction side. The upper callus images show the tissue composition at several healing time points.

4. Discussion

The work presented included three steps to gain a higher level of validity for numerical predictions of bone healing processes under highly diverse loading conditions. Confirming our hypothesis, our numerical fracture-healing model regulated by local distortional and dilatational strains [4,5] was able to predict the course of IFM and tissue distribution of different healing situations under axial compression, torsion, shear loading and bending after calibrating the input parameters within reasonable ranges.

During the first step, the model was calibrated based on automated parameter optimization processes on the IFM, because callus stiffness is the most clinically relevant factor for monitoring the healing process and directly depends on the course of IFM over the healing time. Within previous published ranges for the input parameter values, the optimization process detected model-specific optima for the simulation of four different load cases. Numerical models can thereby be adjusted by finding appropriate values for those input parameters typically related to high uncertainties. Primarily, the calibration procedure delivers more accurate values especially for function-defining parameters (i.e. rule of mixtures and fuzzy membership functions) which were generally based on previous assumptions. The benefit of the first step calibration method presented is the ability to quantitatively decide on the basis of the respective outcome whether or not other mechanisms of the model need to be considered to improve the predictions. For optimization purposes, a nature-inspired particle swarm algorithm was used due to the high complexity and nonlinearity of the problem [57]. This procedure is characterized by a direct calculation method, which in contrast to approximation or deterministic methods such as response surface algorithms [58,59] requires numerous design calculations and thus, is more expensive. On the other hand, the optimization results are definite solutions of the respective problem and are not based on mathematical approximations.

The applied calibration method was not aimed at the determination of reliable material properties for the involved tissues. However, we used the large variability for each of the material parameters shown by literature data to define bounds representing physiological ranges for each tissue property. All resulting parameter values are located sufficiently between their upper and lower bounds, except Young's modulus of bone, which is (still physiologically) close to its lower bound, as well as the fuzzy threshold between ‘decrease’ and ‘stay unchanged’ for bone fraction, which is the lower bound. Owing to the use of uniform distributed parameter values within their bounds, also the bounds themselves represent reasonable values, provided they were defined physiologically. The resulting mechanical properties for cartilage represent the behaviour of fibrocartilage, which is usually found in fracture-healing areas. These results are not comparable with mechanical properties of hyaline articular cartilage (i.e. Young's modulus much smaller, Poisson's ratio much higher).

The calibration method presented requires data of well-characterized and defined in vivo load cases to converge to reasonable parameter values. Furthermore, only isolated load cases with clinically relevant IFM were considered. For axial compression, several experimental datasets were available, particularly from Claes et al. [23]. For torsional rotation, the experiments were rare and only one load case from Bishop et al. [24] was sufficiently accurate to be retrievable for calibration. Similarly, only one well-documented in vivo condition of translational shear was available from Augat et al. [25]. However, we strived for predictions of fracture healing under load cases that were as diverse as possible. Therefore, we chose compressive as well as shear load cases (including two different shear conditions) for the calibration and corroborated the resulting model on further compressive load cases and bending, although the experimental data of the latter were limited to radiographical evaluations only.

The calibration procedure had to exclusively focus on the IFM, because other possible objectives, such as histological or radiographical data for tissue distribution, could not be implemented in the automatic optimization procedure owing to the lack of respective quantifiable experimental data. This shortcoming was attended in the second step, where the model was evaluated concerning a physiological prediction of spatial and temporal tissue distribution during the healing process. These evaluations were performed on the histology data of the underlying in vivo experiments and additional findings of Vetter et al. [51] and Peters et al. [52].

Based on these investigations, we detected non-physiological amounts of intramedullary cartilage formation in the large axial compression load case in our simulations. By increasing the threshold of negative destructive dilatational strain from −5 per cent to −3 per cent (figure 1b) within the underlying tissue differentiation hypothesis of Claes & Heigele [8], we were able to limit cartilage development to areas of smaller strains (i.e. −3% up to −0.85%). This did not influence bone formation, which was not critical in our findings. Adjustment of this single parameter led to enhanced predictions of tissue differentiation within the axial compressive load case B, as expressed by less intramedullary cartilage development in weeks 2 and 3 (figure 3, second column), as well as less advanced bony bridging at week 6. Also for load case A, slightly less cartilage is formed during the first five weeks (figure 3, first column) but still intramedullary cartilage appears. This effect is not reported by Vetter et al. [51], however, the eight-week histology data of the underlying in vivo experiment [34] show distinct fractions of endosteal calcified cartilage for case A, but not case B. Hence, intramedullary cartilage seems to be physiological for load cases with small initial IFM, but not for load cases with large initial IFM. Owing to the approximate absence of cartilage, both shear load cases C and D were not altered by this modification (figure 3, third and fourth column). Furthermore, this adjustment had negligible influence on the simulated mechanics (i.e. courses of IFM over the healing time) for all load cases (figure 2). Because the value of the adjusted threshold was previously based on assumptions, our method was able to refine it resulting in more physiological tissue distribution.

Under torsional loading, we predict intramedullary bone formation, which was not observed in vivo. However, this bone formation is plausible under pure rotational loading because the low local distortional strains, i.e. regions where bone formation is possible, were located at the axis of rotation and at the periosteal surface at some distance to the fracture gap [12]. Therefore, all differentiation hypotheses used in numerical models for fracture-healing simulations predict early intramedullary bone formation (cf. figure 6 in Isaksson et al. [12]). Our calibrated model was not able to impede this effect, however it appeared later in the healing phase (figure 3), starting around week 4.

As demonstrated during the third step, the model was corroborated on also being able to physiologically predict mechanics and tissue distributions of various other loading conditions (V1–V6), especially further axial compressive load cases. The calibrated model represented the respective healing processes with reasonable accuracy. Only case V4 showed large deviations to the in vivo results, which might be caused by ill-conditioned experiments, because from our experience the respective in vivo conditions (i.e. gap size of 2.7 mm and IFS of 19%) should result in faster healing than experimentally measured. Accordingly, other load cases with worse conditions (e.g. case B with gap size of 3.3 mm and IFS of 40%) show faster healing experimentally.

In contrast to models by Garcia-Aznar et al. [17], our model does not simulate callus growth itself. Instead, within a predefined healing region (filled up with connective tissue), bone is formed up to a certain level depending on the mechanical conditions. The resulting bony volume represents the expected effective bony callus size, which cannot exceed the predefined healing region, quantified by the mCI. It is generally accepted that callus size increases with increasing IFM (i.e. decreasing fixation stiffness) [17,54–56], therefore we assumed that for case V5 the effective callus size will exceed the predefined size of the healing region because it represents a loading condition with a large gap and large IFS (IFM of 3.99 mm with gap size 9.9 mm). This might represent a critical size defect with delayed healing [23]. Hence, we defined a larger healing area for this case which led to reasonable results (figure 6). For all the other load cases, additional computations however showed that there were no differences compared with simulations with larger healing regions, concluding that the mCI cannot be too large but only too small.

We were also able to simulate secondary fracture healing under isolated asymmetrical bending according to the respective in vivo data from Hente et al. [26]. This is of specific interest, because we showed that our model is able to clearly distinguish between negative and positive pressures on the opposite sides of the bended fracture callus owing to the use of dilatational strain as stimulus in the tissue differentiation hypothesis of Claes & Heigele [8].

In summary, we applied an optimization process to calibrate input parameters of our existing numerical fracture-healing model to gain a higher level of validity. Thus, we showed that the resulting enhanced model is able to predict fracture-healing processes under various loading conditions. Other models were able to simulate healing under physiological complex loading [4,10], but were not validated against isolated loading scenarios. To the best of our knowledge, this is the first time that ovine fracture healing under axially symmetric as well as asymmetrical isolated loading conditions has been simulated by one numerical model. On the basis of our results, models can be enhanced to also predict healing under complex loading conditions.

5. Conclusion

We were able to confirm our hypothesis that the previously developed model regulated by distortional and dilatational strains is able to predict ovine fracture healing processes under diverse loading conditions (i.e. axial compression, torsional rotation, translational shear and asymmetrical bending), after calibration of the input parameters within reasonable ranges.