Statistical Methods for Analyzing Drosophila Germline Mutation Rates

Abstract

Most studies of mutation rates implicitly assume that they remain constant throughout development of the germline. However, researchers recently used a novel statistical framework to reveal that mutation rates differ dramatically during sperm development in Drosophila melanogaster. Here a general framework is described for the inference of germline mutation patterns, generated from either mutation screening experiments or DNA sequence polymorphism data, that enables analysis of more than two mutations per family. The inference is made more rigorous and flexible by providing a better approximation of the probabilities of patterns of mutations and an improved coalescent algorithm within a single host with realistic assumptions. The properties of the inference framework, both the estimation and the hypothesis testing, were investigated by simulation. The refined inference framework is shown to provide (1) nearly unbiased maximum-likelihood estimates of mutation rates and (2) robust hypothesis testing using the standard asymptotic distribution of the likelihood-ratio tests. It is readily applicable to data sets in which multiple mutations in the same family are common.

SPERM and eggs experience many divisions after the fertilized egg, and mutations may occur each time a cell divides. Little is known about the patterns of mutations during development of the germline cell lineage. This is partly due to the scarcity of appropriate experimental data and to lack of proper statistical methods for analyzing such data. Recently, Gao et al. (2011) reported that mutation rates differ dramatically during germline development in Drosophila, with the rate for the first cell division the highest. But the method developed by Gao et al. (2011) is limited to handling only families with at most two mutations each. Also, their conclusions relied heavily on hypothesis testing and the statistical properties of the likelihood-ratio test they used are not known under such circumstances. Furthermore, their coalescent algorithm is too simplistic, not taking into consideration the details of spermatogenesis. Since the ability to make inferences about mutation rates at the level of single-cell division would be a significant step forward, it is desirable to make the inference rigorous and applicable for analysis of data in which more than two mutations per family are common.

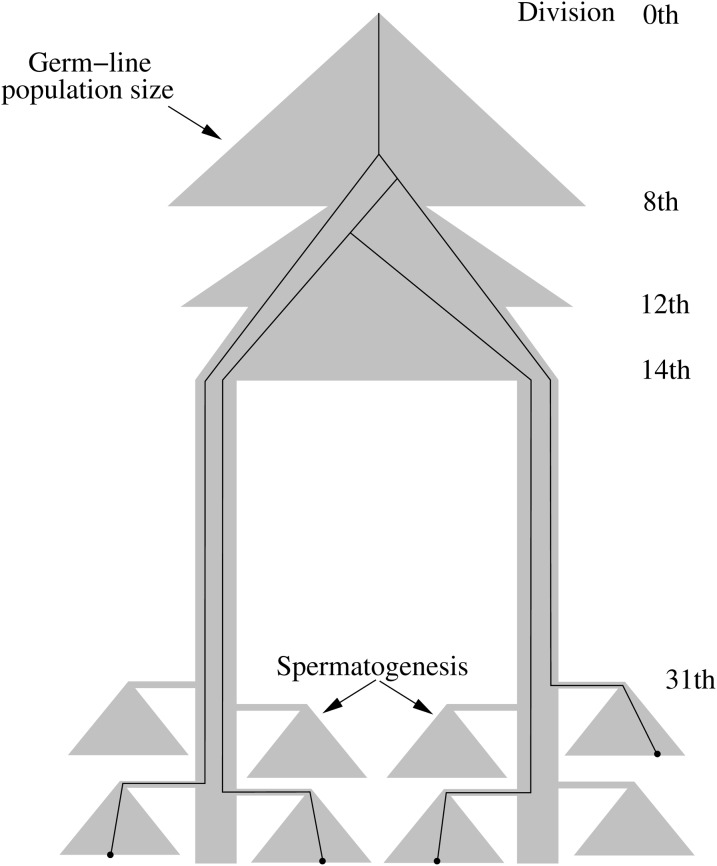
Knowledge of development of the germline lineage is essential for inferring mutation rates. For Drosophila melanogaster males, each sperm from a young adult has experienced ≥36 divisions. The first 14 divisions occur in the cleavage stage characterized by fast cell divisions; the last 5 occur during spermatogenesis; those in between occur during gastrulation and organogenesis when the germline stem cells (GSC) divide asymmetrically. For Drosophila, it is well known (Drost and Lee 1995, 1998; Gilbert 2003) that (1) after the 8th cell division, ∼4–6 cells become the primordial germ cells (PGC); (2) after the 12th division, the number of PGCs ranges from 23 to 52; (3) after the 14th division there are 5–6 PGCs in each gonad; and (4) from the 15th division to just before spermatogenesis the number of PGCs remains more or less constant. After the 31st division one of the two daughter cells of each stem cell remains as a stem cell; the other one differentiates into 64 sperm. Thus, if sperm are sampled after the 36th division, all have experienced exactly 36 divisions, but if they are sampled after, for example, the 38th division, some would have experienced 36 divisions, some 37, and some 38 divisions. The algorithm developed by Gao et al. (2011), using the principle of coalescence (Kingman 1982; Ewens 2004), does not account for these differences.

To develop a thorough understanding of mutational patterns during germline development requires obtaining an estimate of mutation rate for each cell division and testing various hypotheses about mutation rates. This article describes further development of the inference framework, which overcomes previous shortcomings, investigates its statistical properties, improves the coalescent algorithm, and reanalyzes the published data. The improved inference framework has the advantage of being adaptable to analyzing mutation patterns in nucleotide polymorphism data, such as generated by next-generation DNA sequencing.

The Theory

Definitions and notations

Consider a sample of families, each consisting of a number of offspring (or sperm) from the same father. For each family with n sampled offspring, a mutation pattern is observed and represented by 〈i₁, i₂, … , i_k〉 such that each element represents an identified mutation, its value equal to the number of mutants for the mutation, where k is the number of mutations. For example, 〈1〉 represents a mutation in a family that leads to only one mutant; 〈3, 2〉 represents two mutations, where one leads to three mutants and another to two mutants. Also we use 〈〉 to represent the case in which no mutation is observed.

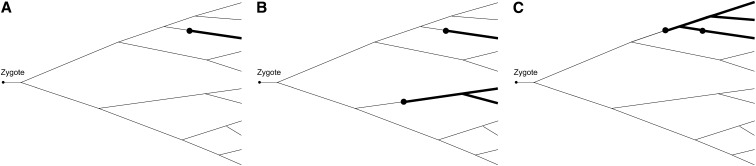
Sequencing the same region of the genome among all sampled offspring in the same family will yield a mutation pattern. Alternatively, such information can be obtained from traditional experiments, particularly for some model organisms. For Drosophila, multigeneration mutation screening has been well developed (Muller 1928; Woodruff et al. 1984, 1996; Ashburner 1989; Greenspan 1997) and one such system was used by Gao et al. (2011) for the purpose of identifying recessive lethal or nearly lethal mutations. More experimental detail can be found in Gao et al. (2011) and for the main purpose of this article, it should suffice to outline the structure of information and the type of mutation being examined. The recessive lethality d of a recessive mutation is defined as one minus the maximal percentage of the homozygote (among all survival offspring) for that mutation. The data reported by Gao et al. (2011) correspond to those mutations with recessive lethality equal to 99%, that is, no more than 1% of survival offspring are z/z homozygote. Once a cell acquires a mutation with recessive lethality d, further mutation(s) is much more likely to increase lethality than to reverse it. Consequently recessive lethal mutations have a masking effect such that only the earliest one is identifiable. Figure 1 shows examples of how mutations in a genealogy lead to different mutation patterns.

Figure 1.

Examples of mutations and resulting mutation patterns. (A) Single mutation leading to mutation pattern 〈1〉; (B) two mutations leading to mutation pattern 〈2, 1〉; (C) two mutations leading to mutation pattern 〈3〉 due to the second mutation being masked by the first one.

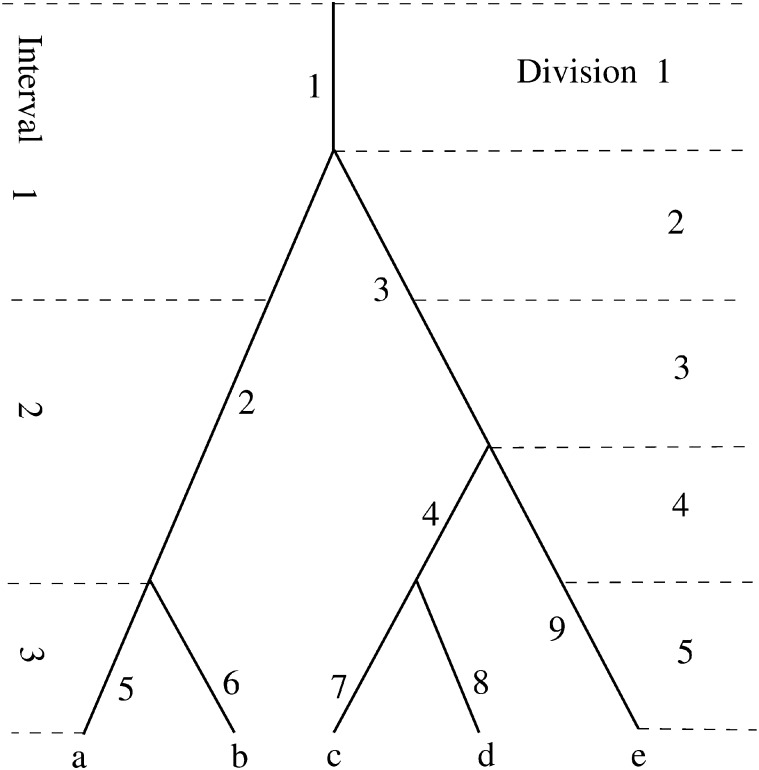
Suppose branches of a sample genealogy are labeled by integers. For branch i, define Ω(i) as the set of branches consisting of the branch i and all its descendant branches, which are referred to as the subtree of the branch i. For the genealogy shown in Figure 2, for example, Ω(2) = {2, 5, 6} and Ω(3) = {3, 4, 7, 9, 8, 9}. Therefore, two mutations, respectively on branches i and j, are both observable if and only if Ω(i) ∩ Ω(i) = Ø.

Figure 2.

An example of the genealogy of five alleles (a−e) sampled from the cell population after the fifth division. Each branch is identified by a nearby integer. The sizes of the branches are ϕ(1) = 5, φ(2) = 2, φ(3) = 3, φ(4) = 2, φ(5) = φ(6) = φ(7) = φ(8) = φ(9) = 1; $b_1^T=\left(1,0,0\right),b_2^T=\left(1,2,0\right)$, $b_3^T=\left(1,1,0\right),b_4^T=\left(0,1,0\right)$, $b_5^T=b_6^T=b_7^T=b_8^T=\left(0,0,1\right)$, and $b_9^T=\left(0,1,1\right)$.

Suppose the germ cell divisions from a fertilized egg to sperm are divided into I intervals. Let [i, j] represent the interval from the ith to the jth cell divisions. Suppose the mutation rate per cell division for the lth interval is u_l and define u = (u₁, … , u_I)^T. For a given sample of sperm, there is a genealogy connecting them to the fertilized egg. Suppose each branch in the genealogy is identified by an unique integer (how branches are numbered is immaterial). Define for the ith branch, b_ij as the number of divisions it contains from the jth interval and b_i as a vector with elements b_ij, j = 1, … , I. That is, b_i = (b_i1, … , b_iI)^T. Define φ(i) as the size of the ith branch, i.e., the number of descendants of the branch that are observed in the sample, and

$$a_k={\displaystyle \sum _{i:\phi \left(i\right)=k}{b}_i}\hspace{1em}\text{and}\hspace{1em}t={\displaystyle \sum _{k=1}^n{a}_k}.$$ (1)

Then a_kj is the total number of cell divisions from the jth interval that are of size k and the kth element, t_k, of t is the total number of cell divisions from the kth interval. For branch i, let w_i be the sum of lengths of all the branches in Ω(i), excluding the branch i itself. That is, $w_i=-b_i+{\displaystyle {\sum }_{k:\Omega \left(i\right)}{b}_k}$. Figure 2 illustrates the aforementioned quantities in a genealogy of five alleles taken after the fifth division. It follows that $a_1={\displaystyle {\sum }_{k=5}^9{b}_i}={\left(0,1,5\right)}^T$, a₂ = b₂ + b₄ = (1, 3, 0)^T, a₃ = b₃ = (1, 1, 0)^T, a₄ = 0, a₅ = b₁ = (1, 0, 0), and an example of w is that w₄ = b₇ + b₈ and w₃ = b₄ + b₇ + b₈ + b₉.

In addition to a and t, we will encounter other quantities that are functions of b_i, i = 1, … , which will be defined as they are introduced. Each of these quantities has a value for a given genealogy, and often we need to evaluate its expectation (mean) over all genealogies. We use a bar over the variable to represent its expectation. For example,

$$\overline{\mathbf{t}}={\displaystyle {\int }_{g}t\hspace{0.17em}dg},\hspace{1em}{\overline{\mathbf{a}}}_k={\displaystyle {\int }_g{a}_k\hspace{0.17em}dg.}$$ (2)

Probability of a mutation pattern

Assume that the number of mutations in a branch of the sample genealogy g is a Poisson variable. Then the probability of no mutation in a family is equal to $e^{-{\mathit{t}}^{T}u}$. Since a single mutation leading to an observed pattern 〈i〉 must occur on a branch of size i, it follows that

$$\begin{array}{c}Pr\left(\langle i\rangle |g\right)={\displaystyle \sum _{k:\phi \left(k\right)=i}{e}^{-{\left(t-b_k-w_k\right)}^{T}u}\left(1-e^{-b_k^{T}u}\right)}\\ ={\displaystyle \sum _{k:\phi \left(k\right)=i}{e}^{-{\left(t-w_k\right)}^{T}u}\left(e^{b_k^{T}u}-1\right)},\end{array}$$ (3)

where the summation is taken over all the branches of size i. In the summation, the first term $e^{-{\left(t-b_k-w_k\right)}^{T}u}$ is the probability that there is no mutation outside the subtree of branch k and the second term $\left(1-e^{-b_k^{T}u}\right)$ is the probability there is at least one mutation in branch k. This is because any mutation in the subtree will be masked by the mutation in branch k and thus not observable. In general, we have for a mutation pattern 〈i₁, … , i_l〉 that

$$Pr\left(\langle i_1,\dots ,i_l\rangle |g\right)={\displaystyle \sum _{\left(k_1,\dots ,k_l\right)\hspace{0.5em}\in \hspace{0.5em}{\mathcal{J}}_g\left(i_1,\dots ,i_l\right)}\left[e^{-{\left(t-w_{k_1,\dots ,k_l}\right)}^{T}u}{\displaystyle \prod _{i=1}^l\left(e^{b_{k_i}^{T}u}-1\right)}\right]},$$ (4)

where $w_{k_1,\dots ,k_l}={\displaystyle {\sum }_i{w}_{k_i}}$ and $\mathcal{J}$_g(i₁, … , i_l) is the collection of the branch sets of genealogy g on which mutations can lead to the observed mutational pattern. That is,

$$\begin{array}{l}{\mathcal{J}}_g\left(i_1,\dots ,i_l\right)=\{\left(k_1,\dots ,k_l\right):\phi \left(k_j\right)=i_j\hspace{0.5em}\text{for}\hspace{0.5em}i=1,\dots ,l\hspace{0.5em}\\ \text{and}\hspace{0.5em}\Omega \left(k_i\right)\mathrm{\cap }\Omega \left(k_j\right)=\mathrm{Ø}\text{for}\hspace{0.5em}i\ne j\}.\end{array}$$ (5)

Since sample genealogy is generally unobservable, one needs to consider all the possible sample genealogies from which the given mutational pattern can be generated, which leads to the general unconditional probability of the mutational pattern 〈i₁, … , i_l〉 as

$$Pr\left(\langle i_1,\dots ,i_l\rangle \right)={\displaystyle {\int }_g{\displaystyle \sum _{\left(k_1,\dots ,k_l\right)\hspace{0.5em}\in \hspace{0.5em}{\mathcal{J}}_g\left(i_1,\dots ,i_l\right)}\left[e^{-{\left(t-w_{k_1,\dots ,k_l}\right)}^{T}u}{\displaystyle \prod _{i=1}^l\left(e^{b_{k_i}^{T}u}-1\right)}\right]dg}}.$$ (6)

This formula provides the basis for the proposed inferences and detailed analysis of Drosophila data. For any given mutation pattern 〈i₁, … , i_l〉 and u, the probability can be evaluated as the average of Pr(〈i₁, … , i_l〉|g) [which is given by (4)] over a reasonably large set of simulated sample genealogies. However, it is generally not efficient and often impractical to use the above formula directly if hundreds or even thousands of different u need to be evaluated.

Approximation to the Probability of a Mutation Pattern

Since Equation 6 is computationally expansive to use in general, accurate and yet-fast approximations to the probabilities of various mutation patterns are important and often necessary for large-scale data analysis. Gao et al. (2011) found approximations to the probabilities for up to two mutations in a family, using the Taylor expansion. For example, $e^{-t^{T}u}\approx 1-t^{T}u+\frac{1}{2}{u}^T\left(t{t}^T\right)u$. Define $A_{ij}=a_i{a}_j^T,A_i=a_i{t}^T\text{,}\hspace{0.5em}\text{and}\hspace{0.5em}{A}_0=t{t}^T$. Then the probabilities p₀ = Pr(〈〉), p_i = Pr(〈i〉), and p_ij = Pr(〈i, j〉) can be approximated (Gao et al. 2011) by

$$p_0\approx 1-{\overline{\mathbf{t}}}^{T}u+\frac{1}{2}{u}^T{\overline{\mathbf{A}}}_{0}u,$$ (7)

$$p_i\approx {\overline{\mathbf{a}}}_i^{T}u-u^T{\overline{\mathbf{A}}}_{i}u,$$ (8)

$$p_{ij}\approx \frac{2-{\delta }_{i-j}}{2}{u}^T{\overline{\mathbf{A}}}_{ij}u,$$ (9)

where δ_i−j = 1 if i = j and 0 otherwise. This method of approximation is referred to as the approximation by Taylor expansion (ATE). Although these approximations cover up to two mutations per family, in principle a reasonably accurate approximation to the probability of any given mutation pattern can be obtained if a sufficient number of Taylor expansion terms are included. With increasing mutation rate, the number of required terms for each case will also increase, and due to the need to estimate a large number of coefficients in higher-order terms, their computations make the ATE inefficient.

Since typically $b_k^{T}u\ll 1$ in Equation 6, $e^{b_{k_i}^{T}u}-1\approx b_k^{T}u$. Furthermore one can simplify the expression by replacing w for each combination of branches by its average value and arrive at

$$Pr\left(\langle i_1,\dots ,i_l\rangle |g\right)\approx {\displaystyle \sum _{\left(k_1,\dots ,k_l\right)\hspace{0.5em}\in \hspace{0.5em}{\mathcal{J}}_g\left(i_1,\dots ,i_l\right)}\left[e^{-{\left[t-w_{k_1,\dots ,k_l}\right]}^{T}u}{\displaystyle \prod _{i=1}^l{b}_{k_i}^{T}u}\right]}$$ (10)

$$\approx e^{-{\left[t-w\left(\langle i_1,\dots ,i_l\rangle \right)\right]}^{T}u}S\left(\langle i_1,\dots ,i_l\rangle ,u\right),$$ (11)

where w(〈i₁, … , i_l〉) is defined as the average value of $w_{k_1,\dots ,k_l}$ over the set $\mathcal{J}$_g(i₁, … , i_l) and

$$S\left(\langle i_1,\dots ,i_l\rangle ,u\right)={\displaystyle \sum _{\left(k_1,\dots ,k_l\right)\in {\mathcal{J}}_g\left(i_1,\dots ,i_l\right)}\left({\displaystyle \prod _{i=1}^l{b}_{k_i}^{T}u}\right)}={\displaystyle \sum _{l_1,\dots ,l_m}{a}_{l_1\dots l_m}{u}_{l_1}\dots u_{l_m},}$$ (12)

where $a_{l_1\dots l_m}={\displaystyle {\sum }_{\left(k_1,\dots ,k_l\right)\hspace{0.5em}\in \hspace{0.5em}{\mathcal{J}}_g\left(i_1,\dots ,i_l\right)}{b}_{k_1{l}_1}\dots b_{k_m{l}_m}}$, which leads to an approximation of Equation 6 as

$$Pr\left(\langle i_1,\dots ,i_l\rangle \right)\approx {\displaystyle {\int }_g{e}^{-{\left[t-w\left(\langle i_1,\dots ,i_l\rangle \right)\right]}^{T}u}S\left(\langle i_1,\dots ,i_l\rangle ,u\right)dg}.$$ (13)

A further simplification and approximation can be obtained by moving the integration inward and replacing each quantity by its integral (that is, its expectation). This leads to the approximation

$$Pr\left(\langle i_1,\dots ,i_l\rangle \right)\approx e^{-{\left[\overline{\mathbf{t}}-\overline{\mathbf{w}}\left(\langle i_1,\dots ,i_l\rangle \right)\right]}^{T}u}\overline{S}\left(\langle i_1,\dots ,i_l\rangle ,u\right),$$ (14)

where $\overline{\mathbf{w}}\left(\langle i_1,\dots ,i_l\rangle \right)$ is the mean value of w(〈i₁, …, i_l〉) over all genealogies, and $\overline{S}$ is the mean of S over all genealogies, which can be computed as

$$\overline{S}\left(\langle i_1,\dots ,i_m\rangle ,u\right)={\displaystyle \sum _{l_1,\dots ,l_m}{\overline{a}}_{l_1\dots l_m}{u}_{l_1}\dots u_{l_m},}$$ (15)

where ${\overline{a}}_{l_1\dots l_m}$ is the mean of $a_{l_1\dots l_m}$ over all possible genealogies. This new approach is referred to as the approximation by inward integration (AII).

Let S(〈〉, u) = 1 and w({}) = 0. Then Equation 14 is applicable to any mutation pattern. The computation of Equation 14 is quite manageable now. In particular, for up to two mutations, we have

$$S\left(\langle i\rangle ,u\right)={\displaystyle \sum _{\left(k\right)\in {\mathcal{J}}_g\left(i\right)}{b}_k^{T}u=a_k^{T}u,}$$ (16)

$$S\left(\langle i,j\rangle ,u\right)={\displaystyle \sum _{\left(k,l\right)\in {\mathcal{J}}_g\left(i,j\right)}\left(b_k^{T}u\right)\left(b_l^{T}u\right)=u^T{B}_{ij}u,}$$ (17)

where $B_{ij}={\displaystyle {\sum }_{\left(k,l\right)\hspace{0.5em}\in \hspace{0.5em}{\mathcal{J}}_g\left(i,j\right)}{b}_k{b}_l^T}$. Therefore, the corresponding new approximations up to two mutations are

$$p_0\approx e^{-{\overline{\mathbf{t}}}^{T}u},$$ (18)

$$p_i\approx e^{-{\left[\overline{\mathbf{t}}-\overline{\mathbf{w}}\left(\langle i\rangle \right)\right]}^{T}u}\left({\overline{\mathbf{a}}}_i^{T}u\right),$$ (19)

$$p_{ij}\approx e^{-{\left[\overline{\mathbf{t}}-\overline{\mathbf{w}}\left(\langle i,j\rangle \right)\right]}^{T}u}\left(u^T{\overline{\mathbf{B}}}_{ij}u\right),$$ (20)

where ${\overline{\mathbf{B}}}_{ij}$ is the mean B_ij over all genealogies. Note that B_ij is not the same as A_ij due to constraints on the pair of branches that are compatible with the observed pattern. Gao et al. (2011) recognized the masking effect of mutations and estimated A_ij by B_ij. We show in a later section that when three or more mutations in a family are rare, then both the ATE and the AII give excellent approximations to the true probabilities. With an increasing number of families with more than two mutations, we find that the new approach provides a more accurate approximation to Equation 6 than those by Gao et al. (2011).

The Likelihood Inference

Suppose there are in total m different mutation patterns in the data set, c₁, … , c_n, and n_i is the occurrence of pattern c_i. Then, the likelihood of the data is

$$L={\displaystyle \prod _{i=1}^{m}Pr{\left(c_i\right)}^{n_i},}$$ (21)

where Pr(c_i) is the probability of pattern c_i. Based on the new scheme for estimating the probabilities of each pattern, the maximum-likelihood estimates, $\widehat{\mathbf{u}}$, of u can be derived from ln(L), which is

$$\text{ln}\left(L\right)=-{\displaystyle \sum _{i=1}^m{n}_i{\left[\overline{\mathbf{t}}-\overline{w}\left(c_i\right)\right]}^{T}u}+{\displaystyle \sum _{i=1}^m{n}_i\text{ln}\left[\overline{S}\left(c_i,u\right)\right]}.$$ (22)

The asymptotic covariance of the estimates $\widehat{\mathbf{u}}$ can also be obtained as the inverse of matrix $V=-{\left({\partial }^2\text{ln}\hspace{0.17em}L/\partial u_k\partial u_l\right)|}_{u=\widehat{\mathbf{u}}}$, whose computation is described in the Appendix. Let r^T = (r₁, … , r_I), where r_k is the number of cell divisions in the kth interval. Then per generation mutation rate u can be estimated as

$$\widehat{u}=r_1{\widehat{u}}_1+r_2{\widehat{u}}_2+\dots +r_I{\widehat{u}}_I.$$ (23)

The variance of this estimate is $\text{Var}\left(\tilde{u}\right)=r^T{V}^{-1}r$. Suppose the total number of mutant lines in the experiment is M and the total number of lines screened is N. Then an alternative estimate of u is $\tilde{u}=M/N$, which is unbiased regardless of whether mutation rates during development are the same (Fu and Huai 2003). A hypothesis can be tested through the likelihood-ratio test. For example, for testing the null hypothesis (H₀) that mutation rates at different cell divisions are all equal, against the alternative hypothesis H₁ that rates have no constraint, the test statistic

$$\text{Lr}=-2\left(\text{ln}\left(L_0\right)-\text{ln}\left(L_1\right)\right)$$ (24)

follows asymptotically the χ²-distribution with I − 1 d.f.

Cell Propagation and Simulation of Cell Genealogy

A discrete generation model is used for the propagation of cells in the germline lineage. We introduce two alternative modes of cell propagation.

Let N(i) be the size of the ith population, which can be divided into two groups, one [size N₀(i)] without a sister cell and one [size N₁(i)] with one sister cell [N(i) = N₀(i) + N₁(i)]. The first mode of propagation assumes that for each cell in the ith population, the probability of having k(k = 0, 1, 2) daughter cell(s) in the ith population is p_k.

This mode of cell propagation is fully determined when the values of p_i are specified. p₂ = 1 corresponds to the case in which each cell yields two daughter cells, which is considered to be the default situation. Another special case is that every cell produces at least one daughter cell, which corresponds to p₀ = 0. For two randomly selected cells from the ith population, the probability that they will coalesce in the i − 1th population is

$$\frac{N_1\left(i\right)}{N\left(i\right)\left(N\left(i\right)-1\right)}.$$ (25)

That is, two cells will coalesce if and only if the first cell selected has a sister cell [with probability N₁(i)/N(i)] and the second cell selected is its sister cell [with probability 1/(N(i − 1) − 1]. When there are multiple pairs of cells being considered, multiple coalescence can occur, which is usually not allowed in the conventional coalescent theory. The exact probabilities of any particular pattern of coalescence (for example, two pairs of coalescence, five pairs of coalescence, etc.) can be given analytically although they are not necessary for our purpose. What is critical is a proper algorithm to simulate this process as is discussed later in this section.

An alternative mode of cell propagation is as follows. Assume that each cell in the (i − 1)th population divides to yield two daughter cells and the cells in the ith population are a random sample (without replacement) from these 2N(i − 1) daughter cells. This mode of cell propagation is recognized when a range condition, such as N(i) ∈ [a, b], is specified. In such a case, N(i) is assumed to be a random integer in the given range [a, b]. Then the probability that two randomly selected cells from the ith population will coalesce in the (i − 1)th population is

$$\frac{1}{2N\left(i-1\right)-1},$$ (26)

which occurs only if the second cell selected is the sister cell of the first one. Again the probability of multiple coalescence can be derived. However, the sampling process will also yield N(i) and N₁(i); thus the coalescent probability is also given by Equation 25.

Simulation algorithms

A forward–backward two-step algorithm was used in Gao et al. (2011) and will continue to be used here. The first (forward) step is to simulate a history of the population sizes and the second (backward) step is to simulate the genealogy given the history of the populations sizes as follows.

Forward algorithm: Simulation of cell population dynamics:

Given the value of N(i − 1), the value of N(i) is simulated according to the transition mode. Meanwhile, the values of N_k(i), (k = 1, 2) are recorded.

Backward algorithm: Simulation of cell genealogy:

Given a collection of n cells from the ith population:

1. Create an array of N(i) integers as follows: N₁(i) integers from 1 to N₁(1) and two copies of each integer from N₁(i) + 1 to N₁(i) +N₂(i).

2. Take a random sample of size n from the above array. If two integers in the sample are the same, a coalescent event occurs.

3. Update the collection of cells and repeat steps 1 and 2 until the 0th population (the zygote) is reached.

In the forward step, the cell lineage splits into two subpopulations after the 14th division and enters the stem cell lineage, which is specified by mode 1 with p₁ = 1 − e, p₂ = 2 for small values of e. After the 31st division, each of the differentiated cells from stem cells goes into spermatogenesis, resulting in 64 sperm. After the 37th cell division, the sperm population consists of sperm that are derived from differentiated cells that have experienced different numbers of divisions. Therefore, the number of cell divisions for each of the sperm in a random sample can be different.

Numerical Results

To investigate statistical properties of the inference framework, the 36 cell divisions are divided into four intervals: [1, 3], [4, 14], [15, 31], and [32, 36], representing, respectively, the early cleavage, late cleavage, the stem-cell stage, and the spermatogenesis stage. Situations with maximal cell divisions >36 are also considered, so that different sperm in a sample might have experienced different numbers of divisions (see Figure 3). In such situations, the meaning of the last two intervals needs to be modified. For example, if a maximum of 38 divisions is allowed, then the last interval corresponds to the last 5 cell divisions, which for some lineages are from the 34th to the 38th division, while for some they are from the 32nd to the 36th division; and the second interval thus includes the 15th division in whatever is not included in the last interval.

Figure 3.

Population dynamics and an example of the genealogy of four sperm.

Simulation of sample genealogy

As pointed out earlier, the process of simulating a sample genealogy is similar to that in Gao et al. (2011), with the exception of the gametogenesis stage. The process consists of forward and backward steps. The former is guided by a number of constraints about the population sizes mentioned in the Introduction. For example, after the 8th division, there are 256 cells from which only 4–7 cells become PGCs. Table 1 lists all the used constraints for population sizes during germline development. After the 31st division in the forward process, each of the differentiated cells will go into gametogenesis, which progresses through 5 additional divisions to produce 64 sperm. This aspect of the development is now explicitly modeled.

Table 1. Constraints during the germline development of a male Drosophila melanogaster.

Constraint no.	Detail
1	N(8) ∈ [4, 6]
2	N(12) ∈ [23, 52]
3	Population split into two with each N ∈ [5, 9]
4	Stem-cell stage starts from the 15th division onward with p2 = 0.001
5	Differentiated cells after the 31st division starts spermatogenesis

The backward process of the simulation is the same as that in Gao et al. (2011) except that the efficiency of the program has been improved. The resulting population dynamics with relation to the sample genealogy are illustrated in Figure 3. It is important to simulate a large number of genealogies from which the values of various coefficients in the inference framework can be obtained. To deal with up to four mutations in a family, we found that in general 250,000 genealogies are sufficient.

Accuracy of the approximations to the probabilities of mutation patterns

Since the expected numbers of occurrences and the difference in the expected numbers of occurrences are critical to the statistical inference, we use the following index to measure the accuracy of the approximations,

$$D_i=N\left(P_i-{\widehat{P}}_i\right),$$ (27)

where P_i is the exact probability for a mutation pattern with i mutations, ${\widehat{P}}_i$ is its approximation, and N is the number of families, which is set to 8625. The probabilities were estimated with 2 million simulated genealogies. Table 2 gives the results for several mutation rates. In all cases the AII is better than the ATE; the AII performs well for a wide range of mutation rates, including a very large mutation rate. The ATE appears to be sufficient for a mutation rate up to ∼u × 10⁻⁴, but with a rate closer to 10 × 10⁻⁴, its errors becomes too large, in addition to not being able to handle more than two mutations. We focus on further studying the statistical properties of the AII because of its obvious superiority.

Table 2. The expected numbers of mutation patterns and quality of approximations in 8625 families, each having 20 offspring.

		i =
u(× 104)		0	1	2	3	4	5	6	7
1	NPi	8,326.5	293.9	4.6	0.0	0.0	0.0	0.0	0.0
	Di	−0.1	0.1	0.0	0.0	0.0	0.0	0.0	0.0
	D′i	0.2	−0.1	−0.1
5	NPi	7,232.6	1,286.7	100.9	4.7	0.1	0.0	0.0	0.0
	Di	−1.7	1.4	0.3	0.0	0.0	0.0	0.0	0.0
	D′i	−1.7	14.1	−17.4
10	NPi	6,067.3	2,179.3	344.1	32.2	2.0	0.1	0.0	0.0
	Di	−5.7	3.8	1.6	0.2	0.0	0.0	0.0	0.0
	D′i	−38.6	131.9	−127.5
50	NPi	1,504.0	2,950.4	2,468.7	1,206.0	389.8	88.8	14.7	1.5
	Di	−31.3	−25.5	12.7	23.8	13.6	4.5	1.0	0.1
	D′i	−4,901.0	11,637.7	−8,438.5

u, mutation rate; NP_i, expected number of occurrences based on exact probability; D_i, D values based on the AII; D′_i, D values based on the ATE.

Maximum-likelihood estimate of u

One major outcome of the inference is the maximum-likelihood estimate of the mutation rate u; thus it is important to understand the properties of the estimates, which were carried out using simulations. Table 3 shows the means and standard deviations of the maximum-likelihood estimates of u₁, u₂, u₃, and u₄ for several cases. The results show that the maximum-likelihood estimates are slightly biased but the bias decreases with increase in family number, which is expected from the well-known properties of the maximum-likelihood method. The standard errors of estimating u₁, … , u₄ differ from each other, with those for u₃ and u₄ being the smallest and that for u₁ the largest. This pattern agrees with the fact that there are many more mutations that result in a smaller mutant size, most of which likely occurred during the third and fourth time intervals. As a result, there are more observations from these two intervals that lead to more accurate estimates.

Table 3. Maximum-likelihood estimates of u₁, u₂, u₃, and u₄(× 10⁴) with 20 offspring from each of n families.

u1, u2, u3, u4	n = 1,000	n = 10,000
4, 4, 4, 4	4.21, 3.86, 4.04, 3.98a	3.95, 3.94, 4.02, 3.97
	4.80, 2.57, 1.37, 1.51b	1.80, 0.99, 0.48, 0.62
8, 4, 4, 4	7.83, 4.11, 3.93, 4.04	7.95, 3.94, 4.02, 3.97
	6.50, 3.02, 1.51, 1.53	2.35, 1.11, 0.53, 0.50
4, 4, 4, 8	4.19, 3.83, 4.07, 7.91	3.97, 3.94, 4.02, 7.96
	4.77, 2.62, 1.44, 1.72	1.84, 0.97, 0.50, 0.56
6, 4, 4, 6	5.93, 3.97, 4.01, 5.97	5.99, 3.92, 4.04, 5.95
	5.68, 2.82, 1.47, 1.62	2.11, 1.04, 0.52, 0.53
3, 6, 6, 3	3.67, 5.58, 6.13, 2.96	3.03, 5.83, 6.06, 2.95
	4.73, 3.00, 1.62, 1.67	1.75, 1.07, 0.56, 0.55

Result for each case is based on 1000 simulated data sets.

^aMean estimates.

^bStandard deviations.

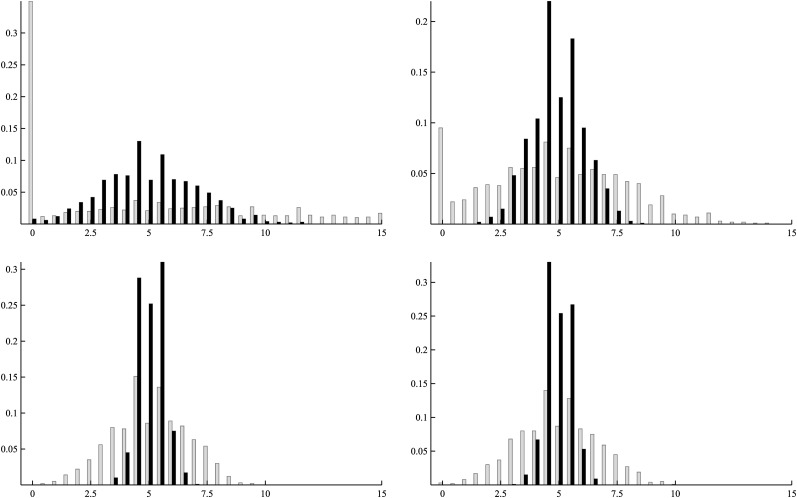
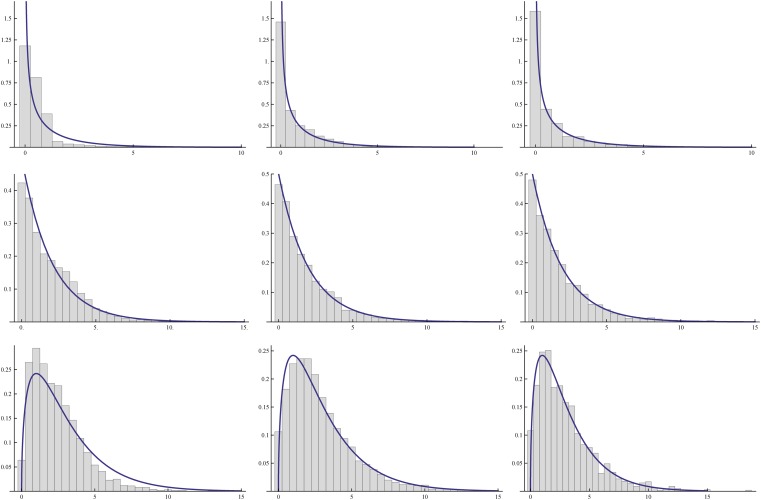
Figure 4 shows the distributions of estimates of mutation rates corresponding to the first row of Table 3. Two obvious features from these distributions are as follows. The first is that with increased family number, each distribution becomes more concentrated around the true mutation rate. The second is that judging from the spread of the distributions, the quality of estimations for u₃ and u₄ is better than that for u₁ and u₂. Among the four, the quality of estimating u₁ is the poorest. These features agree well with the patterns of standard deviations in Table 3.

Figure 4.

Distributions of the estimates for u₁, u₂, u₃, and u₄ (from top down). In each of the plots, shaded bars correspond to 1000 families and solid bars to 10,000 families (labels for the x-axis are multiplied by 10⁴).

Likelihood-ratio test

Being able to obtain maximum-likelihood estimates under different assumptions also allows us to examine the distribution of the likelihood-ratio test. Various hypotheses about the pattern of mutation rates can be tested, as reported in Gao et al. (2011); however, the following four are representative, one for each value of the degrees of freedom: H₀, rates are constant; H₁, the last three are the same; H₂, the first two are the same; and H₃, no constraint.

Let L_ij be the log-likelihood ratio statistics between the ith and jth hypotheses. When H₀ is true, it is expected that L_0,1, L_0,2, and L_0,3 follow asymptotically χ²-distributions with 1, 2, and 3 d.f., respectively. In the simulations, constant mutation rates are used and for each simulated sample, the maximum likelihood under each hypothesis is found, which leads to the likelihood-ratio statistics. Table 4 shows the upper-tail critical values for these three statistics. Comparing these critical values with the critical values of χ with 1, 2, and 3 d.f., respectively, indicates that the these critical values agree reasonably well with the asymptotic values with sample sizes as small as 500. The distributions of these statistics are given in Figure 5 for two different sample sizes, which shows the overall excellent agreement of the empirical density with asymptotic ones.

Table 4. Critical values for likelihood-ratio tests with μ = 0.0004.

	Asmpt		n = 1,000		n = 5,000		n = 10,000
Li,j	c5	c1	c5	c1	c5	c1	c5	c1
L0,1	5.99	9.21	6.18	9.56	6.17	9.35	6.23	9.44
L0,2	3.84	6.64	3.47	5.26	3.96	6.88	3.93	6.66
L0,3	7.82	11.35	7.51	10.55	8.01	11.42	8.21	11.98

c₅ and c₁ are, respectively, the upper 5% and 1% critical values. Simulation results for each case are based on 10,000 replicates.

Figure 5.

Distributions of likelihood-ratios L_0,1 (top three), L_0,2 (middle three), and L_0,3 (bottom three) for 200 (left), 1000 (center), and 10,000 (right) families (bottom), with smooth curves being the χ² densities.

Reanalysis of the data

The data being reanalyzed here consist of those presented in Table 1 of Gao et al. (2011) and 7 additional families, 3 of which have three mutations and 1 of which has four mutations, giving thus a total of 8,625 families. For convenience of comparison, we used the same division of intervals: [1, 1], [2, 2], [3, 14], [15, 31], and [32, 36]. Table 5 shows the maximum-likelihood estimates using both the ATE and the AII (for the sake of space, only the results for four of the eight hypotheses considered in Gao et al. 2011 are given), while Table 6 gives the results of the likelihood-ratio tests. Comparing the entries of the ATE in these tables to those in Tables 4 and 5 of Gao et al. (2011), one can see that the differences are minimal. Furthermore, comparing the estimates by the ATE to those by the AII shows that the differences are also minor in almost all cases. Therefore, the improved method does not change the conclusions made previously. These analyses also included the case in which 38 cell divisions were assumed. In such situations, the patterns of the likelihood-ratio tests (Table 6) suggest that the mutation rates for the second, third, and fourth intervals may also be different, although the evidence is only marginal.

Table 5. Maximum-likelihood estimates of u × 10³ under several hypotheses.

Hypothesis	u1	u2	u3	u4	u5	−ln(L)
H1	0.347a	0.347	0.347	0.347	0.347	4519.0
	0.343b	0.343	0.343	0.343	0.343	4494.8
	0.321c	0.321	0.321	0.321	0.321	4441.9
H3	2.284	2.284	0.001	0.001	1.217	4153.2
	2.284	2.284	0.001	0.001	1.217	4129.0
	2.249	2.249	0.001	0.046	1.050	4126.4
H5	4.864	0.001	0.007	0.007	1.217	4139.6
	4.864	0.001	0.007	0.007	1.217	4115.4
	4.655	0.001	0.037	0.037	1.050	4113.1
H8	5.072	0.001	0.002	0.007	1.217	4139.5
	4.864	0.001	0.002	0.007	1.217	4115.4
	4.815	0.001	0.001	0.058	1.032	4110.8

H₁, u₁ = … = u₅; H₂, u₂ = u₃ = u₄; H₃, u₁ = u₂; H₄, u₂ = u₃; H₅, u₃ = u₄; H₆, u₄ = u₅; H₇, u₁ = u₅; and H₈, no constraint.

^aEstimates based on the ATE.

^bEstimates based on the AII.

^cEstimates based on the AII with 38 divisions.

Table 6. The values of the log-likelihood ratio test of various hypotheses listed in Table 5.

	i =
Contrast	2	3	4	5	6	7	8
H1 vs. Hi	758.8	731.6	758.9	758.8	293.2	714.8	758.9
	758.7	731.7	758.8	758.7	292.7	714.6	758.8
	657.1	630.9	662.1	657.5	293.6	609.9	662.1
Hi vs. H8	0.1	27.3	0.0	0.1	465.7	44.2
	0.1	27.1	0.0	0.1	466.1	44.2
	5.0	31.2	0.0	4.6	368.6	52.3

While it is comforting that the reanalysis reinforces the conclusions made earlier, this should not be regarded as the AII lacking importance. When the number of families with more than two mutations increases, one can expect to see increasing differences and a more rigorous new method than the ATE will become necessary. To illustrate, we simulated sets of 8625 families with four intervals of cells [1, 1], [2, 14], [15, 33], and [34, 38], using two sets of mutation rates, one being equal rates for all the intervals and the other being one that produces mutational patterns resembling those from the experiment, which will be subjected to detailed analysis elsewhere. Table 7 shows the comparison of the two methods from which it is obvious that the ATE leads to underestimation of mutations rates. In the first case (equal mutations rates), the bias in estimating u_i increases with i and u₄ is about two-thirds of the true value. MSEs of the estimates also suggest that the AII performs considerably better (except for u₁ for which there is little difference between the two methods). For the second case, the downward bias in the estimates by the ATE is also obvious in all u_i and the MSEs by ATE are appreciably larger than those by the AII. Another shortcoming of the ATE is that due to differential degrees of underestimation of u_i, it can lead to rejection of certain hypotheses more often than specified by the given nominal level of significance. For example, for testing the hypothesis u₁ = u₄, the ATE in the first case leads to nearly 12% rejection while the AII has <5% rejection at the 5% significance level. These results agree well with an earlier conclusion made from Table 2, which is that when the mean mutation rate is >10⁻⁴, the ATE starts to lose accuracy.

Table 7. Comparison of estimates of u based on the ATE and the AII when mutation rates are relatively high.

Rates	Values (×104)	AII	MSE	ATE	MSE
u1	2.000	2.098	0.648	1.923	0.627
u2	2.000	1.898	0.031	1.602	0.186
u3	2.000	2.015	0.007	1.587	0.177
u4	2.000	1.934	0.016	1.417	0.348
u1	20.000	19.581	2.4772	18.904	3.4325
u2	0.200	0.203	0.0086	0.139	0.0111
u3	0.167	0.165	0.0020	0.152	0.0021
u4	5.000	4.943	0.0112	4.315	0.4742

MSE, mean square error. For each parameter set, 500 sets of 8625 families were generated.

Discussion

This article presents a significantly improved framework for statistical inference of germline mutation rates, with specific reference to D. melanogaster. This framework includes coalescent theory and an improved algorithm for simulating sample genealogies to obtain various coefficients, a method for computing the probabilities of mutation patterns, and a likelihood method for estimating mutation rates and testing hypotheses about the pattern of mutation rates. Statistical properties of the inference framework were investigated through simulation. The new approximation method for computing the probabilities of mutation patterns is more accurate than the previous method by Gao et al. (2011), particularly when mutation rates are high. Nevertheless, the previous method is sufficiently accurate for the data reported by Gao et al. (2011), and thus all major conclusions remain intact. The new likelihood-based inference exhibits desirable and expected properties, including reduced bias and smaller standard deviation with increasing number of families. The asymptotic χ²-distribution for the likelihood-ratio test is sufficiently accurate when the number of families is reasonably large and for the sample size reported in Gao et al. (2011).

This theoretical study paves the way for analysis of data from families with three and four mutations. Furthermore, the theoretical framework reported here can be adapted for studying germline mutational distribution in other organisms and for analyzing data generated through DNA typing or sequencing sperm samples. To apply the framework to other organisms the nature and mode of cell propagation of their germline populations would need to be determined. Application to data generated by DNA typing or sequencing will likely have its own issues, such as data accuracy, but since it is more economical to sequence larger regions with fewer samples than shorter regions with larger samples, observing multiple mutations will likely be the norm. Therefore, the statistical framework of inference described here will be relevant.

Appendix

Asymptotic Covariance of the Maximum-Likelihood Estimates

The asymptotic covariance matrix of the maximum-likelihood estimates $\widehat{\mathbf{u}}$ is the inverse of the following matrix:

$$V={-\left(\frac{{\partial }^2\text{ln}\hspace{0.17em}L}{\partial u_k\partial u_l}\right)|}_{u=\tilde{\mathbf{u}}}.$$

Since

$$\text{ln}\left(L\right)=-{\displaystyle \sum _{k=0}^m{n}_k{\left(t-s_k\right)}^{T}u}+{\displaystyle \sum _{k=0}^m{n}_k\text{ln}\left(S_k\right),}$$

it follows that

$$\frac{\partial \text{ln}\left(L\right)}{\partial u_i}={\displaystyle \sum _{k=0}{n}_k\left[S_k^{-1}\frac{\partial S_k}{\partial u_i}-{\left(t-s_k\right)}_i\right]}$$ (A1)

$$\frac{{\partial }^2\text{ln}\left(L\right)}{\partial u_i\partial u_j}={\displaystyle \sum _{k=1}{n}_k{S}_k^{-2}\left[S_k\frac{{\partial }^2{S}_k}{\partial u_i\partial u_j}-\frac{\partial S_k}{\partial u_i}\frac{\partial S_k}{\partial u_j}\right]}.$$ (A2)

Since S is of the form

$$S={\displaystyle \sum _{i_1,i_2,\dots ,i_k}t\left(i_1,i_2,\dots ,i_k\right)u_{i_1}\dots u_{i_k},}$$

where t(i₁, i₂, … , i_k) is constant, it follows that

$$\frac{\partial S}{\partial u_i}={\displaystyle \sum _{i_1,i_2,\dots ,i_k}t\left(i_1,i_2,\dots ,i_k\right)\frac{\partial u_{i_1}\dots u_{i_k}}{\partial u_i}}$$ (A3)

$$\frac{{\partial }^{2}S}{\partial u_i\partial u_j}={\displaystyle \sum _{i_1,i_2,\dots ,i_k}t\left(i_1,i_2,\dots ,i_k\right)\frac{{\partial }^2{u}_{i_1}\dots u_{i_k}}{\partial u_i\partial u_j}}.$$ (A4)

Furthermore, let n_i be the number of i in i₁, … , i_k; then

$$\frac{\partial u_{i_1}\dots u_{i_k}}{\partial u_i}=\frac{n_i{u}_{i_1}\dots u_{i_k}}{u_i}$$ (A5)

$$\frac{{\partial }^2{u}_{i_1}\dots u_{i_k}}{\partial u_i\partial u_j}=\frac{n_i{n}_j{u}_{i_1}\dots u_{i_k}}{\left(u_i{u}_j\right)}$$ (A6)

$$\frac{{\partial }^2{u}_{i_1}\dots u_{i_k}}{\partial u_i\partial u_i}=\frac{n_i\left(n_i-1\right)u_{i_1}\dots u_{i_k}}{\left(u_i^2\right)}.$$ (A7)

Putting the results of Equations A3–A7 into Equation A2, together with u replaced by $\widehat{\mathbf{u}}$, will lead to the numerical value of ${\partial }^2\text{ln}\hspace{0.17em}L/\partial u_k\partial u_l$.