Complete Numerical Solution of the Diffusion Equation of Random Genetic Drift

Abstract

A numerical method is presented to solve the diffusion equation for the random genetic drift that occurs at a single unlinked locus with two alleles. The method was designed to conserve probability, and the resulting numerical solution represents a probability distribution whose total probability is unity. We describe solutions of the diffusion equation whose total probability is unity as complete. Thus the numerical method introduced in this work produces complete solutions, and such solutions have the property that whenever fixation and loss can occur, they are automatically included within the solution. This feature demonstrates that the diffusion approximation can describe not only internal allele frequencies, but also the boundary frequencies zero and one. The numerical approach presented here constitutes a single inclusive framework from which to perform calculations for random genetic drift. It has a straightforward implementation, allowing it to be applied to a wide variety of problems, including those with time-dependent parameters, such as changing population sizes. As tests and illustrations of the numerical method, it is used to determine: (i) the probability density and time-dependent probability of fixation for a neutral locus in a population of constant size; (ii) the probability of fixation in the presence of selection; and (iii) the probability of fixation in the presence of selection and demographic change, the latter in the form of a changing population size.

RANDOM genetic drift occurs when genes of a given type are transmitted to the next generation with random variation in their number. It occurs when the relevant number of genes is finite and not effectively infinite. The process of random genetic drift plays a fundamental role in molecular evolution and the behavior of genes in finite populations (Crow and Kimura 1970; Kimura 1983). Beyond this, some of the ideas and techniques used in random genetic drift have a wider use, for example, with applications to cancer (Zhu et al. 2011; Traulsen et al. 2013) and range expansion (Slatkin and Excoffier 2012).

To set the stage for the present work, consider a single locus with genetic variation due to the segregation of more than one allele in the population. The population size is assumed finite, so random genetic drift generally occurs, and the number of copies of a particular allele at the locus changes randomly over time. The genetic composition of the population exhibits a particular sort of random walk and a distribution describing such walks can be analyzed under an approximation where it obeys a diffusion equation. This treatment of random genetic drift is naturally known as the diffusion approximation and was introduced into population genetics by Fisher (1922) and Wright (1945) and substantially extended and developed by Kimura (1955a); the diffusion approximation continues to be developed and applied in a variety of situations (Ewens 2004).

The diffusion approximation is often applied to the Wright–Fisher model (Fisher 1930; Wright 1931), where both time and the possible frequencies of an allele take discrete values. Such a “discrete” model has a mathematical description involving matrices and vectors, and numerical results for simple situations can be directly obtained on the computer. A comparison of Wright–Fisher and diffusion results suggest that the diffusion approximation is usually very accurate. It is known to work well when the number of individuals is not large (∼10) when selection is not strong (Ewens 1963). Generally, however, the accuracy of the diffusion approximation depends on the population size and the strength of selection, as discussed in the book by Ewens (2004). The book by Gale (1990) also discusses limitations of this approximation.

For an appreciable population size, or in complex situations, such as a changing population size, the diffusion equation, should, in principle at least, come into its own right, and be preferable to the Wright–Fisher model. For example, if the population size changes over time, the Wright–Fisher model becomes complicated by its matrix of transition probabilities changing size over time (the size of the matrix depends on the size of the population). By contrast, in a diffusion analysis only a parameter in the diffusion equation changes over time; the form and description of the diffusion equation are not dependent on the value of this parameter. The diffusion approximation has some other advantages.

In some cases the diffusion equation can yield explicit mathematical results; however, beyond this, the diffusion equation has the property of accessibly displaying key parameters of a problem (e.g., the effective population size, the strength of selection, mutation rates,...). A consequence is that the diffusion equation can be subject to mathematical transformations that expose the dependence of a solution on important combinations of these parameters. As an example, consider an unlinked locus with two alleles, which is subject to semidominant selection of strength s (with |s| ≪ 1) and two-way mutation at rate u. It can be shown that the diffusion equation leads, after the rescaling of time by the effective population size, N_e, to an equation that depends on the composite parameters N_es and N_eu, rather than separately depending on N_e, s, and u. Thus one conclusion that may be immediately drawn, without actually solving the diffusion equation, is that the equilibrium distribution of the allele frequency (which does not involve time) depends only on the composite parameters N_es and N_eu. Hence a locus with N_e = 100, s = 10⁻², and u = 10⁻⁵ and another with N_e = 1000, s = 10⁻³, and u = 10⁻⁶ will both, under the diffusion approximation, be described by the same equilibrium distribution of the allele frequency, because both have N_es = 1 and N_eu = 10⁻³. More generally, the ability to mathematically transform the diffusion equation can lead to understanding of the properties of whole sets of solutions (in the above example, all equilibrium solutions with given values of N_es and N_eu) along with other properties (Waxman 2011b).

While knowledge of the distribution of the allele frequency is important and useful, exact time-dependent solutions of the diffusion equation for two alleles are known in only a relatively small number of cases, such as under neutrality, where Kimura (1955b) obtained the part of the solution associated with segregating alleles, while McKane and Waxman (2007) derived the corresponding solution that also includes fixation and loss. Other known solutions incorporate migration or mutation (Crow and Kimura 1956, 1970). To analyze interesting new situations, which are constantly arising (for example, see Wylie et al. 2009) requires additional solutions of the diffusion equation and a numerical approach appears to be the simplest way forward.

In this work we present a scheme for numerically solving the diffusion equation. This approach can benefit from the advantages, alluded to above, of the diffusion approximation. In our view, the numerical scheme provides a viable way of investigating problems in random genetic drift; as we show, it can be simply applied to complex situations.

The numerical scheme is designed to lead to a normalized probability distribution in which the total probability sums (or integrates) to unity at all times. We describe solutions of the diffusion equation, whose total probability is unity, as complete. Thus the numerical method presented here produces complete solutions. Before we say more about the numerical scheme, let us discuss features of complete solutions.

A key feature of a complete solution of the diffusion equation is that all possible outcomes are included, by virtue of the total probability of the distribution summing to unity. Thus if fixation and loss are possible, then populations with fixed, lost, and segregating alleles are all, necessarily, included in a complete solution.

There are fundamental reasons for wishing to consider complete solutions of the diffusion equation, apart from the fact that they conserve probability and constitute a complete description. Such solutions have properties that are in extremely close correspondence with those of the model underlying the diffusion approximation—the Wright–Fisher model. As an example, in a Wright–Fisher model for a neutral locus, the expected value of the (relative) frequency of an allele, at any time, coincides with the initial value of its frequency (which is assumed known precisely). Under a diffusion analysis, exactly the same property of the expected value of the allele frequency holds only when a complete solution of the diffusion equation is used to carry out the average; using a solution that covers only populations with segregating alleles will not lead to the expected frequency of an allele coinciding with its initial value. Such an expectation requires an average that is taken not only over populations in which alleles are segregating, but also must include populations in which alleles have fixed or been lost.

When the phenomena of loss and fixation can occur, mathematical treatments of the diffusion equation lead to complete solutions that have been found to contain singularities—sharp spikes (i.e., Dirac delta functions) at the frequencies zero and one (McKane and Waxman 2007; Chalub and Souza 2009; Waxman 2011a). The spikes in the solution are distributions with zero width but finite area. They represent probability densities of lost and fixed alleles. The spikes are the way the probabilities of the terminal frequencies of the Wright–Fisher model arise within the diffusion approximation (Waxman 2011a).

Consider now previous approaches to solving the diffusion equation. We note that numerical approaches (see, e.g., Barakat and Wagener 1978; Wang and Rannala 2004), and the mathematical approach of Kimura (1955b), yield solutions that describe populations with segregating alleles, but populations with fixed or lost genes are not explicitly included (for a discussion of this see Waxman 2011a). As a consequence the resulting solutions of the diffusion equation decay away over time, and such solutions account for a total (or integrated) probability that is generally less than unity; they do not constitute complete solutions.

The numerical approach presented here technically involves solving the forward diffusion equation (Otto and Day 2007) for the probability distribution of the frequency of an allele. In contrast to the previous approaches, we look for a complete solution that conserves probability. However, at first sight it is unclear how to determine such a numerical solution if fixation or loss are possible, since singular spikes are present in the exact solution, and these appear to be numerically intractable, given their zero width. Furthermore, even solutions that do not possess singular spikes may have very sharp features at the boundary frequencies of zero and one due, e.g., to low mutation rates.

The numerical method of this work evades problems by not directly dealing with actual values of a solution, which would diverge at any spikes present. Rather, the method deals with frequency averages. A solution of the diffusion equation is discretized into frequency bins of finite width, and the value of this solution across a bin is a constant that represents an average of the exact solution across the bin. Since this average value, when multiplied by the bin width, represents a probability, it has a finite value, irrespective of any singular behavior of the underlying exact solution. The resulting discretized/averaged solution is treated by a so-called “finite volume” numerical scheme, which is of a type used for fluids. Such a scheme conserves the total probability, in the same way that the volume of a fluid of constant density is conserved. Given that this numerical method is based on a discretization, it cannot explicitly show the presence of singular, zero width spikes within the solution. However, in the Results we show that it is possible to clearly demonstrate the presence and contribution of such singular features within a solution.

Overall, a complete numerical solution of the diffusion equation, as presented in this work, allows a wide range of problems to be addressed, including time-dependent selection and changing population sizes, within a single inclusive and mathematically consistent framework.

Diffusion Equation

To proceed, let us consider the standard case of a single unlinked locus in a randomly mating diploid sexual population. The locus has two alleles, denoted A and B, and generations are taken to be non overlapping. The processes occurring in one generation are given in the following lifecycle:

$$\begin{array}{cc}\begin{array}{c}Adults\\ \left(\text{generation}\hspace{0.5em}t\right)\end{array}& \\ \downarrow & \text{reproduction},\hspace{0.5em}\text{followed}\hspace{0.5em}\text{by}\hspace{0.5em}\text{the}\hspace{0.5em}\text{death}\hspace{0.5em}\text{of}\hspace{0.5em}\text{all}\hspace{0.5em}\text{adults}\\ Zygotes& \\ \downarrow & \text{selection}\\ Juveniles& \\ \downarrow & \text{thinning}\hspace{0.5em}\left(\text{population}\hspace{0.5em}\text{number}\hspace{0.5em}\text{regulation}\right)\\ \begin{array}{c}Adults\\ \left(\text{generation}\hspace{0.5em}t+1\right)\end{array}& \end{array}$$

Based on the assumption that each adult contributes to a very large number of zygotes, the processes of both reproduction and selection are treated as being deterministic in character, meaning that there are negligible deviations from expected behaviors.

The individuals who survive selection (juveniles) are subject to a nonselective process of ecological thinning. In this process, N individuals are randomly picked, without regard to genotype, from an assumed much larger number of individuals, to become the N adults of the next generation. All randomness in the lifecycle, which directly arises from random genetic drift, occurs during the thinning stage of the lifecycle.

The proportion of all genes at the locus, in adults, that are the A allele is the relative frequency of this allele. Henceforth we refer to the relative frequency as just the frequency. The process of thinning generally results in the frequency varying randomly from generation to generation and we write its value at time t as X(t). This random variable generally takes different values in different copies of a population. Statistics of the frequency are described by a Wright–Fisher model (Fisher 1930; Wright 1931) and are expressed in terms of a discrete probability distribution, which can be thought of as describing the behavior of X(t) in a very large number of replicate populations. Under a diffusion approximation, however, both time and the frequency are treated as continuous quantities, and the statistical description of the allele frequency is given in terms of a probability density (but following common usage we use the phrases probability density and probability distribution interchangeably in what follows). The probability density of the frequency of the A allele at time t, when the value of the frequency is x, is written as f(x, t), and this obeys the diffusion equation

$$-\frac{\partial }{\partial t}f\left(x,t\right)=-\frac{1}{4N_{\text{e}}\left(t\right)}\frac{{\partial }^2}{\partial x^2}\left[x\left(1-x\right)f\left(x,t\right)\right]+\frac{\partial }{\partial x}\left[M\left(x,t\right)f\left(x,t\right)\right]$$ (1)

(Kimura 1955a, 1964). In this equation, the function M(x, t), which is typically a polynomial in x, incorporates the forces of migration, mutation, and selection, which are acting at time t (and in an infinite population M(x, t) would drive changes in the allele frequency), while N_e(t) denotes the variance effective population size at time t.

Note that theoretically, the variance effective size, N_e(t), is determined from processes that occur over a single generation (Ewens 2004). We use N_e(t) to refer only to this quantity, and in particular, we do not make use of averages of the effective population size, such as the harmonic mean, which summarize the values taken by the effective population size over multiple generations.

When mutation may be neglected, but AA, AB, and BB genotype individuals have relative fitnesses of 1 + s, 1 + hs, and 1, respectively, assuming |s| and |sh| are small (≪1), we have M(x) = sx(1 − x)[x + h(1 − 2x)] (Ewens 2004). A special case of this scheme of selection, termed semidominant selection, occurs when h = $\frac{1}{2}$. Furthermore, semidominant selection, with s → 2s, is closely equivalent to genic selection, in which the relative fitnesses of the three genotypes are (1 + s)², 1 + s, and 1, respectively, in which case M(x) = sx(1 − x).

Numerical Scheme

Equation 1 can be written in the form

$$\frac{\partial f\left(x,t\right)}{\partial t}+\frac{\partial j\left(x,t\right)}{\partial x}=0,$$ (2)

where

$$j\left(x,t\right)=-\frac{1}{4N_{\text{e}}\left(t\right)}\frac{\partial }{\partial x}\left[x\left(1-x\right)f\left(x,t\right)\right]+M\left(x,t\right)f\left(x,t\right)$$ (3)

is the probability current density. The quantity j(x, t) represents a flow of probability and Equation 2 ensures that probability is rather like a fluid, in the sense that all changes in the probability contained in a region of x occur only because of a flow of probability, via the probability current, in or out of that region.

In the diffusion equation, conservation of total probability follows from the appropriate specification of the probability current at the terminal allele frequencies x = 0 and x = 1. Following McKane and Waxman (2007), we impose conditions that ensure that there is no flow of probability beyond the terminal allele frequencies, by requiring the probability current density to vanish at both x = 0 and x = 1. These conditions, combined with Equation 2 ensure that the total probability, ${\displaystyle {\int }_0^{1}f\left(x,t\right)dx}$, has a constant value for all times. A consequence of this is that fixation and loss are naturally included within the solution (McKane and Waxman 2007; Waxman 2011a). In this work, we present a numerical scheme for the solution of the diffusion equation where the total probability is conserved at all times. The scheme is similar to the sort used on fluids of constant density, where conservation of the total quantity of the fluid (analogous to the total probability) is maintained at all times.

Implementation of the numerical scheme

We first give a direct statement of the numerical scheme. Detailed aspects of the scheme are discussed immediately afterward.

The values of the frequency, x, are discretized into a grid with spacing ε. The grid points lie at x_i = i × ε, where i = 0, 1, 2, …, K, and we take ε = 1/K; hence the values of the x_i range from 0 to 1. Times are also discretized, with a step size of τ and grid points at t_n = n × τ, where n = 0, 1, 2, ….

The numerical scheme determines an approximate, discretized form of the allele frequency’s probability density, f(x, t). In particular, the scheme determines quantities we write as $f_i^n$, with each $f_i^n$ representing the approximate value of f(x, t_n), when averaged over a range of x near x_i (see Interpretation of the numerical scheme for a more detailed explanation of the $f_i^n$). We call the K + 1 values of $f_0^n$, $f_1^n$, …, $f_K^n$ the representation of the distribution f(x, t_n).

Given the K + 1 values of the representation of f(x, t_n), the numerical scheme determines the K + 1 values of the representation of f(x, t_n+1), namely $f_0^{n+1}$, $f_1^{n+1}$, …, $f_K^{n+1}$. The numerical scheme can be compactly written as the matrix equation

$$f^{\left(n+1\right)}={\left[1+\alpha R^{\left(n+1\right)}\right]}^{-1}\left[1-\alpha R^{\left(n\right)}\right]f^{\left(n\right)}.$$ (4)

In this equation:

1. f⁽ⁿ⁾ denotes a K + 1 component column vector for time step t_n. The elements of f⁽ⁿ⁾ are $f_i^n$ with i = 0, 1, 2, …, K and so f⁽ⁿ⁾ contains the representation of f(x, t_n).

2. α is a constant, arising from the discretization of x and t, and takes the form

   $$\alpha =\frac{\tau }{2{\epsilon }^2}.$$ (5)
3. R⁽ⁿ⁾ is a matrix of size (K + 1) × (K + 1) that generally depends on the time, t_n. To define R⁽ⁿ⁾ we introduce

   $$U_i^n=-\frac{x_i\left(1-x_i\right)}{4N_{\text{e}}\left(t_n\right)}+\frac{\epsilon M\left(x_i,t_n\right)}{2},V_i^n=\frac{x_i\left(1-x_i\right)}{4N_{\text{e}}\left(t_n\right)}+\frac{\epsilon M\left(x_i,t_n\right)}{2}.$$ (6)

Then elements of R⁽ⁿ⁾ are written as $R_{i,j}^{\left(n\right)}$ where i, j = 0, 1, 2, …, K. The only nonzero $R_{i,j}^{\left(n\right)}$ have i = j and i = j ± 1; hence R⁽ⁿ⁾ has the form of a tridiagonal matrix. For example, for K = 4 the nonzero elements are

$$R^{(n)}=\left(\begin{array}{ccccc}\blacksquare & \blacksquare & & & \\ \blacksquare & \blacksquare & \blacksquare & & \\ & \blacksquare & \blacksquare & \blacksquare & \\ & & \blacksquare & \blacksquare & \blacksquare \\ & & & \blacksquare & \blacksquare \end{array}\right).$$

Generally, the nonzero elements of R⁽ⁿ⁾ are

$$\begin{array}{lll}\text{Leading}\hspace{0.5em}\text{upper}\hspace{0.5em}\text{diagonal}:\hfill & \begin{array}{l}{R}_{0,1}^{\left(n\right)}=2U_1^n\\ R_{i,i+1}^{\left(n\right)}=U_{i+1}^n\end{array}\hfill & \text{for} \hspace{0.5em}1\le i\le K-1\hfill \\ \text{Main}\hspace{0.5em}\text{diagonal}:\hfill & \begin{array}{l}{R}_{0,0}^{\left(n\right)}=2V_0^n\\ R_{i,i}^{\left(n\right)}=V_i^n-U_i^n\\ R_{K,K}^{\left(n\right)}=-2U_K^n\end{array}\hfill & \text{for} \hspace{0.5em}1\le i\le K-1\hfill \\ \text{Leading}\hspace{0.5em}\text{lower}\hspace{0.5em}\text{diagonal}:\hfill & \begin{array}{l}{R}_{i,i-1}^{\left(n\right)}=-V_{i-1}^n\\ R_{K,K-1}^{\left(n\right)}=-2V_{K-1}^n.\end{array}\hfill & \text{for}\hspace{0.5em} 1\le i\le K-1\hfill \end{array}$$

Using R⁽ⁿ⁾ within Equation 4 completes the specification of the numerical scheme.

Equation 4 generally relies on inverting the matrix 1 + αR⁽ⁿ⁾. When the condition |s| ≤ K/[2N_e(t_n)] applies, the matrix is invertible for all values of the constant α of Equation 5. We have used values of α as large as α = 1000 with good results. Full details of the derivation of the numerical scheme are given in Appendix A.

Interpretation of the numerical scheme

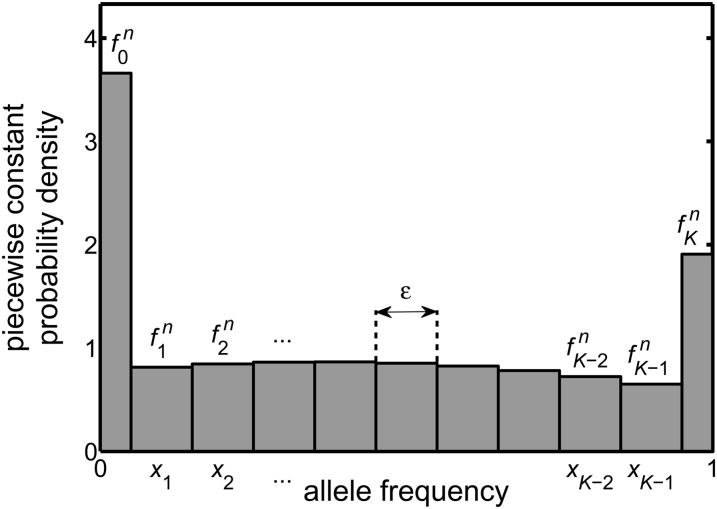
If the probability density f(x, t) were a smooth function of the frequency, x, then its behavior at a given time would be reasonably summarized by the approximate values it takes at the discrete points x_i. Potentially, however, we have a distribution that contains spikes (Dirac delta functions), i.e., singular features that change arbitrarily rapidly. For this reason, we first replace f(x, t) with a probability density that is piecewise constant. This is obtained by splitting the range of possible frequencies, 0 ≤ x ≤ 1, into a set of intervals and replacing f(x, t) in each interval by a constant that equals its average value over the interval. The numerical scheme presented here determines an approximation of these average values, at the discrete times t_n. The quantity $f_i^n$ thus denotes the approximate value of f(x, t_n), after it has been averaged over a range of x near x_i. To be specific:

1. The quantity $f_0^n$ is the approximate value of f(x, t_n), when averaged over x in the range x₀ ≡ 0 to x_1/2, i.e., over a range of width ε/2. This is equivalent to saying ${\displaystyle {\int }_0^{x_{1/2}}f\left(x,t_n\right)dx}\approx \left(\epsilon /2\right)f_0^n$.

2. For i = 1, 2, …, K − 1, the quantity $f_i^n$ represents the approximate value of f(x, t_n), when averaged over x in the range x_i−1/2 to x_i+1/2, i.e., over a range of width ε. This is equivalent to saying ${\displaystyle {\int }_{x_{i-1/2}}^{x_{i+1/2}}f\left(x,t_n\right)}dx\approx \epsilon f_i^n$.

3. The quantity $f_K^n$ represents the approximate value of f(x, t_n), when averaged over x in the range x_K−1/2 to x_K ≡ 1, i.e., over a range of width ε/2. This is equivalent to saying ${\displaystyle {\int }_{x_{K-1/2}}^{1}f\left(x,t_n\right)dx}\approx \left(\epsilon /2\right)f_K^n$.

Figure 1 illustrates the piecewise constant probability density that is determined by the $f_i^n$.

Figure 1.

The numerical approximation replaces the exact probability density of the diffusion equation at time t_n, namely f(x, t_n), by the approximate piecewise constant probability density shown in the figure. This approximate distribution is determined by discretizing, averaging, and approximating the equation obeyed by f(x, t) and then iterating the resulting equation. It leads to the quantities $f_i^n$, each of which is a numerical approximation of the average value of f(x, t_n), with the average taken over a range of x near the grid point x_i (see Interpretation of the numerical scheme). The numerical scheme is designed so that the total probability of the approximate distribution takes the value of unity for all values of the time index, n. The piecewise constant probability density in the figure is an actual output of the numerical method where the following apply. The type of selection acting is genic [hence M(x) = sx(1 − x)] and is of strength s = 0.02, the effective population size is N_e = 10, the initial frequency is 0.4, the time step is τ = 0.01, the number of control volumes is K = 10, and hence the spacing of the frequency grid is ε = 1/K = 0.1. The distribution shown has been evolved for n = 1200 time steps of the numerical scheme, i.e., 12 generations.

We can use the numerical approximation of the probability density, f(x, t), to calculate the average of a quantity such as G(X(t)), where X(t) is the random value of the allele frequency at time t. We work under the assumption that the function G(x) is continuous. The expected or average value of G(X(t)) is written as E[G(X(t)], and under the diffusion approximation $E\left[G(X\left(t\right)\right]={\displaystyle {\int }_0^{1}G\left(x\right)f\left(x,t\right)dx}$. Using the numerical approximation we take

$$E\left[G(X\left(t_n\right)\right]\approx \frac{\epsilon }{2}G\left(0\right)f_0^n+\epsilon {\displaystyle \sum _{i=1}^{K-1}G\left(x_i\right)f_i^n}+\frac{\epsilon }{2}G\left(1\right)f_K^n.$$ (7)

Note that conservation of probability means that the total probability has a value of unity $\left({\displaystyle {\int }_0^{1}f\left(x,t\right)dx}=1\right)$, independent of the value of time, t. This result, in conjunction with Equation 7, suggests that

$$C\left(t_n\right)\stackrel{\text{def}}{\equiv }\frac{\epsilon }{2}{f}_0^n+\epsilon {\displaystyle \sum _{i=1}^{K-1}{f}_i^n}+\frac{\epsilon }{2}{f}_K^n,$$

which is the numerical analog of ${\displaystyle {\int }_0^{1}f\left(x,t_n\right)dx}$, takes the value of unity, independent of the value of the time t_n. In Appendix B we show that the numerical scheme given above yields C(t_n) = 1 for all t_n.

Results

Determining the solution of the diffusion equation

We first apply the numerical scheme of Equation 4 to the fundamental problem of determining the solution of the diffusion equation at time t and frequency x, given an initial distribution at time t = 0. This solution, which is a probability density, can be used to determine the expected value of any statistic that depends on the allele frequency at time t.

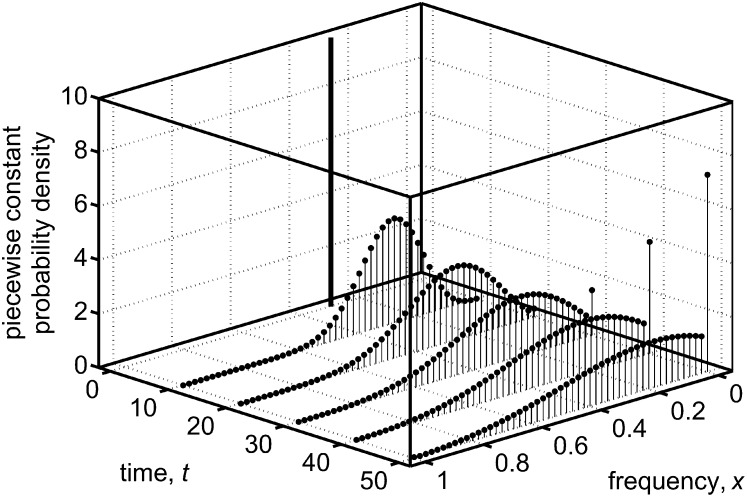
For an initial distribution that is very narrowly peaked around a single frequency, the behavior of the numerically calculated distribution is illustrated in Figure 2 indicates spike-like parts of the solution developing over time.

Figure 2.

Solutions of the diffusion equation at different times that were obtained using the numerical method of this work. The figure covers the neutral case, with no selection, mutation, or migration, and the effective population size adopted was N_e = 100. When implementing the numerical method, we arbitrarily chose a time step of τ = 0.1 and a frequency step of ε = 0.02 (i.e., K = 50). The initial time was taken as t = 0 and the initial distribution had only a single of the $f_i^0$ being nonzero, corresponding to an initial frequency of y = 0.3. Such an initial distribution is indistinguishable from the initial frequency being uniformly distributed over an interval of width ε that is centered at y = 0.3. We note that during the time interval used in the figure (50 generations), spike-like parts of the distribution appear at the frequency 0. As shown in the text, these are fully consistent with the presence of a spike (Dirac delta function) in the full diffusion solution at x = 0, representing populations that have lost the A allele. Evaluating the solution for a longer time (results not shown) also leads to a spike-like part developing at x = 1, signaling populations where fixation occurs. Exact properties of the diffusion solution are that: (i) the distribution remains normalized for all times and (ii) the expected value of the frequency at time t, given an initial distribution that is symmetric about the frequency y, obeys E[X(t)] = y (this result is particular to the neutral case). We find that properties i and ii are both obeyed by the numerical solution to an accuracy of approximately one part in 10¹⁴, which is close to the precision of the software used in the calculations (MATLAB).

Evidence of spikes in the solution

In the analysis of McKane and Waxman (2007) and Waxman (2011a), it was indicated that when the total probability is conserved, exact solutions of the diffusion equation describe populations where alleles are fixed, lost, or are segregating and that these solutions generally contain spikes. However, the numerical approach presented above is obtained by discretizing the frequency into finite-width bins. Thus it is clear that no spike, which has zero width, can be directly seen under the numerical approach. To investigate the content of the numerical approach, let us consider the last two bins on the right in Figure 1. These are bin K −1 and bin K and the corresponding values of the distribution are $f_{K-1}^n$ and $f_K^n$. These bins cover the frequency ranges x_K−3/2 to x_K−1/2 and x_K−1/2 to x_K and hence have widths of ε and ε/2, respectively. Let us write the probability of finding the frequency in these intervals, as calculated from the numerical scheme, as p_K−1(ε) and p_K(ε) respectively, then $p_{K-1}\left(\epsilon \right)=\epsilon f_{K-1}^n$ and $p_K\left(\epsilon \right)=\left(\epsilon /2\right)f_K^n$. The behavior we observe, on progressively reducing ε and hence the width of both bins, is shown in Figure 3.

Figure 3.

We show how the probabilities associated with the numerically determined probability density change when the spacing of discrete frequencies, ε, is reduced. We considered the piecewise constant probability distribution at a discrete time corresponding to t = 100 generations. To make the numerical calculation of all probabilities as comparable as possible, we set the ratio α of Equation 5, which characterizes the numerical scheme, to have the value α = 500. We then determined the time step, for a given value of ε, from τ = 2ε²α and the time index from n = 100/τ. Thus different points of the figure are associated with different ε and hence different τ and n, but the values of t and α are held fixed. The probabilities associated with the last two bins on the right in Figure 1, namely bin K − 1 and bin K, are $p_{K-1}\left(\epsilon \right)=\epsilon f_{K-1}^n$ and $p_K\left(\epsilon \right)=\left(\epsilon /2\right)f_K^n$, respectively. We observe in Figure 3 that when ε approaches 0, the probability p_K−1(ε), associated with bin K − 1, converges to a small number that, within numerical error, may be taken as zero. However the probability p_K(ε), associated with the end bin, approaches an appreciable nonzero value. This is precisely what we would expect if the end bin contains a spike (a Dirac delta function) whose entire weight is located at x = 1 and which always contributes to the probability of the bin, as long as its width is positive. By contrast, the probability associated with the adjacent bin (bin K − 1) has the behavior we would expect of a smooth probability distribution, i.e., one that does not contain a spike. The lines through the data points in the figure result from fitting a quadratic function of ε to p_K−1(ε) and a linear function of ε to p_K(ε).

For the parameters adopted for Figure 3, the behavior of the probabilities exhibited are very well described by

$$\begin{array}{c}{p}_{K-1}\left(\epsilon \right)=a\times \epsilon +b\times {\epsilon }^2\\ p_K\left(\epsilon \right)=c+d\times \epsilon ,\end{array}$$ (8)

where a, b, c, and d are independent of ε but depend on the time at which the distribution is evaluated. The significant fact is that as ε → 0 the probability p_K−1(ε) associated with bin K −1 tends toward a very small number that cannot be meaningfully distinguished from zero but the probability of the end bin, p_K(ε), tends to a constant (namely c). Since p_K−1(ε) and p_K(ε) are numerical estimates of ${\displaystyle {\int }_{x_{K-3/2}}^{x_{K-1/2}}f\left(x,t_n\right)dx}$ and ${\displaystyle {\int }_{x_{K-1/2}}^{1}f\left(x,t_n\right)}dx$, the behaviors exhibited in Figure 3 and Equation 8, as ε → 0, are fully consistent with the theoretical prediction that the distribution f(x, t) contains a spike (a Dirac delta function) whose weight is located at x = 1; so p_K(ε) obtains the entire contribution from the spike but p_K−1(ε) obtains no contribution.

The quantity c = c(t_n), which is the limiting value of p_K(ε) as ε approaches 0, is a numerical estimate of the probability that the frequency x = 1 has been reached by time t_n. It is thus an estimate of the probability of fixation by time t_n and can also be described as the time-dependent probability of fixation. In addition to this numerical result, we have Kimura’s result for the time-dependent probability of fixation, which was derived from the diffusion equation for the neutral case (Kimura 1955b). In Table 1 we give results of both methods of calculation of the time-dependent probability of fixation and find small percentage differences in a variety of different cases.

Table 1. Results for the time-dependent probability of fixation at a neutral locus when the effective population size is N_e = 100.

Time, t (generations)	Initial frequency, y	Time dependent probability of fixation				Error of the numerical result (%)
		Numerical result, c(t)	Kimura’s result	Wright–Fisher result		Relative to Kimura’s result	Relative to the Wright–Fisher result
100	0.05	2.51× 10−4	2.70 × 10−4	2.88 × 10−4		6.9	12.7
	0.10	8.81 × 10−4	9.37 × 10−4	9.95 × 10−4		6.0	11.5
200	0.05	0.0076	0.0077	0.0079		1.3	3.8
	0.10	0.0177	0.0180	0.0184		1.7	3.8
300	0.05	0.0205	0.0207	0.0209		1.0	1.9
	0.10	0.0437	0.0440	0.0444		0.7	1.6
400	0.05	0.0312	0.0313	0.0315		0.3	1.0
	0.10	0.0644	0.0645	0.0649		0.2	0.8
500	0.05	0.0384	0.0385	0.0386		0.3	0.5
	0.10	0.0780	0.0781	0.0784		0.1	0.5
600	0.05	0.0429	0.0430	0.0431		0.2	0.5
	0.10	0.0866	0.0867	0.0868		0.1	0.2

This table gives results for the time-dependent probability of fixation at a neutral locus when the effective population size is N_e = 100. It covers different values of the initial frequency, y, and different values of the time, t. The results were obtained from the numerical scheme of this work, Kimura’s expression for the time-dependent probability of fixation, which took the form of an infinite sum (Kimura 1955b), and the Wright–Fisher model. For the numerical calculations, we fixed the ratio α, Equation 5, at the value α = 500 and determined the probability associated with bin K at a sequence of progressively smaller values of the spacing of discrete frequencies, ε. Extrapolating a straight line through the data yielded the values given in the table (cf. Figure 3). The final two columns of the table contain the magnitude of the error of the numerical approach, relative to Kimura’s result and the Wright–Fisher result.

Inclusion of selection

Table 1 and Figures 2 and 3 cover the random genetic drift of alleles at a neutral locus. We can, additionally, test the accuracy with which the numerical method can deal with selection. For genic selection (where AA, AB, and BB genotype individuals have relative fitnesses of (1 + s)², 1 + s, and 1, respectively) the probability of ultimate fixation (t → ∞) from an initial frequency of y is given, under the diffusion approximation, by

$$P_{\text{fix}}\left(y\right)=\frac{1-e^{-4N_{\text{e}}sy}}{1-e^{-4N_{\text{e}}s}}$$ (9)

(Kimura 1962). In Table 2 we compare the result of the numerical method with Equation 9. Very reasonable agreement is seen in Table 2 between the numerical results and the exact diffusion results.

Table 2. Results for the probability of ultimate fixation at a locus subject to genic selection when the effective population size is N_e = 100.

4Nes	Initial frequency, y	Probability of ultimate fixation		Relative error (%)
		Numerical result, c(∞)	Kimura’s result
−1	0.05	0.0297	0.0298	0.3
	0.10	0.0608	0.0612	0.7
0	0.05	0.0496	0.0500	0.8
	0.10	0.0993	0.1000	0.7
10	0.05	0.3934	0.3935	< 0.1
	0.10	0.6321	0.6321	< 0.1

This table gives results for the probability of ultimate fixation at a locus subject to genic selection when the effective population size is N_e = 100. It covers different values of the initial frequency, y, and different values of the strength of selection, s. The results were obtained from (i) the numerical scheme of this work, in the limit of long times, and (ii) Kimura’s expression for the probability of fixation, Equation 9. The final column of the table contains the magnitude of the error of the numerical approach, relative to Kimura’s result. For the column containing the numerical results, we fixed the ratio α, Equation 5, at the value α = 500 and determined the probability associated with bin K at a sequence of progressively smaller values of the spacing of discrete frequencies, ε. Extrapolating a straight line through the data yielded the values given in the table (cf. Figure 3). This procedure leads to a value of c(t), which is the probability of fixation by time t. The value adopted for t was such that the sum c(t)+ (probability of loss by time t) was greater than 0.999. Theoretically, and in accordance with our numerically findings, this sum increases monotonically with t, hence the probability of ultimate fixation, c(∞), should differ from c(t) by <10⁻³.

Demographic change

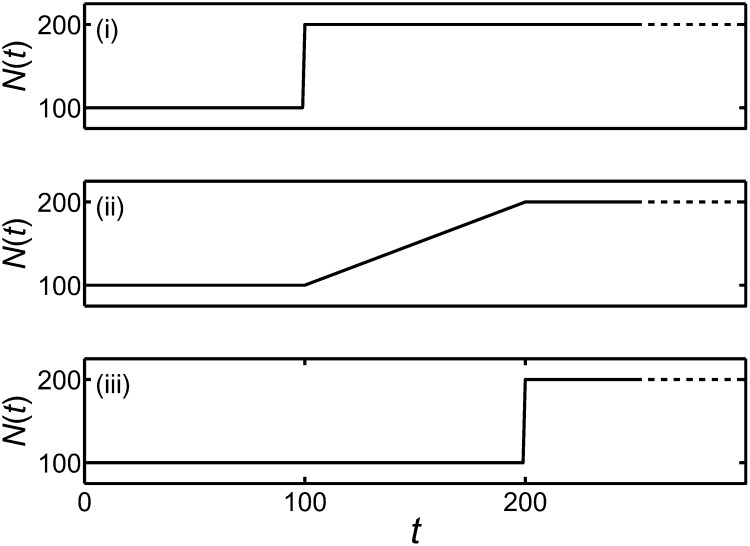
As a final test of the numerical method, let us investigate some nontrivial cases with no known explicit results. We consider the probability of ultimate fixation, under genic selection of strength s, when the population size changes over time. For the purposes of this test, we assume that the effective population size coincides with the census size and consider the population-size behaviors given in Figure 4.

Figure 4.

Different scenarios of population size change that are used in a test of the numerical method of this work. The corresponding results for the probability of ultimate fixation are given in Table 3.

With P_fix(y) the probability of ultimate fixation from an initial frequency of y at time 0, we use three different approaches to estimate this quantity:

1. A direct approach: Use the numerical scheme to determine the probability density of the frequency at very long times. The distribution then reduces to only the terminal bins having nonzero probability. The probability associated with bin K, namely the large n limit of $\left(\epsilon /2\right)f_K^n$, can be used to estimate of the probability of fixation.

2. A less direct, but efficient approach: Use a special case of a result of Waxman (2011b), which is based on the diffusion approximation. When the population size has arbitrary changes from time 0 to time T, but remains constant after time T, the probability of fixation is

   $$P_{\text{fix}}\left(y\right)={\displaystyle {\int }_0^1\frac{1-e^{-4N\left(T\right)sx}}{1-e^{-4N\left(T\right)s}}}f\left(x,T;y\right)dx.$$ (10)

   Here we have extended the notation slightly and used f(x, T; y) to denote the complete probability density of the frequency at time T, given that the initial frequency at time 0 is y. Note that f(x, T; y) is the probability density after the population size has stopped changing. Equation 10 has the advantage that it requires only the distribution at time T. Thus for populations that change according to Figure 4, it requires only the distribution of the frequency for finite values of T (namely 100 and 200 generations) and not for longer times. This considerably reduces the amount of computation compared with the direct method of approach i.

   Since Equation 10 follows from an average of Kimura’s result for the fixation probability, Equation 9, we refer to Equation 10 as the “averaged Kimura result.” In Appendix C we give further details of how the fixation probability is determined by this method.

3. Simulation: As the third and final method of estimating the fixation probability, we simulated a large number of replicate populations, which all started with an A allele frequency of y. All simulations were made within the framework of a Wright–Fisher model (Fisher 1930; Wright 1931); for more details see the caption of Table 3. The simulations were continued until all populations either fixed or lost the A allele. An estimate of P_fix(y) was then obtained from the proportion of all of the replicate populations where the A allele had fixed.

Table 3. Comparison of the effects of different scenarios of demographic change on the probability of ultimate fixation when the initial frequency is y = 0.1.

Description		Probability of Ultimate Fixation				Error of Numerical Result (%)
Scenario	s	Numerical Result	Averaged Kimura Result	Simulation Result		Relative to the Averaged Kimura Result	Relative to the Simulation Result
Reference case: Constant population size, N = 100	−0.001	0.0830	0.0830	0.0853		0.0	2.7
	0.000	0.1000	0.1000	0.1044		0.0	4.2
	0.010	0.3358	0.3358	0.3365		0.0	0.2
Reference case: Constant population size, N = 200	−0.001	0.0676	0.0680	0.0689		0.6	1.9
	0.000	0.0995	0.1000	0.0987		0.5	0.8
	0.010	0.5508	0.5509	0.5513		0.0	0.1
Figure 4 (i): Population size discontinuously increases from N = 100 to N = 200 at t = 100	−0.001	0.0747	0.0750	0.0713		0.4	4.8
	0.000	0.0996	0.1000	0.1000		0.4	0.4
	0.010	0.3841	0.3841	0.3866		0.0	0.6
Figure 4 (ii): Population size continuously increases	−0.001	0.0731	0.0734	0.0711		0.4	2.8
	0.000	0.0996	0.1000	0.0998		0.4	0.2
	0.010	0.4029	0.4030	0.4010		0.0	0.5
Figure 4 (iii): Population size discontinuously increases from N = 100 to N = 200 at t = 200	−0.001	0.0763	0.0771	0.0768		1.0	0.7
	0.000	0.0997	0.1000	0.0952		0.3	4.7
	0.010	0.3638	0.3638	0.3707		0.0	1.9

This table compares the effects of different scenarios of demographic change on the probability of ultimate fixation when the initial frequency is y = 0.1. It includes two reference cases (populations of constant size) and three cases where the population size changes over time, which are illustrated in Figure 4. For the long-time numerical calculations (column “Numerical result” in the table), we fixed the ratio α, Equation 5, at the value α = 1000 and determined the probability associated with bin K at a sequence of progressively smaller values of the spacing of discrete frequencies, ε. Extrapolating a straight line through the data yielded the values given in the table (cf. Figure 3). The values in the column “Averaged Kimura result,” were obtained using the approach in Appendix C; these values used the entire distribution of the frequency and provide some evidence of its numerical accuracy. The simulations for this table were made within the framework of a Wright–Fisher model (Fisher 1930; Wright 1931). In such a framework, selection is treated as a deterministic process, and only the process of population thinning in the life cycle, corresponding to the random sampling of individuals without regard to type (i.e., random genetic drift) is treated stochastically. The simulation results were obtained from 10⁴ replicate populations and simulations were continued until all populations either fixed or lost the A allele.

The results obtained from approaches i, ii, and iii are summarized in Table 3. The overall conclusion is that all three methods of calculation agree well with one another.

Discussion

In this work we have presented a method of numerically solving the diffusion equation for the random genetic drift of the frequency of an allele. We imposed “zero current” boundary conditions at the frequencies x = 0 and x = 1 to ensure that the total probability associated with the distribution remains independent of time. Such an approach automatically leads to the incorporation of fixation and loss into the distribution of allele frequencies—when it is possible for these to occur. In situations where fixation and loss cannot occur, such as when there is two-way mutation, the zero current boundary conditions lead to solutions of the diffusion equation that, theoretically, do not possess singular spikes. In this case, we find that under the numerical scheme, the probability associated with any bin decreases as the splitting of discrete frequencies, ε, decreases (results not shown), giving similar behavior to that of bin K − 1 in Figure 3. This behavior is consistent with there being no spike present in the solution. It thus appears that zero current boundary conditions appear to capture all aspects of the genetic drift process.

The numerical scheme introduced in this work was applied to a number of different problems, as summarized in Tables 1, 2, and 3, including the time development probability of fixation and the probability of ultimate fixation when the population size changes over time. For relatively modest population sizes we found very reasonable results. For example, in Table 3, differences between simulation results and the numerical results were of the order of a few percent. These results give us good confidence in the validity and robustness of the numerical scheme.

The mathematical aspects of this problem involve singular spikes (Dirac delta functions) in exact solutions of the diffusion equation and direct manifestations of these features are seen in the numerical solutions. These ultimately result from the boundary condition imposed on the solutions, namely there being zero probability current density at the frequencies x = 0 and x = 1. In Appendix D we discuss the possibility of other boundary conditions. It turns out that “natural” boundary conditions, which do not need to be externally imposed and, indeed, follow directly from the diffusion equation, are another possibility, and these have been implicitly adopted in the past (Kimura 1955b; Barakat and Wagener 1978; Wang and Rannala 2004). However, these boundary conditions do not result in conservation of probability or the presence of singular spikes in solutions.

The numerical approach has another aspect that we have not pursued: it gives an expression for the probability current density (see Equation A.11). Thus, unlike the Wright–Fisher model, it is possible to determine the numerical value of the probability current density at any time and at any frequency. This might have some interest in its own right.

The diffusion equation for random genetic drift has been in existence for a considerable period of time. The present work provides, we believe, the first method for directly finding a complete numerical solution (i.e., a distribution with a total probability of unity). The delay in finding such a solution may be attributable to the diffusion equation having singular features, i.e., zero width spikes, which lie beyond the features normally encountered in the literature. We have illustrated the accuracy of the numerical solution with a number of examples (see Tables 1, 2, and 3). The numerical method presented here can be easily and rapidly implemented; we believe it should have applications in the analysis and exploration of random genetic drift in genetics and related subjects, wherever the diffusion equation occurs.

Appendix A

Numerical scheme

In this appendix we provide details of the numerical scheme used in this work to solve the forward diffusion equation. The scheme has the property that it conserves probability, in the sense that it leads to a probability density whose total integrated probability has the value of unity for all times.

Finite volume scheme

With t denoting time and x denoting the allele frequency, we consider the continuity equation

$$\frac{\partial f\left(x,t\right)}{\partial t}+\frac{\partial j\left(x,t\right)}{\partial x}=0,x\in \left(0,1\right),t>0.$$ (A.1)

Here f(x, t) is the probability density and j(x, t) is the probability current density, which characterizes flow of probability. The probability current density takes the form

$$j\left(x,t\right)=-\frac{1}{4N_{\text{e}}\left(t\right)}\frac{\partial }{\partial x}\left[x\left(1-x\right)f\left(x,t\right)\right]+M\left(x,t\right)f\left(x,t\right).$$ (A.2)

Following McKane and Waxman (2007) and Waxman (2011a), we impose the boundary conditions that the probability current density vanishes at x = 0 and x = 1, for all times:

$$j\left(0,t\right)=0,\hspace{1em}\hspace{1em}j\left(1,t\right)=0.$$ (A.3)

In applications of the numerical method, an initial probability density, e.g., f(x, 0), needs to be specified for 0 ≤ x ≤ 1.

We now present a finite volume numerical scheme (Morton and Mayers 2005) for the above problem; see also Engelmann et al. (2011) for use of a finite volume scheme to numerically solve a diffusion equation in financial mathematics.

First, we discretize the frequencies, x, with a uniform grid. This is achieved using a grid spacing of ε = 1/K and the grid points x_i = i × ε, with 0 ≤ i ≤ K; we also make use of x_i+1/2 = (i + 1/2)ε. Time is uniformly discretized, with a step size of τ, and the grid points t_n = n × τ with n = 0, 1, 2,….

Let $j_i^n$ be the numerical approximation of j(x_i, t_n) and let $f_i^n$ be the numerical approximation of an average of f(x, t_n), with the average taken over x in the vicinity of x_i. To make the definition of $f_i^n$ precise and to also determine how $f_i^n$ determines $f_i^{n+1}$, we proceed as follows.

For an inner mesh point x_i (1 ≤ i ≤ K − 1), the region of x and t we consider (the control volume) is ${\mathcal{D}}_{i,n}$ = {(x, t)|x_i−1/2 ≤ x ≤ x_i+1/2, t_n ≤ t ≤ t_n+1}. Integrating Equation A.1 over ${\mathcal{D}}_{i,n}$, we obtain

$${\displaystyle {\int }_{x_{i-1/2}}^{x_{i+1/2}}\left[f\left(x,t_{n+1}\right)-f\left(x,t_n\right)\right]dx}+{\displaystyle {\int }_{t_n}^{t_{n+1}}\left[j\left(x_{i+1/2},t\right)-j\left(x_{i-1/2},t\right)\right]dt}=0.$$ (A.4)

The first term on the left-hand side of Equation A.4 is approximated as

$${\displaystyle {\int }_{x_{i-1/2}}^{x_{i+1/2}}\left[f\left(x,t_{n+1}\right)-f\left(x,t_n\right)\right]dx}\approx \left[x_{i+1/2}-x_{i-1/2}\right]\left(f_i^{n+1}-f_i^n\right)\equiv \epsilon (f_i^{n+1}-f_i^n);$$

thus for an inner mesh point, $f_i^n$ is a numerical approximation of the average $\left[1/\left(x_{i+1/2}-x_{i-1/2}\right)\right]{\displaystyle {\int }_{x_{i-1/2}}^{x_{i+1/2}}f\left(x,t_n\right)dx.}$

The second term on the left-hand side of Equation A.4 is approximated by evaluating the currents at the mean time (t_n + t_n+1)/2 = t_n+1/2 and this leads to

$${\displaystyle {\int }_{t_n}^{t_{n+1}}\left[j\left(x_{i+1/2},t\right)-j\left(x_{i-1/2},t\right)\right]dt}\approx \tau \left(j_{i+1/2}^{n+1/2}-j_{i-1/2}^{n+1/2}\right).$$ (A.5)

We then have

$$\epsilon \left(f_i^{n+1}-f_i^n\right)+\tau \left(j_{i+1/2}^{n+1/2}-j_{i-1/2}^{n+1/2}\right)=0.$$ (A.6)

For the left boundary point (x = 0), the control volume is ${\mathcal{D}}_{0,n}$ = {(x, t)|x₀ ≤ x ≤ x_1/2, t_n ≤ t ≤ t_n+1}. We integrate Equation A.1 over ${\mathcal{D}}_{0,n}$ to obtain

$${\displaystyle {\int }_{x_0}^{x_{1/2}}\left[f\left(x,t_{n+1}\right)-f\left(x,t_n\right)\right]dx}+{\displaystyle {\int }_{t_n}^{t_{n+1}}\left[j\left(x_{1/2},t\right)-j\left(x_0,t\right)\right]dt}=0;$$

imposing the boundary condition j(0, t) = 0 leads to

$$\frac{\epsilon }{2}\left(f_0^{n+1}-f_0^n\right)+\tau j_{1/2}^{n+1/2}=0,$$ (A.7)

where $f_0^n$ is a numerical approximation of the average $\left[1/\left(x_{1/2}-x_0\right)\right]{\displaystyle {\int }_{x_0}^{x_{1/2}}f\left(x,t_n\right)dx}$.

At the right boundary point (x = 1) Equation A.1 is analogously discretized,

$$\frac{\epsilon }{2}\left(f_K^{n+1}-f_K^n\right)-\tau j_{K-1/2}^{n+1/2}=0,$$ (A.8)

where $f_K^n$ is a numerical approximation of the average $\left[1/\left(x_K-x_{K-1/2}\right)\right]{\displaystyle {\int }_{x_{K-1/2}}^{x_K}f\left(x,t_n\right)dx}$.

To obtain a fully discrete scheme, we need to approximate the term $j_{i+1/2}^{n+1/2}$, for i = 0, …, K − 1. First we use

$$j_{i+1/2}^{n+1/2}\approx \frac{j_{i+1/2}^{n+1}+j_{i+1/2}^n}{2},$$ (A.9)

and then for n = 1, 2. … take

$$j_{i+1/2}^n\approx -\frac{1}{4N_{\text{e}}\left(t_n\right)}\frac{x_{i+1}\left(1-x_{i+1}\right)f_{i+1}^n-x_i\left(1-x_i\right)f_i^n}{\epsilon }+\frac{M\left(x_{i+1,}{t}_n\right)f_{i+1}^n+M\left(x_{i,}{t}_n\right)f_i^n}{2}.$$ (A.10)

We write this equation as

$$j_{i+1/2}^n=\frac{U_{i+1}^n{f}_{i+1}^n+V_i^n{f}_i^n}{\epsilon },$$ (A.11)

where we have defined

$$\begin{array}{l}{U}_i^n=-\frac{x_i\left(1-x_i\right)}{4N_e\left(t_n\right)}+\frac{\epsilon M\left(x_i,t_n\right)}{2},\\ V_i^n=\frac{x_i\left(1-x_i\right)}{4N_e\left(t_n\right)}+\frac{\epsilon M\left(x_i,t_n\right)}{2}.\end{array}$$ (A.12)

Substituting (A.9)–(A.11) into (A.6), (A.7), and (A.8), we obtain (K + 1) linear equations with respect to the (K + 1) unknowns $f_0^{n+1},\cdots ,f_K^{n+1}$, which take the form

$$\left(1+2\alpha V_0^{n+1}\right)f_0^{n+1}+2\alpha U_1^{n+1}{f}_1^{n+1}=\left(1-2\alpha V_0^n\right)f_0^n-2\alpha U_1^n{f}_1^n,$$ (A.13)

$$\begin{array}{l}\left(1+\alpha \left[V_i^{n+1}-U_i^{n+1}\right]\right)f_i^{n+1}+\alpha \left[U_{i+1}^{n+1}{f}_{i+1}^{n+1}-V_{i-1}^{n+1}{f}_{i-1}^{n+1}\right]\\ =\left(1-\alpha \left[V_i^n-U_i^n\right]\right)f_i^n-\alpha \left[U_{i+1}^n{f}_{i+1}^n-V_{i-1}^n{f}_{i-1}^n\right],\text{for} \hspace{0.5em}1\le i\le K-1\end{array}$$ (A.14)

and

$$\left(1-2\alpha U_K^{n+1}\right)f_K^{n+1}-2\alpha V_{K-1}^{n+1}{f}_{K-1}^{n+1}=\left(1+2\alpha U_K^n\right)f_K^n+2\alpha V_{K-1}^n{f}_{K-1}^n.$$ (A.15)

We can write Equations A.13, A.14, and A.15 as the matrix equation

$$\left[\mathbf{1}+\alpha R^{\left(n+1\right)}\right]f^{\left(n+1\right)}=\left[\mathbf{1}-\alpha R^{\left(n\right)}\right]f^{\left(n\right)},$$ (A.16)

where f⁽ⁿ⁾ denotes a column vector whose elements are $f_i^n$ with i = 0, 1, 2, …, K, and R⁽ⁿ⁾ is a (K + 1) × (K + 1) matrix, whose elements are $R_{i,i}^{\left(n\right)}$ with i, j = 0, 1, 2, …, K. The form of R⁽ⁿ⁾ can be read off from Equations A.13–A.15 and the only nonzero elements are $R_{0,1}^{\left(n\right)}=2U_1^n$, $R_{0,0}^{\left(n\right)}=2V_0^n$, $R_{K,K}^{\left(n\right)}=-2U_K^n$, and $R_{K,K-1}^{\left(n\right)}=-2V_{K-1}^n$, and for 1 ≤ i ≤ K − 1, $R_{i,i+1}^{\left(n\right)}=U_{i+1}^n$, $R_{i,i}^{\left(n\right)}=V_i^n-U_i^n$, and $R_{i,i-1}^{\left(n\right)}=-V_{i-1}^n$.

Matrix inverse

To determine f⁽ⁿ⁺¹⁾ in Equation A.16 in terms of f⁽ⁿ⁾, it is necessary to invert the matrix 1 + αR⁽ⁿ⁺¹⁾. Taking M(x, t) = sx(1 − x) we employ Gershgorin’s circle theorem (Demmel 1997) and it quickly follows that when

$$\left|s\right|\le \frac{K}{2N_{\text{e}}\left(t_{n+1}\right)},$$ (A.17)

the inverse of the matrix 1 + αR⁽ⁿ⁺¹⁾ exists for all values of α, with all eigenvalues of the matrix having a real part that is ≥ 1.

Appendix B: Conservation of the Total Discretized Probability

In this appendix we show that the finite volume scheme introduced in this work conserves the total probability.

It is natural to define the total discretized probability at time t_n as $C\left(t_n\right)=\left(\epsilon /2\right)f_0^n+\left(\epsilon /2\right)f_K^n+\epsilon {\displaystyle {\sum }_{i=1}^{K-1}{f}_i^n}$ (see Figure 1 and Equation 7 with G(x) = 1). We then use Equations A.6–A.8 to establish that

$$\begin{array}{c}C\left(t_{n+1}\right)-C\left(t_n\right)=\frac{\epsilon }{2}\left(f_0^{n+1}-f_0^n\right)+\frac{\epsilon }{2}\left(f_K^{n+1}-f_K^n\right)+\epsilon {\displaystyle \sum _{i=1}^{K-1}\left(f_i^{n+1}-f_i^n\right)}\\ =-\tau j_{1/2}^{n+1/2}-\tau {\displaystyle \sum _{i=1}^{K-1}\left(j_{i+1/2}^{n+1/2}-j_{i-1/2}^{n+1/2}\right)+\tau j_{K-1/2}^{n+1/2}}=0,\end{array}$$ (B.1)

i.e., C(t_n+1) = C(t_n). Thus assuming C(t₀) = 1, the numerical scheme conserves probability in the sense that C(t_n) = 1 for all t_n > 0.

Appendix C: Probability of Fixation when the Population Size Changes

In this appendix, we express the result for the probability of fixation with a varying population size in terms of the numerically determined piecewise constant distribution of frequency of the present work.

We begin with the result of Waxman (2011b) for the probability of ultimate fixation, when specialized to a population whose size changes up to time T, when subject to genic selection with constant strength s. The result can be written as

$$P_{\text{fix}}\left(y\right)=E\left[\frac{1-e^{-4N_{\text{e}}\left(T\right)sX\left(T\right)}}{1-e^{-4N_{\text{e}}\left(T\right)s}}|X\left(0\right)=y\right].$$ (C.1)

In Equation C.1, E[…|X(0) = y] denotes an average over replicate populations that all start with an initial frequency of y at time t = 0, while X(T) is the random value of the allele frequency at time T, i.e., after the population size has stopped changing. In this appendix we extend the notation slightly and use f(x, T; y) to denote the probability density of the frequency at time T, given that the frequency had the value y at time 0 [i.e., f(x, 0; y) = δ(x − y)]; then we can write Equation C.1 as

$$P_{\text{fix}}\left(y\right)={\displaystyle {\int }_0^1\frac{1-e^{-4N_{\text{e}}\left(T\right)sx}}{1-e^{-4N_{\text{e}}\left(T\right)s}}}f\left(x,T;y\right)dx\equiv \frac{1-{\displaystyle {\int }_0^1{e}^{-4N_{\text{e}}\left(T\right)sx}f\left(x,T;y\right)dx}}{1-e^{-4N_{\text{e}}\left(T\right)s}}.$$ (C.2)

Using Equation 7 of the main text, with $G\left(x\right)=e^{-4N_{\text{e}}\left(T\right)sx}$, the integral in Equation C.2 can be approximately written in terms of the numerically determined piecewise constant probability density as

$${\displaystyle {\int }_0^1{e}^{-4N_{\text{e}}\left(T\right)sx}}f\left(x,T;y\right)dx\approx \frac{\epsilon }{2}{f}_0^n+\epsilon {\displaystyle \sum _{i=1}^{K-1}{e}^{-4N_{\text{e}}\left(T\right)s{x}_i}{f}_i^n}+\frac{\epsilon }{2}{e}^{-4N_{\text{e}}\left(T\right)s}{f}_K^n.$$ (C.3)

The time index, n, is chosen so that t_n = T and implicitly, the $f_i^n$ are determined from the $f_i^0$, where of the $f_i^0$, except one, are zero. The single nonzero $f_i^0$ has the value 1/ε and corresponds to the bin containing the frequency y. Using Equation C.3 in Equation C.2 yields the required approximation for P_fix(y).

Appendix D: Boundary Conditions

In this appendix, we discuss the boundary conditions imposed on the solution of the diffusion equation.

For Equation 2 to conserve the total probability, a zero current boundary condition, Equation A.3, was imposed. It is important to ask if any other boundary condition could be imposed. To answer this, we first rewrite Equation A.1 in the standard convection–diffusion form. For simplicity, we take M(x) and N_e to be independent of time and omit the factor 1/(4N_e) in the diffusion equation. We then have

$$\frac{\partial f\left(x,t\right)}{\partial t}-\frac{\partial }{\partial x}\left(D\left(x\right)\frac{\partial }{\partial x}f\left(x,t\right)\right)+\frac{\partial }{\partial x}\left(W\left(x\right)f\left(x,t\right)\right)=0,$$ (D.1)

where the diffusion coefficient is D(x) = x(1 − x) and the convection velocity is W(x) = M(x) + (2x − 1). For the class of problems we consider in this appendix we assume that M(0) = M(1) = 0.

Note that Equation D.1 is a degenerate parabolic equation, since the diffusion coefficient D(x) vanishes at x = 0 and x = 1; i.e., it is degenerate at the boundary points. By the standard theory of degenerate partial differential equations for a well-posed problem (Oleinik and Radkevic 1973), whether a boundary condition should be imposed depends on the direction of the velocity W(x). At the left boundary, x = 0, if W(0) > 0 and then a boundary condition must be imposed; otherwise, no boundary condition is needed and the solution at the boundary will be naturally determined by the differential equation itself. At the right boundary, x = 1, if W(1) < 0 and then a boundary condition must be imposed; otherwise, no boundary condition is needed.

In the problem at hand, we have W(0) = M(0) −1 = −1, i.e., W(0) < 0, and W(1) = M(1) + 1 = 1, i.e., W(1) > 0. Hence, for a well-posed problem, no boundary conditions can be imposed and a regular solution results. However, conservation of total probability will be destroyed since direct calculation, for such a regular solution, leads to a probability current density at x = 0, which is j(0, t) = −f(0, t) and hence j(0, t) < 0. The probability current density at x = 1 is j(1, t) = f(1, t), i.e., j(1, t) > 0. This means that the total probability decreases over time. In fact, just integrating Equation A.1 with respect to x ∈ (0, 1) leads, for any t > 0, to

$$\frac{d}{dt}{\displaystyle {\int }_0^{1}f\left(x,t\right)dx}=j\left(0,t\right)-j\left(1,t\right)<0.$$ (D.2)

Returning to the zero current boundary condition, Equation A.3, if we impose these conditions, we actually impose boundary conditions on a system for which boundary conditions are unnecessary. This means that we cannot expect the problem, Equations A.1–A.3, to be well posed. This is also, apparently, the reason why singularities develop, and compelling evidence for their presence is seen in the numerical solutions. As is clear from the results in the main text, the singularities are not an artifact, but an essential and meaningful aspect of the problem.