Fiber clustering versus the parcellation-based connectome

Abstract

We compare two strategies for modeling the connections of the brain’s white matter: fiber clustering and the parcellation-based connectome. Both methods analyze diffusion magnetic resonance imaging fiber tractography to produce a quantitative description of the brain’s connections. Fiber clustering is designed to reconstruct anatomically-defined white matter tracts, while the parcellation-based white matter segmentation enables the study of the brain as a network. From the perspective of white matter segmentation, we compare and contrast the goals and methods of the parcellation-based and clustering approaches, with special focus on reviewing the field of fiber clustering. We also propose a third category of new hybrid methods that combine aspects of parcellation and clustering, for joint analysis of connection structure and anatomy or function. We conclude that these different approaches for segmentation and modeling of the white matter can advance the neuroscientific study of the brain’s connectivity in complementary ways.

1. Introduction

Computational methods that attempt to answer questions about the function and structure of the human brain are increasingly popular. Many methods aim to describe the structural connectivity or wiring diagram of the brain, where processing streams in the brain’s functional regions are interconnected by white matter fiber tracts. Diffusion magnetic resonance imaging (dMRI) [3] is the only available in-vivo mapping technique for measuring white matter connection structure. Based on dMRI data, the fiber tracts can be virtually reconstructed or traced throughout the brain using computational methods called tractography (e.g. [15,43,54,85,2,86,45,6,52]). Tractography methods trace trajectories (commonly known as “fibers”) by following probable tract orientations. Each fiber trajectory is an estimate of part of the course of some anatomical fiber tract (mm diameter), and has no direct correspondence to smaller features like individual axons (µ m diameter).

Today, two popular styles of analysis of dMRI tractography data generate a quantitative descripition of the white matter connections, a “connectome.” One style, fiber clustering, describes the connections of the white matter as clusters of fiber trajectories. The clusters give anatomical regions in which properties of the white matter structure may be measured. The second analysis style is parcellation-based and uses tractography to estimate the “structural connectivity” between pairs of parcellated cortical regions. The pairwise connectivities are encoded in a matrix that models networks in the brain [69].

These two popular styles of analysis of dMRI tractography data both perform a segmentation of the white matter, but with different goals. Fiber clustering aims to reconstruct tracts corresponding to anatomical divisions of the white matter, while parcellation-based segmentation divides tracts according to the cortical regions, or nodes, that they connect. In this article we compare these two styles of white matter modeling from the perspective of comparing segmentation methods for white matter tractography. We especially focus on reviewing the fiber clustering field, as parcellation-based connectome approaches are thoroughly covered elsewhere in this special issue.

The rest of the article is structured as follows. We first discuss the problem of white matter segmentation. Next we describe the two main categories of parcellation-based and clustering methods, followed by a third category that we propose: hybrid methods that combine aspects of both categories. Finally, we compare the parcellation and clustering approaches by discussing how their outputs correspond to the brain’s anatomical structure and function. We conclude with an assessment of the impact of the parcellation and clustering methods, demonstrating that these different approaches can advance the study of the brain’s connectivity in complementary ways.

2. The white matter segmentation problem

The ultimate goal of any white matter segmentation approach is to classify or delineate anatomical structures in an accurate and consistent way across subjects. Furthermore, because the white matter tracts carry signals between cortical regions, it is important to segment the white matter in a fashion that increases correspondence between structural and functional information. Here we restrict our interest to the segmentation of the white matter as represented by tractography, also known as the tractogram, as opposed to other representations of the white matter such as a white matter mask. Computational analysis and description of the brain’s structural connections is a lofty goal, and is made more difficult by the complex structure of the white matter anatomy.

The white matter contains three types of fiber tract: commissural, association, and projection. A commissure is a crossing site for fibers which connect similar areas [55], so commissural tracts connect related regions of the two cerebral hemispheres, coordinating their activity. Association fibers connect regions in the same hemisphere and come in various sizes: the smallest fibers are completely within the cortex, the medium ones called u-fibers or arcuate fibers connect one gyrus to the next, and the longest association bundles connect different lobes [55]. Finally, projection fibers connect the cortex and subcortical structures such as the thalamus, basal ganglia, and spinal cord. The connections to and from the cerebellum are also called projection tracts [29].

Segmentation of white matter structures is further complicated because the borders of a particular tract are often not clearly defined. For example, the structure of an association tract can be like a superhighway with entrances and exits, rather than a discrete connection from one point to another [55]. This is the case, for example, in the cingulum bundle, where it is common to see tractography trajectories that exit the central portion of the tract. Segmentation is also complicated by the fact that the tracts often cross each other. Overall, the white matter is now thought to contain crossing fibers in up to 90% of its volume [39], and its structure was recently described as a continuous grid that may be orthogonal [84,12].

Thus the white matter segmentation problem does not have one inherent, clear definition. Is the goal to detect and locate the central, more clearly defined portions of each fiber tract? Or is the goal to label the full extent of the connections of the tract, even though they may share space with and cross other tracts? Or is the goal to organize tracts based on the regions they connect, without considering their central portions?

Computational methods for white matter tract segmentation, such as the parcellation and fiber clustering methods, aim to reach one or more of these various goals. Parcellation methods are more cortex-centric: they segment the white matter according to the locations of fiber termini in or near cerebral cortex. Fiber clustering methods, on the other hand, are more white-matter-centric and group tractography trajectories according to some property or properties of the entire trajectory. Generally, clustering methods do not incorporate anatomical or functional information at fiber termini or elsewhere, and parcellation methods do not take into account the full fiber trajectory. Recently, hybrid methods have been proposed for modeling structure and function that combine aspects of both approaches.

3. White matter tract segmentation methods

We review many of the methods that have been proposed for segmenting white matter tractography. We focus on parcellation and fiber clustering, two approaches that analyze tractography from every subject of interest. It is worth noting that several important alternative approaches have been proposed that, instead of performing tractography in the individual subject, segment the white matter using a tract atlas (e.g. [89,28,34,81,88]) or a white matter skeleton [66], thus avoiding the issues of anatomic and tractographic variability of fiber tracts.

1. Parcellation-based methods

In general, parcellation-based approaches for white matter segmentation address the question of what regions a fiber trajectory may connect. These approaches take advantage of additional information in the form of a cortical parcellation into regions of interest (ROIs) that define network nodes, enabling analysis of the brain as a network [10,37,68,70]. Once the nodes are defined, segmentation of tractography is straightforward and is based simply on connections between ROIs. The question of how to define the nodes thus corresponds to our fundamental question (in this article) of how to segment the white matter. The white matter segmentation problem is crucial, as the most important methodological decision in parcellation-based connectome research is thought to be the definition of the network nodes [68].

Node definition has two main aspects which vary in the literature: choice of parcellation method and choice of parcellation size scale. A cortical parcellation from Freesurfer ([22,18]; http://surfer.nmr.mgh.harvard.edu) has been used in many approaches [11,35,38]. Other approaches employed a different cortical template [27]. Several groups have instead proposed nodes that aim to parcellate the cortex randomly or equally, for example using each voxel in the gray/white matter boundary [4], many equal-sized patches [36], equal-sized subdivisions of Freesurfer regions itephoney2009predicting, or random patches of voxels [4]. Nested multiscale parcellations were recently proposed for investigating connectivity at different size scales [11]. The ROIs from the parcellation may be limited to the cortex (e.g. [27]) or may include many subcortical structures such as the thalamus and brainstem (e.g. [11]). It is beyond the scope of this article to more fully review methods for node definition, as this is covered elsewhere in the special issue. These examples demonstrate that it is an active area of research and illustrate the importance of node definition in the parcellation-based white matter segmentation.

The white matter segmentation induced by the parcellation is almost completely dependent on the parcellation itself (additional non-trivial variables that would affect the segmentation include, for example, any dMRI distortion correction and the quality of the registration of the parcellation to the dMRI space). In general, once the parcellation is determined, giving ROIs that are nodes of the connectome graph, segmentation of tractography is straightforward and is based on the intersection of the fibers with the ROIs. Fibers are simply divided into bundles that connect each pair of ROIs. Fibers which do not intersect ROIs are excluded from the analysis. The actual segmentation that is induced in the white matter by the parcellation is usually not reported, in the sense that individual tracts or fiber trajectories are not generally visualized. However the effect of the choice of tractography algorithm on the edge weights of the connectome graph was recently studied, and the authors proposed viewing the induced segmentation in selected regions as a “connectome dissection quality control” [4].

2. Fiber clustering methods

Clustering approaches generally address the goal of detecting the central, anatomically named portions of each fiber tract, without reference to cortical regions. These approaches do not enable graphical analysis of the brain networks, but rather focus on measuring properties of the anatomy of the fiber tracts. Here we present a brief review of the field of fiber clustering.

1. Initial work in fiber clustering

Early work in tractography clustering had the goal of organizing the fibers within a single subject into fiber tracts or bundles. The problem was divided into two parts: choice of clustering method, and choice of similarity or distance metric for comparing fibers. Many approaches were proposed.

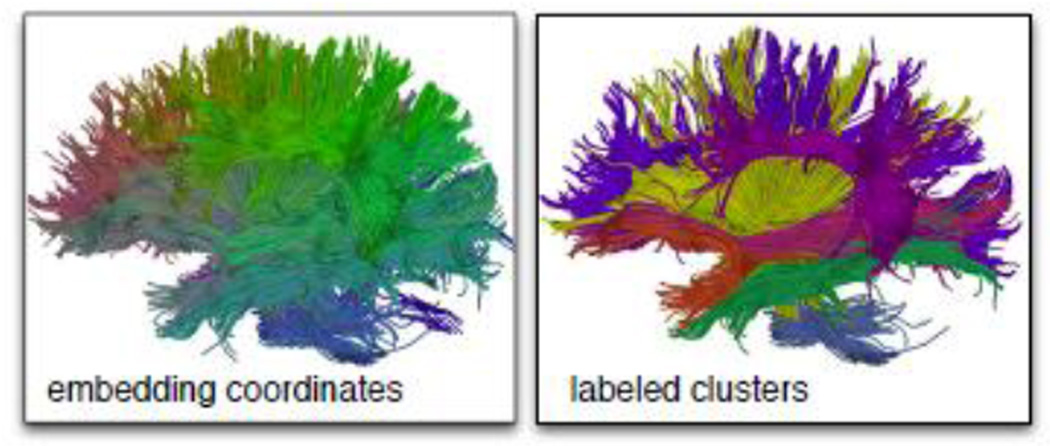
The earliest fiber clustering approach, to our knowledge, relied on a common seeding plane (where tractography was initialized) to give point correspondences across fibers, and clustered fibers according to the mean distance between corresponding points [20]. In the earliest work to analyze the full white matter, Brun et al. performed spectral embedding based on distances between fiber endpoints, then colored fibers using their embedding coordinates to give a soft visual perception of connectivity [9]. This style of spectral embedding of fibers (Figure 1) was extended by [8] and [56] to perform clustering using several other fiber distance measures.

Figure 1.

In one popular approach to fiber clustering, a spectral embedding is used to color (left) and to cluster fibers (right). These images are example results from a multiple subject clustering method for atlas creation [59].

Many different pairwise fiber distance and similarity measures were proposed and tested, for example: measures related to the Hausdorff distance [26,16], the mean suprathreshold distance between pairs of closest points [91], the Euclidean distance between covariance matrices of points on each trajectory [8], and a fiber similarity measure based on the number of times two fibers shared the same voxel [41]. Hausdorff fiber distances were extended using a measure based on dual-rooted graphs [73]. Many authors employed some type of chamfer distance, the mean distance between pairs of closest points on two fibers [16,20,26,56,91,87], and it was found to be the most effective distance in a small study where the ground truth clusters were known [53].

During this initial development period of fiber clustering, hierarchical [16,26,91] and spectral clustering [8,41,58,56] were popular approaches for analysis of the pairwise fiber distances or similarities. Most work during this period focused on single-subject clustering, however one approach performed simultaneous spectral clustering across subjects with the goal of detecting homologous structures [58], while another approach used an atlas to initialize clusters in each subject [49].

2. Advances in fiber clustering

More recent work in tractography clustering has focused on enabling white matter tract analysis for neuroscientific studies. This has included the development of algorithms for clustering data from many subjects, the creation of atlases, and the design of new models for tractography.

Clustering large multiple subject or high resolution tractography datasets has required the development of multi-step or multi-level methods to handle a high number of fibers. In fact, clustering has mainly been limited to deterministic tractography, but with these methods it may be possible to cluster a high number of streamlines from probabilistic tractography. An early approach used random sampling of input fibers and the Nystrom method to approximate computation of all pairwise fiber distances, performed clustering, then used the clusters as an atlas to label the full input data [59]. Recent approaches have employed several different strategies. [33] considered fibers at different length scales separately and combined voxel and fiber clustering. [80] proposed modeling of bundles in voxel space to avoid pairwise fiber distance computation. [74] repeatedly clustered subsets or partitions of the data then analyzed the cluster assignments to create a final clustering of all data in a scalable way. Other groups proposed clustering in individual subjects then matching clusters across subjects [91,82].

Once the large dataset size problem was addressed in some way, fiber clustering became successful for bootstrapping white matter atlas creation. In an early approach, spectral clustering was extended to create an atlas in embedding space, where each fiber was represented by a point, and data from new subjects could be segmented according to the spectral embedding of the new fibers [59]. This approach created an atlas containing fibers from many subjects. More recent clustering approaches have also been applied to create “multi-atlases” that contain information from multiple subjects, thus modeling the anatomical variability in each fiber tract (e.g. [93,33]). After clustering, several groups have incorporated expert labels into the atlas to group clusters according to anatomical naming conventions [59,31] and to select matching clusters across subjects [82]. This creates a multiscale atlas, where the smallest scale is a cluster, and larger scales group clusters into anatomical tracts. Given a tractography multi-atlas, methods have been proposed for clustering individual subjects by using the atlas for classification or as a prior [59,32,40,31]. One approach segmented even the more difficult short association bundles [32].

Other recent fiber clustering work has focused on modeling of fiber tracts. To facilitate quantitative analysis, an algorithm was proposed for finding pointwise correspondences along fiber tracts during fiber clustering [48], and this approach was extended to handle sheet-like tracts [50]. Registration and atlas creation were performed iteratively using an EM algorithm, using labeled clusters as initial input, and incorporating outlier rejection [93] ziyan2009consistency. Outlier rejection was also proposed in the partition-based method [74]. Modeling of tracts in voxel space was proposed: as Gaussian processes incorporating blurred indicator functions [82], as a distribution over voxels and orientations [80], and for efficient clustering [33]. Some approaches have included white matter atlases that were defined in voxel space as additional information for fiber clustering [51,61].

3. Hybrid approaches

It is certainly of interest to inquire what might be the relationship between a parcellation-based and a clustering-based segmentation, and if these approaches may inform each other in some useful fashion. Recently, a third category of hybrid methods has developed that combine aspects of the parcellation and clustering approaches, in that they seek to model cortical, anatomical, or functional information along with structural connection information.

The earliest hybrid approach for white matter segmentation used a gray matter atlas to generate a parcellation that was used to initialize fiber clustering [87]. This style of analysis was expanded to initialize clusters based on a white matter and gray matter parcellation, followed by a spectral embedding and clustering to separate nearby fibers [47]. Several recent hybrid approaches have been proposed in the last year. An approach incorporating anatomical ROI information clustered fibers based on an “associativity vector,” a sequence of numbers between 0 and 1 that described whether a fiber passed through or near each ROI [79]. Another approach employed fiber clusters to build a new type of multimodal atlas that recorded the spatial location of the fiber tracts relative to fMRI and anatomical landmarks; the new style of atlas was then employed to detect fiber tracts based on fMRI, in healthy subjects and surgical patients [57]. A multimodality approach to parcellation and clustering was proposed that used a novel fiber bundle model based on tangent vectors in order to identify corresponding cortical landmarks across subjects [92]. These landmarks were used to do an initial clustering of fibers [25]. The same group also proposed to cluster fibers based on the correlation of their resting state fMRI data (a measure of functional connectivity) epge2012group,ge2012resting.

Other work related to the hybrid category has performed gray matter segmentation using information from tractography. The pioneering paper segmented the thalamus according to its connectivity to the cortex [5]. More recent approaches have employed connectivity profiles to subdivide cortical regions [1,44,72,65], to parcellate the entire cortical surface [64], or to improve an existing parcellation [14].

Many of the described “hybrid” approaches model tractography and anatomic or functional information in a joint fashion, often taking advantage of multimodal input data. We note that further development of hybrid approaches to defining cortical parcellations may be of interest in the future, as a recent study concluded that for representation of fMRI networks, node definition based on structural atlases is “inappropriate” [67]. Furthermore we note that these new styles of multimodal white matter segmentation algorithm are quite varied, as it is not yet known how to best model such multimodal data. Multimodal modeling is itself an important goal for the field of neuroimage analysis [71].

4. Parcellation versus clustering

We defined the ultimate goal of any white matter segmentation approach to be: to classify or delineate anatomical structures in an accurate and consistent way across subjects. Furthermore, we stated that: because the white matter tracts carry signals between cortical regions, it is important to segment the white matter in a fashion that increases correspondence between structural and functional information. Now it is of interest to ask, how do the parcellation and clustering approaches compare at reaching these goals?

1. Comparison to anatomy

The anatomical accuracy of any method is limited by the accuracy of the underlying tractography. Studies have been performed to validate anatomical structures traced by tractography with some success, for example by comparison to tracer studies or electrocortical stimulation [21,19,46]. The clustering approaches have been developed to output structures consistent with expected neuroanatomy, and studies using expert raters have shown that clustering performs comparably to manual interactive segmentation of tractography [53,77,47,90]. On the other hand, most parcellation-based approaches ignore the course of the segmented bundles, thus their anatomical interpretation is hard to assess. However, one recent validation study proposed using submatrices of the connectome matrix to dissect several anatomical tracts, including known connections and false positive connections, giving a powerful framework for estimation of sensitivity and specificity and showing that models incorporating multiple fiber directions give superior results [4].

With regards to the consistency of the white matter segmentation across subjects, many clustering methods have been shown to produce anatomically consistent multi-atlases including data from many subjects, as well as consistent segmentations across subjects (e.g. [59,48,93,82,33,31,40]). After performing parcellation-based segmentation the correspondence across subjects is straightforward and consistent based on the parcellation, and it is standard practice to average the (highly correlated) connection matrices across subjects (e.g. [11]).

The anatomical accuracy of a segmentation method also depends on its assumptions relative to the input tractography. As the parcellation approach uses the terminal region of each fiber, it would be more sensitive to fiber endpoints. Because the clustering approach uses the full length of the trajectory, it would be expected to detect the body of the tract even if the endpoints are not accurate. In fact, clustering has been usefully employed with basic diffusion tensor data, where many or most fiber endpoints do not reach the cortex, whereas parcellation-based approaches require significantly higher quality data and tractographic reconstruction.

As a concrete example, we consider the arcuate fasciculus (AF). Classically thought to connect anterior (Broca’s) and posterior (Wernicke’s) lauguage regions, the AF is a C-shaped structure connecting temporal, parietal, and frontal lobes. In a recent study that employed single-tensor dMRI tractography, the failure of this C-shaped arc to reach Broca’s anterior language area was noted, and it was proposed that the AF instead connects to motor and premotor areas [7]. Low colocalization of the AF with posterior language regions was also observed in a study of cortical stimulation sites for language mapping in epilepsy patients, which demonstrated wide spatial dispersal of positive stimulation sites [19]. However, despite uncertainty and anatomical variability associated with its endpoints and related functional regions, the overall trajectory of the arcuate has been segmented and studied using single-tensor tractography (e.g. [13]) and fiber clustering [60,62].

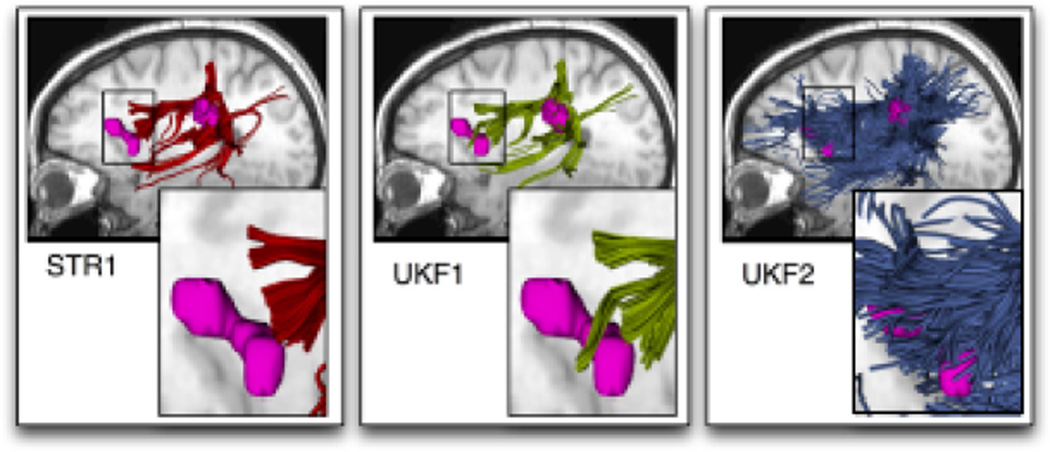
We note that in our experience, the failure of tractography to connect to Broca’s area (of interest for neuroanatomical research and surgical planning) can be ameliorated using a higher-order model (a model derived from the diffusion data that is able to represent more complicated fiber configurations than the single tensor). Our example results from one- and two-tensor dMRI models in a single healthy subject, with reference to subject-specific functional MRI (fMRI), show that fibers passing through the putative Wernicke’s area robustly reach putative Broca’s area only with the two-tensor model (Figure 2). There seems to be an effect of crossing motor fibers that is avoided using the two-tensor model. Other groups have used high angular resolution models for dMRI tractography of the AF, proposing a more nuanced view of the language pathways [23,63].

Figure 2.

Tractography in the vicinity of language activations illustrates sensitivity to diffusion modeling and tractography methods. Three methods were applied throughout the entire brain of a healthy subject: single-tensor streamline (STR1 in red, left), single-tensor unscented Kalman filter (UKF1 in yellow, middle), and two-tensor unscented Kalman filter (UKF2 in blue, right). The UKF methods fit the model to the diffusion data while tracking, taking advantage of prior trajectory information for tracking through areas of fiber crossing [52]. Top images: All fibers passing through putative Wernicke’s area (defined using subject-specific fMRI, rightmost pink blob) were selected for display. Bottom images: The zoomed region shows the putative Broca’s area (anterior language activation) from subject-specific fMRI (pink). In this subject, STR1 does not intersect the anterior language activation and exactly 1 fiber trajectory from UKF1 intersects, however UKF2 traces many fibers connecting both activations (and many other regions). The middle region of the arcuate fasciculus (not visible at right) was relatively similar across methods, despite the difference in anterior endpoints.

This example of one crucial tract illustrates the importance of choosing a tractography algorithm and/or modeling method that accounts for crossing fibers [42,4], as well as the inherent uncertainty in mapping of thebrain’s connections via neuroimaging, especially the difficulty of correlating structure with function. Furthermore, it illustrates that methods which segment fiber tracts based on their endpoints, where the diffusion anisotropy is generally lowest, have the potential to be more sensitive to possible anatomical errors in tractography. These errors would still be present in a clustering approach, but would be expected to have lower impact on the final result. Recent work performing quality control analysis using connectome dissection of individual anatomical structures appears to be very valuable in examining any possible issues with the underlying tractography [4]. In fact, such assessment of the connections in matrix form is well-suited to quantify the important problem of false negative connections (tracts erroneously not traced) as these are effectively invisible in a clustering approach.

2. Comparison to function

The parcellation-based methods are designed to enable comparison of structural and functional connectivity over the entire cortex. Comparison of the connection matrix from dMRI to that from functional connectivity derived from resting state fMRI indicates that structural and functional connectivity are positively correlated, but there is functional connectivity in regions with little structural connectivity [38,17].

It is not clear that there is one best substrate or anatomical model for comparison of structure and function. Tractography itself has been compared to function in many ways, including somewhat successful clinical validation using electrocortical stimulation (e.g. [19,46]) and comparison of fibers to functionally connected regions from fMRI [30]. Trajectory-based clustering may correspond to function in the sense that, like a parcellation, if the size scale of clustering is suitable, the function is not expected to change drastically within a cluster. Specific fiber tracts segmented via clustering have been compared to measures of function. For example, AF lateralization measured from fiber clustering was related to fMRI lateralization [62], and fractional anisotropy of regions of the corpus callosum, segmented via clustering, was inversely related to signal propagation induced by transcranial magnetic stimulation [75].

These example studies comparing connection matrices and fiber clusters to different measures of function illustrate that the parcellation-based and clustering methods output complementary descriptions of the connectome, and that each model (connection matrix and fiber clusters) can be highly useful in studies of the brain’s structure and function.

5. Conclusion

We have compared two methods for segmenting the white matter of the brain that have been extensively developed within the past decade, the fiber clustering approach and the parcellation-based approach. Each approach produces a compact summary of the brain’s connection structure, in the form of a connection matrix for analysis of the brain as a network, or as fiber clusters for analysis of the white matter anatomy. Both the parcellation and clustering approaches have employed strategies for analysis of large amounts of data, and for multiscale representations of white matter structure. The clustering approach considers the full course of each fiber trajectory and is quite robust in that the cores of large bundles can be segmented from any type of streamline tractography, enabling quantitative analysis of white matter tracts. The parcellation-based approach requires high-quality high angular resolution data and tractography, and enables sophisticated analyses of the entire brain as a network and comparison to cortical functional measurements. A third category of hybrid approaches under development includes new methods that aim to jointly model neural connections and additional multimodal data such as fMRI.

Each approach has had a neuroscientific impact. For example, the fiber clustering approach has been employed to study schizophrenia [76,83], aging [78], heritability of white matter tract shapes [39], brain asymmetry [60,62], and the role of the corpus callosum in neural signaling [75]. The graph-theoretic brain network analysis enabled by the parcellation-based approach has inspired wide adoption of this technique, and many recent articles review its important impact [17,10,37,68,70]. We conclude that these approaches to white matter segmentation and analysis are complementary and powerful, and that both methods enable the study of the connections of the human brain in health and disease.

Highlights.

We review the fiber clustering field.

We compare clustering to the parcellation-based approaches.

We show that the approaches are complementary and have different strengths.