Abstract
Background
The intention-to-treat (ITT) comparison is the primary, if not the only, analytic approach of many randomized clinical trials (RCTs).
Purpose
To review the shortcomings of ITT analyses, and of “as treated” and “per protocol” analyses as commonly implemented, with an emphasis on problems that are especially relevant for comparative effectiveness research.
Methods and Results
In placebo-controlled RCTs, ITT analyses underestimate the treatment effect, and are therefore non-conservative for both safety trials and non-inferiority trials. In RCTs with an active comparator, ITT estimates can overestimate a treatment’s effect in the presence of differential adherence. In either case, there is no guarantee that an ITT analysis estimates the clinical effectiveness of treatment. Inverse probability (IP) weighting, g-estimation, and instrumental variable (IV) estimation can reduce the bias introduced by non-adherence and loss to follow-up in “as treated” and “per protocol” analyses.
Limitations
IP weighting and g-estimation require untestable assumptions and time-varying data on confounders and adherence. IV estimation requires a dose-response model and time-varying data on adherence.
Conclusions
We recommend that all RCTs with substantial lack of adherence or loss to follow-up are analyzed using different methods. These include an ITT analysis to estimate the effect of assigned treatment, and “as treated” and “per protocol” analyses to estimate the effect of treatment after appropriate adjustment via IP weighting or g-estimation.
Keywords: randomized clinical trials, intention to treat analysis, as treated analysis, per protocol analysis, effectiveness, safety
1. Introduction
Randomized clinical trials (RCTs) are widely viewed as a key tool for comparative effectiveness research [1], and the intention-to-treat (ITT) comparison has long been regarded as the preferred analytic approach for many RCTs [2].
Indeed the ITT, or “as randomized,” analysis has two crucial advantages over other common alternatives—for example, an “as treated” analysis. First, in double-blind RCTs, an ITT comparison provides a valid statistical test of the hypothesis of null effect of treatment. [3, 4] Second, in placebo-controlled trials, an ITT comparison is regarded as conservative because it underestimates the treatment effect when participants do not fully adhere to their assigned treatment.
Yet excessive reliance on the ITT approach is problematic, as has been argued by others before us [5]. In this paper we review the problems of ITT comparisons with an emphasis on those are especially relevant for comparative effectiveness research. We also review the shortcomings of “as treated” and “per protocol” analyses as commonly implemented in RCTs, and recommend the routine use of analytic approaches that address some of those shortcomings. Let us start by defining two types of causal effects that can be estimated in RCTs.
2. The effect of assigned treatment versus the effect of treatment
Consider a double-blind clinical trial in which participants are randomly assigned to either active treatment (Z=1) or placebo (Z=0) and are then followed for 5 years or until they die (Y=1 if they die within 5 years, Y=0 otherwise). An ITT analysis would compare the 5-year risk of death in those assigned to treatment with the 5-year risk of death in those assigned to placebo. An ITT comparison unbiasedly estimates the average causal effect of treatment assignment Z on the outcome Y. For brevity, we will refer to this as the effect of assigned treatment.
Trial participants may not adhere to, or comply with, the assigned treatment Z. Some of those assigned to placebo may decide to take treatment, and some of those assigned to active treatment may decide not to take it. We use A to refer to the treatment actually received. Thus, regardless of their assigned treatment Z, some subjects will take treatment (A=1) and others will not take it (A=0). The use of ITT comparisons is sometimes criticized when not all trial participants adhere to their assigned treatment Z, i.e., when Z is not equal to A for every trial participant. For example, consider two RCTs: in the first trial, half of the participants in the Z=1 group decide not to take treatment; in the second trial, all participants assigned to Z=1 decide to take the treatment. An ITT comparison will correctly estimate the effect of assigned treatment Z in both trials, but the effects will be different even if the two trials are otherwise identical. The direction and magnitude of the effect of assigned treatment depends on the adherence pattern.
Now suppose that, in each of the two trials with different adherence, we could estimate the effect that would have been observed if all participants had fully adhered to their treatment assignment. We will refer to such effect as the average causal effect of treatment A on the outcome Y or, for brevity, the effect of treatment. The effect of treatment A appears to be an attractive choice to summarize the findings of RCTs with substantial nonadherence because it will be the same in two trials that differ only in their adherence pattern.
However, estimating the magnitude of the effect of treatment A without bias requires assumptions grounded on expert knowledge (see Sections 4 and 5). No matter how sophisticated the statistical analysis, the estimate of the effect of A will be biased if one makes incorrect assumptions.
3. The effect of assigned treatment may be misleading
An ITT comparison is simple and therefore very attractive.[4] It bypasses the need for assumptions regarding adherence and dose-response by focusing on estimating the effect of assigned treatment Z rather than the effect of treatment A. However, there is a price to pay for this simplicity, as reviewed in this section.
We start by considering placebo-controlled double-blind RCTs. It is well known that if treatment A has a null effect on the outcome, then both the effect of assigned treatment Z and the effect of treatment A will be null. This is a key advantage of the ITT analysis: it correctly estimates the effect of treatment A under the null, regardless of the adherence pattern. It is also well known that if treatment A has a non-null effect (that is, either increases or decreases the risk of the outcome) and some participants do not adhere to their assigned treatment, then the effect of assigned treatment Z will be closer to the null that the actual effect of treatment A [3]. This bias towards the null is due to contamination of the treatment groups: some subjects assigned to treatment (Z=1) may not take it (A=0) whereas some subjects assigned to placebo (Z=0) may find a way to take treatment (A=1). As long as the proportion of patients who end up taking treatment (A=1) is greater in the group assigned to treatment (Z=1) than in the group assigned to placebo (Z=0), the effect of assigned treatment Z will be in between the effect of treatment A and the null value.
The practical effect of this bias varies depending on the goal of the trial. Some placebo-controlled RCTs are designed to quantify a treatment’s beneficial effects—for example, a trial to determine whether sildenafil reduces the risk of erectile dysfunction. An ITT analysis of these trials is said to be “conservative” because the effect of assigned treatment Z is biased towards the null. That is, if an ITT analysis finds a beneficial effect for treatment assignment Z, then the true beneficial effect of treatment A must be even greater. The makers of treatment A have a great incentive to design a high-quality study with high levels of adherence. Otherwise a small beneficial effect of treatment might be missed by the ITT analysis.
Other trials are designed to quantify a treatment’s harmful effects—for example, a trial to determine whether sildenafil increases the risk of cardiovascular disease. An ITT analysis of these trials is anti-conservative precisely because the effect of assigned treatment Z is biased towards the null. That is, if an ITT analysis fails to find a toxic effect, there is no guarantee that treatment A is safe. A trial designed to quantify harm and whose protocol foresees only an ITT analysis could be referred to as a “randomized cynical trial.”
Now let us consider double-blind RCTs that compare two active treatments. These trials are often designed to show that a new treatment (A=1) is not inferior to a reference treatment (A=0) in terms of either benefits or harms. An example of a non-inferiority trial would be one that compares the reduction in blood glucose between a new inhaled insulin and regular injectable insulin. The protocol of the trial would specify a non-inferiority margin, that is, the maximum average difference in blood glucose that is considered equivalent (e.g., 10 mg/dL). Using an ITT comparison, the new insulin (A=1) will be declared not inferior to classical insulin (A=0) if the average reduction in blood glucose in the group assigned to the new treatment (Z=1) is within 10 mg/dL of the average reduction in blood glucose in the group assigned to the reference treatment (Z=0) plus/minus random variability. Such ITT analysis may be misleading in the presence of imperfect adherence. To see this, consider the following scenario.
Scenario 1. The new treatment A=1 is actually inferior to the reference treatment A=0, e.g., the average reduction in blood glucose is 10 mg/dL under treatment A=1 and 22 mg/dL under treatment A=0. The type and magnitude of adherence is equal in the two groups, e.g. 30% of subjects in each group decided not to take insulin. As a result, the average reduction is, say, 7 mg/dL in the group assigned to the new treatment (Z=1) and 15 mg/dL in the group assigned to the reference treatment (Z=0). An ITT analysis, which is biased towards the null in this scenario, may incorrectly suggest that the new treatment A=1 is not inferior to the reference treatment A=0.
Other double-blind RCTs with an active comparator are designed to show that a new treatment (A=1) is superior to the reference treatment (A=0) in terms of either benefits or harms. An example of a superiority trial would be one that compares the risk of heart disease between two antiretroviral regimes. Using an ITT comparison, the new regimen (A=1) will be declared superior to the reference regime (A=0) if the heart disease risk is lower in the group assigned to the new regime (Z=1) than in the group assigned to the reference regime (Z=0) plus/minus random variability. Again such ITT analysis may be misleading in the presence of imperfect adherence. Consider the following scenario.
Scenario 2. The new treatment A=1 is actually equivalent to the reference treatment A=0, e.g., the five-year risk of heart disease is 3% under either treatment A=1 or treatment A=0, and the risk in the absence of either treatment is 1%. The type or magnitude of adherence differs between the two groups, e.g., 50% of subjects assigned to the new regime and 10% of those assigned to the reference regime decided not to take their treatment because of minor side effects. As a result, the risk is, say, 2% in the group assigned to the new regime (Z=1) and 2.8% in the group assigned to the reference regime (Z=0). An ITT analysis, which is biased away from the null in this scenario, may incorrectly suggest that treatment A=1 is superior to treatment A=0.
An ITT analysis of RCTs with an active comparator may result in effect estimates that are biased towards (Scenario 1) or away from (Scenario 2) the null. In other words, the magnitude of the effect of assigned treatment Z may be greater than or less than the effect of treatment A. The direction of the bias depends on the proportion of subjects that do not adhere to treatment in each group, and on the reasons for non-adherence.
Yet a common justification for ITT comparisons is the following: Adherence is not perfect in clinical practice. Therefore clinicians may be more interested in consistently estimating the effect of assigned treatment Z, which already incorporates the impact of nonadherence, than the effect of treatment A in the absence of nonadherence. That is, the effect of assigned treatment Z reflects a treatment’s clinical effectiveness and therefore should be privileged over the effect of treatment A. In the next section we summarize the reasons why this is not necessarily true.
4. The effect of assigned treatment is not the same as the effectiveness of treatment
Effectiveness is usually defined as “how well a treatment works in everyday practice,” and efficacy as “how well a treatment works under perfect adherence and highly controlled conditions.” Thus the effect of assigned treatment Z in post-approval settings is often equated with effectiveness, whereas the effect of treatment Z in pre-approval settings (which is close to the effect of A when adherence is high) is often equated with efficacy. There is, however, no guarantee that the effect of assigned treatment Z matches the treatment’s effectiveness in routine medical practice. A discrepancy may arise for multiple reasons, including differences in patient characteristics, monitoring, or blinding, as we now briefly review.
The eligibility criteria for participants in RCTs are shaped by methodologic and ethical considerations. To maximize adherence to the protocol, many RCTs exclude individuals with severe disease, comorbidities or polypharmacy. To minimize risks to vulnerable populations, many RCTs exclude pregnant women, children, or institutionalized populations. As a consequence, the characteristics of participants in an RCT may be, on average, different from those of the individuals who will receive the treatment in clinical practice. If the effect of the treatment under study varies by those characteristics (e.g., treatment is more effective for those using certain concomitant treatments) then the effect of assigned treatment Z in the trial will differ from the treatment’s effectiveness in clinical practice.
Patients in RCTs are often more intensely monitored than patients in clinical practice. This greater intensity of monitoring may lead to earlier detection of problems (i.e., toxicity, inadequate dosing) in RCTs compared with clinical practice. Thus a treatment’s effectiveness may be greater in RCTs because the earlier detection of problems results in more timely therapeutic modifications, including modifications in treatment dosing, switching to less toxic treatments, or addition of concomitant treatments.
Blinding is a useful approach to prevent bias from differential ascertainment of the outcome [6]. There is, however, an inherent contradiction in conducting a double-blind study while arguing that the goal of the study is estimating the effectiveness in routine medical practice. In real life, both patients and doctors are aware of the assigned treatment. A true effectiveness measure should incorporate the effects of assignment awareness (e.g., behavioral changes) that are eliminated in ITT comparisons of double-blind RCTs.
Some RCTs, commonly referred to as pragmatic trials [7–9], are specifically designed to guide decisions in clinical practice. Compared with highly controlled trials, pragmatic trials include less selected participants and are conducted under more realistic conditions, which may result in lower adherence to the assigned treatment. It is often argued that an ITT analysis of pragmatic trials is particularly appropriate to measure the treatment’s effectiveness, and thus that pragmatic trials are the best design for comparative effectiveness research. However, this argument raises at least two concerns.
First, the effect of assigned treatment Z is influenced by the adherence patterns observed in the trial, regardless of whether the trial is a pragmatic one. Compared with clinical practice, trial participants may have a greater adherence because they are closely monitored (see above), or simply because they are the selected group who received informed consent and accepted to participate. Patients outside the trial may have a greater adherence after they learn, perhaps based on the trial findings, that treatment is beneficial. Therefore the effect of assigned treatment estimated by an ITT analysis may under- or overestimate the effectiveness of the treatment.
Second, the effect of assigned treatment Z is inadequate for patients who are interested in initiating and fully adhering to a treatment A that has been shown to be efficacious in previous RCTs. In order to make the best informed decision, these patients would like to know the effect of treatment A rather than an effect of assigned treatment contaminated by others patients’ nonadherence [5]. For example, to decide whether to use certain contraception method, a couple may want to know the failure rate if they use the method as indicated, rather than the failure rate in a population that included a substantial proportion of non-adherers. Therefore the effect of assigned treatment Z may be an insufficient summary measure of the trial data, even if it actually measures the treatment’s effectiveness.
In summary, the effect of assigned treatment Z—estimated via an ITT comparison—may not be a valid measure of the effectiveness of treatment A in clinical practice. And even if it were, effectiveness is not always the most interesting effect measure. These considerations, together with the inappropriateness of ITT comparisons for safety and non-inferiority trials, make it necessary to expand the reporting of results from randomized clinical trials beyond ITT analyses. The next section reviews other analytic approaches for data from RCTs.
5. Conventional “as treated” and “per protocol” analyses
Two common attempts to estimate the effect of treatment A are “as treated” and “per protocol” comparisons. Neither is generally valid.
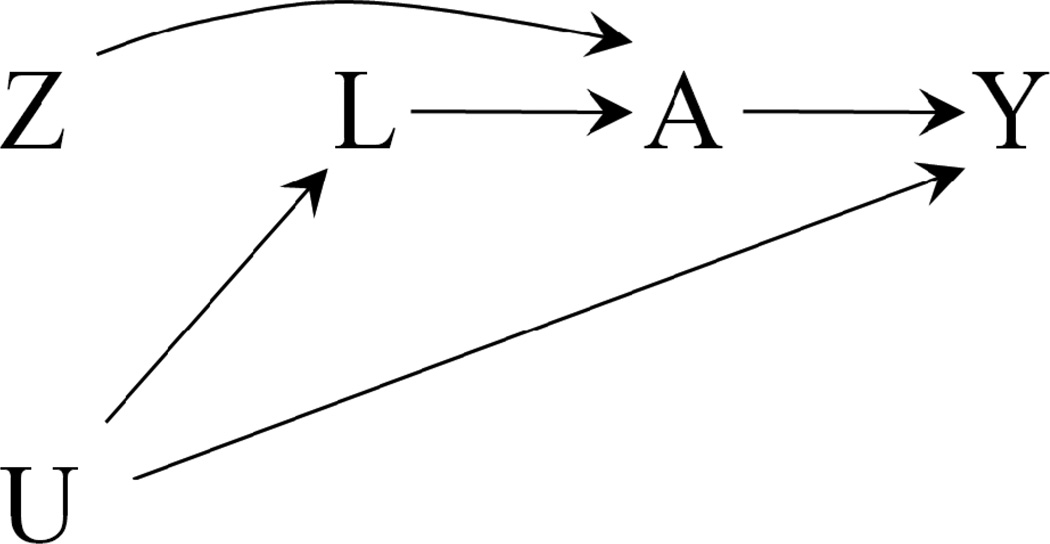
An “as treated” analysis classifies RCT participants according to the treatment that they took (either A=1 or A=0) rather than according to the treatment that they were assigned to (either Z=1 or Z=0). Then an “as treated” analysis compares the risk (or the mean) of the outcome Y among those who took treatment (A=1) with that among those who did not take treatment (A=0), regardless of their treatment assignment Z. That is, an “as treated” comparison ignores that the data come from an RCT and rather treats them as coming from an observational study. As a result, an “as treated” comparison will be confounded if the reasons that moved participants to take treatment were associated with prognostic factors. The causal diagram in Figure 1 represents the confounding as a noncausal association between A and Y when there exist prognostic factors L that also affect the decision to take treatment A (U is an unmeasured common cause of L and Y). Confounding arises in an “as treated” analysis when not all prognostic factors L are appropriately measured and adjusted for.
Figure 1.
Simplified causal diagram for an RCT with assigned treatment Z, received treatment A, and outcome Y. U represents the unmeasured common causes of A and Y. An “as treated” analysis of the A-Y association will be confounded unless all prognostic factors L are adjusted for.
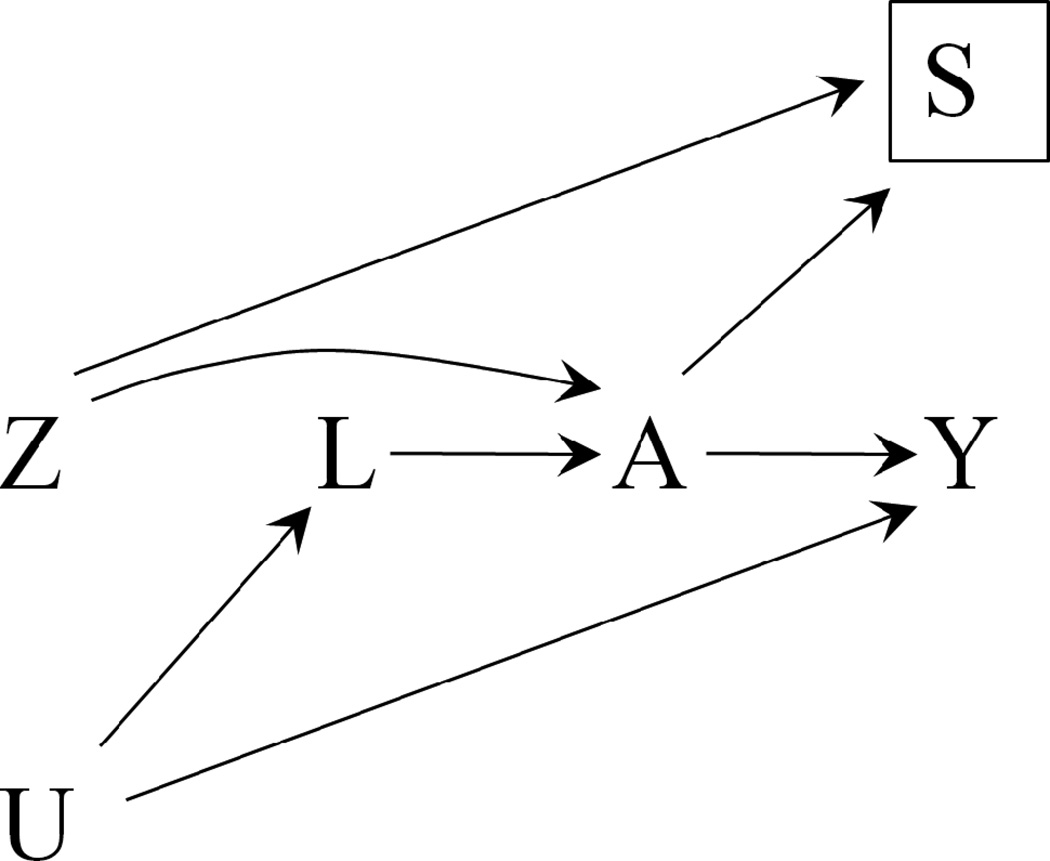
A “per protocol” analysis—also referred to as an “on treatment” analysis— only includes individuals who adhered to the clinical trial instructions as specified in the study protocol. The subset of trial participants included in a “per protocol” analysis, referred to as the per protocol population, includes only participants with A equal to Z: those who were assigned to treatment (Z=1) and took it (A=1), and those who were not assigned to treatment (Z=0) and did not take it (A=0). A “per protocol” analysis compares the risk (or the mean) of the outcome Y among those who were assigned to treatment (Z=1) with that among those who were not assigned to treatment (Z=0) in the per protocol population. This contrast will be affected by selection bias [10] if the reasons that moved participants to adhere to their assigned treatment were associated with prognostic factors L (via A). The causal diagram in Figure 2 includes S as an indicator of selection into the “per protocol” population. The selection indicator S is fully determined by the values of Z and A, i.e., S=1 when A=Z, and S=0 otherwise. The selection bias is a noncausal association between Z and Y that arises when the analysis is restricted to the “per protocol” population (S=1) and not all prognostic factors L are appropriately measured and adjusted for.
Figure 2.
Simplified causal diagram for an RCT with assigned treatment Z, received treatment A, and outcome Y. U represents the unmeasured common causes of A and Y, and S an indicator for selection into the “per protocol” population. The Z-Y association in the “per protocol” population (a restriction represented by the box around S), will be affected by selection bias unless all prognostic factors L are adjusted for.
As an example of biased “as treated” and “per protocol” estimates of the effect of treatment A, consider the following scenario.
Scenario 3. An RCT assigns men to either colonoscopy (Z=1) or no colonoscopy (Z=0). Suppose that undergoing a colonoscopy (A=1) does not affect the 10-year risk of death from colon cancer (Y) compared with not undergoing a colonoscopy (A=0), i.e.., the effect of treatment A is null. Further suppose that, among men assigned to Z=1, those with family history of colon cancer (L=1) are more likely to adhere to their assigned treatment and undergo the colonoscopy (A=1).
Even though A has a null effect, an “as treated” analysis will find that men undergoing colonoscopy (A=1) are more likely to die from colon cancer because they include a greater proportion of men with a predisposition to colon cancer than the others (A=0). This is the situation depicted in Figure 1. Similarly, a “per protocol” analysis will find a greater risk of death from colon cancer in the group Z=1 than in the group Z=0 because the per protocol restriction A=Z overloads the group assigned to colonoscopy with men with a family history of colon cancer. This is the situation depicted in Figure 2.
The confounding bias in the “as treated” analysis and the selection bias in the “per protocol” analysis can go in either direction—for example, suppose that L represents healthy childhood diet rather than family history of colon cancer. In general the direction of the bias is hard to predict because it is possible that the proportions of people with a family history, healthy diet, and any other prognostic factor will vary between the groups A=1 and A=0 conditional on Z.
In summary, “as treated” and “per protocol” analyses transform RCTs into observational studies for all practical purposes. The estimates from these analyses can only be interpreted as the effect of treatment A if the analysis is appropriately adjusted for the confounders L. If the intended analysis of the RCT is “as treated” or “per protocol”, then the protocol of the trial should describe the potential confounders and how they will be measured, just like the protocol of an observational study would do.
6. More general “as treated” and “per protocol” analyses to estimate the effect of treatment
So far we have made the simplifying assumption that adherence is all or nothing. But in reality RCT participants may adhere to their assigned treatment intermittently, e.g., they may take their assigned treatment for 2 months, discontinue it for the next 3 months, and then resume it until the end of the study. Or subjects may take treatment constantly but at a lower dose than assigned, e.g., by taking only one pill per day when they should take two. That is, treatment A is generally a time-varying variable—each day you may take it or not take it—rather than a time-fixed variable—you either always take it or never take it during the follow-up.
An “as treated” analysis with a time-varying treatment A usually needs to include some sort of dose-response model. A “per protocol” analysis with a time-varying treatment A includes all RCT participants but censors them if/when they deviate from their assigned treatment. The censoring usually occurs at a fixed time after nonadherence, say, 6 months. The per protocol population in this variation refers to the adherent person-time rather than to the adherent persons.
Because previous sections were only concerned with introducing some basic problems of ITT, “as treated”, and “per protocol” analyses, it may have been acceptable to consider A as a time-fixed variable. However, this simplification may be unrealistic and misleading in practice. When treatment A is truly time-varying (i) the effect of treatment needs to be redefined, and (ii) appropriate adjustment for the measured confounders L cannot generally be achieved by using conventional methods such as stratification, regression, or matching.
The definition of the average causal effect of a time-fixed treatment involves the contrast between two clinical regimes. For example, we defined the causal effect of a time-fixed treatment as a contrast between the average outcome that would be observed if all participants took treatment A=1 versus treatment A=0. The two regimes are taking treatment A=1 and taking treatment A=0. The definition of the causal effect of a time-varying treatment also involves a contrast between two clinical regimes. For example, we can define the causal effect of a time-varying treatment as a contrast between the average outcome that would be observed if all participants had continuous treatment with A=1 versus continuous treatment with A=0 during the entire follow-up. We sometimes refer to this causal effect as the effect of continuous treatment.
When the treatment is time-varying, so are the confounders. For example, the probability of taking antiretroviral therapy increases in the presence of symptoms of HIV disease. Both therapy and confounders evolve together during the follow-up. When the time-varying confounders are affected by previous treatment—for example, antiretroviral therapy use reduces the frequency of symptoms—conventional methods cannot appropriately adjust for the measured confounders [10]. Rather, inverse probability (IP) weighting or g-estimation are generally needed for confounding adjustment in “as treated” and “per protocol” analyses involving time-varying treatments [11–13].
Both IP weighting and g-estimation require that time-varying confounders and time-varying treatments are measured during the entire follow-up. Thus, if planning to use these adjustment methods, the protocol of the trial should describe the potential confounders and how they will be measured. Unfortunately, like in any observational study, there is no guarantee that all confounders will be identified and correctly measured, which may result in biased estimates of the effect of continuous treatment in “as treated” and “per protocol” analyses involving time-varying treatments.
An alternative adjustment method is instrumental variable (IV) estimation, a particular form of g-estimation that does not require measurement of any confounders [14–17]. In double-blind RCTs, IV estimation eliminates confounding for the effect of continuous treatment A by exploiting the fact that the initial treatment assignment Z was random. Thus if the time-varying treatment A is measured and a correctly specified structural model used, IV estimation adjusts for confounding without measuring, or even knowing, the confounders.
A detailed description of IP weighting, g-estimation, and IV estimation is beyond the scope of this paper. Toh and Hernán review these methods for RCTs [18]. IP weighting and g-estimation can also be used to estimate the effect of treatment regimes that may be more clinically relevant than the effect of continuous treatment [19, 20].
7. Discussion
An ITT analysis of RCTs is appealing for the same reason it may be appalling: simplicity. As described above, ITT estimates may be inadequate for the assessment of comparative effectiveness or safety. In the presence of nonadherence the ITT effect is a biased estimate of a treatment’s effects such as the effect of continuous treatment. This bias can be corrected in an appropriately adjusted “as treated” analysis via IP weighting, g-estimation, or IV estimation. However, IP weighting and g-estimation require untestable assumptions similar to those made for causal inference from observational data. IV estimation requires a dose-response model and its validity is questionable for non-blinded RCTs.
The ITT approach is also problematic if a large proportion of participants drop out or are otherwise lost to follow-up, or if the outcomes are incompletely ascertained among those completing the study. In these studies, an ITT comparison cannot be conducted because the value of the outcome is missing for some individuals. To circumvent this problem, the ITT analysis is often replaced by a pseudo-ITT analysis that is restricted to subjects with complete data or in which the last observation is carried forward. These pseudo-ITT analyses may be affected by selection bias in either direction. Adjusting for this bias is possible via IP weighting if information on the time-varying determinants of loss to follow-up is available, but again the validity of the adjustment relies on untestable assumptions about the unmeasured variables [18].
RCTs with long follow-up periods, as expected in many comparative effectiveness research settings, are especially susceptible to bias due to nonadherence and loss to follow-up. As these problems accumulate over time, the RCT starts to resemble a prospective observational study, and the ITT analysis yields an increasingly biased estimate of the effect of continuous treatment. Consider, for example, a Women’s Health Initiative randomized trial that assigned postmenopausal women to either estrogen plus progestin hormone therapy or placebo [21]. About 40% of women had stopped taking at least 80% of their assigned treatment by the 6th year of follow-up. The ITT hazard ratio of breast cancer was 1.25 (95% CI: 1.01, 1.54) for hormone therapy vs. placebo. The IP weighted hazard ratio of breast cancer was 1.68 (1.24, 2.28) for 8 years of continuous hormone therapy vs. no hormone therapy [22]. These findings suggest that the effect of continuous treatment was more than two-fold greater than the effect of assigned treatment. Of course, neither of these estimates reflects the long-term effect of hormone therapy in clinical practice (e.g., the adherence to hormone therapy was much higher in the trial than in the real world).
When analyzing data from RCTs, the question is not whether assumptions are made but rather which assumptions are made. In an RCT with incomplete follow-up or outcome ascertainment, a pseudo-ITT analysis assumes that the loss to follow-up occurs completely at random whereas an IP weighted ITT analysis makes less strong assumptions (e.g., follow-up occurs at random conditional on the measured covariates). In an RCT with incomplete adherence, an ITT analysis shifts the burden of assessing the actual magnitude of the effect from the data analysts to the clinicians and other decision makers, who will need to make assumptions about the potential bias introduced by lack of adherence. Supplementing the ITT effects with “as treated”or “per protocol” effects can help decision makers [23], but only if a reasonable attempt is made to appropriately adjust for confounding and selection bias.
In summary, we recommend that all RCTs with substantial lack of adherence or loss to follow-up be analyzed using different methods, including an ITT analysis to estimate the effect of assigned treatment, and appropriately adjusted “per protocol” and “as treated” analyses (i.e., via IP weighting or g-estimation) to estimate the effect of received treatment. Each approach has relative advantages and disadvantages, and depends on a different combination of assumptions [18]. To implement this recommendation, RCT protocols should include a more sophisticated statistical analysis plan, as well as plans to measure adherence and other post-randomization variables. This added complexity is necessary to take full advantage of the substantial societal resources that are invested in RCTs.
Acknowledgments
Funding: National Institutes of Health grant R01 HL080644-01
We thank Goodarz Danaei for his comments to an earlier version of this manuscript.
References
- 1.Luce BR, Kramer JM, Goodman SN, Connor JT, Tunis S, Whicher D, Schwartz JS. Rethinking randomized clinical trials for comparative effectiveness research: the need for transformational change. Ann Intern Med. 2009;151:206–209. doi: 10.7326/0003-4819-151-3-200908040-00126. [DOI] [PubMed] [Google Scholar]
- 2.Food and Drug Administration. International Conference on Harmonisation; Guidance on Statistical Principles for Clinical Trials. Federal Register. 1998;63:49583–49598. [PubMed] [Google Scholar]
- 3.Rosenberger WF, Lachin JM. Randomization in Clinical Trials: Theory and Practice. New York, NY: Wiley-Interscience; 2002. [Google Scholar]
- 4.Piantadosi S. Clinical Trials: A Methodologic Perspective. 2nd edition. Hoboken, NY: Wiley-Interscience; 2005. [Google Scholar]
- 5.Sheiner LB, Rubin DB. Intention-to-treat analysis and the goals of clinical trials. Clin Pharmacol Ther. 1995;57:6–15. doi: 10.1016/0009-9236(95)90260-0. [DOI] [PubMed] [Google Scholar]
- 6.Psaty BM, Prentice RL. Minimizing bias in randomized trials: the importance of blinding. Jama. 2010;304:793–794. doi: 10.1001/jama.2010.1161. [DOI] [PubMed] [Google Scholar]
- 7.McMahon AD. Study control, violators, inclusion criteria and defining explanatory and pragmatic trials. Stat Med. 2002;21:1365–1376. doi: 10.1002/sim.1120. [DOI] [PubMed] [Google Scholar]
- 8.Schwartz D, Lellouch J. Explanatory and pragmatic attitudes in therapeutical trials. J Chronic Dis. 1967;20:637–648. doi: 10.1016/0021-9681(67)90041-0. [DOI] [PubMed] [Google Scholar]
- 9.Tunis SR, Stryer DB, Clancy CM. Practical clinical trials: increasing the value of clinical research for decision making in clinical and health policy. Jama. 2003;290:1624–1632. doi: 10.1001/jama.290.12.1624. [DOI] [PubMed] [Google Scholar]
- 10.Hernán MA, Hernández-Díaz S, Robins JM. A structural approach to selection bias. Epidemiology. 2004;15:615–625. doi: 10.1097/01.ede.0000135174.63482.43. [DOI] [PubMed] [Google Scholar]
- 11.Robins JM. Correcting for non-compliance in randomized trials using structural nested mean models. Communications in Statistics. 1994;23:2379–2412. [Google Scholar]
- 12.Robins JM. Correction for non-compliance in equivalence trials. Statistics in Medicine. 1998;17:269–302. doi: 10.1002/(sici)1097-0258(19980215)17:3<269::aid-sim763>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- 13.Robins JM, Finkelstein D. Correcting for non-compliance and dependent censoring in an AIDS clinical trial with inverse probability of censoring weighted (IPCW) Log-rank tests. Biometrics. 2000;56:779–788. doi: 10.1111/j.0006-341x.2000.00779.x. [DOI] [PubMed] [Google Scholar]
- 14.Hernán MA, Robins JM. Instruments for causal inference: an epidemiologist's dream? Epidemiology. 2006;17:360–372. doi: 10.1097/01.ede.0000222409.00878.37. [DOI] [PubMed] [Google Scholar]
- 15.Ten Have TR, Normand SL, Marcus SM, Brown CH, Lavori P, Duan N. Intent-to-Treat vs. Non-Intent-to-Treat Analyses under Treatment Non-Adherence in Mental Health Randomized Trials. Psychiatr Ann. 2008;38:772–783. doi: 10.3928/00485713-20081201-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cole SR, Chu H. Effect of acyclovir on herpetic ocular recurrence using a structural nested model. Contemporary Clinical Trials. 2005;26:300–310. doi: 10.1016/j.cct.2005.01.009. [DOI] [PubMed] [Google Scholar]
- 17.Mark SD, Robins JM. A method for the analysis of randomized trials with compliance information: an application to the Multiple Risk Factor Intervention Trial. Controlled Clinical Trials. 1993;14:79–97. doi: 10.1016/0197-2456(93)90012-3. [DOI] [PubMed] [Google Scholar]
- 18.Toh S, Hernán MA. Causal Inference from Longitudinal Studies with Baseline Randomization. Int J Biostat. 2008;4 doi: 10.2202/1557-4679.1117. Article22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hernán MA, Lanoy E, Costagliola D, Robins JM. Comparison of dynamic treatment regimes via inverse probability weighting. Basic Clin Pharmacol Toxicol. 2006;98:237–242. doi: 10.1111/j.1742-7843.2006.pto_329.x. [DOI] [PubMed] [Google Scholar]
- 20.Cain LE, Robins JM, Lanoy E, Costagliola D, Hernán MA. When to Start Treatment? A Systematic Approach to the Comparison of Dynamic Regimes Using Observational Data. Int J Biostat. 2006;6 doi: 10.2202/1557-4679.1212. Article 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Writing group for the Women's Health Initiative Investigators. Risks and benefits of estrogen plus progestin in healthy postmenopausal women: Principal results from the Women's Health Initiative randomized controlled trial. Jama. 2002;288:321–333. doi: 10.1001/jama.288.3.321. [DOI] [PubMed] [Google Scholar]
- 22.Toh S, Hernández-Díaz S, Logan R, Robins JM, Hernán MA. Estimating absolute risks in the presence of nonadherence: an application to a follow-up study with baseline randomization. Epidemiology. 2010;21:528–539. doi: 10.1097/EDE.0b013e3181df1b69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thorpe KE, Zwarenstein M, Oxman AD, Treweek S, Furberg CD, Altman DG, Tunis S, Bergel E, Harvey I, Magid DJ, Chalkidou K. A pragmatic-explanatory continuum indicator summary (PRECIS): a tool to help trial designers. J Clin Epidemiol. 2009;62:464–475. doi: 10.1016/j.jclinepi.2008.12.011. [DOI] [PubMed] [Google Scholar]