Simplified equation to extract diffusion coefficients from confocal FRAP data

Abstract

Quantitative measurements of diffusion can provide important information about how proteins and lipids interact with their environment within the cell and the effective size of the diffusing species. Confocal FRAP is one of the most widely accessible approaches to measure protein and lipid diffusion in living cells. However, straightforward approaches to quantify confocal FRAP measurements in terms of absolute diffusion coefficients are currently lacking. Here, we report a simplified equation that can be used to extract diffusion coefficients from confocal FRAP data using the half time of recovery and effective bleach radius for a circular bleach region, and validate this equation for a series of fluorescently labeled soluble and membrane-bound proteins and lipids. We show that using this approach, diffusion coefficients ranging over three orders of magnitude can be obtained from confocal FRAP measurements performed under standard imaging conditions, highlighting its broad applicability.

Introduction

Diffusion is a fundamental process that is relevant over all scales of biology. How rapidly diffusion occurs is characterized by the diffusion coefficient D, a parameter that provides a measure of the mean squared displacement per unit time of the diffusing species. At the cellular level, measurements of D can provide important insights into how proteins and lipids interact with their environment, such as the binding of transcription factors with DNA and of proteins and lipids with membrane domains (1,2). In addition, especially for the case of soluble proteins, an accurate measure of D can provide important information about the effective size of the diffusing species (3).

Currently, biologists have at their disposal a wide range of fluorescence-based techniques to monitor the diffusion of biomolecules in cells, including single particle tracking (SPT), fluorescence correlation microscopy (FCS), photoactivation, and fluorescence recovery after photobleaching (FRAP) (4). Of these approaches, many require specialized equipment, analytical tools, or probes. In contrast, confocal FRAP is one of the most accessible methods to measure apparent diffusion (or effective diffusion). In FRAP, the diffusion of a population of fluorescently labeled molecules can be studied by photobleaching the molecules contained within a user-defined region of interest (ROI), and then monitoring fluorescence recovery due to the exchange of bleached molecules within the bleach ROI with the surrounding reservoir of unbleached molecules. Most modern confocal laser scanning microscopes (CLSMs) are equipped to perform FRAP measurements, and FRAP measurements are straightforward to carry out. In addition, FRAP can be performed using many fluorescently tagged proteins or on directly fluorescently labeled molecules (4,5).

Despite the relative ease of performing confocal FRAP measurements, straightforward methods to quantitatively analyze the resulting data are currently lacking. Most current approaches to calculate D’s from confocal FRAP data require fitting of recovery curves with analytical diffusion models using customized programs, a process which often demands a significant level of knowledge of FRAP theory (Table 1). Alternatively, FRAP measurements can be quantified simply in terms of the half time of recovery (τ_1/2), defined as the time required for a bleach spot to recover half way between initial and steady state fluorescence intensities (6-9). An advantage of this approach is that τ_1/2 can be readily extracted from FRAP recovery curves (6-9). However, τ_1/2 is strongly dependent on experimental parameters such as the nominal radius of the user-defined bleach spot (r_n) and the exact bleaching protocol, as well as the characteristic dynamics of the molecule under investigation. Therefore, τ_1/2 is an empirical parameter that cannot be readily compared across studies. In contrast, D provides a quantitative measure of diffusion (10,11). Knowledge of the absolute magnitude of D has many advantages over measurements of τ_1/2. For example, D is uniquely determined by the size of the diffusing molecule as well as its local environment (12). Therefore, discrepancies between the theoretically expected D and measured apparent (or effective) diffusion coefficients may indicate possible molecular interactions or more complex situations. For example, in cell membranes the presence of microdomains prevents proteins from undergoing free diffusion (2). Accurate estimates of D are also a necessary starting point for reaction-diffusion analysis (1,13).

Table 1.

Analytic 2D FRAP models:

References	Bleaching Geometry	Laser Profiles	Postbleach Profile	Diffusion during photobleach	Data types	Microscopy	Target proteins
Kang et al. (17)	circle in R2	Gaussian (rn)	Gaussian (re)	corrected	f(t)	CLSM/ wide-field static	Slow/Fast
Smisdom et al. (24)	circle in R2	Gaussian (ρ)	Uniform with Gaussian edge	Not corrected	f(t)	CLSM	Slow
Axelrod et al. (10)	circle in R2	Gaussian (rn)/Uniform (rn)	Gaussian (rn)/Uniform (rn)	Not corrected	f(t) / τ1/2	wide-field static	Slow
Braga et al. (15)	circle in R2	Uniform (rn)	Gaussian (re)	corrected	f(t)	CLSM	Slow/Fast
Soumpasis (11)	circle in R2	Uniform (rn)	Uniform (rn)	Not corrected	f(t) / τ1/2	wide-field static	Slow
Sprague et al. (25)	circle in R2	Uniform (rn)	Uniform (rn)	Not corrected	f(t)	wide-field static	Slow/Fast
Waharte et al. (26)	circle in R2	NA	Gaussian(re)	corrected	f(x, t)	CLSM	Slow/Fast
Current Study	circle in R2	Gaussian (rn)	Gaussian (re)	corrected	f(t)/τ1/2	CLSM/ wide-field static	Slow/Fast
Angelides et al.(21)	circle in a box	Gaussian (rn)	Gaussian (rn)	Not corrected	f(t)	wide-field static	Slow
Deschount et al. (22)	box in R2	Gaussian (ρ)	Uniform with Gaussian edge	Not corrected	f(t)	CLSM	Slow
Seiffert & Oppermann (23)	circle/line in R2	NA	Gaussian (re)	corrected	f(x,t)/re(t)	CLSM	Slow

R²: infinite 2 dimensional plane, r_n: bleaching spot radius= static laser radius, ρ: scanning laser radius, r_e: effective radius measured from a fluorescent intensity profile, f(t): fluorescence intensity from an ROI, f(x,t): time course of spreading radius of postbleach profiles.

One potential solution to the problem of extracting quantitative D values from confocal FRAP data is to utilize the explicit forms of the classical 2 dimensional FRAP equations for small circular bleaching spots derived by Axelrod for a Gaussian laser (10) and by Soumpasis for a uniform laser (11). Both Axelrod and Soumpasis (10,11) reported equations that relate D, τ_1/2, and r_n for a pure isotropic diffusion model. For example, the Soumpasis equation is given by

$$D_{r_n}=0.224\frac{r_n^2}{{\tau }_{1/2}}$$ (1)

where r_n is the radius of the uniform bleach laser and the coefficient 0.224 was numerically determined (11). However, the derivation of both the Axelrod and Soumpasis FRAP equations assumed that diffusion during photobleaching is negligible. This is not necessarily the case for confocal FRAP. Due to the long scanning time of CLSMs (~s), significant diffusion during the photobleaching may occur in confocal FRAP. r_n thus may not provide an accurate description of the initial conditions required for this equation to be valid. Failure to take this into account can lead to underestimation of D when the Soumpasis or Axelrod equations are used to analyze confocal FRAP data, especially for fast diffusing soluble proteins (14-17). This discrepancy can be resolved using a modified form of the conventional FRAP equations by using the postbleach fluorescence intensity profile to correct for any diffusion that occurs during the photobleaching by incorporating an empirically determined measure, the effective bleach radius r_e from the postbleach profile (17). However, this approach also requires full fitting of the FRAP recovery curves to calculate D. In the current study, we sought to further simplify this approach by deriving an equation to calculate D from confocal FRAP data obtained using circular bleach regions.

Theory

All the parameters and their meanings are summarized in Table 2. For simplicity, we assume that cell are flat enough (as in the case of COS 7 cells) so that both the plasma membrane as well as the cytosol can be treated as 2D objects. We also assume that bleaching spot size is small compared with the cell size, so that we can treat the cell as an infinite plane (R²). Having these, laser intensity profiles for photobleaching lasers in R² are described as either a Gaussian laser:

$$I_{r_n}(x,y)=\frac{2I_0}{\pi r_n^2}\exp \left(-\frac{2(x^2+y^2)}{r_n^2}\right)$$

or a uniform laser,

$$I_{r_n}(x,y)=\frac{I_0}{\pi r_n^2}H(r_n^2-x^2-y^2)$$

where H(·) is the Heaviside function. In both cases, r_n is defined as a nominal radius, and the excitation lasers are represented as εI_rn (x, y) for attenuation factor ε (≪ 1).

Table 2.

List of parameters and their definitions

Parameter	Meaning	Parameter	Meaning
D	Diffusion coefficient	Fi	Prebleach fluorescence intensity
τ1/2	Half time of recovery	F0	Initial postbleach fluorescence intensity
re	Nominal radius = bleaching spot radius =sampling region radius	F∞	Postbleach steady state fluorescence intensity
re	Effective radius = Spreading radius of post-bleach profile	F1/2	Fluorescence intensity at the half of recovery = [F0 + F∞]/2
q	Quantum yield	Mf	Mobile fraction = [F∞ − F0]/[Fi − F0]
ε	Attenuation factor for excitation laser	τD	$\mathrm{Diffusion\; time}=r_e^2/(4D)$
K	Bleaching depth parameter	Drn	D from Soumpasis Eq. using $r_n(D_{r_n}=0.224\frac{r_n^2}{{\tau }_{1/2}})$
γ	The ratio of the nominal and effective radius = rn/re	Dre	D from Soumpasis Eq. using $r_e(D_{r_e}=0.224\frac{r_e^2}{{\tau }_{1/2}})$
Ci	Prebleach fluorescent protein concentration	DConfocal	D from rn, re and ${\tau }_{1/2}(D_{\mathit{confocal}}=\frac{r_n^2+r_e^2}{8{\tau }_{1/2}})$
n	Number of independent experiments	N	Total number of cells for FRAP data collection

If we assume the concentration of fluorescent proteins C(x, y, t) satisfies the diffusion equation

$$C_t=D\mathrm{\Delta }C$$

where D (μm²/s) is a diffusion coefficient and $\mathrm{\Delta }=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$, then the solution can be computed from a convolution of the fundamental solution of the diffusion equation and an initial condition as

$$C(x,y,t)=\mathit{\int }\mathit{\int }C(x-x^{\prime },y-y^{\prime },0){\mathrm{\Phi }}_{\mathit{Dt}}(x^{\prime },y^{\prime })d{x}^{\prime }d{y}^{\prime }$$

where the fundamental solution of the diffusion equation in R² is defined as

$${\mathrm{\Phi }}_{\mathit{Dt}}(x,y)=\frac{1}{4\pi \mathit{Dt}}\exp \left(-\frac{x^2+y^2}{4\mathit{Dt}}\right).$$

Therefore, the fluorescence intensity from the bleach ROI can be computed (10, 17) from

$$F(t)=q\mathit{\int }\mathit{\int }{\mathit{\epsilon I}}_{r_n}(x,y)C(x,y,t)\mathit{dxdy}$$

where q is the quantum yield of the fluorophores and C(x, y, t) describes the concentration of fluorescent proteins within the confocal volume at time t.

It has been empirically demonstrated that a confocal postbleach profile can be described as a simple Gaussian function (constant minus Gaussian) (13);

$$C(x,y,0)=C_i\left(1-K\exp \left(-\frac{2(x^2+y^2)}{r_e^2}\right)\right),$$ (2)

where C_i is the prebleach fluorescent protein concentration, and r_e is the half width at the approximately 14% of bleaching depth from the top. We define r_e as the effective radius of a postbleach profile, in contrast to the nominal radius (r_n) from a user-defined bleaching spot radius.

Following the computation in Axelrod et al. (10,17), for a solution of the diffusion equation with unknown diffusion coefficient D and an initial condition given by Eq. 2, a diffusion FRAP equation for confocal FRAP can be found as

$$F(t)=F_i\left\{1-\frac{K}{1+{\gamma }^2+2t/{\tau }_D}\right\}{M}_f+(1-M_f)F_0.$$ (3)

Where ${\tau }_D=r_e^2/(4D)$ and γ = r_n/r_e. M_f is defined as

$$M_f=\frac{F_{\infty }-F_0}{F_i-F_0}$$

for prebleach fluorescence intensity (F_i), postbleach initial fluorescence intensity(F₀) and postbleach steady state fluorescence intensity (F_∞). K can be computed from Eq. 3 at t = 0 (i.e.F(0) = F₀),

$$\begin{array}{lll}{F}_0& =& F_i\left\{1-\frac{K}{1+{\gamma }^2}\right\}\\ & \Rightarrow & K=\frac{(F_i-F_0)}{F_i}(1+{\gamma }^2).\end{array}$$ (4)

If we let $F_{1/2}=\frac{F_0+F_{\infty }}{2}$, i.e. the fluorescence intensity at the half time of recovery then, by definition, F(τ_1/2) = F_1/2. Since F_1/2 can be related to M_f by

$$F_{1/2}=\frac{(F_i-F_0)}{2}{M}_f+F_0,$$

by setting F(τ_1/2) = F_1/2:

$$\begin{array}{lll}{F}_{1/2}& =& F_i\left\{1-\frac{K}{1+{\gamma }^2+2{\tau }_{1/2}/{\tau }_D}\right\}{M}_f+(1-M_f)F_0\\ & \Rightarrow & 1+{\gamma }^2+2\frac{{\tau }_{1/2}}{{\tau }_D}=\frac{K}{1-\frac{(F_i+F_0)}{2F_i}};\\ & \Rightarrow & 1+{\gamma }^2+2\frac{{\tau }_{1/2}}{{\tau }_D}=\frac{\frac{(F_i-F_0)}{F_i}(1+{\gamma }^2)}{1-\frac{F_i+F_0}{2F_i}},\end{array}$$

where we applied the definition of K in Eq 4. By multiplying 2F_i to both the denominator and numerator in the right hand side, we obtain

$$\begin{array}{c}1+{\gamma }^2+\frac{2{\tau }_{1/2}}{{\tau }_D}=\frac{2(F_i-F_0)(1+{\gamma }^2)}{F_i-F_0}\\ 1+{\gamma }^2+\frac{2{\tau }_{1/2}}{{\tau }_D}=2(1+{\tau }^2);\\ \frac{2{\tau }_{1/2}}{{\tau }_D}=(1+{\gamma }^2).\end{array}$$

Finally, by solving for D in ${\tau }_D=r_e^2/(4D)$, after applying γ = r_n/r_e, we have

$$D_{\mathit{Confocal}}=\frac{r_e^2+r_n^2}{8{\tau }_{1/2}}.$$ (5)

When r_e = r_n in Eq. 4 (i.e., bleaching is instantaneous), we obtain $D=0.25\frac{r_n^2}{{\tau }_{1/2}}$ which is essentially identical to the Soumpasis equation (Eq. 1). The approximately 3% difference in the proportionality constants in Eq. 1 and Eq. 5 is due to the different assumptions on either Gaussian or uniform laser profiles.

Results and discussion

To validate our new FRAP equations (Eqs. 3, 5), we used them to extract D values from confocal FRAP data obtained using an LSCM under standard imaging conditions for a series of proteins and lipid probes localized either to the plasma membrane, or within the cytosol (Fig. 1). The proteins and lipid probes studied included Alexa488 conjugated cholera toxin B-subunit (Alexa-CTxB), a glycolipid binding bacterial toxin commonly studied as a marker of lipid rafts; a model GPI-anchored protein (YFP-GL-GPI); a fluorescent lipid analog (DiIC₁₆); and soluble EGFP in the cytosol (EGFP). Additionally, the protein Flotillin-1, which is diffusely distributed across the cell surface when overexpressed (19) was examined. Previously reported diffusion coefficients for these molecules span over three orders of magnitude (Table 3), covering a range of D values that are physiologically relevant for most studies of protein and lipid dynamics in cells.

Figure 1. Representative images of the subcellular distribution of the proteins and lipids studied.

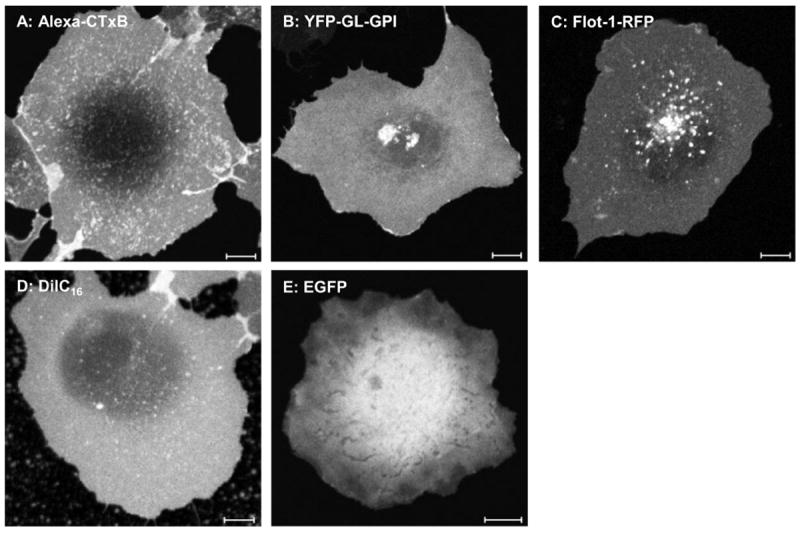
COS7 cells transfected or exogenously labeled with Alexa conjugated cholera toxin B-subunit (Alexa-CTxB), the model GPI-anchored protein (YFP-GL-GPI), Flotillin-1-RFP (Flot-1-RFP), a fluorescent lipid analog (DiIC₁₆), or EGFP. Scale bar = 10 μm.

Table 3.

Diffusion coefficients in cells previously reported in the literature for the molecules examined in the current study by confocal FRAP

Marker	D (μm2/s)	Methods	Reference
CTxB	0.15-0.4	FRAP, FCS	5,27,28
YFP-GL-GPI	0.2-1.3	FRAP,SPT	5,28,29
DiIC16	0.9-5	FRAP, FCS, SPT	5,28,30,31
EGFP	20-70	FRAP, FCS	13,32,33

We performed confocal FRAP analysis of each of these molecules using a circular bleach region with a nominal bleach radius (r_n) of 1.1 μm by repetitively scanning the bleach region. We verified that when diffusion was inhibited by fixing the sample prior to bleaching that the radius of the bleach region was similar to the user-defined nominal bleach radius (Fig. 2). Next, we calculated the effective bleach radius (r_e) and bleach depth (K) from the postbleach fluorescence profile (Fig. 3a,b). For slowly diffusing molecules such as CTxB, the effective bleach radius calculated from the postbleach profile was only slightly larger than the nominal bleach radius (Fig. 2). However, for the majority of molecules examined exchange of fluorescently tagged proteins outside of bleach region was evident. This effect was especially pronounced for the fastest diffusion molecules (Fig. 3a,b). Importantly, the postbleach profiles were well described by an exponential function for all of the molecules examined. This indicates that this approximation provides a reasonable description of the data even for molecules with widely ranging diffusional mobilities and thus that our FRAP equations are valid under these conditions.

Figure 2. Diffusion of Alexa-CTxB on live vs. fixed cells.

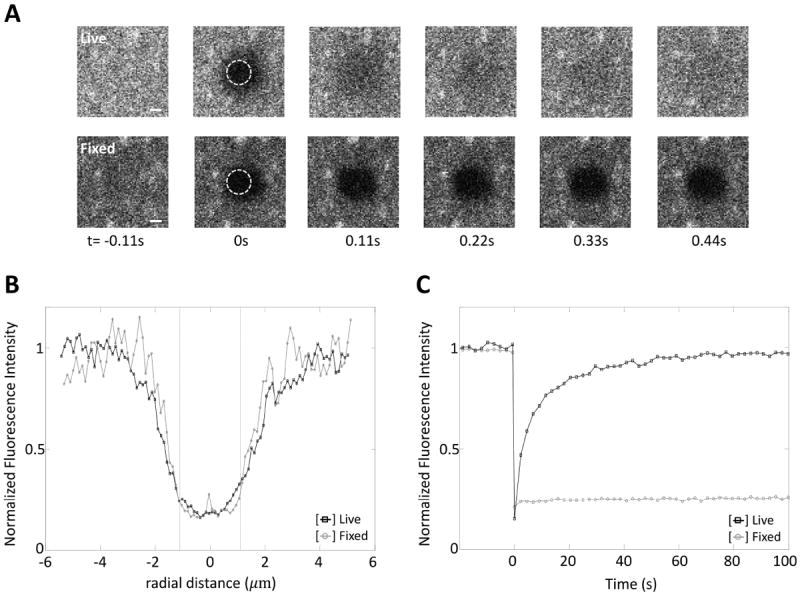
(A) Representative images of Alexa-CTxB on the plasma membrane during a FRAP experiment on either live or fixed cells for r_n=1.1μm. Scale bar = 1 μm. (B) Postbleach profiles of Alexa-CTxB on the plasma membranes of live (□, n=12) and fixed (○, n=5) cells. (C) FRAP data of Alexa-CTxB on the plasma membranes of live (□, n=12) and fixed (○, n=5) cells. Since the bleach ROI is slightly off center in our system as seen in the images of (A) at t=0, a correction was made to align the center of the postbleach profile to determine r_e.

Figure 3. Confocal FRAP data of Alexa-CTxB, YFP-GL-GPI, Flot-1-RFP, DiIC₁₆, and EGFP.

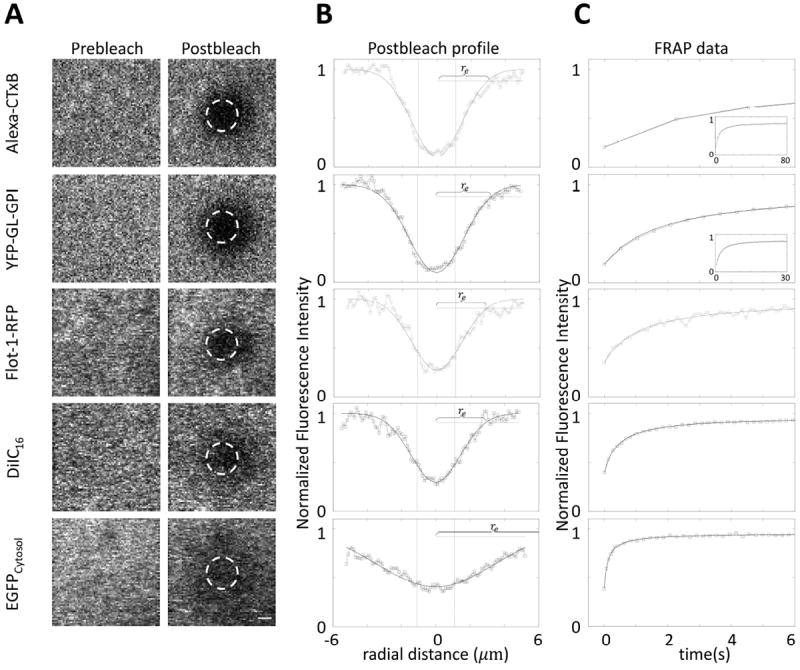
(A) Representative pre- and post-bleach images. Dashed circles represent user-defined bleaching spots with diameter 2.2 μm (i.e. r_n= 1.1 μm). To speed data acquisition for the FRAP analysis, we cropped the imaging window to make it slightly larger than the bleaching spot size. Scale bar, 1 μm. (B) Averaged postbleach profiles for N=12~14 cells along the diagonals of postbleach images (□) and the best fitting Gaussian (Eq. 2, —). Dotted vertical lines show x=±r_n (user defined bleach ROI). Dash-dot horizontal lines are 14% of bleaching depth from the top. (C) Representative FRAP recovery curves (□) and the best fit to Eq. 3 (—). Insets show full FRAP curves for Alexa-CTxB and YFP-GL-GPI. In (B) and (C), y- axes are normalized fluorescence intensities, i.e. F_i = 1. Since the bleach ROI is slightly off center in our system, a correction was made to determine r_e as described in the Materials and Methods.

We next fit the recovery curves to obtain τ_1/2 (Fig. 3c, Table 4), and computed D either by fitting the FRAP data with Eq. 3 (Fig. 3c) or by plugging these numbers directly into the simplified D_Confocal equation (Eq. 5). As illustrated in Figure 4, essentially identical D values were obtained using Eq. 3 (D_fitting) and Eq. 5 (D_Confocal) (Student’s t-test, p>0.05) demonstrating that the two approaches yield similar results as expected. In addition, the D values obtained in this way were in good agreement with the range of values previous reported from studies using more elaborate approaches to quantify D (Table 3). Moreover, the estimated D’s obtained using D_Confocal and D_fitting are independent of experimental conditions as assessed by comparing measurements of EGFP diffusion in the cytoplasm using different bleaching spot size and photobleaching times (Fig. 5 and Table 5, Student’s t-test, p>0.05).

Table 4.

FRAP parameters and measured D’s of various markers.

Markers	Alexa-CTxB (n=5, N=56)	YFP-GL-GPI (n=3, N=36)	RFP-Flot (n=3,N=33)	DiIC16 (n=4, N=58)	EGFP (n=3, N=37)
Parameter
re (μm)	2.7±0.2	3.2±0.1	2.3±0.1	3.0±0.1	7.1±0.2
τ1/2 (s)	4.1±0.7	1.8±0.1	0.97±0.05	0.43±0.28	0.16±0.03
K	0.95±0.04	0.97±0.02	0.79±0.06	0.64±0.06	0.61±0.09
Mf	0.98±0.04	0.99±0.02	0.95±0.04	0.93±0.02	0.95±0.04
Dfitting (μm2/s)	0.26±0.03	0.73±0.04	0.72±0.08	2.7±0.7	41.3±8.2

r_e (μm): effective radius measured from the averaged postbleach profiles. τ_1/2 (s): Halftime-of-recovery of a FRAP curve. K: Photobleaching depth parameter. M_f: Mobile fraction estimated by data fitting. D_fitting: Diffusion coefficient determined by data fitting, n: number of independent experiments, N: total number of cells. Mean ± SD over n.

Figure 4. Comparison of diffusion coefficients determined by various schemes.

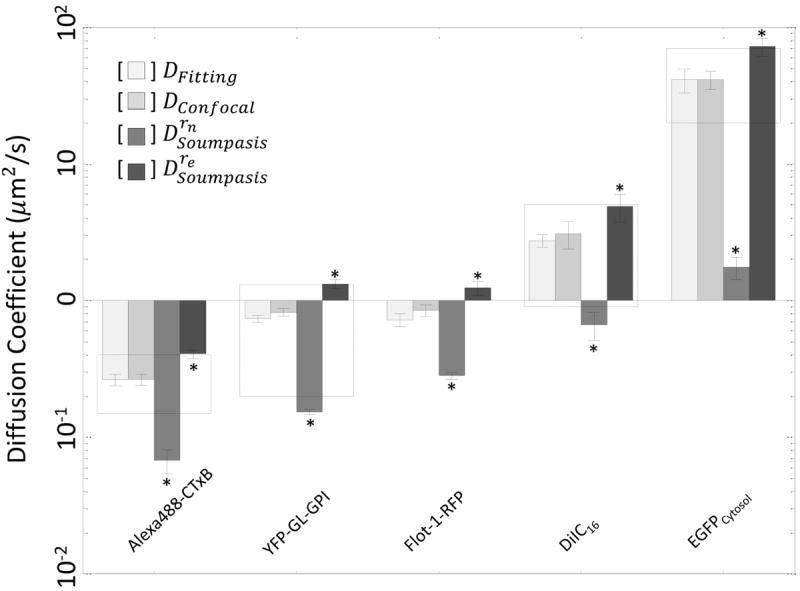
Comparison of diffusion coefficients determined by FRAP data fitting (D_Fitting, Eq. 3), versus the D_Confocal equation (Eq. 5), or the Soumpasis equation using either r_n (D_rn) or r_e (D_re) in log scale. D’s were found from averaged FRAP curves (N≥12 cells per experiment) for three or more separate experiments (n≥3). Error bars represent standard errors. Dashed boxes show D’s reported in the literature (Table 3). *, p<0.05 compared to D_Fitting, Student’s t-test.

Figure 5. Comparison of diffusion coefficients for EGFP in the cytosol obtained by confocal FRAP under different experimental conditions as calculated using the Soumpasis equation or D_Confocal equation.

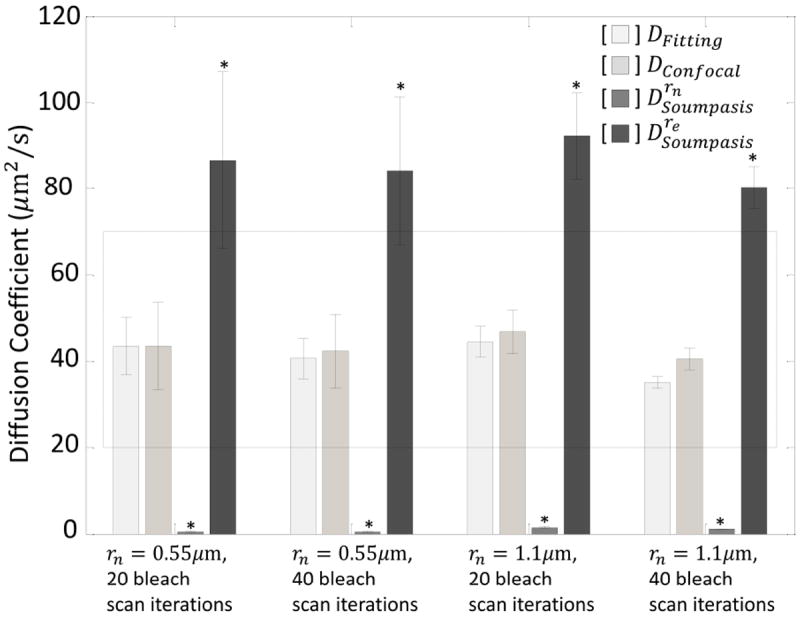
Diffusion coefficients were determined by FRAP data fitting (D_Fitting, Eq. 3), by the D_Confocal equation (Eq. 5), by the Soumpasis equation using r_n (D_rn), and by the Soumpasis equation using r_e (D_re) for individual confocal FRAP curves (N≥6). Dashed box indicates the range of EGFP’s diffusion coefficients in the cytosol reported in the literature. r_e was measured from an averaged postbleach profile (n=1,N=10 cells) and D’s were obtained from individual FRAP data (n=1, N=8,10,10, and 8 cells). *, p<0.05 compared to D_Fitting, Student’s t-test.

Table 5.

Comparison of FRAP parameters for EGFP in the cytosol obtained by confocal FRAP under different experimental conditions

Experimental Setup	1.1 μm diameter ROI		2.2 μm diameter ROI
Parameters	20 iterations (N=8)	40 iterations (N=10)	20 iterations (N=10)	40 iterations (N=8)
rn (μm)	0.55	0.55	1.1	1.1
re (μm)	7.2	7.3	8.6	9.3
τ1/2 (s)	0.28±0.10	0.30±0.12	0.22±0.02	0.28±0.02
K	0.29±0.01	0.32±0.02	0.38±0.01	0.41±0.01
Mf	0.89±0.04	0.89±0.03	0.84±0.01	0.87±0.02

r_n (μm): user defined nominal radius. r_e (μm): effective radius measured from the averaged postbleach profiles. τ_1/2 (s): Halftime-of-recovery of an individual FRAP curve. K: Photobleaching depth parameter. M_f: Mobile fraction calculated by Eq. 3. Iterations: the number of cycles in photobleaching laser scans. FRAP curves (n=1) taken from (17) were re-analyzed without correction for background and photofading. M_f’s found in Table 4 were estimated from data fitting and are therefore larger than M_f’s in Table 5. N: total number of cells. Mean ± SE over N.

To illustrate the importance of using the corrected values of bleach radius to calculate D values, the same FRAP data were analyzed by Soumpasis equation (Eq. 1) using either r_n (D_rn) or r_e (D_re). This approach yielded D’s that were significantly different from those measured using Eq. 3 or Eq. 5 (Fig. 4, Student’s t-test, p<0.05). The relation between D_Confocal and D_rn can be easily seen from 0 < γ ≤ 1 and

$$\frac{D_{r_n}}{D_{\mathit{Confocal}}}=\frac{1.8{\gamma }^2}{1+{\gamma }^2},\frac{D_{r_e}}{D_{\mathit{Confocal}}}=\frac{1.8}{1+{\gamma }^2}$$ (6)

which indicates that

$$D_{r_n}<D_{\mathit{Confocal}}<D_{r_e}.$$ (7)

Therefore, D_rn and D_re can be understood as the upper and lower bounds for D. Importantly, Eqs. 6-7 provide the analytic relations between the equations that relate D and τ_1/2 for conventional and confocal FRAP in terms of γ, the ratio r_n/r_e. This relationship also indicates that τ_1/2 will not scale proportionally with D under conditions where r_e > r_n, providing further evidence that τ_1/2 is not a good approximator of diffusional mobility. For example, depending on the exact imaging conditions used, molecules with similar values of D can demonstrate different values of τ_1/2 (compare results for YFP-GL-GPI and RFP-Flot in Table 4).

The non-fitting method using Eq. 5 heavily hinges on obtaining accurate measurements of r_e and τ_1/2, which can be achieved by analysis of large amount of FRAP data (n>3, and N>10). Here, the statistics of individual r_e, τ_1/2, D, and M_f were carefully compared with the values from the averaged FRAP curve for a set of experiments. We found that there was no significant difference between the values found from averaged FRAP data and mean values of the parameters obtained over multiple individual FRAP data as long as the FRAP dataset size is large (Figure 6, Student’s t-test, p>0.05). Working with averaged FRAP data is more advantageous than using the mean value arising from individual measurements from a computational cost perspective, especially for noisy data from a small ROI size (r_n) or fast diffusion. We also carefully compared D and M_f obtained from individual FRAP data with the values from the averaged FRAP curve for a set of experiments to check if the normalization of the FRAP curves incidently masks biological variability, such as expression level dependent diffusion coefficients (20). However, for the proteins and lipids examined here, D and M_f obtained from individual FRAP data did not show any significant differences from those obtained from the averaged FRAP curves (Figure 6, Student’s t-test, p>0.05).

Figure 6. Comparison of values obtained from averaged FRAP data vs. mean of values from individual FRAP data.

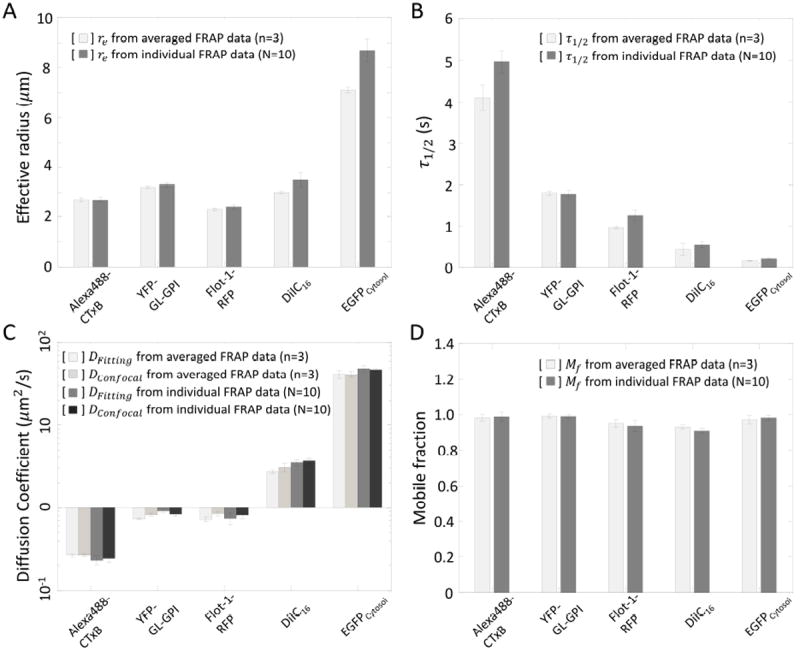
Comparison of Mean±SE of (A) r_e, (B) τ_1/2, (C) D, and (D) M_f determined using averaged FRAP data from more than three independent experiements with 10 cells (n≥3, N=10) or means from 10 individual FRAP data in a single experiment (N=10). Error bars represent standard errors. p>0.05 Cross comparison, Student’s t-test.

In a previous study we found that r_e varies with both r_n and bleaching time, and is more sensitive to r_n than the bleaching time. For larger r_n and longer bleaching time, a larger r_e is obtained (13, 17). In addition, the sensitivity of r_e to experimental definition of r_n and bleaching time is higher for rapidly diffusing proteins (13,17). Nevertheless, variations of r_e and τ_1/2 are constrained by the relation given by Eq. 5 for large range of K as long as the post bleach profiles can be described by a Gaussian (Eq. 2).

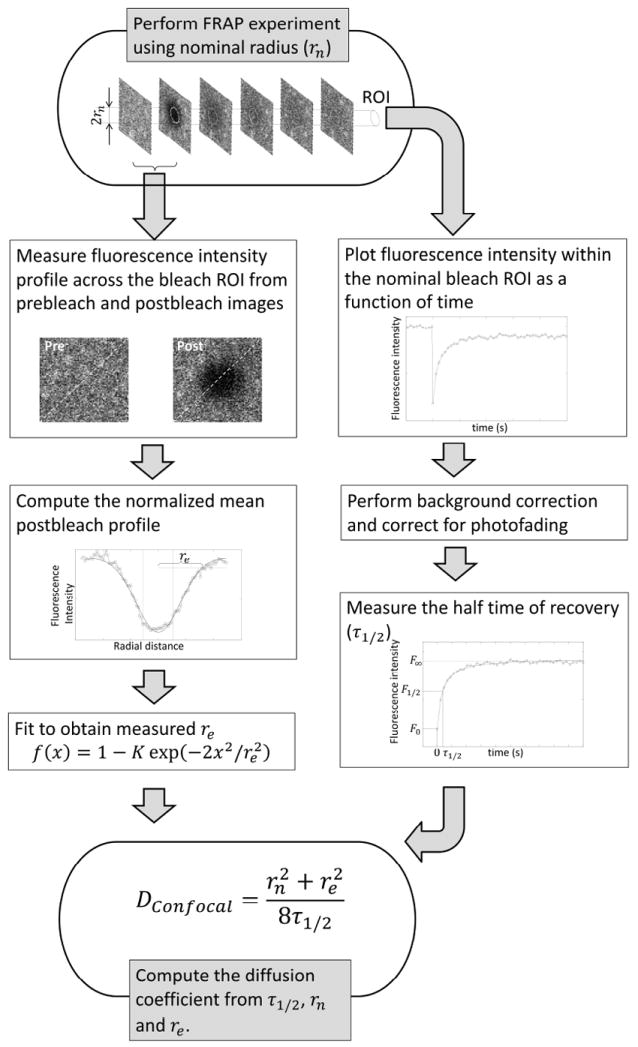
In summary, we derived and tested a new, simplified equation for the quantitative analysis of confocal FRAP data based on the pure isotropic diffusion model. An overall workflow to determine the apparent diffusion coefficient, D from τ_1/2, r_n and r_e is summarized in Figure 7. Taking advantage of widely available technology, this new approach should be accessible to many biologists, since most researchers already have access to CLSMs. Importantly, this method does not require generation of new constructs or the use of specialized fluorescent dyes or labels, and can be applied to both soluble and plasma membrane-associated molecules as illustrated here. Finally, it should be possible to readily incorporate this method into automated approaches to perform and analyze FRAP (18), and thus provide quantitative values for use in systems biology.

Figure 7. Workflow of applying the D_Confocal equation.

Materials and Methods

Cell labeling and reagents

COS-7 cells were acquired from ATCC (Manassas, VA). Cells were maintained in Dulbecco’s modified Eagle medium (DMEM) containing 10% fetal bovine serum at 37°C and 5% CO₂. Cells were plated on coverslips two days prior to experiments. Cells were transfected one day prior to imaging with the model GPI-anchored protein (YFP-GL-GPI) (5), Flotillin-1-RFP (Flot-1-RFP, the gift of Dr. Ai Yamamoto, Columbia University) (21), or EGFP (Clontech, Mountain View, CA) using FuGENE 6 transfection reagent (Roche Diagnostics, Indianapolis, IN). DiIC₁₆ (1,1’-dihexadecyl -3,3,3’,3’-tetramethylindocarbocyanine perchlorate) and Alexa488 fluorophore conjugated cholera toxin B subunit from Vibrio cholerae were obtained from Invitrogen (Carlsbad, CA). For exogenous labeling the cells were rinsed twice with media and then incubated for 5 minutes at room temperature with 100 nM Alexa488-CTxB or 5 μg/ml DiIC₁₆. Cells were then rinsed twice with media and imaged. Cells were maintained in DMEM supplemented with 1 mg/ml Bovine Serum Albumin and 25 mM HEPES buffer during imaging. For FRAP on fixed samples, cell were labeled live with Alexa488-CTxB (as above). Immediately after labeling, cells were fixed with 3.4% paraformaldehyde for 15 minutes at room temperature. Cells were then rinsed with 1x PBS and mounted in Fluoromount G supplemented with 25 mg/ml DABCO (1,4 diazabicyclo[2.2.2]octane) (Sigma-Aldrich) and allowed to solidify overnight prior to imaging.

FRAP methods

FRAP experiments were carried out on a Zeiss LSM510 confocal microscope (Carl Zeiss MicroImaging, Jena, Germany) using filter sets provided by the manufacturer. Imaging was performed using a 40 × 1.3 NA Zeiss Plan-Neofluar objective at 4 × digital zoom. The confocal pinhole was set between 1.78 and 1.81 Airy units. The imaging window was further narrowed to a square observation ROI of 70 × 70 pixel (7.7 μm × 7.7 μm). The 70 × 70 window contained a circular bleach ROI 20 pixels (2.2 μm) in diameter. FRAP conditions were optimized for each molecule under study. Samples were imaged and bleached using a 30 mW Argon laser (488 and 514 laser lines) or 1.0 mW HeNe laser (543 nm laser line). Laser powers for prebleach and postbleach imaging were maintained between 6.8 and 17.1 nW (488 or 514 nm) or between 13.8 and 21.0 nW (543 nm). Bleaching of Alexa 488-CTxB was performed using the 488 nm line at 0.99 μW. EGFP and Flot-1-RFP were bleached using the 488 nm line at 2.28 μW, and YFP-GL-GPI was bleached using the 514 nm line at 1.38 μW. To bleach DiIC₁₆ we combined the 488 nm line (40 nW), 514 line (360 nW), and 543. Bleaching regions were scanned 10 (Alexa-CTxB, YFP-GL-GPI) or 20 times (EGFP, Flot-1-RFP or DiIC₁₆). Prebleach and postbleach images were collected with either no line averaging or with line averaging of 2. Time series images were collect using 2 s delay (Alexa-CTxB), 0.25 s delay (YFP-GL-GPI), or no delay (Flot-1-RFP, DiIC₁₆, EGFP). This resulted in bleach times of 1.12 s (Alexa-CTxB), 0.69 s (YFP-GL-GPI), 0.56 s (Flot-1-RFP), 0.49 s (DiIC₁₆), and 0.27 s (EGFP). During recovery, images were collected every 2.27 s (Alexa-CTxB), 0.52 s (YFP-GL-GPI), 0.14 s (Flot-1-RFP), 0.068 s (DiIC₁₆), or 0.035 s (EGFP). All FRAP was performed at 37 °C using a stage heater.

Correction for background and photofading

To correct for background (F_bk), fluorescence from a cell-free area of the coverslip was measured under the same conditions as FRAP was performed. To correct for observational photofading (F_fading (t)), a time series was collected as for the FRAP studies, except no photobleaching step was performed. The raw FRAP data, F_raw (t) were corrected for background and photofading by

$$F_{\mathit{corrected}}(t)=\frac{F_{\mathit{raw}}(t)-F_{\mathit{bk}}}{F_{\mathit{fading}}(t)-F_{\mathit{bk}}}.$$

Finally, the corrected data were normalized by the prebleach intensity, $F_{\mathit{corrected}}^i$ as

$$F(t)=\frac{F_{\mathit{corrected}}(t)}{F_{\mathit{corrected}}^i}.$$

τ_1/2 measurements

To measure τ_1/2 from the FRAP data a linear interpolation method was used. For the FRAP data {F(0), F(t₁), F(t₂),…, F(t_n)} such that F(0) = F₀ and F(t_n) = F_∞, the fluorescence intensity at half of recovery is defined as F_1/2 = (F₀ + F_∞)/2. If F(t_k) = F_1/2 for some t_k then we chose τ_1/2 = t_k. If F(t_k) < F_1/2 < F(t_k+1) then we chose

$${\tau }_{1/2}=t_k+\frac{\left[F_{1/2}-F(t_k)\right]}{\left[F(t_{k+1})-F(t_k)\right]}(t_{k+1}-t_k).$$

r_e measurements

In order to obtain normalized initial postbleach profiles, fluorescence intensities were measured along a diagonal of the square observation ROIs of 70 × 70 pixel (7.7 μm × 7.7 μm) from the prebleach image obtained immediately prior to and after photobleaching. Between the profiles obtained from two diagonals, the dataset with better symmetry was chosen for analysis. The profiles were then normalized by dividing the postbleach profile by the prebleach profile. The normalized postbleach profiles were averaged over data sets (N=12~14). Since the bleach ROI was slightly off center in some cases, if necessary, the symmetry axis was found and set to be x = 0 from the normalized mean postbleach profile. The mean profiles were then fitted to

$$f_{\mathit{Postbleach}}(x)=1-K\exp \left(-\frac{x^2}{r_e^2}\right)$$

for K and r_e using a nonlinear least-squares fitting routine (nlinfit.m) available in MATLAB^® (version 7.10, R2010a, The Mathworks, Inc.).

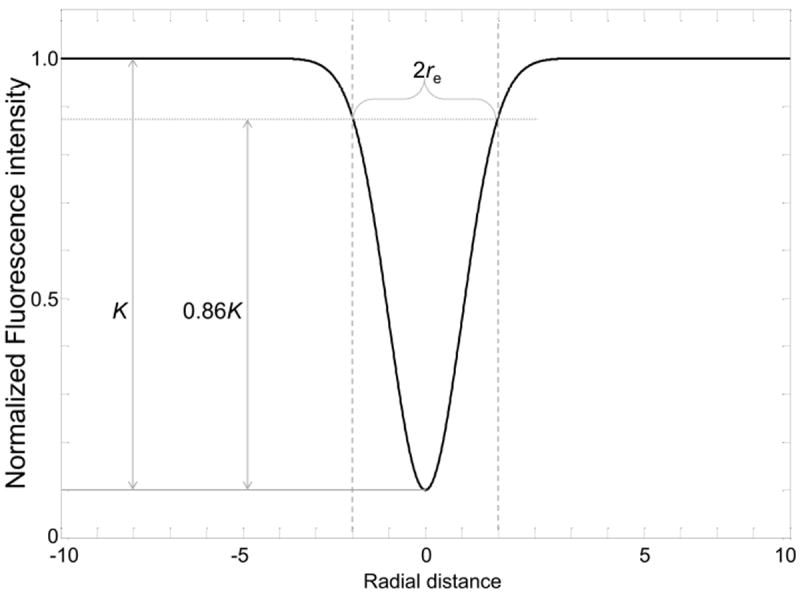
Alternatively, r_e can be determined by direct measurement following three steps. First, K can be determined from the bleaching depth in the nomalized postbleach profile as referred as in Figure 8. Then, the half width of cross-sections between the horizontal line at the height of 0.86K from the bottom of the postbleach profile (Fig. 8) and the postbleach profiles yields r_e without involving any fitting (Fig. 8).

Figure 8. Determination of r_e from a postbleach profile.

FRAP data fitting for D and M_f and weighted residual

The FRAP curves were normalized by the mean prebleach fluorescence intensity (i.e. F_i = 1) and the mean of multiple normalized FRAP data sets was used for data fitting. Data fitting was carried out for D and M_f by a nonlinear least-squares fitting routine (nlinfit.m) available in MATLAB^® (version 7.10, R2010a, The Mathworks, Inc.) minimizing a weighted residual between averaged FRAP data from 10 experiments (F_Data (t)) and a theoretical FRAP curve (F(t), Eq. 3), where the weighted residual is defined by

$$\Vert F_{\mathit{Data}}(t)-F(t)\Vert ={\mathit{\int }}_0^s\frac{\left|F_{\mathit{Data}}(z)-F(z)\right|}{\xi +{\mathit{\int }}_0^s{F}_{\mathit{Data}}(w)\mathit{dw}}\mathit{dz}.$$

If F(0) computed using K from postbleach profile fitting showed any discrepancy from F_Data (0), K was recalibrated using K = (1 + γ²)(1 − F_Data (0)) before data fitting.