Semiparametric regression models for repeated measures of mortal cohorts with non-monotone missing outcomes and time-dependent covariates

Abstract

We propose a semiparametric marginal modeling approach for longitudinal analysis of cohorts with data missing due to death and non-response to estimate regression parameters interpreted as conditioned on being alive. Our proposed method accommodates outcomes and time-dependent covariates that are missing not at random with non-monotone missingness patterns via inverse-probability weighting. Missing covariates are replaced by consistent estimates derived from a simultaneously solved inverse-probability-weighted estimating equation. Thus, we utilize data points with the observed outcomes and missing covariates beyond the estimated weights while avoiding numerical methods to integrate over missing covariates. The approach is applied to a cohort of elderly female hip fracture patients to estimate the prevalence of walking disability over time as a function of body composition, inflammation, and age.

1. Introduction

Our goal is to estimate semiparametric marginal regression models for longitudinal studies with non-monotone missing outcomes and covariates, where missingness may be due to non-response or death. To accommodate deaths, we specify models to estimate associations that are conditioned on being alive [1]. That is, the target of inference is the mean outcome at a particular time conditioned on being alive at that time. Cohorts with data missing due to death are called ‘mortal cohorts,’ and another term for analysis conditioned on being alive, where missingness due to death and non-response is distinguished, is mortal cohort analysis [2]. In contrast, ‘immortal cohort’ analysis does not distinguish between the two reasons for missingness [2]. An analysis approach for mortal cohorts has previously been proposed for continuous outcomes and one time-dependent covariate, where missing data are integrated out of a normal working model [3]. We extend this approach to handle (1) marginal means that are non-linear functions of covariates and (2) a general number of time-dependent covariates with non-monotone missingness. If the model includes continuous covariates with missing data, then integrating over the missing data is intractable, requiring a numerical approach [4]. To avoid computationally intensive methods, we propose a computationally simple extension of weighted estimating equations (WEE). WEE involve multiplying the estimating equation for each observation by the inverse probability of being observed [5, 6]. Motivated by score equations of likelihood-based models for continuous [3, 7] and binary [8] outcomes, we circumvent the integration by replacing missing covariates with simultaneously estimated values.

WEE extends generalized estimating equations (GEE) [9] to better handle the missing data. When there is no selection bias, i.e. data are missing completely at random (MCAR) [10], GEE produces unbiased results. However, GEE produces biased estimates if outcomes are missing not at random (MNAR), i.e. missingness depends on variables that are not fully observed, or are missing at random (MAR), i.e. missingness only depends on fully observed variables [10]. GEE may also be biased if covariates’ missingness depends on outcome data or auxiliary variables (variables not included in the analysis model) that are related to the outcome [5]. An important auxiliary variable in mortal cohorts is survival time. As described in the previous literature [1, 3], MAR-S is a mechanism similar to MAR, except that the probability of missingness at a particular time point depends on (future) time of death. WEE can produce unbiased results if the missingness mechanism is correctly specified [11, 12]. However, the challenge in using WEE to handle the missing data is that the missingness mechanism cannot be identified solely by observed data. Rather, unverifiable assumptions are needed for analyses. Conclusions may not be robust across ranges of assumptions, thus a formal sensitivity analysis is advocated [11–15]. Eliciting assumptions from subject-matter experts about missingness can improve studies by promoting communication between statistical and substantive experts and performing sensitivity analyses over scientifically plausible assumptions.

When using WEE to address the missing data, it is important to distinguish between data that are missing due to death and data that are missing due to non-response (e.g. refusal or missed visits). WEE was originally developed to handle missing covariates [5] and missing outcomes [6, 11] due to non-response. To produce estimates interpreted as conditioned on being alive, weights at each time point are estimated using only data from participants who are alive [1, 3].

The aforementioned data structure and analysis goal are exemplified by longitudinal studies of injured older adults. In one such study, the Baltimore Hip Studies 3 (BHS-3), 205 Caucasian women aged ≥65 years were followed for 1 year after experiencing a hip fracture, with follow-up visits scheduled for 2, 6, and 12 months post-fracture. Our motivating example is an analysis that aims to estimate the associations of interleukin-6 (IL-6), an inflammatory cytokine, and percentage of body fat, a measure of body composition, with self-reported walking disability (defined as inability or requiring human or equipment assistance to walk one block), an activity of daily living (ADL), controlling for age at hip fracture. Body fat and IL-6 are two time-dependent continuous covariates, and walking disability is a binary outcome. Owing to the missing data, unweighted GEE only includes 67, 79, and 68 observations at 2, 6, and 12 months post-fracture, respectively, and data from 110 unique individuals, of whom only 30 had complete data at all three visits. To produce estimates that are conditioned on being alive, WEE only uses information at each visit on the participants who are alive via the estimated weights (inverse probability of being observed among those who are alive) [1, 3]. IL-6, body fat, and ADL information do not have the same missingness pattern at a given visit, and all three variables have non-monotone missing-data patterns. Frequencies of missing-data patterns are found in Table I. Those who miss visits or who refuse to provide serum for measuring IL-6, to undergo dual-energy X-ray absorptiometry (DXA) evaluations for measuring the body composition, or to respond to the questions about ADLs may have greater functional or cognitive decline or may be sicker than those who attend visits and provide complete data; therefore, it is not plausible to assume that data are MAR. MAR-S conditioned on age at hip fracture may be a plausible missingness mechanism, because age at hip fracture is associated with the post-fracture ADL disability, high IL-6 levels, and low body fat. That is, it is plausible that missingness may be independent of unobserved ADL, IL-6, and body fat conditioned on age and time of death.

Table I.

Missing data patterns from BHS-3 by variable and by time of visit.

Variable pattern			Number with variable pattern, by time
RY	$R_{\text{IL}-6}^X$	$R_{\text{Fat}}^X$	2 months	6 months	12 months
1	1	1	67	79	68
1	1	0	6	6	5
1	0	1	23	18	16
0	1	1	21	14	8
0	0	1	10	5	8
0	1	0	1	2	0
1	0	0	17	10	23
0	0	0	53	56	50
D	D	D	7	15	27

Time pattern			Number with time pattern, by variable
R2months	R6months	R12months	Y	XIL-6	XFat
1	1	1	66	51	79
1	1	0	20	19	18
1	0	1	10	3	4
0	1	1	17	20	13
0	0	1	18	8	4
0	1	0	5	8	2
1	0	0	8	15	11
0	0	0	34	54	47
1	1	D	4	2	4
1	0	D	4	2	2
0	1	D	1	1	0
0	0	D	3	7	6
1	D	D	1	3	3
0	D	D	7	5	5
D	D	D	7	7	7

Y = Walking dependence; X_IL-6 = Interleukin 6; X_Fat = Body fat percentage; 1= Observed; 0= Missing; D= Death.

2. Data, models, and estimation

In this section, we describe the data structure, missing-data and analysis models, and estimation procedures for the proposed approach.

2.1. Data

Let Y_{i j} be an outcome at visit j, j = 1, …, J, for participant i, i = 1, …, N, where J is the number of planned follow-up visits, and N is the sample size. Let t _j denote the time of the jth visit, let X_{i j} = {X_{i jk}, k = 1, …, K} be a vector of K incomplete time-dependent covariates in an arbitrary order for participant i, and let V_i be a vector of fully observed baseline covariates for participant i. To handle missing data, let $R_{\mathit{ijk}}^X$ be the response indicator for X_ijk, and let $R_{ij}^Y$ be the response indicator for Y_{i j}. Let S_i be time from baseline until death (e.g. first scheduled study visit after death in the BHS-3 cohort) for participant i. Let A_{i j} be an indicator that participant i is alive at visit j. Lastly, let W_i = {S_i, V_i, X_i, Y_i} denote all relevant data for participant i until death, except for response indicators.

2.2. Models

Consider the expected value of Y_{i j}, given covariates of interest, partly conditioned on being alive [1, 3, 16]:

$${\mu }_{ij}^{Y\mid A,\mathbf{X}}=E[Y_{ij}\mid {\mathbf{X}}_{ij},{\mathbf{V}}_i,t_j,A_{ij}=1].$$

Our goal is to estimate the regression equation

$$g({\mu }_{ij}^{Y\mid A,\mathbf{X}})={\beta }_0+{\mathit{\beta }}_1{\mathbf{X}}_{ij}^t+{\mathit{\beta }}_2{\mathbf{V}}_i^t+{\beta }_3{t}_j,$$ (1)

where g(·) denotes a link function. Estimating survival, f (S_i), is not a primary analysis goal; thus, we aim to estimate the parameters in equation (1) using semiparametric models.

To accommodate the missing data, let ${\mathbf{R}}_{ij}^X=\{R_{\mathit{ijk}}^X,k=1,\dots ,K\}$ be the vector of response indicators for X_{i j}. Also, specifying $R_{i0k}^X$ and $R_{i0}^Y$ to be degenerate, let ${\overline{\mathbf{R}}}_{ij}^Y=\{R_{{ij}^{\prime }}^Y:j^{\prime }=1,\dots ,j-1\}$ denote the history of response indicators for Y_i up through visit j − 1; let ${\overline{\mathbf{R}}}_{ij}^X=\{{\mathbf{R}}_{{ij}^{\prime }}^X:j^{\prime }=1,\dots ,j-1\}$ denote the history of response indicators for X_i up through visit j −1. We consider the following general model for the joint response probabilities at visit j given the history of response probabilities and W_i for participants who are alive (A_{i j} = 1):

$$\begin{array}{l}P({\mathbf{R}}_{ij}^X={\mathbf{r}}_{ij}^X,R_{ij}^Y=r_{ij}^Y\mid {\overline{\mathbf{R}}}_{ij}^X,{\overline{\mathbf{R}}}_{ij}^Y,{\mathbf{W}}_i,A_{ij}=1)\\ =P({\mathbf{R}}_{ij}^X={\mathbf{r}}_{ij}^X\mid {\overline{\mathbf{R}}}_{ij}^X,{\overline{\mathbf{R}}}_{ij}^Y,{\mathbf{W}}_i,A_{ij}=1)\times P(R_{ij}^Y=r_{ij}^Y\mid {\overline{\mathbf{R}}}_{i(j+1)}^X,{\overline{\mathbf{R}}}_{ij}^Y,{\mathbf{W}}_i,A_{ij}=1)\\ =\left[\prod _{k=1}^K{({\pi }_{\mathit{ijk}}^X)}^{r_{\mathit{ijk}}^X}{(1-{\pi }_{\mathit{ijk}}^X)}^{(1-r_{\mathit{ijk}}^X)}\right]\times {({\pi }_{ij}^Y)}^{r_{ij}^Y}{(1-{\pi }_{ij}^Y)}^{(1-r_{ij}^Y)},\end{array}$$

where

$${\pi }_{\mathit{ijk}}^X=P(R_{\mathit{ijk}}^X=1\mid {\overline{\mathbf{R}}}_{ij}^X,R_{ij1}^X,\dots ,R_{ij(k-1)}^X,{\overline{\mathbf{R}}}_{ij}^Y,{\mathbf{W}}_i,A_{ij}=1),$$ (2)

$${\pi }_{ij}^Y=P(R_{ij}^Y=1\mid {\overline{\mathbf{R}}}_{i(j+1)}^X,{\overline{\mathbf{R}}}_{ij}^Y,{\mathbf{W}}_i,A_{ij}=1).$$ (3)

For example, if K = 2 like in the BHS-3 study, then at the first scheduled post-baseline visit (j = 1), the joint probability of observing the outcome and both covariates is

$$\begin{array}{l}P(R_{i11}^X=1,R_{i12}^X=1,R_{i1}^Y=1\mid {\mathbf{W}}_i,A_{i1}=1)=P(R_{i11}^X=1\mid W_i,A_{i1}=1)\times P(R_{i12}^X=1\mid R_{i11}^X=1,{\mathbf{W}}_i,A_{i1}=1)\\ \times P(R_{i1}^Y=1\mid R_{i11}^X=1,R_{i12}^X=1,{\mathbf{W}}_i,A_{i1}=1){\pi }_{i11}^X{\pi }_{i12}^X{\pi }_{i1}^Y.\end{array}$$

The probabilities at j = 2 can condition on the response pattern at j = 1, etc. Conditioning on A_{i j} = 1 implies that equations (2) and (3) are response probabilities only among those who are alive at visit j. As a result, the increasing number of deaths over time will not explicitly diminish response probabilities at later times. Equations (2) and (3) exemplify MNAR mechanisms, because missingness depends on variables with the missing data. Further simplification depends on assumptions about the missing-data mechanism [11]. Also, although the ordering of the K components of X_{i j} is arbitrary for calculating joint response probabilities at visit j, study design aspects may help to simplify the response probability model and inform the ordering (e.g. covariates with a monotone missing-data pattern at visit j) [17].

Let ${\mathbf{W}}_{ij}^{†}=\{S_i,{\mathbf{V}}_i,{\overline{\mathbf{R}}}_{ij}^X{\overline{\mathbf{X}}}_{ij},{\overline{\mathbf{R}}}_{ij}^Y{\overline{\mathbf{Y}}}_{ij}\}$, where ${\overline{\mathbf{R}}}_{ij}^Y{\overline{\mathbf{Y}}}_{ij}=\{R_{{ij}^{\prime }}^Y{Y}_{{ij}^{\prime }}:j^{\prime }=1,\dots ,j-1\}$ and ${\overline{\mathbf{R}}}_{ij}^X{\overline{\mathbf{X}}}_{ij}=\{{\mathbf{R}}_{{ij}^{\prime }}^X{\mathbf{X}}_{{ij}^{\prime }}:j^{\prime }=1,\dots ,j-1\}$. That is ${\mathbf{W}}_{ij}^{†}$ is the collection of relevant observed data for participant i up through visit j − 1, plus survival. The missing-data mechanisms

$${\pi }_{\mathit{ijk}}^X=P(R_{\mathit{ijk}}^X=1\mid {\overline{\mathbf{R}}}_{ij}^X,R_{ij1}^X,\dots ,R_{ij(k-1)}^X,{\overline{\mathbf{R}}}_{ij}^Y,{\mathbf{W}}_{ij}^{†},R_{ij1}^X{X}_{ij1},\dots ,R_{ij(k-1)}^X{X}_{ij(k-1)},A_{ij}=1),$$ (4)

$${\pi }_{ij}^Y=P(R_{ij}^Y=1\mid {\overline{\mathbf{R}}}_{ij}^Y,{\overline{\mathbf{R}}}_{i(j+1)}^X,{\mathbf{W}}_{ij}^{†},A_{ij}=1),$$ (5)

are examples of MAR-S, because the probabilities at time j are functions of observed histories of Y_i and X_i up until j −1 and survival time S_i, an auxiliary variable. If $R_{\mathit{ijk}}^X$ and $R_{ij}^Y$ in equations (4) and (5), respectively, were conditionally independent of S_i, given the fully observed covariates, the equations would simplify to an MAR mechanism.

2.3. Estimation

To estimate the parameters in equation (1), we adapt GEE to accommodate mortality. However, in order for the parameters to be interpreted as partly conditional on being alive, an independence working correlation structure must be specified. A non-independence correlation structure would require specifying pairwise correlations between all visits up until the last visit prior to death. Thus, the parameters in equation (1) would depend on the time of death when S_i ≤ t_J, not just on being alive (A_{i j} = 1) [1, 3, 16]. In the absence of the missing data due to non-response, the independence estimating equation (IEE) to be fit is

$$U(\mathit{\beta })=\sum _{i=1}^N\sum _{j=1}^J{A}_{ij}\frac{\partial {\mu }_{ij}^{Y\mid A,\mathbf{X}}}{\partial \mathit{\beta }}{\text{Var}}_{Y\mid \mathbf{X}}^{-1}(Y_{ij})(Y_{ij}-{\mu }_{ij}^{Y\mid A,\mathbf{X}}),$$ (6)

where Var_{Y |X}(Y_{i j}) is the j, j term, ${\sigma }_{jj}^Y$, of the J × J diagonal working variance–covariance matrix Var_{Y |X}(Y_i). In the presence of missing data due to non-response, the missing-data mechanism can be incorporated into equation (6) via simple inverse-probability-weighted independence estimating equations (simple W-IEE) using

$$U(\mathit{\beta })=\sum _{i=1}^N\sum _{j=1}^J{A}_{ij}\frac{R_{ij}^Y}{{\pi }_{ij}^Y}\left(\prod _{k=1}^K\frac{R_{\mathit{ijk}}^X}{{\pi }_{\mathit{ijk}}^X}\right)\frac{\partial {\mu }_{ij}^{Y\mid A,\mathbf{X}}}{\partial \mathit{\beta }}{\text{Var}}_{Y\mid \mathbf{X}}^{-1}(Y_{ij})(Y_{ij}-{\mu }_{ij}^{Y\mid A,\mathbf{X}}).$$ (7)

In most cases, ${\pi }_{\mathit{ijk}}^X$ and ${\pi }_{ij}^Y$ are not known and need to be estimated. In addition, equation (7) does not efficiently use observations for which at least one of Y_{i j} or X_{i jk}, k = 1, …, K, but not all, are missing. Thus, we consider an estimating equation that can utilize observations with missing variables beyond the estimated weights.

The proposed approach extends equation (7) to utilize observations where X is observed and Y is missing beyond the weights for general models for Y. We first describe the equations for estimating ${\mathit{\pi }}_{\mathit{ijk}}^X$ and ${\mathit{\pi }}_{ij}^Y$ and then introduce the proposed estimating equation for β.

Let ${\mathbf{W}}_{ij}^{\ast Y}$ and ${\mathbf{W}}_{\mathit{ijk}}^{\ast X}$, k =1, … K, denote the vectors of variables associated with $R_{ij}^Y$ and $R_{\mathit{ijk}}^X$, respectively. Let ${\mathit{\gamma }}_j^Y$ and ${\mathit{\gamma }}_{jk}^X$ denote the regression parameters for ${\pi }_{ij}^Y$ and ${\pi }_{\mathit{ijk}}^X$, respectively. Unbiased estimating equations for ${\mathit{\gamma }}_j^Y$ and ${\mathit{\gamma }}_{jk}^X$ are

$$U({\mathit{\gamma }}_j^Y)=\sum _{i=1}^N\frac{A_{ij}}{{\pi }_{ij}^Y}(R_{ij}^Y-{\pi }_{ij}^Y){\mathbf{W}}_{ij}^{\ast Y}$$ (8)

$$U({\mathit{\gamma }}_{jk}^X)=\sum _{i=1}^N\frac{A_{ij}}{{\pi }_{\mathit{ijk}}^X}(R_{\mathit{ijk}}^X-{\pi }_{\mathit{ijk}}^X){\mathbf{W}}_{\mathit{ijk}}^{\ast X},k=1,\dots ,K.$$ (9)

The summands in equations (8) and (9) are multiplied by A_{i j} to ensure that the estimated response probabilities only use data from participants who are alive at visit j. When Y_{i j} (X_ijk) is missing, the summand in equation (8) (equation (9)) simplifies to $-A_{ij}{\mathbf{W}}_{ij}^{\ast Y}(-A_{ij}{\mathbf{W}}_{\mathit{ijk}}^{\ast X})$. Thus, equation (8) can accommodate MNAR Y_ij via user-specified values for the coefficient of Y_ij. Similarly, MNAR X_ijk in equation (9) can be specified via the coefficient of X_ijk.

To estimate β in our proposed method, we utilize observations with missing components of X by plugging in consistent estimates of the missing variables conditioned on the observed covariates. We assume that the mean of X_{i jk} conditioned on being alive, t_j, and fully observed baseline covariates V_i is

$$E[X_{\mathit{ijk}}\mid {\mathbf{V}}_i,t_j,A_{ij}=1]={\mu }_{\mathit{ijk}}^{\mathbf{X}\mid A}={\alpha }_{0k}+{\mathit{\alpha }}_{1k}{\mathbf{V}}_i^t+{\alpha }_{2k}{t}_j.$$

Let ${\mathit{\mu }}_{ij}^{\mathbf{X}\mid A}$ be the K-vector of ${\mu }_{\mathit{ijk}}^{\mathbf{X}\mid A}$. To estimate α_k = {α_0k, α_1k, α_2k}, we posit a weighted independence estimating equation. Let Var(X_i) be the JK × JK block-diagonal working variance–covariance matrix of X_i, which has jth K × K block Var(X_{i j}). Consistent estimates of X_ijk conditioned on V_i, t_j, and observed components of X_ij will be functions of α= {α_k : k = 1, …, K} and components of Var(X_{i j}), with k, k′ component ${\sigma }_{j:{kk}^{\prime }}^X$.

Let ${\mathcal{R}}_j^X$ denote the collection of all possible K-vector missing-data patterns at visit j, ${\mathbf{r}}_j^X=\{r_{jk}^X:k=1,\dots ,K\}$, for ${\mathbf{R}}_{ij}^X$. Thus, $r_{jk}^X=1$ for missing-data patterns in ${\mathcal{R}}_j^X$ indicates X_jk is observed, and $r_{jk}^X=0$ for missing-data patterns in ${\mathcal{R}}_j^X$ indicates X_jk is missing. For example, in the BHS-3 study, K = 2, and all covariate response patterns are possible at all visits; therefore, ${\mathcal{R}}_j^X=\{(0,0),(0,1),(1,0),(1,1)\}$ for all j. Let the terms ${\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{({\mathbf{r}}_j^X)}}$ and ${\text{Var}}_{Y\mid {\mathbf{X}}_{({\mathbf{r}}_j^X)}}(Y_{ij})$ refer, respectively, to the conditional mean and variance of Y_{i j}, with X_{i jk} replaced by ${\mu }_{\mathit{ijk}}^{\mathbf{X}\mid A}$ when $r_{jk}^X=0$. If K = 2 then if, for example, participant i at visit j has observed X_{i j1} and missing X_{i j2} then ${\mathbf{r}}_j^X=(1,0)$ and X_{i j2} is replaced by ${\mu }_{ij2\mid 1}^{\mathbf{X}\mid A}$, which equals $E[X_{ij2}\mid X_{ij1},{\mathbf{V}}_i,t_j,A_{ij}=1]=[{\mu }_{ij2}^{\mathbf{X}\mid A}+{\sigma }_{j:12}^X/{\sigma }_{j:11}^X(X_{ij1}-{\mu }_{ij1}^{\mathbf{X}\mid A})]$, in ${\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(1,0)}}$:

$$\begin{array}{l}g({\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(1,0)}})={\beta }_0+{\beta }_{11}{\mathbf{X}}_{ij1}+{\beta }_{12}{\mu }_{ij2\mid 1}^{\mathbf{X}\mid A}+{\mathit{\beta }}_2{\mathbf{V}}_i^t+{\beta }_3{t}_j\\ ={\beta }_0+{\beta }_{11}{\mathbf{X}}_{ij1}+{\beta }_{12}\left[{\mu }_{ij2}^{\mathbf{X}\mid A}+\frac{{\sigma }_{j:12}^X}{{\sigma }_{j:11}^X}(X_{ij1}-{\mu }_{ij1}^{\mathbf{X}\mid A})\right]+{\mathit{\beta }}_2{\mathbf{V}}_i^t+{\beta }_3{t}_j\\ {\text{Var}}_{Y\mid {\mathbf{X}}_{(1,0)}}(Y_{ij})=\text{Var}(Y_{ij}\mid X_{ij1},{\mu }_{ij2}^{X\mid A},{\mathbf{V}}_i,t_j,A_{ij}=1)\end{array}$$

Also, let ${\mathit{\mu }}_{ij}^{{\mathbf{X}}_{({\mathbf{r}}_j^X)}\mid A}$ denote the subvector of ${\mathit{\mu }}_{ij}^{\mathbf{X}\mid A}$ excluding ${\mu }_{\mathit{ijk}}^{\mathbf{X}\mid A}$ when $r_{jk}^X=0$. Similarly, $\text{Var}({\mathbf{X}}_{ij({\mathbf{r}}_j^X)})$ is the submatrix of Var(X_ij) excluding X_ijk when $r_{jk}^X=0$. Let σ denote the vector of ${\sigma }_{j:k.k^{\prime }}^X$ and ${\sigma }_{jj}^Y$ for j =1, …, J and k, k′ = 1, …, K. Let φ= {β, α, σ}. We consider the following estimating equation for φ:

$$\sum _{i=1}^N\sum _{j=1}^J\sum _{{\mathbf{r}}_j^X\in {\mathcal{R}}_j^X}{A}_{ij}\frac{R_{ij}^Y}{{\pi }_{ij}^Y}\left(\prod _{k=1}^K\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right)U_{ij({\mathbf{r}}_j^X)}^{(1)}(\mathit{\phi })$$ (10)

$$+\sum _{i=1}^N\sum _{j=1}^J\sum _{{\mathbf{r}}_j^X\in {\mathcal{R}}_j^X}{A}_{ij}\left(\prod _{k=1}^K\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right){\mathbf{U}}_{ij({\mathbf{r}}_j^X)}^{(2)}(\mathit{\phi }),$$ (11)

where

$$U_{ij({\mathbf{r}}_j^X)}^{(1)}(\mathit{\phi })=\frac{\partial {\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{({\mathbf{r}}_j^X)}}}{\partial \mathit{\phi }}{\text{Var}}_{Y\mid {\mathbf{X}}_{({\mathbf{r}}_j^X)}}^{-1}(Y_{ij})(Y_{ij}-{\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{({\mathbf{r}}_j^X)}}),$$

and

$${\mathbf{U}}_{ij({\mathbf{r}}_j^X)}^{(2)}(\mathit{\phi })=\frac{\partial {\mathit{\mu }}_{ij}^{{\mathbf{X}}_{({\mathbf{r}}_j^X)}\mid A}}{\partial \mathit{\phi }}{\text{Var}}^{-1}({\mathbf{X}}_{ij({\mathbf{r}}^X)})({\mathbf{X}}_{ij({\mathbf{r}}_j^X)}-{\mathit{\mu }}_{ij}^{{\mathbf{X}}_{({\mathbf{r}}_j^X)}\mid A}).$$

${\mathbf{U}}_{ij({\mathbf{r}}_j^X)}^{(2)}(\mathit{\phi })$ corresponds to the score equation for multivariate normal ${\mathbf{X}}_{ij({\mathbf{r}}_j^X)}$, with ${\mathbf{U}}_{ij(\mathbf{0})}^{(2)}(\mathit{\phi })$ specified to be degenerate (i.e. when ${\mathbf{r}}_j^X=\mathbf{0}$). Although $R_{ij}^Y,\dots ,R_{iJ}^Y$ and components of $R_{ij}^{\mathbf{X}},\dots ,R_{iJ}^{\mathbf{X}}$ can be set to 0 by convention when A_ij = 0 their values do not affect estimates of ${\pi }_{\mathit{ijk}}^X,\dots ,{\pi }_{\mathit{iJk}}^X,{\pi }_{ij}^Y,\dots ,{\pi }_{iJ}^Y$, and φ, because equations (8–11) only use observations where A_{i j} = 1. We show in the Appendix that equations (10) and (11) are unbiased so long as the summands are unbiased.

To understand equations (10) and (11), consider the special case of K = 2. Thus, summing equation (10) over ${\mathcal{R}}_j^X=\{(0,0),(0,1),(1,0),(1,1)\}$ produces four terms because there are four possible covariate response vectors:

$$\begin{array}{l}\sum _{i=1}^N\sum _{j=1}^J{A}_{ij}\frac{R_{ij}^Y}{{\pi }_{ij}^Y}\frac{({\pi }_{ij1}^X-R_{ij1}^X)({\pi }_{ij2}^X-R_{ij2}^X)}{{\pi }_{ij1}^X{\pi }_{ij2}^X}\frac{\partial {\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(0,0)}}}{\partial \mathit{\phi }}{\text{Var}}_{Y\mid {\mathbf{X}}_{(0,0)}}^{-1}(Y_{ij})(Y_{ij}-{\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(0,0)}})\\ +\sum _{i=1}^N\sum _{j=1}^J{A}_{ij}\frac{R_{ij}^Y}{{\pi }_{ij}^Y}\frac{({\pi }_{ij1}^X-R_{ij1}^X)R_{ij2}^X}{{\pi }_{ij1}^X{\pi }_{ij2}^X}\frac{\partial {\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(0,1)}}}{\partial \mathit{\phi }}{\text{Var}}_{Y\mid {\mathbf{X}}_{(0,1)}}^{-1}(Y_{ij})(Y_{ij}-{\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(0,1)}})\\ +\sum _{i=1}^N\sum _{j=1}^J{A}_{ij}\frac{R_{ij}^Y}{{\pi }_{ij}^Y}\frac{R_{ij1}^X({\pi }_{ij2}^X-R_{ij2}^X)}{{\pi }_{ij1}^X{\pi }_{ij2}^X}\frac{\partial {\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(1,0)}}}{\partial \mathit{\phi }}{\text{Var}}_{Y\mid {\mathbf{X}}_{(1,0)}}^{-1}(Y_{ij})(Y_{ij}-{\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(1,0)}})\\ +\sum _{i=1}^N\sum _{j=1}^J{A}_{ij}\frac{R_{ij}^Y}{{\pi }_{ij}^Y}\frac{R_{ij1}^X{R}_{ij2}^X}{{\pi }_{ij1}^X{\pi }_{ij2}^X}\frac{\partial {\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(1,1)}}}{\partial \mathit{\phi }}{\text{Var}}_{Y\mid {\mathbf{X}}_{(1,1)}}^{-1}(Y_{ij})(Y_{ij}-{\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(1,1)}}),\end{array}$$ (12)

where ${\mu }_{ij}^{Y\mid A,{\mathbf{X}}_{(1,1)}}={\mu }_{ij}^{Y\mid A,\mathbf{X}}$, and Var_Y|X(1,1)(Y_ij)=Var_Y|X(Y_ij); therefore the fourth term in equation (12) equals simple W-IEE in equation (7).

Thus, all data points with Y_ij observed contribute information to at least one term in equation (12). However, data points with X_{i j1} and X_{i j2} both observed contribute information to all four terms and are the only data points that contribute information to the fourth term. In contrast, data points with X_{i j1} and X_{i j2} both missing only contribute information to the first term in equation (12).

For general K, equation (10) can be split into 2^K terms (unless some patterns are precluded by study design). Individual i at visit j can contribute information to a particular term ${\mathbf{r}}_j^X\in {\mathcal{R}}_j^X$ if $R_{ij}^Y=1$ and ${\prod }_{k=1}^K{R}_{\mathit{ijk}}^{r_{jk}}=1$. Similarly, equation (11) can be split into 2^K − 1 terms (the term with ${\mathbf{r}}_{\mathbf{j}}^{\mathbf{X}}=\mathbf{0}$ is degenerate; hence, 1 is subtracted). As a result, when K = 2, equation (11) is equal to

$$\begin{array}{l}\sum _{i=1}^N\sum _{j=1}^J{A}_{ij}\frac{({\pi }_{ij1}^X-R_{ij1}^X)R_{ij2}^X}{{\pi }_{ij1}^X{\pi }_{ij2}^X}\frac{\partial {\mathit{\mu }}_{ij}^{{\mathbf{X}}_{(0,1)}\mid A}}{\partial \mathit{\phi }}{\text{Var}}^{-1}({\mathbf{X}}_{ij(0,1)})({\mathbf{X}}_{ij(0,1)}-{\mathit{\mu }}_{ij}^{{\mathbf{X}}_{(0,1)}\mid A})\\ +\sum _{i=1}^N\sum _{j=1}^J{A}_{ij}\frac{R_{ij1}^X({\pi }_{ij2}^X-R_{ij2}^X)}{{\pi }_{ij1}^X{\pi }_{ij2}^X}\frac{\partial {\mathit{\mu }}_{ij}^{{\mathbf{X}}_{(1,0)}\mid A}}{\partial \mathit{\phi }}{\text{Var}}^{-1}({\mathbf{X}}_{ij(1,0)})({\mathbf{X}}_{ij(1,0)}-{\mathit{\mu }}_{ij}^{{\mathbf{X}}_{(1,0)}\mid A})\\ +\sum _{i=1}^N\sum _{j=1}^J{A}_{ij}\frac{R_{ij1}^X{R}_{ij2}^X}{{\pi }_{ij1}^X{\pi }_{ij2}^X}\frac{\partial {\mathit{\mu }}_{ij}^{{\mathbf{X}}_{(1,1)}\mid A}}{\partial \mathit{\phi }}{\text{Var}}^{-1}({\mathbf{X}}_{ij(1,1)})({\mathbf{X}}_{ij(1,1)}-{\mathit{\mu }}_{ij}^{{\mathbf{X}}_{(1,1)}\mid A}),\end{array}$$ (13)

where X_ij(0,1), X_ij(1,0), and X_ij(1,1) are just X_ij2, X_ij1, and X_{i j}, respectively. Similarly, ${\mathit{\mu }}_{ij}^{{\mathbf{X}}_{(0,1)}\mid A},{\mathit{\mu }}_{ij}^{{\mathbf{X}}_{(1,0)}\mid A}$, and ${\mathit{\mu }}_{ij}^{{\mathbf{X}}_{(1,1)}\mid A}$ are just ${\mu }_{ij2}^{\mathbf{X}\mid A},{\mu }_{ij1}^{\mathbf{X}\mid A}$, and ${\mathit{\mu }}_{ij}^{\mathbf{X}\mid A}$, respectively.

As written, equations (10) and (11) only accommodate MNAR mechanisms where R^Y depends on Y, but not components of X and where $R_k^X$ depends on X_k, but not Y or X_−k. However, equations (10) and (11) can be adapted to handle these mechanisms. For example, for components of R^X that depend on Y, the summand in equation (11) is multiplied by $R_{ij}^Y/{\pi }_{ij}^Y$. An implication of this approach is that equation (11) does not use observations with missing Y beyond the weights; thus, more complicated MNAR mechanisms may lead to less efficient estimates. We consider this mechanism and approach in the simulation study and when analyzing the BHS-3 data. When the response probabilities are unknown, the π are replaced with estimates derived from equations (8) and (9).

3. Simulation study

We performed simulation studies to explore the performance of our proposed method and several popular alternatives. We considered K = 1, J = 4, one baseline covariate V, and binary Y. Each study consisted of N = 200 or N = 500 individuals and N_sim = 1000 iterations. Appropriate robust standard errors can be calculated via the information sandwich; however these estimates are not quite correct [2]. Additionally, it has been shown [3] that bootstrap standard errors outperform robust standard errors for WEE; thus the former were calculated with N_bs = 150 bootstrap simulations.

Two different MNAR missing-data mechanisms were explored in this study. The first mechanism, which we call MNAR1, was specified such that the only incomplete variable on which R^X and R^Y depended was X and Y, respectively. In the second mechanism, which we call MNAR2, both R^X and R^Y depended on Y, but only R^X depended on X. To implement estimation assuming MNAR2, the summand in equation (11) was multiplied by $R_{ij}^Y/{\pi }_{ij}^Y$. Both MNAR1 and MNAR2 depended on S.

The simulation proceeded as follows. First, the baseline covariate, V, was simulated from a Normal(1, 4) distribution. We operationalized S as a discrete survival time interpreted as the first visit after death, S ∈ {2, …, J +1}, where all individuals are alive at the first visit, and S = J +1 denotes survival past the end of follow up. S was simulated from a multinomial distribution with a continuation ratio model where logit[P(S_i = s|S_i≥s)]= δ_0s + δ₁V_i, s = 2, 3, 4, δ₀ = {−1.65, −2.00, −2.25}, and δ₁ = −0.25. The time-dependent covariate, X, was simulated from a normal distribution with variance 1, exchangeable correlation 0.5, and mean

$$E[X_{ij}\mid V_i,t_j,S_i]=0.50+0.15V_i+0.50(t_j-1),$$ (14)

where t_j = j (visit number) here.

A Bernoulli distribution assuming a mixed-effects logistic model was specified for Y such that a vector of random effects was simulated from a multivariate normal distribution with mean vector 0, variances 1, and pair-wise correlations 0.5. Y was then simulated, conditional on the simulated random effects, V, X, t, and S. Let b_i denote the random model component. The subject-specific logistic model was

$$\text{logit}\{E[Y_{ij}\mid X_{ij},V_i,t_j,S_i,b_i]\}=-1.0+-0.15X_{ij}+0.20V_i+0.40(t_j-1)+0.40S_i[1+X_{ij}+V_i+(t_j-1)]+b_i,$$ (15)

where b_i = b_i0 + b_i1 X_{i j} + b_i2V_i + b_i4(t _j − 1)+ S_i [b_i5 + b_i6 X_{i j} + b_i7V_i + b_i8(t_j − 1)], and b_i0, …, b_i8 are the random effects. Equation (15) was not the target of estimation, because it is not partly conditioned on being alive. True values of β in equation (1) were found by solving equation (6):

$$\text{logit}({\mu }_{ij}^{Y\mid \mathbf{X},A})=0.066+0.238I_{(t_j=2)}+0.304I_{(t_j=3)}+0.313I_{(t_j=4)}+0.045X_{ij}+0.092V_i.$$

Lastly, among those who are alive, the response indicators were simulated. For both MNAR mechanisms, when A_{i j} = 1, $R_{ij}^X$ was simulated from a Bernoulli distribution with logistic model $\text{logit}({\pi }_{ij}^X)=0.75+0.10S_i-0.10V_i+{\gamma }_{R^X\mid X}{X}_{ij}+{\gamma }_{R^X\mid Y}{Y}_{ij}$, where γ_RX|Y = 0 for MNAR1 and γ_R^X|Y = 0.75 for MNAR2. In both mechanisms, γ_R^X|X = −0.10. For both MNAR mechanisms, when A_{i j} = 1, $R_{ij}^Y$ was simulated from a Bernoulli distribution with logistic model $\text{logit}({\pi }_{ij}^Y)=0.75+0.10S_i-0.10V_i+{\gamma }_{R^Y\mid Y}{Y}_{ij}$, where γ_R^Y|Y = 0.75. We analyzed the data using the proposed method (W-IEE; equations (10) and (11) with K = 1), simple inverse-probability weighting (simple W-IEE; equation (7)), unweighted logistic regression (IEE), and weighted GEE (W-GEE) using an exchangeable correlation matrix.

The MNAR1 model resulted in 21(j = 1) to 51 per cent (j = 4) missing data for X, 22 (j = 1) to 46 per cent (j = 4) missing data for Y, and 37 (j = 1) to 71 per cent (j = 4) missing data for X or Y. The MNAR2 model resulted in 20 (j = 1) to 47 per cent (j = 4) missing data for X, 21(j = 1) to 48 per cent (j = 4) missing data for Y, and 36 (j = 1) to 57 per cent (j = 4) missing data for X or Y. The average cumulative incidences of death at j = 2, 3, 4 specified by the model were 18, 28, and 32 per cent, respectively.

Table II shows results comparing W-IEE, simple W-IEE, W-GEE, and IEE for N = 200 and N = 500. Overall, bias using W-IEE and simple W-IEE was smaller than that when using IEE or W-GEE for both sample sizes. Under the MNAR1 assumption, when α can be estimated using observations with missing Y, W-IEE produced smaller standard errors than simple W-IEE; however, when MNAR2 was assumed, the differences in standard errors were negligible. This result was expected because, under MNAR2, equation (11) only uses observations with Y observed, whereas under MNAR1, inclusion in equation (11) does not depend on whether Y is observed. For both MNAR mechanisms, standard errors using W-GEE and IEE tended to be smaller than those using W-IEE and simple W-IEE. This result for W-GEE was due to the implicit imputation that occurs when specifying GEE to have a non-independence correlation structure in the presence of incomplete data. IEE reflected the MCAR assumption, and observations with Y and X observed varied less than those from the population distribution.

Table II.

Simulation study results (N_sim = 1000, N_bs = 150); percent bias of β̂ 100(β̂ − β)/β (Bias), bootstrap standard error for β̂ (SE), empirical standard error for β̂ (ESE), relative efficiency with simple W-IEE as referent (Rel. Eff.), and 95 per cent confidence interval coverage percent (95 per cent CI Cov.).

Effect	β	N	Method	MNAR1					MNAR2
				Bias	SE	ESE	Rel. eff.	95 per cent CI cov.	Bias	SE	ESE	Rel. eff.	95 per cent CI cov.
Intercept	0.066	200	W-IEE	−12	0.189	0.190	1.3	95.0	14	0.189	0.189	1.0	95.4
			Simple W-IEE	−14	0.217	0.218	1.0	95.0	13	0.192	0.190	1.0	95.7
			IEE	109	0.197	0.199	1.2	93.9	252	0.192	0.189	1.0	88.1
			W-GEE	−239	0.208	0.196	1.2	89.7	−492	0.196	0.189	1.0	65.2
		500	W-IEE	−2	0.117	0.119	1.3	95.2	2	0.116	0.117	1.0	95.8
			Simple W-IEE	−5	0.134	0.136	1.0	94.7	1	0.118	0.119	1.0	95.7
			IEE	114	0.124	0.124	1.2	92.0	256	0.120	0.123	0.9	72.0
			W-GEE	−234	0.121	0.126	1.2	76.7	−490	0.120	0.123	0.9	27.0
I(tj=2)	0.238	200	W-IEE	2	0.186	0.190	1.6	94.8	−1	0.185	0.182	1.0	96.2
			Simple W-IEE	3	0.245	0.244	1.0	96.3	−1	0.186	0.182	1.0	96.2
			IEE	−10	0.167	0.178	1.9	94.3	−18	0.156	0.163	1.2	93.4
			W-GEE	−17	0.184	0.169	2.1	94.7	−27	0.152	0.151	1.4	93.8
		500	W-IEE	−2	0.113	0.110	1.7	95.4	<1	0.113	0.112	1.0	95.2
			Simple W-IEE	−1	0.149	0.145	1.0	96.4	1	0.113	0.112	1.0	95.3
			IEE	−13	0.105	0.110	1.7	93.0	−20	0.098	0.099	1.3	91.5
			W-GEE	−19	0.102	0.100	2.1	91.7	−29	0.093	0.091	1.5	89.0
I(tj=3)	0.304	200	W-IEE	1	0.233	0.230	1.4	96.1	−1	0.232	0.232	1.0	94.4
			Simple W-IEE	<1	0.288	0.277	1.0	96.0	−1	0.233	0.232	1.0	94.6
			IEE	−9	0.179	0.183	2.3	94.1	−19	0.167	0.179	1.7	91.7
			W-GEE	−17	0.197	0.173	2.6	96.3	−30	0.165	0.166	2.0	91.0
		500	W-IEE	<1	0.142	0.138	1.4	95.2	2	0.142	0.141	1.0	96.0
			Simple W-IEE	1	0.175	0.166	1.0	96.1	2	0.142	0.141	1.0	96.1
			IEE	−11	0.113	0.112	2.2	94.9	−19	0.105	0.110	1.6	89.3
			W-GEE	−19	0.110	0.106	2.4	92.8	−30	0.101	0.100	2.0	84.1
I(tj=4)	0.313	200	W-IEE	<1	0.289	0.288	1.4	95.6	<1	0.285	0.280	1.0	95.3
			Simple W-IEE	1	0.339	0.345	1.0	95.9	<1	0.286	0.280	1.0	95.4
			IEE	−9	0.199	0.208	2.8	94.1	−17	0.185	0.192	2.1	91.7
			W-GEE	−17	0.224	0.198	3.0	95.6	−29	0.185	0.177	2.5	93.0
		500	W-IEE	<1	0.175	0.170	1.3	95.6	<1	0.175	0.169	1.0	96.6
			Simple W-IEE	1	0.206	0.195	1.0	97.0	<1	0.175	0.169	1.0	96.7
			IEE	−12	0.125	0.123	2.5	94.6	−18	0.116	0.118	2.0	91.2
			W-GEE	−20	0.122	0.118	2.7	92.0	−30	0.113	0.108	2.4	85.6
X	0.045	200	W-IEE	<1	0.142	0.149	1.0	94.2	−2	0.139	0.136	1.0	95.4
			Simple W-IEE	<1	0.142	0.150	1.0	94.3	−2	0.139	0.136	1.0	95.4
			IEE	−2	0.087	0.094	2.5	93.6	10	0.082	0.085	2.6	95.3
			W-GEE	7	0.099	0.090	2.8	96.0	14	0.084	0.079	3.0	97.0
		500	W-IEE	2	0.086	0.087	1.0	96.0	<1	0.085	0.086	1.0	94.9
			Simple W-IEE	3	0.087	0.088	1.0	96.0	1	0.086	0.086	1.0	94.9
			IEE	4	0.055	0.055	2.6	95.9	2	0.052	0.056	2.4	93.4
			W-GEE	12	0.054	0.053	2.8	96.2	8	0.051	0.052	2.7	94.8
V	0.092	200	W-IEE	8	0.109	0.106	1.2	96.2	7	0.109	0.108	1.1	94.8
			Simple W-IEE	7	0.118	0.115	1.0	96.0	8	0.114	0.114	1.0	94.5
			IEE	25	0.106	0.106	1.2	95.2	26	0.105	0.107	1.1	94.3
			W-GEE	36	0.122	0.114	1.0	96.8	61	0.113	0.114	1.0	94.7
		500	W-IEE	2	0.067	0.066	1.2	95.9	3	0.067	0.067	1.1	95.6
			Simple W-IEE	3	0.072	0.074	1.0	95.1	4	0.070	0.070	1.0	94.9
			IEE	21	0.066	0.066	1.2	95.2	20	0.065	0.066	1.1	94.5
			W-GEE	31	0.070	0.069	1.2	94.0	55	0.069	0.070	1.0	90.1

Comparing estimated standard errors to empirical standard errors shows that the bootstrap with N_bs = 150 performed well. Overall, coverage was slightly closer to the nominal 95 per cent using W-IEE and simple W-IEE compared with IEE or W-GEE. The small decrease in empirical coverage for W-GEE when N = 200 compared with the nominal coverage reflected that the overestimated standard errors using W-GEE (compared with the empirical standard errors) compensated for the large bias. We also explored W-GEE using an unstructured covariance matrix, which resulted in non-convergence problems for N = 200 and little improvement in performance when N = 500 (not shown).

Figure 1 shows the true and estimated proportions (P(Y = 1)), when V_i = 1, its mean, and X_i = (0.65, 1.15, 1.65, 2.15), the means from equation (14), for both MNAR1 and MNAR2 mechanisms when N = 200. In both cases, IEE overestimated the proportion, whereas W-GEE underestimated the proportion, and W-IEE and simple W-IEE produced unbiased estimates.

Figure 1.

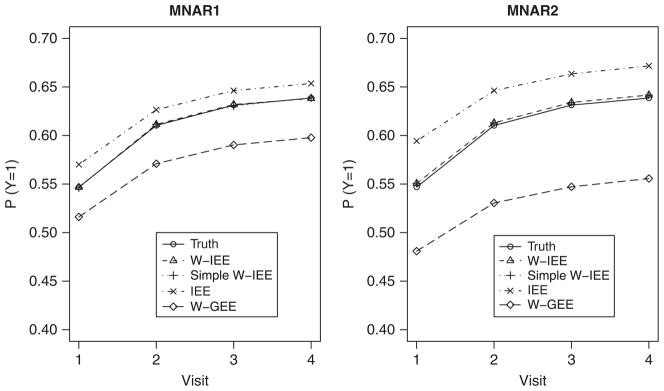
Simulation results, N = 200, N_sim = 1000. Estimated proportions (P(Y = 1)) under two MNAR mechanisms and four estimation methods.

4. BHS-3 data analysis: a sensitivity analysis approach

Our goal was to quantify the association of IL-6 (pg/mL) (X_IL-₆) and body composition (X_Fat) (operationalized as fat mass as a percentage of total mass assessed via DXA evaluations) with prevalence of walking disability (Y) measured at the same time among older women (aged ≥65 years) who experienced a hip fracture, after controlling for age at hip fracture and time since fracture, conditioned on being alive. For this target of inference (i.e. cross-sectional means at time j partly conditional on time-dependent variables at time j, time, and baseline covariates, for j = 1, …, J), independence estimating equations are an appropriate estimation method [18]. Seven, 15, and 27 women died by the 2-, 6-, and 12-month evaluations, respectively. Thus, the impact of deaths on the interpretation of regression coefficients should be considered. One option was to model Y as a trichotomous variable, treating death as a response state of Y as in Miller et al. [19]. However, death was not the primary outcome of interest (if it were, it could be more appropriately handled as a continuous time-to-event variable); thus, we used estimating equations to partly condition on being alive.

In addition to deaths, only 30 participants provided information about Y, X_IL-₆, and X_Fat at all three visits. All 2³ possible missing-data patterns between the three variables were observed during at least one visit (Table I). Within a visit, the variable most commonly missing was IL-6, perhaps because it required the most invasive collection procedure of the three variables; the pattern with only IL-6 collected was the least common. Only 51 participants provided serum at all three visits, compared with 66 and 79 participants who self-reported ADLs and underwent DXA evaluations, respectively, at all three visits. Although less common than longitudinal monotone patterns within a variable, 10, 3, and 4 women provided information at only 2 and 12 months post-fracture (missing at six months) for ADLs, IL-6, and body composition, respectively. Similarly, 5, 8, and 2 women provided information at six months only for ADLs, IL-6, and body composition, respectively. Monotone patterns whereby women missed early visits, but returned at later visits were almost as common as drop outs. We assumed that those with missing observations were in worse physical condition than those providing information. Therefore, these patterns may reflect the competing forces of recovery post-fracture and aging-related physical decline.

We analyzed the BHS-3 data using the proposed W-IEE approach (equations (10) and (11) with K = 2), simple W-IEE (equation (7)), W-GEE, and IEE (logistic regression). Weights were estimated using the following MNAR2 models:

$${\pi }_{ij(\text{IL}-6)}^X=P(R_{ij(\text{IL}-6)}^X=1\mid R_{i(j-1)(\text{IL}-6)}^X,X_{ij(\text{IL}-6)},Y_{ij},V_i,S_i,A_{ij}=1),$$ (16)

$${\pi }_{ij(\text{Fat})}^X=P(R_{ij(\text{Fat})}^X=1\mid X_{ij(\text{Fat})},Y_{ij},V_i,S_i,A_{ij}=1),$$ (17)

$${\pi }_{ij}^Y=P(R_{ij}^Y=1\mid R_{i(j-1)}^Y,{\mathbf{R}}_{ij}^X{\mathbf{X}}_{ij},Y_{ij},V_i,S_i,A_{ij}=1).$$ (18)

Arbitrarily assigning k = 1 for IL-6, and k = 2 for body fat, we did not include $R_{ij(\text{IL}-6)}^X$ or $R_{i(j-1)(\text{Fat})}^X$ in equation (17) due to sparseness. MNAR1 was specified by excluding Y_{i j} from equations (16) and (17). Both MNAR1 and MNAR2 depended on S. For both MNAR mechanisms, assumptions were needed about ${\gamma }_{R_{\text{IL}-6}^X\mid X_{\text{IL}-6}},{\gamma }_{R_{\text{Fat}}^X\mid X_{\text{Fat}}}$ and γ_R^Y|Y, the coefficients for X_{i j(IL}-₆₎, X_{i j(Fat)}, and Y_{i j} in equations (16)–(18), respectively, because these parameters were not identifiable by observed data. To address this issue, ranges of parameter values were elicited from two subject-matter experts, a geriatrician (RRM) and geriatric physical therapist (GEH), to perform a sensitivity analysis. The experts were interviewed separately (by MS) about their beliefs regarding the parameters. The experts were asked the following set of three questions: (1) ‘Holding all else constant, who is more likely to provide responses about ADLs: those who can independently walk one block, or those who cannot independently walk one block?’, (2) ‘What is a plausible range of values for the odds ratio of providing a response, comparing (group chosen in question 1) to (group not chosen in question 1)?’, and (3) ‘What is your rationale for these beliefs?’ The questions were repeated to compare women whose IL-6 levels differed by 10 pg/mL about providing serum, and to compare women whose body fat levels differed by 5 per cent about undergoing DXA evaluations.

The experts were in agreement about the directions of associations and rationale, but opinions differed regarding the magnitudes of associations. After reaching a consensus by connecting the elicited ranges, the experts believed that those without walking disability (those who could independently walk one block) had 1.0 to 2.0 times greater odds of providing a response compared with those with walking disability. The reasons for this belief were that those without walking disability would be proud to admit so, and those with walking disability would feel embarrassed to admit it. Also, walking independence requires cognitive ability, and those lacking the cognitive ability to walk independently may also lack the cognitive ability to respond to interview questions [20]. Comparing women whose IL-6 levels differed by 10 pg/ml, women with lower IL-6 were thought to have 1.0 to 2.5 times greater odds of providing serum than women with higher IL-6. IL-6 levels tended to be highest in the most frail patients. Also, elevated IL-6 is a marker for lingering adverse effects of the hip fracture; thus, those in worse general health were thought more likely to refuse the needle venopuncture required for providing serum [21, 22]. Lastly, the experts assumed that women would have 1.0 to 1.5 times greater odds of undergoing DXA when compared with women with 5 per cent less body fat. Both experts mentioned that elderly hip fracture patients are rarely overweight, and that those with the lowest fat percentage were most likely underweight, a marker of frailty. Given that DXA evaluations required travel from home or hospital to a location with DXA equipment, those who were most frail were thought most likely to refuse. In summary, those who were in better physical health were thought more likely to provide data than those in worse physical health.

We performed sensitivity analysis using the elicited expert information by assuming MCAR and six MNAR assumptions. We defined MNAR1-Min, MNAR1-Mid, and MNAR1-Max, as MNAR1 mechanisms assuming odds ratios that were the minimum, midpoint, and maximum elicited departures from the null, 1.0. MNAR2 mechanisms were analogously named. For example, elicited values of $exp\{{\gamma }_{R_{\text{Fat}}^X\mid \text{Fat}}\}$ ranged from 1.0 to 1.5; thus, the odds ratios corresponding to the minimum, midpoint, and maximum departures from 1.0 were 1.0, 1.25, and 1.5, respectively. The ranges of elicited odds ratios for all three parameters included 1.0; thus, MNAR1-Min simplified to the MAR-S mechanism. Analyses were performed using W-IEE, simple W-IEE, W-GEE, and IEE.

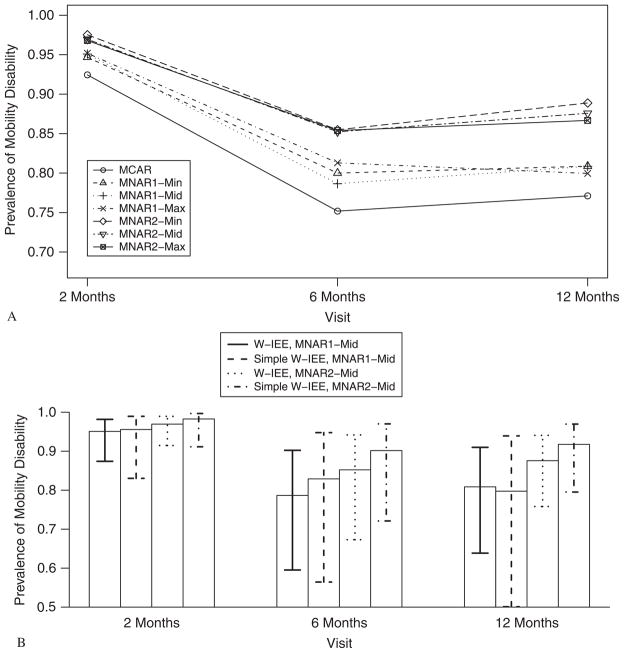
The estimated model parameters are shown in Table III. With the exception of the coefficient for body fat assuming MNAR2-Max using W-IEE, directions of parameters were robust to estimation method or missing-data mechanism. In general, higher levels of IL-6 and body fat and older age were associated with walking disability, adjusted for time since hip fracture and conditioned on being alive. After controlling for IL-6, body fat, and age, estimated prevalence of walking disability using W-IEE for all assumptions except MNAR1-Max was highest at 2 months and lowest at 6 months post-fracture among those who were alive.

Table III.

BHS-3 study results (N = 205, N_bs = 150); estimated coefficients (β̂) and standard errors (SE) relating walking disability (Y = 1) to time since hip fracture, IL-6, body fat, and age. Min, Mid, and Max of $({\gamma }_{R^Y\mid Y},{\gamma }_{R_{\text{IL}-6}^X\mid \text{IL}-6},{\gamma }_{R_{\text{Fat}}^X\mid \text{Fat}})=(0,0,0)$, (−log(1.50), −log(1.75), log(1.25)), and (−log(2.00), −log(2.50), log(1.50)), respectively.

Effect	Assumption	IEE		W-IEE		Simple W-IEE		W-GEE
		β̂	SE	β̂	SE	β̂	SE	β̂	SE
Intercept	MCAR	−8.04	2.94
	MNAR1-min			−8.05	3.44	−10.44	4.48	−10.96	4.62
	MNAR1-mid			−8.95	3.65	−11.75	4.05	−12.35	4.44
	MNAR1-max			−8.16	3.86	−13.13	4.89	−13.66	5.08
	MNAR2-min			−8.81	3.27	−10.04	3.45	−10.99	3.65
	MNAR2-mid			−7.26	3.27	−12.01	4.47	−12.52	4.76
	MNAR2-max			−6.13	2.96	−10.70	4.38	−11.14	4.48
6 months	MCAR	−1.41	0.40
	MNAR1-min			−1.49	0.48	−1.49	0.61	−1.24	0.54
	MNAR1-mid			−1.64	0.64	−1.49	0.73	−1.43	0.61
	MNAR1-max			−1.49	0.67	−1.32	0.86	−1.35	0.73
	MNAR2-min			−1.89	0.61	−2.04	0.64	−1.82	0.56
	MNAR2-mid			−1.68	0.76	−1.82	0.84	−1.77	0.80
	MNAR2-max			−1.60	0.71	−1.75	0.81	−1.70	0.73
12 months	MCAR	−1.33	0.41
	MNAR1-min			−1.45	0.50	−1.15	0.53	−1.07	0.41
	MNAR1-mid			−1.50	0.55	−1.72	0.72	−1.65	0.65
	MNAR1-max			−1.57	0.64	−2.06	0.96	−2.03	0.87
	MNAR2-min			−1.60	0.53	−2.03	0.64	−1.89	0.57
	MNAR2-mid			−1.46	0.65	−1.65	0.72	−1.61	0.70
	MNAR2-max			−1.46	0.50	−1.75	0.60	−1.71	0.57
IL-6 (per 10 pg/mL)	MCAR	0.08	0.10
	MNAR1-min			0.11	0.08	0.12	0.08	0.16	0.09
	MNAR1-mid			0.14	0.07	0.14	0.09	0.16	0.15
	MNAR1-max			0.11	0.07	0.12	0.09	0.13	0.10
	MNAR2-min			0.12	0.18	0.15	0.17	0.18	0.15
	MNAR2-mid			0.14	0.08	0.12	0.08	0.13	0.09
	MNAR2-max			0.15	0.07	0.16	0.08	0.18	0.08
Body fat (per 5 per cent)	MCAR	0.20	0.17
	MNAR1-min			0.14	0.20	0.18	0.27	0.18	0.26
	MNAR1-mid			0.10	0.19	0.22	0.22	0.23	0.22
	MNAR1-max			0.02	0.16	0.32	0.20	0.34	0.20
	MNAR2-min			0.14	0.20	0.08	0.22	0.08	0.23
	MNAR2-mid			0.02	0.21	0.18	0.24	0.18	0.26
	MNAR2-max			−0.01	0.20	0.04	0.24	0.04	0.24
Age (years)	MCAR	0.11	0.03
	MNAR1-min			0.12	0.04	0.15	0.04	0.15	0.05
	MNAR1-mid			0.14	0.04	0.16	0.04	0.17	0.05
	MNAR1-max			0.13	0.04	0.18	0.06	0.18	0.06
	MNAR2-min			0.14	0.03	0.16	0.04	0.18	0.04
	MNAR2-mid			0.13	0.03	0.18	0.05	0.19	0.05
	MNAR2-max			0.12	0.03	0.18	0.04	0.18	0.04

Magnitudes of parameters were sensitive to estimation method for a given missing-data mechanism. For example, the coefficient for IL-6 assuming MNAR2-Min ranged from 0.12 (W-IEE) to 0.18 (W-GEE). The parameters were also sensitive to assumptions about the missing-data mechanism for a given method. The coefficient for body fat using W-IEE varied from −0.01 (MNAR2-Max) to 0.14 (MNAR1-Min and MNAR2-Min). Overall, estimates using W-GEE and simple W-IEE fluctuated across assumptions about missing data more than those using W-IEE, perhaps because the former methods used fewer observations than W-IEE. This reason is also a plausible explanation why estimated associations for IL-6 and body fat were stronger more often using simple W-IEE and W-GEE than those using W-IEE. Among those for whom $R_{ij}^Y{R}_{ij(\text{IL}-6)}^X{R}_{ij(\text{Fat})}^X=1$, the prevalences of walking disability at 2, 6, and 12 months post-fracture were 0.90, 0.72, and 0.72, respectively, whereas the analogous prevalences among those for whom $R_{ij}^Y(1-R_{ij(\text{IL}-6)}^X{R}_{ij(\text{Fat})}^X)=1$ (data only used by W-IEE beyond the weights) were 1.00, 0.82, and 0.84. Similarly, the means of IL-6 among those with $R_{ij}^Y{R}_{ij(\text{IL}-6)}^X{R}_{ij(\text{Fat})}^X=1$ at 2, 6, and 12 months post-fracture were 21.0, 16.6, and 17.5 pg/mL, whereas the means of those with $R_{ij(\text{IL}-6)}^X(1-R_{ij}^Y{R}_{ij(\text{Fat})}^X)=1$ (data only used by W-IEE beyond the weights) were 17.8, 22.1, and 12.0 pg/mL. Finally, the means of body fat percentage among those with $R_{ij}^Y{R}_{ij(\text{IL}-6)}^X{R}_{ij(\text{Fat})}^X=1$ at 2, 6, and 12 months post-fracture were 29.5, 30.2, and 31.4 per cent, whereas the means among those with $R_{ij(\text{Fat})}^X(1-R_{ij}^Y{R}_{ij(\text{IL}-6)}^X)=1$ (data only used by W-IEE beyond the weights) were 28.7, 29.1, and 29.5 per cent. These estimates cannot be interpreted as time-specific prevalences of walking disability owing to the missing data; however, with the exception of 2- and 12-month IL-6, these descriptive statistics correspond with the assumption that healthier participants were more likely to provide observations.

Estimates in general fluctuated more across MNAR2 assumptions than MNAR1 assumptions. This result was expected because weights for R^X assuming MNAR2, unlike MNAR1, depended on assumptions about Y, and fewer observations were used in MNAR2 than in MNAR1. Estimated adjusted time-specific prevalences of walking disability are shown in Figure 2 Panel A for IEE and W-IEE for a hypothetical participant with IL-6, age, and body fat at the observed time-specific mean levels. The lowest estimated prevalences of walking disability were derived using IEE, reflecting the MCAR assumption that those providing data were representative of those with missing data. Estimated prevalences were higher assuming MNAR2 than when assuming the analogous MNAR1 mechanism due to the dependence of R^X on Y. Despite the sensitivity of parameter estimates on assumptions about the missing data, all mechanisms except MNAR1-max suggested some recovery from walking disability by 6 months post-fracture followed by incident disability at twelve months, perhaps due to advancing age. Panel B of Figure 2 compares the estimated prevalence of walking disability and 95 per cent confidence intervals between W-IEE and simple W-IEE for MNAR1-mid and MNAR2-mid mechanisms. For MNAR1-mid, the 95 per cent confidence interval was wider when using simple W-IEE than when using W-IEE, but the confidence intervals were of similar width between the two methods under MNAR2-mid. Also, when assuming MNAR2-mid, the estimated prevalences of walking disability were higher when using simple W-IEE than when using W-IEE at each time point.

Figure 2.

BHS-3 results. Panel A: estimated prevalence of walking disability (P(Y = 1)) at 2, 6, and 12 months post-fracture for MCAR (IEE) and six MNAR (W-IEE) mechanisms. Panel B: estimated prevalence and 95 per cent confidence interval of walking disability (P(Y = 1)) at 2, 6, and 12 months post-fracture for MNAR1-mid and MNAR2-mid mechanisms from W-IEE and simple W-IEE. Min, mid, and max of $({\gamma }_{R^Y\mid Y},{\gamma }_{R_{\text{IL}-6}^X\mid \text{IL}-6},{\gamma }_{R_{\text{Fat}}^X\mid \text{Fat}})=(0,0,0)$, (−log(1.50), −log(1.75), log(1.25)), and (−log(2.00), −log(2.50), log(1.50)), respectively.

5. Discussion

We proposed a computationally simple approach to marginal modeling of longitudinal studies with deaths and non-monotone missing outcomes and covariates partly conditioned on being alive. This approach is flexible enough to handle a general number of missing covariates and data that are MNAR, and it does not require performing numerical integration over missing covariates. Also, the simulation study shows that the proposed method performs well for sample sizes as small as N = 200 and results in more efficient estimates than when using simple W-IEE assuming MNAR1. If the missing-data mechanism of each incomplete variable is specified to depend on Y and all components of X, then the proposed method simplifies to simple W-IEE. Otherwise, the proposed simultaneous estimating equations can provide some efficiency benefits by using more data than simple W-IEE for deriving estimates.

The simulation study and example focused on the scenario when all components of X are continuous to motivate use of a multivariate normal working model for X. When some incomplete covariates are categorical, this model is not correct. However, so long as π, μ^{Y | A,X}, and μ^X|A are correctly specified, the proposed estimating equation is unbiased. Previous empirical research focusing on continuous outcomes also suggests that WEE performs well when a normal working model for X is incorrectly specified [7]. Although the simulation study shows no bias for both W-IEE and simple W-IEE, the BHS-3 analysis shows that results from a particular study may vary between the two methods; thus, it is preferable to use as many observations as possible.

An important limitation of our method is that the number of parameters to estimate can become large when several incomplete covariates are included in the model or when there are many follow-up visits. However, this limitation can be overcome by making plausible assumptions to control the number of parameters, for example by assuming that ${\gamma }_{\mathit{ijk}}^X={\gamma }_{{ij}^{\prime }k}^X$ for j, j′ ∈ {1, …, J}, j ≠ j′. Also, as is always the case for missing data, the missing-data mechanism cannot be identified from the observed data; thus, untestable assumptions are required for performing the analysis. No statistical method accommodating missing data is more beneficial than data collection methods that can minimize the missing data. Therefore, efforts should be made to reschedule missed appointments and obtain responses to interview questions. If missing data remain, a sensitivity analysis should be performed to assess the impact of assumptions about the missing-data mechanism on scientific conclusions. Such an analysis can be facilitated by collecting information to understand the reasons for missingness. For example, those who miss visits due to poor health conditions may differ from those who miss visits due to inclement weather. Additionally, missingness may be due to reasons that are not related to the study participants. For example, some variables may be collected from clinicians as part of the standard clinical care, whereas others may only be collected as part of a research protocol. Thus, reasons for missingness should also be collected from clinicians. This information can be used when estimating weights. Finally, the method is only appropriate for studies with prescheduled visits (i.e. discrete time). Otherwise, data should be analyzed within the framework of informative observation times [23].

The analysis goal that motivated the proposed method was to estimate cross-sectional marginal prevalence of walking disability generalized to those who are alive as a function of simultaneously measured body fat percentage and IL-6, at 2, 6, and 12 months post-fracture. In this case, a W-IEE analysis can provide unbiased estimates if the missing-ness mechanism is correctly specified. However, if the investigator is interested in whether body fat percentage and IL-6 causally affect walking disability, the proposed W-IEE method needs to be adapted to handle time-dependent confounders. For example, if body fat percentage or IL-6 are endogenous (walking disability affects body fat percentage or IL-6 at later times), then previous walking disability is a time-dependent confounder. To address this issue, our proposed method can easily be adapted by using inverse probability of treatment weights (IPTW) [24]. In the BHS-3 example, this would involve multiplying the summand in equation (10) by the inverse joint density of body fat percentage and IL-6 conditional on previous walking disability and other time-dependent confounders. Also, if the investigator is interested in generalizing inferences to the whole cohort, not just those who are alive, then methods for estimating survivor average causal effects are needed to address healthy survivor bias [25]. Additional considerations regarding the use of IPTW can be found elsewhere [24, 26].

One challenge for performing a sensitivity analysis is determining a plausible range of assumptions to explore. The best sources for these assumptions are subject-matter experts. In the BHS-3 example, a geriatrician and a physical therapist were interviewed to obtain plausible assumptions about why hip-fracture patients may refuse to respond to interview questions, provide serum, or undergo DXA evaluations. Although estimates varied, weak to marginal evidence was found across assumptions about the relationship of IL-6 and body fat with walking disability conditioned on being alive, controlling for age and time since hip fracture.

Our proposed method is an example of a selection model, where the probability of response conditional on potentially missing variables and fully observed variables is modeled [27]. Eliciting information interpreted as odds ratios of response for selection models from subject-matter experts may be difficult. An alternative approach, which may be easier for subject-matter experts to interpret, is to specify missing-data mechanisms using pattern-mixture models, where means of a variable are specified separately for those with missing and observed data [13, 15, 27]. However, the pattern-mixture model would require parameterizing models conditional on response pattern. Future research involves marginalized pattern-mixture models conditioned on being alive to retain the benefits of both selection and pattern-mixture models. Additionally, the proposed method was motivated by mortal cohorts where survival status is known for all participants during the study period. Thus, future research involves extending the method to handle possible censoring of mortality. In this case, assumptions about the censoring mechanism would be needed to account for missing values of vital status.

Appendix

In this Appendix, we establish that equations (10) and (11) are unbiased if ${\pi }_{ij}^Y,{\pi }_{\mathit{ijk}}^X,{\mathit{\mu }}_{ij}^{\mathbf{X}\mid A}$, and ${\mu }_{ij}^{Y\mid A,\mathbf{X}}$ are correctly specified, irrespective of the missing-data mechanism. Let ${\mathbf{W}}_{ij}^{\ast }={\mathbf{W}}_{ij}^{\ast Y}\cup {\mathbf{W}}_{ij}^{\ast X}$, where ${\mathbf{W}}_{ij}^{\ast X}=\{{\mathbf{W}}_{\mathit{ijk}}^{\ast X}:k=1,\dots ,K\}$. Using iterated expectations on equation (10),

$$\begin{array}{l}{E}_{(R_{ij}^Y\mid {\overline{\mathbf{R}}}_{ij}^Y,{\overline{\mathbf{R}}}_{i(j+1)}^X,{\mathbf{W}}_{ij}^{\ast },A_{ij}=1,Y_{ij},{\mathbf{X}}_{ij},{\mathbf{V}}_i)}\left[A_{ij}\frac{R_{ij}^Y}{{\pi }_{ij}^Y}\left(\prod _{k=1}^K\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right)U_{ij({\mathbf{r}}_j^X)}^{(1)}(\mathit{\phi })\right]\\ =A_{ij}\left(\prod _{k=1}^K\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right)U_{ij({\mathbf{r}}_j^X)}^{(1)}(\mathit{\phi })E_{(R_{ij}^Y\mid {\overline{\mathbf{R}}}_{ij}^Y,{\overline{\mathbf{R}}}_{i(j+1)}^X,{\mathbf{W}}_{ij}^{\ast },A_{ij}=1,Y_{ij},{\mathbf{X}}_{ij},{\mathbf{V}}_i)}\left[\frac{R_{ij}^Y}{{\pi }_{ij}^Y}\right]\\ =A_{ij}\left(\prod _{k=1}^K\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right)U_{ij({\mathbf{r}}_j^X)}^{(1)}(\mathit{\phi })1,\end{array}$$

because

$$E_{(R_{ij}^Y\mid {\overline{\mathbf{R}}}_{ij}^Y,{\overline{\mathbf{R}}}_{i(j+1)}^X,{\mathbf{W}}_{ij}^{\ast },A_{ij}=1,Y_{ij},{\mathbf{X}}_{ij},{\mathbf{V}}_i)}\left[\frac{R_{ij}^Y}{{\pi }_{ij}^Y}\right]=\frac{{\pi }_{ij}^Y}{{\pi }_{ij}^Y}=1.$$

Next,

$$\begin{array}{l}{E}_{({\mathbf{R}}_{ij}^X\mid {\overline{\mathbf{R}}}_{ij}^Y,{\overline{\mathbf{R}}}_{ij}^X,{\mathbf{W}}_{ij}^{\ast },A_{ij}=1,Y_{ij},{\mathbf{X}}_{ij},{\mathbf{V}}_i)}\left[A_{ij}\left(\prod _{k=1}^K\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right)U_{ij({\mathbf{r}}_j^X)}^{(1)}(\mathit{\phi })\right]\\ =A_{ij}{U}_{ij({\mathbf{r}}_j^X)}^{(1)}(\mathit{\phi })E_{({\mathbf{R}}_{ij}^X\mid {\overline{\mathbf{R}}}_{ij}^Y,{\overline{\mathbf{R}}}_{ij}^X,{\mathbf{W}}_{ij}^{\ast },A_{ij}=1,Y_{ij},{\mathbf{X}}_{ij},{\mathbf{V}}_i)}\left[\prod _{k=1}^K\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right]\\ =A_{ij}{U}_{ij({\mathbf{r}}_j^X)}^{(1)}(\mathit{\phi })I_{({\mathbf{r}}_j^X=\mathbf{1})},\end{array}$$

where $I_{({\mathbf{r}}_j^X=\mathbf{1})}$ is the indicator that ${\mathbf{r}}_j^X$ is the member of ${\mathcal{R}}_j^X$ where $r_{jk}^X=1$ for k = 1, …, K because

$$E_{({\mathbf{R}}_{\mathit{ijk}}^X\mid {\overline{\mathbf{R}}}_{ij}^Y,{\overline{\mathbf{R}}}_{\mathit{ijk}}^X,{\mathbf{W}}_{\mathit{ijk}}^{\ast },A_{ij}=1,Y_{ij},{\mathbf{X}}_{ij},{\mathbf{V}}_i)}\left[\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right]=r_{jk}^X\forall k=1,\dots ,K.$$

Finally, $E_{(Y_{ij}\mid A_{ij}=1,{\mathbf{X}}_{ij},{\mathbf{V}}_i)}[A_{ij}{U}_{ij(\mathbf{1})}^{(1)}(\mathit{\phi })]=0$, where $U_{ij(\mathbf{1})}^{(1)}(\mathit{\phi })$ is $U_{ij({\mathbf{r}}_j^X)}^{(1)}(\mathit{\phi })$ for ${\mathbf{r}}_j^X=\mathbf{1}$.

Similarly, we use iterated expectations to show that equation (11) has mean 0. First,

$$\begin{array}{l}{E}_{({\mathbf{R}}_{ij}^X\mid {\overline{\mathbf{R}}}_{ij}^X,{\overline{\mathbf{R}}}_{ij}^Y,{\mathbf{W}}_{ij}^{\ast },A_{ij}=1,{\mathbf{X}}_{ij},{\mathbf{V}}_i)}\left[A_{ij}\left(\prod _{k=1}^K\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right){\mathbf{U}}_{ij({\mathbf{r}}_j^X)}^{(2)}(\mathit{\phi })\right]\\ =A_{ij}{\mathbf{U}}_{ij({\mathbf{r}}_j^X)}^{(2)}(\mathit{\phi })E_{({\mathbf{R}}_{ij}^X\mid {\overline{\mathbf{R}}}_{ij}^X,{\overline{\mathbf{R}}}_{ij}^Y,{\mathbf{W}}_{ij}^{\ast },A_{ij}=1,{\mathbf{X}}_{ij},V_i)}\left[\prod _{k=1}^K\frac{{(R_{\mathit{ijk}}^X)}^{r_{jk}^X}{({\pi }_{\mathit{ijk}}^X-R_{\mathit{ijk}}^X)}^{(1-r_{jk}^X)}}{{\pi }_{\mathit{ijk}}^X}\right]\\ =A_{ij}{\mathbf{U}}_{ij({\mathbf{r}}_j^X)}^{(2)}(\mathit{\phi })I_{({\mathbf{r}}_j^X=\mathbf{1})}.\end{array}$$

Next, $E_{({\mathbf{X}}_{ij({\mathbf{r}}_j^X)}\mid A_{ij}=1,{\mathbf{V}}_i)}[A_{ij}{\mathbf{U}}_{ij({\mathbf{r}}_j^X)}^{(2)}(\mathit{\phi })]=0$. Thus, equations (10) and (11) are unbiased so long as ${\pi }_{ij}^Y,{\pi }_{\mathit{ijk}}^X,{\mu }_{ij}^{\mathbf{X}\mid A}$, and ${\mathit{\mu }}_{ij}^{Y\mid A,\mathbf{X}}$ are correctly specified, even if the distributions of X_{i j} and Y_{i j} are not correctly specified.