Prediction and Modulation of Platelet Recovery by Discontinuous Centrifugation of Whole Blood for the Preparation of Pure Platelet-Rich Plasma

Abstract

The aim of this study was to describe the behavior of the separation of red blood cells (RBCs) by discontinuous centrifugation (DC) of whole blood to modulate and control the platelet recovery in the preparation of pure platelet-rich plasma (P-PRP). P-PRP is a platelet-rich plasma (PRP) in which the white blood cell layer is not included. To achieve this goal, an analytical model was derived that takes into account the packing of RBCs and predicts the behavior of platelet and plasma recovery efficiencies (PtPlRE) based on the volume of whole blood, the hematocrit, and the volume of supernatant, as a function of the operating variables, centrifugal acceleration, and time. The model was derived from the basic equation of DC, which originates from the equilibrium balance of forces on a particle, and included the addition of one factor that corrected the terminal velocity of RBCs and was also correlated to the PtPlRE in the supernatant. This factor was the ratio between the fractional volume concentrations of plasma and RBCs in the centrifugation pellet after centrifugation. The model was validated and the variability of the data was determined using experimental data from 10 healthy donors in the age range of 25–35 years. The predicted behavior for the packing of RBCs and the PtPlRE was consistent with the behavior seen in the experimental data. Thus, the PtPlRE could be modulated and controlled through centrifugal acceleration, time, and hematocrit. Use of this model based on a physical description of events is the first step of a reliable standardization of PRP preparations.

Introduction

Platelet-rich plasma (PRP) is defined as an autologous preparation from whole blood (WB), in which platelets are concentrated in a small fraction of plasma. This broad definition is considered to be the consensus definition by the International Olympic Committee in sports medicine.¹

Platelets are rich in growth factors, which are critical for tissue regeneration.^2,3 Specifically, growth factors are released from activated platelets at sites of injury; the amount and activity of the growth factors depend on the recovery and preservation of platelets during PRP preparation.¹

In general, PRP preparation is a sequential three-step process that involves blood collection, centrifugation to separate and concentrate the platelets, and activation of the platelets. Accordingly, PRP quality and efficiency is highly dependent on the protocol used for its preparation.^1,4–6 There are a multitude of PRP preparation protocols in the literature, which differ in terms of the conditions used in the preparation steps, such as centrifugal acceleration and time, the number of centrifugation steps, the type of anticoagulant, and the type of platelet agonist.^7–11

Due to this variation, it is difficult to compare the biological effects that are reported in different studies, even for a specific use, which can lead to doubts that compromise the credibility of PRP-based therapies.¹

For the preparation of PRP, blood collection must be performed without trauma to the vessel wall to ensure the integrity of the platelets. Centrifugation is the first step in PRP preparation, which requires the recovery of a large number of intact platelets. Thus, both platelet activation and the final properties of the PRP preparation are influenced by the centrifugation step.

Studies on centrifugation for the preparation of PRP are scarce in the literature. The authors attempt to determine the optimal centrifugation conditions for the recovery of platelets using experimental data from a limited number of experimental conditions. In general, the physical phenomena involved in centrifugation as well as the integrity of platelets are not considered in the interpretation of the experimental data.^12–15

Adding to the complexity, one of the great challenges in studying an autologous product like PRP is to extract a maximum of information from experiments performed with raw material that is not abundant for each donor and exhibits variability among and within individual donors. Given this context, the prediction of the system behavior based on the phenomenological behavior becomes essential.

Accordingly, the objective of the current work was to study the separation of red blood cells (RBCs), platelets, and plasma by discontinuous centrifugation (DC) of WB, with the aim of determining centrifugation conditions that modulate and maximize the efficiency of the recovery of platelets in the supernatant, or upper layer (UL), from a well-established pellet of red blood cells (RBCs) in the bottom layer (BL). Our approach was to develop a mathematical model to predict the platelet and plasma recovery efficiencies (PtPlRE) as a function of the operating variables of the DC and the initial data from the WB samples. To our knowledge, there is no model in the literature that predicts the PtPlRE from DC for the preparation of PRP. In this study, we focused on the preparation of pure (P)-PRP, a type of PRP in which the buffy coat (BC) is not included.

Material and Methods

Experimental

All experiments were approved by the Ethics Committee of the Medical Sciences School of the University of Campinas (UNICAMP; CAAE: 0972.0.146.000-11).

The centrifugation assays were conducted in a Rotina 380R centrifuge (Hettich Lab Technology). The concentration of the WB components was determined using a hematological counter, the Micros ES 60 (Horiba). Blood was collected into 3.5-mL vacuum tubes (Vacuette^®) containing sodium citrate (3.2%) as an anticoagulant, in the volumetric proportion 9:1 blood:sodium citrate. After counting the RBCs and platelets, the WB was centrifuged for 10 min at 70, 100, 190, 280, 370, 460, 550, and 820 g. The supernatant (not including the BC layer) was carefully pipetted to measure the volume and transferred to another tube to determine the platelet concentration. After that, the BC layer was also carefully collected and added to the UL fraction, and the new volume and platelet concentration were determined. The platelet concentration in the BC was determined by the difference in the platelet counts in the volumes with and without BC.

Recovery efficiencies of plasma and platelets

The plasma recovery efficiency in the UL, E_(Pl)UL, was calculated using Equation 1.

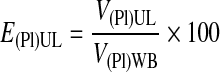(1)

V_(Pl)WB was estimated as V_WB(1 − H), where V_WB is the volume of whole blood and H is the hematocrit. RBCs were defined here as the total blood cells (RBCs are 99% of the total cells in WB).

The platelet recovery efficiency, E_(Pt)UL, or the percentage of platelets in the UL was calculated using Equations 2–4.

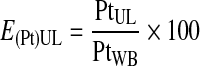(2)

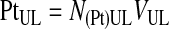(3)

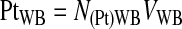(4)

Concentration factor of platelets

The concentration factor of platelets, F_CP, defined by Equation 5, is the ratio between the concentrations of platelets in the UL and in the WB.

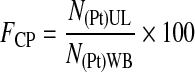(5)

The analytical model

The analytical model for the prediction of the PtPlRE in the UL was derived from a description of the separation of RBCs from WB under DC, as follows (Eqs. 6–18).

Initially, the separation of the components of WB under a centrifugal field was evaluated in terms of the settling velocities at infinite dilution (v_∞) in the Stokes regime (Eqs. 6 and 7).¹⁶ Integration of Equation 6 yields Equation 8, which represents the displacement of a particle between two points, x₁ and x_2, in a centrifugal tube, with the settling velocities taken at infinite dilution.

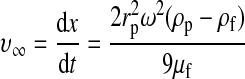(6)

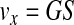(7)

where G is the centrifugal acceleration, S is the sedimentation coefficient, and the subscripts p and f refer to the particle (blood component) and fluid (WB), respectively. For the calculations, we used the physical properties of various blood components as reported by Brown,¹⁷ except for the blood viscosity¹⁸ (0.03 g/[cm·s]) and the platelet density¹⁹ (1.06 g/cm³).

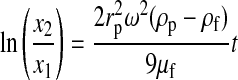(8)

Equation 8 is the basic equation of DC. In Equation 8, ω² must be written in terms of G×g, where G×g=ω²r_r and r_r is the radius of the axis of the rotor.

Next, to consider the backflow of the cell suspension, instead of only the backflow of plasma, the settling velocity of RBCs was corrected. Thus, in a second step, a correlation was obtained between the ratio of the actual setting velocity of RBCs to the predicted settling velocity at infinite dilution and a correction factor, (1 − H_BL)/H_BL, where H_BL is the RBC concentration in the BL (Eq. 9). The correction factor represents the fractional volume concentrations of plasma and RBCs in the centrifugal pellet, or BL. It also represents the packing of RBCs in the BL. To generate the correlation, the settling velocity of RBCs was determined experimentally by measuring the height of the UL in the centrifugation tube and dividing by the time of centrifugation.

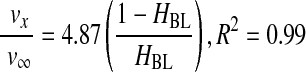(9)

Third, H_BL, the concentration of RBCs in the BL, was determined based on the conservation of RBCs from the WB to the BL and was written as function of V_UL (Eqs. 10–12). V_UL was calculated as a function of the operating variables centrifugal acceleration (G) and time (t), using the basic equation of DC and including v_∞ as corrected by the factor (1 − H_BL)/H_BL. Therefore, H_BL and V_UL were calculated by an iterative process that determined x_2, which is the distance from the axis of the centrifugal head (or rotor), through Equations 10–15.

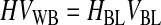(10)

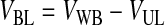(11)

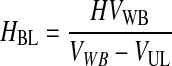(12)

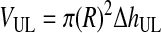(13)

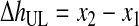(14)

(15)

In a fourth step, the ratio of platelet and plasma recovery efficiencies also was correlated with the factor (1 − H_BL)/H_BL (Eq. 16), and the PtPlRE values were calculated using Equations 1–15. Finally, the model for the prediction of the ratio of platelet and plasma recovery efficiencies was written as a function of V_WB, H, and V_UL (Eqs. 17 and 18).

(16)

(17)

(18)

Note that to establish this model, WB was first collected from a single donor. The model was then validated using data from 10 healthy individuals who were in the age range of 25–30 years. The assumptions for the model are as follows: isothermal centrifugation (25°C), RBCs considered as spherical and rigid particles, range of G 50–820 g and time 1 to 10,000 sec (plausible conditions for preparation of PRP), discontinuous centrifugation with brake off, and sodium citrate as anticoagulant.

Results

Separation of the components of WB

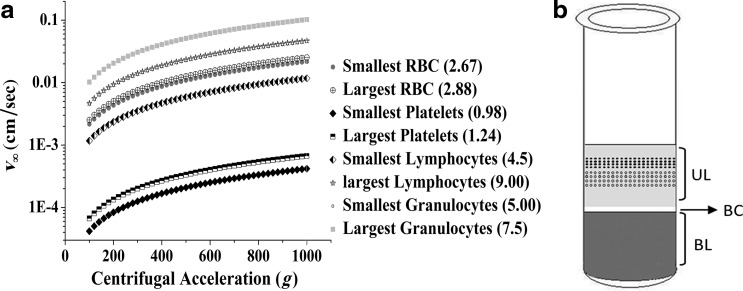
We initially used the physical properties of WB to calculate the settling velocities at infinite dilution (v_∞) as a function of G for the various WB components: RBCs, white blood cells (WBCs), and platelets. Figure 1a shows these settling velocities for WB cells as a function of G. The v_∞ values increased with G for the types of blood cells considered, reaching different plateaus. Platelets, which are the smallest cells, moved more slowly than the other cells, allowing them to be separated from the RBCs. Figure 1b shows the positions of the cells in a centrifuge tube schematically; the positions reflect the theoretical cell separation after centrifugation, without consideration of the interactions among particles. We observed a supernatant, or UL, composed mainly of platelets plus some WBCs dispersed in the plasma; a pellet, or BL, in which all RBCs settled, but which also contained platelets and WBCs and an intermediate thin layer, or BC, that was between the UL and the BL and was rich in WBCs.

FIG. 1.

(a) Settling velocities at infinite dilution, v_∞, as a function of centrifugal acceleration (G) for the various cells in whole blood (size×10⁻⁴ cm) and (b) relative positions of the blood cells inside the centrifuge tube after discontinuous centrifugation. Plasma (light gray), platelets (cells dispersed in plasma), buffy coat (BC; intermediate white blood cell layer), and concentrated red blood cells (RBCs) and other kinds of cells (dark gray) are positioned as shown.

Experimental parameters

Table 1 summarizes the experimental results (i.e., the UL and the UL+BC volumes) as well as the platelet concentrations and the factor of platelet concentration, F_CP, in the UL.

Table 1.

Experimental Data and Calculated Parameters

G (g)	N(Pt)WB(Pt/mm3×10−3)	VUL(mL)	N(Pt)UL(Pt/mm3×10−3)	N(Pt)UL+BC(Pt/mm3×10−3)	FC(UL)	HBL	E(Pl)UL(%)	E(Pt)UL(%)
50	230	1.0	481	361	2.1	0.52	45.3	60.0
70	264	1.2	540	396	2.0	0.59	55.9	70.1
100	245	1.3	467	379	1.9	0.63	62.0	70.8
190	246	1.4	350	174	1.4	0.66	66.7	56.9
280	241	1.7	178	117	0.7	0.77	81.0	35.9
370	230	1.8	117	57	0.5	0.82	85.7	26.2
460	235	1.8	92	82	0.4	0.82	85.7	20.1
550	260	1.9	114	128	0.4	0.87	90.5	23.8
820	247	1.9	36	109	0.1	0.87	90.5	7.9

Experimental data include platelet concentrations in the whole blood, upper layer, and upper layer plus buffy coat, as well as the volume of the upper layer. Calculated parameters include the platelet concentration factor, the packing of the red blood cells in the bottom layer, and the platelet and plasma recovery efficiencies as a function of centrifugal acceleration.

G, centrifugal acceleration; N_(Pt)WB, number of platelets per unit volume in whole blood; N_(Pt)UL, number of platelets per unit volume in the upper layer; N_(Pt)LP+BC, number of platelets per unit volume in the upper layer + buffy coat; V_UL, volume of the upper layer; F_C(UL), platelet concentration factor; H_BL, packing of the red blood cells in the bottom layer; E_(Pl)UL and E_(Pt)UL, plasma and platelet recovery efficiencies, respectively.

As expected, the UL volume increased with increasing G. At values of G ranging from 70 to 100 g, the platelet concentration in the UL was ∼500×10⁻³ platelets/mm³, while the platelet concentration decreased markedly at higher G. Although the total BC volume was the same for all of the samples (0.6 mL), the platelet concentration in the UL+BC was lower at up to 460 g. However, it was higher in the UL+BC than in the UL at the highest values of G (550 and 820 g). These results show that at 550 and 820 g, the platelets stayed mainly in the BC. As a consequence, the F_CP had a maximum value of 2.0 in the UL at G up to 100 g, and it decreased at higher values of G.

Table 1 also shows the calculated values for H_BL and the recovery efficiencies of plasma (E_(Pl)UL) and platelets (E_(Pt)UL) in the UL as a function of G. From a hematocrit of ∼0.4, H_BL increased up to 0.87, which shows the packing of the RBCs into the BL. E_(Pl)UL increased with increasing G up to 90.5%, while E_(Pt)UL increased from 60% to 70% for G up to 100 g and then decreased sharply to 8% as G rose toward 820 g

Recovery efficiencies of platelet and plasma

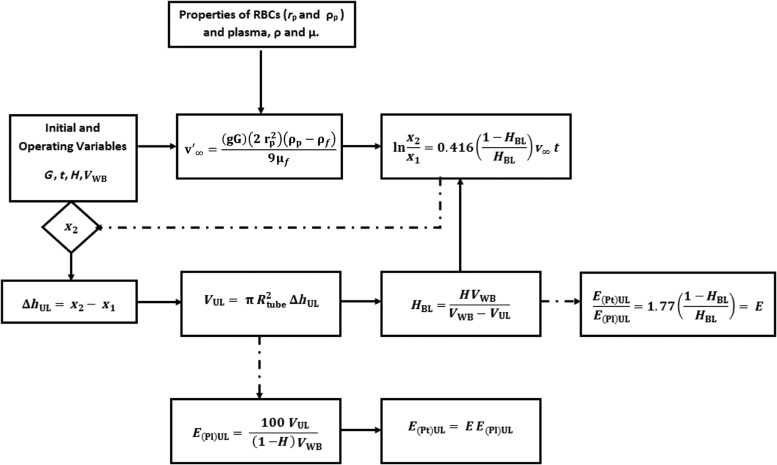
The analytical model (Eqs. 17 and 18) allowed us to predict the PtPlRE for a given volume of collected WB, V_WB, with hematocrit H, subjected to a given G for a defined time period. The model allows for the prediction of the PtPlRE.

Figure 2 shows the algorithm used for calculating the E_(Pt)UL and E_(Pl)UL using the derived model.

FIG. 2.

Algorithm for the calculation of plasma and platelet recovery efficiencies, E_(Pt)UL and E_(Pl)UL, respectively, using the derived model for the platelet and plasma recovery efficiencies (Equations 17 and 18).

Validation and performance of the model

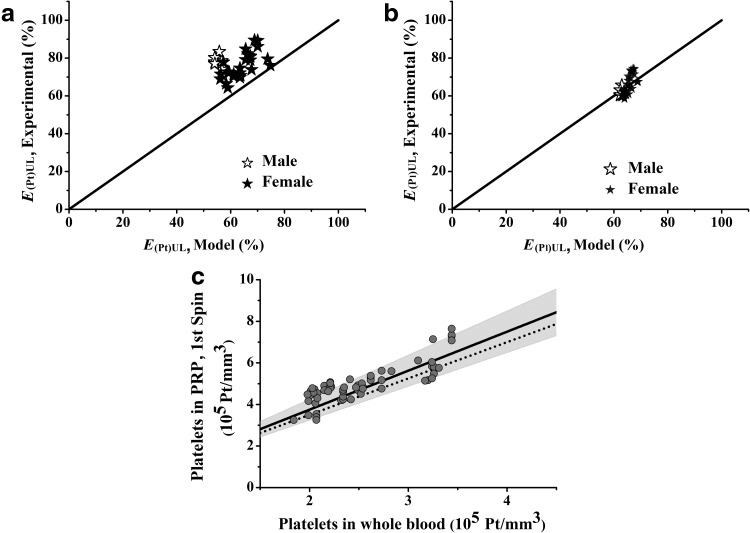
Figure 3 shows the experimental data and the predicted values for the E_(Pt)UL (Fig. 3a) and the E_(Pl)UL (Fig. 3b). Notably, there were variations in the experimental data because there were several blood donors and because blood was collected on different days. The predicted E_(Pl)UL fitted the experimental data better than the predicted E_(Pt)UL did. For the latter, the model underestimated the experimental data.

FIG. 3.

Validation and performance of the derived model with experimental data. The derived model was obtained from Equations 6–18. The experimental data were from 10 healthy individuals in the age range of 25–30 years, whose blood was centrifuged at 100 g for 600 sec. (a) Recovery efficiencies of platelets. (b) Recovery efficiencies of plasma. (c) Performance of the model in terms of the platelet concentrations before and after centrifugation. The solid line represents the experimental average of the platelets; the dashed line depicts the platelet concentrations predicted by the model; and the grey zone is the dispersion of the experimental data.

Figures 3c shows the performance of the model in terms of platelet concentration compared with the average of the experimental data. This graphical result is useful because it directly provides the platelet concentration for the preparer of PRP, and it also evaluates the performance of the centrifugation process.

Predicted behaviors

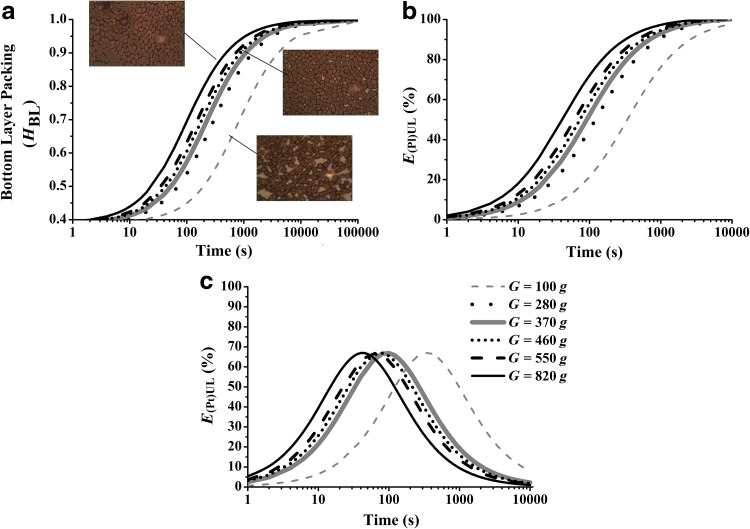
Figure 4 illustrates the behaviors for H_BL, E_(Pl)UL, and E_(Pt)UL, which were predicted using the model.

FIG. 4.

Influence of the operating variables G and time on (a) the packing of red blood cells in the bottom layer, (b) the recovery efficiency of plasma in the upper layer, and (c) the recovery efficiency of platelets on the upper layer.

The curves in Figure 4 show a sharp influence of both G and time on the separation behavior of RBCs, platelets, and plasma. In Figure 4a, H_BL increases with G and time and asymptotically approaches 1, which is the maximum packing of RBCs, at a time of approximately 10,000 sec. The inset micrographs show the differences in the RBC packing at 600 sec for values of G equal to 100, 280, and 820 g. A more porous BL was formed at 100 g, while at 820 g, a denser BL was obtained. In addition, it seems that at low values of G, the RBCs settle and pack in a configuration different from that of the individual elongated cells seen in the micrographs generated at higher G. This behavior recalls the effect of the natural rouleaux formation of RBCs at low shear rates. This is reflected by a rise in the RBC sedimentation rate, as previously reported.¹⁸ This is consistent with the correlation described by Equation 9, in which at low G (low H_BL), the settling velocity v_x is higher than the terminal velocity determined for individual RBCs. Figure 4a also shows that at times less than 50 sec, the BL is still incipient, with an H_BL of ∼0.5. A well-established BL of RBCs can be defined as having an H_BL≥0.6 and facilitates the removal of the V_UL for the preparation of PRP.

Similarly, for the recovery of plasma (Fig. 4b), the curves increase with both G and time and reach the maximum (100% of plasma in the UL) at a time of ∼10,000 sec.

For platelets (Fig. 4c), the recovery efficiencies also increase with G and time, but they reach a maximum of 70% at times that are dependent on the value of G. The maxima of the curves correspond to times ranging from 50 to 400 sec, in which the packing of RBCs in the BL is approximately 60% (Fig. 4a).

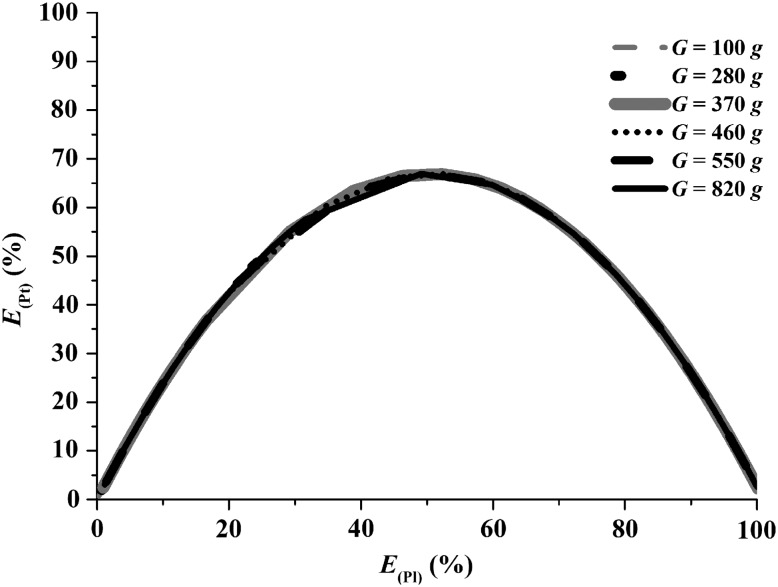
Figure 5 shows the recovery efficiencies of platelets and plasma as predicted by the model (Eqs. 17 and 18) at various Gs and times for a V_WB of 3.5 mL and an average H equal to 0.4. It can be seen the overlapping of the curves at various Gs and times. The figure also defines a point of maximum recovery of platelets, 70%, which corresponds to a recovery of 50% of the plasma. Therefore, the region around this point corresponds to the optimal condition for the recovery of platelets and plasma from WB by DC. Note that at E_(Pl)UL<50%, the E_(Pt)UL is higher than the E_(Pl)UL.

FIG. 5.

Behavior of the recovery efficiencies of platelets and plasma at centrifugal accelerations from 100 to 820 g and times from 1 to 10,000 sec for an average hematocrit 0.4. There is overlapping of the curves at the various Gs and times.

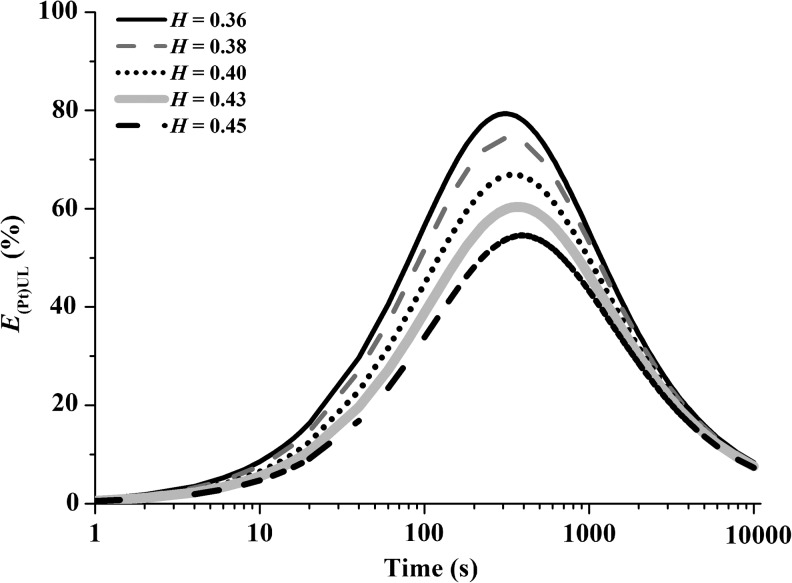
For a G of 100 g, the influence of the hematocrit on the recovery of platelets, as well as on the packing of RBCs and on the V_UL, is shown as a function of time in Figure 6. The recovery of the platelets decreases as the hematocrit increases, and this effect is most pronounced at the region of the maximum recovery of platelets.

FIG. 6.

Influence of hematocrit and time on the recovery efficiency of platelets with centrifugal acceleration G=100 g.

Modulation and Control

The modulation and control of the PtPlRE from centrifugation can be achieved through the operating variables G, time, and hematocrit. Figure 4c shows that the maximum recovery of platelets can be obtained at higher Gs and shorter times, or lower Gs and longer times. However, high Gs may affect the integrity of the platelets, a phenomenon that should be investigated. Therefore, low values of G, such as 100 g, provide a maximum recovery of platelets and should also preserve the integrity of the platelets. For 100 g, the times of maximum recovery of platelets are from 300 to 400 sec. These times should also determine the amount of WBCs such as lymphocytes, neutrophils, and granulocytes in the UL, which must also be investigated. The control of the hematocrit can be achieved by dilution, which can be made with PRP. Such dilution enhances the recovery of platelets in the UL, as seen from the trend of the curves in Figure 6.

Discussion

As expected, centrifugation separated the cells of WB based on their physical properties, which resulted in different settling velocities (Fig. 1a). However, the combined effects of density, viscosity, and backflow of the suspension yielded Equation 9, which corrected the settling velocity of RBCs at infinite dilution by a factor that relates the concentration of voids to the concentration of RBCs in the BL. Since this factor took into account the partition of plasma between the BL and the UL, it also correlated well with the ratio of recovery efficiencies of the platelets and plasma. Surprisingly, at low G, the terminal velocity did not overestimate the actual speed of RBCs, a fact that we attribute to the effect of rouleaux formation, which increased the sedimentation rate, provided a more porous packing of RBCs in the BL, and increased the recovery of platelets. Greater Gs and times produced higher H_BL values, a decrease in the porosity of the BL and a sharp decrease in platelet recovery.

In discontinuous centrifugation, the cells are distributed in the tube in three phases: an UL, a BC fraction, and a BL (Fig. 1b). The concentrations of platelets in the UL and in the UL+BC showed that the retention of platelets in the BC layer was only ∼10%, except when G was 820 g, which yielded a retention of 20% (Table 1). We used only the platelet concentration in the UL to derive the model for P-PRP. An important result from the experimental data was that a G equal to 100 g and a time of 600 sec resulted in the highest concentration of platelets in the UL, with an average concentration factor, F_CP, of 2.0. For other values of G, the F_CP was less than 1. The maximum F_CP corresponded to an H_BL of ∼0.6, in which the fraction of plasma was 0.4 and the recovery efficiency of platelets was maximal, ∼70% (Table 1). Therefore, lower G favored the recovery of platelets in the UL. In contrast, fast and dense packing of RBCs at higher G caused platelet losses of approximately 30%–40% (Table 1). Therefore, the packing of the RBCs (H_BL) influenced the platelet separation from WB. As shown in Figure 3, the behavior predicted by the model was consistent with the trends in the experimental data. Therefore, although the model underestimated the recovery efficiency of platelet relative to the experimental data, we considered these predictions to be effective in light of the complexity and variability of an autologous product such as PRP. The advantage of the model is primarily its practicality because it includes the initial data of hematocrit and volume of WB, the upper volume generated as a function of the operating variables G and time, as well as the ease of the algorithm used to perform the calculations. In addition, the predictions from the model provide an understanding of the behavior of the separation and the modulation of the recovery of platelets using less blood as a raw material than could a solely experimental study.

A comparison of our results with those reported in the literature revealed that the recovery efficiencies of platelets and plasma in DC do not follow the 45° straight line that was described by Brown¹⁷ for continuous centrifugation. With respect to the results reported for just one centrifugation by Kahn et al.¹⁴ (100% recovery efficiency, G of 2300–3000 g, and centrifugation time of 1 min) and Jo et al.¹³ (92% recovery efficiency, G of 900 g, and centrifugation time of 5 min), although the range of G they used is outside the range we studied, our experimental and predicted tendencies did not agree with theirs. Rather, our results indicate that for Gs and times of this order of magnitude, the RBC packing still is incipient, the separation is not well established, and it is difficult to assure reproducible data for the platelet recovery efficiency (Fig. 4).

Landesberg et al.¹⁵ obtained an F_CP of 2 when centrifuging 5 mL of WB for 10 min at G=100 g, and Araki et al.¹² obtained a platelet recovery efficiency of 70%–80% using G=70 g for 10 min. Both of these results are in agreement with our results.

Finally, the predictions of the behavior of separation of RBCs, platelets, and plasma by DC allowed us to modulate and to control the recovery of platelets in terms of G, time, and hematocrit.

These findings contribute to the preparation of PRP under a scientific basis and controlled conditions as well as the standardizing the PRP as an autologous product for specific applications. Studies to account for the effects of variations in the age range and the state of health of the individuals, as well as the integration of the centrifugation step with the activation step in the preparation of PRP, are ongoing in our group. These studies will allow a refinement of the model derived in this work for P-PRP.

Conclusions

This study showed that discontinuous centrifugation for the recovery of platelets, which is a crucial step in the preparation of PRP, can be described by a mathematical model that is based on a physical description of events. The model allowed us to predict the behavior of the separation of RBCs and to maximize, modulate, and control the recovery efficiency of platelets through G, time, and hematocrit by identification of the regions in which the efficiency of platelet recovery is maximal. Adopting these predicted conditions in P-PRP protocols will ensure that the composition of the P-PRP is controlled and reproducible and can even be modulated. These findings contribute to the standardization of the quality of P-PRP in a scientific basis for in vitro biological assays. The characterization and the interconnection between the quality and biological properties of PRP form the basis for further clinical studies.

Acknowledgments

The authors appreciate the participation of the volunteer blood donors and thank the state financial agency, FAPESP (Fundação de Amparo a Pesquisa do Estado de São Paulo), Brazil, which supported this work.

Disclosure Statement

There are no competing financial interests to declare.