Abstract
Diabetes is a chronic and complex multifactorial disease caused by persistent hyperglycemia and for which underlying pathogenesis is still not completely understood. The mathematical modeling of glucose homeostasis, diabetic condition, and its associated complications is rapidly growing and provides new insights into the underlying mechanisms involved. Here, we discuss contributions to the diabetes modeling field over the past five decades, highlighting the areas where more focused research is required.
Introduction
Modern and sedentary lifestyles result in the increased prevalence of systemic diseases, such as diabetes and obesity. According to the latest International Diabetes Federation report, ~8.3% of the global population has diabetes, with this figure expected to rise to 9.9% by 2030 (S1). In addition, the International Diabetes Federation has also estimated that several million people have the condition but are unaware of it. Diabetes, and the complications associated with it, has imposed significant economic consequences and social burdens on individuals, families, health systems, and countries (S2). Numerous studies are being carried out toward improving the quality of life for patients struck by this systemic disease.
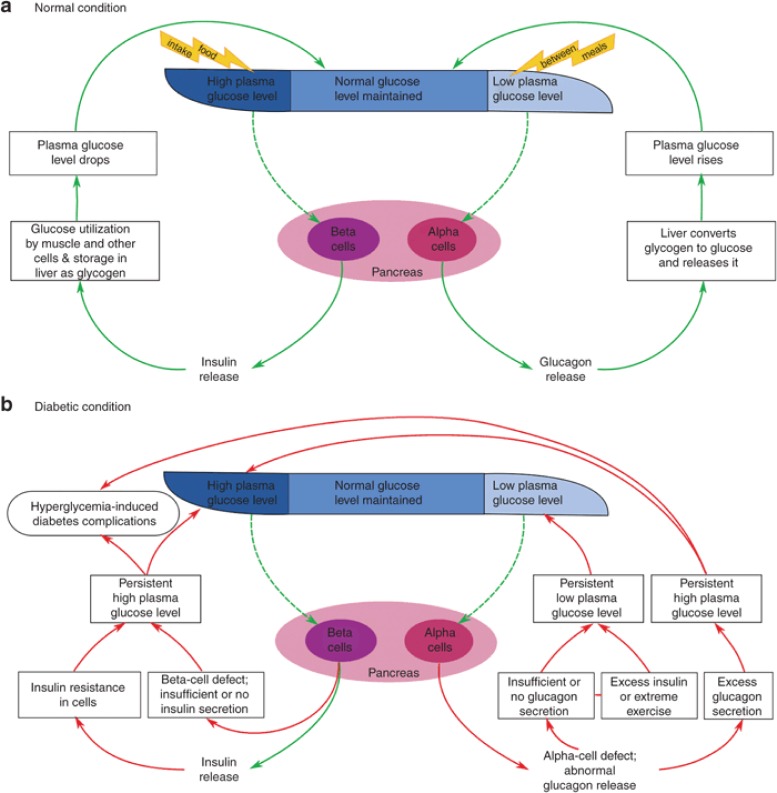
Diabetes is a condition that occurs when the normal insulin–glucose–glucagon regulatory mechanism is affected. Plasma glucose levels are normally maintained within a narrow range through the combined antagonistic action of the two pancreatic hormones, insulin and glucagon. In normal individuals, high blood glucose levels induce the release of insulin, which enables its target cells to take up glucose. In low-glucose conditions, glucagon induces the breakdown of glycogen into glucose (Figure 1a). In diabetic individuals, this synchronized mechanism is disrupted, which results in persistent hyperglycemia (Figure 1b) (see Supplementary Data online). The major concern associated with diabetes is its multietiological and systemic nature. Long-term persistence of diabetes can result in multiple micro- and macrovascular damages, leading to several systemic complications (S3).
Figure 1.
General overview of the glucose homeostasis mechanism under normal and diabetic condition. Plasma glucose level is maintained within a narrow range through the combined antagonistic action of two pancreatic hormones: insulin and glucagon. (a) In normal individuals, high plasma glucose level induces the release of insulin from pancreatic β-cells, which enables the muscle and other cells to take up glucose for energy or to store it as glycogen in liver. On the other hand, at low plasma glucose level, glucagon secreted from α-cells counterregulates the glucose level by inducing the breakdown of glycogen into glucose. (b) In diabetic individuals, the synchronized mechanism between insulin and glucagon secretion is disrupted. Insufficient or lack of insulin production by β-cells, or insulin sensitivity in muscle and other cells, leads to persistent high plasma glucose level (hyperglycemia). This condition is often accompanied by absolute or relative excess level of glucagon, which causes a higher rate of hepatic glucose production than utilization, favoring hyperglycemia (S123–S125). Another defect that is seen in diabetic patients is the impaired secretory response of α-cells to release glucagon when the plasma glucose level drops, leading to the risk of episodes of severe hypoglycemia (S126). This often occurs due to exposure to excess insulin during treatment or to extreme physical activities carried out as part of self-management, accompanied with compromised glucose counterregulation (see Supplementary Data online, for details).
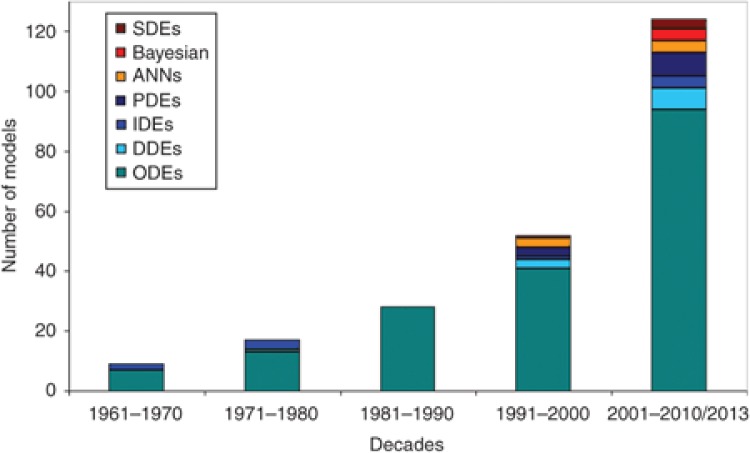
Mathematical models play an increasingly important role in understanding the dynamic behavior and the mechanism underlying diverse and complex biological systems. Numerous mathematical models, statistical methods, and computer algorithms are being developed, which focus on different aspects of diabetes, ranging from molecular and cellular biology through clinical science to health service research. The increase in the types of modeling approaches and the number of models generated over the past five decades are shown in Figure 2.
Figure 2.
Modeling approaches vs. the number of models in relation to diabetes and associated complications, over the past five decades. There has been a significant increase in the number of models, as well as in the diversity of the modeling approaches applied toward addressing diabetes. ANNs, artificial neural networks; DDEs, delay differential equations; IDEs, integro-differential equations; ODEs, ordinary differential equations; PDEs, partial differential equations; SDEs, stochastic differential equations.
Despite the availability of numerous models that attempt to address the complexity of this disease, an imbalance still exists between the current knowledge obtained from experimental approaches and their mathematical representation. To overcome this, it is important to revisit the progress made so far toward diabetes modeling. In this review, we discuss the models that have been developed over the past five decades. Mathematical models of diabetes are grouped based on the purpose for which they are developed and the biological process they address. This classification is then used to generate a comprehensive model relationship map (Figure 3) for each category. Considering the importance of sharing and reuse of models in the field of diabetes research, we encoded several of these models using a standard model description language SBML (systems biology mark-up language) (S4). In addition, some of these models were also curated and annotated with terms from controlled vocabularies and cross-referenced to external data resources (S5). These models (highlighted in green in Figure 3) can be accessed from BioModels Database,1 an online resource for storing and sharing quantitative models of biological processes. Finally, we identify and discuss research challenges (Figure 4) in the field of diabetes modeling. This review aims to serve as an information resource and concludes by addressing directions that need to be better understood.
Figure 3.
Model relationship map. Models that describe diverse aspects of glucose homeostasis and diabetes are broadly classified into clinical (I) and nonclinical (II) models based on the data used, the level of complexity, and the biological description. Within each of these categories, these models are further subclassified based on the purpose for which they are developed and the physiological scale utilized in the models. The subclassification of models are as follows: I-a, diagnosis; I-b, control; I-c, progression; I-d, complications; II-a, whole-body insulin–glucose dynamics; II-b, hepatic glucose dynamics; II-c, brain glucose dynamics; II-d, beta-cell insulin release; II-e, glucagon dynamics; II-f, macrophage action; II-g, beta-cell electrophysiology; II-h, insulin receptor dynamics; II-i, insulin signaling; II-j, multiscale/level hierarchical models. A landscape of how the different models are related and evolve from each other is shown. The models are named with the first author's surname followed by the year of publication and the reference number. The models that are highlighted in green are available in BioModels Database. The arrow (→) is used to link models that are derived/adopted from one or more parent models. In other words, these models share common structures or equations. The line (—) is used to link models representing similar biological phenomenon but that are not derived from any other models. Models that are listed without any connections belong to the corresponding subclass, but do not share significant common components. The models that are repeated (models that fit in more than one subclass) more than once are displayed in red fonts. Models that are boxed red belong to a different category but are displayed as they serve as base models in the existing category. Reference numbers with prefix S can be found in Supplementary Data online. The figure illustrates the importance of sharing and reuse of mathematical models, to leverage on past work.
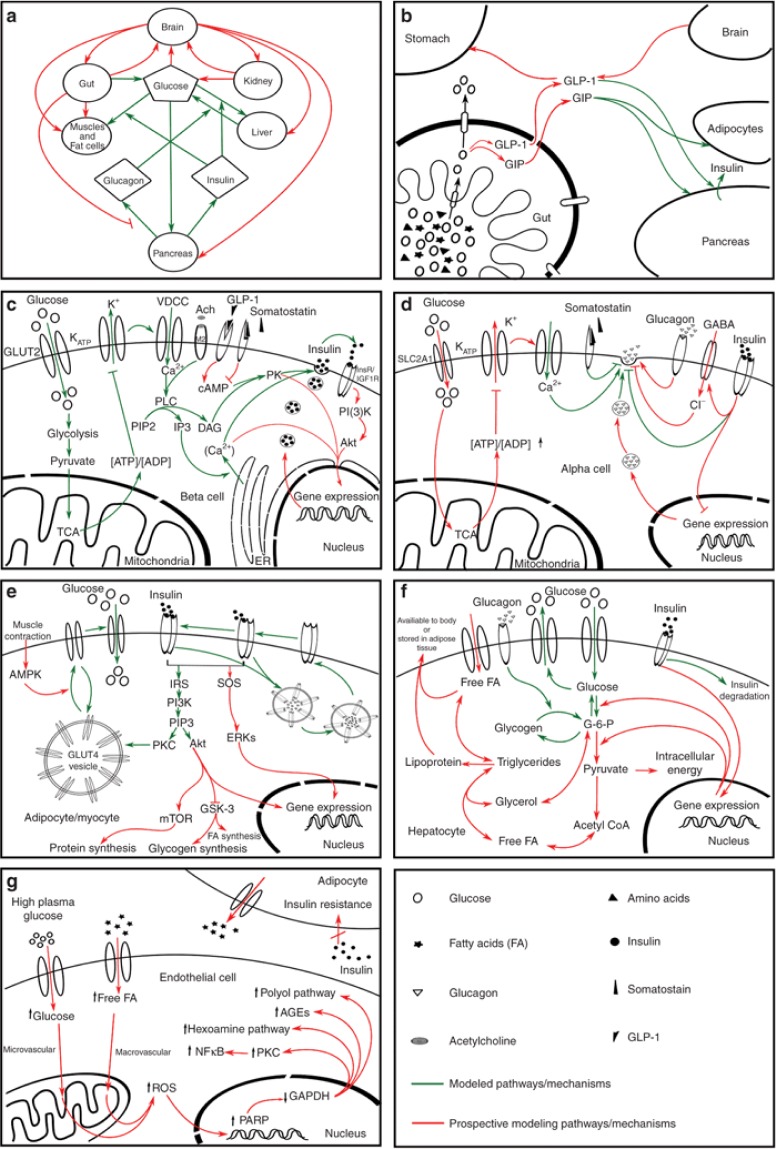
Figure 4.
Diagrammatic representation of the pathways involved in the maintenance of glucose homeostasis (a–f) and hyperglycemia-induced tissue damage pathway (g) at different biological scales (i.e., molecular, cellular, and physiological level). (a) Whole-body glucose homeostasis, (b) glucose absorption from gut, (c) glucose-stimulated insulin secretion by pancreatic β-cells, (d) glucose-mediated glucagon secretion and regulation, (e) insulin-dependent uptake of glucose in adipocytes and myocytes, (f) utilization and storage of glucose as lipid and glycogen in liver, and (g) hyperglycemia-induced tissue damage pathway, which is the cause of diverse diabetic complications. The figure illustrates a simplified representation of the pathways involved at molecular, cellular, and physiological levels. Connectors in red indicate prospective pathways for mathematical modeling while green indicates the previously modeled pathways. It should be noted that pathways denoted in green in each box do not necessarily represent a single model. Rather, they should be seen as a collection of models aimed at addressing these pathways. This figure highlights pathways that need to be targeted by future modeling studies. For detailed explanation of this figure, see Supplementary Data online.
Mathematical Models of Diabetes
Mathematical models of diabetes available in the literature can broadly be classified into clinical and nonclinical categories, based on complexity, depth of biological description, and the data (individual or population scale) used in the model. Clinical models are structurally simple and emulate clinical data by considering only essential biological description. Due to their nature, clinical models form an ideal candidate for evaluating diagnostic tests, developing glucose controllers, understanding disease progression, and predicting risks for complications. Nonclinical/knowledge-based models are more complex in nature and account for the mechanistic description of the biological systems, eventually aimed at being used for clinical purposes.
Within clinical and nonclinical categories, models can be subclassified further based on the biological processes and purpose for which they are proposed. Figure 3 provides a complete picture of models and their relationship to each other (see figure legend for details), for each subclassification. Classification of models describing systemic diseases cannot be definitive due to their complex nature, and hence, some models fit into multiple classes. Moreover, as certain subclasses include a plethora of models, only representative models are presented here.
Clinical Models
A wide range of clinical diabetes models focusing on predicting and understanding different stages of the disease, such as diagnostics, control, progression, and complication are being developed. These models are discussed in this section.
Models for diagnostic tests
To evaluate the diabetic and prediabetic condition in an individual, different glucose tolerance tests, such as intravenous glucose tolerance test (IVGTT), oral glucose tolerance test (OGTT), and meal glucose tolerance test have been devised. The aim of these tests is to obtain an estimate of insulin sensitivity (SI), glucose effectiveness (SG), insulin secretion, and β-cell function.
Insulin sensitivity (SI) and glucose effectiveness (SG). Earlier models for insulin–glucose systems are mainly focused at evaluating different diagnostics tests. Following the pioneering model of Bolie,2 a series of mathematical models illustrating insulin–glucose dynamics were developed (S6–S9). However, a major breakthrough in diabetes modeling occurred with the development of the physiological model3 for glucose disappearance following IVGTT. Being parsimonious and simple, this model is generally known as the “minimal model.” This classical model was developed as two parts, namely, the glucose minimal model4 and the insulin minimal model (S10), which account for glucose uptake and insulin release, respectively. The comparison between the assessment of SI using the glucose clamp technique (S11) and minimal models is discussed by Bergman et al.5 The structural simplicity and ability to evaluate significant physiological parameters has led to more than 1,000 publications related to minimal model.6
Despite their extensive usage, there are several limitations in the use of minimal models including overestimation of SG and underestimation of SI (S12, S13). To overcome these limitations, an additional compartment for glucose kinetics was incorporated into the model along with labeled IVGTT (S14–S18) experiments. Although these bicompartment models allow precise estimation of SI and SG, the additional cost and technology involved in using labeled IVGTT make it impractical to be applied to the general population. To overcome this, Bayesian approaches were employed in the bicompartmental model (S19). This approach improved the accuracy of the estimated SI and SG. Further addressing the limitations of Bergman minimal model,4 De Gaetano and Arino7 formulated a novel semi-mechanistic dynamic model by employing delay differential equations. The resulting model estimates glucose and insulin concentration simultaneously, by considering the feedback relationship between them. Later, Li et al. (S20) proposed a generalized version of ref. 7.
On the basis of the model by De Gaetano and Arino,7 Silber et al.8 proposed an integrated insulin–glucose model to describe IVGTT data from healthy as well as diabetic individuals, using a bidirectional insulin–glucose feedback mechanism. As OGTT closely resembles the physiological condition, this model was extended further by incorporating the description for glucose absorption and incretin effects following a meal (S21). Further extensions were made to (S21), by including data from healthy individuals (S22). Subsequently, Jauslin et al. (S23) developed a model describing the whole-day insulin–glucose profiles following multiple meal tests.
Unlike IVGTT, OGTT accounts for slow glycemic changes that correspond to the rate of glucose appearance in systemic circulation. To gain a more realistic view of glucose dynamics, mixed meal and oral glucose minimal models were extended upon IVGTT minimal models by parametrically defining the rate of glucose appearance in the plasma (S24–S26). The oral glucose test and meal test are increasingly being used for their experimental simplicity and for generating the explicit measure of SI under physiological conditions (S26–S28). Subsequently, a minimal model for labeled MOGTT was proposed (S29).
To incorporate different physiological processes associated with insulin–glucose dynamics, different variations and extensions of the classical minimal model have been developed.9,10 Besides these, there are several physiology-based paradigm models available for diagnosis, such as HOMA,11 CIGMA (S30), MATSUDA (S31), and QUICKI (S32).
Insulin secretion and β-cell function. Since the liver degrades more than a half of the secreted insulin before it is utilized by other body tissues, accurate estimation of prehepatic insulin secretion, hepatic insulin extraction, and clearance are essential for evaluating insulin secretion and β-cell function under normal and diseased conditions. Plasma C-peptide, a part of preproinsulin peptide and therefore secreted in equimolar amounts as insulin by β-cell, acts as an indicator for insulin secretion. However, peripheral C-peptide has a longer half-life and can limit the accurate estimation of insulin secretion. To address this problem, several mathematical models and model-based methods are proposed and reviewed.12 The most commonly used methods/models for estimating the rate of insulin secretion include the deconvolution method13 (S33) and combined models assuming single-(S34) and double-(S35) compartmental disappearance kinetics of both the peptides. In addition, to quantify β-cell activity under different pathological conditions, Thomseth et al. (S36) developed a model to determine the peripheral concentrations of insulin, C-peptide, and islet amyloid polypeptide during OGTT.
Later, Hovorka et al. (S37) formulated a computational method, namely, Insulin SECretion, by implementing a constrained regularization method of deconvolution. Furthermore, the Van Cauter algorithm was applied in Insulin SECretion to estimate C-peptide kinetic parameters (S38). Besides these, some minimal models that include C-peptide kinetics were also proposed for determining insulin secretion (S25, S39–S41) and hepatic insulin extraction (S42–S43). Investigating the relationship between the OGTT-based minimal model and the subcellular events for insulin secretion, Pedersen et al.14 proposed a model that links the insulin secretion model (S44) with the OGTT-based β-cell function models (S25, S45, S46).
The potentiation of insulin secretion, resulting from repeated glucose stimuli, is an important physiological aspect incorporated in early modeling studies. However, simplification of models resulted in the loss of this aspect. Recognizing its significance, Mari et al. (S47) proposed a glucose control model to quantify β-cell function using mixed meal test. This model provided a good approximation to the experimental data.
Models for control
The regulation of blood glucose concentration within safer limits in diabetic patients is achieved by effective dietary planning, physical exercise, and insulin administration. Mathematical models describing insulin administration and absorption kinetics, subcutaneous glucose absorption and gut glucose dynamics, and the effect of diet and exercise on controlling the blood glucose concentration are discussed in this section. Such simulation or virtual-patient models, representing input–output relationship between external inputs, such as insulin delivery, meal, or exercise and corresponding glucose response, forms an essential part of computational simulators.15
Insulin administration and absorption kinetics. Injecting appropriate doses of insulin based on blood glucose concentration is important; failure to do so may lead to hypoglycemia (due to overdosage) and hyperglycemia (due to underdosage). Wang et al. (S48, S49) developed insulin therapy models for both type 1 diabetes mellitus (T1DM) and type 2 diabetes mellitus (T2DM) and demonstrated that exogenous insulin infusion can effectively mimic pancreatic insulin secretion. Huang et al.16 extended the model of Li et al. (S50) (discussed in the section on Models for β-cell insulin release) that illustrates physiological oscillatory insulin secretion stimulated by elevated glucose, to include the effect of impulsive insulin injection administered either periodically or by monitoring the plasma glucose concentration level.
The most common control for diabetes is by subcutaneous injection of insulin or insulin analogues through insulin pumps. Several models (S51–S55) were proposed to estimate the plasma insulin concentration, following such administrations.
The heterogeneity associated with subcutaneous insulin absorption kinetics is a major concern when administering insulin exogenously. To address this issue, Mosekilde et al. (S56) proposed a model elucidating the relationship between different insulin oligomers and their absorption kinetics, and this model was simplified by Trajanoski et al. (S57). Subsequently, several quantitative models for subcutaneous insulin absorption (S58, S59) were developed. Along similar lines, Berger and Rodboard (S60) developed a computer program simulating insulin–glucose dynamics after subcutaneous insulin injection. Models of insulin administration and absorption kinetics are plentiful and are extensively reviewed.17,18
Subcutaneous glucose absorption and gut glucose dynamics. Understanding subcutaneous glucose dynamics is important for continuous in vivo glucose monitoring. To quantify the physiological processes associated with the interstitial and plasma glucose dynamics, Freeland and Bonnecaze (S61) and Wilinska et al. (S62) have postulated models accounting for subcutaneous glucose kinetics. Apart from this, another process that significantly affects the whole-body glucose dynamics is the glucose absorption from the gut. Considering this, Worthington (S63) and Arleth et al. (S64) developed models that illustrate the rate of glucose absorption from the gut and its appearance in the systemic circulation.
Apart from the models discussed in this section, another broader category of models that links the input data to the output results with empirical formula has evolved in the past two decades. Such models predict the prospective plasma glucose level in patients and are efficiently used in automated glucose controllers. Various algorithms, stochastic (S65–S67) and artificial neural network approaches, have been implemented towards devising such models and are discussed in a review by Balakrishnan et al.19 Furthermore, a wider range of pharmacokinetic/pharmacodynamic models to study the effects of antidiabetic drugs on insulin–glucose homeostasis are available and are reviewed by Landersdorfer and Jusko.9
Meal, exercise, and free fatty acid effect on insulin–glucose dynamics. Hovorka et al.20 developed a nonlinear predictive controller model to maintain normal glucose level during fasting conditions in T1DM patients, by using their previous model for glucose kinetics (S18) along with a Bayesian parameter estimation technique. On the basis of the minimal models by Bergman et al.3 and Cobelli et al. (S68), Fabietti et al. (S69) proposed a model for insulin–glucose dynamics in T1DM that can efficiently be used to design glucose feedback control algorithms for an artificial pancreas and was later validated using clinical data (S70).
By extending their previous model (S71), Dalla Man et al.21 suggested a model for whole-body insulin–glucose dynamics with a view to capture different physiological events following a meal. Later, the model was implemented in the development of a simulation tool, namely, Glucose Insulin Model (S72). In 2009, a Glucose Insulin Model simulator developed for performing in silico preclinical trials in T1DM subjects, named as “UVa simulator” was accepted by the US Food and Drug Administration for studying insulin treatments on animals (S73). Similar to this, Wilinska et al. (S74) presented a model for evaluating insulin delivery in T1DM patients.
Following Liu and Tang (S75) (described in the section on Models for insulin signaling), György et al. (S76) proposed a Quasi model (a T1DM linear model) to develop an optimal design controller framework for investigating T1DM. With minimal physiological states taken into account, the model was able to grasp the characteristic behavior and efficiently regulate the unbalanced glucose–glucagon–insulin system. The model was validated by generating the state of glucose absorption adopted from Dalla Man et al. (S72) and tested on models developed by Liu and Tang (S75) and Parker et al. (S77).
Physical exercise causes a transient increase in SI and glucose uptake by muscles (S78). On the basis of the model by Sorensen22 (discussed in the section on Models for whole-body insulin-glucose dynamics), Parker et al. (S79) postulated a predicative glucose control algorithm by incorporating the influence of meal and exercise, while Hernández-Ordoñez and Campos-Delgado (S80) proposed a model to reproduce variations in the blood glucose concentration induced by exercise in diabetic patients. Similarly, Derouich and Boutayeb (S81) and Breton (S82) extended the minimal model of Bergman et al.4 with the closed loop control systems to predict the dynamic changes in glucose level during exercise. Furthermore, Roy and Parker (S83, S84) incorporated the effect of plasma free fatty acid dynamics and exercise on insulin–glucose dynamics, respectively, into the minimal model proposed by Bergman et al. in 1981.3 In addition to this, they proposed a composite model incorporating both effects (S85). Moreover, Kim et al. (S86) and Li et al. (S87) built a multiscale physiological model for exercise effect (discussed in the section on Multiscale/level hierarchical models).
Besides these models, some commercial models, namely, “Archimedes” (S88) and “T1DM PhysioLab” platform (S89) have been developed. These complex simulation models are aimed at predicting the long-term effects of treatments for controlling the disease while evaluating the health-care strategies.
Models for progression
Most models discussed so far assume a constant state of the disease, which is nonrealistic in cases of chronic progressive diseases like diabetes. Moreover, efforts toward the development of new antidiabetic agents are focused at the drugs that can alter diabetes progression. Therefore, it is important to include disease progression in the model in order to study the long-term effect of antidiabetic agent at different stages of progression. Disease progression models specific for diabetes incorporating long-term population studies with antidiabetic agents have been developed (S90–S92) and are reviewed in ref. 9.
Deficits in β-cell mass have been characterized in both T1DM and T2DM. It is observed that chronic hyperglycemia can lead to the growth of the β-cell mass, whereas extreme hyperglycemia can lead to the reduction of the β-cell mass. Evaluating β-cell response and the processes involved in the reduction of β-cell mass under certain physiological conditions, Topp et al.23 developed a model by considering β-cell mass as a dynamic variable along with insulin and glucose concentration. Extending this model, Ribbing et al. (S93) proposed a semi-mechanistic pharmacokinetic/pharmacodynamic model, illustrating the dynamics of fasting plasma glucose, fasting insulin, SI, and β-cell mass along with the effect of antidiabetic treatments in the heterogeneous population.
De Gaetano et al.24 formulated a long-term diabetes progression model that recapitulates the pathophysiological processes involved in T2DM. This model describes the simultaneous evolution of β-cell mass, pancreatic β-cell replication reserve, prevailing glycemia and prevailing insulinemia on the basis of parameters representing insulin-dependent tissue glucose uptake, hepatic net glucose output, β-cell insulin secreting ability, and insulin elimination from plasma. Recently, Hardy et al. (S94) evaluated the performance of this model using the results obtained from the Diabetes Prevention Program Study.
Recently, Nie et al. (S95) developed a population-based mechanistic model for muscle pyruvate dehydrogenase kinase-4 mRNA changing over time, while quantifying the progression of the disease, and the effect of diet and plasma factors on pyruvate dehydrogenase kinase-4 mRNA. As application of epidemiological models for noncommunicable diseases is rare, only few age-structured models (S96, S97) and population models (S98, S99) have been developed.
Models for complications
Individuals with T1DM or T2DM have an increased risk of developing micro/macrovascular complications, the underlying cause of retinopathy and nephropathy, which contributes to the etiology of neuropathy and to the amputation of ulcerated limbs. It can also lead to myocardial infarction and stroke. Mathematical models for predicting and understanding different diabetes complications, such as wound healing,25,26 obesity,27,28 retinopathy (S100), foot ulcer (S101), nephropathy (S102), and coronary heart disease (S103, S104), have been developed. Models for diabetes wound healing, foot ulcer, and obesity (described in the sections on Models for macrophage action and Models for whole-body insulin-glucose dynamics) are physiology-based models, whereas diabetic retinopathy, nephropathy, and coronary heart disease are risk-predictive population-based models. Unfortunately, due to range of ambiguities and complexity associated with diabetes complications, at present, mathematical models in this arena are rare.
Non-Clinical Models
A wide range of mathematical models illustrating the mechanisms underlying insulin–glucose dynamics at different physiological scales, from whole-body through to organ, cellular and subcellular levels are discussed in this section.
Models for whole-body insulin–glucose dynamics
In 1980, Tiran et al. (S105) developed a combined circulatory and organ model of glucose and insulin dynamics by building upon their previous glucose29 and insulin (S106) models. The model isolates glucose uptake in the periphery, liver, brain, and gut and allows a direct comparison of glucose disposal along various routes. An extension to this model was developed to include separate compartmentalization of red blood cells with vascular space (S107). Guyton et al.30 followed the model of Tiran et al.29 and developed a compartmental model for insulin–glucose metabolism in normal individuals, which was further used by Cobelli et al. (S108) to derive an integrated whole-body model for short-term glucose regulation. To further test the validation technique, this model was modified to incorporate the submodels for unit processes involved in glucose regulation (S109).
Sorensen22 developed a physiology-based model for glucose metabolism by adopting features from various models (see Figure 3 for details), which serves as a reference and starting point for several other models. With the inclusion of incretin effect in the model by Sorensen,22 Alvehag and Martin31 proposed a model and validated it with clinical data. By integrating the effect of insulin resistance on glucose regulation under the influence of free fatty acid, Al-Hashmi et al.27 extended the model to incorporate the conditions of obese individuals. To develop a clinical based insulin–glucose interaction model for T1DM individuals, Lehmann et al. (S110) replaced the pharmacodynamic element of the model by Berger and Rodbard (S60) with the Guyton et al.30 glucose model. Recently, Toghaw et al.28 developed a model describing the dynamics of the insulin–glucose–incretin system. The model reproduces both known and supposed effects of bariatric surgery on insulin secretion.
Models for hepatic glucose dynamics
To investigate the role of hepatic glycogen regulation, Xu et al. (S111) suggested a physiological model describing whole-body bioenergetics and glycogen circuitry involved in maintaining blood glucose homeostasis. Recently, Koenig et al.32 presented a novel kinetic model of human hepatic glucose metabolism. This model includes glucose metabolic pathways in human hepatocytes along with the hormonal control of these pathways by insulin, glucagon, and epinephrine. To address the mechanism underlying the cause of repetitive episodes of hypoglycemia in patients with strict insulin treatment and the role of liver in this circumstance, Koenig and Holzhuetter33 used their previous model32 to simulate metabolic alterations in T2DM.
Models for brain glucose homeostasis
It has been established that maintenance of stable glucose level in the brain is more important than that in the blood (S112). Assuming that this regulation of brain glucose homeostasis is the ultimate goal of the insulin–glucose–glucagon regulatory system, Gaohua and Kimura34 presented a brain-centered compartment model consisting of both peripheral insulin–glucose–glucagon interaction as well as brain–endocrine cross talk. The model describes the relationship between brain glucose homeostasis and hyperglycemia in diabetes, and accounts for the effects of stress and blood–brain barrier adaptation to dysglycemia.
Models for β-cell insulin release
Besides early minimal models, a few maximal models were developed for evaluating β-cell function and insulin secretion, for use as controllers to mimic the natural phenomenon. The pioneering models developed by Grodsky et al.35,36 illustrated the detailed cellular processes involved in pancreatic insulin response to glucose stimuli. These models assume that, at a certain threshold level of glucose, insulin-filled granules are stored in reserved and liable pools in β-cells. These granules sequentially secrete insulin, which correspond to the first and the second phase of insulin secretion. Although the model agreed well with the observed data, it was confined to simulation due to its complexity.
In contrast to storage-limited models, Cerasi et al. (S113) adopted the formulation developed by Silvers et al. (S114) and introduced a signal-limited model, which resulted in a biphasic insulin secretion that occurred due to time-dependent inhibitory and potentiating signals. O'Connor et al. (S115) developed another signal-limited model to describe pancreatic insulin release from perfused rat pancreas. Combining the above storage-limited35 and signal-limited (S115) models, Landahl and Grodsky (S116) developed a model for insulin secretion. Further models were developed by extending the model of Grodsky36 with updated knowledge of insulin secretion and β-cell function (S44, S117–S119).
Experimental studies have revealed the biphasic, i.e., rapid (pulsatile) and slow (ultradian), oscillatory nature of the insulin secretion by the β-cells. To understand the effects of insulin on glucose utilization and production, and vice versa, Sturis et al.37 proposed a nonlinear ordinary differential equation model illustrating the ultradian oscillation of insulin secretion. This model was further modified by Tolic et al.38 with the inclusion of insulin receptor dynamics, to provide a more realistic view of the system. To interpret the physiological delay in plasma insulin secretion, Bennett et al. (S120) introduced an explicit time delay for glucose dynamics in the model of Tolic et al.38 This was followed by models with single delay and double explicit time delays for ultradian insulin secretory oscillations proposed by Drozdov et al. (S121) and Li et al. (S50), respectively. By adopting the mechanism of insulin secretion formulated by Maki and Keizer (S122), Keener39 proposed a diffusion model to analyze in vitro insulin secretion by pancreatic β-cells cultured in a flow-through reactor.
Models for glucagon dynamics
When compared with the overwhelming findings about insulin and β-cells, the efforts on investigating glucagon and α-cell functions are relatively sparse, despite their importance in hyperglycemia (S123–S125) and hypoglycemia (S126). As a result, the modeling studies in this area are also limited. The first set of models, exploring the glucagon counterregulation mechanism, were proposed by Farhy and McCall,40 (S127, S128) based on rodent studies. As all the components of these models were clinically measurable, these models identify the role of delayed feedback from α-cells in glucagon counterregulation mechanism.41 Furthermore, the model was evaluated using clinical data, illustrating the relationship between basal glucagon level and different aspects of glucagon counterregulation responses to insulin-induced hypoglycemia in T1DM conditions (S129).
Recently, Gonzalez-Velez et al. (S130) proposed a simple model of glucagon secretion from pancreatic α-cells by considering Ca2+ dynamics in response to changes in glucose levels. Quantitatively reproducing the rate of glucagon secretion, the model highlighted the role of Ca2+ and glucose in regulating glucagon release.
Models for macrophage action
Focusing on the immunological manifestation of diabetes, one of the earliest hypotheses dealing with initiation of T1DM was proposed by Nerup et al. (S131) and is popularly known as the “Copenhagen model.” This model was mathematically formulated by Freiesleben De Blasio et al.42 as a set of ordinary differential equations describing the interplay between macrophages, β-cell proteins, and T cells leading to the onset of T1DM. By extending this model and addressing its limitations, Marée et al.43 postulated the DuCa model, which accounts for the effects of macrophage crowding on β-cell destruction. Building upon the assumptions made in the Copenhagen model, Magombedze et al. (S132) proposed a model involving β-cells, autolytic and regulatory T cells. This model mainly focused on helper T-cell–mediated destruction of β-cells and regulatory T-cell–mediated suppression of T-cell trafficking, thereby performing qualitative analysis for diabetes in the islets.
Focusing on the inflammatory process associated with wound healing, Waugh et al.25 developed a mathematical model to address the complex process involved in diabetic wound healing based on the altered distribution of macrophage phenotypes in normal and diabetic individuals. The model was extended to examine the effect of possible treatments on the wound-healing process in diabetics.26 Furthermore, Mi et al. (S101) proposed an agent-based model, focusing on the inflammation and healing processes in diabetic foot ulcer.
Models for β-cell electrophysiology
The sequence of events that occurs in β-cells, following an elevation of plasma glucose levels, includes depolarization, which results from the closure of ATP-sensitive K+ channels, the opening of voltage-dependent Ca2+ channels, and an increased intracellular Ca2+ that triggers the exocytosis of insulin. Subsequent repolarization of the membrane is mediated by voltage-dependent K+ and Ca2+ sensitive voltage-dependent K+ channel activation. This distinctive periodic pattern of electrical activity, known as bursting electrical activity (S133), depends on the extracellular glucose concentration. Recognizing the importance of β-cell membrane potential on glucose homeostasis, several groups attempted to model the mechanisms behind this process.44,45,46,47
Bursting electrical activity. Following the pioneering investigation by Dean et al. (S134), Atwater et al. (S135) postulated the first biophysical qualitative model for bursting electrical activity. To understand these interactions quantitatively, Chay and Keizer (S136) proposed the first mathematical model of bursting electrical activity by modifying the classical Hodgkin and Huxley (S137) model designed for the squid giant axon. Despite the limited availability of electrophysiological data, the model was able to simulate bursting electrical activity successfully.
The classical Chay and Keizer (S136) model is characterized by five components that include three ion channels and two Ca2+ concentration dynamics. This model was reduced by replacing the equations for voltage-dependent Ca2+ channels activation and inactivation with corresponding steady-state values, along with minor changes in the parameter values to reproduce the essential results.48 In 1986, Chay (S138) modified their reduced model48 by removing the low-conductance ATP-inhibited K+ channel and demonstrated that the bursting activity in β-cells results from the activation of the K+ channel along with voltage-dependent Ca2+ channels. Subsequently, Himmel et al. (S139) tested this hypothesis and discovered that under low glucose concentrations, the current generated by the low-conductance ATP-inhibited K+ channel dominates; whereas during bursting, the current generated by the high-conductance K+ channel (s) dominates the silent phase.
Due to limited availability of data, all the models discussed so far were based on the classical Hodgkin Huxley (S137) model for the squid giant axon. Overcoming this limitation, the data obtained from voltage clamp studies by Rorsman and Trube (S140), led to the development of more realistic models incorporating the properties of the voltage-gated K+ and Ca2+ channels. One such model, proposed by Chay (S141) used an inward voltage-activated Ca2+ current that was activated by intracellular Ca2+ ions and an outward K+ current that was activated by the membrane potential and described the burst activity of the pancreatic β-cell. Sherman et al.49 modified the channel kinetics of the model of Chay (S138) by incorporating voltage clamp data from Rorsman and Trube (S140), and extended it by including stochasticity in Ca2+-activated K+ channels to study the effects of channel sharing between cells, and to describe irregularities in the electrical activities of single cells and those in small clusters. Following this, Sherman and Rinzel (S142) suggested a multicell model with a finite gap junctional conductance. Later using the model of Sherman et al.,49 De Vries and Sherman50 performed a stochastic simulation to understand the emergent bursting phenomenon in β-cells, concluding that this phenomenon scaled up with cluster size, being more robust with larger numbers of cells.
Adopting the model of Sherman et al.,49 Keizer and Magnus (S143) proposed a mixed model of bursting electrical activity in β-cells by considering both ATP-sensitive as well as Ca2+-activated K+ conductance. On the other hand, Magnus and Keizer51 developed a minimal model to illustrate Ca2+ management by mitochondria in β-cells and later integrated it with the model of Keizer and Magnus (S143), describing the interaction of mitochondrial Ca2+ control and electrical activity in β-cells (S144, S145). The latter model was extended further and re-evaluated by Fridlyand and Philipson52 (S146), using the experimental characterizations of the processes involved. This comprehensive model for β-cell glucose sensitivity elucidates the role of cytoplasmic and mitochondrial processes involved in insulin secretion and reactive oxygen species generation mechanism in β-cells. This model can be envisioned to provide an elaborate overview of glucose-sensing mechanisms, which are central to the physiology and pathology of pancreatic β-cells.
In early 1990s, the reduced model of Chay and Keizer48 was upgraded by replacing the slow process with the voltage-dependent inactivation of the Ca2+ current (S147, S148). These models assume that the intracellular Ca2+ concentration varies rapidly and in synchrony with the rapidly oscillating membrane potential. Observing the incompatibility between the slow voltage-dependent inactivation hypothesis and the available data, Smolen and Keizer (S149) suggested a model and concluded that the slow process depends on ATP or ADP concentrations.
It has been suggested that depolarization of the plasma membrane by acetylcholine is mediated by a Ca2+ release–activated current. Examining this hypothesis, Bertram et al.53 developed a model of muscarinic effects, which successfully illustrated the biphasic electrical response of β-cell to the change in glucose levels and accounted for the effect of acetylcholine on pancreatic β-cells. The model was marginally modified by Mears et al.54 to further validate the hypothesis. It was concluded that Ca2+ depletion in the endoplasmic reticulum at a basal glucose level initiates Ca2+ release–activated nonselective currents, while stimulatory glucose results in endoplasmic reticulum filling deactivation of the current. This eventually leads to a biphasic electrical response as the result of altered glucose concentration.
In 1996, Chay (S150) introduced a second slow variable in his previous reduced model,48 to represent Ca2+ concentration in the endoplasmic reticulum. This dramatically influences the electrical activity, Ca2+ oscillations, and insulin secretion. In addition, the model demonstrates the role of acetylcholine in the neuronal control of insulin secretion. The model was later extended to study the role of extracellular Ca2+ on the electrical activity in β-cells.55 Furthermore, Giugliano et al. (S151) developed a detailed model illustrating glucose-induced insulin secretion by including four dynamic subsystems representing glucose transport, insulin secretion, cytosolic Ca2+ kinetics, and the excitable electrophysical behavior of β-cells. This model was insightful in studying the behavior of single β-cells as well as the population of coupled cells and successfully described various dynamic phenomena.
Later, Bertram et al.56 generalized the concept of two slow variables with the proposal of the phantom burster model, showing that a strong electrical coupling between a fast burster and a slow burster produces synchronized medium bursting. This suggests that islets may be composed of cells that are intrinsically either fast or slow, with few or none that are intrinsically medium. The phantom burst model,56 in association with the model of Chay (S150), was later implemented to illustrate the control of oscillations by cytosolic Ca2+ through both direct and indirect feedback pathways (S152).
Examining an alternative hypothesis, to investigate the role of slow glycolytic oscillations in controlling electrical activity in β-cells, Weirschem and Bertram (S153) coupled the minimal models of glycolytic oscillation (S154) and electrical bursting in islets (S136). Following this, Bertram postulated a more realistic model by incorporating the contribution of mitochondria in regulating glycolysis and the feedback mechanism representing the action of Ca2+ on metabolism.57 Extending this model, Bertram et al. (S155) proposed the dual oscillator model for β-cell activity, which included more details on mitochondrial metabolism. Later, Chew et al. (S156) integrated this dual oscillatory model (S155) with the whole-body glucose regulation model proposed by (S108). The model provided a deeper understanding of the oscillatory electrical activity in β-cells, which play an important role in insulin secretion and is lost or distributed in diabetes patients. As a unique approach, Nittala et al. (S157) proposed a hexagonal closed packing model to quantitatively investigate the role of islet cytoarchitecture in the synchronization of β-cell bursting.
Basic metabolism in β-cell. Focusing on the glycolytic component of β-cells, Aslanidi et al. (S158) developed a reaction-diffusion model to describe the spatiotemporal dynamics of the intracellular species involved in initiating insulin secretion from β-cells. Developed by incorporating glucose diffusion equations from the model of Bertram et al. (S159) into their previous work (S160), it mainly focused on the electrical/Ca2+ activity in the islets. Moreover, revising the model developed by Smolen et al. (S161) on the gycolytic oscillations in skeletal muscle, Westermark and Lansner58 proposed a similar model for β-cells, predicting the oscillatory behavior of β-cell glycolysis. Furthermore, employing the phosphofructokinase-1–mediated glycolytic oscillation model (S161) alongside β-cell glycolytic oscillation models,57 (S155), Merrin et al. (S162) presented a mathematical model to study the role of the bifunctional enzyme 6-phosphofructokinase-2-kinase/fructose-2,6-bisphosphatase in altering islet bursting oscillations.
In 2007, Jiang et al.59 postulated a detailed kinetic model of the core processes involved in glucose-stimulated insulin secretion by considering the complete insulin secretion pathway starting from glycolysis and through to ATP production. This model highlighted the relationship between ATP output and glucose input concentrations, as well as the oscillations of metabolite concentration in the glycolysis pathway.
The vastness of available models for β-cell electrophysiology is beyond the limit of this review. However, we have extensively discussed the models starting from the evolution of the classical model by Chay and Keizer (S136) to the most updated model by Fridlyand and Philipson (S146).
Models for insulin receptor dynamics
Studies have revealed that under pathological conditions, such as obesity and diabetes, there is a deficit in cell surface insulin receptor levels, as well as in their functionality. To complement experimental studies on insulin receptor dynamics, several models were proposed. Quon and Campfield60 proposed a mathematical model that describes the molecular processes involved in insulin receptor dynamics, such as receptor binding, endocytosis, and recycling. Later, Wanant and Quon61 suggested a model for insulin receptor binding kinetics by explicitly representing both divalent insulin receptor and receptor aggregation.
To gain further insight into insulin receptor dynamics, Hori et al. (S163) postulated a model specifically focusing on intracellular insulin receptor trafficking dynamics. This model involves all the known kinetics processes, from the activation to deactivation of the extracellular insulin receptors by intracellular proteins and hence played a productive role in investigating insulin action at different steps involved in endosomal trafficking. On the basis of in vivo studies on human hepatocytes, Koschorreck et al.62 suggested a model that explicitly described the molecular processes involved in insulin receptor dynamics, along with those associated with insulin degradation and clearance.
In addition, Kiselyov et al.63 proposed a mathematical model that describes the kinetic properties of insulin and insulin-like growth factor 1 receptor binding and activation, by considering the combinatorial complexity arising from multivalent binding to multiple receptor conformations. Brännmark et al.64 developed a framework by integrating experimental and mathematical modeling approaches to characterize the complex signaling networks involved in the early phase of insulin signaling in human adipocytes. Using this modeling framework, Nyman et al. (S164) tested the time courses for insulin receptor and insulin receptor substrate-1 phosphorylation upon insulin simulation in murine primary adipocytes and compared it to that of human adipocytes. Recently, Brännmark et al. (S194) developed a dynamic model based on experimental data from human adipocytes, which yielded a molecular basis of insulin resistance in T2DM individuals.
Models for insulin signaling
Insulin regulates essential physiological functions by binding to its cell surface receptors, thereby activating signal transduction pathways that mediate cellular responses. Therefore, initial receptor dynamics are important to gain a complete overview of the insulin-signaling pathway. Most models discussed in this section use the insulin receptor dynamic models (discussed in the section on Models for insulin receptor dynamics) as a foundation.
Quon et al. (S165, S166) proposed two models that describe the molecular processes regulating insulin-sensitive glucose transporter dynamics in adipocytes and myocytes. Integrating these models, along with those representing insulin receptor binding kinetics61 and receptor recycling,60 Sedaghat et al.65 proposed a mechanistic model illustrating the post–receptor signaling pathway. Furthermore, Chew et al. (S167) integrated the model proposed by Sedaghat et al.65 with the simple whole-body glucose homeostasis model (S109). Luni et al. (S168) built a multiscale model by incorporating the detailed insulin receptor interaction model63 into the phenomenological insulin-signaling model.65
Subsequently, a simplified version of the Sedaghat model,65 representing insulin and glucagon receptors dynamics, was developed by Liu and Tang (S75). This model involves only two components, insulin and glucose, and ignores the cross talk and feedback between multiple signaling pathways. Despite such simplification, the model was able to reproduce liver glucose and glycogen kinetics, as well as insulin and glucagon receptors dynamics, at the molecular level. The model was then elaborated as a compartmental model describing glucose transporter kinetics, glucose mobilization processes in liver, and insulin-signaling pathway.66
Multiscale/level hierarchical models
As models become more complete and realistic, detailed modules for crucial cellular processes, exemplified by subsystem models, can potentially be merged into whole-body physiology-based models. The result of such a merge is a multilevel or hierarchical model, where the same submodel or module may be described at different levels of complexity. This modeling approach provides a link between different model systems and in vivo human conditions, thereby allowing evaluation of the relevance of in vitro data at physiological levels.67
Taking this into consideration, a “whole-body” hierarchical model was developed by Nyman et al.,68 linking the insulin/insulin receptor dynamics models63,64 to the glucose transport-insulin signaling model65 and subsequently incorporating this dynamic module in a whole-body glucose homeostasis21 model. The model successfully describes the relationship between in vitro insulin signaling in primary human adipocytes and in vivo whole-body glucose homeostasis. Remarkably, the Nyman model is an ideal example representing a modular modeling approach.
Hetherington et al.69 developed a composite model for glucagon/insulin-driven liver glucose homeostasis by linking together a series of subsystem models corresponding to different aspects of physiology. This model has been used further to explore the behavior of glucose homeostasis systems by modulating the liver SI and diet glucose level (S169).
Kim et al. (S86) developed a multiscale model illustrating hormonal control of whole-body glucose homeostasis during exercise. Moreover, extending their previous model (S170), Li et al. (S87) proposed a multiscale cellular model to investigate the intracellular metabolic responses of skeletal muscle to insulin, corresponding to human glucose clamp studies.
Although multiscale, hierarchical, and composite modeling approaches are new, they can be envisioned as a roadmap toward achieving a holistic mechanistic view of the glucose homeostasis system from subcellular to a “whole-body” level, which could eventually lead to better control and treatment methods for diabetes.
Discussion and Future Directions
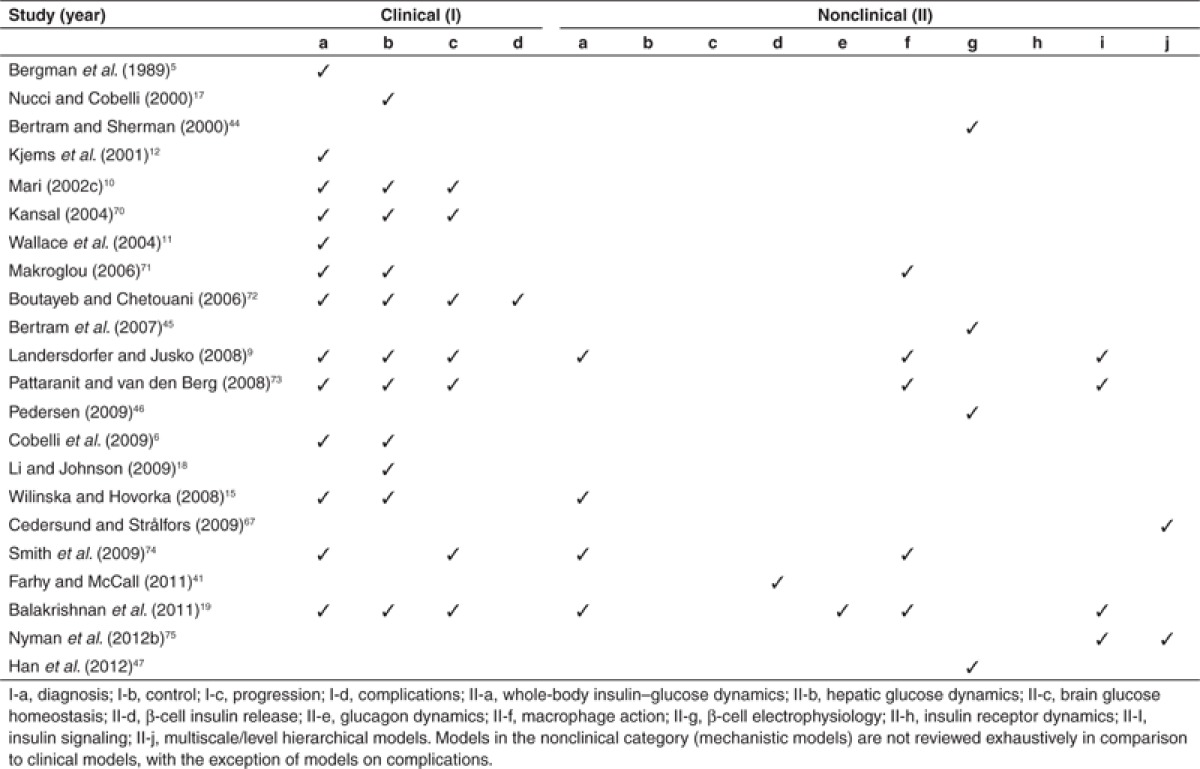
To improve the clinical diagnosis and treatment of systemic diseases, a complete understanding of the complex network underlying the onset and progression of the disease is essential. Such an understanding would enable the identification of fragile points that exist within the network, which can then be targeted for further studies. Since the development of the first mathematical model of insulin-glucose dynamics in the early 1960s,2 there has been a massive breakthrough, both in the number and complexity of models, and in the modeling approaches developed to understand the underlying mechanisms in glucose homeostasis, diabetic conditions, and associated complications. The model relationship map (Figure 3) provides a complete overview of the evolution of most diabetes models available in the literature to-date and highlights the significance of sharing and reuse of models. Reviews about diabetes models, with their coverage of the different biological categories, are listed in Table 1.5,6,9,10,11,12,15,17,18,19,41,44,45,46,47,67,70,71,72,73,74,75 As can be seen from Table 1, models in the nonclinical category are not reviewed exhaustively in comparison to clinical models, with the exception of models on complications.
Table 1. List of reviews with their coverage of different subclasses under clinical (I) and nonclinical (II) categories.
Although modeling studies related to diabetes and its associated complications are abundant, not all aspects of diabetes are mathematically represented, and of those that are, not all are represented equally. This is reflected in Figure 3, where certain model categories are densely populated, while others are sparse. This is presumably due to the lack of experimental data and/or effort in that domain, or the lack of integration with existing experimental knowledge. The following sections attempt to highlight the research opportunities in understanding the mechanism underlying the pathogenesis of diabetes, involving more components and compartments.
Need of more mathematical models to represent the existing knowledge
Immense experimental research over the past decades on diabetes and associated complications led to our current understanding that the ultimate clinical presentation of the disease results from the interaction of multiple cell types and organ systems (S171). To determine the molecular basis of the abnormal secretion of insulin and glucagon, and on insulin resistance in the poor maintenance of glucose homeostasis, it is important to understand the relative contribution of liver, muscle, adipose tissue, α-cell, and β-cell in the onset and progression of diabetes. The role of multiple cell types and organ systems in the maintenance of glucose homeostasis is represented in Figure 4a–f. In addition, the mechanisms underlying hyperglycemia-induced tissue damage is illustrated in Figure 4g. The aim of this figure is to identify the mechanism underlying glucose homeostasis and the pathogenesis of diabetes that needs to be targeted by future modeling studies. Connectors in red indicate prospective pathways for mathematical modeling, whereas green indicates the previously modeled pathways that are discussed in this review, under different subclasses. It should be noted that pathways represented by green connectors in each box do not necessarily represent a single model. Rather, they should be seen as the collection of models aimed at addressing these pathways. Each box with details of the interactions involved is explained in the Supplementary Data online.
Apart from pancreatic hormones, glucose homeostasis is also controlled by various mechanisms involving the autonomic nervous system (S172–S174), genetics (S175, S176), mitochondrial (S177), and endoplasmic reticulum (S178) functions. These are further influenced by environmental factors, such as diet, chronic stress, micronutrient deficiency, and sedentary life style, which offer further areas for modeling.
Genetic studies in simple organisms have convincingly shown the link between aging and insulin (S179, S180). When insulin levels are kept low, cells are stronger, staving off infection and age-related diseases such as cancer, dementia, and stroke. Higher intake of insulin can cause faster aging and accumulate the diseases associated with aging. This happens in most diabetic patients due to overexposure to insulin. Moreover, the mammalian target of rapamycin (mTOR) signaling pathway is also found to control cell growth and tissue aging and has a potential impact on lifespan, insulin resistance, and metabolic adaptation to hyperglycemia in T2DM (S181). These findings could act as a foundation to investigate the integral role of insulin in diabetes and aging through modeling.
Obesity represents a major risk factor in insulin resistance (S182, S183) via inflammation, and it is important to understand the molecular basis by which obesity drives insulin resistance. Several experimental works along this line have been carried out and have determined the role of leptin (S184, S185), resistin (S186), and other proinflammatory cytokines (S187–S189). Although there are a few models that account for obesity and diabetes, the numbers are negligible.
Clinical investigations have identified a strong relationship between hyperglycemia and micro- and macrovascular complications (S3, S190, S191) via inflammation. This results in several secondary diseases causing irreversible damage to various organs. Moreover, diabetes, being a chronic disease, requires efficient self-management strategies, which specifically include lifestyle modifications, through diet (S192), physical activity (S78), and smoking cessation (S193). Conducting modeling studies describing the mechanisms behind the onset and progression of these complications, as well as possible intervention points to prevent acute and chronic complications and that limit risk through self-management, would have a significant impact.
Need of standards in modeling
The usage and implementation of existing mathematical models could become impractical if they are not available in standard formats. Utilizing resources like BioModels Database1 for sharing and reusing models can simplify the development of holistic models. Another recently launched effort, Drug Disease Model Resources (DDMoRe; www.ddmore.eu) (S195), a pioneer innovative medicines initiative founded effort, aims to design a mark-up language for encoding drug and disease models with associated metadata and ensuring interoperability between existing tools along with the development of novel disease models, for instance, diabetes.
Conclusions
The ultimate aim of developing models of diabetes is to understand the dynamics of the complex network underlying its etiology and to use that knowledge to efficiently identify potential therapeutic targets for its control and treatment. In the past five decades of modeling in this field, how far have we advanced? Do we know all the interacting components and intermediates? What could be the role of unknown components, if such exists? How far are we from the complete description of a perturbed network leading to the disease? Regarding the complications associated with diabetes, what is less understood is the consequence of prolonged hyperglycemia acting differently in different individuals, i.e., the types of complications associated with diabetes differs between individuals. What are the reasons? Genetics studies along this line would play a critical role.
So far, mathematical modeling tightly linked to experiments had a great impact in our understanding of diabetes. Efforts on merging subsystem models,68,69 although tricky, could pave the way toward discovering the entire regulatory network. We anticipate that this review would enable further studies and development in diabetes research.
Conflict of interest
The authors declared no conflict of interest.
Acknowledgments
This review was written as part of a curation work for BioModels Database, focusing on mathematical models of diabetes and associated complications. I.A., C.L., and N.L.N. were supported by the European Molecular Biology Laboratory (EMBL); M.S. was supported by DDMoRe; and V.C. was supported by the BBSRC. We thank Nick Juty for proof reading.
Supplementary Material
References
- Li C., et al. BioModels Database: an enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst. Biol. 2010;4:92. doi: 10.1186/1752-0509-4-92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolie V.W. Coefficients of normal blood glucose regulation. J. Appl. Physiol. 1961;16:783–788. doi: 10.1152/jappl.1961.16.5.783. [DOI] [PubMed] [Google Scholar]
- Bergman R.N., Phillips L.S., Cobelli C. Physiologic evaluation of factors controlling glucose tolerance in man: measurement of insulin sensitivity and beta-cell glucose sensitivity from the response to intravenous glucose. J. Clin. Invest. 1981;68:1456–1467. doi: 10.1172/JCI110398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergman R.N., Ider Y.Z., Bowden C.R., Cobelli C. Quantitative estimation of insulin sensitivity. Am. J. Physiol. 1979;236:E667–E677. doi: 10.1152/ajpendo.1979.236.6.E667. [DOI] [PubMed] [Google Scholar]
- Bergman R.N., et al. Assessment of insulin sensitivity in vivo: a critical review. Diabetes. Metab. Rev. 1989;5:411–429. doi: 10.1002/dmr.5610050501. [DOI] [PubMed] [Google Scholar]
- Cobelli C., Man C.D., Sparacino G., Magni L., De Nicolao G., Kovatchev B.P. Diabetes: models, signals, and control. IEEE Rev. Biomed. Eng. 2009;2:54–96. doi: 10.1109/RBME.2009.2036073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Gaetano A., Arino O. Mathematical modelling of the intravenous glucose tolerance test. J. Math. Biol. 2000;40:136–168. doi: 10.1007/s002850050007. [DOI] [PubMed] [Google Scholar]
- Silber H.E., Jauslin P.M., Frey N., Gieschke R., Simonsson U.S., Karlsson M.O. An integrated model for glucose and insulin regulation in healthy volunteers and type 2 diabetic patients following intravenous glucose provocations. J. Clin. Pharmacol. 2007;47:1159–1171. doi: 10.1177/0091270007304457. [DOI] [PubMed] [Google Scholar]
- Landersdorfer C.B., Jusko W.J. Pharmacokinetic/pharmacodynamic modelling in diabetes mellitus. Clin. Pharmacokinet. 2008;47:417–448. doi: 10.2165/00003088-200847070-00001. [DOI] [PubMed] [Google Scholar]
- Mari A. Mathematical modeling in glucose metabolism and insulin secretion. Curr. Opin. Clin. Nutr. Metab. Care. 2002c;5:495–501. doi: 10.1097/00075197-200209000-00007. [DOI] [PubMed] [Google Scholar]
- Wallace T.M., Levy J.C., Matthews D.R. Use and abuse of HOMA modeling. Diabetes Care. 2004;27:1487–1495. doi: 10.2337/diacare.27.6.1487. [DOI] [PubMed] [Google Scholar]
- Kjems L.L., Vølund A., Madsbad S. Quantification of beta-cell function during IVGTT in type II and non-diabetic subjects: assessment of insulin secretion by mathematical methods. Diabetologia. 2001;44:1339–1348. doi: 10.1007/s001250100639. [DOI] [PubMed] [Google Scholar]
- Eaton R.P., Allen R.C., Schade D.S., Erickson K.M., Standefer J. Prehepatic insulin production in man: kinetic analysis using peripheral connecting peptide behavior. J. Clin. Endocrinol. Metab. 1980;51:520–528. doi: 10.1210/jcem-51-3-520. [DOI] [PubMed] [Google Scholar]
- Pedersen M.G., Toffolo G.M., Cobelli C. Cellular modeling: insight into oral minimal models of insulin secretion. Am. J. Physiol. Endocrinol. Metab. 2010;298:E597–E601. doi: 10.1152/ajpendo.00670.2009. [DOI] [PubMed] [Google Scholar]
- Wilinska M.E., Hovorka R. Simulation models for in silico testing of closed-loop glucose controllers in type 1 diabetes. Drug Discov. Today Dis. Mod. 2008;5:289–298. [Google Scholar]
- Huang M., Li J., Song X., Guo H. Modeling impulsive injections of insulin: towards artificial pancreas. SIAM J. Appl. Math. 2012;72:1524–1548. [Google Scholar]
- Nucci G., Cobelli C. Models of subcutaneous insulin kinetics. A critical review. Comput. Methods Programs Biomed. 2000;62:249–257. doi: 10.1016/s0169-2607(00)00071-7. [DOI] [PubMed] [Google Scholar]
- Li J., Johnson J.D. Mathematical models of subcutaneous injection of insulin analogues: a mini-review. Discrete Continuous Dyn. Syst. Ser. B. 2009;12:401–414. doi: 10.3934/dcdsb.2009.12.401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balakrishnan N.P., Rangaiah G.P., Samavedham L. Review and analysis of blood glucose (BG) models for type 1 diabetic patients. Ind. Eng. Chem. Res. 2011;50:12041–12066. [Google Scholar]
- Hovorka R., et al. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiol. Meas. 2004;25:905–920. doi: 10.1088/0967-3334/25/4/010. [DOI] [PubMed] [Google Scholar]
- Dalla Man C., Rizza R.A., Cobelli C. Meal simulation model of the glucose-insulin system. IEEE Trans. Biomed. Eng. 2007;54:1740–1749. doi: 10.1109/TBME.2007.893506. [DOI] [PubMed] [Google Scholar]
- Sorensen J.T. A Physiologic Model of Glucose Metabolism in Man and Its Use to Design and Assess Improved Insulin Therapies for Diabetes. Massachusetts Institute of Technology; 1985. [Google Scholar]
- Topp B., Promislow K., deVries G., Miura R.M., Finegood D.T. A model of beta-cell mass, insulin, and glucose kinetics: pathways to diabetes. J. Theor. Biol. 2000;206:605–619. doi: 10.1006/jtbi.2000.2150. [DOI] [PubMed] [Google Scholar]
- De Gaetano A., et al. Mathematical models of diabetes progression. Am. J. Physiol. Endocrinol. Metab. 2008;295:E1462–E1479. doi: 10.1152/ajpendo.90444.2008. [DOI] [PubMed] [Google Scholar]
- Waugh H.V., Sherratt J.A. Macrophage dynamics in diabetic wound dealing. Bull. Math. Biol. 2006;68:197–207. doi: 10.1007/s11538-005-9022-3. [DOI] [PubMed] [Google Scholar]
- Waugh H.V., Sherratt J.A. Modeling the effects of treating diabetic wounds with engineered skin substitutes. Wound Repair Regen. 2007;15:556–565. doi: 10.1111/j.1524-475X.2007.00270.x. [DOI] [PubMed] [Google Scholar]
- Al-Hashmi S., Ekanayake M., Martin C.Type II diabetes and obesity: a control theoretic model. Emergent Problems in Nonlinear Systems and Control Vol. 393eds. Ghosh B., Martin C., Zhou Y.1–19.Springer, Berlin/Heidelberg; 2009 [Google Scholar]
- Toghaw P., Matone A., Lenbury Y., De Gaetano A. Bariatric surgery and T2DM improvement mechanisms: a mathematical model. Theor. Biol. Med. Model. 2012;9:16. doi: 10.1186/1742-4682-9-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tiran J., Galle K.R., Porte D., Jr. A simulation model of extracellular glucose distribution in the human body. Ann. Biomed. Eng. 1975;3:34–46. doi: 10.1007/BF02584487. [DOI] [PubMed] [Google Scholar]
- Guyton J.R., et al. A model of glucose-insulin homeostasis in man that incorporates the heterogeneous fast pool theory of pancreatic insulin release. Diabetes. 1978;27:1027–1042. doi: 10.2337/diab.27.10.1027. [DOI] [PubMed] [Google Scholar]
- Alvehag K., Martin C.The feedback control of glucose: on the road to type II diabetes. Decision and Control45th IEEE Conference, 2006685–690.
- König M., Bulik S., Holzhütter H.G. Quantifying the contribution of the liver to glucose homeostasis: a detailed kinetic model of human hepatic glucose metabolism. PLoS Comput. Biol. 2012a;8:e1002577. doi: 10.1371/journal.pcbi.1002577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koenig M., Holzhuetter H.G. Kinetic modeling of human hepatic glucose metabolism in T2DM predicts higher risk of hypoglycemic events in rigorous insulin therapy. J. Biol. Chem. 2012b. [DOI] [PMC free article] [PubMed]
- Gaohua L., Kimura H. A mathematical model of brain glucose homeostasis. Theor. Biol. Med. Model. 2009;6:26. doi: 10.1186/1742-4682-6-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grodsky G.M., Curry D., Landahl H., Bennett L. [Further studies on the dynamic aspects of insulin release in vitro with evidence for a two-compartmental storage system]. Acta Diabetol. Lat. 1969;6 suppl. 1:554–578. [PubMed] [Google Scholar]
- Grodsky G.M. A threshold distribution hypothesis for packet storage of insulin and its mathematical modeling. J. Clin. Invest. 1972;51:2047–2059. doi: 10.1172/JCI107011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sturis J., Polonsky K.S., Mosekilde E., Van Cauter E. Computer model for mechanisms underlying ultradian oscillations of insulin and glucose. Am. J. Physiol. 1991;260:E801–E809. doi: 10.1152/ajpendo.1991.260.5.E801. [DOI] [PubMed] [Google Scholar]
- Tolic I.M., Mosekilde E., Sturis J. Modeling the insulin-glucose feedback system: the significance of pulsatile insulin secretion. J. Theor. Biol. 2000;207:361–375. doi: 10.1006/jtbi.2000.2180. [DOI] [PubMed] [Google Scholar]
- Keener J.P. Diffusion induced oscillatory insulin secretion. Bull. Math. Biol. 2001;63:625–641. doi: 10.1006/bulm.2001.0235. [DOI] [PubMed] [Google Scholar]
- Farhy L.S., McCall A.L. Pancreatic network control of glucagon secretion and counterregulation. Meth. Enzymol. 2009;467:547–581. doi: 10.1016/S0076-6879(09)67021-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farhy L.S., McCall A.L. Optimizing reduction in basal hyperglucagonaemia to repair defective glucagon counterregulation in insulin deficiency. Diabetes. Obes. Metab. 2011;13 suppl. 1:133–143. doi: 10.1111/j.1463-1326.2011.01455.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freiesleben De Blasio B., Bak P., Pociot F., Karlsen A.E., Nerup J. Onset of type 1 diabetes: a dynamical instability. Diabetes. 1999;48:1677–1685. doi: 10.2337/diabetes.48.9.1677. [DOI] [PubMed] [Google Scholar]
- Marée A.F., Kublik R., Finegood D.T., Edelstein-Keshet L. Modelling the onset of Type 1 diabetes: can impaired macrophage phagocytosis make the difference between health and disease. Philos. Trans. A. Math. Phys. Eng. Sci. 2006;364:1267–1282. doi: 10.1098/rsta.2006.1769. [DOI] [PubMed] [Google Scholar]
- Bertram R., Sherman A. Dynamical complexity and temporal plasticity in pancreatic beta-cells. J. Biosci. 2000;25:197–209. [PubMed] [Google Scholar]
- Bertram R., Sherman A., Satin L.S. Metabolic and electrical oscillations: partners in controlling pulsatile insulin secretion. Am. J. Physiol. Endocrinol. Metab. 2007;293:E890–E900. doi: 10.1152/ajpendo.00359.2007. [DOI] [PubMed] [Google Scholar]
- Pedersen M.G. Contributions of mathematical modeling of beta cells to the understanding of beta-cell oscillations and insulin secretion. J. Diabetes Sci. Technol. 2009;3:12–20. doi: 10.1177/193229680900300103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han K., Kang H., Kim J., Choi M. Mathematical models for insulin secretion in pancreatic ß-cells. Islets. 2012;4:94–107. doi: 10.4161/isl.19569. [DOI] [PubMed] [Google Scholar]
- Chay T.R., Keizer J. Theory of the effect of extracellular potassium on oscillations in the pancreatic beta-cell. Biophys. J. 1985;48:815–827. doi: 10.1016/S0006-3495(85)83840-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherman A., Rinzel J., Keizer J. Emergence of organized bursting in clusters of pancreatic beta-cells by channel sharing. Biophys. J. 1988;54:411–425. doi: 10.1016/S0006-3495(88)82975-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Vries G., Sherman A. Channel sharing in pancreatic beta cells revisited: enhancement of emergent bursting by noise. J. Theor. Biol. 2000;207:513–530. doi: 10.1006/jtbi.2000.2193. [DOI] [PubMed] [Google Scholar]
- Magnus G., Keizer J. Minimal model of beta-cell mitochondrial Ca2+ handling. Am. J. Physiol. 1997;273:C717–C733. doi: 10.1152/ajpcell.1997.273.2.C717. [DOI] [PubMed] [Google Scholar]
- Fridlyand L.E., Philipson L.H. Glucose sensing in the pancreatic beta cell: a computational systems analysis. Theor. Biol. Med. Model. 2010;7:15. doi: 10.1186/1742-4682-7-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram R., et al. A role for calcium release-activated current (CRAC) in cholinergic modulation of electrical activity in pancreatic beta-cells. Biophys. J. 1995;68:2323–2332. doi: 10.1016/S0006-3495(95)80414-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mears D., Sheppard N.F., Jr, Atwater I., Rojas E., Bertram R., Sherman A. Evidence that calcium release-activated current mediates the biphasic electrical activity of mouse pancreatic beta-cells. J. Membr. Biol. 1997;155:47–59. doi: 10.1007/s002329900157. [DOI] [PubMed] [Google Scholar]
- Chay T.R. Effects of extracellular calcium on electrical bursting and intracellular and luminal calcium oscillations in insulin secreting pancreatic beta-cells. Biophys. J. 1997;73:1673–1688. doi: 10.1016/S0006-3495(97)78199-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram R., Previte J., Sherman A., Kinard T.A., Satin L.S. The phantom burster model for pancreatic beta-cells. Biophys. J. 2000;79:2880–2892. doi: 10.1016/S0006-3495(00)76525-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram R., Satin L., Zhang M., Smolen P., Sherman A. Calcium and glycolysis mediate multiple bursting modes in pancreatic islets. Biophys. J. 2004b;87:3074–3087. doi: 10.1529/biophysj.104.049262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westermark P.O., Lansner A. A model of phosphofructokinase and glycolytic oscillations in the pancreatic beta-cell. Biophys. J. 2003;85:126–139. doi: 10.1016/S0006-3495(03)74460-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang N., Cox R.D., Hancock J.M. A kinetic core model of the glucose-stimulated insulin secretion network of pancreatic beta cells. Mamm. Genome. 2007;18:508–520. doi: 10.1007/s00335-007-9011-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quon M.J., Campfield L.A. A mathematical model and computer simulation study of insulin receptor regulation. J. Theor. Biol. 1991a;150:59–72. doi: 10.1016/s0022-5193(05)80475-8. [DOI] [PubMed] [Google Scholar]
- Wanant S., Quon M.J. Insulin receptor binding kinetics: modeling and simulation studies. J. Theor. Biol. 2000;205:355–364. doi: 10.1006/jtbi.2000.2069. [DOI] [PubMed] [Google Scholar]
- Koschorreck M., Gilles E.D. Mathematical modeling and analysis of insulin clearance in vivo. BMC Syst. Biol. 2008;2:43. doi: 10.1186/1752-0509-2-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiselyov V.V., Versteyhe S., Gauguin L., De Meyts P. Harmonic oscillator model of the insulin and IGF1 receptors' allosteric binding and activation. Mol. Syst. Biol. 2009;5:243. doi: 10.1038/msb.2008.78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brännmark C., Palmér R., Glad S.T., Cedersund G., Strålfors P. Mass and information feedbacks through receptor endocytosis govern insulin signaling as revealed using a parameter-free modeling framework. J. Biol. Chem. 2010;285:20171–20179. doi: 10.1074/jbc.M110.106849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sedaghat A.R., Sherman A., Quon M.J. A mathematical model of metabolic insulin signaling pathways. Am. J. Physiol. Endocrinol. Metab. 2002;283:E1084–E1101. doi: 10.1152/ajpendo.00571.2001. [DOI] [PubMed] [Google Scholar]
- Liu W., Hsin C., Tang F. A molecular mathematical model of glucose mobilization and uptake. Math. Biosci. 2009;221:121–129. doi: 10.1016/j.mbs.2009.07.005. [DOI] [PubMed] [Google Scholar]
- Cedersund G., Strålfors P. Putting the pieces together in diabetes research: towards a hierarchical model of whole-body glucose homeostasis. Eur. J. Pharm. Sci. 2009;36:91–104. doi: 10.1016/j.ejps.2008.10.027. [DOI] [PubMed] [Google Scholar]
- Nyman E., et al. A hierarchical whole-body modeling approach elucidates the link between in Vitro insulin signaling and in Vivo glucose homeostasis. J. Biol. Chem. 2011;286:26028–26041. doi: 10.1074/jbc.M110.188987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hetherington J., et al. A composite computational model of liver glucose homeostasis. I. Building the composite model. J. R. Soc. Interface. 2012;9:689–700. doi: 10.1098/rsif.2011.0141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kansal A.R. Modeling approaches to type 2 diabetes. Diabetes Technol. Ther. 2004;6:39–47. doi: 10.1089/152091504322783396. [DOI] [PubMed] [Google Scholar]
- Makroglou A. Mathematical models and software tools for the glucose-insulin regulatory system and diabetes: an overview. Appl. Numer. Math. 2006;56:559–573. [Google Scholar]
- Boutayeb A., Chetouani A. A critical review of mathematical models and data used in diabetology. Biomed. Eng. Online. 2006;5:43. doi: 10.1186/1475-925X-5-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pattaranit R., van den Berg H.A. Mathematical models of energy homeostasis. J. R. Soc. Interface. 2008;5:1119–1135. doi: 10.1098/rsif.2008.0216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith J.M., et al. Mathematical modeling of glucose homeostasis and its relationship with energy balance and body fat. Obesity (Silver Spring) 2009;17:632–639. doi: 10.1038/oby.2008.604. [DOI] [PubMed] [Google Scholar]
- Nyman E., Cedersund G., Strålfors P. Insulin signaling - mathematical modeling comes of age. Trends Endocrinol. Metab. 2012b;23:107–115. doi: 10.1016/j.tem.2011.12.007. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.