Abstract
Although stimulus-frequency otoacoustic emissions (SFOAEs) offer compelling advantages as noninvasive probes of cochlear function, they remain underutilized compared to other evoked emission types, such as distortion-products (DPOAEs), whose measurement methods are less complex and time-consuming. Motivated by similar advances in the measurement of DPOAEs, this paper develops and characterizes a more efficient SFOAE measurement paradigm based on swept tones. In contrast to standard SFOAE measurement methods, in which the emissions are measured in the sinusoidal steady-state using discrete tones of well defined frequency, the swept-tone method sweeps rapidly across frequency (typically at rates of 1 Hz/ms or greater) using a chirp-like stimulus. Measurements obtained using both swept- and discrete-tone methods in an interleaved suppression paradigm demonstrate that the two methods of measuring SFOAEs yield nearly equivalent results, the differences between them being comparable to the run-to-run variability encountered using either method alone. The match appears robust to variations in measurement parameters, such as sweep rate and direction. The near equivalence of the SFOAEs obtained using the two measurement methods enables the interpretation of swept-tone SFOAEs within existing theoretical frameworks. Furthermore, the data demonstrate that SFOAE phase-gradient delays—including their large and irregular fluctuations across frequency—reflect actual physical time delays at different frequencies, showing that the physical emission latency, not merely the phase gradient, is inherently irregular.
INTRODUCTION
Stimulus-frequency otoacoustic emissions (SFOAEs) evoked by low-level tones are thought to arise by coherent reflection from a localized region near the peak of the traveling wave (e.g., Zweig and Shera, 1995). Because of their spatial and mechanistic specificity, SFOAEs are often easier to interpret than other evoked emissions, such as distortion-product otoacoustic emissions (DPOAEs), whose generation mechanisms are inherently nonlinear and generally more complex. Since SFOAEs are usually measured at sound levels suitable for probing outer-hair-cell contributions to cochlear amplification, SFOAEs may be more sensitive to mild and moderate hearing loss than DPOAEs. For similar reasons, SFOAEs are also well suited for examining the function of the olivocochlear efferent system (reviewed in Guinan, 2006). In addition, recent theory and empirical evidence suggest that SFOAE delays provide valuable information about cochlear frequency selectivity (e.g., Shera and Guinan, 2003; Shera et al., 2002; Schairer et al., 2006; Shera et al., 2010; Bergevin et al., 2010; Bentsen et al., 2011; Joris et al., 2011). Finally, ongoing efforts to test theoretical models of the cochlea using SFOAEs have provoked years of fruitful debate and refined both theories of OAE generation and our basic understanding of cochlear mechanics.
Although SFOAEs are attractive as probes of cochlear function, they are less widely used than other evoked emissions, both because the measurement paradigms are more complex and the necessary responses (e.g., measurements with and without a suppressor tone) can be time-consuming to acquire. Improved measurement techniques that increase the speed of data acquisition while remaining robust to artifacts would enhance the power and utility of SFOAE measurements. For example, faster SFOAE measurement methods would ease the collection of the high-resolution SFOAE phase-versus-frequency functions needed for exploring the tuning of cochlear filters over a broad range of frequency and level.
The recent development of measurement paradigms in which the stimulus frequencies are swept continuously from one frequency to another has significantly reduced measurement times for both DPOAEs and SFOAEs (e.g., Long et al., 2008; Choi et al., 2008; Bennett and Özdamar, 2010). In contrast to traditional discrete-tone methods, in which different frequency components of the emission are measured step-wise in the sinusoidal steady state, swept-tone techniques pass quickly over the full targeted frequency range (e.g., 0.5–8 kHz). Although swept-tone measurements are certainly faster, their interpretation must not be overhasty. In particular, current interpretations of swept-tone SFOAEs rely on the assumption—convenient but unexplored and potentially problematic—that the measured emissions are identical to those evoked by pure tones. Here, we test this assumption by comparing discrete-tone SFOAEs (DT-SFOAEs) with the emissions evoked using our implementation of a swept-tone SFOAE measurement paradigm (ST-SFOAEs).
METHODS
Overview
We measured SFOAEs using two stimulus paradigms, each described in detail in subsequent sections. In the “discrete-tone” case (Shera and Guinan, 1999), the evoking stimulus was a pure tone, and emissions at different frequencies were evoked and measured individually. In the “swept-tone” case, the stimulus was a chirp-like waveform whose instantaneous frequency changed smoothly with time, typically at rates of 2 Hz/ms or greater. In both cases, the stimuli were repeated and the responses recorded and averaged until a specified minimum number of artifact-free responses were acquired at each time point. No signal-to-noise (SNR) criteria were employed for these measurements. The emission was subsequently extracted from the averaged response.
Because the stimulus and emission overlap in both time and frequency, extracting the emission from the measured pressure waveform constitutes the principal methodological challenge in measuring SFOAEs. Among the strategies proposed for recovering the emission (Kalluri and Shera, 2007a), we here employed the interleaved suppression method (e.g., Kemp and Chum, 1980; Guinan, 1990; Shera and Guinan, 1999) for both the discrete- and swept-tone paradigms. The suppression paradigm typically presents stimuli during two adjoining intervals. The first interval contains only the evoking probe waveform; the second contains an additional suppressor stimulus. To minimize the effect of earphone nonlinearities, probe and suppressor waveforms are presented using different sound sources. During the first, or “probe-alone” interval, the measured ear-canal pressure contains both the probe stimulus and any emission it evokes. The additional suppressor presented during the second, or “probe + suppressor” interval is chosen to reduce or eliminate the emission evoked by the probe. In principle, then, the emission can be found by computing the difference, at the probe frequency, between the probe-alone and probe + suppressor waveforms. Since the emission is derived by combining measurements made at different times, we sought to reduce the effects of time-dependent drifts by interleaving the probe-alone and probe + suppressor intervals. In most measurements reported here, we also interleaved the discrete-tone and swept-tone paradigms to facilitate their comparison.
Discrete-tone paradigm
The discrete-tone (DT) paradigm has been detailed previously (Shera and Guinan, 1999; Kalluri and Shera, 2007a,b). In the version implemented here, the probe stimulus was a pure tone of frequency fp, level Lp, and minimum duration of approximately Navg × 100 ms, where Navg is the number of artifact-free responses to be recorded and averaged. (The total duration was extended when segments of the response were identified as artifacts and excluded from the average.) During presentation of the continuous probe tone, the suppressor tone (of frequency fs = fp − 50 Hz and level Ls) was cycled on and off at intervals of roughly 200 ms (duty cycle of one half), thereby interleaving probe-alone and probe + suppressor segments, which were extracted from the response and averaged separately. The emission, PSFOAE, was then obtained as the complex (vector) difference between the probe-frequency Fourier components of the ear-canal pressure in the averaged probe-alone (Pp) and probe + suppressor intervals (Pps). In other words,
| (1) |
where the phases of and were adjusted to compensate for any differences in the starting phase of the probe stimulus in the two analyzed intervals (Shera and Guinan, 1999). The superscript DT identifies SFOAEs obtained using the discrete-tone method. Recorded response waveforms were screened for artifacts in real time by computing the difference between the current data buffer and a previously stored artifact-free reference buffer. When the rms difference exceeded a user-defined criterion, the data buffer was rejected; otherwise, it was added to the averaging buffer. Continual replacement of the reference buffer minimized the effects of slowly varying drifts in the baseline signal.
Swept-tone paradigm
In the swept-tone (ST) paradigm, both the probe and the suppressor stimulus pressure have the form
| (2) |
where O(t) is an overall ramping window used to taper the tone onset and offset, is the pressure amplitude, and is the instantaneous phase (in cycles). The instantaneous frequency is then , where the diacritical dot represents a time derivative. The phase can have many forms. Here, we used sweeps whose instantaneous frequency varied linearly with time, so that , where and b is the sweep rate (e.g., in Hz/s).1 If the rate is chosen so that , then . With these definitions, the phase becomes
| (3) |
where is an adjustable starting phase. The onset/offset window, O(t), is unity on the interval and tapers quickly to zero outside that range. We used the amplitude and phase of the ear-canal calibration curves to adjust the voltage waveform driving the earphones in order to produce the desired stimulus pressures, .
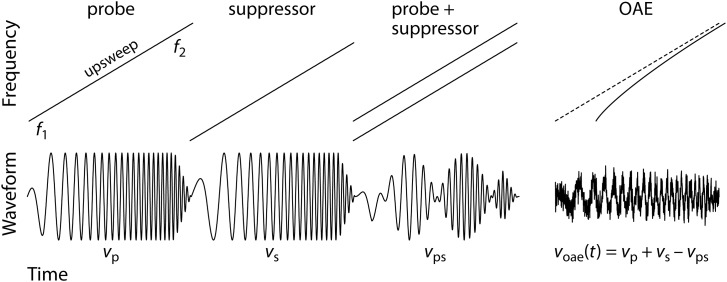
To simplify the later analysis and facilitate comparison with the discrete-tone case, we interleaved three stimulus intervals, consisting of a probe-alone sweep, a suppressor-alone sweep, and a probe + suppressor sweep.2 The paradigm is schematized Fig. 1. As in the discrete-tone case, the instantaneous frequency of the suppressor sweep was maintained at 50 Hz below that of the probe. (In some measurements we employed other values to examine the influence of suppressor placement.) The three-interval stimulus blocks were repeated to acquire a specified number of artifact-free responses at each frequency (anywhere from 32 to 256, depending on probe level and sweep rate). We denote the voltage waveforms recorded from the probe microphone during the three intervals of block number m by , , and , respectively. (Note that the superscripts here throughout this paragraph are indices, not exponents.) The “OAE waveform” was then computed using the formula
| (4) |
The final, mean waveform was obtained by averaging over blocks: . A corresponding noise waveform was computed from the difference between successive OAE waveforms: , with . Microphone calibrations were applied later, after the emission frequency was determined, to obtain the ear-canal emission and noise pressures.
Figure 1.
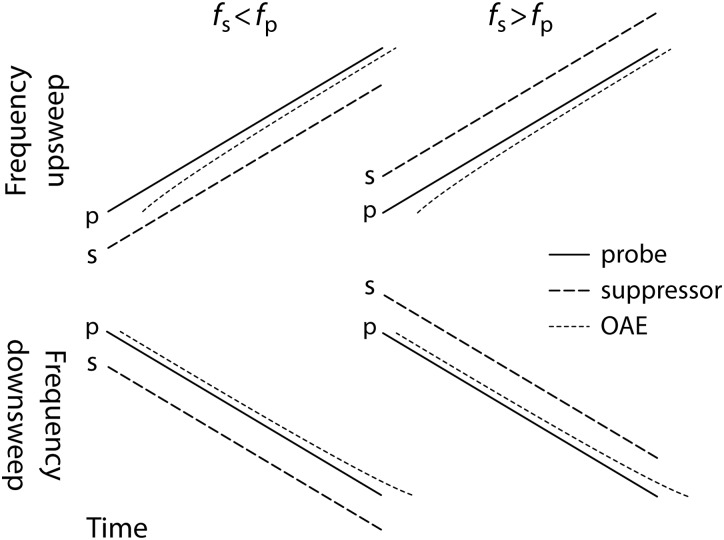
Schematic of the swept-tone paradigm. Stimuli are presented in three interleaved intervals comprising, respectively, the probe, suppressor, and probe + suppressor waveforms. The instantaneous frequencies of the probe and suppressor waveforms are shown increasing linearly with time. The OAE waveform, whose instantaneous frequency also varies with time, is obtained by computing sums and differences of the responses to the three stimulus waveforms. Because of cochlear dispersion, the OAE sweep (rightmost panel, solid line) is delayed relative to the probe sweep (dashed line) by an amount that varies with frequency (i.e., with time).
The principle used to obtain the emission waveform via Eq. 4 is similar to that used in the discrete-tone case. The voltage waveform measured during the probe-alone sweep, vp(t), contains, in addition to background noise, both the probe and the evoked emission. Likewise, the waveform vs(t) contains the suppressor and any emission evoked by the suppressor. During the probe + suppressor interval, we expect the emission evoked by the probe to be greatly reduced, whereas that evoked by the suppressor to remain largely unchanged. (Since Lp is generally substantially lower than Ls, the probe has little effect on the suppressor or its emission.) Thus, the waveform vps(t) consists of the probe, the suppressor, and the suppressor-evoked emission.3 Combining the three waveforms according to Eq. 4 thus yields the time waveform of the emission evoked by the probe sweep; the probe sweep itself, the suppressor sweep, and the suppressor-evoked emission all cancel out.
We implemented artifact rejection for the swept-tone paradigm using a thresholding criterion in the time domain. The strategy was guided by the observation that in our subjects (all adults) the most troublesome artifacts were transients, usually less than 5 ms in duration. Artifacts were identified as blips in the emission time waveform whose amplitude exceeded a user-specified criterion. The criterion varied from subject to subject according to baseline noise levels and could be changed as necessary during the session. When an artifact was detected, an interval extending 3 ms before and after the artifact was zeroed out (erased) prior to adding the buffer to the accumulating average. Thus, ostensibly artifact-free data in the same buffer are preserved while only a small segment surrounding the artifact is deleted. (The corresponding segment was erased from the probe-alone, suppressor-alone, and probe + suppressor intervals, no matter where the artifact actually occurred.) Note that with this implementation the effective number of measured responses can vary with time within the sweep. In order to compute the average, we kept track of the number of contributing waveforms at each time point.
Spectral estimation
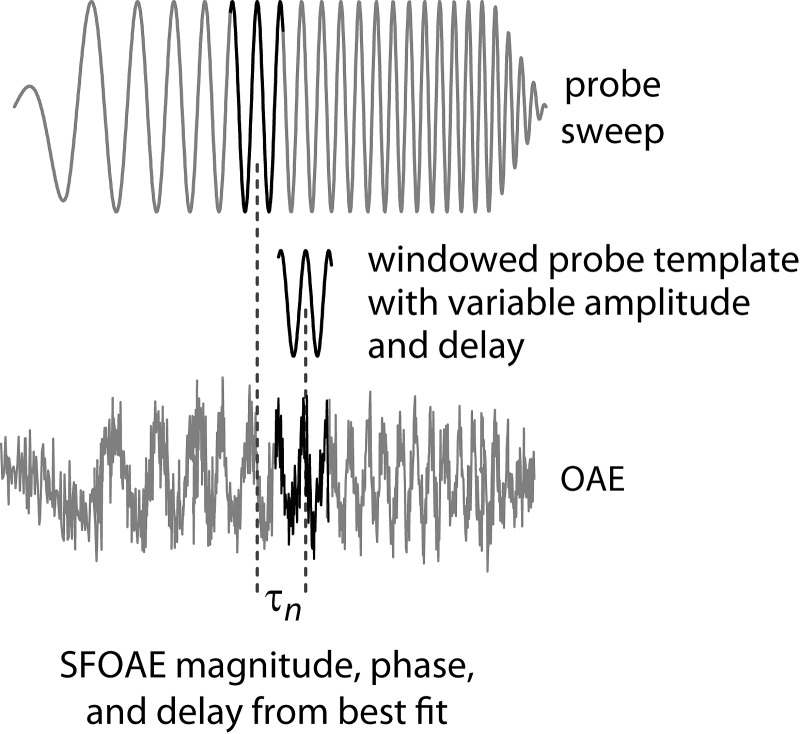
In the swept-tone paradigm, we estimate the SFOAE spectrum from the time waveform by fitting a model to the measurement, as illustrated in Fig. 2. Like the probe stimulus that evoked it, the voltage waveform is a frequency sweep, albeit one whose instantaneous frequency is slightly delayed relative to that of the probe. To determine the emission magnitude, phase, and delay at time tn, we consider the surrounding segment of the emission voltage waveform:
| (5) |
where the segment is defined by the analysis window, , which is centered about tn and has nominal duration . We model the measured emission segment as a scaled, delayed, and phase-shifted version of the windowed probe sweep. Thus, we model the voltage waveform using the equation
| (6) |
where cn and sn are, respectively, the coefficients of the in-phase and quadrature components and τn is the overall delay. Equation 6 models the waveform as comprising a single OAE component of unknown amplitude, phase, and delay; if desired, additional terms could be included to account for other possible components of the waveform (e.g., contributions from multiple, higher-order reflections).
Figure 2.
Finding SFOAEs from the swept-OAE waveform. SFOAE magnitude, phase, and delay are found by determining the parameters of a “template waveform” that yield the best match with a given segment of the measured OAE waveform. The template is a windowed version of the probe sweep with variable amplitude, phase shift, and delay. The window illustrated here is effectively rectangular; for the actual analysis, we applied a taper to emphasize frequency components occurring near the center of the window.
At each analysis time, tn, we determine the three unknown parameters by least-squares fitting4; that is, by minimizing the root-mean-square (rms) value of the residual between measurement and model, . The summation in the mean extends over those (discrete) measurement times t for which . For linear sweeps (i.e., constant sweep rate, b), the nominal window duration corresponds to a frequency bandwidth given by . The bandwidth . represents the approximate range of emission frequencies included in the fitting procedure. Unless otherwise specified, our standard parameters were b = −2 Hz/ms (a downsweep) and ms, equivalent to an analysis bandwidth of 80 Hz.
In terms of the best-fit parameters , the SFOAE at frequency fn has the value
| (7) |
where and is the complex-valued microphone calibration, including compensation for any phase shifts introduced by the A/D converter, with units of Pa/Vpk. An estimate of the on-frequency noise was obtained by applying the same analysis5 to the noise waveform, . Although other methods of estimating PSFOAE are possible—and some (e.g., heterodyning or fast Fourier transforms) are more computationally efficient—the approach outlined here has the benefit, important for our purposes, of providing an accurate and intuitive measure of the emission delay, τn, obtained directly in the time domain, rather than from phase gradients.
Subjects
All procedures were performed at the House Research Institute and approved by the institutional review board at St. Vincent Medical Center. Acoustic signals were delivered to and recorded from the ears of adult human subjects (one ear each) while they were comfortably seated in a sound-attenuating chamber. Subjects reported normal hearing and were screened for measurable reflection-source OAEs using 80 dB peSPL clicks in the linear mode. Only subjects with click-evoked OAE (CEOAE) levels averaging at least 6 dB above the noise floor on the interval 0.5–4 kHz were selected for further study. Because our goal was to test for differences between two SFOAE measurement paradigms, no additional audiometric criterion were applied. Of the 17 subjects screened, 14 passed and completed the study (4 male, 10 female; 18–37 yr old), two failed the screening, and one did not return. In 11 of the 14 studied subjects, we measured SFOAEs at frequencies on the interval 0.5–4.5 kHz at probe and suppressor levels of 40 and 60 dB sound pressure level (SPL), respectively. In a subset of 4 subjects, we also made measurements at probe levels of 20 dB SPL. In a different, partially overlapping subset of 4 subjects, we made additional measurements spanning a higher frequency range (4–8.5 kHz; 40 dB SPL probe).
Stimulus generation and recording
Stimulus waveforms were generated and responses acquired and averaged digitally using a National Instruments 4461 data-acquisition board (100 kHz sampling rate) and an ER10C probe system (Etymōtic Research, Elk Grove Village, IL). The hardware was controlled using custom software written in LabVIEW (National Instruments, Austin, TX) and matlab (The Mathworks, Natick, MA). In situ earphone calibrations were performed using chirps at regular intervals throughout a measurement session. The calibration curves were used to deliver stimuli with the desired ear-canal sound-pressure level and starting phase.6 Real-time artifact rejection was implemented for both discrete-tone and swept-tone paradigms. To reduce the unnecessary rejection of buffers specifically due to low-frequency noise, the microphone signal was filtered using a highpass filter with a cutoff frequency of 250 Hz.
RESULTS
Equivalence between swept- and discrete-tone SFOAEs
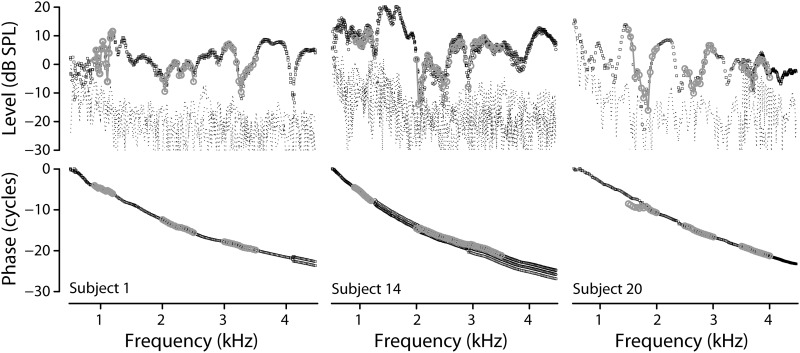
Figure 3 compares SFOAEs measured using the ST and DT paradigms. Spectral magnitudes (top row) and phases (bottom) of (small black symbols) and (filled gray symbols) are shown for three subjects, one per column. Stimulus frequencies ranged from 0.5–4.5 kHz and probe and suppressor levels were 40 and 60 dB SPL, respectively. To minimize the effect of drift, the ST and DT measurements were interleaved with each other and with in-the-ear calibrations (C). For example, the measurements shown in Fig. 3 were collected by repeating the sequence three times in succession. The ST results were obtained by averaging 64 artifact-free sweep responses at each time point; the DT results by averaging 64 artifact-free responses at each frequency. To speed the data collection, the three DT measurements were performed over three, more limited frequency spans distributed over the range of the ST measurement (DT1 on 0.75–1.25 kHz, DT2 on 2–2.5 kHz, and DT3 on 3–3.5 kHz). The analysis windows used to obtain were fixed at 40 ms duration, matching the buffer length of the fast Fourier transform used to compute . Since the two paradigms were interleaved within a short time period, the repeated measurements of illustrate the run-to-run variability of the swept-tone measurement while providing an estimate of the minimum expected variation between and .
Figure 3.
Magnitudes (top) and phases (bottom) of swept-tone and discrete-tone SFOAEs (black and gray symbols, respectively) in three subjects. Probe and suppressor levels were 40 and 60 dB SPL, respectively. In the ST paradigm, the probe frequency was swept from 4.5 down to 0.5 kHz at 2 Hz/ms. Repeated measurements of (up to three in each subject) are shown overlaid. In the DT paradigm, measurements were made over three, more limited frequency spans (DT1 on 0.75–1.25 kHz, DT2 on 2–2.5 kHz, and DT3 on 3–3.5 kHz). Black dashed and gray dashed lines show the noise floors of the ST and DT measurements, respectively.
The data in Fig. 3 indicate that the magnitude and phase of the DT and ST measurements match closely, even down to the detailed spectral variations. A similar match between and was found in all 11 subjects in whom we measured SFOAEs with these parameters (0.5–4.5 kHz, 40 dB SPL probe). In some subjects, we also made measurements at 20 dB SPL (n = 4), and the results from the two paradigms match equally well at this lower stimulus level. Although possible higher-order contributions to the SFOAE arising from multiple internal reflection within the cochlea are neglected in the ST analysis employed here [i.e., in the model of Eq. 6], they are at least partially captured by the DT method when the combined settling and measurement times are longer than twice the OAE delay, as they were here. Among other things, the good agreement between the DT and ST measurements thus suggests that any higher-order contributions to the SFOAE are small, at least in the subjects measured here.
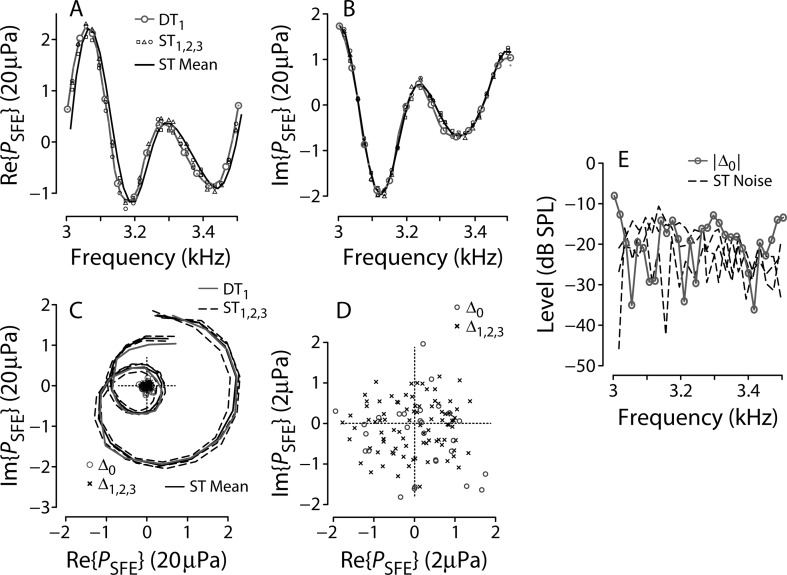
Figure 4 zooms in on the data from Subject 1 to examine differences between the DT and ST measurements more closely. Panels A and B plot the real and imaginary parts, respectively, of , the DT measurement obtained during the first of the three repeated sequences; the three ST measurements, , obtained from , , ; and their mean, . To look for possible systematic differences between the two paradigms, we computed the complex differences
| (8) |
and
| (9) |
Thus, at every frequency, Δ0 and Δ1,2,3 represent the vector differences (in Pa) between the individual measurements and the mean of the three ST sweeps. Figure 4C shows , , , Δ0, and Δ1,2,3, all plotted in complex coordinates. The four sets of complex difference pressures cluster near the origin, where they superpose and appear essentially indistinguishable when plotted on the same scale as the DT and ST measurements. In other words, all difference pressures—whether method-to-method or run-to-run—are small compared to the SFOAE pressures themselves. Both Δ0, and Δ1,2,3 are normally distributed about the origin, and their mean magnitudes are statistically identical (t-test, p = 0.5). Thus, the pressure differences Δ0 between SFOAEs measured using the two paradigms are typically no larger than the run-to-run variability in the sweep measurements themselves. Equivalently, differences between the DT and ST SFOAEs are of the same order as the noise in the swept-tone measurement [Fig. 4E].
Figure 4.
Differences between and . (A) and (B) The real and imaginary parts, respectively, of (gray symbols and line), the three repeated measurements of (small open symbols), and their mean, (solid black line). (C) These same pressures in a polar plot, together with the complex difference pressures and defined by Eqs. 8, 9, respectively. (D) The difference pressures on an expanded scale (, so that tick marks represent intervals of 2 μPa). (E) Compares the pressure magnitude , expressed in dB SPL, with the noise floors computed during each ST measurement. The data are from Subject 1.
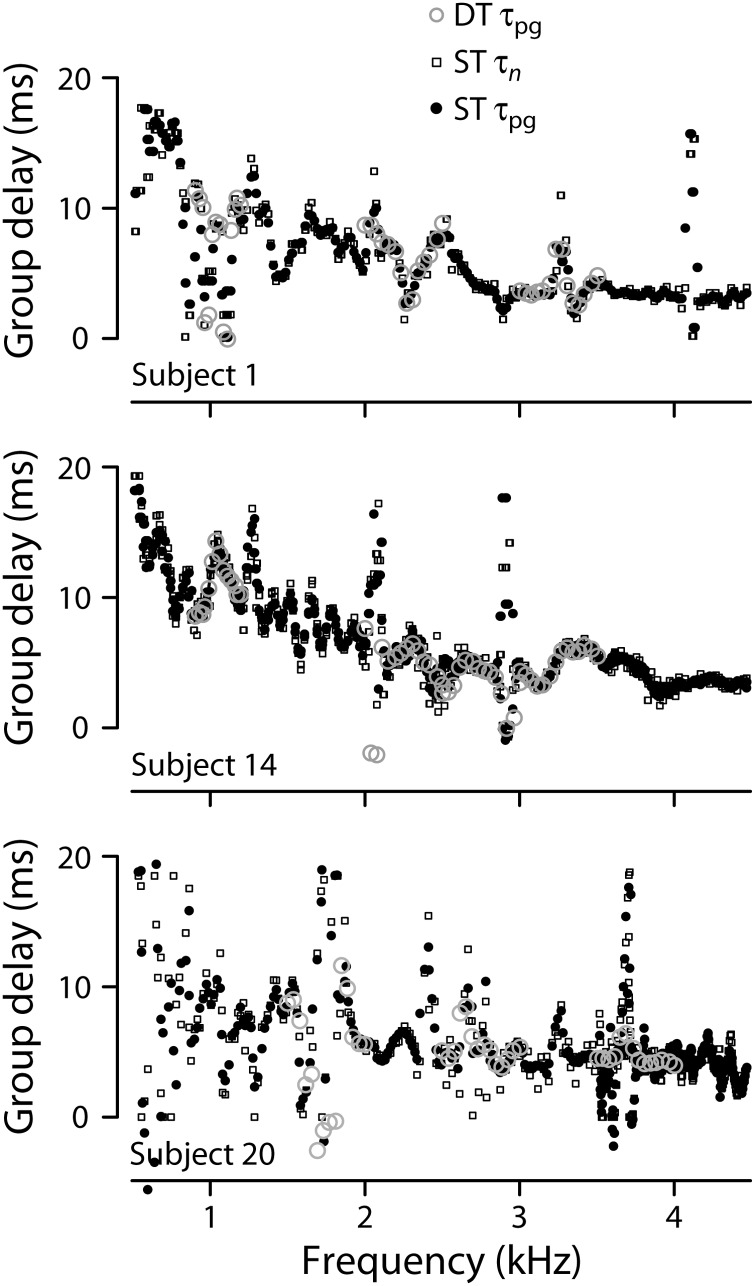
Group delays of swept- and discrete-tone SFOAEs
We compared the group delays of swept- and discrete-tone SFOAEs by computing the gradient of their respective phase-versus-frequency functions. The phase-gradient delay is defined as , where is SFOAE phase in cycles. Figure 5 shows that the phase-gradient group delays of DT (open gray circles) and ST (filled dots) SFOAEs are very similar, essentially overlapping even in their microstructural details. In addition to providing phase-gradient delays computed in the frequency domain, the ST method allows the estimation of group delay directly from the time waveform (see the discussion of τn in Sec. 2). Although the comparison in Fig. 5 does suggest small differences between τn (squares) and τpg (dots)—some of which are due to the constraint that the physical delay, τn, cannot be negative and some of which occur near spectral notches where the variability is always high—on the whole, the delays computed in the time domain appear strikingly similar to the delays, τpg, computed from SFOAE phase. Thus, SFOAE delays measured using the two different measurement protocols and computed using two different analysis methods yield nearly equivalent results.
Figure 5.
Equivalence of group delay of swept- and discrete-tone SFOAEs. The circular symbols show the phase-gradient delays, , for the DT (open gray circles connected by lines) and ST (filled dots) emissions. The open squares show values of , the ST group delay obtained directly in the time domain using the least-squares fitting procedure. Delays are from the same three subjects shown in Fig. 3.
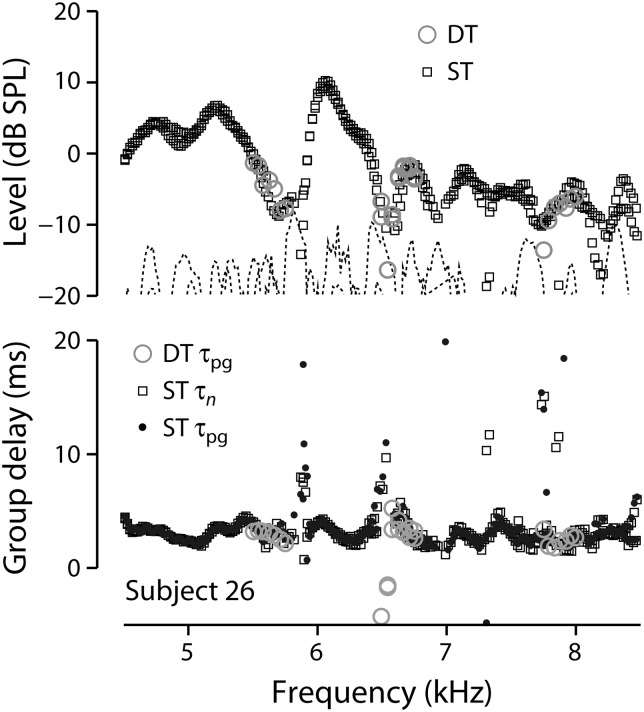
SFOAEs at higher frequencies
Figure 6 demonstrates the efficacy of the ST paradigm at high frequencies by comparing ST and DT SFOAEs measured from 4.5–8.5 kHz. High-frequency data were obtained and analyzed in four subjects, one from the previous group of 11 subjects and three additional subjects recruited for the purpose. All gave results comparable to those shown here. Mean SFOAE levels are typically smaller at frequencies above 4.5 kHz than at those below. In addition, we found that the high-frequency measurements were generally less repeatable from session-to-session, and even from run-to-run, than their low-frequency brethren. Since the calibrations interleaved between each measurement were less stable at high frequencies, the increased measurement variability likely arises from small movements of the probe that occur sporadically during the measurement. High frequency measurements, where sound wavelengths are shorter, are expected to be especially sensitive to such movements. Despite the increased variability, the overall match in magnitude and group delay between the ST and DT paradigms remains strong.
Figure 6.
Swept- and discrete-tone SFOAEs at high frequencies. The two panels show SFOAE level and group delay at frequencies from 4.5 to 8.5 kHz for both the DT (open circles) and ST (squares) paradigms. In the bottom panel, the circular symbols show phase-gradient delays, , for the DT (open circles) and ST (filled dots) emissions. The open squares show values of , the ST group delay obtained directly in the time domain using the least-squares fitting procedure. To improve the SNR at these higher frequencies, the ST emissions were obtained using an analysis window of 80 ms duration.
Effects of parameter variations
As shown in Sec. 3A, our standard measurement and analysis parameters yield swept-tone SFOAEs that are nearly indistinguishable from discrete-tone SFOAEs. Although the results are not especially sensitive to the exact values of these parameters, large changes in parameters can affect the results. Here we discuss some of the principal parameters and how changes in their values influence the measured SFOAEs.
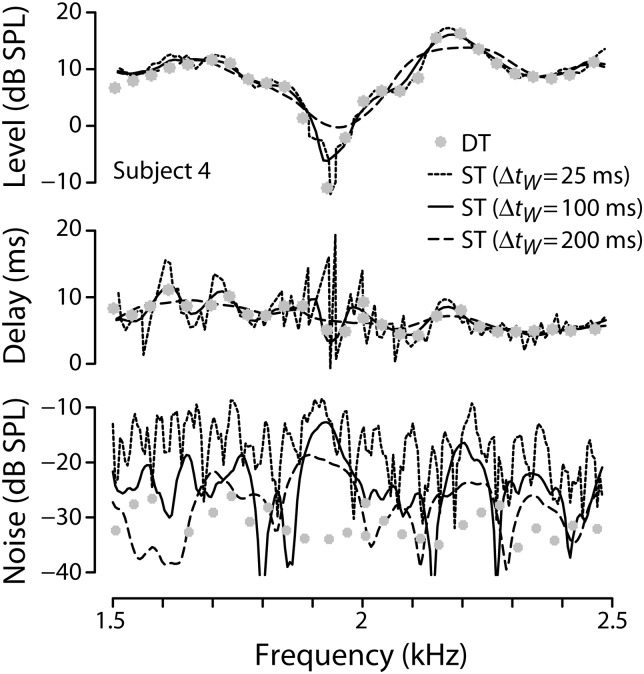
Duration of the analysis window
Figure 7 shows the SFOAE spectral magnitude, group delay, and noise floor obtained from a single ST measurement using analysis windows of three different durations (namely, 25, 100, and 200 ms). Discrete-tone SFOAEs measured in the same subject are shown for comparison. When the sweep rate is held constant, the duration, , of the analysis window controls the analysis bandwidth, , and thus determines the range of frequencies constraining the fit and influencing the estimate of the SFOAE at each analysis time. Longer analysis windows effectively average the emission over a larger bandwidth and thus produce smoother, more slowly varying SFOAE spectra. The OAE waveform analyzed in Fig. 7 was measured using a sweep rate, b, of −1 Hz/ms. Although the two shorter analysis windows preserve much of the fine spectral detail (e.g., near the notch at 1.9 kHz), the longest window has an effective bandwidth of roughly 200 Hz and produces considerable smearing at frequencies where the emission level varies most rapidly. Thus, if the analysis window is made too long, spectral detail is smoothed away. On the plus side, however, longer analysis windows result in lower mean noise floors, reducing the variance of the measurement and aiding the detection of low-level emissions. At the other extreme, if the window is made too short, uncertainties in the fitting procedure grow and the estimates become noisy and unreliable.
Figure 7.
Dependence of swept-tone SFOAEs on the duration of the analysis window. The three panels show the SFOAE spectral level, group delay, and noise floor obtained from a single ST measurement (sweep rate = −1 Hz/ms) using analysis windows of duration 25, 100, and 200 ms. Discrete-tone SFOAEs measured in the same subject are shown for comparison (gray dots).
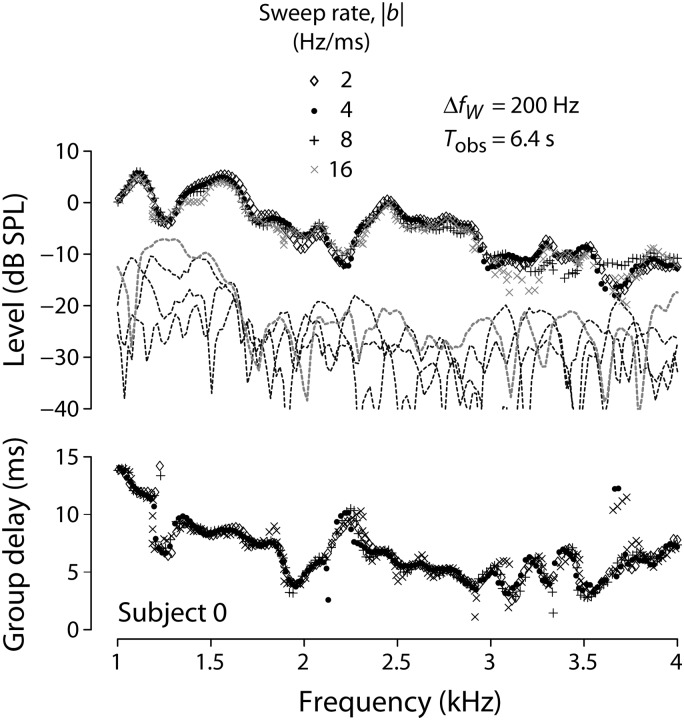
Sweep rate
The effective analysis bandwidth can also be changed by fixing the duration of the analysis window, , while varying the sweep rate, b. Changing in this way produces results similar to varying at fixed b. For example, with fixed, faster rates yield smoother SFOAE spectra (not shown). Figure 8 shows the effect of varying (from 2 to 16 Hz/ms) while maintaining equivalent spectral resolution by fixing the analysis bandwidth, at 200 Hz. Thus, when we doubled the sweep rate, we halved the duration of the analysis window. In addition to fixing , we attempted to preserve the measurement SNR by fixing the total observation time . Since , fixing Tobs requires increasing the number of averages in proportion to the sweep rate. Although the measurements become somewhat noisier at the fastest rate (−16 Hz/ms), Fig. 8 indicates that SFOAEs measured at fixed bandwidth and observation time are otherwise largely insensitive to the sweep rate, at least over the eightfold range explored here. Similar results were seen in all five subjects in whom emissions at different sweep rates were measured.
Figure 8.
Effect of sweep rate at constant analysis bandwidth and observation time. The two panels show SFOAE level and group delay measured using sweep rates of 2, 4, 8, and 16 Hz/ms (all were downsweeps with b < 0). The analysis bandwidth was fixed at 200 Hz and the total observation time was fixed at 6.4 s. The measurement noise floors are shown with short-dashed lines. Measurements at the highest sweep rate are shown in gray.
The observed elevation of the noise floor at the fastest rate suggests a breakdown in our attempt to control the SNR of the measurement by varying the number of averages in proportion to the rate. Part of the problem, we suspect, is that the analyzed noise waveform, , may comprise more than random noise. Recall that we define as the average difference between successive OAE waveforms. Because of imperfect cancellation between buffers, the noise waveform can contain trace and variable amounts of the stimulus tones, as well as snippets of the emission itself. These “non-Gaussian contaminants,” which may arise from temporal drift in the calibration or small shifts in probe placement in the ear canal, can affect the outcome of the least-squares fitting procedure. The resulting errors in signal (or noise) estimation are generally largest at the highest sweep rates, where the analysis windows are the shortest and the number of data points constraining the fit the fewest.
Sweep direction and suppressor placement
Most results reported here were obtained using stimulus downsweeps (b < 0). To explore the possible influence of sweep direction, we compared results obtained using interleaved sweeps of opposite directions and found nearly identical results. As illustrated in Fig. 9, changing the sweep direction also changes the distance in the time-frequency plane between the OAE and the suppressor. Because the OAE is always delayed relative to the probe, the relative locations of the OAE and the suppressor depend both on the sweep direction and on whether the suppressor frequency is less than or greater than the probe. In general, the OAE and the suppressor are closest when the quantities b and have opposite signs (i.e., for an upsweep with or a downsweep with ). (In our standard protocol, a downsweep with , they have the same sign.) In one subject, we performed a series of measurements designed to examine effects of sweep direction, suppressor placement, and their possible interactions. We measured all four combinations of direction and placement on each of three different days. An analysis of variance (ANOVA) on the resulting SFOAE levels found no significant dependence on session number (day), sweep direction, or suppressor placement but did reveal a significant interaction between sweep direction and suppressor placement , . In particular, measurements with sgn were significantly different from those with sgn , especially in regions of low SNR. The pattern of the interaction suggests that the operative variable is the time-frequency distance between OAE and suppressor. A pattern like this could emerge if the OAE waveform were contaminated by incomplete cancellation of the suppressor (see Sec. 4C), and if the effect of the suppressor residual on the fitting procedure depends on its distance from the OAE.7 This is consistent with our observation that removing data points with low SNR greatly reduced the apparent interaction term in the analysis (i.e., the dependence on sgn ); for data with SNR > 4 dB, the interaction becomes nonsignificant [F(1, 2186) = 3.67, p > 0.05]. We conjecture that in regions of low SNR, the fitting procedure has greater difficulty extracting the emission when the suppressor residual is nearby and thus is more easily confused with the OAE itself.
Figure 9.
Time-frequency schematic showing relative probe, suppressor, and OAE waveforms for the four different combinations of linear sweep direction (rows) and relative suppressor frequency (columns). Solid lines represent the probe, dashed lines the suppressor, and dotted lines the OAE. Note that the OAE is closer to the suppressor in the upper left and lower right panels, where b and have opposite signs.
DISCUSSION
This study demonstrates that SFOAEs measured using swept tones (ST) are essentially indistinguishable from those measured using standard discrete-tone (DT) methods. We compared ST and DT measurements at low-to-moderate stimulus intensities (20–40 dB SPL) over a wide frequency range (0.5–8.5 kHz) and found that differences between the two methods are comparable to the run-to-run variability of either method alone. In addition, the match appears relatively insenstive to changes in measurement parameters such as sweep rate and direction.
Although exploring possible differences between ST and DT SFOAEs required the robust alignment of many methodological ducks, our ultimate conclusion that the results match closely appears entirely consistent with previous findings of the near equivalence of discrete-tone SFOAEs and CEOAEs (Kalluri and Shera, 2007b). If discrete-tone stimuli lie at the slow-end extreme of the swept-tone method (b → 0), then the clicks used to evoke CEOAEs occupy the other, where the sweep is so fast that all frequencies are presented simultaneously (see also Bennett and Özdamar, 2010). One useful measure of the “sweepiness” of a given measurement/analysis combination is the ratio of the size of the window bandwidth (Sec. 2C1), , to the frequency scale, , characteristic of variations in the SFOAE spectrum. A convenient measure of the latter interval is the reciprocal of the emission delay, . Over the interval , the emission phase varies by approximately one cycle. When the ratio is much less than one, the measurement is effectively discrete; when γ is much greater than one, the measurement approaches that of a click-evoked emission (CEOAE). The measurements reported here explore the middle ground near γ ∼1 where the swept-tone designation is appropriate.
Our measurement and analysis methods differ in some respects from previous studies that have used swept-tone stimuli to measure SFOAEs (Choi et al., 2008; Bennett and Özdamar, 2010). For example, whereas previous studies used either much faster8 (Bennett and Özdamar, 2010) or slower (Choi et al., 2008) sweep rates, we generally employed intermediate rates corresponding to γ ∼1. Unlike Choi et al. (2008), we adopted an interleaved, three-interval paradigm to help cancel out the suppressor and used least-squares fitting, rather than digital heterodyning, to extract the emission from the time waveform. Although we believe that these modifications help to make the measurement more robust (see Sec. 4C), we have no reason to believe that the agreement we find between discrete- and swept-tone SFOAEs should not apply to OAEs obtained using these other methods.
Advantages of the swept-tone method
The swept-tone method offers many advantages for acquiring high-resolution SFOAE data. First among them is the substantial increase in measurement efficiency compared to the DT method. Although the ST method eliminates much of the overhead (e.g., gaps, ramps, and settling time) needed to transition the stimulus from one frequency to another, most of the savings comes from the way the ST method exploits the smoothness and local redundancy typical of SFOAE spectra. To measure the SFOAE at any given frequency, the DT method relies on measurements made at that frequency alone. The ST analysis procedure, by contrast, makes use of measurements spanning a frequency band determined by the sweep rate and the duration of the analysis window. As a result, the method can provide high frequency resolution, and noise floors comparable to those of the DT method, in shorter times. For example, the ST measurements shown in Fig. 3 span a larger frequency range at higher resolution than the DT data but took essentially the same amount of time to collect (about 6.5 min for 64 averages acquired using the relatively slow sweep rate of −2 Hz/ms). The improved measurement efficiency has beneficial side effects, such as reducing subject fatigue and the concomitant movements and other artifacts that contaminate or prolong the measurement. We have found that artifacts and rejected buffers tend to occur more often toward the end of a long run as subjects become restless and noisy. Thus, in addition to requiring more time per frequency point, broadband DT measurements typically require multiple breaks and recalibrations, both of which can be significantly reduced, although not entirely eliminated, using the faster ST method.
Another compelling advantage of the ST method is that the discrete frequencies at which SFOAE values are ultimately obtained during the analysis stage need not be set in advance. Indeed, they can be changed at any time by reanalyzing the OAE sweep waveform. This makes the ST method convenient when employing data-analysis procedures, such as the ϕFFT for isolating or removing OAE components (Shera and Bergevin, 2012), that require knowing SFOAE values at a set of frequencies unknown at the time of measurement. In effect, reanalysis of the OAE sweep waveform provides an accurate interpolation scheme capable of estimating SFOAE values at any desired frequency. Since total DT measurement times depend on the desired frequency resolution, which for the ST method can be adjusted post hoc at whim, quantitative comparisons of total measurement times are generally not all that useful. In the time T needed to acquire probe-alone and probe + suppressor data at one probe frequency using the DT method, the linear ST method provides data spanning a frequency interval of width , where the factor of 2/3 reduction arises from use of the interleaved, three-interval paradigm.
The sweep rate and analysis window determine the effective spectral resolution and noise floor of the measurement. Although the results presented here all derive from linear sweeps analyzed using windows of fixed bandwidth, these parameters can be chosen, or varied with time, to suit the specific application. For example, log or power-law sweeps can be used to improve measurement SNRs at low frequencies. For the analysis stage, it may prove beneficial to match the window bandwidth to the expected spectral features of the SFOAE. In particular, the spectral density of SFOAE notches and the rate of phase accumulation generally decrease at higher frequencies, roughly in proportion to the emission delay. Varying the analysis bandwidth with frequency [e.g., so that , where is the expected delay trend] would therefore result in more uniform smoothing and a reduction in any frequency-dependent bias. The needed delay trend could be obtained from published measurements [see Eq. 14] or tailored to individual subjects based on an initial analysis of the OAE waveform.
Compensating for cochlear dispersion
Because of cochlear frequency dispersion, the instantaneous frequency of the emission waveform is not simply that of the stimulus evaluated at a fixed delay. As illustrated in Fig. 1, for example, even when the instantaneous frequency of the probe varies uniformly with time, that of the emission varies nonuniformly because emissions at low frequencies are more delayed than those at high frequencies. As a result of this dispersion, the time dependence of the emission's instantaneous frequency forms a curve rather than a line (see right panel of Fig. 1). In addition to having an overall curvature whose form presumably depends on the species, the delay in each individual ear displays considerable microstructure (see Fig. 5). According to the coherent-reflection model (Shera et al., 2005), the microstructure depends on the particular pattern of micromechanical irregularities manifest in the individual ear. Although the microstructure cannot be known and compensated for in advance, estimates of the overall curvature can be obtained from prior measurements in the same or similar species. In principle, these estimates can therefore be used to optimize the measurement or analysis parameters.
Consider, for example, the problem of choosing the duration of the analysis window, , so that it corresponds with a desired frequency bandwidth, . For a linear sweep, the two are related by the formula , where b is the sweep rate. Although this relationship holds for the stimulus, cochlear dispersion modifies it for the OAE. To see how, note that although the instantaneous frequency of the probe stimulus is , the instantaneous frequency of the OAE waveform varies due to temporal dispersion. In general, the instantaneous frequency, , of the OAE waveform can be written
| (10) |
where τ(f) is the OAE delay. Computing the time derivative using the chain rule yields
| (11) |
Assuming a linear sweep and solving for yields
| (12) |
where quantifies the degree of dispersion. Thus, to first order, the intervals and are related by
| (13) |
Whenever q is nonzero, Eq. 13 deviates from the simple relationship, , applicable to the stimulus waveform. The deviation increases with the sweep rate and depends on its direction. Since q > 0, the window corresponding to a fixed bandwidth is shorter for upsweeps (b > 0) than for downsweeps (b < 0). To find the magnitude of the dispersive effect, we compute q(f) using the empirical power-law form for the delay trend, , derived from SFOAE measurements (Shera and Guinan, 2003). When expressed as the equivalent number of stimulus periods, the emission delay trend has the approximate form
| (14) |
Consequently,
| (15) |
which is zero when reduces to a constant delay . Plugging in the numbers, one finds that dispersive effects on the window duration are small at the sweep rates employed here, even at low frequencies, where is largest. For example, at f ∼1 kHz (where and ) the deviations are only about 10% at b = 16 Hz/ms and proportionally smaller at lower rates.
Alternatives to least-squares fitting
We explored two alternatives to the least-squares fitting procedure for obtaining the SFOAE spectrum from the OAE waveform. Although both alternatives—digital heterodyning (Choi et al., 2008) and Fourier analysis—proved more computationally efficient than the least-squares procedure, both also appeared more susceptible to noise or artifacts in the waveform. Consider, for example, the Fourier-based procedure, which yields the estimate
| (16) |
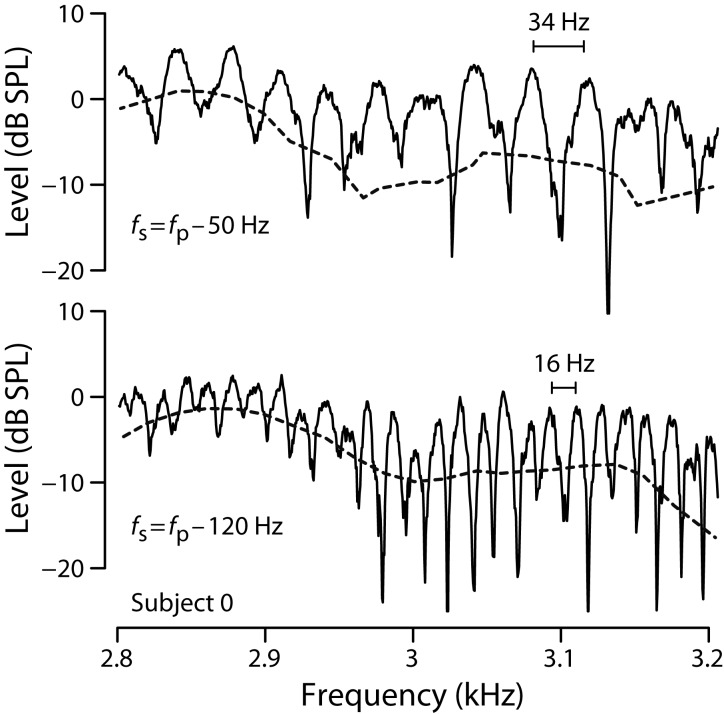
where represents the discrete Fourier transform and . Figure 10 plots a typical SFOAE spectral magnitude computed in this way. Unlike the estimates of obtained using least-squares fitting (dashed lines), the Fourier estimates from Eq. 16 manifest quasiperiodic spectral oscillations reminiscent of an interference pattern. (To facilitate visualization of the interference pattern, we smoothed the spectrum, which has a native resolution of 0.5 Hz, using a 10-Hz running complex average.) Since oscillations in the frequency domain correspond to a delay in the time domain, the pattern suggests that the waveform contains two major components: the OAE itself and a signal resembling the OAE but delayed in time.
Figure 10.
Estimates of obtained by Fourier analysis. In both panels, the solid lines show SFOAE levels obtained using Eq. 16; the dashed lines show values obtained using our standard least-squares fitting algorithm. The data in the two panels were obtained using different values for the relative frequency of the suppressor. In the top panel, the suppressor frequency is 50 Hz below the probe; in the bottom panel it is 120 Hz below. To aid the visualization of the spectral structure, the Fourier estimates were smoothed using a 10-Hz running complex average.
What is the origin and identity of the delayed component? Ideally, the linear combination of measurements used to define the OAE waveform [Eq. 4] achieves total cancellation of the probe and suppressor stimuli. In practice, however, the cancellation can never be perfect. Not only are the measurements of finite precision and affected by nonlinearities in the transducers, but small drifts in calibration or shifts in probe position during the measurement can also prevent complete cancellation of the stimuli. The presence of uncanceled stimulus components in the OAE waveform can interfere with the analysis of the OAE. Being the larger of the two stimulus waveforms, the suppressor might be expected to be the dominant contaminant.
Indeed, comparison of the two panels in Fig. 10 demonstrates that the period of the oscillation—and hence the delay of the interfering component—depends on the frequency of the suppressor tone. For example, the spectral oscillation period is smaller when the suppressor frequency is positioned farther away from the probe. Because of the sweep, the stimulus and emission frequencies in the waveform vary with time, and differences in frequency therefore correspond to differences in time (e.g., to delays). Computation of the oscillation period, based on the known delays of the emission and suppressor, confirms this diagnosis. The emission delay, relative to the probe, is given by the corresponding SFOAE phase-gradient delay, . To find the suppressor delay, note that for linear sweeps performed with the suppressor at a fixed distance from the probe, the time delay between a particular frequency component in the probe and its appearance in the suppressor waveform is simply
| (17) |
The delay can be either positive or negative, depending both on the relative suppressor frequency and on the direction of the sweep. When is negative, the delay is actually an advance—frequencies in the suppressor waveform occur before they appear in the probe. The oscillation period due to interference between the emission and the suppressor is just the reciprocal of the total delay between them:
| (18) |
The measurements in Fig. 10 were collected using standard downsweeps (b = −2 Hz/ms) with the suppressor below the probe . Hence, for these data. According to the data in Fig. 8, the typical value of near 3 kHz in this subject is about 4 ms. Substituting these numbers into Eq. 18 yields the estimates Hz and Hz for relative suppressor frequencies of 50 and 120 Hz, respectively. The scale bars provided in Fig. 10 show that these values provide good estimates of the oscillation period. This analysis confirms that the additional, delayed component in the OAE waveform is an uncanceled, contaminating remnant of the suppressor.
The absence of spectral oscillations in the estimate of obtained from the same OAE waveform using the least-squares fitting procedure (dashed line in Fig. 10) indicates that the least-squares analysis method is substantially more robust to artifactual contamination by stimulus remnants. The reason for this is simple: unlike Fourier analysis, the fitting procedure uses prior knowledge to construct a reliable model for the OAE and its variation with time. The model provides additional constraints that enable a more robust estimation of the SFOAE. In effect, the model-based method implements a filter that helps separate the OAE signal of interest from possible contaminants in the measured waveform (see also Long et al., 2008).
The swept-tone compression method
Although the suppression-based sweep method employed here is already substantially faster than the discrete-tone method, measurement times can be decreased another 33% simply by adopting a swept-tone version of the compression paradigm (Kemp and Chum, 1980; Kalluri and Shera, 2007a). Whereas the swept-tone suppression method uses a suppressor to help extract the emission, the swept-tone compression method exploits the compressive growth of SFOAE amplitude by employing probe-alone sweeps presented at two different levels: the probe level, , and a higher, “probe-compressor” level, . The OAE waveform is then defined using a modified form of Eq. 4:
| (19) |
where . By subtracting off a linearly scaled-down version of the high-level response to the swept compressor, Eq. 19 removes the stimulus contribution to the waveform while largely preserving the emission evoked by the probe. Analysis of the OAE waveform proceeds just as it does in the swept-suppressor case. By eliminating the need for a third stimulus interval (i.e., the suppressor-alone segment), the swept-tone compression method reduces the measurement time by roughly one third.
Although the compression method outlined above is considerably more efficient, we chose to employ the suppression method for the present study. In the discrete-tone case, the suppression and compression paradigms have been shown to yield nearly equivalent results (Kalluri and Shera, 2007a). However, to facilitate comparisons between discrete- and swept-tone measurements, we sought to use the same basic paradigm, suppression or compression, for both. Unfortunately, the discrete-tone version of the compression paradigm is quite sensitive to earphone nonlinearities of the sort that bedevil the Etymōtic ER10c (Schairer et al., 2003); for that reason, we adopted the suppression paradigm throughout. Perhaps surprisingly, however, the swept-tone compression method is considerably more tolerant of earphone nonlinearities than its discrete-tone counterpart. This convenient contrast arises from the different ways the emissions are distinguished and separated from the stimulus in the two cases. In the discrete-tone case, the probe and the emission occur simultaneously, and the analysis relies on the nonlinear growth of the emission to extract it from the measured waveform. As a result, nonlinearities in the earphone directly contaminate the estimate of the SFOAE, and the accuracy of the emission measurement depends critically on the linearity of the transducers. In the swept-tone case, however, the emission is separated from the probe directly in the time domain by exploiting the emission delay.
In principle, the measurement and subtraction of the high-level probe-compressor waveform is entirely unnecessary. Indeed, by including representations of both the emission and the probe in the fitted model [i.e., in Eq. 6], it is often possible to extract the SFOAE directly from the low-level, probe-alone waveform, , without need of subtracting out the probe stimulus, as in Eq. 19. By eliminating the need to measure , this reduces the measurement time by another 50%. We have found, however, that the estimation of the SFOAE is much more robust—especially at low emission levels or at high frequencies where OAE delays are short and the emission therefore more difficult to distinguish from the probe—if the probe stimulus can be largely removed from the analyzed waveform prior to fitting. By subtracting the rescaled probe-compressor measurement one reduces the amount of the stimulus waveform that leaks through the equivalent filter created by the model estimation procedure.
Equivalence of phase-gradient and physical delay
The close correspondence between phase-gradient and time-domain estimates of SFOAE latency evident in Fig. 5 demonstrates that the irregularity characteristic of SFOAE delays is robust to the method of measurement and not merely the artifactual result of taking the derivative of a noisy signal. Furthermore, the match demonstrates that SFOAE phase-gradient delays—including their large and irregular fluctuations across frequency—reflect the actual physical time delays of the emission at different frequencies. The physical emission latency, not merely the phase gradient, is inherently irregular. A previous comparison, in frogs, between SFOAE phase-gradient delays and emission onset latencies measured in the time domain is consistent with this result (Meenderink and Narins, 2006). Although that study compared data pooled across animals, rather than point-by-point in individuals, the two different delay measures manifest a similar frequency dependence in their overall magnitude and variance.
Before finding the close match between phase-gradient delay and physical SFOAE latency, we had expected the physical latency to vary rather more smoothly with frequency. Indeed, we feared at first that the irregularity apparent in our estimates of physical latency reflected a hypersensitivity to unrejected artifacts lurking in the data or some elusive error in our least-squares fitting procedure. Our expectations regarding smoothness of the physical latency had been shaped, in part, by measurements of the latencies of click-evoked OAEs, which are often summarized by smooth curves. The possibility that physical latencies, but not phase gradients, would vary smoothly with frequency also appeared consistent with theoretical arguments. According to filter theory, the correspondence between phase gradients and actual physical time delays in any given frequency band depends to some degree on the constancy of the response amplitude (in this case, emission level) in that band (Papoulis, 1962, Sec. 7-5). Since much of the irregularity across frequency in emission phase gradients is associated with wobbles or notches in emission magnitude (e.g., Sisto et al., 2007), our working hypothesis was that the phase gradients and physical latencies would differ, with physical latencies showing considerably less variability across frequency. In retrospect, however, this theoretical constraint appears less restrictive than we hypothesized, and our impressions of underlying smoothness in published CEOAE delays were unwarranted. As we realized, many studies report only group trends, in which much of whatever irregularity there may be is ironed out. Even in those studies that report CEOAE delays in individual ears (e.g., Sisto et al., 2007), the delays are often extracted from the measured time waveform using time-frequency analysis averaged over a frequency band (e.g., 1/3 octave), thereby smoothing the result. Finally, the frequency resolution of the analysis is often insufficient to capture fine frequency fluctuations, whose effects therefore appear smoothed.
The irregular frequency dependence of SFOAE delays corroborates predictions of the coherent-reflection model of OAE generation. Factorization of model-generated SFOAE spectra into minimum-phase and all-pass components (e.g., Papoulis, 1962, Sec. 10-3) demonstrates that, like the empirical SFOAE latencies reported here, the all-pass (or pure delay) component of simulated SFOAEs is inherently irregular (Shera and Bergevin, 2012). In the model, the irregular frequency dependence of SFOAE magnitude and delay originates in the irregular spatial dependence of the micromechanical perturbations responsible for wave scattering. Because of micromechanical irregularity, emissions at nearby frequencies can have strikingly different latencies, even though they originate in adjacent or overlapping regions of the cochlea.
ACKNOWLEDGMENTS
We thank Carolina Abdala and John Guinan for their helpful comments on the manuscript. This work was supported by grants R01 DC03687, P30 DC05209, and P30 DC10743 from the National Institutes of Health.
Footnotes
Because the evoked emission is delayed relative to the stimulus, satisfactory estimates of the SFOAE can often be obtained directly from an analysis of just the probe-alone waveform. In such cases, the suppressor-only and probe + suppressor waveforms are not strictly needed. See Sec. 4D for more details.
Emissions resulting from nonlinear interactions between the probe and suppressor are assumed small enough to be ignored here; their contributions to the estimate of the probe-evoked emission are reduced further by the subsequent signal processing.
Note that the optimization needed to determine the best-fit values of the parameters can become singular if all three parameters are allowed to vary simultaneously. The problem occurs because small changes in τn can be compensated for by small changes in the ratio . As a result, simultaneous optimization of all three parameters may not converge. To circumvent this numerical problem we proceed in two steps. First, we determine the best-fit values of the two parameters at multiple fixed values of . to determine how they and the corresponding minimum rms residual, , vary as a function of . Then, we define the optimal value of as that which minimizes . To expedite the computation, was constrained to the interval [0,20] ms.
Analysis of the noise waveform is identical except that, rather than being varied, the value of the delay τn, and hence of the emission frequency, is fixed at the value determined from the emission waveform.
Because our principal aim was to compare the discrete and swept-tone paradigms, rather than obtain baseline SFOAE data at known stimulus levels, we made no attempt to compensate for uncertainties in the calibration arising from ear-canal standing waves (e.g., Scheperle et al., 2011).
Although we did not explore the possibility here, the time-frequency distance between the OAE and the suppressor may also influence the magnitude of olivocochlear efferent effects.
The sweep rates employed by Bennett and Özdamar (2010) are fast enough that their paradigm is perhaps better thought of as measuring a chirp-evoked CEOAE than a swept-tone SFOAE.
References
- Bennett, C. L., and Özdamar, Ö. (2010). “ Swept-tone transient-evoked otoacoustic emissions,” J. Acoust. Soc. Am. 128, 1833–1844. 10.1121/1.3467769 [DOI] [PubMed] [Google Scholar]
- Bentsen, T., Harte, J. M., and Dau, T. (2011). “ Human cochlear tuning estimates from stimulus-frequency otoacoustic emissions,” J. Acoust. Soc. Am. 129, 3797–3807. 10.1121/1.3575596 [DOI] [PubMed] [Google Scholar]
- Bergevin, C., Velenovsky, D. S., and Bonine, K. E. (2010). “ Tectorial membrane morphological variation: Effects upon stimulus frequency otoacoustic emissions,” Biophys. J. 99, 1064–1072. 10.1016/j.bpj.2010.06.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi, Y. S., Lee, S. Y., Parham, K., Neely, S. T., and Kim, D. O. (2008). “ Stimulus-frequency otoacoustic emission: measurements in humans and simulations with an active cochlear model,” J. Acoust. Soc. Am. 123, 2651–2669. 10.1121/1.2902184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guinan, J. J. (1990). “ Changes in stimulus frequency otoacoustic emissions produced by two-tone suppression and efferent stimulation in cats,” in Mechanics and Biophysics of Hearing, edited by Dallos P., Geisler C. D., Matthews J. W., Ruggero M. A., and Steele C. R. (Springer-Verlag, New York: ), pp. 170–177. [Google Scholar]
- Guinan, J. J. (2006). “ Olivocochlear efferents: Anatomy, physiology, function, and the measurement of efferent effects in humans,” Ear Hear. 27, 589–607. 10.1097/01.aud.0000240507.83072.e7 [DOI] [PubMed] [Google Scholar]
- Joris, P. X., Bergevin, C., Kalluri, R., Mc Laughlin, M., Michelet, P., van der Heijden, M., and Shera, C. A. (2011). “ Frequency selectivity in Old-World monkeys corroborates sharp cochlear tuning in humans,” Proc. Natl. Acad. Sci. 108, 17516–17520. 10.1073/pnas.1105867108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalluri, R., and Shera, C. A. (2007a). “ Comparing stimulus-frequency otoacoustic emissions measured by compression, suppression, and spectral smoothing,” J. Acoust. Soc. Am. 122, 3562–3575. 10.1121/1.2793604 [DOI] [PubMed] [Google Scholar]
- Kalluri, R., and Shera, C. A. (2007b). “ Near equivalence of human click-evoked and stimulus-frequency otoacoustic emissions,” J. Acoust. Soc. Am. 121, 2097–2110. 10.1121/1.2435981 [DOI] [PubMed] [Google Scholar]
- Kemp, D. T., and Chum, R. A. (1980). “ Observations on the generator mechanism of stimulus frequency acoustic emissions—Two tone suppression,” in Psychophysical Physiological and Behavioural Studies in Hearing, edited by Brink G. V. D. and Bilsen F. A. (Delft University Press, Delft, The Netherlands: ), pp. 34–42. [Google Scholar]
- Long, G. R., Talmadge, C. L., and Lee, J. (2008). “ Measuring distortion product otoacoustic emissions using continuously sweeping primaries,” J. Acoust. Soc. Am. 124, 1613–1626. 10.1121/1.2949505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meenderink, S. W., and Narins, P. M. (2006). “ Stimulus frequency otoacoustic emissions in the Northern leopard frog, Rana pipiens pipiens: Implications for inner ear mechanics,” Hear. Res. 220, 67–75. 10.1016/j.heares.2006.07.009 [DOI] [PubMed] [Google Scholar]
- Papoulis, A. (1962). The Fourier Integral and Its Applications (McGraw-Hill, New York: ), pp. 1–318. [Google Scholar]
- Schairer, K. S., Ellison, J. C., Fitzpatrick, D., and Keefe, D. H. (2006). “ Use of stimulus-frequency otoacoustic emission latency and level to investigate cochlear mechanics,” J. Acoust. Soc. Am. 120, 901–914. 10.1121/1.2214147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schairer, K. S., Fitzpatrick, D., and Keefe, D. H. (2003). “ Input-output functions for stimulus-frequency otoacoustic emissions in normal-hearing adult ears,” J. Acoust. Soc. Am. 114, 944–966. 10.1121/1.1592799 [DOI] [PubMed] [Google Scholar]
- Scheperle, R. A., Goodman, S. S., and Neely, S. T. (2011). “ Further assessment of forward pressure level for in situ calibration,” J. Acoust. Soc. Am. 130, 3882–3892. 10.1121/1.3655878 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., and Bergevin, C. (2012). “ Obtaining reliable phase-gradient delays from otoacoustic emission data,” J. Acoust. Soc. Am. 132, 927–943. 10.1121/1.4730916 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., and Guinan, J. J. (1999). “ Evoked otoacoustic emissions arise by two fundamentally different mechanisms: A taxonomy for mammalian OAEs,” J. Acoust. Soc. Am. 105, 782–798. 10.1121/1.426948 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., and Guinan, J. J. (2003). “ Stimulus-frequency-emission group delay: A test of coherent reflection filtering and a window on cochlear tuning,” J. Acoust. Soc. Am. 113, 2762–2772. 10.1121/1.1557211 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., and Oxenham, A. J. (2002). “ Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements,” Proc. Natl. Acad. Sci. 99, 3318–3323. 10.1073/pnas.032675099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., and Oxenham, A. J. (2010). “ Otoacoustic estimation of cochlear tuning: Validation in the chinchilla,” J. Assoc. Res. Otolaryngol. 11, 343–365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., Tubis, A., and Talmadge, C. L. (2005). “ Coherent reflection in a two-dimensional cochlea: Short-wave versus long-wave scattering in the generation of reflection-source otoacoustic emissions,” J. Acoust. Soc. Am. 118, 287–313. 10.1121/1.1895025 [DOI] [PubMed] [Google Scholar]
- Sisto, R., Moleti, A., and Shera, C. A. (2007). “ Cochlear reflectivity in transmission-line models and otoacoustic emission characteristic time delays,” J. Acoust. Soc. Am. 122, 3554–3561. 10.1121/1.2799498 [DOI] [PubMed] [Google Scholar]
- Zweig, G., and Shera, C. A. (1995). “ The origin of periodicity in the spectrum of evoked otoacoustic emissions,” J. Acoust. Soc. Am. 98, 2018–2047. 10.1121/1.413320 [DOI] [PubMed] [Google Scholar]