Catalytic micromotor generating self-propelled regular motion through random fluctuation

Abstract

Most of the current studies on nano/microscale motors to generate regular motion have adapted the strategy to fabricate a composite with different materials. In this paper, we report that a simple object solely made of platinum generates regular motion driven by a catalytic chemical reaction with hydrogen peroxide. Depending on the morphological symmetry of the catalytic particles, a rich variety of random and regular motions are observed. The experimental trend is well reproduced by a simple theoretical model by taking into account of the anisotropic viscous effect on the self-propelled active Brownian fluctuation.

INTRODUCTION

Living organisms on the earth generate active motion by dissipating chemical energy under isothermal conditions, being much different from thermal combustion engine such as gasoline engine. Thus, studies on chemical motors directly converting chemical energy into mechanical energy is of scientific, as well as technological, importance. As the main conductors in life system^{1, 2} are minute-sized proteins, trial to fabricate nano/micro chemical motors working under isothermal conditions has been a hot (and challenging) topic in biotechnology and nanotechnology for the last decade because they can be applied in various applications, e.g., biomedicine³ and nanodevices.^{4, 5} In 2004, Paxton et al. succeeded in constructing a nanosized motor system with catalytic particles in a solution containing reactants.⁶ Typical objects have been nanorods consisting of composites with different metal species, in which one of them has catalytic activity. The driving force that propels the rod-shaped particles arises from diffusiophoresis or self-electrophoresis by a catalytic reaction with a chemical composition gradient along a particle.^{7, 8, 9, 10} Since then, several research groups have attempted to prepare nano/microsized motors that exhibit regulated motion (e.g., translation, spin, and rotation) by other mechanisms such as microbubble,^{11, 12, 13, 14} magnetic,^{15, 16} and ultrasound¹⁷ propulsions. Because these minute systems have ultralow Reynolds numbers (Re ≪ 1), they need a continuous driving force or torque to maintain their motions. To obtain this force (in forward or backward direction) or torque (in a clockwise or counterclockwise direction), all previous motors possess compositional asymmetry, which increases operational factors.

In this study, we propose a nano/microscale motor system, being simpler than that of Paxton et al.⁶ The present motor is made of a single metal (Pt) instead of composite rods, so only the morphology of Pt particles is a key operational factor. The mechanism moving the particle is definitely different from that discussed in previous papers^{7, 8, 9, 10} because the stationary gradient of the chemical composition along a particle is not formed for noncomposite particles. Nevertheless, we demonstrate that particles show various regulated motions depending on their morphology. We experimentally explore the motion of Pt particles in a solution containing hydrogen peroxide to elucidate how the motion is determined and controlled.

EXPERIMENTAL

Catalytic particles made of Pt were obtained from Nilaco Corp. Using a scanning electron microscope (SEM) (JSM-7500FA field emission SEM, JEOL), we confirmed that the primary particles are almost spherical with submicron size (Fig. 1). Pt particles were dispersed in deionized water by ultrasonication, and the median diameter of the particles in the solution was 5.8 × 10² nm as measured by a dynamic light scattering spectrophotometer (MCLS-1000, Otsuka Electronics). The median size corresponded to the size of primary particles in Fig. 1, indicating that the primary particles were well dispersed in the solution through the procedure of ultrasonication. The particle suspension was mixed with hydrogen peroxide water and poured into a μ-Slide (Nippon Genetics Co, Ltd.). The decomposition of hydrogen peroxide (2H₂O₂ → 2H₂O + O₂) proceeds on the surface of the Pt particles, which leads to non-Brownian motion of the particles. After the convection calmed down (a few minutes), we observed the movement of the Pt particles and their aggregates in hydrogen peroxide water at room temperature (20–25 °C) using an optical microscope (Olympus IX71, Olympus Co.) and a high-speed CCD (charge-coupled device) camera (120 frames/s). O₂ microbubbles were not observed on the surface of the Pt particles or aggregates, and the bulk concentrations of hydrogen peroxide remained unchanged during the observation, although macroscopic bubbles appeared on the surface of the bulk hydrogen peroxide solution.

Figure 1.

SEM image of Pt particles used in our experiments.

RESULTS AND DISCUSSIONS

Movement of spherical particles

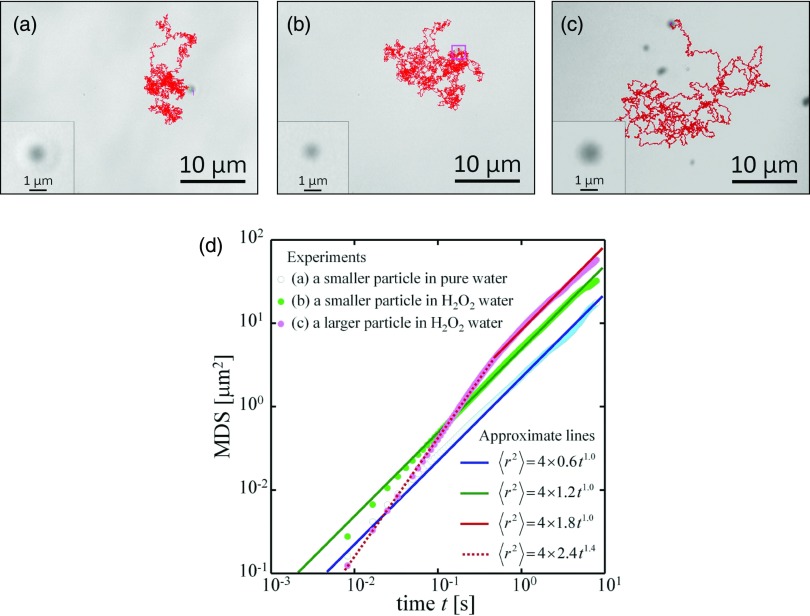
In pure water, colloidal particles exhibit the usual Brownian motion, i.e., fluctuation under thermal equilibrium [Fig. 2a]. Likewise, in 1% hydrogen peroxide water, Pt particles show random motion [Figs. 2b, 2c]. Although it was difficult to evaluate the actual size of the particles owe to the blurring effect on the microscopic image for the fluctuating particles, the insets of Figs. 2a, 2b, 2c indicate that particles in (a) and (b) are almost the same in their sizes. On the other hand, the particle in Fig. 2c is about double in the diameter. According to the two-dimensional Einstein–Smoluchowski equation on Brownian motion under equilibrium, the mean square displacement (MSD: ⟨r²⟩) at random motion is given as

$$⟨r^2⟩=4Dt,$$ (1)

where D represents the diffusion coefficient, and t represents the time. Thus, we have analyzed the fluctuating motion as in Fig. 2d by taking the log-log plot beween ⟨r²⟩ and t. MSD is calculated from the trajectory shown in Figs. 2a, 2b, 2c. There are two remarkable observations seen in Fig. 2d. In the case of particles in Figs. 2a, 2b, a plot of log(⟨r²⟩) vs. log(t) gives a straight line whose slope is almost 1.0 [the green and blue approximate lines in Fig. 2d], corresponding to the stochastic fluctuation without any memory effect regardless the difference between thermal equilibrium in Fig. 2a and dissipative condition in Fig. 2b. From the difference of the intercept on the vertical axis, the apparent diffusion constants D's are evaluated as 0.6 μm²/s for the actual Brownian motion and 1.2 μm²/s for the active Brownian motion. From the value of 0.6 μm²/s, the hydrodynamic diameter is calculated to be 7 × 10² nm according to the Stokes–Einstein equation, which agrees well with the results of SEM (Fig. 1) and dynamic light scattering. It is noted that the apparent diffusion constant of the active Brownian motion is almost twice larger than the normal diffusion constant for the same-sized object. In other words, the fluctuating motion of the active Brownian particle is characterized by two-times higher temperature (∼600 K) based on the consideration of the Einstein-Stokes relationship. In the past studies on the chemical motors, such kind of fluctuation have been attributed to chemically heterogeneous structures^{7, 8, 9, 10} owe to stationary unbalance from the generation of invisible O₂ nanobubbles by the decomposition of hydrogen peroxide, or from diffusiophoresis due to the stationary chemical composition gradient.

Figure 2.

Trajectory of the motion of primary particles in (a) pure water and (b) and (c) 1% hydrogen peroxide water for 1 min. Insets show the expanded figure. The particles in (a) and (b) have almost the same diameter, while the particle in (c) is larger. (d) Relationship between time and mean square displacement obtained from the trajectory of (a)–(c). Solid lines and the dotted line show approximate lines of slope 1.0 and 1.4, respectively.

Another noticeable observation is that the slope of log(⟨r²⟩) vs. log(t) changes at t < 1 s for the larger particle shown in Fig. 2c. The particle shows random motion for time scales over 1 s because the slope is almost 1.0. On the contrary, the particle has a ballistic character in its propelled motion at a short time scale less than 1 s since the slope for this motion (1.4) is larger than that for random motion (1.0). This result demonstrates that the larger particle exhibits the tendency to cause ballistic motion for the time scale less than 1 s. Such a characteristic enables to make particle motion regulated for longer time scale by the control of its morphology or spatially confined field.¹⁸

Self-propelled motion of aggregates

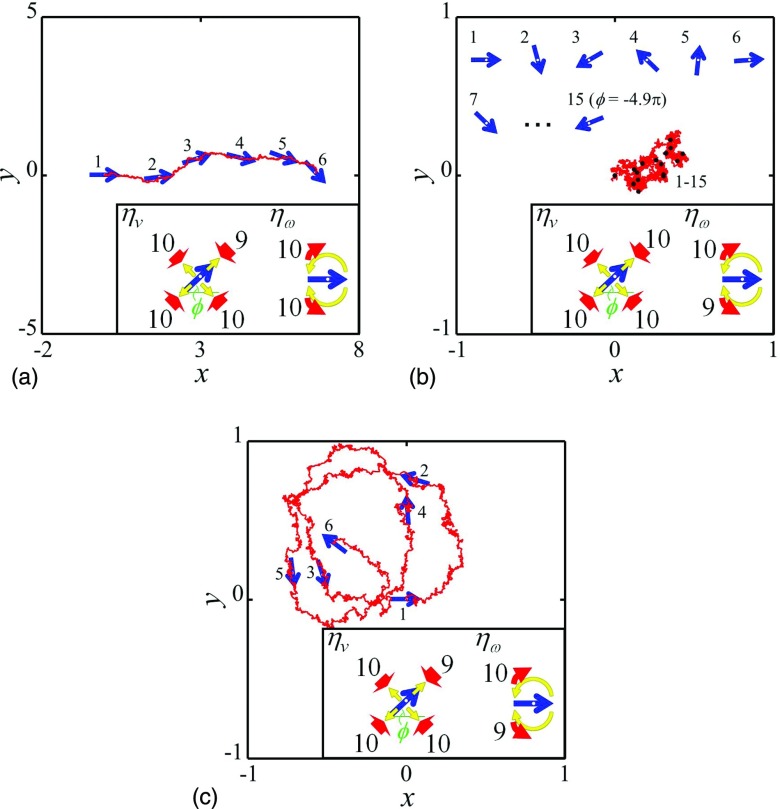
Aggregates, which consist of many (10²–10³) primary particles, exhibit two-dimensional motion at the bottom of the μ-slide. Figure 3 shows the trajectory of Pt aggregates with several types of morphology in 1% hydrogen peroxide water (see videos of the supplementary material).¹⁹ The aggregates exhibit various motions depending on their shape; for example, aggregates that are streamlined [Fig. 3a] or those that resemble a windmill [Fig. 3b] or a boomerang [Fig. 3c] exhibit translation, spin, and rotation motions, respectively. The mechanism responsible for these motions can be explained by two assumptions. First, spatial unbalance of force or torque affects nonspherical particles. If catalytic activity depends on the crystal face of an aggregate, constant force and torque are produced in the same manner as in composite motors.^{7, 8} Second, the directions of translation and rotation affect drag, although the time average of random force and torque is zero. For example, a streamlined or a windmill-shaped object may have a direction-dependent drag force in translation and rotation motions, respectively. We consider the latter assumption to be more reasonable in consideration of the calculation results shown in Sec. 3C.

Figure 3.

Trajectory and snapshots of (a) translation, (b) spin, and (c) rotation motions of Pt aggregates in 1% hydrogen peroxide water. The scale bar indicates 10 μm.

Analysis of the aggregate shape

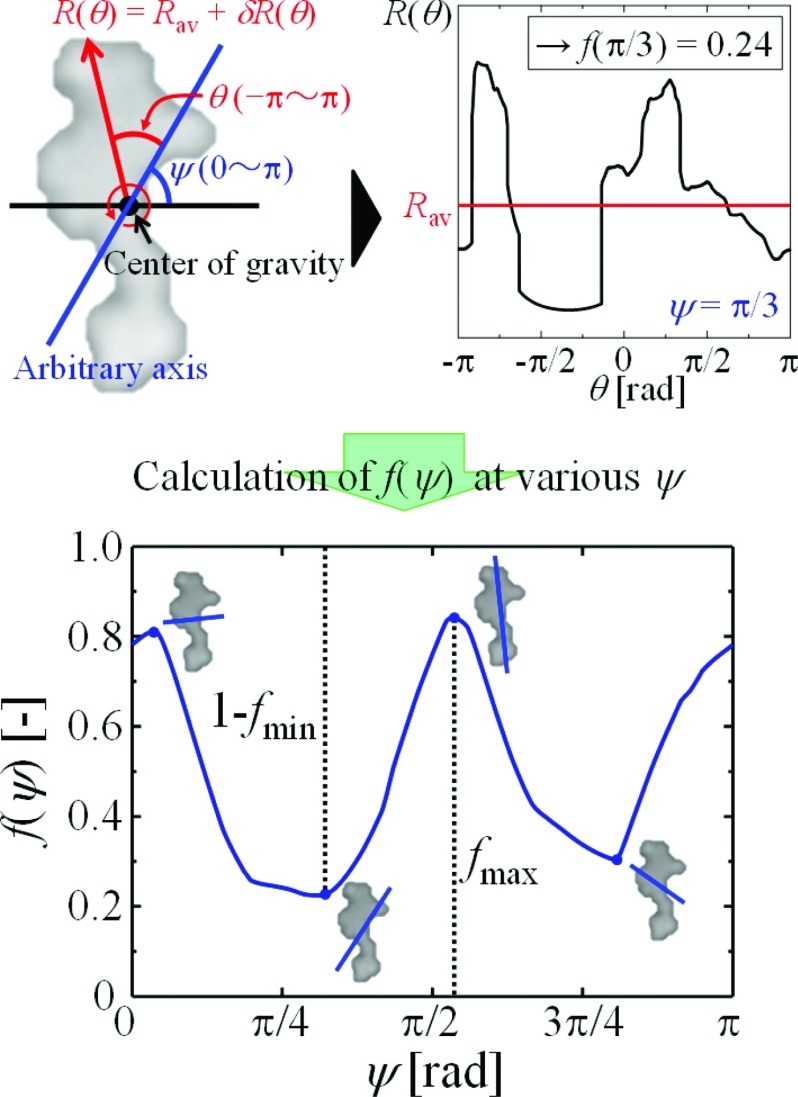
The aggregate motion correlates with aggregate morphology. The quantitative analysis of the aggregate shape is necessary to describe the relationship between morphology and the motion type. Aggregate shape is characterized in two dimensions by a method similar to that of Hiraiwa et al.²⁰R(θ) is the length between the center of gravity and the edge at angle θ (−π ≤ θ ≤ π) from a certain axis tilted at angle ψ (0 ≤ ψ ≤ π) in a counterclockwise direction (see Fig. 4 top). R(θ) is given as

$$R\left(\theta \right)=R_{\mathrm{av}}+\delta R\left(\theta \right),$$ (2)

where R_av is the mean radius of a particle and is calculated by the following equation:

$$R_{\mathrm{av}}=\frac{{\int }_{-\pi }^{\pi }R\left(\theta \right)\mathrm{d}\theta }{2\pi }.$$ (3)

δR(θ) is expressed by the Fourier series as follows:

$$\delta R\left(\theta \right)=\sum _{n=1}^{\infty }(a_n\cos n\theta +b_n\sin n\theta ),$$ (4)

where the cosine term shows the axial symmetry of the particle with respect to an axis of the azimuthal angle ψ. On the contrary, the sine term, which is an odd function, shows the point symmetry. The ratio of the axial symmetry of the shape, f(ψ), can be defined as

$$f\left(\psi \right)=\frac{\sum _{n=1}^{\infty }{a}_n^2}{\sum _{n=1}^{\infty }{a}_n^2+\sum _{n=1}^{\infty }{b}_n^2}.$$ (5)

The value of f(ψ) ranges from zero to unity. A value near unity means that the particle has a high degree of axial symmetry at that axis. On the contrary, the degree of axial symmetry is lower at lower values of f(ψ) (f ∼ 0). The graph at the bottom of Fig. 4 shows the calculation result for f(ψ) of an arbitrary axis at various angles (ψ) for a streamlined aggregate. Interestingly, the axis with the largest value of f(ψ), f_max, corresponds to the translational direction [compare the axis with the translational direction in Fig. 3a]. For an aggregate with rotational motion, the axis also agrees with the tangential direction of the trajectory. It is unclear in which direction along the axis of symmetry (forward or backward) the particle moves; however, particles appear to move toward the edge generating the lower drag force (Fig. 3). The drags arising due to flow separation in the boundary layer are known to become greater at higher Reynolds numbers (Re > 1); however, vortexes have been observed in both simulations and experiments even at ultralow Reynolds numbers (Re ≪ 1).^{21, 22} Although our nano/microsized motor system has a significantly low Reynolds number (Re ≅ 10⁻⁴–10⁻⁵), the occurrence of vortexes along aggregates would have a prominent effect on their drags.

Figure 4.

Typical example of quantitative analysis of particle morphology [using the particle from Fig. 3a]. Top: (left) schematic representation of quantitative analysis of particle morphology and (right) profiles of R(θ) (−π ≤ θ ≤ π) from an axis tilted at angle ψ (ψ = π/3). Bottom: calculation result for f(ψ) of an arbitrary axis at various angles ψ (0 ≤ ψ ≤ π).

The appearance of spin-type motion can be associated with the minimum value of f(ψ), f_min. The axial symmetry–asymmetry balance (SAB) of particles can be defined as

$$\mathrm{SAB}=f_{\max }/(1-f_{\min }).$$ (6)

Table 1 summarizes the SAB values and motion types. We analyzed various particles including those in Figs. 3a, 3b, 3c (see detailed analysis of SAB values and motion types of supplementary material).¹⁹ At SAB < 1, the aggregates tend to spin. In addition, aggregates show rotational and translational modes at SAB ∼ 1 and SAB > 1, respectively. Detailed analysis of particle morphology indicates that the dynamical mode is based on SAB, which characterizes aggregate morphology, and that the direction of the consequent motion is selected for direction-dependent viscous dissipation. The mechanism is quite interesting because it is different from the mechanism of previously reported motors with constant forces or torques.

Table 1.

Summary of SAB values and motion types in Fig. 3

Aggregate	fmax [-]	1 − fmin [-]	SAB [-]	Dynamical mode
Fig. 3a	0.84	0.78	1.08	Translation
Fig. 3b	0.92	0.97	0.94	Spin
Fig. 3c	0.95	0.96	0.99	Rotation

Model of particle motion

The above discussion on particle motions such as translation, spin, and rotation motions can be described by the following differential equations.²³ The equation for translation is

$$m\frac{\mathrm{d}\mathit{\nu }\left(t\right)}{\mathrm{d}t}=\mathit{F}\left(t\right)-{\eta }_v\mathit{\nu }\left(t\right)+\mathit{\xi }\left(t\right),$$ (7)

while that for rotation is

$$I\frac{\mathrm{d}\omega \left(t\right)}{\mathrm{d}t}=N\left(t\right)-{\eta }_{\omega }\omega \left(t\right)+\xi \left(t\right).$$ (8)

F(t) and N(t) denote the driving force and torque, respectively. They work at any time and in any random direction (time average: ⟨F(t)⟩ = 0 and ⟨N(t)⟩ = 0). In the above equations, the term “thermal fluctuations: ξ(t)” is negligible for larger aggregates. I is the moment of inertia, m represents the mass of the aggregates, and v(t) and ω(t) denote the translation velocity and angular velocity, respectively [ω(t) = dϕ/dt; ϕ is the angular displacement of rotation]. In the above set of equations, overall drags of translation and rotation, η_ν and η_ω, respectively, depend on the motion direction. For example, a streamlined aggregate has different η_ν's depending on whether the direction is forward or backward, and a windmill-shaped aggregate has different η_ω's depending on whether the direction is clockwise or counterclockwise (insets in Fig. 5). Figure 5 shows the calculation results of Eqs. 7, 8 with various parameters. The results agree with the trajectory observed by experiments, demonstrating that a few percent differences (only 10%) in direction-dependent drags can generate various regulated motions from the random force.

Figure 5.

Calculated result of trajectory t (0 ≤ t ≤ 1.5 × 10⁴) for (a) translation, (b) spin, and (c) rotation motions of Pt aggregates based on Eqs. 7, 8. Blue arrows represent particles with the angular displacement of rotation (ϕ) [see the insets in (a)–(c)]. All parameters, excluding drag, η_v, and η_ω, are fixed as follows: ⟨|F(t)|²⟩ = 1/6, ⟨N(t)²⟩ = 1/3, x(0) = y(0) = v_x(0) = v_y(0) = ϕ(0) = ω(0) = 0, m = 0.5, and I = 1.0. Values of direction-dependent drag are described in the insets of (a)–(c).

CONCLUSION

In conclusion, we have demonstrated that simple catalytic particles without forming composite with different material, which do not produce a constant driving force or torque, show regulated motions in a solution containing a reactant. The nano/microsized motors in our system exhibit various motions by a mechanism different from that of previous motors. The occurrence of regular motion in these particles is ascribed to random force and torque by a catalytic reaction, and the dynamical mode (i.e., translation, spin, and rotation) can be controlled up to only a few percent difference for drags, depending on the motion direction. Such a simple system might enhance the controllability of particles. Furthermore, the design of more universal nanomotors, which previously have had a chemically heterogeneous structure as well as a shape-controlled structure, will be possible because the former structure affects the driving force, while the latter mainly affects the viscous dissipation.