Preliminary evaluation of multifield and single-field optimization for the treatment planning of spot-scanning proton therapy of head and neck cancer

Abstract

Purpose: Spot-scanning proton therapy (SSPT) using multifield optimization (MFO) can generate highly conformal dose distributions, but it is more sensitive to setup and range uncertainties than SSPT using single-field optimization (SFO). The authors compared the two optimization methods for the treatment of head and neck cancer with bilateral targets and determined the superior method on the basis of both the plan quality and the plan robustness in the face of setup and range uncertainties.

Methods: Four patients with head and neck cancer with bilateral targets who received SSPT treatment in the authors' institution were studied. The patients had each been treated with a MFO plan using three fields. A three-field SFO plan (3F-SFO) and a two-field SFO plan (2F-SFO) with the use of a range shifter in the beam line were retrospectively generated for each patient. The authors compared the plan quality and robustness to uncertainties of the SFO plans with the MFO plans. Robustness analysis of each plan was performed to generate the two dose distributions consisting of the highest and the lowest possible doses (worst-case doses) from the spatial and range perturbations at every voxel. Dosimetric indices from the nominal and worst-case plans were compared.

Results: The 3F-SFO plans generally yielded D95 and D5 values in the targets that were similar to those of the MFO plans. 3F-SFO resulted in a lower dose to the oral cavity than MFO in all four patients by an average of 9.9 Gy, but the dose to the two parotids was on average 6.7 Gy higher for 3F-SFO than for MFO. 3F-SFO plans reduced the variations of dosimetric indices under uncertainties in the targets by 22.8% compared to the MFO plans. Variations of dosimetric indices under uncertainties in the organs at risk (OARs) varied between organs and between patients, although they were on average 9.2% less for the 3F-SFO plans than for the MFO plans. Compared with the MFO plans, the 2F-SFO plans showed a reduced dose to the parotids for both the nominal dose and in the worst-case scenario, but the plan robustness in the target of the 2F-SFO plans was not notably greater than that of the MFO plans.

Conclusions: Compared with MFO, 3F-SFO improves plan robustness in the targets but degrades dose sparing in the parotids in both the nominal and worst-case scenarios. Although 2F-SFO improves parotid sparing compared with MFO, it produces little improvement in plan robustness. Therefore, considering its tolerable target coverage and sparing of OARs in worst-case scenarios, the authors recommend MFO as the planning method for the treatment of head and neck cancer with bilateral targets.

INTRODUCTION

In spot-scanning proton therapy (SSPT), the narrow proton pencil beam is steered magnetically to cover the lateral extension of the target, while its energy is changed to cover the target in depth. The radiation dose is deposited as individual spots, each corresponding to a proton Bragg peak at a certain location and energy. The amount of dose deposited by each spot is related to the weight assigned to the spot. The prescribed target dose and required normal tissue sparing in SSPT are achieved by selecting the appropriate spot positions and energies and by optimizing the weights of the spots.

The optimization method of SSPT treatment planning can be either multifield optimization (MFO) or single-field optimization (SFO). MFO, usually referred to as intensity-modulated proton therapy,¹ fully utilizes the flexibility of the spot-scanning technique to create highly modulated dose distributions. In MFO, spots from all the proton fields are optimized together; as a result, the dose from each individual field can be highly inhomogeneous, with large gradients both outside and inside the targets. Unlike in fixed range modulation proton therapy, the goal of MFO optimization is not to create spread-out Bragg peaks (SOBPs) from each field. The inhomogeneous dose from each field is summed up to create homogeneous target coverage. In this way, MFO can create complex dose distributions to achieve optimal sparing of organs at risk (OARs). A major drawback of MFO is that, owing to its large dose gradients from its individual fields, MFO plans are highly sensitive to setup and range uncertainties, and these large in-field dose gradients cannot be addressed by the use of safety margins around the targets.²

SFO, also known as single-field uniform dose (SFUD),^{3, 4} optimizes the spots of each proton field individually and creates a more uniform dose distribution from each beam than MFO. A constant range modulation width laterally across the field does not necessarily result from a SFO field because SFO does have the flexibility to create different dose levels in the targets by assigning different weights to the spots, but there are fewer and lower dose gradients, especially inside the targets, than with MFO because of the much lower degree of modulation. Therefore, SFO plans are expected to be more robust to uncertainties than MFO plans. However, it is often difficult for SFO to achieve the level of OAR sparing that MFO does because of SFO's limited modulations.

A range shifter can reduce the range of the proton beam and is sometimes used clinically to cover shallow targets.⁵ On the other hand, it adjusts the lateral size of the beam spots passing through it.⁶ According to Titt et al.,⁶ a 5 cm thick range shifter made of polymethyl methacrylate (PMMA, C₅O₂H₈, ρ = 1.19 g cm⁻³), which is close to the 6.7 cm thick range shifter used in our institution, results in smaller lateral spot size at a given residual range than without a range shifter up to a residual range of 16 cm.⁶ This is because a higher energy beam must be used if a range shifter is inserted and the higher energy beam generally has a smaller spot size. For a typical proton beam for head and neck cancer, the majority of the pencil beams have a residual range of less than 16 cm when a range shifter is used. Therefore, reduced lateral spot sizes are expected for most of the pencil beams. Withsmaller lateral spot sizes, better normal tissue sparing without sacrificing target coverage is expected to be obtained. However, whether this improvement is equivalent to that afforded by MFO has not, to our knowledge, been tested. Therefore, we used a range shifter in the design of the SFO plans in this study to help improve their OAR sparing. In addition, higher energy protons have wider Bragg peaks,⁶ so fewer energy layers are required to cover the same thickness of target, resulting in a higher delivery efficiency.

In this work, we compared the two SSPT optimization methods, MFO and SFO (with a range shifter), for the treatment of head and neck cancer with bilateral targets and determined the superior method, in terms of both plan quality and plan robustness in the face of setup and range uncertainties.

METHODS AND MATERIALS

Study design

This study was performed based on data from four patients with head and neck cancer who received SSPT at The University of Texas MD Anderson Cancer Center Proton Therapy Center between July and December 2011. Institutional review board approval was obtained for the use of this data. All four patients had been prescribed at three dose levels administered using the simultaneous integrated boost technique to bilateral targets. Here, we refer to the targets, from the highest to the lowest prescribed dose, as clinical target volume 3 (CTV 3), CTV 2, and CTV 1. CTVs were delineated by physicians, with CTV 3 defined as the high risk microscopic disease volume (gross disease or postop tumor bed with nonuniform 5–10 mm margin), CTV 2 encompassing a 10–15 mm margin beyond CTV 3 and the high-risk nodal volume adjacent to gross disease in the neck, and CTV 1 encompassing a 10–15 mm margin beyond CTV 2 for patients with pharyngeal tumors and uninvolved nodes in the neck considered to be at risk of harboring subclinical disease. We used the CTVs in both the plan optimizations and evaluations; no PTV concept was employed. Each patient had been treated with a three-field MFO plan generated by an experienced physicist from the MD Anderson Proton Therapy Center. All the MFO plans had used similar beam configurations, with a posterior beam, a left superior-lateral oblique beam, and a right superior-lateral oblique beam. The prescribed dose levels and the target volume of each dose level along with the gantry and couch angles for each patient are listed in Table 1.

Table 1.

Patient prescriptions, target volumes, and beam angles.

		Prescribed dose (Gy)			Target volume (cm3)			Beam angles (gantry, couch)
Patient	Number of fractions	CTV 3	CTV 2	CTV 1	CTV 3	CTV 2	CTV 1	Field 1	Field 2	Field 3
1	30	66	60	54	96.8	218.5	141.8	180°, 0°	295°, 20°	65°, 340°
2	33	70	63	57	206.9	426.7	227.6	180°, 0°	300°, 20°	60°, 340°
3	33	70	63	57	166.2	276.5	212.7	180°, 90°	300°, 15°	60°, 345°
4	33	70	63	57	138.7	253.3	282.3	180°, 0°	290°, 15°	70°, 345°

We retrospectively generated a three-field SFO plan (3F-SFO) for each patient using the same beam orientations as in the MFO plan. Since all the patients involved in this study had large target thickness in the lateral direction and large lateral separation between the targets on the left and right sides, each of the two lateral fields (fields 2 and 3) was optimized to cover only the left or right target whichever was closer to the beam entrance. Field 1 (the posterior field) was optimized to cover the entire target. The total dose of the 3F-SFO plan was the weighted sum of the doses from the three fields. The best weights were found to be 60% from the posterior field and 40% from each of the lateral fields (the target doses from the two lateral fields do not add together since they each cover a separate target region).

Our previous experience has shown that it is difficult for SFO with two lateral fields to provide good parotid sparing because of its limited modulation and the high entrance dose. Therefore, we also retrospectively created a two-field SFO plan (2F-SFO) for each patient, with the two lateral fields of the 3F-SFO plan replaced by an anterior oblique beam (gantry angle, 13° or 25°; couch angle, 90°). Both fields were optimized to cover the entire target, and the total dose consisted of 50% from each field.

Both the 3F-SFO and 2F-SFO plans were calculated with a 6.7-cm range shifter modeled in the beam line. All the MFO and SFO plans were generated on the Eclipse treatment planning system (Varian Medical Systems, Inc., Palo Alto, CA).

Robustness analysis

We evaluated the robustness of the MFO and SFO plans to setup and range uncertainties using a worst-case analysis approach.² The setup uncertainty for proton therapy of head and neck cancer in our practice is estimated to be 3 mm. The range uncertainty due to stopping power conversion error, computed tomography artifacts, and patient anatomy changes is assumed to be 3.5% of the nominal beam ranges. The perturbations included six spatial shifts along the three major axes (left–right, posterior–anterior, and superior–inferior), two range shifts, six spatial shifts with positive range shift, and six spatial shifts with negative range shift—a total of 20 perturbed dose distributions. Dose distributions were recalculated in Eclipse for each of the above described 20 perturbed situations. We extracted the highest and the lowest dose values in each voxel from the nominal and the 20 perturbed dose distributions, forming a hot dose distribution with the highest values and a cold dose distribution with the lowest values. The dose distributions derived in this way provided an estimate of the robustness of the delivered dose to spatial and range uncertainties.⁷

Banded dose-volume histograms (DVHs) were plotted for the MFO and SFO plans (Fig. 2). The original DVH of each structure from the nominal dose distribution was overlaid by a shaded area that was bounded by the DVHs from the cold and the hot dose distributions obtained from the robustness analysis. The width of the DVH bands corresponds to the plan robustness for the structure indicated.

Figure 2.

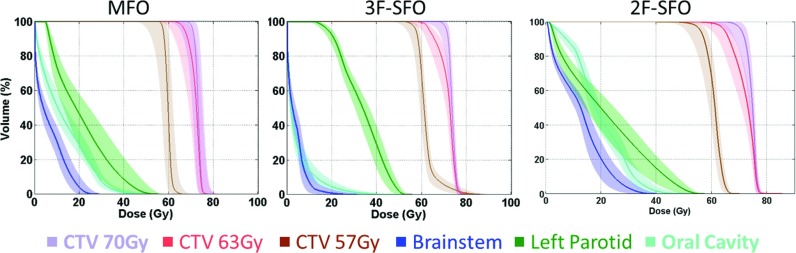
Banded DVHs of the 3F-MFO, 3F-SFO, and 2F-SFO plans for patient 3. The solid lines are DVHs for the nominal doses, and the shaded areas (the bands) are bounded by the DVHs for the cold and hot doses obtained from the robustness analysis.

Column charts were created to show the dosimetric indices from the nominal dose distributions, and the error bars were created to represent variations of each index in the face of uncertainties. The maximum and minimum of each error bar were taken from the hot and cold dose distributions, respectively, that were calculated from the robustness analysis, indicating the lowest and highest values each index could be when encountering uncertainties. Since D95 of the targets measures the minimum dose that 95% of the target received, the cold dose distribution gives the worst-case value for D95; conversely, the hot dose distribution gives the worst-case values for D5 and the OAR indices. Therefore, we use the differences between the nominal value and minimum and between the nominal value and maximum (E₋ and E₊, respectively) to estimate the robustness of target D95 index and the rest of the indices in the worst-case scenario.

RESULTS

Figure 1 shows typical transverse dose distributions from the MFO and SFO plans and the beam orientations of each plan (these data were for patient 3). The hot spots appearing between the two lateral targets in the 3F-SFO plan were due to the superposition of the two lateral fields, which tended to overshoot to the gap area between the two separated targets and reach the boundary of the target on the opposite side. Figure 2 shows the banded DVHs of the MFO and SFO plans for the same patient, showing typical differences between these plans.

Figure 1.

Dose distributions from the MFO (left), 3F-SFO (middle), and 2F-SFO (right) plans for patient 3. The arrows indicate the angles of the proton beams.

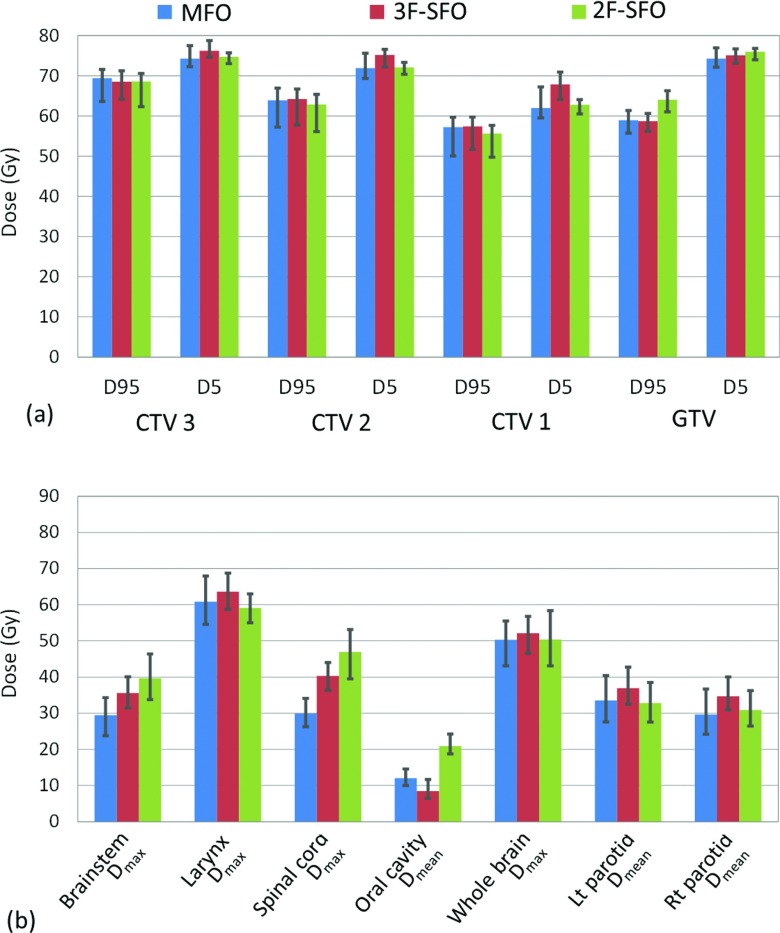
The 3F-SFO plans all achieved the prescribed dose to the targets, with slightly lower coverage than the MFO plans in the two CTVs with lower prescribed dose levels (CTV 1 and CTV 2). As shown in Fig. 3, 3F-SFO plans generally yielded D95 and D5 values in the targets similar to those yielded by the MFO plans, but they also tended to produce hot dose regions in CTV 1 where the two lateral fields meet, as shown by the higher D5 value in CTV 1. In terms of OAR sparing, 3F-SFO plans consistently had lower doses to the oral cavity than the MFO plans in all four patients, with an average reduction of 9.9 Gy (range, 2.0–15.5 Gy); conversely, doses to the two parotids were higher by an average 6.7 Gy (range, 2.8–12.7 Gy) for the 3F-SFO plans than for the MFO plans in all four patients [Fig. 3b]. For the other OARs, the 3F-SFO plans did not consistently produce higher or lower doses than the MFO plans.

Figure 3.

Dosimetric indices in the targets (a) and the OARs (b) from the MFO, 3F-SFO, and 2F-SFO plans averaged over the four patients. The maximums and minimums of each error bar were taken from the hot and cold plans, respectively, calculated from the robustness analysis. Lt: Left; Rt: Right.

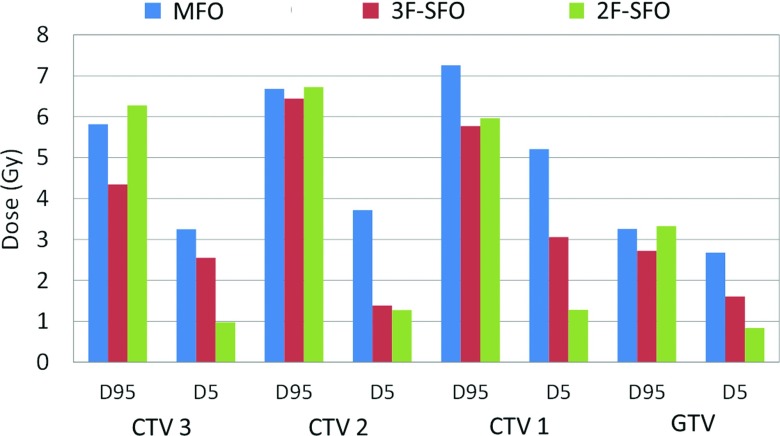
Figure 4 and the error bars on each column in Fig. 3 demonstrate the variations of each dosimetric index under uncertainties. In the targets of the 3F-SFO plans, E₋ of D95 was an average of 1.0 Gy less and E₊ of D5 an average of 1.2 Gy less than in the MFO plans. Overall, 3F-SFO plans reduced the error bar size (E₊ + E₋) in the targets by 22.8% compared with the MFO plans. E₊ in the OARs varied between organs and between patients, although they were on average 9.2% less for the 3F-SFO plans than for the MFO plans.

Figure 4.

Length of the worst-case error bars in the targets displayed in Fig. 3. For D95, it is given by the minimum error, and for D5, the maximum error.

In the worst-case scenario, which is represented by the minimum error of D95 and the maximum errors of D5 and the OAR indices, the 3F-SFO plans’ doses were on average 0.6 Gy higher in D95 and 1.1 Gy higher in D5 compared with the MFO plans. For the OARs, the indices varied between the patients and between organs, but the 3F-SFO plans’ doses were, in general, higher than those of the MFO plans in the worst-case scenario, except for the doses to the oral cavity and the whole brain. These results suggest that 3F-SFO plans are generally more robust than MFO plans in the face of uncertainties.

The results for the 2F-SFO plans are also shown in Fig. 3. The target coverage for the 2F-SFO plans was generally acceptable, with some cold spots in CTV 1. The 2F-SFO plans for all four patients successfully kept the dose to at least one of the parotids lower than the dose limit (D_mean < 26 Gy), and the mean parotid dose was, on average, 0.6 Gy lower than that of the MFO plans. The 2F-SFO plans did show higher doses to the brain stem, spinal cord, and oral cavity than the MFO plans for all the patients, as shown in Fig. 3b, but those doses were all within tolerance limits.

In terms of robustness, the 2F-SFO plans resulted in E₊ values of the target D5 an average of 1.7 Gy less than those of the MFO plans for all targets and a slightly lower average D5 under worst case, averaged among all targets (Fig. 4). However, the 2F-SFO plans showed no improvement over the MFO plans in the E₋ of the target D95, and hence the average target D95 for 2F-SFO in the worst case was similar to that of the MFO plans in the worst case, although we did observe a higher D95 in the gross target volume (GTV) from the 2F-SFO plans than for the MFO plans. For the OARs, the 2F-SFO plans resulted in an average of 1.4 Gy less dose to the left and right parotids in the worst-case scenario than the MFO plans, owing to the 2F-SFO plans’ lower nominal doses and lower E₊ in the parotids.

DISCUSSION

In this work, we investigated the potential of using SFO with a range shifter in the beam line to create acceptable plan quality and to improve the plan robustness for spot-scanning proton therapy for head and neck patients with bilateral targets in comparison with MFO. As expected, the plan quality of SFO was highly determined by the beam orientations selected. Since all spots from a field are optimized to cover the selected target, the OAR sparing largely depends on the path and penumbra of the beam. With the use of a range shifter, the SFO plans better spared the part of OARs that were in the penumbra area of the beam, but they did not provide much help sparing OARs directly in the beam path. As a result, the 3F-SFO plans yielded a higher dose to the parotids than the MFO plans in all four patients since the parotids are right in the paths of the two lateral fields. In contrast, the 2F-SFO plans yielded lower doses to at least one of the parotids than the MFO plans because the two lateral fields were replaced by an anterior field. Since target coverage could be achieved and the doses to the brainstem and the spinal cord were well within tolerance for these patients, dose to the parotids became a major concern. Therefore, the 2F-SFO plans were superior to the 3F-SFO plans. However, both 3F-SFO and 2F-SFO plans were inferior to MFO plans in terms of overall plan quality due to their limited modulation.

On measures of robustness, a more complex pattern emerged. The target dose in the 3F-SFO plans generally showed smaller variations than did the target dose in the MFO plans with the introduction of uncertainties and preserved the target coverage better in the worst-case scenario. This result is clinically important because it suggests 3F-SFO would lead to a lower chance of local failure.⁸ The 2F-SFO plans, although expected to be more robust than the MFO plans, showed no improvement in the target coverage under the worst-case scenario, probably because the anterior beam passed through less homogeneous tissue than the two lateral beams did. In terms of the robustness in the OARs, SFO plans did not show a consistent reduction in the dose variations (E₊), although their average variations were lower among the four patients. In the worst-case scenario, the MFO plans still showed superior dose sparing in most of the OARs mainly because of the lower doses in the nominal dose distributions.

Beam orientations play an important role in the plan robustness. Beams passing through heterogeneous tissues and organs tend to be more sensitive to uncertainties than beams passing through homogeneous media; beams coming from some directions may be more prone to patient setup uncertainties than others because of uncertainties in patient immobilizations (for example, the anterior beam used in the 2F-SFO plans versus the lateral beams used in the 3F-SFO); patient organ motions and anatomical changes may also cause more severe perturbations to the delivered dose for some beam orientations than for others. Furthermore, beam angles that result in higher robustness do not necessarily produce better plan quality and vice versa. As shown here, the 3F-SFO plans were generally more robust than the 2F-SFO plans in the targets but unavoidably yielded higher doses to the parotids. On the opposite, the 2F-SFO replaced the two lateral fields with an anteroposterior beam to achieve better sparing in the parotids but it resulted in degraded plan robustness due to the high heterogeneity in the beam pathway. Also, the optimal beam orientations for a MFO plan and a SFO plan can be quite different. The beam configurations utilized in this work may not be optimal, but with the large bilateral target and the complex distribution of OARs in the head and neck area, it is not straightforward to determine the optimal beam angle configuration that achieves the best balance between plan quality and plan robustness under uncertainties. It is one of the objectives of this work to find out whether a 3F- or 2F-SFO plan is superior in comparison to a 3F-MFO plan. More thorough investigations should be done in the beam angle optimization problem with considerations on the trade-off between plan quality and the plan robustness to uncertainties for both MFO and SFO.

The robustness analysis method used in this study was adopted from the worst-case analysis method proposed by Lomax et al.² In addition to the proton range errors, it accounted for setup errors along the three major axes, without considering any nonrigid patient movements, movements in directions other than the major axes, or changes in patient anatomy. Such simplifications may have led us to underestimate the spatial uncertainties of the proton beams. On the other hand, the worst-case dose distributions generated from this method consisted of the worst dose in each voxel out of all 20 perturbed doses and the nominal doses, which may have led us to overestimate the uncertainty. For example, the worst-case dose may include contributions from spatial perturbations along both positive and negative directions along an axis. A more thorough analysis of the plan robustness could be performed by an exhaustive sampling approach,⁷ at a much higher computational cost. The current approach is more practical and, as has been shown, can provide a reasonable estimate of the worst-case dose distributions under uncertainties.⁷ With better imaging techniques to be implemented in the proton treatment machine later on, real time CT surveillance data obtained during the treatment course may become available to us. They will provide more accurate information on patient setup error and anatomy change, so that greatly help us to estimate the delivered dose to the patient. In addition, a more thorough estimate of the range uncertainty can be employed to include the beam energy variation and the off-axis thickness variation of the range shifter.

A range shifter can also be applied to MFO plans to improve their quality and delivery efficiency. However, the additional neutron dose to the patient caused by a range shifter is still to be determined for SSPT in our facility,⁹ although a reduction in neutron dose was observed by another group from their facility.¹⁰ In addition, the use of a range shifter reduces the air gap between the delivery nozzle and the patient surface, resulting in an increased chance of collisions.

CONCLUSIONS

SFO using the same three proton fields as MFO yields improved plan robustness in the targets but degrades dose sparing in the parotids both in the nominal plan and in the worst-case scenario. SFO using two fields improves parotid sparing but produces little improvement in plan robustness. Therefore, considering its tolerable target coverage and OAR sparing in the worst-case scenario, we recommend MFO as the planning method for head and neck cancer treatment with bilateral targets. More extensive study on a larger patient population should be performed in order to provide statistical support for the findings of this work. To achieve a better trade-off between plan quality and robustness to uncertainties, planners can apply optimization techniques that take robustness into account during the plan optimization;^{8, 11, 12, 13, 14} this solution would be ideal but is yet to be implemented for routine clinical applications.