“Ultra-high resolution optical trap with single fluorophore sensitivity”

Abstract

We present a single-molecule instrument that combines a timeshared ultra-high resolution dual optical trap interlaced with a confocal fluorescence microscope. In a demonstration experiment, individual single-fluorophore labeled DNA oligonucleotides were observed to bind and unbind to complementary DNA suspended between two trapped beads. Simultaneous with the single-fluorophore detection, coincident angstrom-scale changes in tether extension could be clearly observed. Fluorescence readout allowed us to determine the duplex melting rate as a function of force. The new instrument will enable the simultaneous measurement of angstrom-scale mechanical motion of individual DNA-binding proteins (e.g., single base pair stepping of DNA translocases) along with the detection of fluorescently labeled protein properties (e.g., internal configuration).

Introduction

Single-molecule techniques have evolved into powerful tools to study many fundamental biological processes. They have been utilized to quantify the mechanical properties, conformational dynamics, and interactions of biological macromolecules providing a level of precision and clarity previously unobtainable^1–4. In particular, single-molecule fluorescence microscopy and optical “tweezers” have provided crucial insights into the mechanism of a wide range of nucleic acid binding proteins and molecular motors involved in genome maintenance.

Fluorescent approaches are varied⁵. With a single fluorophore, fluorescence microscopy is used to detect the presence or absence of a single labeled protein⁶, to count the number of subunits in a protein complex⁷, or track the movements of proteins with nanometer precision⁸. With two fluorophores, fluorescence resonance energy transfer (FRET) between pairs of molecules provides a spectroscopic measurement of inter-pair distances^9,10, enabling the detection of conformational dynamics in a doubly-labeled protein or translocation of a labeled motor protein along a labeled nucleic acid substrate¹¹. In optical trap measurements, a single molecule of DNA or RNA can be tethered between two attachment points, and its extension monitored by the trap (or traps). The tether is designed so that changes in its extension relay information about the biological system under study, for example the binding of a molecule or the motion of a molecular motor.

In many cases, a detailed understanding of the proteins involved in genome maintenance requires sensitivity to base pair (bp) length scales. For example, molecular motors that translocate along DNA or RNA (e.g., polymerases and helicases) likely move in discrete steps on the order of only a single base pair: only 3.4 Å in duplex DNA. The direct detection of such steps provides an important clue into the inner workings of these proteins. The recent technical development of ultra-high resolution optical tweezers^12–14 has made possible, for the first time, the direct observation of molecular motion on the scale of 1 base pair of DNA. This technique is only beginning to be applied to biological questions^12,15–18.

Despite such advances, single-molecule techniques currently have important limitations. For example, the operation of motor proteins consists of complex internal conformational transitions driving translocation along a substrate. Though optical traps can provide ultra-high spatial resolution of motor translocation over long distances, they cannot reveal the internal state (conformation or number) of the protein. In contrast, single-molecule fluorescence techniques are well-suited to probe the conformational state of a protein of interest, but (in the case of FRET) have much more limited spatial range. More generally, current single-molecule techniques are often ill-equipped to capture the multi-faceted and three-dimensional dynamics of protein complexes, as they typically project all motion onto a single measurement axis. In the case of FRET, for instance, molecular conformational changes are measured along the vector between donor and acceptor fluorophores; in optical trap measurements, movements are detected only along the direction of applied tension. These limitations motivate the development of hybrid techniques that allow for simultaneous measurement of multiple observables. Moreover, in order to probe these dynamics on relevant length scales and to be applicable to a large class of biological processes—particularly those associated with DNA metabolism—it is essential that they resolve motions on sub-nanometer length scales.

Hybrid instruments combining fluorescent capabilities and mechanical manipulation provide a promising direction to attain this goal^19–24. Though such instruments have long existed in the field, they have suffered from two major limitations: 1) they lack the sensitivity to detect individual fluorescent molecules, and/or 2) they are unable to measure displacements with adequate (sub-nanometer) mechanical resolution, and are thus limited in their applicability to biological problems. We combined ultra-high resolution dual-trap optical tweezers formed from a single laser beam with a single-molecule confocal fluorescence microscope to measure the fluorescence of labeled molecules immobilized on the tether between the beads with single-fluorophore sensitivity (Fig. 1a). The design provided angstrom-scale stability necessary for high resolution by eliminating the most common source of noise found in traditional optical tweezers—the drift between the microscope stage and the optical trap. We demonstrated our instrument’s ability to detect individual fluorophores and resolve sub-nanometer motion simultaneously by measuring the hybridization of a probe strand of single-stranded DNA (ssDNA) oligonucleotides to a complementary sequence.

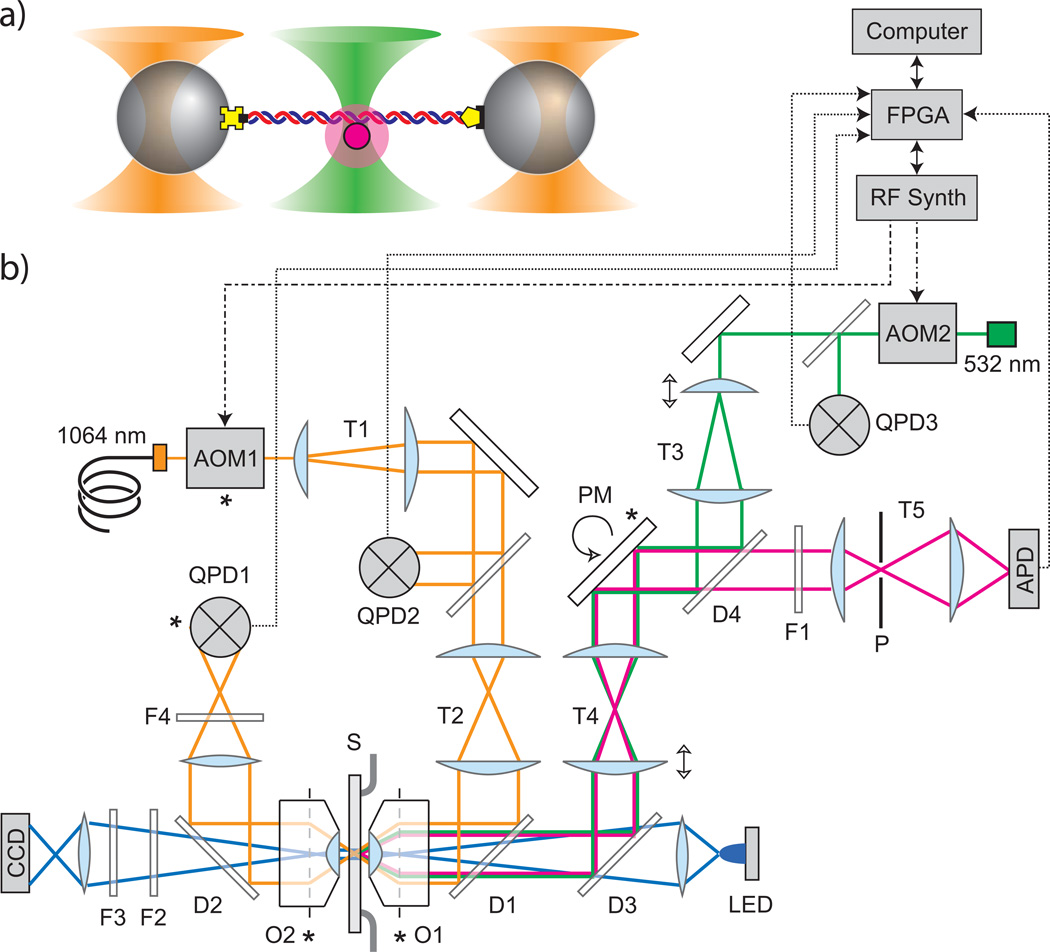
Figure 1.

Combined ultra-high resolution optical trap and single-molecule fluorescence microscope setup. (a) Schematic of experimental setup showing dual optical traps (orange cones) trapping two beads with DNA tethered between them and confocal laser excitation and detection (green cone) measuring fluorescence from a single fluorophore-labeled molecule (magenta disk) bound to the DNA. Bead-DNA attachments are made via biotin (DNA) - streptavidin (bead) and digoxigenin (DNA) - anti-digoxigenin (bead) linkages. (b) Instrument layout showing optical paths for 1064-nm trapping laser (orange), 532-nm fluorescence excitation laser (green), collected fluorescence (magenta) and blue light-emitting diode (LED) for brightfield imaging (blue). Lasers are interlaced by acousto-optic modulators (AOM1 and 2 interlaced the trap and fluorescence lasers respectively) driven by radio frequency (RF) synthesizers directly controlled by a field programmable gate array (FPGA) chip-based data acquisition and control pc card.

Synchronous with laser modulation, the FPGA reads three quadrant photodiodes (QPD) that measure trapped bead positions (QPD1) and trap and fluorescence excitation laser intensities (QPD2 and QPD3 respectively, enabling laser intensity stabilization) along with a single photon counting avalanche photodiode (APD) measuring fluorescence. Additional component abbreviations: dichroic mirror (D), filter (F), objective lens (O), pin hole filter (P), piezo mirror stage (PM), sample chamber (S), telescope (T). Conjugate image planes indicated by *. See Supplementary Note online for a complete parts list.

Results

Instrument Design

Combining optical tweezers with single-molecule fluorescence detection poses a severe and well-documented technical challenge: decreased fluorophore lifetime due to enhanced photobleaching. This enhanced photobleaching is believed to be due to absorption of the near-IR optical trap photons while in the excited state²⁵. One solution to this problem is to separate the optical trap and fluorophore by a large distance^20,21 However this approach is not practical for measuring angstrom-scale changes in tether extension, as tethers must be as stiff as possible and hence must be kept short (typically ≤ 3 kbp or 1 µm in length). Instead we minimized photobleaching by combining the optical tweezers and confocal microscope via interlacing: the optical traps and confocal microscope are turned ON and OFF in sequence so that they are never both on simultaneously²⁶.

Interlacing the optical tweezers while achieving ultra-high resolution required modifications to previously successful ultra-high resolution optical tweezers designs²⁷. In order to maintain sufficient trap stiffness while interlacing the traps must be turned ON and OFF at rates >10 kHz²⁶. However, ultra-high resolution optical tweezers operate near noise thresholds and have extremely low tolerance for additional vibrational noise. Acousto-optic devices are all-electronic devices that can switch laser intensities at >100 kHz rates and are commonly used in lower resolution optical traps^26,28. We used an acousto-optic modulator (AOM1) to directly control the intensity of the trap laser (i.e., the trap stiffness) and whether it is ON or OFF (Fig. 1b). Though not widely recognized, an AOM can deflect a laser beam similar to an acousto-optic deflector. We used a water immersion microscope objective to focus the beam deep inside the sample chamber (~50 µm from the coverslip) and we used the AOM to rapidly switch the trap laser between two deflection angles to create traps at two positions, a technique known as “timesharing”²⁹. This depth provided improved stability by decoupling the trap position and stiffness from the chamber position²⁷. Scattered laser light from the trapped beads was collected by a second identical objective and imaged onto a quadrant photodiode detector (QPD) which measured the bead positions (see Methods). The optical trap portion of the instrument could clearly resolve artificially generated single base pair steps (Supplementary Fig. 1).

For the confocal microscope we interlaced a 532-nm fluorescence excitation laser via a second AOM (AOM2), while a piezo mirror stage deflected the excitation beam and provided lateral positioning of the confocal volume as well as raster-scan fluorescence imaging capability. Fluorescence from within the confocal volume was collected by the front objective, directed backwards along the excitation laser path, focused through a 100-µm pinhole, and imaged onto a single photon-counting avalanche photodiode detector (APD).

We used a field-programmable gate array (FPGA)-based data acquisition and control system to interlace the optical traps and confocal microscope at 66 kHz. This provided high-speed synchronous control of beam modulation and data acquisition (Fig. 2). Each of the two traps was ON in sequence for only 1/3 of the repetition cycle. Fluorescence was excited and collected only during the final 1/3 of the cycle when both traps were OFF. To control the optical traps (e.g., timing, positioning and intensity) the FPGA communicated digitally with a home-built RF synthesis device to drive the trap laser AOM (see Methods and Supplementary Fig. 2). The FPGA sampled the two trapped bead positions discretely in sequence once per trap ON interval at each interval midpoint (Fig. 2). In order to accurately measure bead positions during interlacing we used special IR-enhanced detectors that respond to µs-timescale IR switching (Supplementary Fig. 3). To control the excitation laser intensity, the FPGA controled a digital gate and analog intensity control input of a commercial AOM driver. A counter on the FPGA collected single photon counts from the APD which was gated by the FPGA to collect light only during the fluorescence excitation ON interval. In addition, the FPGA controled PID feedback routines by utilizing QPD beam monitors to maintain constant excitation and trap laser intensities (including while scanning the trap position, see Supplementary Fig.4).

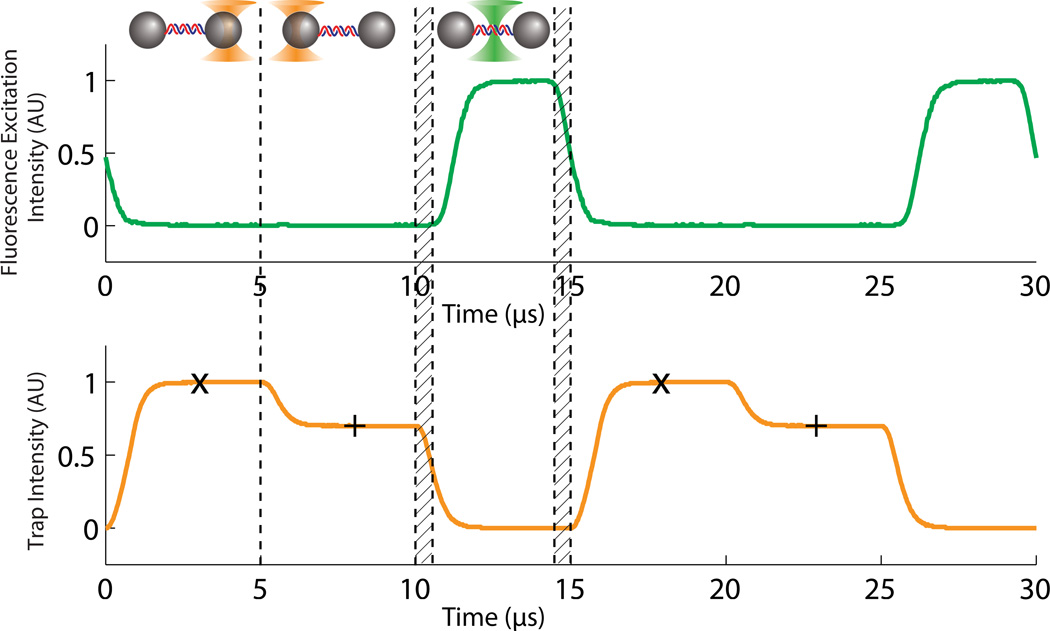
Figure 2.

Interlacing and timesharing of optical trap and fluorescence excitation lasers. Two optical traps are created in sequence during time intervals A and B via the trap AOM switching between two trap laser intensities and deflection angles (traps in intervals A and B were set to different intensities for clarity in the figure). Trap data acquisition occurs at time points indicated by ‘x’ and ‘+’ for traps 1 and 2 respectively. The fluorescence excitation laser is only ON during time interval C while the trap laser is OFF. There are 625 ns delays (hatched intervals) between switching optical traps OFF (ON) and fluorescence excitation ON (OFF). Fluorescence is only collected during time interval C. Laser intensities in the plots were measured by photodetectors and recorded by a digital oscilloscope.

Instrument Demonstration

To test the capabilities of our new instrument we measured fluorescently labeled single-stranded DNA (‘probe strand’) binding and unbinding to complementary ssDNA tethered between two beads (Fig. 3a). Since the mechanical properties of ssDNA and double-stranded DNA (dsDNA) differ, the binding and unbinding reactions can give rise to angstrom-scale changes in the tethered DNA extension, depending on the DNA tension¹. The probe strand was 9 nucleotides (nt) long and was labeled with a single Cy3 fluorophore at the 3’ end. The tether was constructed from two dsDNA sections (1.5 and 1.7 kbp long each) linked through a single 19-nt ssDNA section whose center 9 nt are complementary to the probe strand. Solution conditions were chosen to optimize binding and unbinding rates. During all experiments the optical traps were held at a constant separation at approximately 0.2 pN/nm stiffness. The fluorescence excitation power was approximately 3 µW (average power including interlacing) and was chosen to give sufficient detected single fluorophore fluorescence while ensuring that the photobleaching of fluorophores was negligible on the time scales of probe strand unbinding (< 60 s).

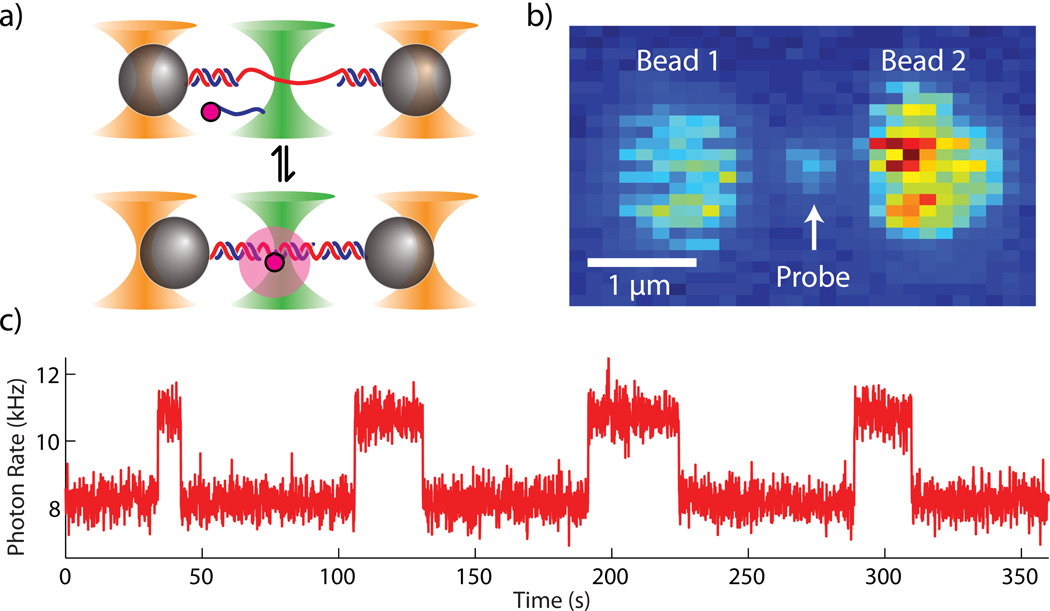
Figure 3.

Single fluorophore-labeled oligonucleotides hybridization experiment. (a) Schematic of experimental setup. Two beads held in dual traps are tethered together by dsDNA (3 kbp) with a short ssDNA (19 nt) portion near the center. ssDNA probe strands diffuse in the surrounding solution and bind-unbind to the complementary tethered ssDNA. (b) Fluorescence image of the experiment acquired by the instrument. A probe strand bound to the tethered DNA is observed as a fluorescent spot localized between the two beads. (c) Fluorescence vs. time with the confocal measurement localized between the two beads at the probe strand binding location. Digital increases (decreases) in fluorescence indicate the binding (unbinding) of a probe strand.

We observed individual probe strands binding to the tethered DNA by confocal microscopy (Fig. 3b). The two trapped beads are clearly visible due to non-specific binding of probe strands to bead surfaces, while the DNA tethered between them is not. Freely diffusing probe strands surrounding the tethered beads gave rise to a diffuse fluorescence background (~10 nM probe strand concentration). When a probe strand bound to the tethered ssDNA it became immobilized and could be seen in the fluorescence image as a bright spot centered between the two beads. The confocal microscope focus could be positioned at this spot to monitor binding and unbinding of individual probe strands with the tether over time, as indicated by the stepwise increases and decreases in fluorescence intensity in Fig. 3c.

Simultaneous with fluorescence measurement we could detect angstrom-scale changes in the DNA tether extension with the optical tweezers portion of the instrument. The mechanical properties of DNA dictate that the end-to-end extension of n base pairs of dsDNA should be shorter than that of n nucleotides of ssDNA above a critical tension, and longer below that tension¹. Figure 4a shows one example of simultaneous measurement for the case of a tether held at 10-pN tension. As a stepwise increase in fluorescence was detected, indicating the binding of a probe strand, a coincident stepwise 3 Å decrease in the tether extension was observed by the optical tweezers. Further, we could see multiple, reversible hybridization reactions on the same DNA tether (e.g., Fig. 4b). We observed many individual reactions on many individual tethers and quantified the difference in the tether extension averaged over the 3 s before and after the binding or unbinding reaction as determined by a stepwise change in fluorescence (Fig. 4c). The extension change distributions associated with binding and unbinding were nearly symmetrical and of opposite sign, as expected. The widths of the distributions can be attributed to trap measurement noise (Supplementary Fig. 5). Note that occasionally the trap measurement noise was greater than that seen in the examples of Fig. 4a–b such that the moment a probe strand binds or unbinds became difficult to assign. The fluorescence signal thus served as an unambiguous indication of the binding or unbinding reaction.

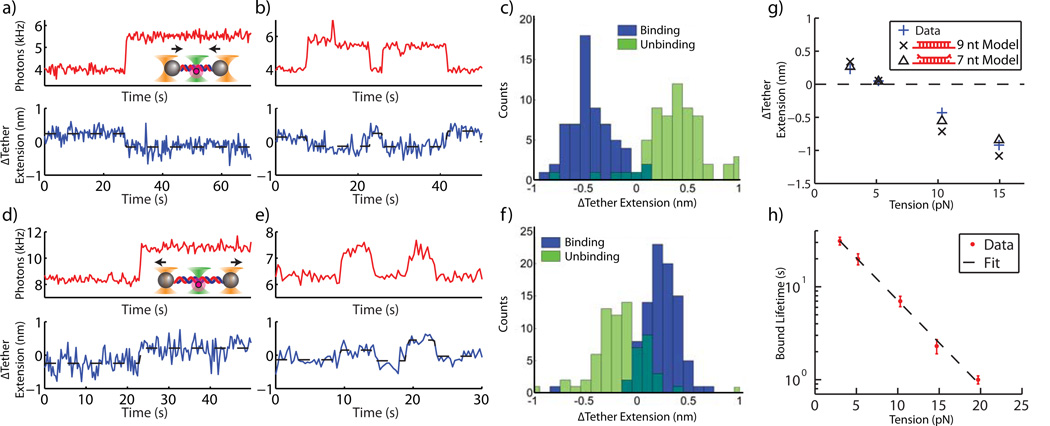
Figure 4.

Combined measurement of fluorescence and DNA tether extension. (a) – (b) and (d) – (e) Fluorescence (red, 333 ms per data point) and DNA tether extension (blue, acquired at 66 kHz, boxcar averaged to 3 Hz) are measured simultaneously. The binding (unbinding) of probe strands is indicated by stepwise increases (decreases) in fluorescence and is coincident with angstrom-level stepwise changes in DNA tether extension. (c) and (f) Change in tether extension for many binding and unbinding events for 10 pN (c) and 3 pN (f) tensions. (g) Mean change in tether extension upon binding and unbinding vs. tether tension. Data points at ~3, 5 and 10 pN include only binding events (avoiding confusing unbinding with photobleaching). ~15 pN data point includes only unbinding events (photobleaching does not occur given short bound probe lifetime and insufficient counts of binding were obtained since acquisition was made using a “Wait-and-Yank” technique, see Methods). Standard error bars are smaller than symbol sizes (n = 90, 114, 63, 19, and 14 for 3, 5, 10, 17, and 20 pN respectively). Measurements in (g) and (h) at 3, 5, 10, 17, and 20 pN, are derived from 71, 35, 20, 17, and 16 unique tether molecules respectively. Models assume 9 nt or 7 nt (best fit to data) of the 9 nt probe strand stably bind to the tethered DNA. (h) Semilog plot of duplex lifetime vs. tension (s.e.m, n = 156, 68, 52, 35, and 34 for 3, 5, 10, 17, and 20 pN respectively). Dashed line is linear fit. ~15 and 20 pN data in (g) and (h) acquired with Wait-and-Yank technique.

In contrast to the high tension case (above), at low tension (3 pN) we observed that upon probe strand binding the DNA tether expanded (Fig. 4d–e), and the extension change distribution associated with binding and unbinding reversed (Fig. 4f). We repeated these measurements at additional tether tensions and determined the mean change in tether extension vs. tether tension (Fig. 4g). With increasing tether tension, there is a clear transition from expansion to contraction that occurs at approximately 5.5 pN. It is important to note that near this transition tension, where we do not expect and indeed do not detect a change in tether extension, probe strand binding and unbinding events are identified solely from the fluorescence signal.

By manipulating the tether tension our instrument could also modulate the duplex melting reaction. We measured the force-dependent unbinding rate using fluorescence as the readout. We measured how long a probe strand stays bound to the DNA tether vs. tether tension over a wide range of tension (3–20 pN, Fig. 4h). The lifetime of the bound state followed a simple exponential decay vs. tether tension.

Discussion

Our measurements provide insight into DNA annealing and melting processes and how they are modulated by mechanical force. We first consider the change in extension of the DNA tether upon the binding and unbinding of 9-nt ssDNA probe strands. We model this process using polymer models of ssDNA and dsDNA. We predict the change in DNA tether extension upon annealing by calculating the difference in the extension of 9 bp of dsDNA and 9 nt of ssDNA using the extensible worm-like chain and extensible freely-jointed chain models, respectively (see Methods). Additionally, since the traps are maintained at a constant separation (rather than a constant force), binding and unbinding alters slightly the tension (by 0.03–0.05 pN). Thus, the measured change in tether extension upon binding and unbinding is partitioned between the tether and the trapped beads, which are displaced slightly to attain a new equilibrium tension. The result is that the DNA always contracts or expands less than if it were perfectly rigid, by a factor dependent on the tether and trap compliances. We include this effect of the non-perfectly rigid DNA in our modeling. The modeling agrees with the trend observed for the extension change as a function of tension (Fig. 4g) and with the critical tension (approximately 5.5 pN) where ssDNA and dsDNA have nearly identical mechanical properties and there is no change in extension upon probe binding.

Despite qualitative agreement, the model overestimates the magnitude of tether extension change above and below the critical tension. We do not believe that this discrepancy is due to either instrumentation calibration error or tether modeling error (see Methods and Supplementary Figs. 6 and 7). Instead, we propose that the discrepancy is observed because the bound probe strand is not in the configuration we imagine. In our model we assume that base pairing to the DNA tether occurs for all 9 nt of the probe strand. If instead we treat the number of base paired probe nt as a fitting parameter, we then find that the model best fits the data assuming only 7 ± 1 probe nt base pair (Fig 4h). This may suggest that 1–2 nt at each end of the bound probe strand are not base pairing effectively. They may be either permanently un-paired or dynamically fluctuating. Instability at the ends may arise because of the lack of both nearest neighbor nucleotides for the end nucleotides or perhaps because of an interaction with the neighboring unpaired ssDNA linkers of the tether. We also cannot rule out the possibility that the Cy3 fluorophore at the 3' probe strand end may interfere with base pairing at that end.

Beyond providing insight into the conformation of the hybridized probe strand, the simultaneous measurement of force and fluorescence allowed for a detailed characterization of unbinding kinetics vs. tether tension. The duplex lifetime decreased with applied tether tension exponentially (Fig. 4h). This suggests that the hybridized tether undergoes a fixed (force-independent) expansion from the probe-strand-bound state to the final unbinding transition state³⁰. The lifetime should scale with applied force F as ~exp(-FΔx₀/k_BT), where Δx₀ is the distance to the transition state and 1/ k_BT is the Boltzmann factor. Hence from the slope of our fit we derive Δx₀ = 8.6 ± 0.4 Å. The probe strand may come unbound via fraying from the ends, one base pair at a time. However, the large magnitude of the expansion suggests that a multi-base pair portion of the probe-strand-bound tether expands before melting can occur. If Δx₀ is distributed over the whole dsDNA portion, then the dsDNA needs to be stretched to about 1.3 times the original length before it melts.

We combined the above observations into a model detailing the complete reversible probe strand annealing and melting reaction as a function of DNA extension (Fig. 5). Two free energy contours are plotted vs. the tether extension reaction coordinate, one each describing the bound and unbound probe strand configurations. From the angstrom-resolution tether extension measurements we know that the relaxed unbound and bound probe strand states are separated by a distance Δx_h (Δx_h is linearly related to the measured change in extension, Δext, with a correction factor due to tether compliance, see Methods). Δx_h is tension dependent and for simplicity we only draw the model for one particular tension (above the 5.5 pN transition tension where probe strand binding causes a tether contraction; for other tensions the bound and unbound probe strand free energy contours are horizontally shifted with respect to each other). In the bound state, the probe strand must expand by a distance Δx₀ to the transition state to dissociate. In contrast to Δx_h, Δx₀ is tension independent, based on the observation of the simple exponential force dependence of the unbinding rate.

Figure 5.

Proposed reaction diagram illustrating the complete process of probe strand annealing (binding) and melting (unbinding) with complementary tethered DNA. Two free energy contours vs. DNA tether extension are drawn for both the probe strand unbound (blue) and bound (red) states. The initial annealing (binding) and final melting (unbinding) transitions are indicated by the labeled vertical wavy lines. The location of the annealing transition at the extension of the melting transition is assumed given the reversibility of the reaction, although the precise location is not directly measured. Relaxations and excitations of the DNA tether along the reaction contours are indicated by black arrows. The change in DNA tether extension upon annealing is labeled Δx_h. The distance to the melting transition state is labeled Δx₀.

The combination of angstrom-resolution optical trapping with single-molecule fluorescence microscopy allows for a rich exploration of a biological system. We expect that the instrument can be readily extended to tap into the rich arsenal of single-molecule fluorescence detection methods available—e.g., FRET (a simple two-color fluorescence detection addition that we have already made; data not shown), single molecule localization, polarization anisotropy, and fluorescence lifetime spectroscopy. Thus, we anticipate that this technique will be broadly applicable to the many proteins and protein complexes involved in nucleic acid metabolism. We view this advance as a significant step toward the measurement of complex, multidimensional dynamics of macromolecular machinery at the single-molecule level with angstrom resolution.

Methods

Instrument Design Details

The instrument layout is presented in Fig. 1b. A parts list is available in the Supplementary Note. Briefly, we use an acousto-optic modulator (IntraAction) to modulate a 1064-nm laser (IPG Photonics) for trapping and a microscope objective (O1, Nikon CFI Plan APO VC 60× 1.2 NA water immersion) to focus the beam. A quadrant photodiode detector (Pacific Silicon Devices) was used to measure the bead positions. For the confocal microscope we interlaced a 532-nm fluorescence excitation laser (World Star Tech) via a second AOM (IntraAction), while a piezo mirror stage (Mad City Labs) deflected the excitation beam and provided lateral positioning of the confocal volume as well as raster-scan fluorescence imaging capability. Fluorescence was detected by an APD (PerkinElmer). The instrument is equipped with a visible illumination arm (470-nm LED, Watec CCD camera) that allows for direct observation of beads during tether formation and other trap manipulations within the sample chamber. The camera signal is recorded and displayed on the instrument computer using a frame grabber pc card (Matrix Vision). Excess trap and fluorescence excitation laser light is removed from the visible image by filters F2 (Thorlabs) and F3 (Semrock) respectively. The trap laser light used to measure the bead positions before QPD1 is filtered with a 1064-nm bandpass filter (F4, Newport). Fluorescence is passed through an excitation filter to further remove 532-nm excitation laser light (F1, Chroma Technology). The dichroic mirrors used to combine/separate the optical tweezers, fluorescence microscope, and visible microscope beams are D1 and D2 (CVI SWP-45-RU1064-TUVIS-PW-1025-C), D3 (CVI SWP-45-RU532-TUVIS-PW-1025-C) and D4 (Semrock LPD01–532RS-25). The relative collimation of the trap and excitation beams determines the relative depth of focus of the optical traps and confocal volume. We align the confocal excitation volume in the plane of the optical traps by adjusting the positions of the first lens of telescope T3 (course adjustment) and the second lens of telescope T4 (fine adjustment). Achromatic lenses (Newport Precision Achromatic Doublets) are used in telescope T4 and for the pinhole focusing lens (T5, left side lens) to ensure that a wide spectrum of fluorescence co-focuses on the pinhole to maximize fluorescence collection vs. background rejection efficiency. The use of water immersion microscope objectives to focus the excitation laser and collect fluorescence reduces the confocal microscope efficiency and we are able to collect approximately 25% as much fluorescence as a similarly designed confocal microscope using an oil immersion objective described in Ref. ²¹).

RF Synthesis for Trap AOM

A diagram showing the main components of the RF synthesis electronics for the optical trap AOM and their connectivity is shown in Supplemental Fig. 1a. The RF synthesizer board (Analog Devices) is an ‘evaluation’ board provided by Analog Devices that provides an easy interface to their AD9852 digital RF synthesizer integrated circuit. We power the board with a 3.3 VDC regulated linear power supply (Acopian). A reference clock signal must be provided and we mount directly to the board a 49.152 MHz temperature compensated crystal oscillator (TCXO) with 1 ppm stability (Conner-Winfield). The RF synthesizer board is controlled by the FPGA pc card (National Instruments, LabVIEW 2009 programming) via the FPGA digital output lines. We use the parallel digital communication option of the synthesizer board to set board parameters. On startup of the instrument, we set the following synthesizer operating parameters: 6x system clock, phase locked loop (PLL) range low, PLL enabled, output shape keying (OSK) enabled, unramped frequency shift keying (FSK) mode, manual update clock. The RF synthesizer board output is amplified to the final AOM input power via a low noise RF power amplifier (Mini-Circuits).

We use the following strategy to achieve precise RF switching to produce precise timesharing/interlacing. The RF synthesizer has buffers where updated frequency and amplitude values can be loaded sequentially prior to near-synchronous updating of all board values. While an interlacing interval is executing, we load the RF synthesizer buffers with the desired settings for the next interval (e.g., while trap 1 is ON we load the settings for trap 2). One complication is that the board does not update both RF frequency and amplitude as synchronously as we require. Therefore we use two independent trigger signals to switch the RF frequency and amplitude. Using the FSK operating mode we use the FSK digital input to switch the frequency. The amplitude gets updated in the normal way triggered by an Update Trigger digital input. We tune a delay in the FPGA timing between the triggering of these two inputs to synchronize the switching of RF amplitude and frequency. The RF output of the synthesizer is amplified to the desired AOM operating power (~2 W average) using a low-noise, fixed-gain RF power amplifier (Mini-Circuits, 5 W max output, 40 db gain). We power the amplifier with a 24 VDC linear regulated power supply (Acopian). We connect the amplifier to the AOM and deliver the RF using low noise RF cables (Mini-Circuits).

Instrument Calibration and Consideration of Timesharing

Trapped bead position measurements are calibrated via a power spectrum measurement of bead Brownian motion to give the position of a bead relative to the trap center^28,31. Bead positions and forces are measured and calibrated using the near-IR trapping laser itself. To cross-check this calibration method, we also co-aligned a second laser to simultaneously measure the beads and these two independent bead measurements agree to better than 5%.

However, calibration occurs before the beads are tethered. After bead tethering and upon the application of tension to the tether, the motion of the pair of beads becomes coupled and is perturbed by the timesharing/interlacing of the optical traps. This is because during an interlacing time period in which one or both traps are switched OFF, the force exerted by the stretched DNA tether is not balanced by the traps. As a result, the tethered beads are pulled in the direction of the applied tension during each interlacing cycle. The sequential ON/OFF switching of the traps leads to the oscillation of beads plus tether at the timesharing/interlacing rate (Supplementary Fig. 5). Due to this effect, data acquisition timing was carefully adjusted so that bead position is measured at the center of the ON time period in order to measure the true average tether extension (Fig. 2 and Supplementary Fig. 5). Because the amplitude of the oscillation decreases with increasing rate (Supplementary Fig. 5a) we also chose an interlacing rate (66 kHz) as high as is practical. To verify proper calibration under tension and that bead oscillations were not impacting measurements, we measured the force-extension properties of both the DNA tethers used in the hybridization experiment and also DNA tethers containing a hairpin (see Tether Construct methods, below). These measurements achieve good agreement with our polymer modeling (see Polymer Modeling methods, below), and the observed hairpin unzipping force agrees to better than 0.1% with independent measurements on a separate optical trap (Supplementary Fig. 6). Together, these controls indicate that bead position and force calibration errors cannot account for the systematic discrepancy between the measured and modeled extension change with probe strand binding vs. tension (Fig. 4g).

Experiment Solution Conditions

Experiments were conducted in an imaging buffer containing an oxygen scavenging system to increase both tether³² and fluorophore lifetimes (glucose oxidase, Sigma-Aldrich, and catalase, Calbiochem)^32,33 along with a triplet state quencher to prevent fluorophore blinking (Trolox, Sigma-Aldrich)³⁴. In addition, the buffer contained 20 mM Tris-HCl, 100 mM NaCl, and 20 mM MgCl₂. Salt conditions were chosen to optimize the probe strand binding/unbinding rates.

Tether Constructs: Synthesis and Attachment to Beads

Three different DNA tether construct designs were used in the experiments presented in this paper: the ‘artificial stepping construct’, the ‘hairpin construct’, and the ‘hybridization construct’. The artificial stepping construct was prepared via polymerase chain reaction (PCR) amplification of a 3.4 kbp section of phage lambda DNA using PCR primers functionalized on their 5’ ends with either digoxigenin or biotin. The final construct has one digoxigenin and one biotin functional group on opposing ends for eventual linkages to anti-digoxigenin- and streptavidin-coated beads, respectively (Spherotech, 860 nm and 790 nm for the streptavidin- and anti-digoxigenin-coated beads, respectively).

The hairpin and hybridization constructs are more complicated and very similar to each other in their design and synthesis. Each construct design consists of two ~ 1.5-kbp long dsDNA ‘handle’ sections (denoted handle ‘left’ and handle ‘right’) joined together by a central DNA segment unique to each design. This design is modular in that the central joining DNA segment can be tailored with consideration to the particular experiment in mind while minimizing overall changes in the construct synthesis protocol. The handles were synthesized by initially amplifying a section of phage lambda or pBR322 DNA via PCR using PCR primers functionalized on their 5’ ends with either digoxigenin (handle right) or biotin (handle left). These PCR products were then digested by a restriction enzyme to select the final length of the handle and to expose ssDNA overhangs to which the central joining DNA segment was ligated.

The hybridization construct contains a central joining segment consisting of a ssDNA segment complementary to the labeled probe strands (sequence: 5' - ACA AGT CCT - 3' - Cy3) flanked on each end by 5-nt poly dT linkers (tether insert sequence: 5' - TTTTT AGG ACT TGT TTTTT - 3'). The handle left and handle right construct segments are 1.5- and 1.7-kbp long respectively (total tether length is 3.2 kbp). This construct was used for all probe strand binding (hybridization) experiments discussed in the paper. Detailed synthesis information for the hybridization construct is to be published. The hairpin construct contains a central joining segment consisting of an 89-bp long dsDNA hairpin. The handle left and handle right construct segments are both 1.5-kbp long (total tether length is 3.0 kbp). This tether was used only in control experiments as an instrument calibration test tether and is represented only the data of Supplementary Fig. 6. Detailed synthesis information for the hairpin construct can be found in Ref. ³².

In order to tether beads together with the construct, first streptavidin-coated beads were incubated with the constructs in order to form DNA-construct-coated beads (care was taken not to load too much DNA onto the beads or else additional noise was observed during experiments). Next, an individual trapped DNA-construct-coated bead was tethered to an individual trapped anti-digoxigenin-coated bead in situ within the sample chamber by the instrument user immediately preceding an experiment. A computer automated ‘fishing’ algorithm was used to efficiently create and test for tether formation.

“Wait-and-Yank” Data Acquisition Technique

We developed a special computer automated scheme to measure the force-dependent unbinding rates of the probe strand from the DNA tether. At high tensions (>10 pN), tethers are susceptible to prematurely breaking (ending an experiment) and thus we used this measurement technique to minimize the average tether tension and maximize measurement efficiency. With this “wait-and-yank” scheme, we held the tether at a low tension (< 5 pN) while waiting for a probe strand to bind. The computer control program detected the stepwise increase in fluorescence coincident with probe strand binding and “yanked” the tether to a higher tension. The new tension was chosen at random from a set of tensions to minimize systematic measurement error.

Polymer Modeling

We model the predicted extensions of our DNA tethers vs. tether tension using standard polymer models. The modeling consists of numerical calculations performed using MATLAB (The MathWorks, version 2010a). The total extension of the tether can be decomposed into the sum of the extensions of the segments of the tether that form the complete tether. We decompose the model tethers into ds- and ssDNA segments and compute the extension of these segments separately. We use the extensible worm-like chain (XWLC) and extensible freely jointed chain (XFJC) models to compute the extensions of the ds- and ssDNA segments respectively (as described previously^35,36). For all calculations used in this paper we use the same polymer parameters (i.e., these parameters are NOT fitted). For XWLC calculations: persistence length of dsDNA = 53 nm, stretch modulus for dsDNA = 1200 pN, and the contour length per single dsDNA base pair = 0.338 nm/bp³⁶. For XFJC calculations: persistence length of ssDNA = 0.75 nm, stretch modulus of ssDNA = 800 pN, and the contour length per single ssDNA nucleotide = 0.59 nm/nt³⁵. For modeling the construct force vs. extension curves (for both the hybridization construct and the hairpin construct) one single fitting parameter was used: an extension offset between the data and model. The offset was approximately 70 ± 10 nm (the error is the standard deviation seen between different bead-tether sets). The measured tether extension is calculated from the known trap separation (calibrated by video microscopy²⁷), the bead positions measured relative to the trap centers (calibrated by power spectrum measurements for each bead pair³¹), and the radii of the trapped beads (provided by bead manufacturer, see above). The consistent offset we observe is likely due mostly to inaccuracy in the bead sizes.

The measured change in tether extension upon probe strand binding depends only on the segment of tether that changes configuration upon hybridization. Importantly, it is independent of the absolute trap separation and bead sizes, and thus of any offsets needed to fit the construct force-extension behavior. The predicted change in tether extension upon probe strand binding at a given force F, Δx_h (F), is thus calculated from the difference in the extension of n nt of ssDNA and n bp of dsDNA at that force (n = 9 for the case of the entire probe strand annealing), based on the polymer models described above. The measurements were performed with the traps held at constant positions, however, not at constant force, and hence the relative compliance of the entire tether compared to the two traps must be taken into account. The experiment can be modeled as a pair of springs in series (tether + traps). It can be easily shown that the measured change in tether extension, Δext(F) (Fig. 4g), is related to Δx_h(F) as Δext(F) = Δx_h(F) · 2 k_tether (F)/(k_trap + 2k_tether(F)), where k_tether and k_trap are the tether and trap stiffness, respectively¹³. k_trap is determined from calibration and k_tether(F) ≡ dF_tether/dx|_F is defined as the slope of the force-extension curve of the entire construct evaluated at the force of interest, calculated using the above tether modeling. Note that we observed via tether force-extension measurements that a significant portion of our tethers were softer than they ought to be (i.e., the measured k_tether < modeled k_tether), which would reduce the observed change in extension upon probe strand binding for these tethers. However, we estimate that this inaccuracy can at most account for 1/3 of the discrepancy between the extension change vs. force model and data (Fig. 4g). Note also that we have also performed more exact calculations and such higher order corrections only negligibly change the result.