Comparative assessment of bone mass and structure using texture-based and histomorphometric analyses

Abstract

The purpose of this study was to develop a methodology for quantitatively assessing bone quantity and anisotropy based on texture analysis using Gabor wavelets. The wavelet approach has the capability to simultaneously examine the images at low and high resolutions to gain information on both global and detailed local features of the bone image. The program that implemented the texture analysis gave measures of density (M_Density) and anisotropy (M_Anisotropy). It also allowed us to examine the texture energy at four orientations (0°, 45°, 90°, 135°) to gain insight about the details of the anisotropy. Analysis of templates of four simulated patterns, which had same number of dots but with differing orientations, demonstrated how the texture-based analysis differentiated between these templates. The measures of M_Anisotropy discriminated between the four simulated patterns. The M_Density measures were similar across all patterns. These outcomes matched the design intent of the simulated patterns. We also compared the trabecular bone images obtained from a previous study, in which the right forelimbs of normal female retired breeder beagle dogs (5–7 years old) were cast for 12 months to induce bone loss, using both histomorphometry and texture analysis. Both histomorphometry and the texture analysis detected significant differences in the trabecular bone of the distal metatarsal between the control and disuse groups. Percent trabecular bone (Tb.Ar/T.Ar) and the textural density parameter (M_Density) were highly correlated (r =0.962). M_Anisotropy was decreased (3.9%) after the 12-month disuse protocol, but was not significantly different from normal. However, the texture energy values at all orientations (0°, 45°, 90° and 135°) were significantly decreased in the disuse group. Therefore, texture analysis was able to assess anisotropy, which could not be extracted from histomorphometric parameters. We conclude that texture analysis is an effective tool for assessing 2D bone images that yields information regarding the quantity of bone as well as the orientation of the trabecular structure that can augment our ability to discriminate between normal and pathological bone tissue.

Introduction

Quantitative measures of bone strength, which is dependent on mass, material and architecture, are necessary to investigate factors affecting bone strength development during growth and bone loss resulting from aging and disease. Histomorphometric analysis of trabecular bone has been used to quantify bone mass as well as the rate of bone formation and resorption [28]. However, these measures were only designed to assess surface cellular activity, not the quantification of trabecular and cortical bone architecture. Multiple approaches have been utilized in characterizing the structure of trabecular bone from two-dimensional images, particularly in describing orientation disparity or anisotropy. Mean intercept length (MIL) was defined as the ratio between the total line length (in a linear grid) divided by the number of intersections, which when calculated as a function of direction, gave information about the anisotropy of a bone sample [34]. Anisotropy can then be quantified by the principle radii of a fabric ellipse, which was based either on MIL [34,35] or equivalently on a fabric tensor [8,12,33]. The MIL method, however, failed to recognize a visible anisotropy in a simulated image whose pattern had an isotropic interface (circles were used) between the bone and marrow phases [24]. Volume-based methods including the volume orientation (VO) method and star volume distribution (SVD) provided measures of trabecular bone around a point in the trabecula and were able to recognize anisotropy when MIL-based methods failed, but they only recognized the anisotropy when the correct phase was chosen to avoid the isotropic interface [24].

Power spectrum techniques based on Fourier analysis have been utilized to assess trabecular structure, primarily on radiographic images [2,4,13,25,36]. Fourier series of an image represent a sinusoidal decomposition of the image intensity variations. Each sinusoid is associated with an amplitude at a frequency related to some dominant harmonic. The power spectrum is the square of the amplitudes and gives a measure of the power at each frequency [15]. Oxnard (1993) [25] used Fourier analysis to analyze the structure of the human lumbar vertebra (mid-sagittal section of the L2 vertebra), and the data suggested that healthy bone was oriented at 0° (vertical trabeculae) and 90° (horizontal trabeculae) as indicated by a pronounced cross-like orthogonal shape of the power spectrum. In contrast to healthy bone, images of bone with marked osteoporosis had a diffuse and isotropic power spectrum distribution. Chappard et al. [4] derived an anisotropy index based on visually examining the Fourier power spectrum and manually drawing lines to define sectors which identify high energy areas. These sectors represented the spreading angles of the longitudinal and the transverse trabeculae, from which their anisotropy measure was derived. Instead of finding angles, Wigderowitz et al. [36] used rectangular regions to identify power spectrum disparities between longitudinal and transverse trabeculae. While Fourier techniques may be able to discern orientation differences, they lack the ability to identify local structural features. Furthermore, Fourier series require an infinite number of terms to describe a non-trivial pattern.

Recent advances in imaging technologies such as high-resolution magnetic resonance (MR) imaging [20], peripheral quantitative computed tomography (pQCT) and micro-computed tomography (micro-CT) [1] have enabled three-dimensional structural assessment of both trabecular and cortical bone. These analysis methods rely on extensions to the line intercept method which does not discriminate between individual trabecula but provides a statistical sampling of the trabecular mass and its orientation [17]. Therefore, these methods have the same limitation that the MIL methods exhibit. The algorithms used in 3D analysis also have been found to overestimate trabecular thickness and bone volume [5]. Thus, a methodology that provides a reliable assessment of the bone architecture of two-dimensional slices and has the potential for being easily extended to three dimensions would provide important information to complement standard histomorphometry analysis.

Textural properties of microscopic or radiographic bone images, which represent the spatial arrangement of the gray levels of the pixels in a region, produce localized information of bone architectural patterns and could provide more insight into bone structure than previously developed methods [39]. One of the texture approaches is fractal analysis, where a “fractal dimension” was defined as a measure of texture and applied to describing both density and directionality of bone [6,9,10,16,27]. Despite its theoretical attractiveness, this method lacks a uniform approach in its definition and implementation, and the results vary widely [21,23,31].

Gabor filtering is a widely used approach in texture analysis, giving information about local properties of the image and requires a small number of functions in the expansion to describe local behavior. Gabor filters have useful properties such as optimal resolution in both space and spatial frequency, strike a balance between global and local views of an image and provide the basis for a uniform approach to defining texture [14,22]. They also have been utilized to analyze images in three dimensions [38]. A Gabor-based texture scheme is therefore a potentially powerful tool in analyzing trabecular bone texture where orientation, shape and architecture as well as density are the fundamental components. The purpose of this study was twofold. First, we illustrate the texture analysis using Gabor wavelet filters by analyzing 4 simulated patterns. Second, we compare standard histomorphometric outcome variables [26] with the parameters from the texture analysis on trabecular bone in dog metacarpals from a widely accepted model of disuse.

Methods

Template-pattern analysis

A simulated template of four patterns (Fig. 1) previously analyzed using Fourier analysis [28] was analyzed using texture analysis. Each pattern A–D had the same number of dots and the same area fraction but very different orientations.

Fig. 1.

Simulated texture patterns (A–D). Each pattern has the same number of dots and the same area fraction (with permission, Schaffler et al. (1997)). (E) Texture energy along the 0° orientation as a function of varying percentage of bone area from simulated images, where areas of black pixels represent bone. TE_1/2 marks the maximum value of the texture energy, which occurs when the bone area is about 50%.

Trabecular bone analysis

A second analysis involved the trabecular bone of distal dog metacarpals from an accepted model of disuse [19]. The right forelimbs of female retired breeder beagle dogs (5–7 years old) were cast for 12 months to induce bone loss [19]. Coronal slices of the distal segments of the 2nd metacarpal harvested from both immobilized (IM) (n=5) and control (C) (n=8) animals from a previous study were used in the analysis [19]. The metacarpals were fixed in 10% neutral buffered formalin, dehydrated, cleaned and then embedded with methyl methacrylate [26]. Undecalcified frontal sections (10 μm thick) were cut using a microtome (Leica, Nusseloch, Germany), stained (von Kossa) and analyzed with standard histomorphometric methods using the OsteoMeasure system (Osteometrics, Atlanta, GA) [19]. Percent trabecular bone (Tb.Ar/T.Ar, %), trabecular number (Tb.N, #/mm), trabecular width (Tb.Wi, μm) and separation (Tb.Sp, μm) were measured on a 6-mm region of cancellous bone at the distal neck of the metacarpal [19]. These values were correlated (Pearson Product Moment Correlation) to the texture analysis parameters.

The slides of the distal metacarpals were scanned by a Nikon Eclipse E-400 microscope under 2× objective magnification. At this magnification, approximately 8 images per metacarpal were scanned, these images were stitched together (Panavue Image Assembler, Greensburg, PA, USA) using prominent landmarks to give a complete metacarpal image. The gray scales were converted to black and white via a uniformly chosen threshold which was heuristically determined at the mid-point of the gray scale range (Adobe Photoshop v6.0). The cortical regions were erased to avoid potential artifacts in the texture analysis which could be induced due to the sharp transition of black and white along the cortical region of the bone slices (Fig. 2).

Fig. 2.

Frontal section of distal metacarpal with cortical bone erased. The four orientations (0°, 45°, 90°, 135°) used for the texture analysis are indicated. The 0° orientation was perpendicular to the longitudinal trabeculae and the 90° orientation analyzed the horizontal trabeculae. The 45° and 135° orientations assessed trabeculae mid-way between the dominant trabecula orientations.

Gabor wavelet transform

The original image was convoluted with a bank of Gabor filters to produce a series of output images containing Gabor coefficients g_mn(x, y) where m ranges over the sequence of filter center frequencies or scales (1–M) and n ranges over the number of orientations (1–N). A measure of “texture energy”, e_mn, was then calculated based on a Gaussian average of |g_mn(x, y)| [14,37] (see Appendix A for details). The scale parameter refers to the resolution level at which the images are viewed. The higher the scale, the lower the resolution, and more global features of the image are detected. Lower scales correspond to the higher resolutions and “zoom-in” on the details of the image at the expense of the global features. In image processing, the higher scales are related to the low frequency contents of the image.

There are two ways to implement the multiresolution filtering. One way is to keep the image scale the same and vary the scale of the filters, a computationally expensive procedure. An equivalent approach is to maintain the filters the same size and scale the image. We implemented the second approach. The scales of an image can be heuristically determined by choosing the frequency bands with the most prominent power in the power spectrum [37]. We found that, for natural and realistic images, where the power spectrum transition is smooth, the best texture analysis was achieved using 3 frequency bands, which were equivalent to 3 image scales corresponding to 1/2, 1/4 and 1/8 [37]. This heuristic criterion was utilized in this study by choosing the number of scales to be 3 (M=3).

The total number of orientations was chosen to be 4 (N=4). These four orientations included 0°, 45°, 90° and 135° (Fig. 2). Our reason for choosing these particular orientations was that 0° corresponded to the longitudinal trabeculae and 90° corresponded to the transverse trabeculae. The 45° and 135° orientations assessed trabeculae oriented mid-way between the dominant trabecula orientations. Adding more orientations would increase the orientation resolution with which one could identify maximum and minimum values, but whether this would give more information is questionable. Moreover, the fact that the max/min of the texture energy can be only at 0°, 45°, 90° or 135° is not a shortcoming since the primary consideration is the comparisons of the texture energy at these values between control and immobilized bone.

Texture outcome measures

Four properties of the bone images were defined based on texture features derived from the Gabor wavelet transform:

• (1)Density measure (M_Density): this measure described the amount of bone in the image relative to the total area being analyzed. If the total area of bone is less than 50% of the total area, then the bone density can be represented as the averaged texture energy of scales (1–M) and orientations (1–N) as in Eq. (1).

$$M_{\text{Density}}=\frac{{\displaystyle \sum _{m=1}^M}{\displaystyle \sum _{n=1}^N}{e}_{mn}}{M·N}$$ (1)

Using this method, the highest energy occurs when the bone area is 50% and declines for bone areas greater or less than 50%. A simulation of texture energy along a particular orientation as a function of varying percentage of bone area is shown in Fig. 1E. The energy at 50% bone area is defined as TE_1/2. Thus, if the total area of bone struts is greater than 50%, the texture energy would be a characterization of the area of non-bone, M_{Density(nonbone)}. The corresponding bone density when it is greater than 50% of the area would then be given as M_Density =2×TE_1/2 − M_{Density(nonbone)}.

• (2)Texture energy at each orientation 0°, 45°, 90° and 135° (Texture Energy_0°–_135°): This measure described the amount of bone in the image at each of the 4 orientations (Fig. 2). The density measure (M_Density) was the average of these four texture energy values.

$$\text{Texture}{\text{Energy}}_n=\frac{{\displaystyle \sum _{m=1}^M}{e}_{mn}}{M}$$ (2)

The density and energy metrics measure the similarity between the texture pattern of the bone image and the scaled and oriented Gabor filters. They do not have units, and only the relative values and shapes of the energy curves are of importance.

• (3)
  Orientation measure (M_Orientation): this was a pair of angles that represented the orientations with the maximum and minimum texture energy. These angles were obtained by summing up texture energy values of the same orientation and selecting the orientations with the maximum and the minimum texture energy. That is,

  $$M_{\text{Orientation}}=({\theta }_{max},{\theta }_{min})$$ (3)
  where

  $${\theta }_{max}=(n_{max}-1)·180°/N;\left\{n_{\text{Max}}\in (1:N),\sum _{m=1}^M{e}_{{mn}_{\text{Max}}}=max\left({\sum _{m=1}^M{e}_{mn}\mid }_n\right)\right\}$$ (4)

  $${\theta }_{min}=(n_{min}-1)·180°/N;\left\{n_{\mathit{Min}}\in (1:N),\sum _{m=1}^M{e}_{{mn}_{\mathit{Min}}}=min\left({\sum _{m=1}^M{e}_{mn}\mid }_n\right)\right\}$$ (5)
• (4)
  Anisotropy measure (M_Anisotropy): this measure was the difference between the texture energy values of the maximum and minimum orientations, normalized by the averaged texture energy which is M_Density:

  $$M_{\text{Anisotropy}}=\frac{max\left({\frac{{\displaystyle \sum _{m=1}^M}{e}_{mn}}{M}|}_n\right)-min\left({\frac{{\displaystyle \sum _{m=1}^M}{e}_{mn}}{M}|}_n\right)}{M_{\text{Density}}}$$ (6)

A Student’s t-test assessed differences between the control and IM groups at a significance level of p<0.05 (Sigma Stat 3.0, SPSS Chicago, IL, USA). If the analysis detected abnormalities or not being in accordance with the equal variance assumptions, Mann–Whitney Rank Sum Test assessed group differences. Pearson Product Moment Correlations compared relationships between M_Density and percent trabecular bone (Tb.Ar/T.Ar; %) and between Texture Energy_0° and trabecular separation (Tb.Sp; μm) parameters.

Results

Template-pattern results

The density values (M_Density) of patterns A–D were similar with a mean (SD) of 5.81 (0.43) and a coefficient of variation (CV, ratio of standard deviation of the density measure to the mean) of 7.4% (Table 1). However, the difference in directionality of each pattern was detected in the anisotropy parameter. Pattern B was the most anisotropic pattern (M_Anisotropy =1.47) and pattern C the most isotropic (M_Anisotropy = 0.46). The coefficient of variation of the anisotropy variable was 60.3%, indicating a large variability in orientation of patterns A–D. The orientation with maximal and minimal texture energy values was different between the patterns. The M_Orientation for pattern A was (135°, 90°), whereas pattern B was (0°, 45°). Patterns B and C both had θ_max =0°, yet they had the greatest difference in M_Anisotropy. The texture energy at each orientation (0°, 45°, 90° and 135°) further illustrated how the four patterns differed in energy distribution across all orientations, which allowed us to gain insight about the details of the anisotropy. For example, it shows that, for pattern B, the largest value of M_Anisotropy was due to a large span between the texture energy values at 0° (10.58) and 45° (2.90). In contrast, pattern C, with the lowest M_Anisotropy measure, had relatively equal energy values across all orientations (Table 1) and was isotropic along 45° and 135°.

Table 1.

Texture analysis results from simulated patterns A–D shown in Fig. 1

Region	MDensity	MAnisotropy	MOrientation (degree)		Texture Energyn
			θmax	θMin	0°	45°	90°	135°
A	5.78	0.63	135	90	4.84	5.33	4.65	8.32
B	5.21	1.47	0	45	10.58	2.90	4.34	3.04
C	6.11	0.46	0	90	7.22	6.36	4.39	6.49
D	6.13	0.54	0	45	7.37	4.09	7.32	5.75
Mean	5.81	0.78			7.51	4.67	5.17	5.90
SD	0.43	0.47			2.36	1.50	1.44	2.19
CV	7.4	60.3			31.4	32.1	27.8	37.1

Dog metacarpal results

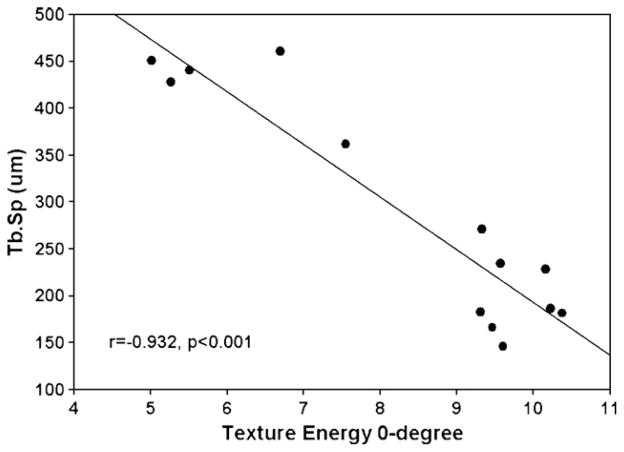
Histomorphometric analysis produced significant decreases in trabecular width (Tb.Wi) in the IM group with a significant increase in trabecular separation (Tb.Sp) (Table 2). The percent of trabecular bone area was also significantly decreased, a result mirrored by the density parameter (M_Density) from the texture analysis (Table 2). Furthermore, texture energy values in all orientations (0°, 45°, 90° and 135°) were significantly decreased in the IM group (Table 2). M_Anisotropy as a measurement of the anisotropy of the bone section was slightly decreased (3.9%) though not significant (p=0.697), after the 12-month disuse protocol. Significant correlations existed between the histomorphometry measurements and the texture parameters. Specifically, percent trabecular bone (Tb.Ar/T.Ar, %) and the density parameter (M_Density) were highly correlated (r=0.962, p<0.001) (Fig. 3). The inverse relationship between trabecular separation (Tb.Sp) and texture energy in the 0° orientation (Texture Energy_0°) was also highly correlated (r = −0.932, p <0.001) (Fig. 4).

Table 2.

Histomorphometry (reported in [19]) and texture parameters of distal metacarpal trabecular bone from a dog model of disuse

Parameters	Groups
	Control (C)	Immobilized (IM)
Texture analysis
MDensity	7.63 (0.11)	4.68 (0.71)a
MAnisotropy	0.48 (0.07)	0.46 (0.10)
Texture Energyn
0°	9.75 (0.43)	6.01 (1.08)b
45°	6.57 (0.28)	4.25 (0.77)a
90°	6.15 (0.28)	3.85 (0.55)b
135°	8.02 (0.49)	4.62 (0.57)b
Histomorphometry
Tb.Ar/T.Ar (%)	32.08 (3.73)	9.30 (2.0)b
Tb.Sp (μm)	199.3 (41.2)	428.2 (39.3)b
Tb.Wi (μm)	92.34 (8.59)	43.47 (7.43)b

Data are expressed as mean (SD). See text for abbreviations of the parameters.

^ap<0.01,

^bp<0.001 vs. Control.

Fig. 3.

Correlation (Pearson Product Moment) between the percentage of trabecular bone (Tb.Ar/T.Ar, %) and texture density (M_Density). r=0.962, p<0.001.

Fig. 4.

Correlation (Pearson Product Moment) between the trabecular separation (Tb.Sp, μm) and Texture Energy_0°. r = −0.932, p <0.001.

We also analyzed the same bone tissue images for an orientation resolution of 30° (0, 30°, 60°, 90°, 120°, 150°). The shape of the texture energy distribution as a function of orientation and the statistics comparing control to immobilized samples at each orientation were the same as when the orientation resolution was 45°. That is, results gave a maximum texture energy at 0° and a minimum at 90°. Thus, the conclusions that the maximal and minimal orientation directions are close to 0° and 90° of the bone sample are unaltered.

Discussion

The results of this study indicate that wavelet-based texture analysis using Gabor functions is an effective tool that could quantify bone architecture as well as bone density in two-dimensional bone slices. The analysis was able to differentiate simulated patterns with similar densities but disparate orientations. Moreover, it differentiated patterns comprised of the identical bone–marrow interfaces (Fig. 1, circles). Thus, it compares favorably with other methods developed to quantify anisotropy of bone structure, such as mean intercept length (MIL), which have been shown to be either unable to detect anisotropy in simulated bone patterns [24] or not sufficiently sensitive in detecting anisotropy [11].

The major advantage of using a multiresolution approach in this application is that it examines the directionality of the texture components at all scales (resolutions) simultaneously and independently. It has been found that, at least in femurs, both structural anisotropy and preferred orientation were strongly dependent on resolution [18]. Some anisotropic features manifest themselves better at a specific resolution and thus can be more easily quantified in the texture energy measure associated with each scale. Moreover, the methodology is not limited to two-dimensional images and can be readily adapted to consider images in 3D to process volumetric data by utilizing 3D Gabor functions [38]. Such an extension of the methodology to 3D images is beyond the scope of this paper.

Another important advantage of this methodology is that the number of scales can be adapted to refine the metrics that are used to determine bone density and directionality. In analyzing the simulated patterns, three scales were utilized. This gave excellent results for differentiating anisotropy between patterns. However, the coefficient of variation (CV) of the bone density metric was 7.4%. When we used 5 scales instead of 3, the CV of the bone density metric dropped by half to 3.6% as data from additional scales provided a more complete representation of the density. A greater number of scales, however, impact the anisotropy measure because “zooming-in” diminishes the directionality of the structure. Therefore, depending on the image and how it was obtained, a compromise on the number of scales could be established for obtaining reasonable measures of density and anisotropy. Alternate methods using multiresolution techniques, which give information about orientation such as steerable filters [29] or steerable pyramids [30] also might give better insight. A complete evaluation of how these different methods for obtaining orientation information and how noise properties and imaging modality (projection radiography, CT, MRI etc.) affect the choice of scale number to optimize the density and anisotropy is beyond the scope of this study.

It should be noted that a simple pixel count of bone per unit area would give an estimate of bone density, but such a method is limited to density estimation and is applicable to only black and white images. The method developed here can discriminate between different bone densities even when gray scale images are considered, if the contrast among gray scale images can be controlled to be at a uniform level. Moreover, the pixel count gives a measure of density by weighting all pixels in a particular region equally. It does not consider the architecture or the non-uniformity of the distribution of pixels. The Gabor function technique weights the pixels closer to a particular point more than it weights the points that are further away and does this at a number of resolutions simultaneously. This technique therefore deals with nonuniform densities of the image in a much more organized manner. Furthermore, as pointed out above, the texture-based approach gives information about bone orientation at a range of scales. We used 4 orientations (0°, 45°, 90°, 135°) because it was sufficient to demonstrate the effectiveness of the method in detecting anisotropy and not because of any physiological constraints. We have found that specifying a finer resolution in orientation did not alter the conclusion about the functioning of the system.

Schaffler et al. (1997) [28] utilized Fourier analysis to show that four simulated patterns, which were stereologically identical, had distinct power spectra as a function of angular position. The anisotropy (M_Anisotropy) and the M_Orientation (θ_max, θ_min) parameters in our texture analysis approach extended these results. The orientations that yielded the maximal power spectrum [28] were the same orientations that yielded maximum texture energy (θ_max). For example, pattern D had maximal power at 0° and 90° which were detected in the texture analysis as large values in texture energy at 0° and 90° (7.37 and 7.32 respectively). While the Fourier analysis was able to identify a structural disparity in stereologically identical patterns, it is limited in that the number of terms of the Fourier expansion needed to adequately describe the structure of the pattern is not known and comparisons are qualitative. The Gabor wavelet analysis of these images not only gave information that was derived from observing the Fourier spectral plots, but also optimized the choice of features that describe these patterns and identified specific orientation metrics that could be used for comparing patterns.

The density measure, M_Density, from the texture analysis correlated well with percent trabecular bone measurements (r=0.962, p <0.001) (Fig. 3). Moreover, the texture analysis was able to directly assess trabecular bone structure in individual orientations. The texture energy for each orientation (0°, 45°, 90°, 135°) yielded information regarding trabecular bone orientation and anisotropy. The texture energy at 0° orientation correlated well with trabecular separation measures (r=−0.932, p<0.001) (Fig. 4). Quantitatively, texture corresponds to the density and orientation of the points that make up an image. Gabor filters are sinusoidal functions, whose amplitude decays as a Gaussian and has a particular orientation. The sinusoids also have a particular spatial frequency of oscillation of black and white regions. The texture energy distribution of a bone image represents how close the image can be described in terms of the Gabor functions. If the bone area is less than 50% of the total area, the denser the bone trabeculae along a direction, the higher the overall texture energy along that direction. A smaller texture energy in a given direction would indicate a larger trabecular separation or thinner trabeculae. When a high texture energy was predominantly along the 0° orientation, it implies that the trabeculae were aligned more longitudinally. The simulated images show these correlations and illustrate the capability of the texture analysis to accurately assess density and orientation of the image. The application to images of normal and immobilized bone shows how pathologies affect features (density and orientation) that contribute to bone quality.

Histomorphometric parameters do not measure direct information regarding trabecular structure, specifically the shape and orientation of the trabecular elements [28]. In contrast, the texture analysis not only detected deficits in the amount of bone following a disuse protocol but the orientations in which the deficit occurred. There was a 38.6% decrease in M_Density after immobilization of the dog forelimb for 12 months. The orientation with the greatest texture energy decrease was 135° (−42.4%). However, the orientation with the largest texture energy, 0°, which was the predominant orientation of trabeculae had a 38.4% decrease in texture energy following immobilization. The trabecular structure became more isotropic following disuse as illustrated by a decreased M_Anisotropy parameter. Similar decreases in anisotropy from a Fourier analysis were found in the vertebral bodies of osteoporotic patients [25]. Even though the M_Anisotropy decreased, the predominant orientation remained at 0°. The anisotropy parameter in conjunction with the texture energy values at each orientation can yield information as to how specifically the orientation of the structure had been altered.

Studies of cancellous bone from proximal femora of women with hip fractures illustrated that fewer trabecular elements were transverse to the primary load axis [7]. These specimens had a significantly greater anisotropic structure than control specimens, even when matched for bone volume. A similar anisotropy relationship has been observed in radiographic images of osteoporotic fractures of the calcaneous, which have preferential deletions of trabeculae in some directions [3]. In contrast, Sugita et al. (2001) found from examination of femoral neck fractures that the bone strength along the longitudinal direction decreased more as density decreased [32], which was in line with the findings of Oxnard (1993) in bone from human lumbar vertebrae. Therefore, when assessing anisotropy, it is necessary to consider the orientation where the anisotropic property was obtained. The texture-based methodology using Gabor wavelets affords such a characterization.

In summary, a Gabor wavelets-based texture analysis is an effective analysis tool for bone images. It yields information regarding the quantity of bone (M_Density) as well as the orientation of the trabecular structure (M_Anisotropy), which can be adapted for a wide range of 2D and 3D imaging techniques.

Appendix A

Gabor coefficients were generated by convoluting the original image with a bank of Gabor filters. An even-symmetric Gabor filter was used, which has the impulse response given as:

$$h(x,y)=\frac{1}{2\pi {\sigma }_x{\sigma }_y}exp\left\{-\frac{1}{2}\left[\frac{x^2}{{\sigma }_x^2}+\frac{y^2}{{\sigma }_y^2}\right]\right\}cos(2\pi u_{0}x)$$ (A1)

where u₀ is the frequency of a sinusoidal plane wave along the x-axis, and σ_x and σ_y are the space constants of the Gaussian envelope along the x and y axes, respectively. Both σ_x and σ_y take on values related to the center radial frequency u₀. Filters with arbitrary orientations (θ) can be obtained via a rigid rotation of the x–y coordinate system:

$$\begin{array}{l}{x}^{\prime }=x\text{cos}\theta +y\text{sin}\theta \\ y^{\prime }=-x\text{sin}\theta +y\text{cos}\theta \end{array}$$ (A2)

From this, a set of Gabor wavelets or filters can be generated which cover the two-dimensional image plane. The Fourier transform representation of each Gabor filter is given by:

$$H(u,\nu )=exp\left\{-\frac{1}{2}\left[\frac{{(u-u_0)}^2}{{\sigma }_u^2}+\frac{{\nu }^2}{{\sigma }_{\nu }^2}\right]\right\}+exp\left\{-\frac{1}{2}\left[\frac{{(u+u_0)}^2}{{\sigma }_u^2}+\frac{{\nu }^2}{{\sigma }_{\nu }^2}\right]\right\}$$ (A3)

where:

$$\begin{array}{l}{\sigma }_x=\frac{1}{2\pi {\sigma }_u}\\ {\sigma }_y=\frac{1}{2\pi {\sigma }_{\nu }}\end{array}$$ (A4)

The design of the Gabor filters entails determining a set of filters so that their support should uniformly cover the area in the frequency domain. A common strategy is to design the filter set so that the half-peak magnitude supports of the filter responses in the frequency spectrum touch each other. Combining this with Eq. (A4), we will have the following [37]:

$$\begin{array}{l}{\sigma }_x=\frac{3\sqrt{2\text{ln}2}}{2\pi u_0}\\ {\sigma }_y=\frac{1}{2\pi \text{tan}\left(\frac{\theta }{2}\right)\sqrt{\frac{u_0^2}{2\text{ln}2}-\frac{1}{4{\pi }^2{\sigma }_x^2}}}\end{array}$$ (A5)

The orientation resolution θ was chosen based on heuristic criteria, while the center frequencies, u₀’s, were chosen so that they were one octave apart, with the highest frequency determined by the Nyquist–Shannon sampling theorem. The choices are given as [37]:

$$\frac{3N_{\text{w}}}{8},\frac{3N_{\text{w}}}{16},\dots ,\frac{3}{1},\frac{3}{2}(\text{cycles}/N_{\text{w}})$$ (A6)

where N_w is the width of the image in pixels.

If the Gabor filter set is composed of filters with M center frequencies, and N orientations, the Gabor coefficients (filter output when Eq. (A1) is convoluted with the given data) are given by g_mn(x, y), where m ranges over the sequence of filter center frequencies (1–M) and n ranges over the number of orientations (1–N). At each coordinate (x, y), a measure of “texture energy” could be defined in terms of g_mn(x, y) [14]:

$$e_{mn}(x,y)=\frac{1}{W^2}\sum _{(x_1,y_1)\in W_{xy}}G(x,y,{\sigma }_x,{\sigma }_y)\mid g_{mn}(x_1,y_1)\mid$$ (A7)

where W_xy is an W×W window centered at the pixels with coordinates (x, y) and G(x, y, σ_x, σ_y) is a Gaussian window centered at (x, y) with standard deviations σ_x and σ_y.