TopNet: a tool for comparing biological sub-networks, correlating protein properties with topological statistics

Abstract

Biological networks are a topic of great current interest, particularly with the publication of a number of large genome-wide interaction datasets. They are globally characterized by a variety of graph-theoretic statistics, such as the degree distribution, clustering coefficient, characteristic path length and diameter. Moreover, real protein networks are quite complex and can often be divided into many sub-networks through systematic selection of different nodes and edges. For instance, proteins can be sub-divided by expression level, length, amino-acid composition, solubility, secondary structure and function. A challenging research question is to compare the topologies of sub- networks, looking for global differences associated with different types of proteins. TopNet is an automated web tool designed to address this question, calculating and comparing topological characteristics for different sub-networks derived from any given protein network. It provides reasonable solutions to the calculation of network statistics for sub-networks embedded within a larger network and gives simplified views of a sub-network of interest, allowing one to navigate through it. After constructing TopNet, we applied it to the interaction networks and protein classes currently available for yeast. We were able to find a number of potential biological correlations. In particular, we found that soluble proteins had more interactions than membrane proteins. Moreover, amongst soluble proteins, those that were highly expressed, had many polar amino acids, and had many alpha helices, tended to have the most interaction partners. Interestingly, TopNet also turned up some systematic biases in the current yeast interaction network: on average, proteins with a known functional classification had many more interaction partners than those without. This phenomenon may reflect the incompleteness of the experimentally determined yeast interaction network.

INTRODUCTION

Protein–protein interactions play a role in nearly all events that take place in a cell. An important idea, in fact, emerging in post-genomic biology is that the cell can be understood as a complex network of interacting proteins (1,2). The set of all such interactions carried out by proteins encoded in a genome has been dubbed the interactome. Complex networks are also used to describe the structure of a number of wide-ranging systems including the internet, power grids, the ecological food web and scientific collaborations. Despite the seemingly huge differences among these systems, it has been shown that they all share common features in terms of network topology (3–11). Thus, networks may provide a framework for describing biology in a universal language understandable to a broad audience.

Network definitions and theories

The topological analysis of the networks provides quantitative insight into their basic organization. Four topological statistics of particular interest in network analysis are as follows (3–11). (i) Average degree (K). The degree of a node is the number of links that this node has with other nodes. The average degree of the whole network is the average of the degrees of all its individual nodes. (ii) Clustering coefficient (C). This is defined as the ratio of the number of existing links between a node’s neighbors and the maximum possible number of links between them (similar to an odds ratio). The clustering coefficient of a network is the average of all its individual coefficients. This statistic can be used to determine the completeness of the network. (iii) Characteristic path length (L). The graph-theoretical distance between two nodes is the minimum number of edges that is necessary to traverse from one node to the other. The characteristic path length of a network is the average of these minimum distances. It gives a measure of how closely nodes are connected within the network. (iv) Diameter (D). The diameter of a network is the longest graph-theoretical distance between any two nodes in the graph. Table 1 explains, in detail, the formulas that are used to calculate these statistics.

Table 1. Overview of the interaction datasets and the analysis: topological statistics.

^aThe values of the topological statistics for the whole yeast interaction network.

Until recently, classical random network theory was used to model complex networks. This was introduced by Erdös and Rényi (6,12). It assumes that any two nodes in the network are connected with random probability p and the degrees of the nodes follow a Poisson distribution, which has a strong peak at the average degree, K. Most random networks are highly homogenous, in that most nodes have the same number of links (degree), k_i ≈ K, where k_i is the degree of the ith node. The chance of having nodes with k links falls off exponentially for large k [i.e. P(k) ≈ e^–k], meaning that it is very unlikely that there will be any nodes of degree significantly larger than average.

To explain the heterogeneous nature of complex networks, Barabási and colleagues recently proposed a ‘scale-free’ model in which the degree distribution in many large networks follows a power-law [P(k) ≈ k^–r] (3,5). A remarkable point about this distribution is that most of the nodes within these networks have very few links, with only a few of them (hubs) being highly connected. Many aspects of genomic biology have such a scale-free structure (13–17). Concurrently, Watts and Strogatz found that many networks can also be described as having a ‘small-world’ property (11), i.e. they are defined as being both highly clustered and containing small characteristic path lengths (large C and small L).

Complex networks, moreover, can be further divided into two broad categories: directed and undirected. In an undirected network, the statement ‘node A is linked to node B’ is the same as ‘node B is linked to node A’. However, the edges of the directed networks have a defined direction. Thus, the clustering coefficient cannot be calculated for directed networks (6).

Biological applications

Currently, large-scale experiments have created a great variety of genome-wide interaction networks, especially in Saccharomyces cerevisiae (18–21). Furthermore, there are also a number of databases [i.e. MIPS (22), BIND (23) and DIP (24)] that have many manually curated interactions for yeast. Finally, beyond the experimentally derived protein–protein interactions, there are also predicted interactions (25), literature-derived interactions (26) and regulatory interactions (27).

These different kinds of interactions give rise to many types of networks. Protein–protein interaction networks are undirected, as opposed to directed regulatory networks. Even for the same network, many meaningful sub-networks can be generated by selecting different types of edges. For example, it has been known that interaction data produced by different methods are of different quality. Thus, the topology of the interaction network determined by yeast two-hybrid experiments is quite different from that determined by in vivo pull-down experiments (28,29). Secondly, proteins can be divided into different classes based on their biological properties, such as expression level, amino acid composition, sub-cellular localization and solubility (see Table 2). Therefore, different sub-networks can also be generated through selecting different classes or groups of nodes (e.g. proteins).

Table 2. Overview of the interaction datasets and the analysis: biological categories.

Category	Reference	URL	No. ORFs covered	No. of groups	Description
Expression	(47)	http://171.65.26.52/yeast_cell_cycle/cellcycle.html	6130	13	Cell-cycle expression data using affymetrix
Protein size	(48)	http://www.yeastgenome.org/	6092	12	Derived from genome sequence
Amino acid composition	(33)	http://us.expasy.org/tools/pscale/PolarityGrantham.html	6092	14	Derived from genome sequence
Subcellular localization	(49)	http://bioinfo.mbb.yale.edu/genome/localize/	2902	4	transposon tagging
Function	(22)	http://mips.gsf.de/proj/yeast/CYGD/db/index.html	3936	2	MIPS Functional catalogs
Sequence conservation	(50)	http://www.ncbi.nlm.nih.gov/COG/	4139	5	COG database
Tertiary structure (fold)	(51)	http://scop.mrc-lmb.cam.ac.uk/scop/	3471	452	SCOP database
Fold class	(51)	http://scop.mrc-lmb.cam.ac.uk/scop/	3471	7	SCOP database
Secondary structure	(41)	http://abs.cit.nih.gov/gor/	6092	7	Predicted by GOR IV
Soluble protein versus membrane protein	(40)	http://www.cbs.dtu.dk/services/TMHMM/	6092	14	Predicted by TMHMM server v 2.0

This great variety of interaction networks presents an interesting challenge: to compare these myriad networks and sub-networks in terms of the topological statistics one has to repeatedly perform the same set of calculations. Although such comparisons are somewhat tedious, it is useful to see the effects of different selections on the results, and comparison of different network topologies could provide clues to basic principles involved in pathway structure. Alternatively, comparing different networks can be used to assess their quality (28,30).

In order to facilitate the analysis of interaction networks, we constructed a web tool, TopNet, to perform comparisons automatically. It is available from: http://genecensus.org/TopNet.

TopNet takes an arbitrary undirected network and a group of node classes as an input to create sub-networks. Then it computes all four topological statistics mentioned above and draws a power-law degree distribution for each sub-network. The results of these calculations are plotted in the same format for each statistic to facilitate direct comparison. TopNet also enables the user to explore complex networks by sections. For example, all neighbors of a certain node can be shown on a simple graph. Alternatively, the user could select two nodes and request that all paths not exceeding some specified length be displayed as an independent graph.

We immediately applied TopNet to the available interaction data and a number of important structural and functional classes for yeast proteins, which are summarized in Tables 2–3. The results reveal several interesting relationships between a protein’s biological properties and its topological statistics within the interaction network. We chose the results of several most interesting and important protein classes for further discussion below. For other results, please find them through the ‘download’ page on the TopNet website.

Table 3. Overview of the interaction datasets and the analysis: interaction datasets.

Dataset	Reference	URL	No. ORFs covered	No. of interactions
MIPS complex catalogs	(22)	http://mips.gsf.de/proj/yeast/CYGD/db/index.html	871	8250
BIND	(23)	http://www.bind.ca/	3789	5965
DIP	(24)	http://dip.doe-mbi.ucla.edu/dip/Main.cgi	4716	15113
Yeast two-hybrid	(18)	http://genome.c.kanazawa-u.ac.jp/Y2H/	3278	4393
Yeast two-hybrid	(21)	http://www.nature.com/cgi-taf/DynaPage.taf?file=/nature/journal/v403/n6770/full/403623a0_fs.html	1044	981
In vivo pull-down	(20)	http://yeast.cellzome.com/	1361	31304
In vivo pull-down	(19)	http://www.mdsp.com/yeast/	1578	25333

RESULTS AND DISCUSSION

Overview of TopNet

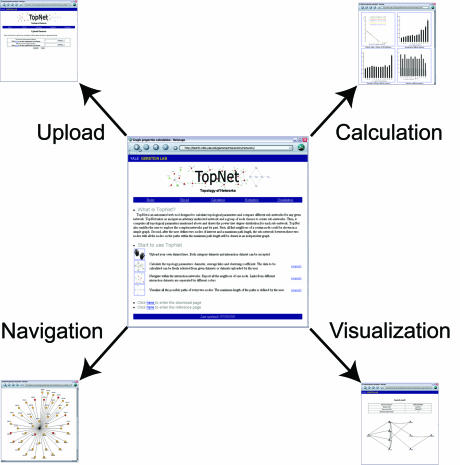
TopNet consists of four major parts (see Fig. 1).

Figure 1.

Overview of TopNet. The whole website consists of four major parts: upload, calculation, navigation and visualization. For details, please refer to the text.

Upload. In the first step (as shown in Fig. 1, ‘upload’), the user can upload: (i) a set of edges and (ii) (optionally) different sub-groups of nodes. The network must be undirected. The groups are defined as the classes of the nodes if the network is composed of unique sub-populations.

A variety of sample networks are available from the website. This includes a comprehensive yeast interaction network and many possible classes of yeast proteins. Because the yeast interaction data produced by different methods differ in many aspects (28), we also divided the yeast network into three parts: (i) data produced by individual experiments (compiled from MIPS, BIND and DIP databases (22–24); the results from the large-scale experiments are excluded); (ii) data produced by large-scale yeast two-hybrid experiments (18,21); (iii) data produced by in vivo pull-down experiments (19,20). Predicted or literature-derived interactions can also be uploaded.

Calculation. As shown in Figure 1, ‘calculation’, TopNet automatically computes the four topological statistics described above. The results are presented in a table for easy downloading and in graphs for direct visualization. Because many real networks are scale-free, the degree distributions for different classes are plotted on a log–log scale. The degree distribution of scale-free networks follows a power-law, i.e. the distribution is a straight line on a log–log plot. The parameters and the correlation coefficients of the regression lines are also given on the graph.

Navigation. As shown in Figure 1, ‘navigation’, TopNet explores the networks node by node, showing all the neighbors of each node as most of the real networks are too complex to discern any information from a global view. Specifically, in the yeast protein–protein interaction network example, different colors are used to indicate the sources of the interaction between a given node and the center node. Interactions that are confirmed by several independent methods haven been shown to be of higher quality (29). TopNet can thus facilitate the determination of reliable interaction partners of a specific gene for use in further investigation.

Visualization. Finally, as discussed above, it is hard to depict the whole network clearly. Although it is useful to show all the neighbors of each node, the user sometimes wants to directly view the topology of a sub-network, where the proteins that the user is interested in are involved. Using TopNet, the user could specify two nodes and a maximum path length. Then the tool will show all possible paths connecting these nodes (as shown in Fig. 1, ‘visualization’) with length less than the specified maximum.

Algorithms in TopNet

Distance calculation. To calculate the diameter and the characteristic path length of each network (or sub-network), distances between any two connected nodes (disconnected nodes are excluded) are calculated first by a greedy algorithm. Simply put, for each source node, all of its neighbors are labeled as having a distance of 1. The nodes that are linked to these neighbors are labeled as having a distance of 2, and so on, until the final node is encountered. Nodes that are encountered multiple times are considered only the first time. This algorithm is referred to as a breadth-first search.

All possible paths calculation. To determine all possible paths between any two nodes, we perform a breadth-first search from the source node (as described above), then a second breadth-first search from the target node, thus identifying all nodes that could be on a path between the source and target of appropriate length. All the neighbors of the source node are placed on the same layer; the neighbors of these nodes are placed on a further layer; and so on. By scoring each node with its shortest distance from both source and target, we can use the relation between the scores of a node and the scores of its neighbors to identify edges on a shortest path in time proportional to the number of edges in the graph.

Choices in embedding a sub-network in larger network. The purpose of TopNet is to allow the researcher to divide the network of interest into many sub-networks, and then compare topological statistics of those sub-networks. However, the issue of embedding a sub-network into a bigger network has a number of complexities. To resolve these complexities we have to make a number of arbitrary but reasonable decisions. Consider the calculation of node degree (a step on the way to calculating the average node degree of a sub-network). Suppose node s in sub-network A has three neighbors also in A, and one neighbor that is not in A. Do we calculate the degree of s as three or four? Likewise, consider the problem of calculating the shortest distance between two nodes in the same sub-network (a necessary step in calculating a sub-network’s diameter). What do we do if the shortest path makes use of nodes not in the sub-network?

We have decided to calculate these values (as well as analogous values for the clustering coefficient) with respect to the entire network. This is illustrated in Figure 2. So for the examples above we calculate the degree as four, and we do use a path involving the nodes outside the sub-network. As we are ultimately interested in the statistics of the sub-networks as they related to the network as a whole, it was logical to go in this direction.

Figure 2.

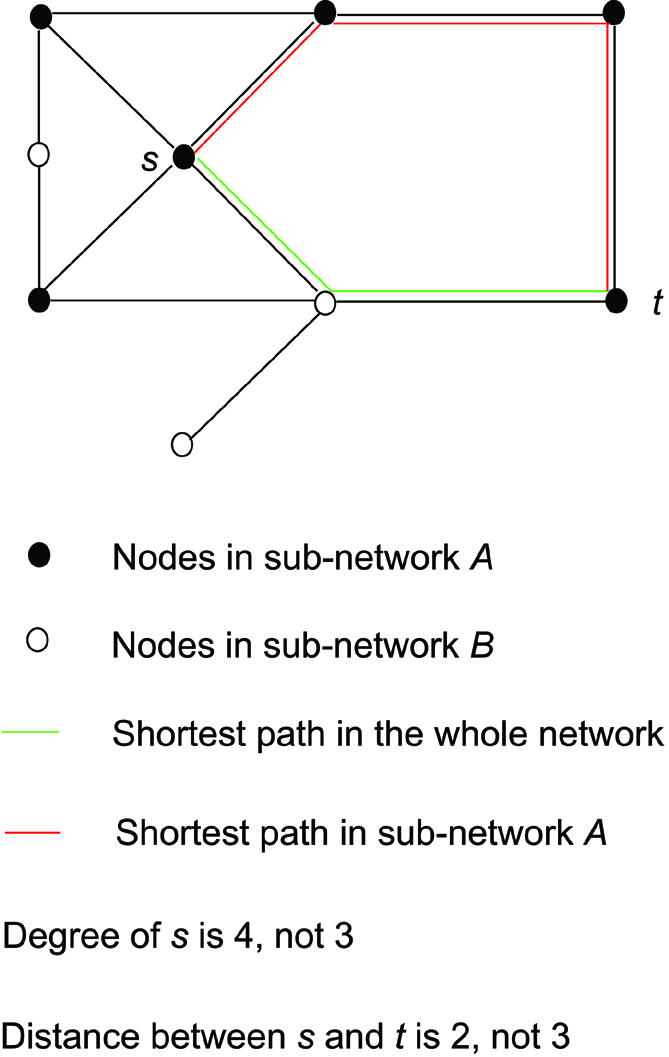
A certain sub-network is embedded in the whole network, when the topological statistics for the nodes in this sub-network are calculated. (A) Node s interacts with three other nodes in sub-network A (shown as solid circles) and one node in sub-network B (shown as open circles). The degree of s is therefore 4 instead of 3. (B) The shortest path between nodes s and t could go through nodes in sub-network B (shown as the green line). Thus, the distance between s and t is 2, not 3.

Application: analysis of different genomic features in yeast

In a direct fashion, we can apply TopNet to the existing interaction datasets and standard sets of protein classes available for yeast. This enables us to find some straightforward but interesting biological correlations. In particular we focused on the following characteristics: (i) mRNA expression, (ii) amino acid composition, (iii) solubility, (iv) secondary structure, (v) function and (vi) protein size.

In order to perform a complete analysis of the whole yeast interaction network, we merged all the available protein–protein interaction datasets to create a comprehensive network for yeast (see Table 3), which consists of 69592 interactions among 4957 proteins (29). Given the high false positive rates of many of the high-throughput interaction screen methods (28), we divided this whole interaction dataset into three sub-datasets (as described above) to further confirm the biological relevance of the results. (i) Two-hybrid sub-dataset, which contains all the interacting pairs identified by yeast two-hybrid experiments (5202 interactions, 7.5% of the total) (18,21). (ii) Pull-down sub-dataset, which contains all the interactions identified by in vivo pull-down techniques (54 663 interactions, 78.5% of the total) (19,20). (iii) Manual sub-dataset, which contains interacting protein pairs identified by individual experiments from MIPS, BIND and DIP (interacting pairs in the first two sub-datasets are excluded; 14 837 interactions, 21.3% of the total) (22–24).

The two-hybrid sub-dataset is known to contain many false positives (28) and it is <10% of our whole dataset. Therefore, the results from the two-hybrid sub-dataset are not as reliable as the manual sub-dataset, which is generally believed to be the most reliable data available (28). Thus, if the result calculated based on the manual sub-dataset agrees with that of the whole dataset, we believe that the result is more trustworthy than if calculated against the two-hybrid set. We repeated all the calculations on these three sub-datasets individually, performing a simple form of sensitivity analysis. With one exception, the results are in strong agreement. Only those results pertaining to protein size are different, as discussed in detail below.

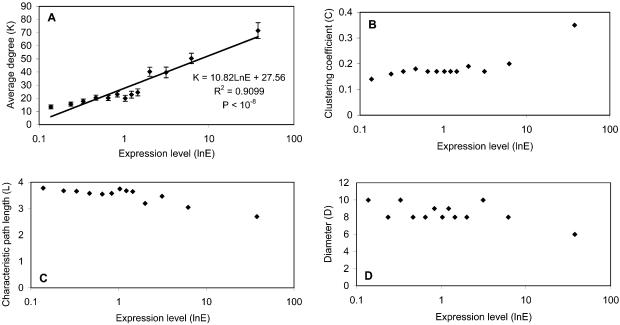
mRNA expression. Starting with a reference dataset for the absolute expression level in yeast [a non-trivial combination of different gene expression datasets (31)] we used TopNet to investigate relationships between expression levels and topological statistics of the network of known interacting yeast proteins. The proteins are divided into 13 groups based on their expression levels. As shown in Figure 3, sub-networks consisting of highly expressed proteins tend to have higher average degrees and clustering coefficients, but smaller diameters and characteristic path lengths. However, some correlations (Fig. 3B–D; statistics C, L and D, respectively) are very poor; therefore, we focused our analysis specifically on relationships between the protein’s biological properties and its degree distribution for all biological features.

Figure 3.

Relationships between expression levels and topological statistics. (A) Protein’s average degree has an exponential relationship with its expression level. The regression equation, R² and P value are shown in the figure. The P value measures the statistical significance of the correlation of regression [R]. (B) Protein’s expression level has a positive relationship with its clustering coefficient. (C and D) Protein’s expression level has a negative relationship with its diameter and characteristic path length.

In Figure 3A, the curve shows an exponential distribution. This result makes sense; proteins with more copies in the cell have a greater possibility of interacting with other proteins by chance alone, although the mRNA level and the abundance of a protein do not always correlate perfectly (32). We also looked at the relationship between expression fluctuation (i.e. through the yeast cell cycle) and topological statistics, but did not find any strong correlations (see the ‘download’ page).

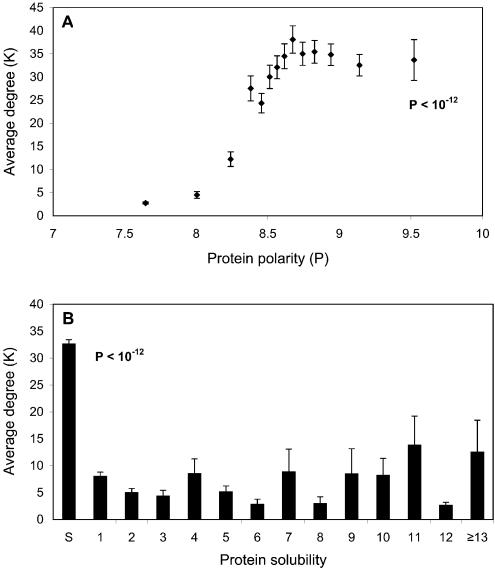
Amino acid composition. As shown in Figure 4A, proteins with more polar amino acids tend, on average, to have higher degrees in the interaction network. [The polarity of a protein can be determined from the average of the polarities of its amino acids using the Grantham scale (33). A similar method has been used to calculate the hydrophobicity of proteins (34)].

Figure 4.

Relationships between average degree and protein polarity, and solubility. (A) Protein polarity is determined as the average polarity of all its composing amino acids. Proteins are binned into 14 groups with approximately the same number of proteins in each group. The P value, calculated by the Mann–Whitney test (a non-parametric T test) (46), measures the difference between the protein groups of highest and lowest polarities. (B) The number of trans-membrane helices is predicted by TMHMM server 2.0. The labels on the x-axis: S, Soluble proteins; the number means different classes of proteins with corresponding number of trans-membrane helices; ≥13, all the proteins with ≥13 trans-membrane helices. The P value, calculated by the Mann–Whitney test, measures the difference between soluble and trans-membrane proteins, which consists of all the proteins with trans-membrane helices.

Three major reasons for this phenomenon could be: (i) polar amino acids tend to be on the protein’s surface (35), therefore the more polar amino acids a protein has, the larger the surface it could potentially have. (ii) One of the most important protein–protein interaction forces is electrostatics. Polar amino acids have a higher tendency to have this kind of interaction (36). Previous studies have shown that, although overall interaction interfaces are hydrophobic, polar amino acid residues are conserved at specific positions as interaction ‘hot spots’ (37). (iii) Most proteins without many polar amino acids are membrane proteins. Because of the inherent bias against membrane proteins in the experimentally determined interaction network, membrane proteins have less interaction partners, as will be discussed in detail below.

In yeast two-hybrid experiments, protein baits have DNA-binding domains and the preys have the activation domains. When the protein baits interact with the preys, the interaction will bring the activation domain to the DNA-binding domain, which will turn on the reporter genes. However, some polar protein baits have activation domain-like acidic regions. It has been shown that these polar protein baits could turn on the reporter genes in the absence of any preys (38,39). Therefore, polar proteins might produce many false positive signals and artificially have more interaction partners. However, we performed the same calculations on the three sub-datasets and the results remain the same. Most importantly, the result based on the manual sub-dataset confirms that the correlation between protein polarity and its degree is real.

Protein solubility. In general, soluble proteins have many more interaction partners than membrane proteins (see Fig. 4B). The most important cause of this phenomenon is that soluble proteins are relatively free to move within the cell and therefore have the ability to interact with many more proteins at different times and localizations. In contrast, a membrane protein’s mobility is largely limited to a two-dimensional surface.

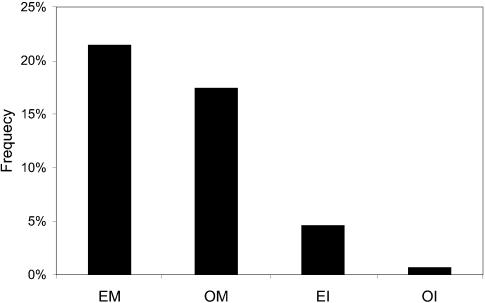
Another significant reason for the large degree of soluble proteins is that these proteins are much more amenable to interaction determination experiments, specifically the yeast two-hybrid (18,21). In the whole merged interaction dataset, there are 463 interacting pairs among 863 membrane proteins. The observed frequencies of the membrane proteins and the interactions between them in the yeast genome are both much lower than random expectation (see Fig. 5). Therefore, in experimentally determined interaction networks the number of interaction partners for membrane proteins is most probably grossly underestimated.

Figure 5.

Expected and observed frequencies of the membrane proteins and the interactions between membrane proteins in the yeast genome. ‘EM’, expected frequency of the membrane proteins; ‘OM’, observed frequency of the membrane proteins; ‘EI’, expected frequency of the interactions between membrane proteins; ‘OI’, observed frequency of the interactions between membrane proteins.

Interestingly, the number of interaction partners for membrane proteins does not seem to have any correlation with the number of trans-membrane helices that they have, as predicted by the TMHMM server 2.0 (40).

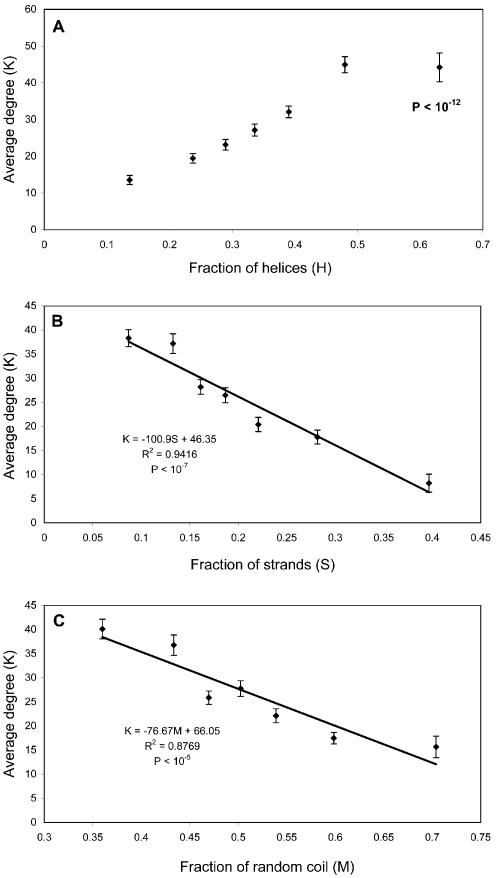
Secondary structure. The secondary structure of proteins was predicted using the GOR IV algorithm (41). It is obvious from Figure 6 that more helical proteins tend to have more interactions. A good example of the involvement of helices in interactions is coiled-coil domains, which consist of two or more alpha-helices that wrap around each other with a slight left-handed superhelical twist (42,43). In the yeast genome, 121 proteins containing coiled-coil regions were identified using the MULTICOIL algorithm (44). In the whole interaction dataset, there are 250 interacting pairs among 119 of these 121 proteins.

Figure 6.

Relationships between average degree and protein secondary structures. The secondary structures of proteins are determined by the GOR IV algorithm. The fraction (i.e. the x-axis) is calculated as the ratio of the number of amino acids with a certain secondary structure over the total length of the protein. Proteins are binned into seven groups with approximately the same number of proteins in each group. The P value in (A), calculated by the Mann–Whitney test, measures the difference between the protein groups of highest and lowest fraction of helices. The regression equations, R² and P values are shown in (B) and (C). The P values measure the statistical significance of the correlation of regression [R].

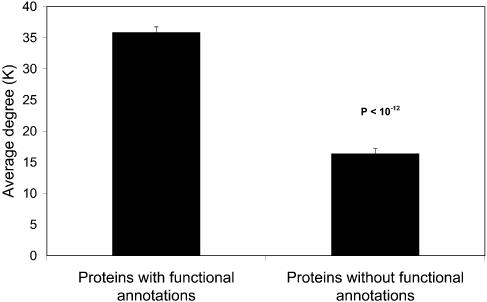
Function. We also observed a very interesting phenomenon in the experimentally determined interaction network: proteins with at least one functional annotation in MIPS database (22) on average had a much higher degree than those without any functional annotation (Fig. 7). This reflects the bias in current interaction datasets, i.e. proteins with functional annotation are preferred as baits, even in large-scale experiments.

Figure 7.

Proteins with at least one functional annotation have many more interaction partners than those without any functional annotations based on MIPS functional classification. The P value, calculated by the Mann–Whitney test, measures the difference between the two groups.

The calculations for the above five characteristics have been repeated for the three sub-datasets. The results remain the same (see Supplementary Material, Figs 1–7), which confirms that they are reliable and free of artifacts of large-scale interaction screen methods.

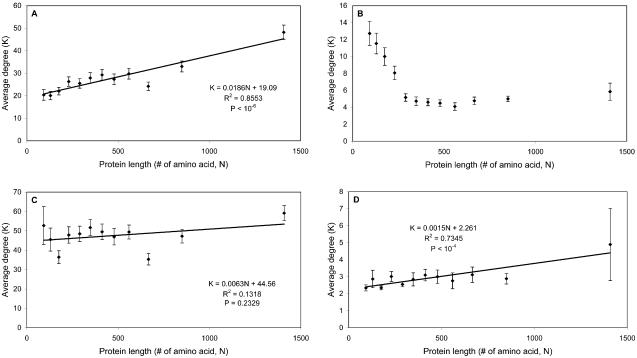
Protein size. To our surprise, the results of our algorithms as applied to different datasets do not agree with each other with respect to protein size (see Fig. 8). In the whole dataset, we found that larger proteins tend to have more interaction partners (see Fig. 8A). Subsequently, we repeated the calculations on the three sub-datasets individually: (i) manual sub-dataset (see Fig. 8B). Protein size has a negative relationship with protein degree, i.e. the larger the protein is, the less interaction partners it has on average. (ii) pull-down sub-dataset (see Fig. 8C). There are no strong relationships between protein size and degree. (iii) two-hybrid sub-dataset (see Fig. 8D). Protein size has a positive relationship with protein degree, i.e. the larger the protein is, the more interaction partners it has on average, which agrees with the result of the whole interaction dataset.

Figure 8.

Relationships between average degree and protein length. Protein length is reflected in the number of amino acids it has. (A) Positive relationship in the whole dataset. (B) Negative relationship in the manual sub-dataset. (C) No significant relationships in the pull-down sub-dataset. (D) Positive relationship in the two-hybrid sub-dataset. The regression equation, R² and P value are shown in (A), (C) and (D). The P value measures the statistical significance of the correlation of regression [R].

As discussed earlier, the manual sub-dataset is the most reliable dataset (28), and the result calculated based on this sub-dataset agrees well with our common knowledge, i.e. some of the most promiscuous proteins are small unspecific repeats such as ubiquitin (45).

The positive relationship observed in the two-hybrid sub-dataset and the whole dataset are generated by the following artifacts. (i) In yeast two-hybrid experiments, some large proteins may not be able to fold correctly in a non-native environment (i.e. nucleus). They might then expose hydrophobic groups and aggregate, producing a false positive signal. (ii) Most importantly, in Figure 8 the proteins are divided into 12 bins based on their lengths; each bin contains approximately 500 proteins. Because of the nature of the in vivo pull-down technique (i.e. identifying complexes instead of binary interacting pairs), the average degree of the proteins in this sub-dataset (47.9) is much higher than those of the other two sub-datasets (2.9 for the two-hybrid subset, 6.6 for the manual subset). Therefore, the average degree of each bin in Figure 8 depends on the number of proteins in the bin that are included in the pull-down subset. The fact that there are few small proteins in the pull-down sub-dataset leads to the artificial positive relationship observed in the whole dataset (see Supplementary Material, Fig. 8).

Summary

In summary, we have given an overview of the design principles and a wide range of possible applications of our automated web tool: TopNet. This tool provides users with the ability to compare the topological statistics of different sub-populations within the same network and to explore complex networks part by part. To demonstrate its use, we applied TopNet to analyze the relationships between a variety of biological classes and a protein’s degree distribution within the yeast protein–protein interaction network. The results illustrated several interesting trends, which could be used to predict protein–protein interactions and ultimately protein function. Furthermore, our analyses also discovered several systematic errors existing in the current large-scale interaction data.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.