Abstract
We have developed a computational method for transcriptional regulatory network inference, CARRIE (Computational Ascertainment of Regu latory Relationships Inferred from Expression), which combines microarray and promoter sequence analysis. CARRIE uses sources of data to identify the transcription factors (TFs) that regulate gene expression changes in response to a stimulus and generates testable hypotheses about the regulatory network connecting these TFs to the genes they regulate. The promoter analysis component of CARRIE, ROVER (Relative OVER-abundance of cis-elements), is highly accurate at detecting the TFs that regulate the response to a stimulus. ROVER also predicts which genes are regulated by each of these TFs. CARRIE uses these transcriptional interactions to infer a regulatory network. To demonstrate our method, we applied CARRIE to six sets of publicly available DNA microarray experiments on Saccharomyces cerevisiae. The predicted networks were validated with comparisons to literature sources, experimental TF binding data, and gene ontology biological process information.
INTRODUCTION
Automated inference of regulatory networks is a crucial step in bridging individual molecule characterization and predictive systems biology. In addition, knowledge of the flow of information through a cell in response to stimuli can be used to predict the effects of novel stimuli and to modulate the cell’s response by altering the activities of specific members of a network. Understanding biology to this degree will require the complete determination of the interactions among genes, proteins and metabolites at many levels of regulation. The transcriptional portion of a cell’s regulatory network is currently the most tractable given the availability of high-throughput gene expression data and the progress in sequence pattern analysis in the bioinformatics community.
Important advances have been made toward understanding transcriptional regulatory networks. One strategy infers global networks directly from whole genome microarray data (1–9). Segal et al. further showed that it was beneficial to also incorporate protein–protein interaction data (10). Another strategy focuses on the identification of shared regulatory motifs in the promoters of co-regulated genes, signified by similar expression profiles. Examples include the identification of statistically overabundant short oligomers (11,12), overabundant transcription factor binding motifs (13–17), and common oligomers via multiple-local alignment of the input promoter sequences (18–32). Palin et al. investigated the overlap between genes that change expression due to a gene deletion and genes with promoters containing binding sites for a particular transcription factor (TF) (33).
Rather than attempting to determine global regulatory networks, here we introduce a method of inferring a specific transcriptional network from the response to a single stimulus or the deletion of a single TF. Accurate predictions of such specific networks are widely applicable since the relationships of genes in the pathway are well defined and the impact of external stimuli can be clearly delineated. Therefore, testable hypotheses can be formed about the method of action of a drug and suggestions can be made regarding later steps in the network to be targeted with a new drug, potentially resulting in fewer side effects.
Our method combines two complementary methods for detecting transcriptional regulation. First, microarray data are used to reveal the genes that respond to a given stimulus through changes in mRNA abundance. These genes are believed to form a co-regulated group. If there are TFs in the group, they are proposed to regulate the observed expression changes of the other genes. Two previous studies correlated the expression profiles of TFs with those of the genes whose promoters contained binding sites for these TFs (34,35). Segal et al. also used the expression levels of candidate regulators to build regression trees for explaining global gene expression (9). Second, we identify TFs with binding sites that are statistically over-represented in the promoter regions of the co-regulated group of genes. Even if their expression levels do not change upon stimulation, these TFs are also predicted to regulate the group. A number of recent papers describe statistical methods for identifying overabundant TF binding motifs (13–17). The main novelty of our approach is the combination of the above two methods in the construction of transcriptional networks, along with technical improvements in the latter method.
Our approach is implemented in a computational tool called CARRIE (Computational Ascertainment of Regulatory Relationships Inferred from Expression). The promoter sequence analysis component of CARRIE is a stand-alone program called ROVER (Relative OVER-abundance of cis-elements). ROVER identifies the TFs most likely to regulate the observed mRNA abundance changes. It also determines which specific genes are regulated by each identified TF. Based on this information and the results of microarray analysis, CARRIE infers a transcriptional regulatory network. The stimulatory or inhibitory impact of each TF on its regulated genes is inferred from the directions of change in their expression levels.
CARRIE was applied to publicly available Saccharomyces cerevisiae microarray data (36–39). These included six experiments: three experiments were performed upon stimulation from extracellular signals and the other three involved wild-type and TF gene deletion strains. A TF gene deletion experiment can be used to determine the signaling network downstream of a TF that is active in the wild-type strain. We predicted transcriptional regulatory networks for these six experiments and evaluated our predictions with publicly available data including a large set of chromatin immunoprecipitation experiments (40) and gene ontology (41) biological process annotations. CARRIE produced cohesive networks that showed significant agreement with experimental results.
MATERIALS AND METHODS
Workflow
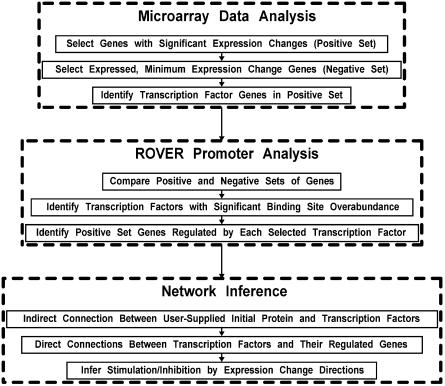
CARRIE is composed of three components: (i) Microarray analysis, (ii) Promoter sequence analysis using ROVER, and (iii) Network inference. Figure 1 summarizes the steps in each of these processes.
Figure 1.
CARRIE workflow. This flowchart demonstrates the three components of the CARRIE network inference tool.
Materials
Six microarray datasets were selected from the SGD Expression Connection (http://db.yeastgenome.org/cgi-bin/SGD/expression/expressionConnection.pl). These represent all available experiments that could be interpreted as two-condition experiments, and were known to involve at least one TF with an annotated binding matrix, which is required by ROVER. Two of the selected data sets have been analyzed by the authors using promoter analysis tools: one (38) with consensus binding sequences, and the other (37) with the ab initio binding site discovery tool MEME (42) in addition to consensus binding sequences.
The promoters for 6221 genes were obtained from SCPD, the Saccharomyces cerevisiae Promoter Database (http://www.cgsigma.schl.org/jian/). The sequences of these promoters were taken to be the 1000 bases upstream of the transcription start sites and were downloaded on 14 April 2003.
The TF binding site matrices were obtained from version 6.4 of TRANSFAC Professional (43). We selected all 43 matrices that were annotated as representing yeast TFs from the binding site matrix description file of TRANSFAC (matrix.dat). Other yeast TFs included in TRANSFAC had descriptions but did not contain binding site matrices.
Microarray analysis
We analyzed six two-color cDNA microarray data sets (Table 1). Each data set represented the differences in gene expression between two conditions. Three data sets compared the wild-type with single TF gene deletion (39). These data sets were also used by Palin et al. to investigate the overlap between genes whose expression changes due to a gene deletion and genes with promoters containing binding sites for a particular TF (33). A single time point, immediately after alpha mating factor stimulation, was taken from a time series data set (36) and used to represent the differences in expression between stimulated and unstimulated cells. Later time points gave similar results (data not shown). The final two data sets represented the gene expression differences between normal growth conditions and either phosphate (38) or zinc starvation (37).
Table 1. Transcription factors identified by CARRIE.
| Perturbation | Known TFsa | Identified TF | Fold changeb | ROVER P valuec | Reference |
|---|---|---|---|---|---|
| Alpha factor stimulation | STE12, MCM1 | STE12 | 3.14 | 7.03E–19 | (36) |
| Deletion of STE12 | STE12 | STE12 | –3.09 | 1.53E–06 | (39) |
| Deletion of GCN4 | GCN4 | GCN4 | –27.86 | 2.68E–40 | (39) |
| AP1 | 1.13 | 6.10E–71 | |||
| TBP | 1.12 | 1.53E–35 | |||
| Deletion of YAP1 | YAP1 | YAP1 | –28.97 | 1.26E–25 | (39) |
| ZAP1 | –1.76 | 4.40E–01 | |||
| ROX1 | –2.17 | 6.20E–01 | |||
| Phosphate starvation | PHO4, PHO2 | PHO4 | 1.2 | 3.06E–17 | (38) |
| Zinc starvation | ZAP1 | ZAP1 | 7.49 | 2.10E–06 | (37) |
| LEU3 | –1.36 | 9.06E–09 |
aTFs previously known to be involved in the response to a given condition or knocked out.
bFold change in mRNA abundance for this TF as measured in the corresponding microarray experiment.
cProbability of observing the overabundance of significant binding sites for this TF, in the promoters of genes in our positive set, by chance, as calculated by ROVER.
Each data set was analyzed to select two equal sized sets of genes. The first set, the positive set, included genes showing significant expression changes between the two conditions being studied. The promoters for the genes in the positive set were all available from SCPD. The second set, the negative set, was composed of genes that showed the least significant changes in expression. For the analyses of two data sets (36,39), absolute fluorescence intensities were available. We limited the negative set to the top 60% of intensity values, roughly indicating expressed genes. We further limited the negative set to those genes with promoter information available in SCPD.
The method for selecting the positive set varied according to the information available for each data source. The TF gene deletion (39) and alpha mating factor induction (36) experiments contained a likelihood of change statistic (P value) for each gene expression ratio, which formed the basis for the positive gene set for these experiments. This measure of confidence took into account the differences in mRNA abundance, error due to a particular instance of background subtraction, and gene-specific error estimated from preliminary experiments. A P value cut-off of 0.005 was selected for the Roberts et al. experiment. A less stringent cut-off of 0.01 was judged to be appropriate for the Hughes et al. experiments. For the phosphate (38) and zinc (37) starvation experiments, the fold change information from the two available replicates formed the basis for the positive set.
ROVER
Given the Position Specific Scoring Matrix (PSSM) of a TF, ROVER calculates a score for each position in an input sequence. This score is the product of the probabilities of observing each base in an L-long subsequence, L being the number of positions in the PSSM. These probabilities are generated from the TF binding matrix obtained from TRANSFAC (43) by dividing the counts for each base in each matrix position by the total number of sequences used to generate the matrix. We followed Laplace’s rule of succession and added one pseudocount to each position in the matrix to avoid multiplying by zero.
The negative set was used to determine the minimum score that would be considered significant in the positive set. This cut-off score, S, was greater than all but 0.1% of the PSSM scores from the sequences in the negative set. In other words, the probability P of a random sequence having a score ≥S was 0.001. ROVER then identified all sub-sequences in the positive set promoters that had scores ≥S. These were returned as significant sites, i.e. potential binding sites for the TF described by the PSSM. ROVER then calculated the probability of observing K or more significant sites in a promoter with N positions using the binomial distribution, assuming that binding sites occur with a probability P = 0.001 (equation 1). The resulting probability of overabundance, P(overabundance), can be interpreted as the likelihood that the TF regulates a particular gene in the positive set.
![]()
A similar calculation was carried out to determine whether binding sites for the TF are significantly overabundant in the entire positive set of promoters. Equation 1 was used, with N set to the sum of the promoter lengths of all sequences in the positive set. The resulting probability can be interpreted as the likelihood that the TF regulates the entire positive set. All binomial distribution calculations were performed using a C function library provided as part of the R statistical language package, version 1.6.2 (http://www.r-project.org).
Recent papers have used similar algorithms to detect the overabundance of binding sites for a particular TF in a group of promoters (14–16). The new features in ROVER include our method for determining the threshold score S and our novel way of selecting the negative set.
Selecting transcription factors
When searching the positive set of genes for TFs, we matched all entries in the microarray data to all TFs in the TRANSFAC database (43), using either standard gene names or SwissProt identifiers, depending on availability.
Evaluation of network cohesiveness
The gene ontology (GO) (41) data were obtained from the Saccharomyces Genome Database (SGD) GO Term Finder (www.yeastgenome.org/cgi-bin/SGD/GO/goTermFinder) on 9 May 2003. We identified the most relevant GO biological process category containing the largest number of genes from each network. The probability of choosing the observed number of genes (or more) from a given category by chance was calculated independently through the hypergeometric distribution. This calculation was performed using the phyper function from the R statistical language package version 1.6 (http://www.r-project.org). It takes into account the total number of genes (G), the number of genes in a particular biological process category (B), the number of genes in the network (T), and the number of genes in the network that are in a particular biological process (I), as described in equation 2.
![]()
RESULTS
Gene expression profiling
Analysis of each microarray data set yielded two equal-sized groups of genes. The first group, the positive set, consisted of genes that showed significant changes in mRNA abundance from one condition to another. The second set of genes, the negative set, consisted of genes that were expressed under both conditions but showed no significant changes in mRNA abundance. The negative sets were used as control sequences, i.e. they did not contain the TF binding sites that were believed to be present in the positive sets. As heterochromatin organization may render the promoter of some genes inaccessible, we required all genes in the negative sets to be expressed.
Identifying transcription factors
Two methods were used to identify the TFs regulating the response to each stimulus. The first method identified TF-encoding genes among the regulated genes from the microarray data. The second method made use of a computer algorithm, ROVER, to identify TFs whose binding sites are overabundant in the promoters of positive set genes. The second method supplemented the first by including TFs that are activated post-transcriptionally.
In five of six stimulation or gene deletion experiments, the first method was sufficient to select the TFs involved in the respective network, according to the original studies (Table 1, all but phosphate starvation). One might suspect that we would fail to identify the first TFs to be activated in a network because the signal transduction pathway would directly modify existing proteins rather than altering mRNA levels. Nonetheless, in two of the three stimulation data sets, the primary TFs, STE12 (36) and ZAP1 (37), also show significant changes in mRNA abundance. Interestingly, both TFs were predicted by ROVER to be auto-regulatory (see below), which is also supported by experimental data in the literature (37,40,44). This increase in mRNA abundance is presumably due to the activation of existing STE12 and ZAP1 proteins. Therefore our first method of TF identification can also succeed in cases where feedback alters mRNA levels for the primary TFs. Our second method, ROVER, can identify TFs that show no detectable changes in expression levels upon stimulation or knockout, as in the case of PHO4 (38).
ROVER
The goal of ROVER is to detect TFs whose binding sites are significantly more abundant in the promoters of the positive set, relative to those in the negative set of genes. Given the binding preferences (PSSMs) of a library of TFs, as in TRANSFAC (43), ROVER can determine both the TFs most likely to regulate the promoters of the relevant genes and the genes likely to be bound by these TFs.
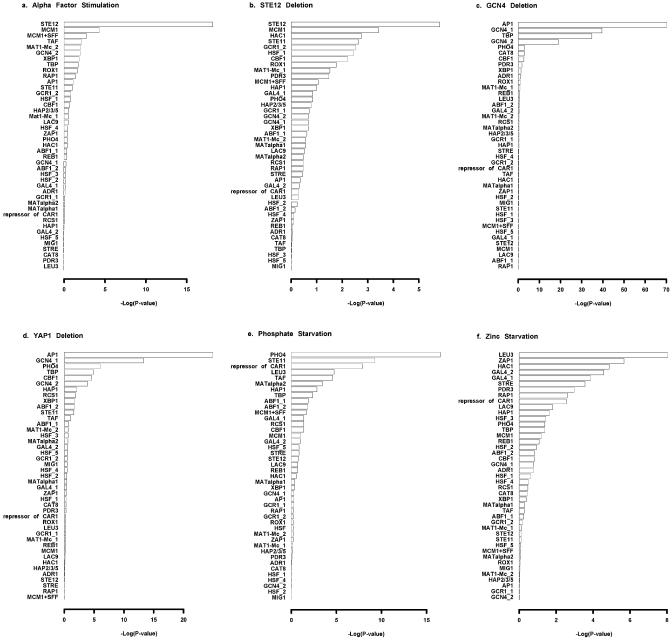
The PSSMs for 43 yeast TFs are available from TRANSFAC (43). Figure 2 shows the overabundance scores [–log(P value), with P value defined by equation 1 in Materials and Methods] for all 43 TFs in the positive sets of promoters, as selected from the six stimulation or knockout experiments. ROVER identifies TFs with significantly over-represented binding sites in all cases. Such TFs are most likely to regulate the groups of genes responsive to the stimulus/knockout. In four of the six conditions, ROVER clearly separates functional TFs from the other TFs. For the alpha mating factor stimulation experiment, the biologically relevant TF, STE12, is the most significant TF, with a P value 14 orders of magnitude more significant than the next TF (Fig. 2a). Seven orders of magnitude separated the regulating TF, PHO4 (38), from the second most significant TF upon phosphate starvation (Fig. 2e). Although PHO2 also regulates responses to phosphate starvation (38), it was not identified because its PSSM was not available from TRANSFAC. The high rankings for both GCN4 and YAP1 (same as AP1) in both the GCN4 and YAP1 knockout experiments may be due to the high degree of similarity in the PSSMs of these two TFs. Figure 2f shows that, in the promoters of genes responsive to zinc starvation, the only TF with a greater overabundance score than ZAP1 is LEU3. ZAP1 is known to regulate gene expression under this condition (37), but the biological relevance of LEU3 is unknown. The PSSMs for ZAP1 and LEU3 have limited similarity.
Figure 2.
Detection of TFs responsible for the gene expression changes in six experimental conditions. Each plot (a–f) depicts –log[P(overabundance)] as defined in equation 1 for each of 43 PSSMs. (a) Alpha Mating Factor Stimulation. STE12 has the most significant overabundance of binding sites, as expected. MCM1, also known to be involved in the response to alpha factor, is represented by the second and third most significant PSSMs. (b) Deletion of STE12. STE12 is the most significant as expected. MCM1 is the second most significant PSSM as in (a). (c) Deletion of GCN4. AP1 (same as YAP1), TBP and GCN4 (there are two TRANSFAC PSSMs for GCN4, indicated as GCN4_1 and GCN4_2) show the most significant P(overabundance) in response to GCN4 deletion. GCN4 and YAP1 have similar binding preferences. (d) Deletion of YAP1. AP1 (YAP1) is clearly the most significant TF. GCN4 is also significant, which may be the result of the similarity between its PSSM and that of AP1. (e) Phosphate starvation. As expected, PHO4 is the most significant TF for this condition. (f) Zinc starvation. ZAP1 is highly significant for this condition, as expected. The biological relevance of LEU3 is unknown.
In summary, ROVER proved to be highly specific in identifying TFs known to respond to the respective stimuli. These predictions were consistent with many of those by the microarray analysis method. In addition, ROVER was able to identify PHO4 as regulating the response to phosphate starvation (38), which was missed by the microarray method.
Finding promoters regulated by the predicted TFs
In addition to predicting the TFs involved in each response, ROVER also determined which of the regulated promoters were likely to be bound by each predicted TF. In this application of ROVER, the P(overabundance) as defined in equation 1 was calculated individually for each promoter in the positive set. P(overabundance) ≤ 0.01 was considered significant.
Inference of transcriptional regulatory networks
After determining (i) the genes with significant expression changes, (ii) the TFs most likely to cause those changes, and (iii) the genes whose promoters are likely to be bound by each of these TFs, we assembled these data to infer a transcriptional regulatory network for each perturbation response.
The network inference proceeds as follows: (i) if the receptor protein responsible for sensing the initial stimulus is known, such as STE2 for alpha mating factor, a link is drawn between the receptor protein and each predicted TF. These links are drawn with a dotted line symbolizing that these connections are likely to be indirect. (ii) Each TF is connected with the genes that it regulates, as predicted by ROVER. These links are drawn as solid lines symbolizing direct regulation of genes by TFs. (iii) The inhibitory/stimulatory relationships between each TF and the genes it regulates are inferred from the direction of gene expression change observed for the regulated gene, and potentially that of the TF, according to the microarray data. For example, if after some stimulus the mRNA abundance for TF A increases, the mRNA abundance for gene 1 decreases, and TF A is shown to bind the promoter of gene 1, then we infer that TF A inhibits the transcription of gene 1.
The above steps were implemented with a computer algorithm called CARRIE. We did not include genes in the network if ROVER predicted them as unlikely to be regulated by the identified TFs in the network, despite significant changes in their mRNA abundance according to the microarray analysis. These genes may be false positives from the microarray analysis or may contain TF binding sites that ROVER could not detect. ROVER could miss a TF if its PSSM were absent from TRANSFAC or if the binding sites in the promoter of the gene were too weak to be detected.
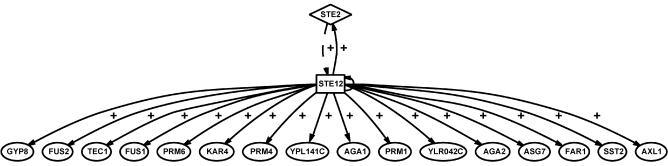
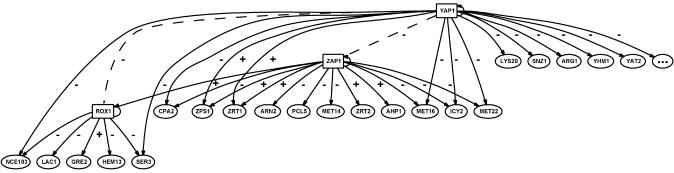
Figures 3 and 4 show two of the networks inferred by CARRIE. The alpha mating factor network shows many known features of the response to this mating factor (Fig. 3). In this network, the TF STE12 up-regulates the expression of its own gene as well as the gene of the alpha factor receptor STE2, forming two positive feedback loops. Additionally, nine of the 18 genes depicted as responsive to stimulation by STE12 are consistent with previous studies on responses to alpha factor stimulation (36). Twelve of the 18 genes are involved in the response to mating factor alpha (mating with conjugation) according to GO (41). The network inferred from STE12 deletion experiment (see Supplemental Material) is highly similar to the network in Figure 3. Since both alpha factor and STE12 knockout target the same TF, this similarity in the inferred network confirms the robustness of CARRIE. Figure 4 shows such a network inferred from the YAP1 deletion experiment. This example demonstrates the potential of discovering more complex regulation using our approach. TFs ROX1 and ZAP1 are expressed at different levels in the wild-type and YAP1Δ strains. CARRIE predicts that ZAP1 and ROX1 are auto-regulatory and that ZAP1 regulates the expression of ROX1. Evidence for the auto-regulation of ZAP1 has been presented previously (37). These relationships indicate that CARRIE can predict multiple levels of regulation.
Figure 3.
Inferred transcriptional regulatory network mediating mating response. These genes have been predicted by CARRIE to respond to alpha mating factor stimulation. Solid arrows represent significant overabundance of binding sites for the TF STE12 (rectangle) in the promoters of the genes. The dotted arrow between STE2 (diamond) and STE12 represents prior knowledge of STE2 as a receptor for the alpha factor stimulus and inferred indirect impacts on downstream TFs. The ‘+’ symbols represent stimulatory relationships.
Figure 4.
Inferred transcriptional regulatory network controlled by YAP1 activity. These genes have been predicted by CARRIE to respond to YAP1 deletion. Solid arrows between the TFs (rectangles) and their target genes represent direct regulation predicted by ROVER. Dotted arrows represent inferred indirect impacts of a known change in the system (ΔYAP1) on downstream TFs. The ‘+’ symbols represent stimulatory relationships and the ‘–’ symbols denote inhibitory relationships. Note that the TF, ZAP1, is shown to directly regulate another TF, ROX1, demonstrating our ability to detect multiple levels of regulation. It was not possible to determine the nature of the regulatory relationship between YAP1 and ZAP1 with the available data. A node with three dots is included to signify that the network has been truncated for display purposes. A full representation of the network is available in the Supplementary Material.
Evaluation of transcription factor binding site predictions
In order to evaluate ROVER’s accuracy in detecting the regulation of a gene by one or more TFs, we compared its predictions to experimental promoter/TF binding data in a global analysis using chromatin immunoprecipitation (ChIP) and microarrays. These data were obtained upon over-expression of TF-myc fusion proteins using an anti-myc antibody (40). The authors compared the relative amount of immunoprecipitated promoter DNA for each of 6270 genes from extracts of S.cerevisiae over-expressing the fusion protein, with the background levels of immunoprecipitated DNA from wild-type cells. This ratio was used to generate a P value of interaction between a given TF and the promoter of a given gene. P values ≤ 0.001 were considered to be significant (40). To judge the similarity between the computational predictions by ROVER and the experimental findings by Lee et al., we determined the intersection between the two data sets for each TF in each of our inferred networks. The statistical significance of the observed intersection was calculated using the hypergeometric distribution (equation 2 in Materials and Methods).
Table 2 indicates that the intersection between the experimental and computational promoter binding results was highly significant except in the case of PHO4, which is involved in the phosphate starvation condition. In this case, zero of the seven promoters identified by ROVER showed significant TF binding in the ChIP data by Lee et al. (40). However, six of these seven predictions were consistent with findings in earlier studies (38,45). For the other five cases, the P values of obtaining the observed computational–experimental intersections were less than 7 × 10–8. The percentage of the genes’ promoters predicted by ROVER to be bound by a given TF was as high as 66% and averaged 35% for the five data sets.
Table 2. Assessment of transcription factor binding predictions.
| Perturbation | Experimentala | ROVERb | Intersectionc | P valued |
|---|---|---|---|---|
| Alpha factor stimulation (STE12) | 56 | 18 | 12 | <3.11E–12 |
| STE12 deletion (STE12) | 56 | 13 | 6 | <3.11E–12 |
| GCN4 deletion (GCN4) | 80 | 61 | 21 | 3.11E–12 |
| YAP1 deletion (YAP1) | 45 | 52 | 6 | 6.34E–08 |
| Phosphate starvation (PHO4) | 62 | 7 | 0e | 1e |
| Zinc starvation (ZAP1) | 24 | 24 | 4 | 2.13E–08 |
aNumber of promoters with significant experimentally measured interactions with the given TF (40).
bNumber of promoters, chosen from the set of genes with significant mRNA abundance changes, with significant binding sites for the given TF, as predicted by ROVER.
cNumber of genes with significant binding shown in vivo and predicted by ROVER.
dProbability of choosing an intersection of this size or larger by chance.
eSix of the seven genes identified by ROVER were also identified as being regulated by PHO4 in the analysis of the microarray data by Ogawa et al. (38). See text for more details.
Evaluation of network cohesiveness
In order to evaluate the quality of our inferred networks, we determined the extent to which the genes in each network were involved in the same biological process as annotated by GO (41). We identified the most relevant GO biological process for the genes in each network using the SGD ‘GO TermFinder’ (see Materials and Methods). The P value of the intersection between the genes in our network and the genes in the selected biological process was calculated using the hypergeometric distribution (equation 2 in Materials and Methods).
The cohesiveness of a network, as measured by the enrichment of genes involved in one biological process, was highly significant for all of our networks (Table 3). On average, 42% of the genes in a particular network were involved in the selected biological process. The probabilities of observing such a large number of genes in these categories, by chance, were extremely small, ranging from 5.3 × 10–8 to 1.1 × 10–11. In five of six cases the most common biological process for the genes in a network was in agreement with previous data for the stimulus or TF (36–39). The significant abundance of genes involved in ‘Amino Acid and Derivative Metabolism’ in the YAP1 deletion network was not directly in line with previous knowledge about the roles of YAP1. This unexpected finding merits further experimental investigation.
Table 3. Assessment of network cohesiveness.
| Perturbation | GO categorya | Genes in GO category | Genes in networkb | Intersectionc | P valued |
|---|---|---|---|---|---|
| Alpha factor stimulation | Conjugation with cellular fusion | 102 | 18 | 12 | 2.19E–11 |
| STE12 deletion | Reproduction | 168 | 13 | 7 | 1.32E–10 |
| GCN4 deletion | Amino acid metabolism | 143 | 61 | 33 | 1.13E–11 |
| YAP1 deletion | Amino acid and derivative metabolism | 155 | 52 | 20 | 1.05E–11 |
| Phosphate starvation | Phosphate transport | 9 | 7 | 2 | 5.33E–08 |
| Zinc starvation | Zinc ion transport | 6 | 24 | 3 | 1.66E–09 |
aThe Gene Ontology Biological Process Category with the largest number of genes from our inferred network.
bNumber of promoters with significant binding sites for the given TF as predicted by ROVER. These promoters were chosen from the set of genes with significant mRNA abundance changes.
cThe number of genes in our network that are annotated as being involved in the given GO biological process category.
dProbability of choosing an intersection of this size or larger by chance.
DISCUSSION
We have presented an integrated method, CARRIE, for automatically inferring the transcriptional portion of a regulatory network starting with global gene expression profiles, and for attaching confidence levels to all connections of the network. The network diagrams generated by CARRIE assist the rapid assimilation of a large volume of data and aid in the design of further experiments. Additionally, the multiple layers of regulation seen in these networks can produce further inferences regarding the temporal relationships of different events in the progression of a signal from cellular receptors to gene expression.
We demonstrated the ability to identify TFs likely to regulate observed changes in mRNA levels in response to a stimulus, either by detection of TF genes with altered expression or by application of our promoter analysis tool ROVER. The two methods are complementary. Previous studies in the inference of response networks (9,34,35) have also shown the validity of identifying TFs by their own changes in expression. However, these studies lacked a method for identification of regulating TFs that are activated by post-transcriptional modifications, which can be detected with our second method ROVER. Recent papers have used similar algorithms to detect the overabundance of binding sites for a particular TF in a group of promoters (14–16). ROVER improves upon these methods with a better choice of the threshold score and a novel way of selecting the negative set. Furthermore, the combination of ROVER with other components of CARRIE is a novel aspect of our approach.
For each perturbation, the TFs predicted by CARRIE were consistent with experimental data in the literature. In five of the six cases, the relevant TFs were identifiable from their own changes in gene expression. Three of these cases were trivial given that the microarray data were obtained from yeast strains in which the genes for the relevant TFs had been deleted. In the other two cases, the stimuli used in the experiments resulted in up-regulation of identified TFs. ROVER provided strong support for both expression-based predictions. In the sixth case, the TF PHO4 was only pinpointed by ROVER, and not by the expression-based method.
Identification of targeted promoters by ROVER is also consistent with global in vivo DNA binding data. The overlap between the ChIP results and our TF binding site predictions was highly significant in five of the six cases (Table 2). The P values of such large overlaps are extremely small (Table 2). ChIP data may not be the ideal gold standard for evaluating the accuracy of ROVER predictions. The rich media growth conditions used in the experiments by Lee et al. (40) may not be compatible with the necessary post-transcriptional activation of certain TFs. For example, PHO4, the critical TF activated by phosphate starvation is phosphorylated under normal growth conditions. Phosphate starvation results in dephosphorylation of PHO4 and its translocation to the nucleus (38). Thus the lack of agreement between the genes we predict to be regulated by PHO4 and the ChIP results is not surprising. Consistent with this interpretation, six of the seven predictions made by ROVER in this case are supported by previous studies (38,45). Another concern with the ChIP data is that the over-expressed TF-myc fusion proteins used in the experiments (40) may display altered DNA binding in vivo. This may also contribute to the discrepancy between ChIP data and ROVER predictions.
Multiple TFs can be identified by ROVER for inclusion in the inferred network. In this study we have selected the TF with the most significant P(overabundance) in each set of regulated promoters. Other TFs that bind a smaller proportion of the promoters in the positive set would also be ranked highly by ROVER. For example, MCM1 was the second most significant TF in regulating the responses to STE12 deletion and alpha factor stimulation. MCM1 is known to assist STE12 in regulating gene expression in response to alpha factor (36). In more complicated networks, subsets of the positive set genes may be involved in multiple pathways. The prioritized TF list and specific TF–promoter relationships provided by ROVER will capture this information. In some cases (e.g. Fig. 2c), a small group of TFs are clearly more significant than all others. In other cases, the cut-offs between significant and insignificant TFs are less clear. Therefore, CARRIE is proposed as a hypothesis generation tool for experimental biologists and we suggest that ROVER’s output be used as a prioritized list to guide further investigations. The method for selecting P(overabundance) cut-offs is currently under development.
The networks generated by CARRIE are cohesive in terms of the biological function of the genes involved. A genetic or environmental stimulus should produce responses specific to that stimulus. We have shown that the networks CARRIE infers contain a highly significant proportion of genes whose GO annotations indicate the involvement in a biological process that is consistent with the original stimulus (Table 3). This is especially indicative of the quality of the networks given the limited amount of such biological process information (9).
One potential circularity problem with our study is that some of the binding sites in the regulated set of promoters may have been utilized to construct the PSSMs of the TFs as supplied by TRANSFAC. This potential overlap of test and training sets might cause ROVER to appear more accurate than it actually is. In our experience, this problem is not as serious as one would expect. For example, five binding sites from three promoters were used to construct the PSSM of STE12. Only STE2 was included in the network and the other two genes were not included because their expression did not change significantly. The binding sites in the 17 other genes in the network were not used by TRANSFAC to construct the PSSM.
CARRIE may not be able to detect all relevant TFs. Its first TF identification method can only detect TFs that are regulated at the level of transcription. Its second method, ROVER, is limited by the completeness of TRANSFAC. Both methods rely on the TF binding matrices in TRANSFAC to determine which genes in the positive set are regulated by the selected TFs. An ab initio binding site discovery tool [e.g. (11,12,18–32)] may serve as a useful supplement to the two methods presented here by identifying binding sites for novel TFs.
In summary, we have presented a new and reliable method that can greatly accelerate the experimental dissection of transcriptional regulatory networks by generating hypotheses about the transcriptional response to stimuli. Starting with microarray data that are both widely available and being generated at an increasingly rapid pace, the methodology described here can be used to quickly infer a large proportion of the total signaling network mediating a response to a cellular stimulus. Our results are provided in an intuitively understandable yet information dense format that permits evaluation of the reliability of each prediction. These networks can be used as road maps for further studies that would not be possible without a global view of the response phenomena.
SUPPLEMENTARY MATERIAL
Supplementary Material is available at NAR Online.
Acknowledgments
ACKNOWLEDGEMENTS
We thank the referees for their thoughtful suggestions. We thank J.Mintseris and C.Haverty for proofreading. This work has been supported in part by NSF grants DBI-0078194, MRI DBI-0116574, IGERT-9870710 and NIH grants P20 GM66401 and 1P20GM066401–01. U.H. was funded in part by R01-CA81157.
REFERENCES
- 1.Liang S., Fuhrman,S. and Somogyi,R. (1998) Reveal, a general reverse engineering algorithm for inference of genetic network architectures. Pac. Symp. Biocomput., 18–29. [PubMed] [Google Scholar]
- 2.Kyoda K.M., Morohashi,M., Onami,S. and Kitano,H. (2000) A gene network inference method from continuous-value gene expression data of wild-type and mutants. Genome Inform. Ser. Workshop Genome Inform., 11, 196–204. [PubMed] [Google Scholar]
- 3.D’Haeseleer P., Liang,S. and Somogyi,R. (2000) Genetic network inference: from co-expression clustering to reverse engineering. Bioinformatics, 16, 707–726. [DOI] [PubMed] [Google Scholar]
- 4.Ihmels J., Friedlander,G., Bergmann,S., Sarig,O., Ziv,Y. and Barkai,N. (2002) Revealing modular organization in the yeast transcriptional network. Nature Genet., 31, 370–377. [DOI] [PubMed] [Google Scholar]
- 5.Rung J., Schlitt,T., Brazma,A., Freivalds,K. and Vilo,J. (2002) Building and analysing genome-wide gene disruption networks. Bioinformatics, 18 (Suppl. 2), S202–210. [DOI] [PubMed] [Google Scholar]
- 6.Soinov L.A., Krestyaninova,M.A. and Brazma,A. (2003) Towards reconstruction of gene networks from expression data by supervised learning. Genome Biol., 4, R6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stuart J.M., Segal,E., Koller,D. and Kim,S.K. (2003) A gene-coexpression network for global discovery of conserved genetic modules. Science, 302, 249–255. [DOI] [PubMed] [Google Scholar]
- 8.Kwon A.T., Hoos,H.H. and Ng,R. (2003) Inference of transcriptional regulation relationships from gene expression data. Bioinformatics, 19, 905–912. [DOI] [PubMed] [Google Scholar]
- 9.Segal E., Shapira,M., Regev,A., Pe’er,D., Botstein,D., Koller,D. and Friedman,N. (2003) Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nature Genet., 34, 166–176. [DOI] [PubMed] [Google Scholar]
- 10.Segal E., Wang,H. and Koller,D. (2003) Discovering molecular pathways from protein interaction and gene expression data. Bioinformatics, 19 (Suppl. 1), I264–I272. [DOI] [PubMed] [Google Scholar]
- 11.Brazma A., Jonassen,I., Vilo,J. and Ukkonen,E. (1998) Predicting gene regulatory elements in silico on a genomic scale. Genome Res., 8, 1202–1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wolfsberg T.G., Gabrielian,A.E., Campbell,M.J., Cho,R.J., Spouge,J.L. and Landsman,D. (1999) Candidate regulatory sequence elements for cell cycle-dependent transcription in Saccharomyces cerevisiae.Genome Res., 9, 775–792. [PMC free article] [PubMed] [Google Scholar]
- 13.Liu R., McEachin,R.C. and States,D.J. (2003) Computationally identifying novel NF-kappa B-regulated immune genes in the human genome. Genome Res., 13, 654–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Aerts S., Thijs,G., Coessens,B., Staes,M., Moreau,Y. and Moor,B.D. (2003) Toucan: deciphering the cis-regulatory logic of coregulated genes. Nucleic Acids Res., 31, 1753–1764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zheng J., Wu,J. and Sun,Z. (2003) An approach to identify over-represented cis-elements in related sequences. Nucleic Acids Res., 31, 1995–2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Elkon R., Linhart,C., Sharan,R., Shamir,R. and Shiloh,Y. (2003) Genome-wide in silico identification of transcriptional regulators controlling the cell cycle in human cells. Genome Res., 13, 773–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sharan R., Ovcharenko,I., Ben-Hur,A. and Karp,R.M. (2003) CREME: a framework for identifying cis-regulatory modules in human-mouse conserved segments. Bioinformatics, 19 (Suppl. 1), I283–I291. [DOI] [PubMed] [Google Scholar]
- 18.Lawrence C.E., Altschul,S.F., Boguski,M.S., Liu,J.S., Neuwald,A.F. and Wootton,J.C. (1993) Detecting subtle sequence signals: a Gibbs sampling strategy for multiple alignment. Science, 262, 208–214. [DOI] [PubMed] [Google Scholar]
- 19.Bailey T.L. and Elkan,C. (1994) Fitting a mixture model by expectation maximization to discover motifs in biopolymers. Proc. Int. Conf. Intell. Syst. Mol. Biol., 2, 28–36. [PubMed] [Google Scholar]
- 20.Roth F.P., Hughes,J.D., Estep,P.W. and Church,G.M. (1998) Finding DNA regulatory motifs within unaligned noncoding sequences clustered by whole-genome mRNA quantitation. Nat. Biotechnol., 16, 939–945. [DOI] [PubMed] [Google Scholar]
- 21.Yada T., Totoki,Y., Ishikawa,M., Asai,K. and Nakai,K. (1998) Automatic extraction of motifs represented in the hidden Markov model from a number of DNA sequences. Bioinformatics, 14, 317–325. [DOI] [PubMed] [Google Scholar]
- 22.Hertz G.Z. and Stormo,G.D. (1999) Identifying DNA and protein patterns with statistically significant alignments of multiple sequences. Bioinformatics, 15, 563–577. [DOI] [PubMed] [Google Scholar]
- 23.Lukashin A.V. and Rosa,J.J. (1999) Local multiple sequence alignment using dead-end elimination. Bioinformatics, 15, 947–953. [DOI] [PubMed] [Google Scholar]
- 24.Tavazoie S., Hughes,J.D., Campbell,M.J., Cho,R.J. and Church,G.M. (1999) Systematic determination of genetic network architecture. Nature Genet., 22, 281–285. [DOI] [PubMed] [Google Scholar]
- 25.Hughes J.D., Estep,P.W., Tavazoie,S. and Church,G.M. (2000) Computational identification of cis-regulatory elements associated with groups of functionally related genes in Saccharomyces cerevisiae.J. Mol. Biol., 296, 1205–1214. [DOI] [PubMed] [Google Scholar]
- 26.Kielbasa S.M., Korbel,J.O., Beule,D., Schuchhardt,J. and Herzel,H. (2001) Combining frequency and positional information to predict transcription factor binding sites. Bioinformatics, 17, 1019–1026. [DOI] [PubMed] [Google Scholar]
- 27.Liu X., Brutlag,D.L. and Liu,J.S. (2001) BioProspector: discovering conserved DNA motifs in upstream regulatory regions of co-expressed genes. Pac. Symp. Biocomput., 127–138. [PubMed] [Google Scholar]
- 28.Thijs G., Lescot,M., Marchal,K., Rombauts,S., De Moor,B., Rouze,P. and Moreau,Y. (2001) A higher-order background model improves the detection of promoter regulatory elements by Gibbs sampling. Bioinformatics, 17, 1113–1122. [DOI] [PubMed] [Google Scholar]
- 29.Horton P. (2001) Tsukuba BB: a branch and bound algorithm for local multiple alignment of DNA and protein sequences. J. Comput. Biol., 8, 283–303. [DOI] [PubMed] [Google Scholar]
- 30.Keich U. and Pevzner,P.A. (2002) Finding motifs in the twilight zone. Bioinformatics, 18, 1374–1381. [DOI] [PubMed] [Google Scholar]
- 31.Buhler J. and Tompa,M. (2002) Finding motifs using random projections. J. Comput. Biol., 9, 225–242. [DOI] [PubMed] [Google Scholar]
- 32.Frith M.C., Hansen,U., Spouge,J.L. and Weng,Z. (2004) Finding functional sequence elements by multiple local alignment. Nucleic Acids Res., 32, 189–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Palin K., Ukkonen,E., Brazma,A. and Vilo,J. (2002) Correlating gene promoters and expression in gene disruption experiments. Bioinformatics, 18 (Suppl. 2), S172–180. [DOI] [PubMed] [Google Scholar]
- 34.Birnbaum K., Benfey,P.N. and Shasha,D.E. (2001) cis element/transcription factor analysis (cis/TF): a method for discovering transcription factor/cis element relationships. Genome Res., 11, 1567–1573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhu Z., Pilpel,Y. and Church,G.M. (2002) Computational identification of transcription factor binding sites via a transcription-factor-centric clustering (TFCC) algorithm. J. Mol. Biol., 318, 71–81. [DOI] [PubMed] [Google Scholar]
- 36.Roberts C.J., Nelson,B., Marton,M.J., Stoughton,R., Meyer,M.R., Bennett,H.A., He,Y.D., Dai,H., Walker,W.L., Hughes,T.R. et al. (2000) Signaling and circuitry of multiple MAPK pathways revealed by a matrix of global gene expression profiles. Science, 287, 873–880. [DOI] [PubMed] [Google Scholar]
- 37.Lyons T.J., Gasch,A.P., Gaither,L.A., Botstein,D., Brown,P.O. and Eide,D.J. (2000) Genome-wide characterization of the Zap1p zinc-responsive regulon in yeast. Proc. Natl Acad. Sci. USA, 97, 7957–7962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ogawa N., DeRisi,J. and Brown,P.O. (2000) New components of a system for phosphate accumulation and polyphosphate metabolism in Saccharomyces cerevisiae revealed by genomic expression analysis. Mol. Biol. Cell, 11, 4309–4321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hughes T.R., Marton,M.J., Jones,A.R., Roberts,C.J., Stoughton,R., Armour,C.D., Bennett,H.A., Coffey,E., Dai,H., He,Y.D. et al. (2000) Functional discovery via a compendium of expression profiles. Cell, 102, 109–126. [DOI] [PubMed] [Google Scholar]
- 40.Lee T.I., Rinaldi,N.J., Robert,F., Odom,D.T., Bar-Joseph,Z., Gerber,G.K., Hannett,N.M., Harbison,C.T., Thompson,C.M., Simon,I. et al. (2002) Transcriptional regulatory networks in Saccharomyces cerevisiae.Science, 298, 799–804. [DOI] [PubMed] [Google Scholar]
- 41.Ashburner M., Ball,C.A., Blake,J.A., Botstein,D., Butler,H., Cherry,J.M., Davis,A.P., Dolinski,K., Dwight,S.S., Eppig,J.T. et al. The Gene Ontology Consortium (2000) Gene ontology: tool for the unification of biology. Nature Genet., 25, 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bailey T.L. and Elkan,C. (1995) Unsupervised learning of multiple motifs in biopolymers using expectation maximization. Machine Learning, 21, 51–80. [Google Scholar]
- 43.Wingender E., Chen,X., Hehl,R., Karas,H., Liebich,I., Matys,V., Meinhardt,T., Pruss,M., Reuter,I. and Schacherer,F. (2000) TRANSFAC: an integrated system for gene expression regulation. Nucleic Acids Res., 28, 316–319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ren B., Robert,F., Wyrick,J.J., Aparicio,O., Jennings,E.G., Simon,I., Zeitlinger,J., Schreiber,J., Hannett,N., Kanin,E. et al. (2000) Genome-wide location and function of DNA binding proteins. Science, 290, 2306–2309. [DOI] [PubMed] [Google Scholar]
- 45.Oshima Y. (1997) The phosphatase system in Saccharomyces cerevisiae.Genes Genet. Syst., 72, 323–334. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.