Abstract
This paper describes a calorimetric study of the association of a series of seven fluorinated benzenesulfonamide ligands (C6HnF5-nSO2NH2) with bovine carbonic anhydrase II (BCA). Quantitative structure-activity relationships between the free energy, enthalpy, and entropy of binding and pKa and log P of the ligands allowed the evaluation of the thermodynamic parameters in terms of the two independent effects of fluorination on the ligand: its electrostatic potential and its hydrophobicity. The parameters were partitioned to the three different structural interactions between the ligand and BCA—the ZnII cofactor-sulfonamide bond (~65% of the free energy of binding), the hydrogen bonds between the ligand and BCA (~10%), and the contacts between the phenyl ring of the ligand and BCA (~25%). Calorimetry revealed that all of the ligands studied bind in a 1:1 stoichiometry with BCA; this result was confirmed by 19F NMR spectroscopy and by X-ray crystallography (for complexes with human carbonic anhydrase II).
Introduction
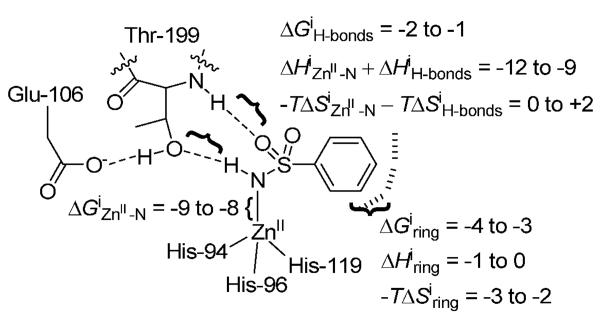
The primary motivation of this paper was to understand the interaction of arylsulfonamides with carbonic anhydrase II (CA, E.C. 4.2.1.1). Arylsulfonamides are the highest affinity and most widely used inhibitors for CA.[1–4] The structure of CA bound to arylsulfonamides has been defined in detail using X-ray crystallography.[1, 2, 5] CA binds most arylsulfonamides with the same geometry: the ionized sulfonamide nitrogen, ArSO2NH−, binds to the ZnII cofactor (with a free energy of ΔGiZn2+ −N)[6], one sulfonamide oxygen and the sulfonamide NH engage in hydrogen bonds with residues of the active site of CA (with a free energy of ΔGiH-bonds), and the aryl ring interacts directly with a hydrophobic pocket of the enzyme (with a free energy of ΔGiring) (Figure 1). While computational approaches have provided rough estimates of the free energies of these interactions,[7] experimental estimates of the free energies of these interactions are still not available.[1] In addition, previous experimental and computational studies have not partitioned the thermodynamic parameters of enthalpy and entropy to the structural interactions between arylsulfonamide and CA.[1, 4]
Figure 1.
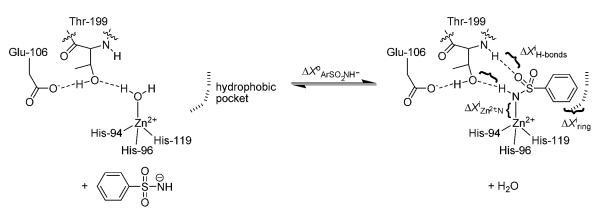
Association of benzenesulfonamide ligands with carbonic anhydrase (CA). The diagram shows the equilibrium between the water-bound form of the enzyme (CA-ZnII-OH2+) and the arylsulfonamide-bound form. We express the thermodynamic parameters (free energy: X = G, enthalpy: X = H, and entropy: X = S) for the association of the arylsulfonamide anion with CA-ZnII-OH2+ in terms of five contributions, as follows: ΔX°ArSO2NH− = ΔXiZn2+−N + ΔXiH-bonds + ΔXiring + ΔX°trans+rot,ArSO2NH− − ΔX° trans+rot,H2O. The terms with superscripts of i are the intrinsic energies for structural interactions between ligand and CA (defined in the text) relative to the reference state of CA-ZnII-OH2+; they are energies for the different interactions in the absence of losses in translational and rotational entropy.[6] ΔX°trans+rot,ArSO2NH− and ΔX°trans+rot,H2O are the translational and rotational costs (primarily, in entropy)[8, 9] of complexation with CA of the arylsulfonamide anion and of the water. We make the assumption that ΔX°trans+rot,ArSO2NH− ≈ ΔX°trans+rot,H2O because of the weak (logarithmic) dependence of this primarily entropic term on molecular-weight.[8] This assumption gives ΔX°ArSO2NH− = ΔXiZn2+−N + ΔXiH-bonds + ΔXiring.
The present study attempts to address these deficiencies in the literature by examining the thermodynamics of binding (free energy, enthalpy, and entropy) of fluorinated benzenesulfonamides (compounds of the form C6HnF5-nSO2NH2) to bovine carbonic anhydrase II (BCA). These results can be used to partition the thermodynamics of binding to the structural interactions between ligand and CA because fluorination of the phenyl ring involves only small changes in size and shape of the ligands. This study, thus, presents a useful perturbational approach to understanding the binding of benzenesulfonamide itself. The disadvantage of a perturbational approach is that the variations in both structures and thermodynamic parameters are small, the data are noisy, and the conclusions are neither highly accurate nor amenable to reliable extrapolation to ligands with significantly different core structures.
A second motivation of this paper was to understand the use of fluorine in drug design. Fluorine has been used extensively in ligands that bind tightly to proteins or that limit metabolism in useful ways.[10, 11] The physical properties of fluorine that have contributed to its use in medicinal chemistry include: its slightly larger (~23% greater Bondi's van der Waals radius, ~27% greater C-X covalent bond length, and ~50% greater surface area for −CX3 groups) size than hydrogen, its high electronegativity (which significantly alters the inductive and electronic properties of fluorinated ligands compared to their non-fluorinated analogs), and its low polarizability.[11, 12] Further, fluorocarbons adopt significantly different conformations than hydrocarbons, and are generally believed to be less polarizable and “more hydrophobic” than the analogous hydrocarbons.[11]
As an aryl subsitituent, fluorine significantly perturbs the electronic properties of the ring. For instance, the quadrupole moment of hexafluorobenzene is equal in magnitude but opposite in sign to that of benzene, and thus the interactions involving the face of hexafluorobenzene, which is partially positively charged, are different than those of benzene, which is partially negatively charged.[11, 13] These myriad effects of fluorine make a clear understanding of the affinity of fluorinated ligands for proteins difficult, and even more difficult than understanding the affinity of their non-fluorinated analogs (the affinity of non-fluorinated ligands for proteins is, to begin with, not well-understood)[14, 15]. Not being able to rationalize why fluorination increases the affinity of ligands makes the rational design of fluorinated ligands for target proteins particularly challenging.
A number of previous studies have examined the binding of fluorinated arylsulfonamide ligands to CA.[12, 16–20] Gao et al. studied the binding of para-substituted benzenesulfonamides with linear hydrocarbon and fluorocarbon tails (p-H2NSO2C6H4CONH(CX2)n-1CX3 where X = H or F and n = 1–6) to BCA.[12] As the length of the tails increased (as n increased from 1 to 6), the values of Kd decreased by a factor of 5 for the hydrocarbon series, and by a factor of 15 for the fluorocarbon series. The contribution of hydrophobicity to affinity for BCA of the two series was the same when normalized to the molecular surface area (calculated by taking into account the larger size of fluorine than hydrogen) of the ligands. The affinities of the two series for BCA were not the same, however: the fluorocarbon ligands bound tighter (by ~0.7 kcal mol−1) than the analogous hydrocarbon ligands because of a hydrogen bond between the carboxamide of the ligand and residues of the active site of CA. This hydrogen bond should be stronger for the fluorocarbon ligands than for the hydrocarbon ligands.
Kim et al. examined the binding of ligands of structure p-H2NSO2C6H4CONHCH2C6HnF5-n (where n = 0–5) to wild-type HCA II and to a mutant of HCA II where Phe-131 was mutated to Val.[16] While the range in values of Kd obs of these ligands for the two proteins was small (factor of <20), the investigators were able to construct a linear free-energy relationship (with R2 = 0.83) between affinity and the distinct electrostatic interactions between CA and the secondary (fluorinated) phenyl ring of the ligands. They determined that no single interaction dominated affinity for all of the ligands in the series, and suggested that the multipole-multipole interactions contributed differently to affinity of the different ligands. Their study emphasized that the effect of fluorination of the ligand on its affinity for CA is quite complicated, and that a number of effects compensate.
Supuran and coworkers studied the activity of arylsulfonamide ligands appended with fluoroalkyl tails or fluoroaryl rings.[17] Several of these ligands had high affinity (~nM) towards HCA II and bovine carbonic anhydrase IV (a membrane-bound, medically relevant isozyme of CA)[1, 2, 4], moderate water solubility, and high activity in a rabbit model of glaucoma. These results suggest that fluorinated sulfonamides could be effective as therapeutic inhibitors of CA, but do not reveal the theoretical basis for this activity.
Gerig and coworkers studied the solution-phase binding of fluorinated benzenesulfonamides to HCA I and II using 19F NMR spectroscopy.[18–20] Their results suggested a stoichiometry of binding of 2:1 for 2-fluorobenzenesulfonamide (2-FBS), 3-fluorobenzenesulfonamide (3-FBS), and 4-fluorobenzenesulfonamide (4-FBS) to wild-type HCA I and II,[19, 20] and were in stark contrast to the 1:1 stoichiometry generally observed for the binding of all other arylsulfonamides to wild-type CA. Reconciling this conflict was a third motivation for our work. Accordingly, we observe 1:1 binding for all of the fluorinated benzenesulfonamides (including 4-FBS) in this study using biophysical and X-ray crystallographic techniques (Figure 2).
Figure 2.
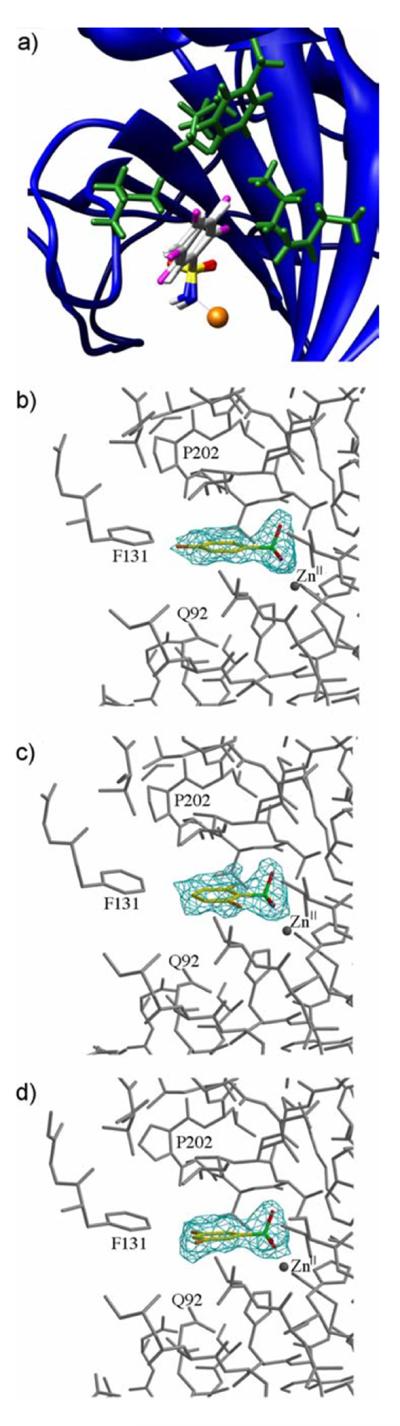
a) Overlay of binding of 4-fluorobenzenesulfonamide (4-FBS), 2,6-difluorobenzenesulfonamide (2,6-FBS), and 3,5-difluorobenzenesulfonamide (3,5-FBS), to human carbonic anhydrase II (HCA). The ligands have been rendered as ball-and-stick models with the fluorines shown in magenta; the phenyl rings of the ligands bind with an invariant orientation (they are co-planar). HCA has been depicted as a blue ribbon diagram with the hydrophobic residues that are within van der Waals contact distance of the ligands displayed in green (Gln-92, Val-121, Phe-131, Leu-141, and Leu-198). The protein backbone and ZnII cofactor (orange sphere) from only one structure is shown to facilitate visualization (the heavy-atom RMSD of the side chains and backbone atoms of the protein in the different structures was < 0.61 Å). b)-d) Difference electron density maps (contoured at 2.2σ) of HCA II complexed with b) 4-FBS, c) 2,6-FBS, and d) 3,5-FBS, calculated with Fourier coefficients |Fo| - |Fc| and phases derived from each final model less the ligand and active-site solvent molecules. This figure was prepared with Bobscript and Raster3D.[22]
Experimental Design
The system of BCA and substituted benzenesulfonamides is the simplest one that we know for studying protein-ligand interactions; this system serves as a model to study the binding of structurally related ligands to a structurally well-defined protein.[1, 4, 5, 21] BCA binds most substituted benzenesulfonamides with the same orientation. This conserved mode of binding has allowed the attribution of binding energies to particular interactions between the ligand and protein and, thus, to structural components of the ligand (for instance, a para substituent on the phenyl ring)[12, 23, 24], and has enabled the physical-organic study of the affinity of arylsulfonamide ligands for CA.[1]
In the work described in this paper, fluorinated benzenesulfonamides constitute a series of simple ligands where the contribution of fluorine to the electrostatic potential and to the hydrophobicity of the ligand, and the manifestations of these effects on affinity for BCA, can be easily separated. The conserved orientation of substituted benzenesulfonamides complexed with HCA II allows the attribution of differences in the thermodynamics of association of the different fluorinated benzenesulfonamides with BCA to differences in the strengths of conserved interactions between BCA and ligand (Figure 1), and not to new, structurally different interactions in each case.
We used isothermal titration calorimetry to follow the binding of the ligands to BCA because it allows the direct measurement of the dissociation constant (Kdobs), enthalpy of binding (ΔH°), and stoichiometry of binding from a single experiment, and the entropy of binding (ΔS°) through the thermodynamic relation (ΔG° = ΔH° − TΔS°).[24, 25] Our results demonstrate that ~65% (~ −8 kcal mol−1) of the free energy of binding is contributed by the ZnII-N bond, ~10% (~ −1 kcal mol−1) by the hydrogen-bond network, and ~25% (~ −3.5 kcal mol−1) by hydrophobic contacts between the phenyl ring and CA.
Given the small range in the thermodynamics of association (values of Kd vary by less than a factor of 10 across the series, and ΔH° and TΔS° by 2.5–3 kcal mol−1), we cannot generalize the quantitative aspects of our conclusions to the binding of arylsulfonamides more structurally complex than fluorinated benzenesulfonamides to CA. We believe, however, that our conclusions are generally qualitatively applicable.
Thermodynamic Framework and Background
The variation of the dissociation constant (Kdobs) with pH for all CA-sulfonamide complexes for which these data are reported gives a bell-shaped curve bounded by two values of pKa—the pKa for the acidic limb (~6.9) is associated with an ionizable group of the enzyme (most likely the ZnII-bound water: ZnII-OH2+ ⇆ ZnII-OH + H+), and the pKa for the basic limb is equal to the pKa of the sulfonamide.[1, 26, 27]
Although in principle an exceptionally simple process, the mechanism of interaction of CA with sulfonamides is still a matter of debate: both displacement of the ZnII–bound water by the sulfonamide anion [Eq. (1)], and displacement of the ZnII–bound hydroxide by the neutral sulfonamide [Eq. (2)], are consistent with the experimental data:
| (1) |
| (2) |
While King and Burgen suggested that the mechanism involves three states (with an intermediate state that is weakly populated and has only hydrophobic contacts between CA and the ligand),[27, 28] the details of the mechanism do not concern us here because we are only interested in the equilibrium between the separated reactants and the end-product complex, and because no intermediate in the pathway has been detected experimentally.[28] We only want to remove the dependence of the equilibrium thermodynamic parameters on the fractions of arylsulfonamide and CA that are present in their active, charged forms (see next section).
We adopt the interaction of the sulfonamide anion (ArSO2NH−) with the ZnII-bound water form of CA (CA-ZnII-OH2+) [Eq. (1); Figure 1] as the standard reaction for the interpretation of thermodynamics because we believe that this is the most likely mechanism.[1]
Results and Discussion
X-ray Crystal Structures of Complexes of Fluorinated Benzenesulfonamides with HCA II
The X-ray crystal structures of HCA II complexed with 4-FBS, 2,6-difluorobenzenesulfonamide (2,6-FBS), and 3,5-difluorobenzenesulfonamide (3,5-FBS) demonstrate an invariant orientation of the sulfonamide group and phenyl ring for these ligands (Figure 2a). Table S.1 shows the data collection and refinement statistics for these structures. Electron density maps of each CA-ligand complex conclusively demonstrate a ligand to CA stoichiometry of 1:1 (Figure 2b–d). The ionized sulfonamide NH group of each ligand coordinates to the active site ZnII cofactor, and donates a hydrogen bond to Thr-199, as in the structures of other substituted benzenesulfonamides complexed with HCA II.[1, 2, 5] Given that the active site architectures of HCA II and BCA are identical, we can interpret the differences in the thermodynamics of association of the fluorinated benzenesulfonamides with BCA in terms of differences in the strengths of the same structural interactions between CA and ligand (Figure 1).
Calculation of Thermodynamic Parameters for the Standard Reaction of the Binding of Sulfonamide Anions to ZnII-OH2+ Form of CA [Eq. (1)]
We use Scheme 1 in order to calculate thermodynamic parameters for the reaction specified in Eq. (1). Eq. (3) shows the fractions (θ) of arylsulfonamide as the anion (ArSO2NH−) and of free (non-arylsulfonamide bound) CA as the ZnII-bound water form (CA-ZnII-OH2+):
| (3a) |
| (3b) |
Here “pKa(ArSO2NH2)” is the acid dissociation constant for the neutral sulfonamide (referred to in the remainder of this paper as “pKa”), “pKa(CA-ZnII-OH2+)” is the acid dissociation constant of the ZnII-bound water, and “pH” is the pH of the solution.
Scheme 1.
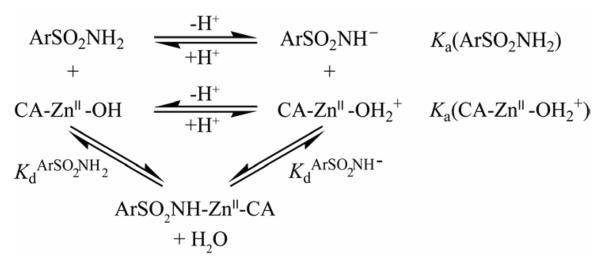
Equilibria for the association of arylsulfonamide ligands (ArSO2NH2/ArSO2NH−) with carbonic anhydrase (CA-ZnII-OH2+/CA-ZnII-OH).
Eqs. (4) and (5), derived in the Supporting Information section, give the dissociation constant (KdArSO2NH−) and enthalpy (ΔH°ArSO2NH−) for the association of ArSO2NH− with CA-ZnII-OH2+ (Scheme 1; Figure 1). Khalifah et al. undertook a similar analysis in their examination of the association of nitrogen heterocycles with HCA I.[29]
| (4) |
| (5) |
Here Kdobs is the experimentally observed dissociation constant of CA-sulfonamide complex, ΔH°obs is the experimentally observed enthalpy of binding of sulfonamide to CA, ΔH°ion,ArSO2NH2 is the enthalpy of ionization of neutral sulfonamide in solution, ΔH°ion,CA−ZnII−OH2+ is the enthalpy of ionization of CA-ZnII-OH2+ in solution, and ΔH°ion,buffer is the enthalpy of ionization in solution of the buffer (here, H2PO4− with ΔH°ion,buffer = 0.86 kcal mol−1).[30]
By titrating the benzenesulfonamides with sodium hydroxide, we measured values of pKa by following the pH, and values of ΔH°ion,ArSO2NH2 by measuring the heat released using isothermal titration calorimetry (Table 1; see Experimental Section). These procedures generate values in good agreement with those in the literature. Table 1 also lists values of pKa and enthalpy of ionization for CA-ZnII-OH2+ that have been reported in the literature.[1, 31, 32]
Table 1.
Physical properties of fluorinated benzenesulfonamides and the ZnII-bound water of BCA (CA-ZnII-OH2+).
| Abbreviation | Titratable molecule | pKa | ΔH°ion (kcal mol−1) | p [a] | Log P[a] |
|---|---|---|---|---|---|
| BS | Benzenesulfonamide | 10.1[b],[c] | 9.10 ± 0.01[d],[e] | 1.94 ± 0.03[f] | 0.29 ± 0.01 |
| 2-FBS | 2-fluorobenzenesulfonamide | 9.6[b] | 7.89 ± 0.03[d] | 1.82 ± 0.04 | 0.26 ± 0.01 |
| 3-FBS | 3-fluorobenzenesulfonamide | 9.7[b] | 8.47 ± 0.06[d] | 4.06 ± 0.12 | 0.61 ± 0.01 |
| 4-FBS | 4-fluorobenzenesulfonamide | 10.0[b] | 8.58 ± 0.03[d] | 3.42 ± 0.14 | 0.53 ± 0.02 |
| 2,6-FBS | 2,6-difluorobenzenesulfonamide | 9.1[b] | 7.81 ± 0.14[d] | 1.45 ± 0.04 | 0.16 ± 0.01 |
| 3,5-FBS | 3,5-difluorobenzenesulfonamide | 9.4[b] | 8.58 ± 0.04[d] | 9.0 ± 0.3 | 0.95 ± 0.02 |
| pentaFBS | Pentafluorobenzenesulfonamide | 8.2[b],[g] | 7.60 ± 0.03[d] | 11.1 ± 0.2 | 1.05 ± 0.01 |
| CA-ZnII-OH2+ | ZnII-water of BCA | 6.9[h] | 6.90[i] | – | – |
Partition coefficient between octanol and sodium phosphate buffer pH 7.5 determined spectrophotometrically.[12] Uncertainties are the maximum deviation of a single measurement from the average of three independent measurements.
Determined potentiometrically (ionic strength, I = 0.052 M with sodium chloride). Uncertainties from this procedure are estimated to be 0.2 pH units.[12]
Literature value of 10.1.[28]
Estimated by isothermal titration calorimetry by titration of sulfonamide with sodium hydroxide at pH 9.6 (near the pKa) with I = 0.052 M with sodium chloride. Uncertainties represent the standard deviation of the mean from 7–9 injections.
Literature value of 8.3 kcal mol−133.
Literature value of 1.63.[28]
Literature value of 8.05.[34]
Estimated from the pH-dependence of BCA-catalyzed hydration of carbon dioxide.[31] We estimate an uncertainty of 0.05 pH unit from other reported values for this parameter.[1]
Estimated from the temperature dependence of the pKa of BCA-catalyzed hydrolysis of p-nitrophenylacetate.[32]
Table 2 lists the thermodynamic parameters that we observed experimentally (Kdobs, ΔH°obs, and −TΔS°obs), and those that we have calculated for the binding of ArSO2NH− to CA-ZnII-OH2+ (KdArSO2NH−, ΔH°ArSO2NH−, and −TΔS°ArSO2NH−). In our analysis, we focus on the calculated thermodynamic parameters (for ArSO2NH−) because they are independent of the fractions of arylsulfonamide and CA in the active forms [specified in Eq. (1)], and thus allow us to ascribe differences in the thermodynamics of binding of the ligands to structural interactions between the ligands and CA.
Table 2.
Thermodynamic parameters for the observed binding of fluormated benzenesulfonamides to BCA, and for the binding of the sulfonamide anion (ArSO2NH−) to the ZnII-bound water (CA-ZnII-OH2+) form of the enzyme [calculated using Eqs. (3) and (4)].
| Ligand | Kdobs[a] (nM) | ΔH°obs[a] (kcal mol−1) | −TΔS°obs[b] (kcal mol−1) | KdArSO2NH−[c] (nM) | ΔH°ArSO2NH−[d] (kcal mol−1) | −TΔS°ArSO2NH−[e] (kcal mol−1) |
|---|---|---|---|---|---|---|
| BS | 730 ± 60 | −9.0 ± 0.5 | +0.7 ± 0.6 | 0.34 ± 0.18 | −12.3 ± 0.6 | −0.6 ± 0.6 |
| 2-FBS | 230 ± 20 | −10.2 ± 0.2 | +1.1 ± 0.2 | 0.39 ± 0.18 | −12.2 ± 0.2 | −0.6 ± 0.4 |
| 3-FBS | 75 ± 8 | −9.0 ± 0.2 | −0.7 ± 0.2 | 0.11 ± 0.05 | −11.6 ± 0.2 | −2.0 ± 0.4 |
| 4-FBS | 590 ± 40 | −7.8 ± 0.5 | −0.7 ± 0.5 | 0.4 ± 0.2 | −10.6 ± 0.5 | −2.2 ± 0.6 |
| 2,6-FBS | 190 ± 14 | −9.4 ± 0.4 | +0.2 ± 0.4 | 1.0 ± 0.5 | −11.2 ± 0.5 | −1.1 ± 0.6 |
| 3,5-FBS | 57 ± 12 | −9.6 ± 0.3 | −0.3 ± 0.3 | 0.16 ± 0.08 | −12.3 ± 0.3 | −1.1 ± 0.5 |
| pentaFBS | 25 ± 4 | −8.9 ± 0.1 | −1.4 ± 0.1 | 0.8 ± 0.4 | −9.5 ± 0.5 | −2.9 ± 0.5 |
Uncertainties are the maximum deviation of one measurement from the average of three independent measurements.
Uncertainties were estimated by propagating errors in Kdobs and ΔH°obs.
Calculated using Eq. (3). Uncertainties were estimated by propagating the errors in all of the parameters in Eq. (3) assuming that they were independent.
Calculated using Eq. (4). Uncertainties were estimated by propagating the errors in all of the parameters in Eq. (4) (except for ΔH°ion,buffer) assuming that they were independent.
Uncertainties were estimated by propagating errors in KdArSo2NH− and ΔH°ArSo2NH−.
Quantitative Structure-Activity Relationships to Determine the Importance of Lewis Basicity and Hydrophobicity of the Fluorinated Benzenesulfonamide Anion
While the ranges in values of the thermodynamic parameters are small (ΔG°ArSO2NH− varies by 1.3 kcal mol−1, ΔH°ArSO2NH− by 2.8 kcal mol−1, and −TΔS°ArSO2NH− by 2.3 kcal mol−1; Table 2), we believe that the application of a quantitative structure-activity relationship (QSAR) to the data clarifies the importance of the different structural interactions between these ligands and BCA. The narrow ranges do not, however, allow us to generalize our results to the association of structurally complex arylsulfonamides with CA. Similar QSAR analyses have been reported by other investigators, but they have not examined the thermodynamic parameters for the association of the arylsulfonamide anion, ArSO2NH−, with CA-ZnII-OH2+.[4, 35]
As discussed in the Introduction, the important interactions between ArSO2NH− and CA are: (i) the bond between the arylsulfonamide nitrogen and ZnII cofactor, (ii) the hydrogen bonds between the –SO2NH group and residues of the active site, and (iii) the contacts between the aryl ring of the arylsulfonamide and the hydrophobic pocket of CA (Figures 1 and 2). The first two of these interactions should be influenced by the Lewis basicity of ArSO2NH−, and thus by the pKa of ArSO2NH2 (assuming a Brønsted relationship). The third interaction should be influenced by the hydrophobicity of the ligand, estimated by the logarithm of the partition coefficient (log P) of the ligand between octanol and sodium phosphate buffer pH 7.5. We estimated values of log P by UV spectroscopy (Table 1) as previously described.[12] We determined that pKa and log P do not correlate with one another (R2 = 0.28).
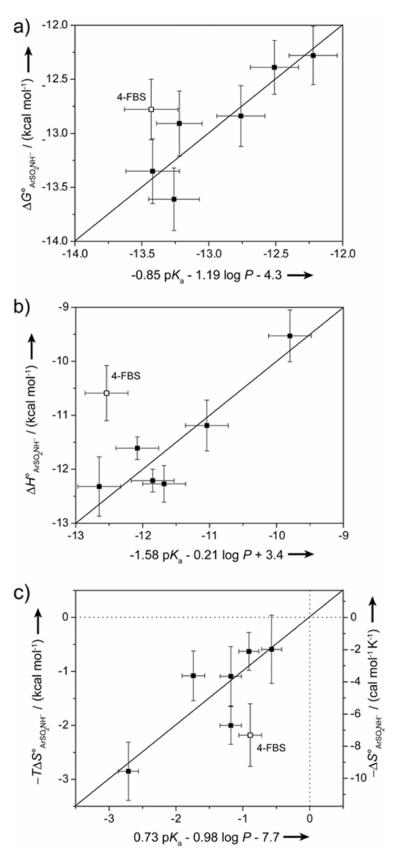
We constructed QSARs between ΔG°ArSO2NH− (KdArSO2NH−), ΔH°ArSO2NH−, or −TΔS°ArSO2NH− and pKa and log P of the benzenesulfonamide ligands in order to determine the relative importance of electrostatic (depending on pKa) and hydrophobic (depending on log P) interactions to the free energy, enthalpy, and entropy of binding (Figure S.1). The fits that we obtained were only modest for all three thermodynamic parameters (R2 = 0.46–0.63). In order to account for the possibility that the set of ligands did not interact in a constant way with CA, and that this inhomogeneity resulted in the poor fits, we also constructed QSARs in which we omitted one of the ligands from the analysis (considering it as an outlier). The best fits that we obtained for ΔG°ArSO2NH− (KdArSO2NH−) and ΔH°ArSO2NH− involved omitting 4-FBS (R2 = 0.83 for both; Figure 3a,b). The best fit for −TΔS°ArSO2NH− involved omitting 3,5-FBS (R2 = 0.83; data not shown), but omitting 4-FBS also gave a reasonable QSAR to the −TΔS°ArSO2NH− data (R2 = 0.70; Figure 3c). As a simplifying approximation, we assume that 4-FBS interacts with CA in a way that is different from that used by the other ligands, and consider it in a separate section below.
Figure 3.
Quantitative Structure-Activity Relationships (QSARs) between a) ΔGArSO2NH−, b) ΔH°ArSO2NH−, and c) −TΔS°ArSO2NH− and pKa and log P for fluorinated benzenesulfonamides. QSARs are shown in which the data for 4-fluorobenzenesulfonamide (4-FBS; shown as open squares) was omitted; QSARs to data for all of the ligands are shown in Figure S.1. The y-error bars are uncertainties described in Table 2, and the x-error bars were obtained by propagating uncertainties in pKa and log P. The horizontal and vertical dotted lines in c) separate favorable (−TΔS° < 0) from unfavorable (−TΔS° > 0) entropy of binding.
Eqs. (6–8) give the QSARs obtained when 4-FBS was omitted from the optimization. We discuss each of the equations, and its implications on the nature of the interactions between the benzenesulfonamide ligands and CA, in turn in the following sections.
| (6) |
| (7) |
| (8) |
While the uncertainties in the parameters are relatively large, we believe that we can cautiously use the QSARs to partition the free energy, enthalpy, and entropy to the structural interactions between CA and ligand in a semi-quantitative way.
Electrostatic Effects of the Benzenesulfonamide Ligands (ZnII-N Bond and Hydrogen-Bond Network) Primarily Influence the Enthalpy of Binding (ΔH°ArSO2NH−)
Eq. (7) shows that ΔH°ArSO2NH− is more sensitive to a change in pKa (electrostatic effects) than to the same change in log P (hydrophobic effects). The weak influence of log P is consistent with the widely-held belief that hydrophobic interactions in protein-ligand binding are manifested as the “hydrophobic effect”, and appear primarily in the entropy of binding with an enthalpy of binding near zero at T = 298 K.[36]
The equilibrium shown in Figure 1 allows the partitioning of ΔH°ArSO2NH− into the structural, component interactions between ArSO2NH− and CA [Eq. (9)].
| (9) |
The first two terms (ΔHiZnII−N and ΔHiH-bonds) are expected to depend only on pKa, and the third term (ΔHiring), which represents van der Waals contacts (induced dipole-induced dipole forces) between the phenyl ring and active site residues of CA, on log P as in Eq. (10).
| (10a) |
| (10b) |
We have disregarded possible interactions between polar and charged residues of the active site of CA and the multipoles (quadrupole and dipole) of the fluorinated rings of the ligands because X-ray crystal structures reveal that there are no such amino acid residues of CA in the vicinity of the ring (Figure 2).[37] There is, of course, the possibility of contacts between nonpolar residues of the active site of CA and the multipoles of the rings of the ligands. We cannot take such contacts into account without overparameterizing the QSAR because of the small number of ligands we have studied. Moreover, Kim et al. previously estimated that contacts between the dipole of the fluorinated phenyl rings of sulfonamide ligands and nonpolar residues of CA contributed <0.4 kcal mol−1 to the free energy of binding.[16] Thus, our approach of neglecting these multipole-induced dipole contacts, while certainly not ideal, is defensible as a first-order approximation.
To solve for the constant c2 in Eq. (10a), we assume that the strength of van der Waals contacts between the phenyl ring and CA disappears when the ring is not present (e.g., for the molecule HSO2NH2, which has a value of clog P of −2.21: ΔHiring = 0 = −2.21B + c2). We solve for c1 by subtraction of this value for c2 from the constant in Eq. (7).
Eq. (11) gives the contributions from electrostatic interactions [Eq. (11a)]—the ZnII-N bond and the hydrogen-bond network—and from hydrophobic interactions [Eq. (11b)] to the enthalpy of association [by combining Eqs. (7) and (10)].
| (11a) |
| (11b) |
Table 3 lists the values, calculated using Eq. (11), of these contributions. The ZnII-N bond and hydrogen-bond network contribute very favorably (~ −11 kcal mol−1) to the enthalpy of association, while the phenyl ring makes a very small (~ −1 kcal mol−1) favorable contribution (presumably due to van der Waals contacts of the phenyl ring).
Table 3.
Free energies, enthalpies, and entropies (all in kcal mol−1) for the different structural interactions between the fluorinated benzenesulfonamide anion and CA-Znn-OH2+ (Figure 1).
| Ligand | Calculated ΔG°ArSo2NH−[a] | ΔGi ZnII-N bond[a],[b] | ΔGi H-bond network[a],[c] | ΔGi Ring contacts[a],[d] | Calculated ΔH°ArSo2NH−[a] | ΔHi ES[a],[e] | ΔHi Ring contacts[a],[f] | Calculated −TΔS°ArSo2NH−[a] | −TΔSi ES[a],[g] | −TΔSi Ring contacts[a],[h] |
|---|---|---|---|---|---|---|---|---|---|---|
| BS | −13 ± 3 | −9 ± 3 | −2 ± 3 | −2.9 ± 0.9 | −12 ± 7 | −12 ± 7 | −1 ± 2 | −1 ± 8 | 2 ± 8 | −2 ± 2 |
| 2-FBS | −13 ± 3 | −8 ± 3 | −1 ± 3 | −2.9 ± 0.9 | −12 ± 7 | −11 ± 7 | −1 ± 2 | −1 ± 7 | 1 ± 8 | −2 ± 2 |
| 3-FBS | −13 ± 3 | −8 ± 3 | −1 ± 3 | −3.3 ± 0.9 | −12 ± 7 | −11 ± 7 | −1 ± 2 | −1 ± 7 | 2 ± 8 | −3 ± 2 |
| 4-FBS | −13 ± 3 | −8 ± 3 | −1 ± 3 | −3.2 ± 0.9 | −12 ± 7 | −12 ± 7 | −1 ± 2 | −1 ± 7 | 2 ± 8 | −3 ± 2 |
| 2,6-FBS | −12 ± 3 | −8 ± 3 | −1 ± 3 | −2.8 ± 0.9 | −11 ± 6 | −10 ± 7 | 0 ± 2 | −1 ± 7 | 1 ± 7 | −2 ± 2 |
| 3,5-FBS | −13 ± 3 | −8 ± 3 | −1 ± 3 | −3.7 ± 1.0 | −12 ± 6 | −11 ± 7 | −1 ± 2 | −2 ± 7 | 1 ± 8 | −3 ± 2 |
| pentaFBS | −12 ± 3 | −8 ± 3 | −1 ± 3 | −3.9 ± 1.0 | −10 ± 6 | −9 ± 6 | −1 ± 2 | −3 ± 7 | 0 ± 7 | −3 ± 2 |
Uncertainties were estimated by propagating uncertainties in all of the parameters in the appropriate equation (assuming that these uncertainties were independent).
From Eq. (14a).
From Eq. (14b).
From Eq. (13b).
ZnII-N bond and hydrogen-bond network from Eq. (11a).
From Eq. (11b).
ZnII-N bond and hydrogen-bond network from Eq. (12a).
From Eq. (12b).
Electrostatic and Hydrophobic Interactions Both Influence the Entropy of Binding (−TΔS°ArSO2NH−
Increasing the Brønsted basicity of ArSO2NH− (that is, increasing the pKa of ArSO2NH2) increases −TΔS°ArSO2NH− [making it less favorable; Eq. (8)] and decreases ΔH°ArSO2NH− [making it more favorable; Eq. (7)]. The observation that increasing the enthalpy of the pKa-dependent structural, component interactions—the ZnII-N bond and the hydrogen-bond network (Figure 1)—lowers the entropy of these interactions is compatible with the phenomenon of enthalpy/entropy compensation.[38, 39] In the physical model for enthalpy/entropy compensation, more exothermic binding occurs with a less favorable (more unfavorable) entropy than less exothermic binding because of the lower mobility (less “tightness”) at the protein-ligand interface for the more exothermic binding event than the less exothermic one.[38]
Eq. (8) shows that increasing the hydrophobicity (that is, increasing the log P) of the benzenesulfonamide ligand decreases −TΔS°ArSO2NH− (making it more favorable). This observation is compatible with the widely-held belief that the hydrophobic effect is primarily an entropic effect when T ~ 298 K.[36]
We solve for the component (intrinsic) entropies of interaction [Eq. (12)] as we did above for the component (intrinsic) enthalpies [Eq. (11)] above (Figure 1).
| (12a) |
| (12b) |
Table 3 shows the calculated results for the component entropies of association. Electrostatic contacts (the ZnII-N bond and hydrogen-bond network) make small, unfavorable contributions to −TΔS°ArSO2NH− (~1–2 kcal mol−1). That these interactions are unfavorable entropically is compatible with the phenomenon of enthalpy/entropy compensation (see above). In line with our intuition, the phenyl ring makes a favorable (~ −3 to −2 kcal mol−1) contribution to −TΔS°ArSO2NH−, presumably due to solvent release as the basis of the hydrophobic effect[36].
Partitioning the Free Energy of Binding (ΔG°ArSO2NH−) Into the Different Structural Interactions between Fluorinated Benzenesulfonamide Anions and CA-ZnII-OH2+
Eq. (13) shows the partitioning of ΔG°ArSO2NH− into the structural, component interactions between ArSO2NH− and CA using an analysis similar to that that we used to partition ΔH°ArSO2NH− and −TΔS°ArSO2NH− above.
| (13a) |
| (13b) |
Koike et al. reported a small molecule model of the active site of CA that consisted of a macrocyclic triamine chelated to ZnII.[40] The triamine provides a good model because it: (i) had a distorted tetrahedral geometry about the ZnII with the fourth site occupied by H2O with a pKa of 7.3 (close to the value for CA-ZnII-OH2+; Table 1)[1, 31, 32], (ii) catalyzed the hydrolysis of p-nitrophenylacetate (a model substrate for CA),[1, 32] and (iii) bound arylsulfonamides as anions. The binding of arylsulfonamides to the triamine only probes the ZnII-N bond (ΔGiZnII−N) with no effects of the hydrogen-bond network or of hydrophobic contacts of the ring (ΔGiring = ΔGiH-bonds = 0; Figure 1). The value of the slope (related to β) of a plot of ΔG°ArSO2NH− for the binding of arylsulfonamides (and monoanions) to the triamine model vs. the pKa of these ligands was −0.40 (the uncertainty in the value of β from the standard error for linear least-squares fitting was 0.07). We take the value of −0.40 to be pKa-dependence of the ZnII-N bond (ΔGiZnII−N) for the binding of fluorinated benzenesulfonamides to BCA. This assumption gives a value for the pKa-dependence of the hydrogen-bond network (ΔGiH-bonds) of −0.44. Interestingly, this analysis suggests that the ZnII-N bond and hydrogen-bond network have the same sensitivity to pKa of the sulfonamide.
Liang et al. have shown that mutating Thr-199 to Ala in HCA II decreases the affinity of of HCA for dansylamide by ~0.8 kcal mol−1, presumably due to the removal of the hydrogen bond between the side chain hydroxyl of Thr-199 of CA and the NH of the sulfonamide (Figure 1).[41] No experimental value is available for the strength of the other hydrogen bond (between the backbone amide of Thr-199 and one of the sulfonamide oxygens). Krebs et al. have examined the catalytic activity of, but not the binding of sulfonamides to, an HCA mutant where Thr-199 was replaced by Pro—a mutation that would be expected to abolish both hydrogen bonds.[42] We assume that the two hydrogen bonds are equal in energy, giving ΔGiH-bonds = −1.5 kcal mol−1 for dansylamide (pKa = 9.8).[43]
These assumptions allow us to divide the effect of electrostatics (from the pKa-dependent terms; Eq. (13a)) on the free energy of binding (ΔG°ArSO2NH−) into contributions from the ZnII-N bond and the hydrogen-bond network bond [Eq. (14)]:
| (14a) |
| (14b) |
Table 3 shows the calculated intrinsic free energies. Most of the binding energy (~75%) for the fluorinated benzenesulfonamides is contributed by electrostatic contacts (with the ZnII-N bond making up ~65% and the hydrogen-bond network ~10 %) with the remainder (~25%) contributed by hydrophobic contacts (mainly in the entropy of association) of the phenyl ring (Figure 4).
Figure 4.
Free energies, enthalpies, and entropies (all in kcal mol−1) for the different structural interactions between a fluorinated benzenesulfonamide anion and CA-ZnII-OH2+ (data from Table 3).
Our results suggest the dominant role of the ZnII-N bond in affinity, and compare extremely well to a computational study of Menziani et al. that reported a value of ~60% for this interaction.[7] Our results differ from those of Menziani et al., however, in that they ascribed the variation of ΔG°ArSO2NH− (for the binding of a series of substituted benzenesulfonamide anions to CA-ZnII-OH2+) to the variation in the strengths of van der Waals contacts between the ligands and CA, with the strength of the ZnII-N bond being relatively constant across the series. Our results suggest that variations in the strengths of the ZnII-N bonds (ΔGiZnII−N) and in the strengths of ring contacts (ΔGiring) are of comparable magnitude, with neither one alone explaining the variation in ΔG°ArSO2NH− (cf. BS and pentaFBS in Table 3).
Entropy (#x2212;TΔS°ArSO2NH−) of Binding Partially Compensates for Enthalpy (ΔH°ArSO2NH−)
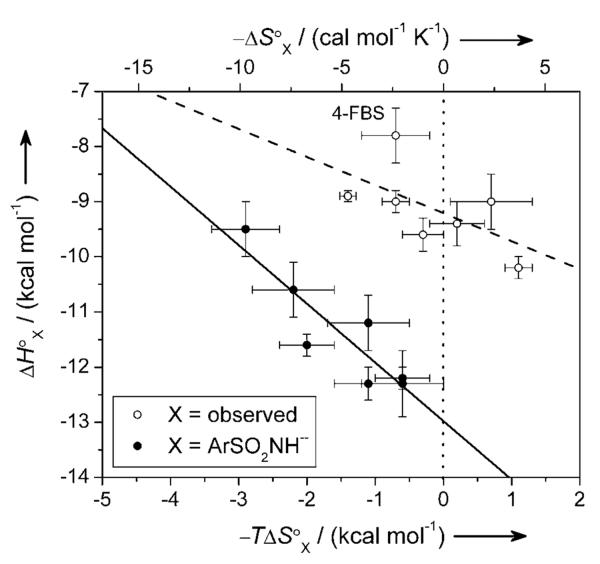
Figure 5 shows a plot between ΔH°ArSO2NH− and −TΔS°ArSO2NH−; the slope gives the compensation (1.1 ± 0.2) between the two. A stronger (more exothermic) ZnII-N bond has a proportionally greater entropic cost of association. The compensation value is slightly greater than unity; this result demonstrates that increasing the exothermicity of binding correlates with increasing the affinity of ArSO2NH− (the sulfonamide anion) for CA-ZnII-OH2+.
Figure 5.
An enthalpy/entropy compensation plot for the binding of fluorinated benzenesulfonamides to BCA. Error bars are uncertainties described in Table 2. The solid and dashed lines are linear fits to the data. For X = ArSO2NH− (closed circles), the best-fit line gave a value for compensation (negative of the slope) of 1.1 ± 0.2, and a value of R2 of 0.88. For X = observed (the experimentally observed data; open circles), the best-fit line gave a value for compensation (negative of the slope) of 0.5 ± 0.3, and a value of R2 of 0.36; the fit improved only marginally when 4-FBS was excluded from the analysis (R2 = 0.45). The poorer fit to the observed data (X = observed) than to the data calculated for the idealized reaction [X = ArSO2NH−; Eqs. (1) and (5)] illustrates the difficulty of rationalizing the thermodynamics for processes that have a number of steps (e.g., ionization of arylsulfonamide and CA, and binding) without first disentangling the thermodynamics of the individual steps. Uncertainties were given by the linear least-squares fitting procedure. The dotted vertical line separates favorable (−TΔS° < 0) from unfavorable (−TΔS° > 0) entropy of binding.
We do not make too much of the linear relationship between enthalpy and entropy, however. The range in ΔG°ArSO2NH− for the series of fluorinated benzenesulfonamides is much less than that in ΔH°ArSO2NH− or in −TΔS°ArSO2NH−, and thus such a linear relationship is required.[44]
The Outlier: 4-Fluorobenzenesulfonamide
The ligand 4-FBS interacts with a less favorable ΔH°ArSO2NH− (Figure 3b) and a more favorable −TΔS°ArSO2NH− (Figure 3c) than that expected based on the QSARs for the other ligands. This deviation suggests either: (i) greater mobility of the CA/4-FBS complex (either of the protein or the ligand in the complex) than expected based on the other ligands of the series, or (ii) greater contribution of hydrophobic contacts with CA of 4-FBS than expected based on the QSAR for the other ligands. Possibility (ii) seems unlikely because the hydrophobicity (log P) of 4-FBS does not differ appreciably from the other ligands (Table 1) and all of the ligands bind in a similar way to CA (Figure 2). We are currently exploring possibility (i) by conducting molecular dynamics simulations of CA/ligand complexes. We will report the results of these studies in due course.
4-Fluorobenzenesulfonamide Binds to BCA II, HCA I, and HCA II with a Stoichiometry of 1:1
ITC provides the stoichiometry of binding of ligand to protein as one of the fitting parameters. The stoichiometries for all CA-FBS complexes examined in this study were unity (1.02 ± 0.05). This observation is in contrast to the results reported by Gerig and coworkers.[19, 20] On the basis of binding titrations followed by 19F NMR spectroscopy, these investigators reported that 2-FBS, 3-FBS, and 4-FBS bound with stoichiometries of ligand to protein of 2:1 in complex with HCA II and HCA I, and that the bound ligands were in fast exchange on the NMR time scale (and thus were likely both in the active site).[19, 20] These results are very surprising given the 1:1 stoichiometry that has been demonstrated for almost all other sulfonamide-wild-type CA complexes by a number of biophysical techniques.[1, 45],[46]
In search for a reconciliation between these conclusions, we speculated that Gerig and coworkers might have been observing a second, weak binding site (Kdobs ~ 5 μM) that we would not observe under the conditions we used for ITC, because of the greater (50 to 100-fold) concentration of CA used in NMR (0.5–1 mM) than what we used in ITC (10 μM).[47] We repeated the ITC measurements with 4-FBS using ~70 μM of BCA to be able to observe a weak secondary binding site (Kdobs ≤ 7 μM). Again, our data fit well to a single-site binding model with a stoichiometry of 1.06 (Figure S.2). The possibility remained that the second ligand bound with an enthalpy below our limit of detection (|ΔH°obs| < 0.2 kcal mol−1).
To address this issue, we attempted to replicate the 19F NMR titration experiments of Gerig and coworkers.[18–20] Our results demonstrate that 4-FBS binds to BCA II with a 1:1 stoichiometry (Figure 6). While BCA II has very high sequence identity (81%) and homology (88%) with HCA II, and is completely identical in its active site with HCA II, there are subtle differences outside of the active site (e.g., I91V, C206S) between the two that could contribute to differences in the binding of ligands.[1],[48]
Figure 6.
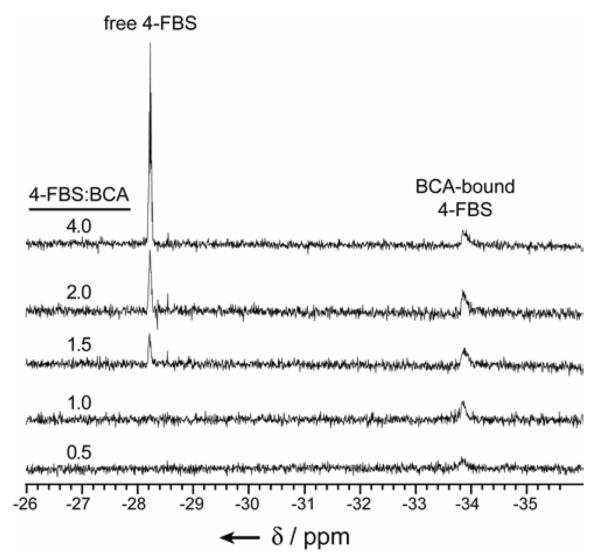
19F NMR spectra of 4-fluorobenzenesulfonamide (4-FBS) in the presence of bovine carbonic anhydrase II (BCA, 0.5 mM). The number of equivalents of 4-FBS to BCA is indicated. Chemical shifts (δ in ppm) are reported relative to trifluoroacetic acid as “external” standard (in a sealed capillary). All samples were in 20 mM Na2D2PO4 (“pH” 7.5) at T = 298 K.
We repeated the 19F NMR titration with HCA I and 4-FBS, and again observed a stoichiometry of binding of 1:1 (Figure S.3). We ensured high activity of the NMR samples of BCA II and HCA I by following fluorometrically the binding of ethoxzolamide (an inhibitor that has been shown to bind 1:1 to CA and to quench the fluorescence of tryptophan residues of the protein)[43, 49]. Our results indicate high activity of both enzymes: ~90% for BCA II and ~82% for HCA I (Figure S.4).
Our solution-phase results are consistent with the crystal structure of 4-FBS in complex with HCA II (Figure 2a); this structure conclusively demonstrates a stoichiometry of binding of 1:1. There is no evidence in the electron density map for a second or an alternative binding conformation of 4-FBS (Figure 2b). The ZnII coordination polyhedron remains tetrahedral in the 4-FBS complex and does not adopt the pentavalent geometry proposed by Gerig and colleagues.[19]
We have no explanation for the difference reported by Gerig and coworkers.[19, 20] Based on our current understanding of the system, we conclude that Gerig's conclusions are incorrect, and based on some unrecognized source of error in the data.
Conclusions
In this paper, we have reported the separated thermodynamic parameters of enthalpy and entropy for the association of fluorinated benzenesulfonamides with BCA. We have used the experimentally observed data to calculate thermodynamic parameters for the idealized reaction of the binding of the sulfonamide anion (ArSO2NH−) to the ZnII-water form of BCA (CA-ZnII-OH2+) (Figure 1). We constructed Quantitative Structure-Activity Relationships (QSARs) for the free energy (ΔG°ArSO2NH−), enthalpy (ΔH°ArSO2NH−), and entropy (−TΔS°ArSO2NH−) of the idealized reaction with pKa and log P of the fluorinated benzenesulfonamides (Figure 3). Using our results and those from others, we semi-quantitatively partitioned these thermodynamic parameters to the different structural interactions (component intrinsic interactions) between ArSO2NH− and CA-ZnII-OH2+ (Figures 1 and 4).
The QSARs demonstrate that increasing fluorination on the benzenesulfonamide has three effects on the dissociation constant (KdArSO2NH−) of ArSO2NH− for CA-ZnII-OH2+: (i) it increases the hydrophobicity (log P) of the ligand, an effect that lowers KdArSO2NH−, (ii) it decreases the Lewis basicity of the anion for the ZnII cofactor of CA (by decreasing the pKa of the neutral sulfonamide), an effect that increases KdArSO2NH−, and (iii) it decreases the strength of the hydrogen-bond network between the −SO2NH group and residues of the active site of CA, an effect that increases KdArSO2NH−. These three effects serve to minimize the variation in KdArSO2NH− (the affinity varies by less than a factor of ten) across the series. This small range in KdArSO2NH− (and in ΔH°ArSO2NH− and −TΔS°ArSO2NH−) does not allow us to generalize these results to the binding of structurally complex arylsulfonamides to CA.
The partitioning of the thermodynamic parameters into the different structural interactions between the benzenesulfonamide ligands and CA have clarified the relative importance of the different interactions: electrostatic contributions are dominant with ~65% (~−8 kcal mol−1) of the free energy being contributed by the ZnII-N bond and ~10% (~ −1 kcal mol−1) by the hydrogen-bond network. Hydrophobic interactions between the aryl ring and CA contribute the remaining ~25% (~ −3.5 kcal mol−1) (Figure 4); this result is consistent with the ~103 (~ −4 kcal mol−1) higher affinity of HCA for benzenesulfonamide than for methanesulfonamide.[1, 50]
One of the ligands, 4-FBS, interacts differently with CA than the others. It binds with a less favorable enthalpy and a more favorable entropy than anticipated from QSARs to the other ligands (Figure 3). We believe that the complex of 4-FBS and CA has greater mobility than the complexes of the other ligands and CA. We are currently pursuing computational studies to test this hypothesis.
Our results highlight the importance of examining the thermodynamic parameters for the association of the arylsulfonamide anion (ArSO2NH−) to CA-ZnII-OH2+ (both ligand and protein in their active forms). Most studies (even QSARs in the literature) have only discussed the experimentally observed thermodynamic parameters. Such analyses confound too many variables: for instance, a lower pKa for an arylsulfonamide increases the fraction present as the anion (active form), but also reduces the Lewis basicity of the anion.
The “best” value for the pKa of the ligand to give the lowest value for the observed dissociation constant (Kdobs) should be near the pH of the solution (~7.4) because of these two competing effects of pKa.[1, 51] Pentafluorobenzenesulfonamide has only a pKa of 8.2, so a better scaffold than a phenyl ring would be a larger ring system (e.g., naphthalene) to allow for the addition of more electron-withdrawing substituents to decrease the pKa to ~7.4. Fluorine is the best choice for these substituents because it will decrease the value of pKa, and also increase the hydrophobicity of the ligand.
Our results show that the different binding interactions between a protein and ligand can be separated experimentally. An examination of the magnitude of these separate interactions for different ligands in a series could allow for the optimization of affinity by tuning the strengths of the different interactions independently. Finally, our results reveal that, even for a well-characterized protein such as CA, there are still outliers that show that our understanding of non-covalent interactions remains painfully incomplete.[14]
Experimental Section
General Methods
Fluorinated benzensulfonamides and proteins (bovine carbonic anhydrase II pI 5.9 (BCA), human carbonic anhydrase I (HCA I), and soybean trypsin inhibitor) were purchased from Sigma-Aldrich (St. Louis, MO). Deuterium oxide (D2O, 99.9% D), hexadeuterated dimethyl sulfoxide (DMSO-d6, 99.9% D), and sodium deuteroxide (NaOD, 99.5% D) were purchased from Cambridge Isotopes (Andover, MA). The benzenesulfonamides were recrystallized from water before use, and the other reagents were used as received. Enzymes were quantified by UV spectroscopy: for BCA ε280 = 55,300 M−1 cm−1, and for HCA I ε280 = 47,000 M−1 cm−1 using molecular-weights of 29.09 kDa and 28.85 kDa, respectively.[1, 52] 19F{1H} NMR experiments were carried out on a Varian Inova spectrometer operating at 376 MHz (19F). Isothermal titration calorimetry was performed using a VP-ITC microcalorimeter from MicroCal (Northampton, MA). UV-Vis spectroscopy was conducted on a Hewlett Packard 8453 spectrophotometer (Palo Alto, CA), and fluorescence spectroscopy on a Perkin-Elmer LS50B fluorometer (Boston, MA) with temperature controlled by a circulating water bath.
Quantification of Stock Solutions of Fluorinated Benzenesulfonamides
The fluorinated benzenesulfonamides (except pentafluorobenzenesulfonamide) were prepared gravimetrically to 10–20 mM in D2O or DMSO-d6. Stock solutions were diluted 1:10 with 2.00 mM maleic acid in D2O (prepared gravimetrically to 1 M and then diluted), and an excess of NaOD was added to facilitate deprotonation of the sulfonamide. Proton resonances due to the benzenesulfonamide were normalized relative to that of maleic acid (allowing a 10 s delay between pulses) to determine accurately the concentration of the stock solutions. Pentafluorobenzenesulfonamide, which had been rigorously dried, was prepared to 10.0 mM gravimetrically.
Measurement of pKa of Fluorinated Benzenesulfonamides
The benzenesulfonamides (5 mM in 52 mM NaCl) were titrated with NaOH, and the pH was monitored with a glass pH electrode. The values of pKa were obtained by fitting the data (treating pH as the independent variable and volume of NaOH added as the dependent variable) to the full solution for the titration using nonlinear least-squares optimization and the activity coefficients for proton and hydroxide at an ionic strength of 0.05 M.[53]
Isothermal Titration Calorimetry to Determine Heats of Ionization of Fluorinated Benzenesulfonamides
Samples of the benzenesulfonamides (~5 mM in 52 mM NaCl with pH adjusted to 9.6: near their values of pKa) were titrated with 10.0 mM NaOH in 52 mM NaCl at T = 298 K. Ten 6.0 μL injections were preceded by one 2.0 μL injection, which was omitted for data analysis. After the injections, it was verified that the pH of the samples had not changed during the titration. The peaks of the thermogram were integrated, subtracted by the background heats, and normalized to the amount of NaOH added. The average and standard deviation, which was taken to be the uncertainty, of these values are reported. To determine appropriate background heats (of dilution and mechanical effects), buffers with values of pKa ~ 9.6 and with well-characterized enthalpies of ionization (values of ΔH°ion,buffer in kcal mol−1: cyclohexylaminoethanesulfonic acid 9.453, 3-(cyclohexylamino)-2-hydroxy-1-propanesulfonic acid 11.15, and ethanolamine 12.05)[30] were titrated as described. The difference between these experimental values and those from the literature gave the background heats, which were very small (<0.3 kcal mol−1) in all cases.
Isothermal Titration Calorimetry to Examine the Binding of Fluorinated Benzenesulfonamide Ligands to BCA
For most experiments, BCA (~10 μM) in 20 mM sodium phosphate buffer pH 7.5 (with 0.6% D2O) was titrated with ~110 μM benzenesulfonamide ligand in the same buffer at T = 298 K. Twenty-five 12.0 μL injections were preceded by one 2.0 μL injection, which was omitted for data analysis. After subtraction of background heats, the data were analyzed by a single-site binding model using the Origin software (provided by Microcal) with the values of binding stoichiometry, ΔH°, and Kd allowed to vary to optimize the fit. Measurements were conducted 3–4 times with a new stock solution of ligand prepared and quantified for each measurement. In order to verify the binding stoichiometry of 4-fluorobenzenesulfonamide (4-FBS) to BCA, BCA (68.2 μM) in 20 mM sodium phosphate buffer (with 5% DMSO-d6) was titrated with 1.00 mM 4-FBS in the same buffer at T = 298 K. Twenty-eight 10.0 μL injections were preceded by one 2.0 μL injection, which was omitted for data analysis. The data were analyzed as described.
19F NMR Binding Titrations to Verify Stoichiometry of 4-FBS to CA
BCA (0.5 mM) or HCA I (0.75 mM) was solubilized in 20 mM sodium phosphate buffer pH 7.5. The sample was lyophilized and then re-dissolved in an equal volume of D2O. Aliquots of 4-FBS (~20 mM in D2O) were added to the sample, and 19F{1H} spectra were acquired using a time between pulses of 2.0 s when the stoichiometry of ligand to protein was less than or equal to unity and 20.0 s otherwise, to take into account the reported values of T1 by Dugad and Gerig.[19] The resonances are reported relative to trifluoroacetic acid in a sealed capillary as external standard. It was verified that the “pH” of the samples had not changed appreciably (<0.2 “pH” units) during the titration.
X-ray Crystal Structures of HCA II-Ligand Complexes
Recombinant HCA II was prepared as described[54] and crystallized by the hanging drop vapor diffusion method. Typically, 5 μL of protein solution [8–12 mg mL−1 protein, 1 mM methyl mercuric acetate, 20 mM Tris-sulfate (pH 8)] and 5 mL of precipitant buffer [2.75 M ammonium sulfate, 50 mM Trissulfate (pH 8)] were combined in a single drop suspended over a 1 mL reservoir of precipitant buffer at 4°C. Crystals appeared within two weeks and belonged to space group P21 with average unit cell parameters a = 43.4 Å, b = 42.2 Å, c = 73.5 Å, b = 104.2°.
Prior to ligand soaking experiments, crystals of HCA II were cross-linked by adding 5 mL of glutaraldehyde solution [0.8% glutaraldehyde (v/v), 4.0 M ammonium sulfate, 50 mM Tris-sulfate (pH 8.0)] to the hanging drop and allowing it to equilibrate at 4°C for 48 hours. Crystals were then transferred to a precipitant buffer containing 1–5 mM of the fluorinated benzenesulfonamide and soaked for 1 week at 4°C.
X-ray diffraction data were collected at room temperature using an R-AXIS IIc image plate detector (Molecular Structure Corporation) mounted on a Rigaku RU-200HB rotating anode X-ray generator (operating at 50 kV and 100 mA) supplying Cu Ka radiation focused with Yale double mirrors. Raw diffraction data were processed using the HKL suite of programs.[55] The 1.54 Å resolution structure of native HCA II retrieved from the Research Collaboratory for Structural Bioinformatics (RCSB accession code 2CBA)[56] was used as the starting coordinate set for the crystallographic refinement of the structure of each enzyme-inhibitor complex. Electron density maps calculated with Fourier coefficients 2|Fo| − |Fc| and |Fo| − |Fc| and phases derived from the in-progress atomic model were generated with X-PLOR and viewed with O;[57] these maps consistently revealed the binding of only one inhibitor molecule per enzyme molecule throughout refinement. Refinement converged smoothly to final crystallographic R factors in the range of 0.211–0.221. Data collection and refinement statistics are recorded in Table S.1. The atomic coordinates of the complexes of HCA with 4-FBS, 2,6-FBS, and 3,5-FBS have been deposited in the RCSB with the accession codes of 1IF4, 1IF5, and IF6, respectively.
Supplementary Material
Acknowledgements
This work was supported by the National Institutes of Health (GM51559, GM30367, and GM49758). V.M.K. and B.R.B. acknowledge support from pre-doctoral fellowships from the NDSEG and NSF, respectively. D.T.M. acknowledges support from a post-doctoral fellowship from the NIH (AI068605).
Footnotes
Supporting information for this article is available on the WWW under http://www.chemasianj.org or from the author.
References
- [1].Urbach AR, Whitesides GM. manuscript in preparation [Google Scholar]
- [2].Supuran CT, Scozzafava A, Casini A. Med. Res. Rev. 2003;23:146–189. doi: 10.1002/med.10025. [DOI] [PubMed] [Google Scholar]
- [3].Mansoor UF, Zhang X-R, Blackburn GM. In: The Carbonic Anhydrases: New Horizons. Chegwidden WR, Carter ND, Edwards YH, editors. Birkhäuser; Verlag: 2000. pp. 437–459. [Google Scholar]
- [4].Supuran CT, Scozzafava A, Conway J. In: Carbonic Anhydrase: Its Inhibitors and Activators. Supuran CT, Scozzafava A, Conway J, editors. CRC Press; Boca Raton, FL: 2004. pp. 67–147. [Google Scholar]
- [5].Christianson DW, Fierke CA. Acc. Chem. Res. 1996;29:331–339. [Google Scholar]
- [6].Jencks WP. Proc. Natl. Acad. Sci. U. S. A. 1981;78:4046–4050. doi: 10.1073/pnas.78.7.4046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Menziani MC, Debenedetti PG, Gago F, Richards WG. J. Med. Chem. 1989;32:951–956. doi: 10.1021/jm00125a005. [DOI] [PubMed] [Google Scholar]
- [8].Mammen M, Choi S-K, Whitesides GM. Angew. Chem. 1998;110:2908–2953. doi: 10.1002/(SICI)1521-3773(19981102)37:20<2754::AID-ANIE2754>3.0.CO;2-3. [DOI] [PubMed] [Google Scholar]; Angew. Chem. Int. Ed. Eng. 1998;37:2755–2794. [Google Scholar]
- [9].Krishnamurthy VM, Estroff LA, Whitesides GM. In: Fragment-Based Approaches in Drug Discovery. Jahnke W, Erlanson DA, editors. Wiley-VCH; Weinheim: 2006. pp. 11–53. [Google Scholar]
- [10].Böhm HJ, Banner D, Bendels S, Kansy M, Kuhn B, Müller K, Obst-Sander U, Stahl M. ChemBioChem. 2004;5:637–643. doi: 10.1002/cbic.200301023. [DOI] [PubMed] [Google Scholar]
- [11].Uneyama K. Organofluorine Chemistry. Blackwell Publishing; Oxford, U.K.: 2006. [Google Scholar]
- [12].Gao J, Qiao S, Whitesides GM. J. Med. Chem. 1995;38:2292–2301. doi: 10.1021/jm00013a005. [DOI] [PubMed] [Google Scholar]
- [13].a) Battaglia MR, Buckingham AD, Williams JH. Chem. Phys. Lett. 1981;78:420–423. [Google Scholar]; b) Williams JH. Acc. Chem. Res. 1993;26:593–598. [Google Scholar]
- [14].Whitesides GM, Krishnamurthy VM. Q. Rev. Biophys. 2005;38:385–395. doi: 10.1017/S0033583506004240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].a) Gohlke H, Klebe G. Angew. Chem. 2002;114:2764–2798. doi: 10.1002/1521-3773(20020802)41:15<2644::AID-ANIE2644>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]; Angew. Chem. Int. Ed. Eng. 2002;41:2645–2676. [Google Scholar]; b) Homans SW. Angew. Chem. 2004;116:292–303. [Google Scholar]; Angew. Chem. Int. Ed. Eng. 2004;43:290–300. [Google Scholar]
- [16].Kim C-Y, Chang JS, Doyon JB, Baird JTT, Fierke CA, Jain A, Christianson DW. J. Am. Chem. Soc. 2000;122:12125–12134. [Google Scholar]
- [17].a) Scozzafava A, Menabuoni L, Mincione F, Briganti F, Mincione G, Supuran CT. J. Med. Chem. 2000;43:4542–4551. doi: 10.1021/jm000296j. [DOI] [PubMed] [Google Scholar]; b) de Leval X, Ilies M, Casini A, Dogne J-M, Scozzafava A, Masini E, Mincione F, Starnotti M, Supuran CT. J. Med. Chem. 2004;47:2796–2804. doi: 10.1021/jm031116j. [DOI] [PubMed] [Google Scholar]
- [18].a) Gerig JT, Moses JM. J. Chem. Soc., Chem. Commun. 1987:482–484. [Google Scholar]; b) Veenstra DL, Gerig JT. Magn. Reson. Chem. 1998;36:S169–S178. [Google Scholar]
- [19].Dugad LB, Gerig JT. Biochemistry. 1988;27:4310–4316. doi: 10.1021/bi00412a018. [DOI] [PubMed] [Google Scholar]
- [20].Dugad LB, Cooley CR, Gerig JT. Biochemistry. 1989;28:3955–3960. doi: 10.1021/bi00435a049. [DOI] [PubMed] [Google Scholar]
- [21].Colton IJ, Carbeck JD, Rao J, Whitesides GM. Electrophoresis. 1998;19:367–382. doi: 10.1002/elps.1150190303. [DOI] [PubMed] [Google Scholar]
- [22].a) Kraulis PJ. J. Appl. Crystallogr. 1991;24:946–950. [Google Scholar]; b) Merritt EA, Murphy MEP. Acta Crystallogr., Sect. D. 1994;50:869–873. doi: 10.1107/S0907444994006396. [DOI] [PubMed] [Google Scholar]; c) Esnouf RM. J. Mol. Graphics & Modelling. 1997;15:132–134. doi: 10.1016/S1093-3263(97)00021-1. [DOI] [PubMed] [Google Scholar]
- [23].a) Jain A, Huang SG, Whitesides GM. J. Am. Chem. Soc. 1994;116:5057–5062. [Google Scholar]; b) Cappalonga Bunn AM, Alexander RS, Christianson DW. J. Am. Chem. Soc. 1994;116:5063–5068. [Google Scholar]
- [24].Krishnamurthy VM, Bohall BR, Semetey V, Whitesides GM. J. Am. Chem. Soc. 2006;128:5802–5812. doi: 10.1021/ja060070r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Wiseman T, Williston S, Brandts JF, Lin L-N. Anal. Biochem. 1989;179:131–137. doi: 10.1016/0003-2697(89)90213-3. [DOI] [PubMed] [Google Scholar]
- [26].a) Kernohan JC. Biochim. Biophys. Acta. 1966;118:405–412. doi: 10.1016/s0926-6593(66)80049-8. [DOI] [PubMed] [Google Scholar]; Lindskog S, Thorslund A. Eur. J. Biochem. 1968;3:453–460. doi: 10.1111/j.1432-1033.1967.tb19552.x. [DOI] [PubMed] [Google Scholar]; b) Coleman JE. Ann. Rev. Pharmacol. Toxicol. 1975;15:221–242. doi: 10.1146/annurev.pa.15.040175.001253. [DOI] [PubMed] [Google Scholar]
- [27].Taylor PW, King RW, Burgen ASV. Biochemistry. 1970;9:3894–3902. doi: 10.1021/bi00822a007. [DOI] [PubMed] [Google Scholar]
- [28].King RW, Burgen ASV. Proc. R. Soc. London, B. 1976;193:107–125. doi: 10.1098/rspb.1976.0034. [DOI] [PubMed] [Google Scholar]
- [29].Khalifah RG, Zhang F, Parr JS, Rowe ES. Biochemistry. 1993;32:3058–3066. doi: 10.1021/bi00063a017. [DOI] [PubMed] [Google Scholar]
- [30].Goldberg RN, Kishore N, Lennen RM. J. Phys. Chem. Ref. Data. 2002;31:231–370. [Google Scholar]
- [31].Kernohan JC. Biochim. Biophys. Acta. 1965;96:304. [PubMed] [Google Scholar]
- [32].Pocker Y, Stone JT. Biochemistry. 1968;7:4139–4145. doi: 10.1021/bi00851a050. [DOI] [PubMed] [Google Scholar]
- [33].Binford JS, Lindskog S, Wadsö I. Biochim. Biophys. Acta. 1974;341:345–356. doi: 10.1016/0005-2744(74)90227-7. [DOI] [PubMed] [Google Scholar]
- [34].Olander J, Bosen S, Kaiser E. J. Am. Chem. Soc. 1973;95:4473. doi: 10.1021/ja00786a042. [DOI] [PubMed] [Google Scholar]
- [35].a) Kakeya N, Yata N, Kamada A, Aoki M. Chem. Pharm. Bull. 1969;17:2000–2007. doi: 10.1248/cpb.17.2000. [DOI] [PubMed] [Google Scholar]; b) Kakeya N, Yata N, Kamada A, Aoki M. Chem. Pharm. Bull. 1969;17:2558–2564. doi: 10.1248/cpb.17.1010. [DOI] [PubMed] [Google Scholar]; c) Hansch C, McClarin J, Klein T, Langridge R. Mol. Pharmacol. 1985;27:493–498. [PubMed] [Google Scholar]; d) Gupta SP. In: Progress in Drug Research. Jucker E, editor. Birkhäuser; Verlag: 2003. pp. 173–204. [Google Scholar]; e) Clare BW, Supuran CT. In: Carbonic Anhydrase: Its Inhibitors and Activators. Supuran CT, Scozzafava A, Conway J, editors. CRC Press; Boca Raton, FL: 2004. pp. 149–181. [Google Scholar]
- [36].a) Southall NT, Dill KA, Haymet ADJ. J. Phys. Chem. B. 2002;106:521–533. [Google Scholar]; b) Dill KA, Bromberg S. Molecular Driving Forces: Statistical Thermodynamics in Chemistry & Biology. Garland Science; New York: 2003. [Google Scholar]; c) Sturtevant JM. Proc. Natl. Acad. Sci. U. S. A. 1977;74:2236–2240. doi: 10.1073/pnas.74.6.2236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Glu-106, Glu-117, and Arg-246 are the closest polar or charged residues of CA, and these are distanced from the phenyl ring of the ligands with enough space for several intervening water molecules.
- [38].a) Dunitz JD. Chem. Biol. 1995;2:709–712. doi: 10.1016/1074-5521(95)90097-7. [DOI] [PubMed] [Google Scholar]; b) Searle MS, Westwell MS, Williams DH. J. Chem. Soc., Perkin Trans. 1995;2:141–151. [Google Scholar]; c) Williams DH, Stephens E, O'Brien DP, Zhou M. Angew. Chem. 2004;116:6760–6782. doi: 10.1002/anie.200300644. [DOI] [PubMed] [Google Scholar]; Angew. Chem. Int. Ed. Eng. 2004;43:6596–6616. doi: 10.1002/anie.200300644. [DOI] [PubMed] [Google Scholar]
- [39].Gilli P, Gerretti V, Gilli G, Borea PA. J. Phys. Chem. 1994;98:1515–1518. [Google Scholar]
- [40].Koike T, Kimura E, Nakamura I, Hashimoto Y, Shiro M. J. Am. Chem. Soc. 1992;114:7338–7345. [Google Scholar]
- [41].Liang ZW, Xue YF, Behravan G, Jonsson BH, Lindskog S. Eur. J. Biochem. 1993;211:821–827. doi: 10.1111/j.1432-1033.1993.tb17614.x. [DOI] [PubMed] [Google Scholar]
- [42].Krebs JF, Ippolito JA, Christianson DW, Fierke CA. J. Biol. Chem. 1993;268:27458–27466. [PubMed] [Google Scholar]
- [43].Chen RF, Kernohan JC. J. Biol. Chem. 1967;242:5813–5823. [PubMed] [Google Scholar]
- [44].Cornish-Bowden A. J. Biosci. 2002;27:121–126. doi: 10.1007/BF02703768. [DOI] [PubMed] [Google Scholar]; Sharp K. Protein Sci. 2001;10:661–667. doi: 10.1110/ps.37801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Gao J, Wu Q, Carbeck J, Lei QP, Smith RD, Whitesides GM. Biophys. J. 1999;76:3253–3260. doi: 10.1016/s0006-3495(99)77477-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].A recent X-ray crystallographic study from Jude et al. revealed that four CuII-containing bivalent arylsulfonamides bound with a 2:1 stoichiometry to HCA II, with one ligand bound to the ZnII cofactor in the active site and the second ligand interacting with residues at the rim of the catalytic cleft (i.e., not in the active site) (see Jude KM, Banerjee AL, Haldar MK, Manokaran S, Roy B, Mallik S, Srivastava DK, Christianson DW. J. Am. Chem. Soc. 2006;128:3011–3018. doi: 10.1021/ja057257n. Kim et al. reported that two molecules of 4-(aminosulfonyl)-N-[(2,3,4,5,6-pentafluorophenyl)methyl]-benzamide bound to one molecule of a mutant of HCA II (Phe-131→Val) in the crystal, with one ligand bound to the ZnII cofactor and the second ligand bound outside of the active site (see ref [16]). This ligand bound with a 1:1 stoichiometry with the HCA mutant in solution.
- [47].From the data of Gerig and coworkers, there was no peak apparent at the chemical shift of free ligand until the stoichiometry of ligand to protein was greater than 2:1. Assuming that free ligand was present at ~7% (but below the limit of detection by 19F NMR) and given the total concentration of CA of 1 mM, we calculate a value for Kdobs for this presumptive secondary site of ~5 μM.
- [48].Computation for sequence alignment was performed at the SIB using the BLAST network service from ExPASy: http://www.expasy.org/cgi-bin/blast.pl.
- [49].Kernohan JC. Biochem. J. 1970;120:26P. doi: 10.1042/bj1200026p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Maren TH, Conroy CW. J. Biol. Chem. 1993;268:26233–26239. [PubMed] [Google Scholar]
- [51].Jencks WP. Catalysis in Chemistry and Enzymology. Dover Publications; Mineola, NY: 1987. [Google Scholar]
- [52].a) Nyman PO, Lindskog S. Biochim. Biophys. Acta. 1964;85:141–151. doi: 10.1016/0926-6569(64)90174-9. [DOI] [PubMed] [Google Scholar]; b) Lindskog S, Henderson LE, Kannan KK, Liljas A, Nyman PO, Strandberg B. In: The Enzymes. Boyer PD, editor. Academic Press: New York: 1971. pp. 587–665. [Google Scholar]
- [53].Harris DC. Quantitative Chemical Analysis. 5th ed W.H. Freeman & Company; 1998. [Google Scholar]
- [54].Nair SK, Calderone TL, Christianson DW, Fierke CA. J. Biol. Chem. 1991;266:17320–17325. [PubMed] [Google Scholar]
- [55].Otwinowski Z, Minor W. Methods Enzymol. 1997;276:307–326. doi: 10.1016/S0076-6879(97)76066-X. [DOI] [PubMed] [Google Scholar]
- [56].Håkansson K, Carlsson M, Svensson LA, Liljas A. J. Mol. Biol. 1992;227:1192–1204. doi: 10.1016/0022-2836(92)90531-n. [DOI] [PubMed] [Google Scholar]
- [57].a) Brünger AT, Kuriyan J, Karplus M. Science. 1987;235:458–460. doi: 10.1126/science.235.4787.458. [DOI] [PubMed] [Google Scholar]; b) Jones TA, Zou JY, Cowan SW, Kjeldgaard M. Acta Crystallogr., Sect. A. 1991;47:110–119. doi: 10.1107/s0108767390010224. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.