Revised UV extinction coefficients for nucleoside-5′-monophosphates and unpaired DNA and RNA

Abstract

Ultraviolet absorption provides the nearly universal basis for determining concentrations of nucleic acids. Values for the UV extinction coefficients of DNA and RNA rely on the mononucleotide values determined 30–50 years ago. We show that nearly all of the previously published extinction coefficients for the nucleoside-5′-monophosphates are too large, and in error by as much as 7%. Concentrations based on complete hydrolysis and the older set of values are too low by ∼4% for typical RNA and 2–3% for typical DNA samples. We also analyzed data in the literature for the extinction coefficients of unpaired DNA oligomers. Robust prediction of concentrations can be made using 38 µg/A₂₆₀ unit for single-stranded DNA (ssDNA) having non-repetitive sequences and 40–80% GC. This is superior to currently used predictions that account for nearest-neighbor frequency or base composition. The latter result in concentrations that are 10–30% too low for typical ssDNA used as primers for PCR and other similar techniques. Methods are described here to accurately measure concentrations of nucleotides by nuclear magnetic resonance. NMR can be used to accurately determine concentrations (and extinction coefficients) of biomolecules within 1%.

INTRODUCTION

Routine methods for determining biochemical concentrations, C, usually rely on measurements of UV absorbance, A. The accuracy of the results is often limited by uncertainty in the material’s extinction coefficient, ε, in the Beer–Lambert law: A = ε·C·l, where l is the pathlength of the cuvette. Complications may arise from UV-absorbing impurities, pH effects and light-scattering due to turbidity. It is also likely that deviations from linear Beer’s law behavior will accompany reorientation of the chromophores due to base pairing, stacking and other conformational changes such as aggregation and formation of complexes with ligands. Given these uncertainties, concentrations within ±10–20% accuracy are often considered acceptable, and this is usually sufficient to prepare solutions for enzyme-catalyzed syntheses and assays, and to make semi-quantitative interpretations of biochemical equilibria. Yet there are occasions where it would be valuable to know concentrations at high accuracy. Our particular concern is in measurements of equilibrium constants and their use in constructing free energy cycles for interacting systems.

Until recently, it has been difficult to accurately measure equilibrium constants for the binding of most ligands to nucleic acid or protein targets. This is not from a lack of interest, but rather it is due to the complicating factors mentioned in the previous paragraph, and that exquisitely pure materials were impossible to isolate for many biological molecules. Now, however, many biomolecules can be obtained in >98% purity by highly efficient techniques such as solid-phase synthesis, affinity tagging, gel electrophoresis and liquid chromatography with high surface area adsorbents. With highly pure materials, it is possible to accurately determine the concentrations of the interacting species, the equilibrium constants and free energies. Accurate free energies would provide great predictive power in thermodynamic cycles for the affinities of related compounds binding to a target. A reliable method is needed to determine concentrations with high accuracy.

Sample concentrations within ±0.05% can be achieved in many chemical analyses, using common laboratory equipment. The standard for analytical assays relies upon four-figure accuracy in weighing materials. Simple adaptation of these techniques, as illustrated here, dramatically reduces errors in biochemical determinations associated with serial dilution via micropipets. It is also shown that nuclear magnetic resonance (NMR) instrumentation available at nearly every major research institution is capable of determining the concentrations of nucleic acids and other biomolecules within ±1%. It is not unreasonable that improvements on the methods can reduce the errors to ±0.1% for compounds with purity >99.9%.

¹H-NMR referencing for accurate determination of concentration

If careful attention is paid to details of acquisition and data processing, the integrated intensity of an NMR peak will accurately reflect the number of corresponding nuclei present in the active region of the NMR transmit/receive coil. All compounds will exhibit equal NMR ‘extinction’ coefficients for non-exchangeable protons. In a biopolymer sample, total NMR signal intensity is not dependent on primary sequence, three-dimensional folding or complex formation. Contaminants and buffer components usually do not interfere with concentration measurements, even when they absorb or scatter UV light.

In the past 10–15 years, dramatic enhancements in the sensitivity of NMR spectrometers have occurred. These result from digital electronics, oversampling of the time-domain signal, and improved probehead and shim coil designs. Using 500+ MHz spectrometers, it is possible to measure C for many biomolecules within ±1–3% at ∼1.0 mM concentrations (1,2). The necessary amounts are produced routinely by DNA/RNA synthesizers (1 µmol scale) or in protein over-expression systems from 1 l cell cultures. Higher accuracy can be achieved using the ∼30 mM concentrations in the present work, together with accurate dilution methods. Determinations at lower concentrations are also feasible with careful attention to sample preparation, data acquisition and signal analysis. It may be possible to increase the sensitivity of NMR-based concentration measurements by another order of magnitude with the advent of cryocooled probe technology, higher magnetic field strengths and other instrumental advances.

We have developed a quantitative NMR methodology based on integration of proton resonances and comparison with a primary standard, cacodylic acid [CA; (CH₃)₂AsO₂H]. CA has a single acidic proton that is used to accurately determine the CA concentration by titration with standardized NaOH. It also has six equivalent methyl protons for comparison with the integrals of NMR signals from analytes. CA has other favorable aspects in that it does not absorb UV light at 260/280 nm, can serve as a pH 7 buffer, and is commonly used to inhibit bacterial growth. The sharp CA NMR singlet located at 1.6–1.7 p.p.m. (depending on pH) can be used to standardize a secondary reference reagent, 3-(trimethylsilyl)propionic-2,2,3,3-d₄-acid sodium salt (d₄-TSP) by integral comparison. TSP has a sharp singlet at 0.00 p.p.m., free from spectral overlap with many analyte molecules.

Many of the details have been published for acquiring and processing the NMR spectra to give accurate concentrations by comparing integrals with CA or TSP (1). Revisions presented here improve the accuracy of manipulations with small volumes and eliminate error-prone serial dilutions (2). The present work also improves upon the accuracy of the UV extinction coefficients of RNA and DNA mononucleotides. This makes it possible to determine concentrations within a few percent from limit hydrolysates of small quantities of RNA and DNA samples.

MATERIALS AND METHODS

General procedures

The published protocols (1) were followed, with exceptions noted below.

Free induction decays (128k real + imaginary) were collected as single scans using a 90° pulse. Delays of at least 2 min separated pulses.

Care must be taken to prevent evaporation of H₂O and D₂O from containers with volumes ∼1 ml or less. Evaporation can affect masses in the 0.1–1 mg range (0.1–1 µl). Standardized reference solutions also require protection from evaporation. CA solutions were stored in Nalgene containers externally sealed with parafilm, and stored in sealed desiccators (no desiccant). All manipulations with 99.996% D₂O were conducted in an argon-filled glove box.

Precisions reported herein are 95% confidence limits based on four or more determinations (1). Intermediate results used in multiplication and division carry more significant digits than are justified by experimental errors.

Cacodylic acid

Note that CA is poisonous; avoid breathing the dust. Use appropriate care in handling and disposal as recommended by the Material Safety Data Sheet.

The concentrations of solutions were calculated from mass-based determinations, rather than using volumes. A primary stock solution, CA_p, was prepared with ∼0.1 mmol CA/g of solution. A single dilution of CA_p by ∼30-fold produced a working NMR stock, CA_w, with an accurately known concentration of equivalent methyl protons, [H_w], in the range of 20–30 mM. H₂O and D₂O densities at 22.5°C were interpolated from tabulated data to be 0.9978 and 1.1044 g/ml, respectively (3).

Standardization of NaOH. A solution of 5.998 mM potassium acid phthalate was prepared from crystals dried for 2 h at 120°C, then dissolved in a 1.000 l volumetric flask. This was used to standardize 10 mM NaOH (VWR or Fisher) in quadruplicate. A typical NaOH concentration was 10.03 ± 0.01 mM. Titrations used a 25 ml class A burette, with NaOH titrant protected from CO₂ in storage and during the titration. A Fisher AR15 pH meter (model 8005) was calibrated with pH 7 and 10 buffers. End points were determined using a numerical approximation to the second derivative of pH versus the volume of NaOH added.

Primary stock CA_p. A typical calculation is illustrated in some detail as the procedure may be unfamiliar to readers accustomed to using molarity and volumetric manipulations. CA (∼1.4 g) was dissolved in ∼100 ml of 99.9% D₂O. Then ∼2 ml of this solution was added to a tared titration flask, and the net weight, 1.9768 g, was measured accurately. About 75 ml of freshly degassed Milli-Q water was added, and this aliquot of primary stock was determined to contain 0.1808 ± 0.0014 mmol of CA by titration against NaOH. Thus, there is 0.0915 mmol CA per g of CA_p solution (0.0921 ± 0.0007 mmol was the average of 13 determinations). This solution is ∼1% CA, so it is not appropriate to use the density of D₂O to convert it to a volume. The units, mmol/g solution, serve to carry high precision measurements to subsequent operations.

Working stock CA_w. This solution was prepared under argon; masses were determined in sealed containers. In a typical dilution, 0.2028 g of CA_p was added to 6.1115 g of 99.996% D₂O. This solution is only 0.04% CA by weight, so its density was approximated as that of D₂O, yielding [H_w] = 19.59 ± 0.16 mM

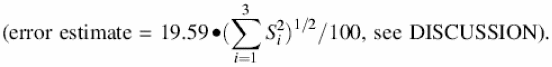
Nucleoside monophosphates

RNA and DNA nucleoside-5′-monophosphates (NMPs) and cytidine-3′,5′-cyclic monophosphate were purchased from Sigma Chemical, Acros Chemical and Fluka Chemical. Each extinction coefficient determination included samples from more than one vendor. Samples were not included in the analysis if substantial impurities were indicated by NMR signals in the aromatic region other than the desired NMP.

NMR-based concentrations. The NMR samples were prepared under argon. For each concentration determination, an indefinite amount between 1 and 6 mg of NMP powder was dissolved in ∼0.700 ml of CA_w (delivered by a micropipet) in a snap-top 1.5 ml microcentrifuge tube. Small amounts of pulverized, anhydrous KOH were added to help dissolve NMPs purchased in the free acid form. The samples were added to an NMR tube sealed with a silicone rubber septum cap wrapped with parafilm. Concentrations varied over a range from 15 to 96 mM, with most near 30 mM.

A Brüker Avance DRX-500 MHz spectrometer was used, as in our published protocol (1). NMR peak integrals were usually measured using Brüker’s Xwin NMR software, although they were occasionally verified using NMRPipe (4).

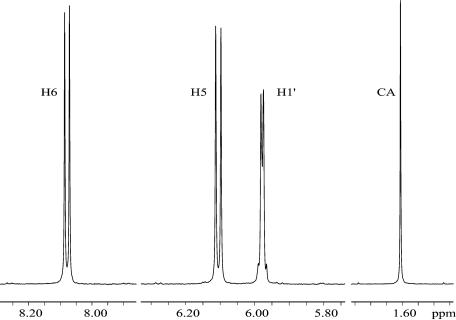
Figure 1 shows the relevant spectral regions for pC. In most biomolecules, more than one proton can be used for quantitative comparison, thus several measurements contribute to the average. The H6, H5 and H1′ signals were used for pC, pU, pdC (2′-deoxycytidine-5′-monophosphate) and <pC (cytidine-3′-5′-cyclic monophosphate); H5 and H1′ were used for pT; H2, H8 and H1′ for pA and pdA; and H8 and H1′ for pG and pdG. H8 is slightly acidic and exchanges significantly with D₂O over several hours at room temperature, so spectra involving A and G were measured within ∼20 min of dissolution in D₂O.

Figure 1.

500 MHz ¹H NMR spectrum (0.5 Hz exponential broadening) for a D₂O sample of 23.0 mM CMP and 19.6 mM cacodylic acid (CA). The CA peak is reduced in height by half (unapodized linewidth = 0.5 Hz). ¹³C-satellites are visible near the baseline.

The calculation of concentrations for the NMPs in NMR samples will be demonstrated with the CMP sample illustrated in Figure 1. The CA methyl integral was set to 1.000, and the three CMP peaks averaged 1.172 ± 0.004 intensity units. This gave [CMP] = 22.97 ± 0.22 mM

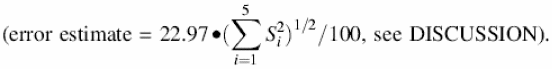
The ¹³C-satellite peaks were excluded from all integration regions, or subtracted as in (1).

Dilution and extinction coefficient determination. UV absorbance was measured on a Beckman DU 640 spectrophotometer blanked against water or 0.10 M phosphate buffer (pH 7). The difference in A₂₆₀ between phosphate buffer and water was less than 0.0005. Oxygen was not flushed from the cell compartment. Dilutions were carried out so that A₂₆₀ readings were between 0.80 and 1.10 to insure high sensitivity using the spectrophotometer. Again, mass-based dilutions reduced volume errors. Final pH values were verified to lie between 6.9 and 7.0. The dilution factors varied from about 100 to 300. UV measurements were made on the same day as NMR concentration determination to minimize the possibility of evaporation, sample degradation or bacterial growth.

In one dilution of the CMP determination under consideration, 0.0188 g of the NMR sample (0.0170 ml of D₂O) was added to 2.9802 g of freshly degassed Milli-Q (Millipore) water (2.9869 ml H₂O) and sealed. This leads to a dilution factor, D = 177. The measured A = 0.926 at 260 nm, with l = 1 cm. The extinction coefficient from

was 7.11 l/mmol/cm or, in units common to biochemical laboratories, 7.11 ODU/µmol. Dilution and A₂₆₀ measurement was repeated at least three more times, and averaged. The average over five NMR samples was ε₂₆₀ = 7.07 ± 0.06 ODU/µmol for pC.

RESULTS

Extinction coefficients

The average extinction coefficient values for the RNA and DNA mononucleotides at 260 nm are collected in the second column of Table 1. Also shown under ‘This work’ are the extinction coefficients and wavelengths for the absorbance maximum nearest 260 nm, the number of independent samples included in the average, N, and the 95% confidence limits for the average ε₂₆₀. Listed under ‘Previous’ are the ε₂₆₀ values that are now in common use for the NMPs (5) together with a correction factor that is the ratio of the ε₂₆₀ values.

Table 1. UV absorbance of RNA and DNA nucleoside-5′-monophosphates.

	This worka					Previous
	ε260	εmax	λmax	Nb	Confc	ε260	fd
pA	15.02	15.04	259	8	0.5%	15.34	1.0210
pdA	15.06	15.08	259	8	0.3%	15.34	1.0183
pC	7.07	8.74	271	5	00.8%	7.60	1.0753
pdC	7.10	8.86	271	5	0.3%	7.60	1.0705
pG	12.08	14.09	252	7	0.3%	12.16	1.0066
pdG	12.18	14.23	252	4	0.4%	12.16	0.9987
pU	9.66	9.78	262	5	0.9%	1.021	1.0570
pT	8.56	9.49	267	5	0.7%	8.70	1.0165

^aUnits of ε (l/mmol/cm or ODU/µmol), units of λ (nm).

^bNumber of determinations.

^c95% confidence limits.

^dCorrection factor for concentrations based on previous ε₂₆₀ values (5).

Spectra

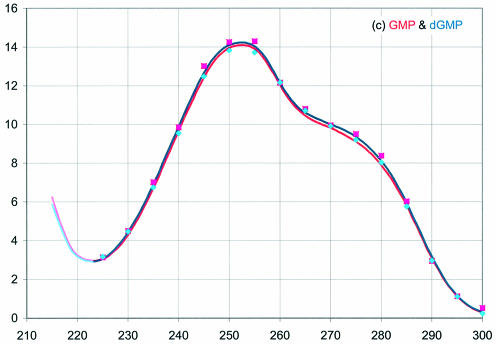
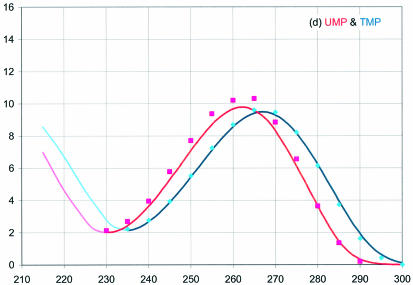
The extinction coefficients are presented in Figure 2 as a function of wavelength from 215 to 300 nm for RNA (red) and DNA (blue). The dark lines are from representative spectra measured in a 1.00 cm cuvette, then normalized to the average ε₂₆₀ in Table 1; the spectra are not averages over many samples. These absorbance values (divided by 10) would be measured for a 0.100 mM solution of the NMP in a 1.00 cm cuvette. The lighter lines at the left of each curve are from previous studies measured in short pathlength cuvettes with oxygen removed from the samples and flushed from the cell compartment (6,7). These curves were normalized to the darker curves at the minimum near 230 nm (at 235 nm for pC and pdC). For comparison with previous work (6,7), data points are also shown at 5 nm intervals normalized to the ε₂₆₀ (Previous) values in Table 1.

Figure 2.

UV absorbance of the RNA (red) and DNA (blue) 5′-mononucleotides, (a) A, (b) C, (c) G and (d) U and T. This work: dark lines right of the minimum near 230 nm. Squares: spectra from Beaven et al. (6) normalized to ε from Gray et al. (5). Diamonds: spectra from Voet et al. (7) normalized to ε from Gray et al. (5). Light lines at short wavelengths: data from Beaven et al. (6) and Voet et al. (7) normalized at the junction to spectra from this work.

Cytidine-3′-5′-cyclic monophosphate

In addition to the data in Table 1 and Figure 2 for the four standard NMPs, the ε-value was determined for <pC. The average of three determinations was ε₂₆₀ = 7.06 ± 0.02 ODU/µmol, identical to that for pC and pdC within experimental error. The spectrum (not shown) was also nearly indistinguishable from pC and pdC in Figure 2b.

DISCUSSION

Comparison with published UV spectral properties

Extinction coefficients. The most definitive set of mononucleotide extinction coefficients to date was collected by Gray et al. (5). Many of the data for that and other compilations (8–14) derive from the work of Beaven et al. (6), which includes exquisite hand-drawn spectra for A, C, G, U and T in the back cover of the book, and Doty and co-workers (7), which also contains data for dA, dC and dG and accurate measurements at short wavelengths; these authors relied on earlier work (15–19) for most of their extinction coefficients. The data were obtained with recrystallized NMP samples with purity analyzed by thin-layer chromatography. It is uncertain whether impurities could be detected at the level of 2–3%. The samples were dried and weighed to estimate concentrations prior to measurement of UV absorbance to determine extinction coefficients.

The most recent improvement to the mononucleotide extinction coefficients comes from the 1975 PhD dissertation of M.Alexis (20), who was a student of E.G.Richards. Their values were included in the Gray et al. publication (5), and are included in Table 1 under ‘Previous’. The Alexis thesis is not routinely available, so we were fortunate to obtain a copy of the relevant chapter from Dr Gray. The information is summarized here very briefly, and in more detail in Cavaluzzi (2).

The Alexis extinction coefficients were derived from titrations of 5–200 mM solutions of the nucleosides and nucleotides. Adenosine, guanosine and cytidine were titrated with perchloric acid dissolved in glacial acetic acid, with the best defined end point occurring for C. In addition, the disodium salts of pG and pU were titrated with HCl in water, and the free acid of pA was titrated with NaOH. All of the titrations involved at least one of the species as a weak acid or base. This leads to uncertainty in locating the equivalence point. Gran analysis (21) added confidence to the determinations, but ambiguity was apparent and often exacerbated by competing equilibria. Overall, Alexis estimated errors of 2–5% in the extinction coefficients, which is in line with the differences expressed in the last column of Table 1. Alexis also verified each of the nucleotide extinction coefficients by a colorimetric phosphomolybdate analysis similar to that in Baginski et al. (22) and Murphy and Trapane (23); the precision of that method appears to be about ±2–5%.

The previous work appears to have assumed that the ε₂₆₀ values are the same for the cognate DNA and RNA mononucleotides. This is probably a good assumption, but was not made in the present work. That the cognate values in the second column of Table 1 all agree to better than 1% is an encouraging sign regarding the precision of the NMR-based concentration determinations.

It is interesting that the largest deviation between the previous extinction coefficients and this work is for C, the very species for which the end point of the non-aqueous titration should be best determined. Given the ∼7% deviation between our results and the previous work, we performed an additional check with <pC. As noted in Results, pC, pdC and <pC have identical extinction coefficients within experimental error.

Spectra. The collection of spectra in Figure 2 shows that there is generally close agreement between the cognate DNA and RNA spectra. The differences between pA and pdA, pC and pdC, and pG and pdG are probably not significant, although the 250–270 nm maxima are always slightly higher for the deoxyribo- than the ribo-species (except for pT and pU). There is also good agreement between the shapes of the spectra in the current versus previous work for all except C. The difference is most pronounced for the shallow valley near 250 nm. It is possible that the samples used in the previous work had a UV-absorbing contaminant with a peak shifted toward shorter wavelengths. That is the most likely explanation for the fact that the previous ε₂₆₀ values were most in error for C. The fact that nearly all of the older ε₂₆₀ values were too high also suggests that small amounts of UV-absorbing impurities contaminated their samples.

Error analysis

Replicate determinations. One procedure for estimating the precision of a result is to replicate the determination many times. These are expressed in the 95% confidence limits of Table 1. It is seen that all of the determinations are precise within 0.3–0.9% by this estimator. That is a substantial improvement over previous work.

Propagation of measurement errors. Another way to analyze errors is to estimate the error in individual measurements that comprise the determination, then to determine how these errors are likely to propagate into the final result. A benefit of this approach is that one can often identify the largest contributor(s), and the precision of future work can be improved with relatively little additional effort. One might assume that there would be few contributions to errors embodied in a Beer’s law determination (see Equation 1). However, there are at least seven individual operations with errors that can affect the final ε₂₆₀ value. We classified the contributions of errors in terms of the major steps: S1 = NaOH standardization; S2 = CA titration; S3 = CA dilution to NMR concentration; S4 = NMR integral comparison; S5 = NMR setup and spectral acquisition; S6 = errors in D; and S7 = errors in the UV measurement. Some of these have several suboperations; our overall best estimates of percentage error are shown in the second column of Table 2, as obtained from repetitive trials (1,2). The square root of the sum of squared errors is generally a good estimate of the effect of error propagation when the result is computed by product (and divisor) operations as in Equation 1 (24). Thus, the error level should be ∼1% in the extinction coefficient determinations. This is in good agreement with 95% confidence limits expressed in Table 1. It should be noted that S6 and S7 apply only to extinction coefficient measurements, not to the general case of concentration determination by NMR.

Table 2. Error analysis.

	%1	%2
S1	0.20	0.04
S2	0.80	0.64
S3	0.05	0.003
S4	0.50	0.25
S5	0.10	0.01
S6	0.02	0.0004
S7	0.40	0.16
Sum	2.07	1.10
(Sum)1/2		1.05

Note that the dilution errors, S3 and S6, are very small. In our previous publication (1), they were the largest sources of error—limited by the ability to dispense highly accurate volumes via micropipets. It is difficult to deliver liquids more accurately than ±2–3%, even with careful control of micropipet calibration, temperature, viscosity, the use of ‘high precision’ tips, etc. With mass-based dilutions using amounts that can be weighed with three- or four-digit accuracy, dilution errors become small compared with other sources. Now S2 (CA standardization), S4 (NMR integral comparison) and S7 (UV spectrophotometer cell positioning, drift, etc.) are the largest sources of error. (Note that S6 may be underestimated: the current dilutions require weighed aliquots of the NMR sample that are 10–30 mg. This transfer was made carefully and quickly to avoid evaporation, but future work would benefit from using 10- to 30-fold dilutions rather than the current 100- to 300-fold. Such experiments would require a more sensitive NMR spectrometer or serial dilution.)

The current procedure for the CA standardization uses titration against standardized 0.0100 M NaOH. Despite all precautions taken (CO₂-free environment, tiny additions of titrant near the end point, the use of a class A burette), titration results cannot be made with high accuracy for such dilute acids and bases. If the concentration of all solutions were increased by 10 or 100, the resultant titration curves would give more definitive equivalence points. This could be accomplished with larger volumes of D₂O to dilute the primary stock CA to the NMR working stock value in one step, using volumetric glassware. Together with mass-based measurements for the smaller volumes, it is realistic to reduce the S1–S3 errors below 0.05% in future work.

Although repetitive estimates of S4 are for ∼0.5% random error, it is more difficult to assess the possibility of subjective bias in phase correction and integration. To evaluate this possibility, two different people produced virtually identical results and percentage errors from independent trial measurements. Although automatic phase correction software is available, results are not sufficiently reproducible for high quality determinations. Similar subjectivity problems arise in evaluating integrals. A readily available tool for minimizing subjectivity in phasing and integration is to implement curve-fitting programs to quantify peak areas with higher degrees of precision. Misshapen peaks are often more readily apparent in comparing the simulations with the real spectrum. The issues in phasing and integration are most severe when the signals are close to the noise level, or there are nearby peaks. S/N problems can be alleviated by working on a cryoprobe, and the issues of S/N and nearby peaks will be reduced by working with a very high field instrument for ¹H measurements. If the S1–S5 errors can be carefully controlled, it may be possible to use NMR to measure concentrations within 0.5% or even 0.1%.

Finally, errors associated with the UV measurement can be reduced to generate highly accurate extinction coefficients. Highly stable ratio-recording dual-beam instruments are available that position the cuvette with great accuracy for every sample.

Impurities

It may be of little value to have a method for measuring concentrations with high accuracy if the compounds themselves are not pure. For instance, if an accurate extinction coefficient is determined, but later samples have a buffer component or other contaminant that absorbs in the UV, the results will be compromised.

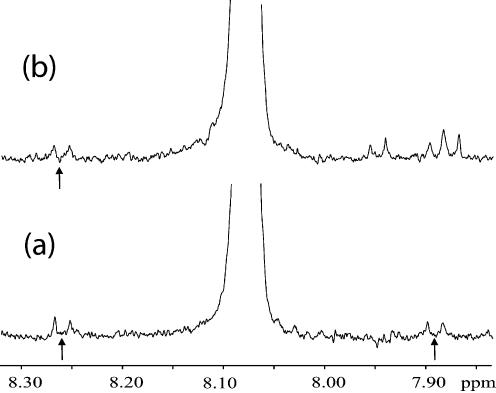
An advantage of NMR for the study of fairly complex biomolecules is that the presence of impurities is often readily apparent. For instance, Figure 3a shows an expansion of the region near the CH6 proton signal from pC in Figure 1. The ¹³C-satellite peaks (arrowed) are symmetrically disposed around the comparatively huge central ¹²C peak. Each satellite peak has 0.55% of the intensity of the central peak, so they make an easy reference to assess impurities in the NMP samples. The pC sample illustrated in Figure 3b clearly shows impurity peaks superimposed upon the rightmost satellite. When the region to the right is integrated, and the contribution of one satellite is subtracted, the impurity constitutes the remainder, i.e. ∼0.8% of the main peak. The contaminant(s) resonate in the aromatic region of the proton spectrum, and probably absorb UV light. Samples that had more than a 1% contribution from impurity peaks were excluded from the averages reported in Table 1. If one were to attempt a further improvement on the accuracy of the extinction coefficients over that in Table 1, it would first be necessary to refine the NMPs to ∼99.9% purity.

Figure 3.

¹³C-satellite (arrows) and impurity peaks surrounding the cytidylate–H6 doublet. (a) Spectrum shown in Figure 1. (b) Spectrum of a sample with impurity peaks overlaid upon the upfield satellite.

Extinction coefficients of DNA and RNA oligomers

A widely accepted method for determining an RNA or DNA extinction coefficient is to compare the absorbance of the intact molecule with that of the limit hydrolysate. RNA can be hydrolyzed overnight in 0.3 M NaOH at 37°C (25); note that this procedure may result in a few percent deamination of C to U. DNA can be hydrolyzed with a mixture of nucleases (26), or the phosphate released in a Kjeldahl apparatus and quantified (23). The latter two methods have been applied to determine ε₂₆₀ values for 18 single-stranded DNA (ssDNA) oligomers of length 9–24 nt (23,26); these measured values are probably accurate within 2–5%. Both determinations were made at room temperature but at different ionic strengths [0.04 M by Murphy and Trapane (23) and 0.11 M by Kallansrud and Ward (26)]. Single-stranded stacking has an insensitive dependence on salt concentration, so changes in UV absorbance should be negligible over this range in ionic strength (the sequences and ε₂₆₀ values are collected in the Supplementary Material available at NAR Online). None of the molecules should form a stable hairpin or duplex (27,28).

The concentrations derived using previous monomer extinction coefficients must be corrected for the new values presented in Table 1. This can be accomplished by multiplying the old concentration by the sum:

X_Af_A + X_Cf_C + X_Gf_G + X_U/Tf_U/T    2

where X_j is the mole fraction of base j, and f_j is the correction factor from Table 1. To correct an extinction coefficient, replace f_j by (f_j)^–1. The f_j factors will differ if a study used a different set of monomer ε₂₆₀ values. The 18 oligomer data set (23,26) used ε₂₆₀ = 15.4, 7.4, 11.5 and 8.7 for dA, dC, dG and T (8–10), so the f_j are 1.0226, 1.0423, 0.9442 and 1.0164, respectively.

The predictions of the three most common methods for calculating extinction coefficients are shown in Figure 4a for the 18 ssDNA data set. Method 1 assumes ε₂₆₀ = 10 ODU/µmol of monomer (33 µg/ODU) for all sequences of short ssDNA (29). For the 18 oligomers, the average of the predicted ε₂₆₀ values is 16% too high (circles in Fig. 4a). [Solid symbols at the left of the Figure are for the ten 15–24mers similar to PCR primers and other DNA probe sequences (GC content from 38 to 80%); open symbols at the right are for the eight 9–16mers with one- or two-base repeating sequences.] Method 2 uses the sum of the monomer extinction coefficients weighted by the number of times each base appears in the sequence (triangles in Figure 4a). Though touted as an improvement over the first method (29), this assumption is usually worse because it ignores hypochromicity effects. In the 18 oligomer test set, the average was 24% too high. Method 3 [squares in Figure 4a (14)] uses nearest-neighbor estimates of extinction coefficients based on mono- and dinucleotide additivity rules (5,8–14). This method also predicts ε₂₆₀ values that are too large, by an average of 14%.

Figure 4.

Deviations between measured and predicted extinction coefficients for 18 ssDNA oligomers. Closed symbols are for non-repetitive (complex) sequences, open symbols for repetitive (simple one- or two-base repeats). (a) Circles have ε₂₆₀ = 10 ODU/µmol of monomer unit (33 µg/ODU); triangles, the weighted sum of mononucleotides; squares, nearest-neighbor estimation (14). (b) Circles have ε₂₆₀ = 8.7 ODU/µmol (38 µg/ODU), and include the correction of Equation 2 for measurements (23,26) that are based on the monomer values of Warshaw (8), Warshaw and Tinoco (9) and Cantor et al. (10). (c) Percentage (A + G) was used to order the 18 DNA sequences. The vertical axis scale is the same for all panels

All three methods predict the complex (non-repetitive) sequences well except for a constant offset of 15–25%. Eliminating the offset and correcting the experimentally derived extinction coefficients (23,26) by Equation 2 provides the excellent fit in Figure 4b. The average error in the prediction using method 1 was adjusted to zero by using ε₂₆₀ = 8.7 ODU/µmol of monomer (38 µg/ODU). The range of errors is only –2% to +3% for the 10 complex sequences (closed circles). We recommend that this value be applied to determine concentrations of non-repetitive ssDNA oligomers. The average of the RNA mononucleotide extinction coefficients is slightly higher than for DNA, primarily due to the larger ε₂₆₀ value for pU than for pT. Therefore, ε₂₆₀ = 8.9 ODU/µmol of monomer (37 µg/ODU) is recommended for complex ssRNA sequences.

In comparing the open circles in Figure 4b and c, it is apparent that the calculated minus experimental ε₂₆₀ values correlate inversely with (A + G) content for ssDNA in simple repetitive sequences. However, the complex sequences display no similar correlation. Thus, the complex sequences appear to have a negligible influence from sequence or single-stranded stacking on the extinction coefficients, while effects are pronounced for the simple sequences. Why should that be? Two possible explanations occur to us: (i) it is possible that some of the simple sequences have unusual base-stacked structures accentuated by a repeating pattern of neighbors; or (ii) variations due to hypochromicity and monomer extinction coefficients may balance in sequences that are complex enough. Hypochromicity effects are largest when A and G are involved as neighbors and smallest with C and U/T (8–10). This tends to cancel the fact that A and G have the largest extinction coefficients. Each of the non-repetitive sequences in the data set has 7–12 of the 16 possible nearest-neighbor combinations, while the simple sequences have only one or two. Thus the ε₂₆₀ values of the simple sequences may skew toward their constituent monomers modulated by only one or two hypochromicity contributions.

At present, there is not sufficient information to reliably predict the extinction coefficients of double-stranded DNA (dsDNA), dsRNA, and mixed double- and single-stranded structures. Our laboratory has engaged in preliminary work directed toward this goal. A procedure to accommodate simple, but accurate corrections for non-standard nucleotides is also of interest.

Significance of NMR-based extinction coefficients and concentrations

What impact will the revisions to mononucleotide extinction coefficients have on the determination of the concentrations of oligomers and polynucleotides? In a limit digest of an RNA molecule of equal amounts of A, C, G and U, the revised extinction coefficients generate a concentration ∼4% higher than expected using the old values. There is a 2–3% increase for an average-composition DNA. Using the data in Table 1, it is possible to obtain extinction coefficients within 2–5% from limit digests of ∼1 ODU of single-, double and mixed double- and single-stranded sequences. The uncertainty may be reduced if it can be established that: digestion is >99% complete; there is little or no deamination of C or other base modification during the hydrolysis; the sample has no UV-absorbing impurities; and volume errors are negligible. NMR, together with mass-based dilution, can be used to obtain concentrations at 1% accuracy with ∼100 ODU of a 20mer using the methods described above. Such quantities are routinely produced by solid-phase synthesis on the 1 µmol scale. Equivalent amounts of a cloned and over-expressed protein are commonly produced from 1–2 l cultures. It should be possible to reduce these amounts by a factor of 10 or more for an NMR spectrometer equipped with a cryoprobe. In many applications, NMR would probably be used to establish an accurate extinction coefficient, which would be used in subsequent concentration determinations.

Carefully determined extinction coefficients will not be necessary for some purposes. The approximations for non-repetitive sequences of 38 µg/ODU for ssDNA and 39 µg/ODU for ssRNA should have wide application. However, poorly approximated extinction coefficients are not sufficient if the intent is to determine an accurate equilibrium constant (and free energy) for an interacting system. An eventual goal is to develop procedures to determine concentrations within ±0.1% accuracy.

NMR is one of the few widely available tools that can determine concentrations of nearly the whole range of biochemical and chemical substances. The ability to make highly accurate measurements of concentration could bring a new level of predictive capacity for the study of interacting systems of proteins, nucleic acids, drug candidates and other important biochemicals.

SUPPLEMENTARY MATERIAL

Supplementary material available at NAR Online includes the UV absorbance data for the nucleoside-5′-monophosphates shown in Figure 2, and the data on which Figure 4 was based.