Abstract
Mesophyll conductance (gm) can markedly limit photosynthetic CO2 assimilation and is required to estimate the parameters of the Farquhar–von Caemmerer–Berry (FvCB) model properly. The variable J (electron transport rate) is the most frequently used method for estimating gm, and the correct determination of J is one of its requirements. Recent evidence has shown that calibrating J can lead to some errors in estimating gm, but to what extent the parameterization of the FvCB model is affected by calibrations is not well known. In addition to determining the FvCB parameters, variants of the J calibration method were tested to address whether varying CO2 or light levels, possible alternative electron sinks, or contrasting leaf structural properties might play a role in determining differences in αβ, the product of the leaf absorptance (α) and the photosystem II optical cross-section (β). It was shown that differences in αβ were mainly attributed to the use of A/Ci or A/PPFD curves to calibrate J. The different αβ values greatly influenced gm, leading to a high number of unrealistic values in addition to affecting the estimates of the FvCB model parameters. A new approach was devised to retrieve leaf respiration in the light from combined A/Ci and A/Cc curves and a framework to understand the high variation in observed gm values. Overall, a background is provided to decrease the noise in gm, facilitating data reporting and allowing better retrieval of the information presented in A/Ci and A/Cc curves.
Key words: A/Ci curve fitting, chlorophyll fluorescence, Coffea arabica, Limonium gibertii, Nicotiana tabacum, variable J method.
Introduction
Photosynthesis is a major process that affects plant growth and crop productivity. In addition to stomatal and biochemical factors, the photosynthetic capacity of leaves is also determined by the mesophyll conductance (gm), which regulates the CO2 flux from the intercellular airspaces to the sites of carboxylation in the chloroplastic stroma (Flexas et al., 2012). Early gas exchange studies assumed infinite and constant gm, implying that the CO2 concentrations in the substomatal cavities (Ci) and chloroplasts (Cc) would be the same (Farquhar et al., 1980). However, the role of finite gm limiting photosynthesis in response to several biotic and abiotic stresses (Flexas et al., 2008), as well as its importance in constraining maximum photosynthetic rates, particularly in evergreen sclerophylls (Warren et al., 2004; Niinemets et al., 2011), is now well established. Actually, there is a general consensus that gm must be incorporated into the Farquhar–von Caemmerer–Berry (FvCB) model of leaf photosynthesis (Farquhar et al., 1980) because this model underestimates the maximum Rubisco carboxylation rate (Vcmax) when gm is considered to be infinite (Ethier and Livingston, 2004; Niinemets et al., 2009a ).
Several methods to estimate gm have been reported (Warren, 2006; Pons et al., 2009). Among them, those based on gas exchange coupled with the chlorophyll fluorescence technique have been extensively used. In particular, the variable J method (where J stands for electron transport rate, usually measured using chlorophyll fluorescence analysis) is the most widespread method because it allows the point-specific estimation of gm as well as tracking how gm supposedly changes in response to varying light or CO2 (Pons et al., 2009). However, the variable J method is highly sensitive to errors in some parameters, especially the CO2 compensation point in the absence of photorespiration (Γ*) and J (Harley et al., 1992). Importantly, J needs to be calibrated due to the uncertainties in both the leaf absorptance (α) and photosystem II (PSII) optical cross-section (β).
The J calibration is based on the analysis of response curves of photosynthetic rates to light [A/photosynthetic photon flux density (PPFD)] or CO2 (A/C
i) under non-photorespiratory conditions, typically under low (1–2%) oxygen conditions. Under these circumstances, the relationship between J calculated through gas exchange (J
A) and chlorophyll fluorescence (J
F) is expected to be linear because electron transport flow is primarily associated with Rubisco carboxylation. Consequently, J
A can be calculated as J
A=4(A+RL) (Warren, 2006). Other assumptions are that αβ or light respiration (R
L) values do not change in response to varying C
i or PPFD. To date, three different approaches have been used to calibrate J: the relationship between the quantum yield of PSII (ФPSII) and CO2 ( ) (Valentini et al., 1995), the relationship between J
A and J
F (Pons et al., 2009), and the plot of A versus PPFD ФPSII/4, which is also used to estimate R
L (Yin et al., 2009). Another point deserving attention is the use of A/PPFD or A/C
i curves under low O2 to perform the calibration; ideally, both curves should give the same results. However, as observed by Yin et al. (2009), fundamental differences exist when choosing A/PPFD or A/C
i curves to calibrate J. First, when using the full A/C
i curve, photorespiration can still occur at low CO2 levels. Alternatively, the excess of energy can increase the rate of alternative electron flow. Both cases can compromise the linearity of the relationship between J
A and J
F. The same problem occurs in A/PPFD curves, where higher PPFD intensities can induce alternative electron flow (depending on g
s, low C
i can occur as well). To overcome this problem, Yin et al. (2009) recommended using the electron transport-limited regions of both curves, namely the combination of low light levels from A/PPFD and high C
i levels from A/C
i, which would ultimately minimize the risk of photorespiration and alternative electron flow.
) (Valentini et al., 1995), the relationship between J
A and J
F (Pons et al., 2009), and the plot of A versus PPFD ФPSII/4, which is also used to estimate R
L (Yin et al., 2009). Another point deserving attention is the use of A/PPFD or A/C
i curves under low O2 to perform the calibration; ideally, both curves should give the same results. However, as observed by Yin et al. (2009), fundamental differences exist when choosing A/PPFD or A/C
i curves to calibrate J. First, when using the full A/C
i curve, photorespiration can still occur at low CO2 levels. Alternatively, the excess of energy can increase the rate of alternative electron flow. Both cases can compromise the linearity of the relationship between J
A and J
F. The same problem occurs in A/PPFD curves, where higher PPFD intensities can induce alternative electron flow (depending on g
s, low C
i can occur as well). To overcome this problem, Yin et al. (2009) recommended using the electron transport-limited regions of both curves, namely the combination of low light levels from A/PPFD and high C
i levels from A/C
i, which would ultimately minimize the risk of photorespiration and alternative electron flow.
More recently, Gilbert et al. (2012) examined the use of A/PPFD or A/Ci curves to calibrate J and demonstrated dramatic changes in g m values estimated using either the A/PPFD or A/C i curves. However, to what extent these calibrations affect estimates of photosynthetic parameters such as V cmax or J max, and whether this effect is dependent on the species studied, remain unresolved. Flexas et al. (2007) found no differences using both calibrations for tobacco, and extrapolated this result to other species where only the A/PPFD calibration was used. Hassiotou et al. (2009), using the calibration based on A/C i curves performed under two light levels, concluded that calibration is light dependent. Other studies did not use the A/PPFD or A/C i calibration, but estimated α using integrating spheres and assumed a β value of 0.5 (e.g. Galmés et al., 2007; Tosens et al., 2012), even though β has been reported to vary (Laisk and Loreto, 1996). Collectively, these results reveal no consensus on how to calibrate J, even though g m estimated by the variable J method is mainly dependent on J. In addition, because the fluorescence signal primarily emanates from the upper mesophyll layers, but gas exchange parameters are volume based (Warren et al., 2006), measured J and estimated g m are most probably less representative of the whole leaf in species with lower specific leaf area (SLA; leaf area per unit dry mass).
The main questions asked in this study were as follows. (i) How do the J calibrations affect g m? (ii) How might these calibrations be translated into the FvCB parameters? (iii) Would the calibrations be dependent on species? To answer these questions, measurements were carried out using three species with contrasting SLA and photosynthetic capacities. The results highlight how g m, V cmax, and J max may be affected by using A/C i or A/PPFD curves under low O2 to calibrate J. The results are discussed in the context of current models of g m estimations.
Materials and methods
Plant material and growth conditions
Limonium gibertii (Senn.) Senn. and Nicotiana tabacum L. seeds were germinated, and plants were grown outdoors under typical Mediterranean climate conditions (Balearic Islands, Spain, 39°38ʹN, 2°38ʹE, 85 m a.s.l.) in 4 litre pots with a commercial substrate (horticultural peat) and perlite at a proportion of 4:1. Seedlings of Coffea arabica L. obtained from seeds were grown outdoors under subtropical conditions in Viçosa (20°45ʹS, 42°15ʹW, 650 m a.s.l.), southeastern Brazil, using 12 litre pots containing a mixture of soil, sand, and composted manure (4:1:1, v/v/v). Plants were irrigated and fertilized as required. Measurements were performed during the summer (growing season) on ~1-year-old plants in the case of C. arabica and L. gibertii, and 1-month-old plants in the case of N. tabacum, on 4–6 plants per species.
Gas exchange and fluorescence measurements
Leaf gas exchange and chlorophyll a fluorescence were measured simultaneously with an open-flow infrared gas-exchange analyser system equipped with a leaf chamber fluorometer (LI-6400XT, Li-Cor, Lincoln, NE, USA). Environmental conditions in the leaf chamber consisted of a leaf-to-air vapour pressure deficit of 1.2–2.0 kPa and a leaf temperature of 25 °C.
In light-adapted leaves, the actual ФPSII was determined by measuring steady-state fluorescence (F s) and maximum fluorescence during a light-saturating pulse of ~8000 μmol m–2 s–1 (F mʹ), following the procedures of Genty et al. (1989):
| ФPSII=(Fmʹ–Fs)/Fmʹ | (1) |
The electron transport rate (JF) was then calculated as:
| JF=αβ PPFD ФPSII | (2) |
where PPFD is the photosynthetically active photon flux density, α is the leaf absorptance, and β is the PSII optical cross-section. The product αβ was determined from the relationship between ФPSII and 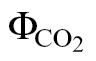 or A and PPFDФPSII/4, obtained by varying either the light intensity or the CO2 concentration under non-photorespiratory conditions in an atmosphere containing <1% O2 (Valentini et al., 1995; Yin et al., 2009).
or A and PPFDФPSII/4, obtained by varying either the light intensity or the CO2 concentration under non-photorespiratory conditions in an atmosphere containing <1% O2 (Valentini et al., 1995; Yin et al., 2009).
Four to six A/C i and A/PPFD curves under <1% O2 (A/PPFD and A/C i) or 21% O2 (only A/C i) were obtained from different plants for each species. In light-adapted leaves, A/C i curves were initiated at an ambient CO2 concentration (C a) of 400 μmol mol–1 under a saturating PPFD of 1500 μmol m–2 s–1. Once steady state was reached, C a was decreased stepwise down to 50 μmol mol–1 air. Upon completion of the measurements at low C a, it was returned to 400 μmol mol–1 air to restore the original A. Next, C a was increased stepwise to 2000 μmol mol–1 air. For the A/PPFD curves, C a was held at 400 μmol mol–1, and the curve was initiated at a PPFD of 1500 μmol m–2 s–1; then, PPFD levels were decreased to 0 μmol m–2 s–1. Both the A/C i and A/PPFD curves consisted of 11–13 different C a values or PPFD intensities.
C c was calculated after Harley et al. (1992) as:
| Cc={Γ*[JF+8(A+RL)]}/[JF–4(A+RL)] | (3) |
where Γ* was determined from the in vitro Rubisco specificity factor (S c/o) (see below) as:
| Γ*=O/Sc/o | (4) |
A was taken from gas-exchange measurements, and the J F values were obtained from chlorophyll a fluorescence yield. The rate of mitochondrial respiration at darkness (R dark) was measured early in the morning in dark-adapted leaves, and it was divided by two (R dark/2) to serve as a proxy for R L.
After estimating C c, g m was calculated as follows (Harley et al., 1992):
| gm=A/(Ci–Cc) | (5) |
From the A/C i and A/C c curves, the maximum carboxylation capacity (V cmax) and maximum capacity for electron transport rate (J max) were calculated on a C i and C c basis using the kinetic parameters of Rubisco described below and, for comparative purposes, those described in Bernacchi et al. (2002). The FvCB model was fitted to the data by applying iterative curve fitting (minimum least square difference) using the Microsoft Excel Solver tool (Microsoft Corporation, Redmond, WA, USA). Additionally, g m, V cmax, and J max were estimated using the Ethier and Livingston (2004) method, which is based on fitting A/C i curves with a non-rectangular hyperbola version of the FvCB model, relying on the hypothesis that g m reduces the curvature of the Rubisco-limited portion of an A/C i response curve. For the method based on fitting A/C i curves, species-specific S c/o values were used as in the Harley method. Corrections for the leakage of CO2 and water vapour into and out of the leaf chamber of the Li-6400–40 have been applied to all gas-exchange data, as described by Rodeghiero et al. (2007). The percentage corrections applied to CO2 and water vapour flux rates are shown in Supplementary Table S1 available at JXB online for the different species.
Calibration relationships
The relationship between J
A and J
F was calibrated using the linear plot of ФPSII and 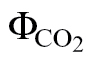 , based on Valentini et al. (1995):
, based on Valentini et al. (1995):
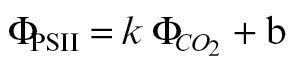 |
(6) |
| JF=4(ФPSII–b) PPFD/k | (7) |
where 4/k=αβ. k and b were obtained through the linear fit of ФPSII versus 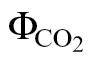 .
.
In addition, the method based on Yin’s approach was also used (Yin et al., 2009), which presents a straightforward way to derive αβ and R L, as follows:
| JA=4 (A+RL) | (8) |
| JF=αβ PPFD ФPSII | (9) |
J A is rewritten as
| A=JA/4–RL | (10) |
Assuming J A=J F under non-photorespiratory conditions gives
| A=αβ PPFD ФPSII/4–RL | (11) |
As Equation 11 has the form of y=ax+b, through the linear fit of A versus PPFDФPSII/4, R L can be retrieved as the y-intercept, and αβ can be retrieved as the slope of the regression. Notably, this equation presented by Yin et al. (2009) has an extension of the FvCB model to account for alternative electron fluxes in the form of pseudocyclic (f pseudo) and cyclic (f cyc) electron flow (see further details in Yin et al., 2004):
| A=αβ PPFD ФPSII {1–[fpseudo/(1–fcyc)]}/4–RL | (12) |
According to the updated model, to accomplish Equation 8, not only are non-photorespiratory conditions required but also the down-regulation of alternative electron fluxes so that low values of f pseudo and f cyc allow Equation 12 to be as close as possible to Equation 11, thus reliably estimating αβ.
Four types of calibration were devised based on the approaches of Valentini and Yin described above. The first and second calibration methods were based on the ФPSII/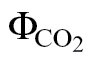 relationship, and the third and fourth methods were based on Yin et al. (2009) as follows:
relationship, and the third and fourth methods were based on Yin et al. (2009) as follows:
(i) ФPSII/
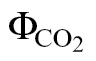 (A/C
i): this calibration is performed using the entire A/C
i curve under low O2, and the PPFD level is that used in the normal A/C
i curve (i.e. 1500 μmol m–2 s–1). The R
L value must be assumed. In this variant, the initial part of the A/C
i curve is the most susceptible region for the occurrence of alternative electron sinks due to a high reductant (ATP and NADPH) supply associated with high PPFD and a limitation on reductant use (low CO2 and O2). Conversely, this variant most resembles the conditions used in the normal A/C
i curve.
(A/C
i): this calibration is performed using the entire A/C
i curve under low O2, and the PPFD level is that used in the normal A/C
i curve (i.e. 1500 μmol m–2 s–1). The R
L value must be assumed. In this variant, the initial part of the A/C
i curve is the most susceptible region for the occurrence of alternative electron sinks due to a high reductant (ATP and NADPH) supply associated with high PPFD and a limitation on reductant use (low CO2 and O2). Conversely, this variant most resembles the conditions used in the normal A/C
i curve.(ii) ФPSII/
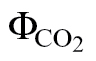 (PPFD >400 μmol m–2 s–1): this is the variant more often reported in the literature and consists of using A/PPFD curves under low O2 and ambient CO2. A disadvantage of this variant is that a loss of linearity occurs at low PPFD, as
(PPFD >400 μmol m–2 s–1): this is the variant more often reported in the literature and consists of using A/PPFD curves under low O2 and ambient CO2. A disadvantage of this variant is that a loss of linearity occurs at low PPFD, as 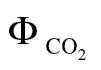 is affected disproportionately by errors in respiration estimations or by the increase in mitochondrial respiration at low light (the Kok-effect; Brooks and Farquhar, 1985). Thus, it is recommended to exclude
is affected disproportionately by errors in respiration estimations or by the increase in mitochondrial respiration at low light (the Kok-effect; Brooks and Farquhar, 1985). Thus, it is recommended to exclude 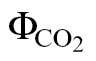 values >0.05 to keep the relationship as linear as possible (Seaton and Walker, 1990; Edwards and Baker, 1993). To meet this criterion, PPFD levels below 400 μmol m–2 s–1 had to be excluded, making this method prone to a high reductant supply (high PPFD) and intermediate reductant use (moderate CO2 and low O2).
values >0.05 to keep the relationship as linear as possible (Seaton and Walker, 1990; Edwards and Baker, 1993). To meet this criterion, PPFD levels below 400 μmol m–2 s–1 had to be excluded, making this method prone to a high reductant supply (high PPFD) and intermediate reductant use (moderate CO2 and low O2).(iii) Yin (PPFD <400 μmol m–2 s–1): this variant was originally described by Yin et al. (2009), and it can also be used to estimate R L. As this method is not based on quantum efficiency plots, there is not the disadvantage of having to exclude the points at low PPFD or assume a given R L value. Actually, it is recommended to use only the points at the linear phase of the A/PPFD (corresponding to PPFD levels <400 μmol m–2 s–1 for the species grown outdoors), which is in the range of a lower reductant supply and where only the basal components of alternative electron sinks exist.
(iv) Yin (PPFD <400 μmol m–2 s–1/C i >500 μmol mol–1 air): this method has the same advantages and assumptions of method (iii). A particularity of this approach resides in the incorporation of data from the A/C i curve with C i above 500 μmol mol–1 air.
Retrieving the respiration value from combined A/C i and A/C c curves
The FvCB model predicts that A/C i curves and their A/C c counterparts share the same CO2 compensation point (Γ), as this parameter is independent of g m:
| Γ=[Γ*+Kc(1+O/Ko)RL/Vcmax]/(1–RL/Vcmax) |
Evans and von Caemmerer (1996) proposed that an averaged g m can be estimated as the slope of the plot of A versus C i–C c. Because the plot goes through the origin, both A and C i–C c must be zero, which is what occurs when Γ is shared by both A/C i and A/C c curves, as predicted by the FvCB model.
It was realized that for some data sets, when R
L was set in advance as required to obtain C
c, the plot of A versus C
i–C
c in the region which was Rubisco limited showed good linearity, although with an intercept differing from zero. Given the predictions of the FvCB model, this difference should be attributed to a biased R
L used to calculate C
c, which in turn leads to different Γ values, as obtained from the A/C
i and A/C
c curves. Given this fact and that the Γ* values in this study were reliably estimated from Rubisco kinetics in purified preparations, it is proposed here that R
L can be obtained as the value that makes the intercept of the plot of A versus C
i–C
c equal zero. The approach was tested using ideal data sets where the respiration values used as inputs were successfully retrieved from the combined A/C
i and A/C
c curves. Consequently, for each curve, R
L was estimated as described below. First, R
L was set to be equal to R
dark/2, as set in previous studies (Niinemets et al., 2005, 2006, 2009b
). To maintain the plot A versus C
i–C
c as linear as possible, only points in the C
i range strictly limited by Rubisco (C
i <200 μmol mol–1 air) were considered. Secondly, the new R
L was obtained as the value that forces the intercept of the plot A versus C
i–C
c to be zero using the Goal Seek function available in Microsoft Excel (see Fig. 1 for an example). The new respiration value obtained in this way is hereafter referred to as 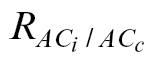 . An Excel spreadsheet (with modelled and real data) is available (see Supplementary Spreadsheet S1 at JXB online) that shows how this method was performed.
. An Excel spreadsheet (with modelled and real data) is available (see Supplementary Spreadsheet S1 at JXB online) that shows how this method was performed.
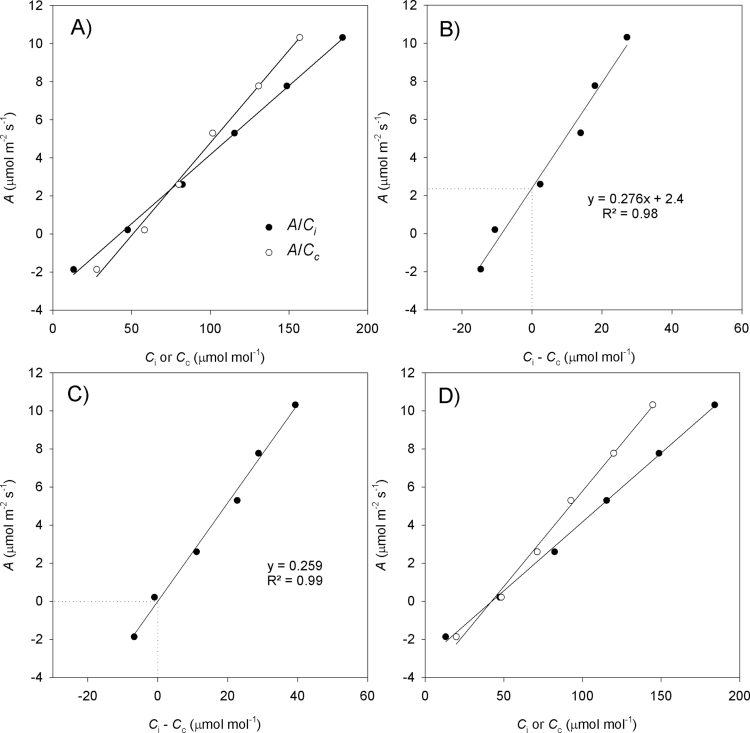
Fig. 1.
Graphical representation of the method utilized to retrieve the respiration value from the combined A/C
i and A/C
c curves (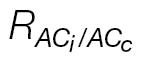 ). The example is based on values measured in an N. tabacum leaf. (A) The initial part of an A/C
i (filled circles) and the respective A/C
c (open circles) curve considering R
L=R
dark/2 (1.1 μmol CO2 m–2 s–1). (B) C
i–C
c from the curves presented in (A) plotted against A. The y-axis positive intercept (2.4) when x=0 (see the dotted lines) means negative g
m for A lower than the intercept because C
i >C
c. The slope of the linear regression (0.276) is an estimation of averaged g
m over the range of C
i used in the linear fit. (C) By adjusting to zero the intercept in the relationship A versus C
i–C
c, a new respiration value,
). The example is based on values measured in an N. tabacum leaf. (A) The initial part of an A/C
i (filled circles) and the respective A/C
c (open circles) curve considering R
L=R
dark/2 (1.1 μmol CO2 m–2 s–1). (B) C
i–C
c from the curves presented in (A) plotted against A. The y-axis positive intercept (2.4) when x=0 (see the dotted lines) means negative g
m for A lower than the intercept because C
i >C
c. The slope of the linear regression (0.276) is an estimation of averaged g
m over the range of C
i used in the linear fit. (C) By adjusting to zero the intercept in the relationship A versus C
i–C
c, a new respiration value, 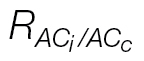 , is obtained (0.4 μmol CO2 m–2 s–1), and the same CO2 compensation point is now shared by both curves (C
i–C
c=0 at A=0). The influence of the new respiration on g
m can be observed as the modified slope (0.259). (D) The modified initial part of the A/C
i and A/C
c curves calculated with
, is obtained (0.4 μmol CO2 m–2 s–1), and the same CO2 compensation point is now shared by both curves (C
i–C
c=0 at A=0). The influence of the new respiration on g
m can be observed as the modified slope (0.259). (D) The modified initial part of the A/C
i and A/C
c curves calculated with 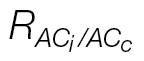 .
.
Rubisco kinetic parameters
The Rubisco kinetic parameters used in this study were measured in vitro, except the S c/o values for N. tabacum and L. gibertii, which were taken from Galmés et al. (2006) and Galmés et al. (2005), respectively. All measurements for the determination of Rubisco kinetic parameters were conducted at 25 °C. The Rubisco specificity factor was measured in highly purified extracts and using wheat Rubisco as a reference normalized to 100, following the procedures described in Galmés et al. (2005). The Michaelis–Menten constants for CO2 (K c) and O2 (K o) and the maximum rate for the carboxylase reaction (V cmax) were measured in rapidly isolated leaf protein extracts (Sharwood et al., 2008). Briefly, ~0.5g fresh weight of leaves were ground in a mortar with 2ml of ice-cold extraction buffer containing 100mM Bicine (pH 8.2), 6% (w/v) polyethylene glycol (PEG) 4000, 2mM MgCl2, 0.1mM EDTA, 1mM benzamidine, 1mM ε-aminocaproic acid, 50mM 2-mercaptoethanol, 10mM dithiothreitol (DTT), 2 μM pepstain A, 10 μM E64, 10 μM chymostatin, 2mM phenylmethylsulphonyl fluoride (PMSF), and 2.5% (w/v) polyvinylpolypyrrolidone (PVPP). The liquidized sample was clarified by centrifugation at 12 842 g for 4min. A 1ml aliquot of clarified extract was eluted using a Sephadex PD-10 column (GE Healthcare, UK) pre-equilibrated with desalt buffer containing 100mM Bicine (pH 8.2), 20mM MgCl2, 10mM DTT, 1mM KH2Pi, 0.5mM EDTA, 1mM benzamidine, 1mM ε-aminocaproic acid, and 10mM NaHCO3. The protein peak (in 1ml) was supplemented with protease inhibitors (4 μM pepstain A, 20 μM E64, and 20 μM chymostatin). Of this extract, 250 μl was supplemented with 2.542 μCi NaH14CO3 and activated for 15min before carboxylase measurements. The remainder was used to assay Rubisco catalytic sites. Measurements of K c and V cmax for the carboxylase activity in nitrogen or air were determined in two sets of eight vials from the amount of 14C incorporated into PGA, as described elsewhere (Bird et al., 1982). Each set of vials used eight different concentrations of bicarbonate chosen to provide CO2 (aq) between 0.7 μM and 75 μM, each with a specific radioactivity of 3.7×1010 Bq mol–1 and containing 375 nmol RuBP. K o was calculated from the relationship K c (air)=K c (N2)×{1+[O2]/K o}. The concentration of Rubisco catalytic sites in the extract was measured from the stoichiometric binding of the inhibitor [14C]CABP to CO2-Mg2+-activated Rubisco active sites (Butz and Sharkey, 1989). Thereafter, the carboxylase catalytic turnover rate K cat c was obtained as K cat=V cmax/[catalytic sites]. The Rubisco kinetic constants are summarized in Table 1.
Table 1.
Rubisco kinetic constants measured for the species studied: specificity factor (Sc/o), CO2 compensation point in the absence of respiration (Γ*), Michaelis–Menten kinetics for CO2 (K c) and O2 (K o), and catalytic turnover rate for the carboxylase reaction (K cat)
| Species | S c/o | Γ* (μbar) | K c (μM) | K o (μM) | K cat (s–1) |
|---|---|---|---|---|---|
| N. tabacum | 98.1±2.6a | 39.7±1.1 | 12.4±0.7 | 274±42 | 3.2±0.3 |
| C. arabica | 98.4±4.3 | 39.6±1.7 | 10.3±1.3 | 479±113 | 3.2±0.1 |
| L. gibertii | 110.5±1.6b | 35.2±0.5 | 8.9±0.5 | 593±75 | 2.7±0.8 |
Values are the means ±standard error of 3–4 replicates per species.
a Taken from Galmés et al. (2006)
b Taken from Galmés et al. (2005).
Statistical analyses
Data are expressed as the means ±standard error. Student’s t-tests were used to compare the photosynthetic parameters calculated with the different sets of Rubisco kinetic constants and to examine whether the intercepts of the regression were significantly different from zero. Linear regression and statistical analyses were carried out using Microsoft Excel.
Results
The effect of the different calibration methods on αβ
The four calibration methods tested here comprised scenarios ranging from a low (Yin PPFD <400 μmol m–2 s–1) to a high reductant supply (ФPSII/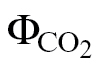 PPFD >400 μmol m–2 s–1), all performed under non-photorespiratory conditions, although potentially affected by the occurrence of an alternative electron flow. Additionally, three species covering a large range in SLA (33±1.4, 14±2.7, and 9.0±1.3 m2 kg–1 for N. tabacum, C. arabica, and L. gibertii, respectively) were selected to assess the extent to which structural changes might play a role in determining the αβ product.
PPFD >400 μmol m–2 s–1), all performed under non-photorespiratory conditions, although potentially affected by the occurrence of an alternative electron flow. Additionally, three species covering a large range in SLA (33±1.4, 14±2.7, and 9.0±1.3 m2 kg–1 for N. tabacum, C. arabica, and L. gibertii, respectively) were selected to assess the extent to which structural changes might play a role in determining the αβ product.
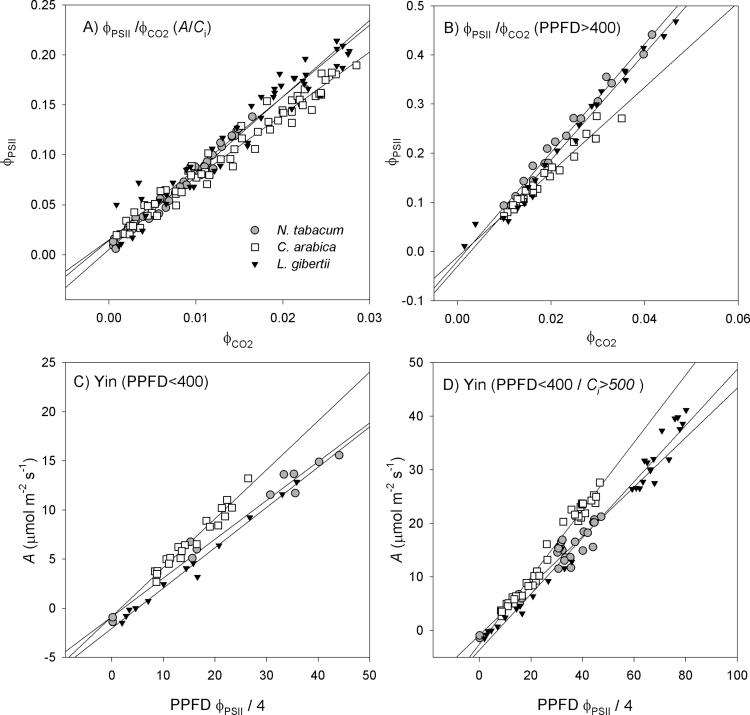
High regression coefficients were obtained for all of the relationships based on the four calibration methods (r
2=0.91–0.98) (Fig. 2). In contrast to expectations, no major differences in the estimation of αβ were found between the methods Yin (PPFD <400 μmol m–2 s–1) and ФPSII/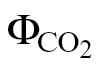 (PPFD >400 μmol m–2 s–1) (Fig. 2B, C) and between ФPSII/
(PPFD >400 μmol m–2 s–1) (Fig. 2B, C) and between ФPSII/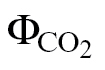 (A/C
i) and Yin (PPFD <400/C
i >500 μmol mol–1 air) (Fig. 2A, D). Thus, the inclusion of data at high PPFD or low C
i, conditions that favour the prevalence of alternative electron fluxes, had slight effects on the estimated αβ. Instead, the major differences among the calibration methods were dependent on the type of data used to perform the calibration [i.e. A/PPFD or A/C
i curves (Table 2)]. Regardless of the studied species, the calibrations using only A/PPFD data gave lower αβ values, ranging from 0.37 to 0.50, whereas those using A/C
i data produced higher αβ values, ranging from 0.46 to 0.62 (Table 2). Notably, the species displaying the most contrasting SLA values (N. tabacum and L. gibertii) showed similar values for αβ, suggesting that leaf structure does not play a major role in determining αβ.
(A/C
i) and Yin (PPFD <400/C
i >500 μmol mol–1 air) (Fig. 2A, D). Thus, the inclusion of data at high PPFD or low C
i, conditions that favour the prevalence of alternative electron fluxes, had slight effects on the estimated αβ. Instead, the major differences among the calibration methods were dependent on the type of data used to perform the calibration [i.e. A/PPFD or A/C
i curves (Table 2)]. Regardless of the studied species, the calibrations using only A/PPFD data gave lower αβ values, ranging from 0.37 to 0.50, whereas those using A/C
i data produced higher αβ values, ranging from 0.46 to 0.62 (Table 2). Notably, the species displaying the most contrasting SLA values (N. tabacum and L. gibertii) showed similar values for αβ, suggesting that leaf structure does not play a major role in determining αβ.
Fig. 2.
Calibration relationships ФPSII versus 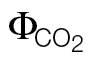 (A and B) and A versus PPFD ФPSII/4 (C and D) measured under non-photorespiratory conditions (<1% O2) by varying PPFD intensities (A/PPFD curves) or substomatal CO2 concentrations (A/C
i curves). For more details on the four calibration methods, see the Materials and methods. In (A), the entire A/C
i curve is utilized; in (B), only values at PPFD >400 μmol m–2 s–1 are considered; in (C), only values at PPFD <400 μmol m–2 s–1 are used; in (D), only values at PPFD <400 μmol m–2 s–1 plus C
i >500 μmol mol–1 are considered. The slope of the lines in all graphs refers to the product αβ, whereas the y-intercept should be interpreted as the presence of alternative electron sinks in A and B and as a measure of R
L in C and D. The values of the slopes and intercepts are summarized in Table 2. Only
(A and B) and A versus PPFD ФPSII/4 (C and D) measured under non-photorespiratory conditions (<1% O2) by varying PPFD intensities (A/PPFD curves) or substomatal CO2 concentrations (A/C
i curves). For more details on the four calibration methods, see the Materials and methods. In (A), the entire A/C
i curve is utilized; in (B), only values at PPFD >400 μmol m–2 s–1 are considered; in (C), only values at PPFD <400 μmol m–2 s–1 are used; in (D), only values at PPFD <400 μmol m–2 s–1 plus C
i >500 μmol mol–1 are considered. The slope of the lines in all graphs refers to the product αβ, whereas the y-intercept should be interpreted as the presence of alternative electron sinks in A and B and as a measure of R
L in C and D. The values of the slopes and intercepts are summarized in Table 2. Only 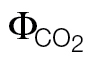 values <0.05 were kept in the plots, as recommended by Seaton and Walker (1990). The scales have different amplitudes according to the calibration. In the plots, data from 4–6 A/PPFD or A/C
i curves are used for the linear regression.
values <0.05 were kept in the plots, as recommended by Seaton and Walker (1990). The scales have different amplitudes according to the calibration. In the plots, data from 4–6 A/PPFD or A/C
i curves are used for the linear regression.
Table 2.
Slopes (αβ) and light respiration following the method of Yin et al. (2011) (R
L,Yin, μmol CO2 m–2 s–1) or intercept values (ФPSII/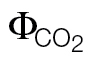 ) obtained under non-photorespiratory conditions according to different approaches, consisting of higher (ФPSII/
) obtained under non-photorespiratory conditions according to different approaches, consisting of higher (ФPSII/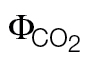 A/C
i or PPFD >400 μmol m–2 s–1) or lower (Yin PPFD <400 or PPFD <400 μmol m–2 s–1 and C
i >500 μmol mol–1 air) susceptibilities to alternative electron sinks
A/C
i or PPFD >400 μmol m–2 s–1) or lower (Yin PPFD <400 or PPFD <400 μmol m–2 s–1 and C
i >500 μmol mol–1 air) susceptibilities to alternative electron sinks
For comparison, the original slopes (k) obtained when using the ФPSII/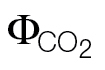 relationship were already converted to αβ (αβ=4/k); the intercept refers to the parameter b in the equation: ФPSII = k
relationship were already converted to αβ (αβ=4/k); the intercept refers to the parameter b in the equation: ФPSII = k 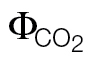 +b.
+b.
| Slope (αβ) | Intercept (ФPSII/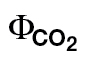 ) ) |
R L,Yin | ||
|---|---|---|---|---|
| N. tabacum | ФPSII/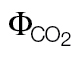 (A/C
i) (A/C
i) |
0.52±0.013 | 0.005±0.002 | |
ФPSII/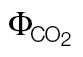 (PPFD >400) (PPFD >400) |
0.36±0.011 | –0.02±0.008* | ||
| Yin (PPFD <400) | 0.39±0.017 | 0.87±0.47 | ||
| Yin (PPFD <400 C i >500) | 0.46±0.026 | 0.87±0.87 | ||
| C. arabica | ФPSII/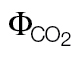 (A/C
i) (A/C
i) |
0.64±0.014 | 0.015±0.002* | |
ФPSII/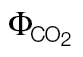 (PPFD >400) (PPFD >400) |
0.46±0.018 | –0.011±0.007 | ||
| Yin (PPFD <400) | 0.50±0.025 | 0.84±0.41 | ||
| Yin (PPFD <400 C i >500) | 0.63±0.015 | 2.55±0.45* | ||
| L. gibertii | ФPSII/ФCO22 (A/C i) | 0.56±0.019 | 0.014±0.004* | |
ФPSII/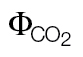 (PPFD>400) (PPFD>400) |
0.37±0.011 | –0.03±0.009* | ||
| Yin (PPFD<400) | 0.41±0.013 | 2.04±0.25* | ||
| Yin (PPFD <400 C i >500) | 0.50±0.018 | 3.14±1.02* |
Values are the means ±standard error of four replicates per species.
An asterisk denotes respiration or intercepts significantly different from zero (P < 0.05).
Mesophyll conductance as affected by the J calibration methods and respiration estimations
Given that no major differences were found between the ФPSII/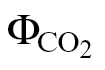 relationship and the Yin method, g
m was estimated using the methods covering the extremes of αβ values, namely ФPSII/
relationship and the Yin method, g
m was estimated using the methods covering the extremes of αβ values, namely ФPSII/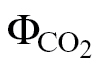 (A/C
i) and ФPSII/
(A/C
i) and ФPSII/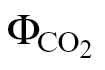 (PPFD >400 μmol m–2 s–1). Because these methods consider only A/PPFD (ФPSII/
(PPFD >400 μmol m–2 s–1). Because these methods consider only A/PPFD (ФPSII/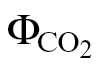 , PPFD >400 μmol m–2 s–1) or A/C
i data [ФPSII/
, PPFD >400 μmol m–2 s–1) or A/C
i data [ФPSII/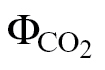 (A/C
i)], the g
m estimated using either method is hereafter referred to as the g
m obtained with the A/PPFD or A/C
i
J calibration. Once the two J calibrations to be used were defined, an R
L value next had to be chosen to calculate C
c. Because there was no consistency in the R
L estimated via the Yin approach using A/PPFD (PPFD <400 μmol m–2 s–1) or A/C
i (PPFD <400 μmol m–2 s–1 or C
i >500 μmol mol–1 air) (Table 2), R
dark/2 was preferred because it is the unique respiration value actually measured in planta. To check the consistency of the respiration value used, a new approach was also tested to find an alternative proxy for R
L (
(A/C
i)], the g
m estimated using either method is hereafter referred to as the g
m obtained with the A/PPFD or A/C
i
J calibration. Once the two J calibrations to be used were defined, an R
L value next had to be chosen to calculate C
c. Because there was no consistency in the R
L estimated via the Yin approach using A/PPFD (PPFD <400 μmol m–2 s–1) or A/C
i (PPFD <400 μmol m–2 s–1 or C
i >500 μmol mol–1 air) (Table 2), R
dark/2 was preferred because it is the unique respiration value actually measured in planta. To check the consistency of the respiration value used, a new approach was also tested to find an alternative proxy for R
L (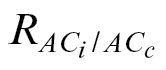 ) as the value forcing the CO2 compensation point (Γ) to be equal when calculated from A/C
i and A/C
c curves. The estimated
) as the value forcing the CO2 compensation point (Γ) to be equal when calculated from A/C
i and A/C
c curves. The estimated 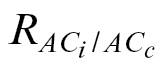 values were always lower than their corresponding R
dark/2 counterparts (Table 3).
values were always lower than their corresponding R
dark/2 counterparts (Table 3).
Table 3.
Dark respiration measured at pre-dawn (R
dark) and light respiration estimated from combined A/C
i and A/C
c curves ( )
)
All values are in μmol CO2 m–2 s–1.
| Species | R dark |
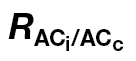 a
a
|
|---|---|---|
| N. tabacum | 2.2±0.1 | 0.3±0.1 |
| C. arabica | 0.9±0.1 | 0.2±0.1 |
| L. gibertii | 4.0±0.3 | 1.7±0.4 |
Values are the means ±standard error of four replicates per species.
a For 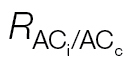 , the values are averages from the A/C
c curves calibrated using the A/PPFD or A/C
i curves.
, the values are averages from the A/C
c curves calibrated using the A/PPFD or A/C
i curves.
Due to the high amount of negative and extremely high g
m values at low or high C
i, respectively (Table 4), a filter was next applied to keep the valid g
m estimates, here defined as those values in the range of 0 <g
m <1mol CO2 m–2 s–1. As expected, the use of 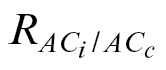 significantly reduced the amount of negative values of g
m at low C
i (
significantly reduced the amount of negative values of g
m at low C
i (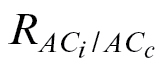 in Table 4), as the rationale for this method works at this C
i range (Fig. 1). Conversely, the use of A/C
i
J calibration improved the g
m estimation at high C
i (Table 4) due to a lowering of C
c values (Fig. 3A). Thus, the highest percentage of data excluded (i.e. unrealistic g
m values) was found when combining the A/PPFD J calibration with R
dark/2 (88, 56, and 42% for N. tabacum, C. arabica, and L. gibertii, respectively), whereas the lowest percentage of data excluded was obtained with the A/C
i
J calibration and
in Table 4), as the rationale for this method works at this C
i range (Fig. 1). Conversely, the use of A/C
i
J calibration improved the g
m estimation at high C
i (Table 4) due to a lowering of C
c values (Fig. 3A). Thus, the highest percentage of data excluded (i.e. unrealistic g
m values) was found when combining the A/PPFD J calibration with R
dark/2 (88, 56, and 42% for N. tabacum, C. arabica, and L. gibertii, respectively), whereas the lowest percentage of data excluded was obtained with the A/C
i
J calibration and 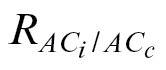 (17% for N. tabacum and 0% for the other species) (Table 4).
(17% for N. tabacum and 0% for the other species) (Table 4).
Table 4.
Mesophyll conductance (g m, mol CO2 m–2 s–1) for several intervals of C i and percentage of data excluded (DE) after applying a restriction (g m restricted to the range of 0 <g m <1mol CO2 m–2 s–1)
The A/C
i or A/PPFD J calibration refers to the ФPSII/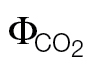 (A/Ci) or A/PPFD methods, respectively.
(A/Ci) or A/PPFD methods, respectively. 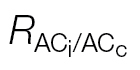 is the light respiration estimate from the combined A/Ci and A/Cc curves proposed in this study, and Rdark/2 is the dark respiration divided per two to account for the observed reduction in Rdark under light (Niinemets et al., 2005). Note the high DE at low Ci for Rdark/2 and at high Ci for the A/PPFD J calibration.
is the light respiration estimate from the combined A/Ci and A/Cc curves proposed in this study, and Rdark/2 is the dark respiration divided per two to account for the observed reduction in Rdark under light (Niinemets et al., 2005). Note the high DE at low Ci for Rdark/2 and at high Ci for the A/PPFD J calibration.
| A/C i J calibration | A/PPFD J calibration | |||||||
|---|---|---|---|---|---|---|---|---|
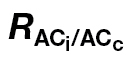
|
R dark/2 |
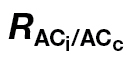
|
R dark/2 | |||||
| g m | DE (%) | g m | DE (%) | g m | DE (%) | g m | DE (%) | |
| N. tabacum | ||||||||
| C i <100 | 0.290±0.065 | 17 | 0.243±0.033 | 58 | 0.345±0.132 | 17 | 0.203±0.031 | 67 |
| C i 100–350 | 0.213±0.021 | 0 | 0.287±0.037 | 6 | 0.468±0.064 | 50 | 0.504±0.262 | 88 |
| C i >350 | 0.038±0.005 | 0 | 0.045±0.007 | 0 | 0.262±0.024 | 65 | 0.132±0.130 | 70 |
| C. arabica | ||||||||
| C i <100 | 0.131±0.018 | 0 | 0.202±0.042 | 10 | 0.164±0.028 | 0 | 0.202±0.035 | 20 |
| C i 100–350 | 0.117±0.006 | 0 | 0.124±0.007 | 0 | 0.186±0.029 | 0 | 0.191±0.029 | 6 |
| C i >350 | 0.052±0.004 | 0 | 0.053±0.004 | 0 | 0.219±0.038 | 41 | 0.194±0.039 | 56 |
| L. gibertii | ||||||||
| C i <100 | 0.235±0.027 | 0 | 0.270±0.050 | 7 | 0.310±0.041 | 7 | 0.275±0.079 | 27 |
| C i 100–350 | 0.214±0.014 | 0 | 0.228±0.020 | 0 | 0.371±0.044 | 7 | 0.406±0.083 | 21 |
| C i >350 | 0.071±0.011 | 0 | 0.073±0.012 | 0 | 0.226±0.063 | 32 | 0.162±0.044 | 42 |
Values are the means ±standard error of 4–6 A/C i curves per species. The SE was calculated according to the points that remained in each C i interval after applying the restriction.
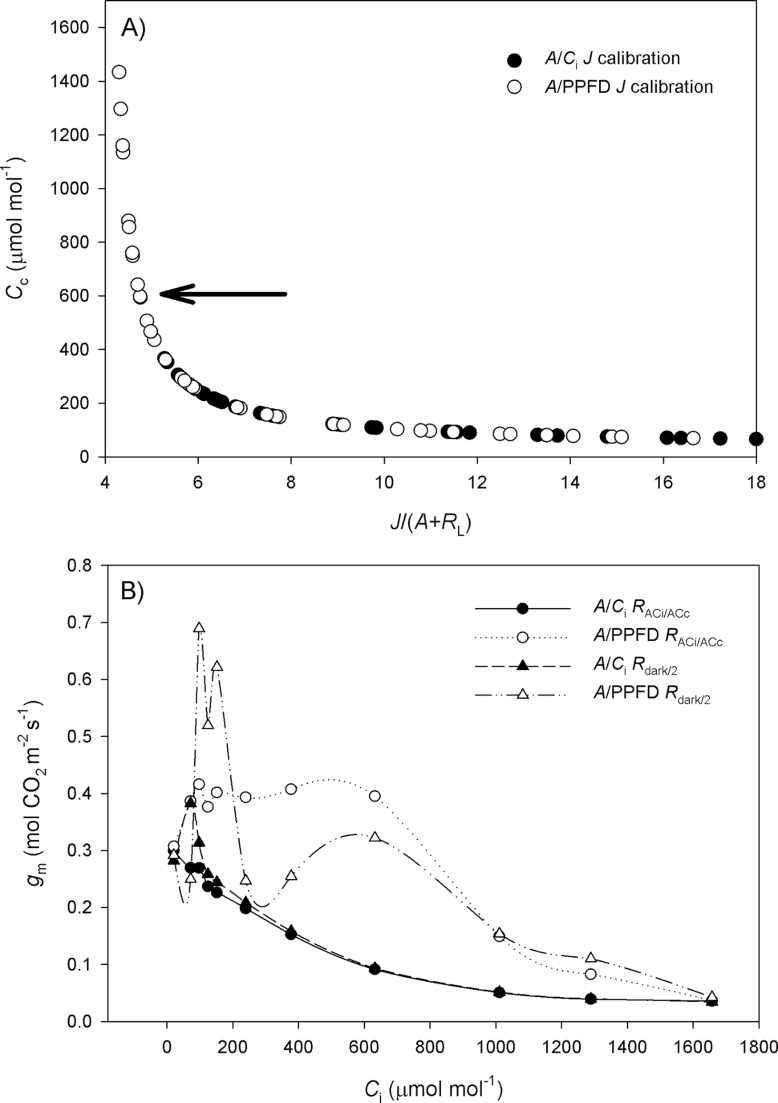
Fig. 3.
(A) Relationship between C
c and J/(A+R
L), as affected by the J calibration using the A/PPFD (open circles) or A/C
i curves (filled circles). As J/(A+R
L) approaches four (likely to occur at high C
i), C
c tends to infinity, thus increasing the probability of being higher than C
i and resulting in negative g
m values. The arrow indicates the C
c upper limit (~600 μmol mol–1) observed for the A/C
i
J calibration, being much lower than its A/PPFD counterpart which can reach C
c values >1600 μmol mol–1. (B) g
m response to C
i as affected by the A/C
i (filled symbols) or A/PPFD (open symbols) J calibration method and the light respiration estimations [R
dark/2 (triangles) or 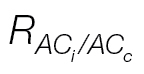 (circles)]. It is remarkable how there are ‘spikes’ in g
m at low C
i when using R
dark/2 and how these are alleviated when using
(circles)]. It is remarkable how there are ‘spikes’ in g
m at low C
i when using R
dark/2 and how these are alleviated when using 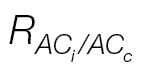 . The curves are from L. gibertii, and the points are averages from four plants for g
m between 0 and 1mol CO2 m–2 s–1. The A/C
i or A/PPFD J calibration refers to the αβ obtained from the curves shown in Fig. 2A and B, respectively.
. The curves are from L. gibertii, and the points are averages from four plants for g
m between 0 and 1mol CO2 m–2 s–1. The A/C
i or A/PPFD J calibration refers to the αβ obtained from the curves shown in Fig. 2A and B, respectively.
The different calibrations also affected the magnitude of g m in response to C i. There was no general trend at C i <100 μmol mol–1 air, whereas at C i >100 μmol mol–1 air, lower g m values (up to 50%) were observed using the A/C i J calibration (Table 4). In addition, when plotting g m versus C i, a high amplitude in g m, depending on the calibration used, was revealed (Fig. 3B). Such amplitude led to a reasonable disagreement between the averaged g m at C i of 100–350 μmol mol–1 air and the single point g m at CO2 ambient (400 μmol mol–1) (Supplementary Tables S2, S3 at JXB online), which suggests that care must be exercised when reporting single point g m data. In Supplementary Table S4, in addition to the filter keeping the values in the range of 0 <g m <1mol CO2 m–2 s–1, the Harley et al. (1992) criteria were also applied, considering the g m data in the range of 10 <dC c/dA <50 as reliable to see whether they corresponded to the data presented in Table 4. Overall, the g m values presented in Table 4 and those obtained after applying the Harley criteria varied accordingly, but some exceptions were noticed such as the g m values estimated at C i >350 μmol mol–1 air for L. gibertii which were substantially higher than the g m data shown in Supplementary Table S4. Most importantly and irrespective of this difference, the amount of data excluded using the Harley criteria was always higher (up to 100%) even when the same estimates presented in Table 4 had 0% of data excluded together with small standard errors. Additionally, the Harley criteria worked differently depending on the species, J calibration, and C i range, given that some species were more affected than others.
To obtain an independent estimate of g m that was not affected by the need for calibrating J, g m was also estimated using an alternative approach, namely the A–C i curve analysis method suggested by Ethier and Livingston (2004). The g m values obtained following this approach are given in Table 5.
Table 5.
Maximum carboxylation rate of Rubisco (V cmax, μmol CO2 m–2 s–1), maximum electron transport rate from gas exchange (J max, μmol e– m–2 s–1), mesophyll conductance (g m Ethier, mol CO2 m–2 s–1) according to Ethier and Livingston (2004), and electron transport rate estimated from chlorophyll fluorescence (Jflu, μmol e– m–2 s–1)
All of the photosynthetic parameters were calculated on a Ci basis from the A/Ci curves or on a Cc basis from the A/Cc curves using the measured Rubisco kinetic constants (Γ*, Kc, and Ko) in this study (as reported in Table 1) or the standard Rubisco kinetics for tobacco from Bernacchi et al. (2002). A/Ci J cal and A/PPFD J calibration denote the photosynthetic parameters calculated for A/Cc curves using the αβ retrieved from ФPSII/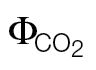 (A/Ci) or (A/PPFD) J calibrations. Note that Jflu is independent of Rubisco kinetics.
(A/Ci) or (A/PPFD) J calibrations. Note that Jflu is independent of Rubisco kinetics.
| Measured kinetic constants | Bernacchi constants | |||||
|---|---|---|---|---|---|---|
| N. tabacum | C. arabica | L. gibertii | N. tabacum | C. arabica | L. gibertii | |
| V cmax C i basis | 71.7±4.6 | 41.7±2.4* | 70.5±1.6* | 59.8±3.8 | 49.8±2.7 | 104.0±2.4 |
| V cmax C c basis A/Ci J cal | 106.3±8.9 | 73.9±3.6* | 133.4±11.9* | 87.0±7.1 | 89.8±4.4 | 210.1±20.8 |
| V cmax C c basis A/PPFD J cal | 80.2±5.7 | 59.8±3.8* | 101.7±8.2* | 66.7±4.6 | 70.3±3.1 | 155.8±14.0 |
| V cmax Ethier | 91.8±14.7 | 80.2±4.0* | 124.8±5.0* | 81.7±9.2 | 102.1±5.4 | 164.6±11.7 |
| J max C i basis | 87.2±7.4 | 110.7±3.4 | 175.3±7.3 | 86.6±7.4 | 110.7±3.4 | 176.6±7.4 |
| J max C c basis A/C i cal | 103.2±10.5 | 136.6±7.1 | 228.6±8.7 | 101.4±10.3 | 136.6±7.1 | 233.4±8.9 |
| J max C c basis A/PPFD cal | 84.9±7.3 | 113.7±5.7 | 177.0±5.8 | 84.4±7.3 | 113.1±5.3 | 178.2±5.8 |
| J max Ethier | 99.5±3.3 | 115.0±3.2 | 179.8±8.9 | 99.5±3.3 | 114.4±3.2 | 179.8±8.9 |
| J flu A/Ci J cal | 117.5±11.4 | 139.2±6.7 | 236.0±9.7 | – | ||
| J flu A/PPFD J cal | 94.7±7.9 | 113.1±4.8 | 181.7±6.4 | – | ||
| g m Ethier | 0.412±0.045 | 0.108±0.006 | 0.226±0.036 | 0.296±0.015 | 0.101±0.005 | 0.257±0.048 |
Values are the means ±standard error of 4–6 A/C i or A/C c curves per species.
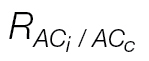 was used when needed.
was used when needed.
An asterisk denotes differences in the respective photosynthetic parameter calculated using the different set of Rubisco kinetics.
The graphical representation of the A/C i and A/C c curves is shown in Supplementray Figure S1 at JXB online.
Maximum Rubisco carboxylation and electron transport rate as affected by αβ
In contrast to the g
m estimates that could be greatly affected by the use of either R
dark/2 or 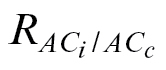 (Table 4, Fig. 3B), the V
cmax and J
max estimates were minimally affected by the use of different respiration values (~6% at most; Table 5; Supplementary Table S5 at JXB online).
(Table 4, Fig. 3B), the V
cmax and J
max estimates were minimally affected by the use of different respiration values (~6% at most; Table 5; Supplementary Table S5 at JXB online).
Irrespective of species, V cmax and J max on a C c basis were always higher for the A/C i J calibration than for its A/PPFD J counterpart (Table 5). These higher V cmax and J max values are in agreement with the lower g m values found, in general, with the A/C i J calibration (Table 4). The V cmax obtained using the Ethier and Livingston method was closer to the V cmax on a C c basis calculated using the A/C i J calibration for L. gibertii and C. arabica, whereas for N. tabacum an intermediate value between those obtained with the A/PPFD or A/C i J calibration was found (Table 5). Apart from the J max calculated with the A/C i J calibration, which had the higher values for all species and reflected the higher αβ found (Table 3), there were no major differences among the other calculated values of J max. The use of the standard Rubisco kinetics (K c, K o, and Γ*) originally obtained for N. tabacum by Bernacchi et al. (2002) would lead to an overestimation of V cmax by ~30% and 20% for L. gibertii and C. arabica, respectively. The other photosynthetic parameters for these two species were unaffected by the use of different Rubisco kinetic constants (Table 5). No significant differences were observed for N. tabacum when using the different set of Rubisco kinetics, with the exception of g m (Ethier and Livingston method), which was 28% lower when using the Rubisco kinetics of Bernacchi et al. (2002).
Discussion
To the best of the authors’ knowledge, this study is the first to address the idea that the use of A/C i or A/PPFD curves under low O2 to calibrate J can significantly affect the estimations of g m, V cmax, and J max, as demonstrated in species with contrasting leaf structural properties and photosynthetic capacities. A background is also provided to understand potential factors that could be translated into unrealistic g m values at low and high C i, and recommendations to improve g m estimations accordingly.
Sensitivity of the variable J method to αβ
The high sensitivity of the variable J method has been known since its introduction by Harley et al. (1992). However, among the several sources of error, more attention has been given to an accurate determination of Γ* (Warren et al., 2006; Pons et al., 2009) than to J per se, given the variety of ways in which J can be calibrated. Despite the J calibration based on A/PPFD curves being the most common method in the literature, here it is shown that this calibration produced a higher number of unrealistic g m estimates than its counterpart based on A/C i curves (Table 4). Additionally, it was demonstrated that g m misestimations could be directly associated with the J calibration method at high C i on the one hand, and the proper choice of Γ* and R L at low C i on the other hand. Notably, the need to develop useful criteria to improve g m estimations and to understand the high g m variability is crucial considering that the only existing indicator, the Harley et al. (1992) criteria which consider that reliable g m estimations are those situated in the range of dC c/dA (10–50), performed poorly in retrieving acceptable data in addition to being dependent on the species, applied C i range, and J calibration (Supplementary Table S4 at JXB online).
It can be deduced from the relationship between C c and J/(A+R L) (Fig. 3A) that C c approaches infinity as J/(A+R L) approaches four (number of electrons per CO2 molecule fixed). In contrast, C c is negative when the ratio is less than four [the lower C c threshold for positive J/(A+R L) is defined by the parameter Γ*]. Therefore, as J/(A+R L) approaches four as photorespiration and other alternative electron sinks tend to decrease (at high C i, for example), extremely high C c values are to be expected, leading to a greater probability of estimating negative values of g m. Thus, for the same (A+R L), the higher the αβ, the higher the J, ultimately resulting in a greater probability of obtaining positive g m values due to a lowering of C c, whereas the opposite holds true for a lower αβ.
At low C
i (<100 μmol mol–1 air), misestimations of g
m are unlikely to be affected by J/(A+R
L), as this ratio tends to achieve higher values with decreasing C
i. In any case, reliable estimations of g
m at low C
i are extremely challenging given that the estimations are highly dependent on the proper choice of values of Γ* or R
L, which can ultimately affect C
c. In the present study, the authors are quite confident about their Γ* values because they were estimated from Rubisco kinetics in purified preparations. Given this, it was possible to retrieve a respiration estimate (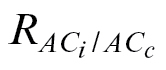 ) as the value forcing the intercept of the linear relationship of A versus C
i–C
c to zero, which is equivalent to forcing the Γ to be the same. It is believed that
) as the value forcing the intercept of the linear relationship of A versus C
i–C
c to zero, which is equivalent to forcing the Γ to be the same. It is believed that 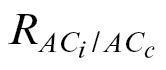 obtained in this way is a valid estimate, as its magnitude was lower than that of R
dark (Table 3), in agreement with the general consensus that respiration is inhibited in the light (Tcherkez et al., 2005). In addition, the use of
obtained in this way is a valid estimate, as its magnitude was lower than that of R
dark (Table 3), in agreement with the general consensus that respiration is inhibited in the light (Tcherkez et al., 2005). In addition, the use of 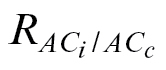 significantly improved the number of valid g
m estimates (Table 4), highlighting the importance of respiration in estimating g
m at low C
i, with the advantage of better matching a biochemical prediction of the FvCB model, namely A/C
i and A/C
c sharing the same Γ.
significantly improved the number of valid g
m estimates (Table 4), highlighting the importance of respiration in estimating g
m at low C
i, with the advantage of better matching a biochemical prediction of the FvCB model, namely A/C
i and A/C
c sharing the same Γ.
An a priori weakness regarding 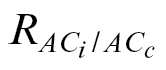 resides in whether g
m is kept constant at a low C
i range. However, the authors argue in favour of a constant g
m where a high linearity can be observed when plotting A versus C
i–C
c, in the region strictly limited by Rubisco (Fig. 1C). Furthermore, it can also be noted that g
m estimated using the variable J method is closer to the constant g
m, as the individual points are close to the regression line in the plot of A versus C
i–C
c. The apparent variability of g
m that might be identified using the variable J method could simply be a result of the high sensitivity of A, C
i, or C
c to random errors at this low C
i range. This conclusion is supported when comparing the data of Flexas et al. (2007), who showed a high variability of g
m at low C
i using the variable J method, with those recorded by Tazoe et al. (2011), who found almost constant values of g
m using the isotopic method.
resides in whether g
m is kept constant at a low C
i range. However, the authors argue in favour of a constant g
m where a high linearity can be observed when plotting A versus C
i–C
c, in the region strictly limited by Rubisco (Fig. 1C). Furthermore, it can also be noted that g
m estimated using the variable J method is closer to the constant g
m, as the individual points are close to the regression line in the plot of A versus C
i–C
c. The apparent variability of g
m that might be identified using the variable J method could simply be a result of the high sensitivity of A, C
i, or C
c to random errors at this low C
i range. This conclusion is supported when comparing the data of Flexas et al. (2007), who showed a high variability of g
m at low C
i using the variable J method, with those recorded by Tazoe et al. (2011), who found almost constant values of g
m using the isotopic method.
Why do A/C i and A/PPFD curves result in different αβ?
Given that α can be measured and that large changes in this parameter during the execution of A/PPFD or A/C i curves are unlikely to occur, the uncertainty in J is particularly related to β. Eichelmann and Laisk (2000) found β varying from 0.38 to 0.51 in N. tabacum under varying light and temperature conditions. Similar results were reported by Loreto et al. (2009) while studying the effect of blue light on g m. Hassiotou et al. (2009) also concluded that J calibration is light dependent. Collectively, all of this information highlights the importance of irradiance in determining the β value and helps explain the apparently better suitability of the A/C i-based J calibration: it is performed under the same irradiance used in the normal A/C i curves. In fact, another advantage of keeping a fixed irradiance during the calibration is to avoid changes in the profiles of light absorption through the leaf that may occur under changing irradiance (Evans, 2009; Oguchi et al., 2011); this can be especially important for the Li-Cor LED-based fluorescence/light source which consists of blue and red light with narrow bandwidths. However, to what extent changes in spectral light could be responsible for differences in β is unclear (Evans, 2009). Further explanations for this statement might be linked to the engagement of alternative electron sinks and the fluorescence signals that might not be representative of the whole leaf, in contrast to the gas-exchange signals (Hassiotou et al., 2009). Even if the uncertainty about the fluorescence signal could be resolved using calibration curves, as in this study, conflicting information on the possible effects of alternative electron sinks on g m measurements has been reported. Whereas several authors (e.g. Loreto et al., 1994; Ruuska et al., 2000; Flexas and Medrano, 2002) showed circumstantial evidence suggesting that alternative electron sinks play no major role in g m estimations, other investigators reported that up to 24% of the total electron flux can be associated with alternative sinks (see Gilbert et al., 2012, and references therein). In any case, the present results argue against the relevance of alternative electron sinks as potential bias for proper g m estimations, given that the calibration methods most likely to be affected by these sinks (calibrations performed at high PPFD and low C i) did not differ from others which used a range of data under strictly limited electron transport (low PPFD and high C i).
Mesophyll conductance, maximum velocity of Rubisco carboxylation, and electron transport rate
The choice of the method to calibrate J can significantly affect the estimation of photosynthetic parameters and even alter their interpretation in the context of the diffusive versus biochemical limitations to photosynthesis. In N. tabacum, the use of A/PPFD calibration would lead to the conclusion that the assumption of infinite g m is plausible because no difference in V cmax on a C i or C c basis was observed (Table 5). In sharp contrast, the use of A/C i calibration points to a finite g m and a higher V cmax value (33%) in relation to the V cmax on a C i basis. For C. arabica and L. gibertii, higher V cmax values were observed using both A/C i and A/PPFD J calibrations compared with V cmax on a C i basis, but the degree of underestimation varied considerably (Table 5). It is important to bear in mind that such alterations also imply changes in biochemical aspects of the leaf because V cmax is related to the amount of activated Rubisco, whereas J max is associated with components of the electron transport chain, and both parameters can affect the leaf nitrogen economy (Niinemets and Tenhunen, 1997). Thus, it is highly unlikely that both calibrations can hold true, as they can considerably change the leaf biochemical signature and hence ultimately pose uncertainties on how to decide which calibration to use. To address this issue, a first cut-off point is to check if the minimum requirement of four electrons per carboxylation is attained, which can be achieved by dividing J by A. If this ratio is less than four, the calibration is, on a theoretical basis, inadequate. This criterion allowed the exclusion of the standard αβ for C. arabica (Supplementary Table S2 at JXB online) and the A/PPFD calibration for N. tabacum. In addition, g m and the FvCB photosynthetic parameters were estimated using the J-independent Ethier and Livingston method. Interestingly, the values of V cmax and g m obtained with this method reasonably matched those obtained with the A/C i J calibration for L. gibertii and C. arabica. In N. tabacum, the V cmax calculated from the Ethier approach presented intermediate values between the V cmax from the A/PPFD or A/C i J calibration, and, given the high standard errors in its g m estimate, it is believed that, even in this species, the A/C i J calibration might be a better option to recommend, as it allows the retrieval of a greater number of realistic g m estimations regardless of the respiration value (Tables 4, 5). Therefore, it is proposed that the A/C i J calibration seems to be more reliable than its A/PPFD counterpart in terms of producing acceptable data, in accordance with the results of Gilbert et al. (2012).
Regarding the use of Rubisco kinetic constants, a considerable overestimation of V cmax (~30%) would occur in L. gibertii if standard values of those constants (Bernacchi et al., 2002) were used (Table 5). Importantly, even if good fits could be obtained irrespective of the kinetic constants, the relationship between V cmax and leaf nitrogen might be compromised. Thus, if the main goal is to use the FvCB model to characterize photosynthetic capacities and relate them to nitrogen partitioning (e.g. Xu et al., 2012), species-specific kinetic constants for Rubisco should be implicitly used.
Further recommendations to improve g m estimation
Given the uncertainties in g m estimations, criteria were provided to assess the consistency of Γ* and R L through the determination of Γ (by definition, Γ must be higher than Γ*) or by plotting A versus C i–C c and analysing the intercept of the linear relationship. In addition, provided that the estimates of Γ and Γ* are reliable, it is possible to retrieve a respiration estimate from A/C i and A/C c curves. The respiration value was the focus here because of the availability of the current methods to estimate R L using gas exchange and/or chlorophyll fluorescence (see Yin et al., 2011), all of which were performed under low irradiance conditions that do not match those used in A/C i curves, which ultimately makes the choice of a proper respiration value a very complicated task.
If an inconsistency between Γ for the A/C
i curve and Γ* (Γ lower than Γ*) is found, or if the value of respiration retrieved by forcing the intercept of A versus C
i–C
c to zero is negative, four potential sources of error need to be checked: (i) correction for CO2 and water vapour leakage through the chamber gaskets is crucial to the determination of Γ and very important for species with low photosynthetic potential (see Rodeghiero et al., 2007); (ii) the influence of lateral diffusion which can become significant (especially for homobaric leaves) with large gradients of CO2 inside and outside the chamber in addition to the lower fluxes of CO2 near the compensation point (Morison and Lawson, 2007); (iii) Γ* determination; and (iv) Rubisco deactivation. The first two sources of error are particularly dependent on the leaf chamber size and, given the magnitude of the corrections in A at low C
i (Supplementary Table S1 at JXB online), the need to use larger leaf chambers to obtain more reliable g
m, Γ, and 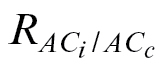 estimates is emphasized. For species displaying low respiration rates, it is possible to obtain an estimate of Γ* by fixing R
L, inputting a test Γ*, and changing this parameter to obtain the intercept of A versus C
i–C
c closest to zero. All of these hints provide a good framework to extract as much information as possible from the A/C
i and A/C
c curves. Nevertheless, because all of these adjustments rely on fitting processes, proper judgement about the biological meaning of the obtained estimates is obviously required.
estimates is emphasized. For species displaying low respiration rates, it is possible to obtain an estimate of Γ* by fixing R
L, inputting a test Γ*, and changing this parameter to obtain the intercept of A versus C
i–C
c closest to zero. All of these hints provide a good framework to extract as much information as possible from the A/C
i and A/C
c curves. Nevertheless, because all of these adjustments rely on fitting processes, proper judgement about the biological meaning of the obtained estimates is obviously required.
Regarding the J calibration, independent of it being based on A/C i, A/PPFD, or both, one should first check whether all of the positive J/A values are higher than four. If not, there is an inconsistency with the calibration because this implies that fewer than four electrons would be used per carboxylation event. If yes, the next step is to verify the suitability of the respiration value by checking if all of the positive J/(A+R L) values are still higher than four. If not, there is an inconsistency for the same reason stated previously. Another checkpoint is to verify that the maximum observed C c is at least equal to the maximum C i that would implicate infinite g m. If C c values higher than the maximum C i are present for positive A, there is again an inconsistency with the calibration, as Fick’s first law of diffusion predicts a drawdown of CO2 between C i and C c. In fact, it is theoretically possible to define an upper limit for αβ which would be the value making the A/C i and A/C c curves identical, implicating infinite g m.
Conclusion
This work brings new information to the growing amount of published papers trying to improve g m estimation. Criteria are provided to examine the amount of unrealistic g m data and identify inconsistencies with the biochemical model utilized, leading to a higher amount of acceptable data. In addition, the need for additional measurements to validate the J calibration to improve the estimation of photosynthetic parameters is emphasized. Moreover, given the observed high variability in g m, it is important that comparisons among studies reporting data consider the variability due to the J calibration method, and, if necessary, normalize data according to the reported αβ values.
Supplementary data
Supplementary data are available at JXB online.
Figure S1. Graphical representation of the A/C i and their respective A/C c curves calibrated with the A/C i or A/PPFD J calibration.
Table S1. Leakage correction for CO2 and water vapour.
Table S2. Averaged mesophyll conductance (g m) for the interval of C i ranging from 100 to 350 μmol mol–1 air and the single point g m at ambient CO2 concentration (400 μmol mol–1 air) using R dark/2 in the g m estimation.
Table S3. The same as in Table S1, using 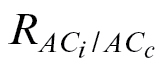 rather than R
dark/2 to estimate g
m.
rather than R
dark/2 to estimate g
m.
Table S4. Mesophyll conductance (g m, mol CO2 m–2 s–1) for several intervals of C i and percentage of data excluded (DE) after applying two restrictions (g m restricted to the range of 0 < g m<1mol CO2 m–2 s–1 and dC c/dA of 10–50 [the Harley et al. (1992) criteria].
Table S5. Maximum carboxylation rate of Rubisco (V cmax) and maximum electron transport rate from gas exchange (J max), as affected by the different J calibrations and calculated with R dark/2.
Spreadsheet S1. An Excel spreadsheet is provided that allows the user to retrieve the leaf respiration from combined A/C i and A/C c curves.
Acknowledgements
This research was supported by the National Council for Scientific and Technological Development (CNPq) (grant 302605/2010-0) to FMD and Plan Nacional (Spain) (grant AGL2009-07999) to JG. A PhD scholarship granted by CNPq to SCVM is also gratefully acknowledged.
References
- Bernacchi CJ, Portis AR, Nakano H, Von, Caemmerer S, Long SP. 2002. Temperature response of mesophyll conductance. Implications for the determination of Rubisco enzyme kinetics and for limitations to photosynthesis in vivo . Plant Physiology 130, 1992–1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bird IF, Cornelius MJ, Keys AJ. 1982. Affinity of RuBP carboxylases for carbon dioxide and inhibition of the enzymes by oxygen. Journal of Experimental Botany 33, 1004–1013 [Google Scholar]
- Brooks A, Farquhar GD. 1985. Effect of temperature on the CO2/O2 specificity of ribulose-1,5-bisphosphate carboxylase/oxygenase and the rate of respiration in the light. Planta 165, 397–406 [DOI] [PubMed] [Google Scholar]
- Butz ND, Sharkey TD. 1989. Activity ratios of ribulose-1,5-bisphosphate carboxylase accurately reflect carbamylation ratios. Plant Physiology 89, 735–739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichelmann H, Laisk A. 2000. Cooperation of photosystems II and I in leaves as analyzed by simultaneous measurements of chlorophyll fluorescence and transmittance at 800 nm. Plant and Cell Physiology 41, 138–147 [DOI] [PubMed] [Google Scholar]
- Edwards GE, Baker NR. 1993. Can CO2 assimilation in maize leaves be predicted accurately from chlorophyll fluorescence analysis? Photosynthesis Research 37, 89–102 [DOI] [PubMed] [Google Scholar]
- Ethier GJ, Livingston NJ. 2004. On the need to incorporate sensitivity to CO2 transfer conductance into the Farquhar–von Caemmerer–Berry leaf photosynthesis model. Plant, Cell and Environment 27, 137–153 [Google Scholar]
- Evans JR. 2009. Potential errors in electron transport rates calculated from chlorophyll fluorescence as revealed by a multilayer leaf model. Plant and Cell Physiology 50, 698–706 [DOI] [PubMed] [Google Scholar]
- Evans JR, von Caemmerer S. 1996. Carbon dioxide diffusion inside leaves. Plant Physiology 110, 339–346 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farquhar GD, von Caemmerer S, Berry JA. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78–90 [DOI] [PubMed] [Google Scholar]
- Flexas J, Barbour MM, Brendel O, et al. 2012. Mesophyll diffusion conductance to CO2: an unappreciated central player in photosynthesis. Plant Science 193–194 70–84 [DOI] [PubMed] [Google Scholar]
- Flexas J, Diaz-Espejo A, Galmés J, Kaldenhoff R, Medrano H, Ribas-Carbo M. 2007. Rapid variations of mesophyll conductance in response to changes in CO2 concentration around leaves. Plant, Cell and Environment 30, 1284–1298 [DOI] [PubMed] [Google Scholar]
- Flexas J, Medrano H. 2002. Energy dissipation in C3 plants under drought. Functional Plant Biology 29, 1209–1215 [DOI] [PubMed] [Google Scholar]
- Flexas J, Ribas-Carbó M, Diaz-Espejo A, Galmés J, Medrano H. 2008. Mesophyll conductance to CO2: current knowledge and future prospects. Plant, Cell and Environment 31, 602–621 [DOI] [PubMed] [Google Scholar]
- Harley PC, Loreto F, Di, Marco G, Sharkey TD. 1992. Theoretical considerations when estimating the mesophyll conductance to CO2 flux by analysis of the response of photosynthesis to CO2 . Plant Physiology 98, 1429–1436 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hassiotou F, Ludwig M, Renton M, Veneklaas EJ, Evans JR. 2009. Influence of leaf dry mass per area, CO2, and irradiance on mesophyll conductance in sclerophylls. Journal of Experimental Botany 60, 2303–2314 [DOI] [PubMed] [Google Scholar]
- Galmés J, Flexas J, Keys AJ, Cifre J, Mitchell RAC, Madgwick PJ, Haslam RP, Medrano H, Parry MAJ. 2005. Rubisco specificity factor tends to be larger in plant species from drier habitats and in species with persistent leaves. Plant, Cell and Environment 28, 571–579 [Google Scholar]
- Galmés J, Medrano H, Flexas J. 2006. Acclimation of Rubisco specificity factor to drought in tobacco: discrepancies between in vitro and in vivo estimations. Journal of Experimental Botany 57, 3659–3667 [DOI] [PubMed] [Google Scholar]
- Galmés J, Medrano H, Flexas J. 2007. Photosynthetic limitations in response to water stress and recovery in Mediterranean plants with different growth forms. New Phytologist 175, 81–93 [DOI] [PubMed] [Google Scholar]
- Genty B, Briantais JM, Baker NR. 1989. The relationship between the quantum yield of photosynthetic electron-transport and quenching of chlorophyll fluorescence. Biochimica et Biophysica Acta 990, 87–92 [Google Scholar]
- Gilbert ME, Pou A, Zwieniecki MA, Holbrook NM. 2012. On measuring the response of mesophyll conductance to carbon dioxide with the variable J method. Journal of Experimental Botany 63, 413–425 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laisk A, Loreto F. 1996. Determining photosynthetic parameters from leaf CO2 exchange and chlorophyll fluorescence. Plant Physiology 110, 903–912 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loreto F, Marco G, Tricoli D, Sharkey T. 1994. Measurements of mesophyll conductance, photosynthetic electron transport and alternative electron sinks of field grown wheat leaves. Photosynthesis Research 41, 397–403 [DOI] [PubMed] [Google Scholar]
- Loreto F, Tsonev T, Centritto M. 2009. The impact of blue light on leaf mesophyll conductance. Journal of Experimental Botany 60, 2283–2290 [DOI] [PubMed] [Google Scholar]
- Morison JIL, Lawson T. 2007. Does lateral gas diffusion in leaves matter? Plant, Cell and Environment 30, 1072–1085 [DOI] [PubMed] [Google Scholar]
- Niinemets U, Cescatti A, Rodeghiero M, Tosens T. 2005. Leaf internal diffusion conductance limits photosynthesis more strongly in older leaves of Mediterranean evergreen broad-leaved species. Plant, Cell and Environment 28, 1552–1566 [Google Scholar]
- Niinemets U, Cescatti A, Rodeghiero M, Tosens T. 2006. Complex adjustments of photosynthetic potentials and internal diffusion conductance to current and previous light availabilities and leaf age in Mediterranean evergreen species Quercus ilex . Plant, Cell and Environment 29, 1159–1178 [DOI] [PubMed] [Google Scholar]
- Niinemets U, Díaz-Espejo A, Flexas J, Galmés J, Warren CR. 2009. a Role of mesophyll diffusion conductance in constraining potential photosynthetic productivity in the field. Journal of Experimental Botany 60, 2249–2270 [DOI] [PubMed] [Google Scholar]
- Niinemets U, Flexas J, Peñuelas J. 2011. Evergreens favored by higher responsiveness to increased CO2 . Trends in Ecology and Evolution 26, 136–142 [DOI] [PubMed] [Google Scholar]
- Niinemets U, Tenhunen JD. 1997. A model separating leaf structural and physiological effects on carbon gain along light gradients for the shade-tolerant species Acer saccharum . Plant, Cell and Environment 20, 845–866 [Google Scholar]
- Niinemets U, Wright IJ, Evans JR. 2009. b Leaf mesophyll diffusion conductance in 35 Australian sclerophylls covering a broad range of foliage structural and physiological variation. Journal of Experimental Botany 60, 2433–2449 [DOI] [PubMed] [Google Scholar]
- Oguchi R, Douwstra P, Fujita T, Chow WS, Terashima I. 2011. Intra-leaf gradients of photoinhibition induced by different color lights: implications for the dual mechanisms of photoinhibition and for the application of conventional chlorophyll fluorometers. New Phytologist 191, 146–159 [DOI] [PubMed] [Google Scholar]
- Pons TL, Flexas J, Von, Caemmerer S, Evans JR, Genty B, Ribas-Carbó M, Brugnoli E. 2009. Estimating mesophyll conductance to CO2: methodology, potential errors, and recommendations. Journal of Experimental Botany 60, 2217–2234 [DOI] [PubMed] [Google Scholar]
- Rodeghiero M, Niinemets U, Cescatti A. 2007. Major diffusion leaks of clamp-on leaf cuvettes still unaccounted: how erroneous are the estimates of Farquhar et al. model parameters? Plant, Cell and Environment 30, 1006–1022 [DOI] [PubMed] [Google Scholar]
- Ruuska SA, Badger MR, Andrews TJ, von Caemmerer S. 2000. Photosynthetic electron sinks in transgenic tobacco with reduced amounts of Rubisco: little evidence for significant Mehler reaction. Journal of Experimental Botany 51, 357–368 [DOI] [PubMed] [Google Scholar]
- Seaton GGR, Walker DA. 1990. Chlorophyll fluorescence as a measure of photosynthetic carbon assimilation. Proceedings of the Royal Society B: Biological Sciences 242, 29–35 [Google Scholar]
- Sharwood RE, von Caemmerer S, Maliga P, Whitney SM. 2008. The catalytic properties of hybrid Rubisco comprising tobacco small and sunflower large subunits mirror the kinetically equivalent source Rubiscos and can support tobacco growth. Plant Physiology 146, 83–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tazoe Y, von Caemmerer S, Estavillo GM, Evans JR. 2011. Using tunable diode laser spectroscopy to measure carbon isotope discrimination and mesophyll conductance to CO2 diffusion dynamically at different CO2 concentrations. Plant, Cell and Environment 34, 580–91 [DOI] [PubMed] [Google Scholar]
- Tcherkez G, Cornic G, Bligny R, Gout E, Ghashghaie J. 2005. In vivo respiratory metabolism of illuminated leaves. Plant Physiology 138, 1596–1606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tosens T, Niinemets Ü, Westoby M, Wright IJ. 2012. Anatomical basis of variation in mesophyll resistance in eastern Australian sclerophylls: news of a long and winding path. Journal of Experimental Botany 63, 5105–5119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentini R, Epron D, Angelis P, Matteucci G, Dreyer E. 1995. In situ estimation of net CO2 assimilation, photosynthetic electron flow and photorespiration in Turkey oak (Q. cerris L.) leaves: diurnal cycles under different levels of water supply. Plant, Cell and Environment 18, 631–640 [Google Scholar]
- Warren CR, Adams MA. 2004. Evergreen trees do not maximize instantaneous photosynthesis. Trends in Plant Science 9, 270–274 [DOI] [PubMed] [Google Scholar]
- Warren CR. 2006. Estimating the internal conductance to CO2 movement. Functional Plant Biology 33, 431–442 [DOI] [PubMed] [Google Scholar]
- Xu C, Fisher R, Wullschleger SD, Wilson CJ, Cai M, McDowell NG. 2012. Toward a mechanistic modeling of nitrogen limitation on vegetation dynamics. PLoS One 7, e37914 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin X, Struik PC, Romero P, Harbinson J, Evers JB, van der Putten PEL, Vos J. 2009. Using combined measurements of gas exchange and chlorophyll fluorescence to estimate parameters of a biochemical C3 photosynthesis model: a critical appraisal and a new integrated approach applied to leaves in a wheat (Triticum aestivum) canopy. Plant, Cell and Environment 32, 448–464 [DOI] [PubMed] [Google Scholar]
- Yin X, Sun Z, Struik PC, Gu J. 2011. Evaluating a new method to estimate the rate of leaf respiration in the light by analysis of combined gas exchange and chlorophyll fluorescence measurements. Journal of Experimental Botany 62, 3489–3499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin X, van Oijen M, Schapendonk AHCM. 2004. Extension of a biochemical model for the generalized stoichiometry of electron transport limited C3 photosynthesis. Plant, Cell and Environment 27, 1211–1222 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.