Abstract
Melatonin is endogenously produced and released in humans during nighttime darkness and is suppressed by ocular light exposure. Exogenous melatonin is used to induce circadian phase shifts and sleep. The circadian phase-shifting ability of a stimulus (e.g., melatonin or light) relative to its timing may be displayed as a phase response curve (PRC). Published PRCs to exogenous melatonin show a transition from phase advances to delays approximately 1 h after dim light melatonin onset. A previously developed mathematical model simulates endogenous production and clearance of melatonin as a function of circadian phase, light-induced suppression, and resetting of circadian phase by light. We extend this model to include the pharmacokinetics of oral exogenous melatonin and phase-shifting effects via melatonin receptors in the suprachiasmatic nucleus of the mammalian hypothalamus. Model parameters are fit using 2 data sets: (1) blood melatonin concentration following a 0.3- or 5.0-mg dose, and (2) a PRC to a 3.0-mg dose of melatonin. After fitting to the 3.0-mg PRC, the model correctly predicts that, by comparison, the 0.5-mg PRC is slightly decreased in amplitude and shifted to a later circadian phase. This model also reproduces blood concentration profiles of various melatonin preparations that differ only in absorption rate and percentage degradation by first-pass hepatic metabolism. This model can simulate experimental protocols using oral melatonin, with potential application to guide dose size and timing to optimally shift and entrain circadian rhythms.
Keywords: melatonin, modeling, circadian rhythms, pharmacokinetics, phase shift, exogenous dose, phase response curve
Mathematical modeling of biological processes may improve understanding of underlying physiology, suggest areas of further investigation, and provide useful predictions. Melatonin is an excellent candidate for modeling because of the growing body of published research and its many current uses, including treatment of jet lag and phase-shift disorders (Sanchez-Barcelo et al., 2010). Current clinical studies with only 1 or 2 dose sizes cannot guide dosing of the dozens of over-the-counter dose sizes and preparations available to the public. We chose to model the circadian phase resetting effects of exogenous melatonin to provide a method for guiding effective timing and dosage of administration relative to preparation.
Melatonin
The hormone melatonin (N-acetyl-5-methoxy-tryptamine) is secreted into the bloodstream by the pineal gland, starting approximately 2 h before habitual bedtime, continuing throughout nighttime darkness, and decreasing to daytime levels around habitual wake time (Burgess et al., 2008). Ocular light exposure suppresses melatonin secretion in humans in an intensity-dependent manner, even in ordinary room light of ~100 lux (Zeitzer et al., 2000). Suppression is mediated via the suprachiasmatic nucleus (SCN) of the hypothalamus, the site of the mammalian circadian pacemaker (Zucker et al., 1976; Rusak, 1977), which also regulates the onset of melatonin secretion with a circadian periodicity. The melatonin rhythm persists in the absence of a sleep-wake or light-dark cycle (Czeisler and Khalsa, 2000). Endogenous melatonin has multiple physiological functions, including tracking time of year based on scotoperiod (Hui et al., 1992). Because of its tight regulation by the SCN and minimal masking by factors besides light, melatonin is the most accurate known marker of human circadian phase (Klerman et al., 2002).
Exogenous melatonin is currently used for shifting circadian phase and inducing sleep. Here we focus on the effects on circadian phase. Phase shifts are mediated by melatonin receptors in the SCN (Reppert et al., 1988); the direction and magnitude of phase shifts depend on the initial phase at melatonin delivery (Lewy et al., 1998; Burgess et al., 2008). Phase response curves (PRCs) have been determined for oral doses ranging from 0.5 mg to 3.0 mg (Lewy et al., 1992; Zaidan et al., 1994; Lewy et al., 1998; Burgess et al., 2008; Burgess et al., 2010). These PRCs show relatively weak (type 1) resetting (Winfree, 1980); the point of transition from phase advances to phase delays occurs approximately 1 h after dim light melatonin onset (DLMO), that is, approximately 1 h before habitual bedtime in normally entrained individuals. By comparison, type 1 PRCs to ocular light stimuli (e.g., Khalsa et al., 2003) show this transition point occurring close to the core body temperature nadir, approximately 2 h before habitual wake. The phase-resetting effects of light and exogenous melatonin are therefore approximately 8 h out of phase. Whereas light causes phase delays during early biological night and phase advances during late biological night, exogenous melatonin has the opposite effect. Since light exposure and melatonin production typically occur at different times of day, endogenous melatonin may augment light-based entrainment (Lewy et al., 1998).
Mathematical Modeling
Brown et al. (1997) introduced a physiologically based model of the diurnal variation of pineal and plasma melatonin concentration for calculating melatonin phase and peak amplitude. This model also provided information about melatonin infusion and clearance rates within the pineal gland and blood plasma. To incorporate the ocular light effects on melatonin production and rhythm, this model was integrated with an existing mathematical model of the effects of light on the human circadian pacemaker (St. Hilaire et al., 2007a, 2007b).
Here, we extend this model to incorporate (1) pharmacokinetics of two preparations of oral melatonin and (2) effects of combined endogenous and exogenous melatonin on the circadian pacemaker to predict the phase shift induced by a given dose at any circadian phase.
MATERIAL AND METHODS
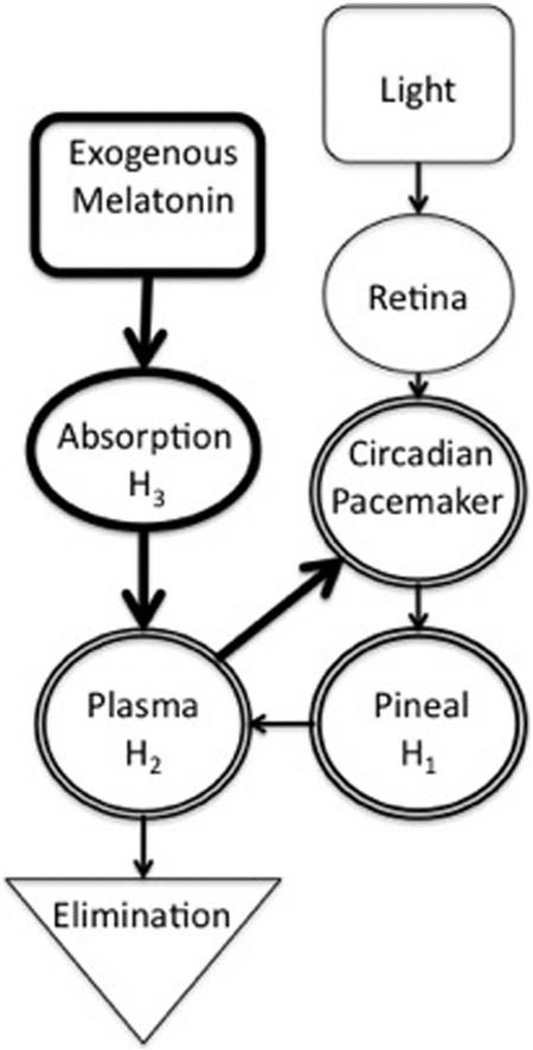
In this section, we introduce previously published model equations, our modifications to these equations, and new model equations, which together comprise the current model. Figure 1 is a schematic of our new model. Table 1 summarizes the data sets used.
Figure 1.
Schematic diagram of the multicompartment melatonin model. A drive generated by light is transmitted to the circadian pacemaker via the retinohypothalamic tract, generating light-dependent phase resetting. Light also suppresses endogenous melatonin production at the pineal via the circadian pacemaker. Melatonin synthesis in the pineal is initiated by signals from the circadian pacemaker. Melatonin then diffuses into the plasma. Melatonin in the plasma has a phase-resetting effect on the circadian pacemaker. Plasma levels are increased by exogenous melatonin doses and decreased by elimination via the kidneys. Before reaching the plasma and acting on the circadian pacemaker, exogenous melatonin goes through an absorption stage during which ~90% of the dose is degraded. Bold lines indicate model additions from previously published work. The double lines around the circadian pacemaker, pineal, and plasma compartments indicate that together they comprise the pathway of endogenous melatonin production.
Table 1.
Summary of data sets used in this article.
| Pharmacokinetic Data Sets | |
|---|---|
| Wyatt et al.(2006) |
Summary: Determined the physiological half-life and time to peak of exogenous gelatin-capsule melatonin by studying 0.3- and 5.0-mg doses. Found that the time to peak is roughly 1.2 h and the half-life is approximately 1.0 h. Use in the article: The Wyatt exogenous melatonin preparation appeared to be the most similar to the preparation used by Burgess et al. Therefore, the values of pharmacokinetic parameters fit to the Wyatt data were used in fitting the model to the Burgess PRCs. |
| Aldhous et al. (1985) |
Summary: Compared 2.0-mg doses of melatonin in 3 different preparations to demonstrate the effect of preparation on pharmacokinetics. Found that the time to peak for gelatin-capsule melatonin is approximately 50 min and the half-life is approximately 40 min. Use in the article: Used to demonstrate the model’s versatility and ability to reproduce a second pharmacokinetic profile from only minor changes to 2 parameters. Additionally, the demonstration that 2 gelatin-capsule preparations (Aldhous et al. and Wyatt et al.) produced inconsistent pharmacokinetic profiles reinforces our point that preparation has a significant impact on the resultant PRC and therefore should be reported in all studies examining melatonin’s phase resetting effects. |
| Phase Response Curve (PRC) Data Sets | |
| Burgess et al. (2008) |
Summary: Produced a PRC to three 3.0-mg doses of gelatin-capsule exogenous melatonin in a light-controlled environment. Use in the article: This is the PRC to which the model is fit. |
| Burgess et al. (2010) |
Summary: Produced a PRC to three 0.5-mg doses of gelatin-capsule exogenous melatonin in a light-controlled environment to demonstrate the effect of dose size on maximum phase shift. Found that relative to the 3.0-mg PRC, the 0.5-mg PRC’s peak is phase advanced. Use in the article: Used to demonstrate that our model can reproduce the effects of multiple dose sizes without additional parameter manipulation. |
| Lewy et al. (1992, 1998) |
Summary: Produced a PRC to four 0.5-mg doses of exogenous melatonin in an uncontrolled light environment. Use in the article: Used as a second data set to show that our model can reproduce multiple protocols without manipulating model parameters. Demonstration of the effects of multiple light intensities during the uncontrolled light portion of the protocol demonstrates the importance of reporting light environments in interpreting PRC results. |
Model of Light’s Effects on the Circadian Pacemaker
The Kronauer et al. (1999) model of the effects of light on the human circadian pacemaker includes a light preprocessor in the retina, Process L, and the circadian pacemaker in the SCN, Process P. When light reaches the retina, it activates photoreceptors that project via the retinohypothalamic tract to SCN neurons.
In the model, photoreceptors exist as “activated” or “ready” (since transition time between states is negligible). Photoreceptors are activated at rate
| (1) |
where I0 and I1 are constants, and I represents environmental light intensity in lux. The value for p was empirically determined by Kronauer et al. (1999) and updated by St. Hilaire et al. (2007a, 2007b). Activated photoreceptors are converted back to the ready state at constant rate β (Kronauer et al., 1999; St. Hilaire et al., 2007a, 2007b). The fraction of activated photoreceptors, n, is modeled by
| (2) |
The resultant photic drive, B, to the circadian pacemaker is assumed to be proportional to the rate, α(1 − n), at which photoreceptors are activated:
| (3) |
In these equations, x represents circadian pacemaker activity, and xC is a complementary variable. G is a constant that modifies photic drive strength, and (1 − bx)(1 − bxC) modulates circadian phase dependence of light sensitivity through parameter b (Kronauer et al., 1999). The value b = 0.4 was chosen by Kronauer et al. (1999) to achieve a photic sensitivity maximum-to-minimum ratio of ~3:1 with maximum sensitivity approximately 3.8 h before the core body temperature nadir.
Two coupled differential equations model Process P (St. Hilaire et al., 2007b):
| (4) |
| (5) |
Parameter κ modifies photic drive B’s strength, τCrepresents intrinsic period, γ determines the oscillator’s stiffness (i.e., how quickly it returns to its limit cycle after perturbation) (Kronauer, 1990), and f is a correction term included to fix the period at precisely τC(Forger et al., 1999).
Constants η and ξ in Equations 4 and 5 modify the strength of the melatonin drive, M. Their values are experimentally determined (see the Results section) to achieve correct PRC shape.
Oscillator phase, φ, uses the standard polar definition
| (6) |
Endogenous and Exogenous Melatonin
The multicompartmental melatonin concentration model includes the pineal gland (H1), blood plasma (H2), and oral absorption site (H3). The first 2 are adapted from St. Hilaire et al. (2007b), whereas absorption site is our addition. These compartments are modeled by the following differential equations:
| (7) |
| (8) |
| (9) |
During biological night, the SCN induces the pineal gland to produce melatonin, which infuses into plasma at rate βIP. Melatonin is cleared from plasma by the kidneys at rate βCP. Absorption of exogenous melatonin into plasma happens at rate βAP; this new parameter’s value is determined by experimental measures of time to peak (details below). Parameter values for a, βIP, and βCP, used in Equations 7, 8, 10, and 11, were previously estimated by St. Hilaire et al. (2007b). Minor updates to these parameters’ values were derived for our new model as described below.
A(φ) in Equation 7 represents pineal melatonin production and is defined below. (1 − mB)S(H1,B) models melatonin suppression by light input, B, where m is a constant modifying B’s strength, originally derived by St. Hilaire et al. (2007b). S is a step function that prevents H1 from falling below 0 in response to strong light stimuli, since a negative concentration is unphysiological. When (1 − mB) ≥ 0, S = 1, but when H1 < 0.001 pmol/L (threshold chosen to approximate 0) and (1 − mB) < 0, S = 0.
At the time of a dose delivery, the value of H3 is increased by an amount proportional to the exogenous dose at a rate determined by the pharmacokinetic parameters in Equations 7, 8, and 9 To convert dose mass to an effective blood concentration, we assume equal distribution across 5 L of blood volume (Nadler et al., 1962), the accepted “average” adult’s blood volume. To account for dose loss by first-pass hepatic metabolism (Claustrat et al., 2005), we multiply the effective blood concentration by a parameter 0 ≤ ε ≤ 1, which represents the fraction of the dose that is absorbed into the bloodstream. This parameter may be different for different dose preparations. An alternative approach would be to explicitly model first-pass metabolism by adding an additional compartment; this is not necessary for the results presented here.
Serotonin to melatonin conversion is catalyzed by arylalkylamine N-acetyltransferase (AA-NAT). This enzyme-catalyzed melatonin precursor is then O-methylated by hydroxyindole O-methyltransferase (HIOMT), producing melatonin. This circadian phase dependent process is modeled by A(φ) (St. Hilaire et al., 2007b):
| (10) |
| (11) |
The phases φon and φoff are those at which melatonin synthesis is turned on and off. The function M2π(x) returns x modulo 2π (cycle period). The constant r converts from time to phase, for consistency with previous work in which melatonin onset and offset times were used rather than phases (St. Hilaire et al., 2007b).
The melatonin drive to the SCN represents input to melatonin receptors from both endogenous and exogenous melatonin blood plasma. It is modeled by the sigmoid function,
| (12) |
where M decreases to a negligible value as H2 decreases and approaches Mmax as H2 increases. The midpoint of this rising portion of the function occurs at H2 = Hsat and M = Mmax/2. The curve becomes steeper for smaller values of σ.
A sigmoid function was chosen to simulate receptor saturation. The value of Hsat was estimated from dose-responses of several studies (Zhdanova, 2005; Dollins et al., 1994; Stone et al., 2000; Burgess et al., 2010). Stone et al. (2000) compared the effects of 0.1-, 0.5-, 1.0-, 5.0-, and 10.0-mg doses on sleep onset and observed no dose-dependence over the range 0.5 to 10.0 mg. Studies by Dollins et al. (1994) and Zhdanova et al. (1995) found that doses between 0.3 and 10.0 mg produce effects of similar magnitude. Dollins et al. (1994) found that the physiological concentration of melatonin during the biological night was roughly 200 pg/mL, a concentration that could be duplicated during the biological day by administering a dose between 0.1 and 0.3 mg. Zhdanova et al. (1995) found that above a 0.3-mg dose there was no significant increase in response. Together, these findings suggest that melatonin receptors are saturated at levels above ~200 pg/mL. These findings are consistent with a more recent study (Burgess et al., 2010) in which only minimal dose-dependence in phase shifting was observed between 0.5 mg and 3.0 mg. We therefore take 200 pg/mL (861 pmol/L) to be the value of Hsat. Other studies have also reported saturation of melatonin receptors; results from Deacon and Arendt (1995), who looked at acute effects on core body temperature, suggest that the half-maximal response occurs between 0.05 mg and 0.5 mg, which after digestion and metabolism produce plasma concentrations of ~430 pmol/L and ~4300 pmol/L, respectively, consistent with the value of Hsat chosen here.
After fixing a nominal value for Hsat, we constrained σ based on dose responses observed experimentally. Burgess et al. (2010) derived phase response curves for 3 consecutive daily doses of 0.5 mg or 3.0 mg, finding a 4% increase in PRC amplitude for the higher dose. These findings place an upper bound of ~103 for σ. Larger values of σ would result in a flatter sigmoid curve, and therefore a more gradual dose response, which would not be consistent with experimental data. Therefore, a nominal value of σ = 50 pmol/L was chosen. To achieve tighter constraints on σ, PRC data are needed from doses well below Hsat. Those PRCs have not been produced, however, and doses used clinically (including those modeled below) are large enough to saturate melatonin receptors. At these concentrations, the model is insensitive to the precise value of σ.
The values of Mmax and other parameters were determined by fitting our model to the PRC of Burgess et al. (2008) for a 3.0-mg dose of exogenous melatonin, described below in the “PRC Methods” section
Pharmacokinetics Methods
Melatonin’s pharmacokinetics are determined by 3 parameters: ε (preabsorption metabolism), βCP (effective clearance rate), and βAP(effective absorption rate). To fit values to βAP and βCP, we compared the model to blood plasma melatonin concentration data from Wyatt et al. (2006). Specifically, we required that the model accurately reproduce both time to peak (i.e., time from ingestion to peak concentration) and physiological half-life, for both 0.3-mg and 5.0-mg doses. Their data showed a half-life of ~1.0 h and a time to peak of ~1.2 h. Consistent with this, Waldhauser et al. (1984) found the half-life of melatonin to be ~50 min. Wyatt et al. (2006) analyzed melatonin’s pharmacokinetic profile at 2 different circadian phases, one in which endogenous melatonin was present and one in which endogenous melatonin was absent. Although concentrations were slightly higher during the exogenous melatonin-present trials, the time to peak and clearance rate were not affected by circadian phase. Therefore, we did not model difference in pharmacokinetics with circadian phase. Parameter ε modifies the amplitude of melatonin’s concentration profile over time. Its value was set to 0.1 based on the findings of Claustrat et al. (2005) and confirmed after fitting values for βAP and βCPto the Wyatt et al. (2006) data. The value of ε and the values of βCP and βAPwere used to simulate the Burgess et al. (2008, 2010) protocols below.
Exogenous melatonin pharmacokinetics are preparation dependent; therefore, a single parameter set will never fit all data. Aldhous et al. (1985) showed that for an equal dose of 2 mg in gelatin capsules, corn oil, and a slow-release pill, different plasma concentration profiles resulted, presumably because of different degrees of preabsorption metabolism and rates of absorption. Comparison of gelatin preparations used by Aldhous et al. (1985) and Wyatt et al. (2006) reveals further differences. Wyatt et al. (2006) used a gelatin capsule in which 5.0 mg of melatonin was suspended in cellulose, whereas Aldhous et al. (1985) used a gelatin capsule in which 2.0 mg of melatonin was suspended in lactose. The 2 studies show different times to peak and half-lives. These differences cannot be accounted for by changing dose size and instead must be accounted for by changing pharmacokinetic parameters, because the model’s solution to a single dose is a biexponential equation, in which time to peak and half-life are independent of dose size. To illustrate the model’s ability to reproduce different plasma melatonin profiles, we modeled a 2-mg dose for both the Aldhous and Wyatt gelatin preparations by fitting values of ε and βAP for each.
PRC Methods
We simulated the Burgess et al. (2008) PRC protocol to fit the model’s sensitivity to exogenous melatonin. The protocol began with 7 days of habitual sleep schedules, followed by 5 days on a 4.0-h ultradian sleep-wake and light-dark cycle alternating between 1.5 h of permitted sleep with lights off and 2.5 h kept awake in room light (>150 lux). The ultradian cycle minimized phase-shifting effects of light by evenly distributing light exposure across circadian phases. For the first three 24-h days of this ultradian cycle, participants were given a 3.0-mg gelatin-based capsule of oral melatonin (Burgess et al., 2008) or a placebo at the start of a wake episode at the same clock time each 24-h day. A PRC was constructed based on the last day’s phase assessment. Values of parameters Mmax, η, and ξ in Equations 4, 5, and 12, which together determine the strength of the phase resetting effect, were explored over a range of 1 order of magnitude above and below final values and optimized using a least-square data-fitting method to fit the 3.0 mg PRC. The 3-dimensional parameter space spanned by Mmax, η, and ξ was explored using a fixed grid loop algorithm written in MatLab 7.11.0 (The MathWorks, Natick, MA) that simulated a PRC at each coordinate of the parameter space. Residuals were calculated as the vertical distance between experimental data points and the simulated PRC. The final set of model parameters is listed in Table 2.
Table 2.
Model parameters.
| Parameter | Value and Units (Previous Value) |
Parameter | Value and Units (Previous Value) |
|---|---|---|---|
| I0 | 9500 lux (9500 lux) |
η | 0.04 |
| I1 | 100 lux | ζ | 0.54 |
| α0 | 0.1 sec (0.05 sec) |
βIP | 7.83 × 10−4 sec−1 (7.83 × 10−4 sec−1) |
| β | 0.007 sec (0.0075 sec) |
βCP | 3.35 × 10−4 sec−1 (4.17 × 10−4 sec−1) |
| p | 0.5 | βAP | 1.62 × 10−4 sec−1 |
| r | 15.36 sec | a | 1.0442 × 10−3 sec−1 |
| G | 37 | ϕon | 6.113 |
| b | 0.4 | ϕoff | 4.352 |
| γ | 0.13 | δ | 600 sec |
| κ | 12/π h | Mmax | 0.019513 |
| τc | 24.1 h | Hsat | 861 pmol/L |
| f | 0.99729 | σ | 50 pmol/L |
| m | 7 sec−1 | ε | 0.10 |
Best fit parameter values are given in the order that they appear in the Methods section. Previously used parameter values from St. Hilaire et al. (2007b) are given when applicable, even if the values are unchanged.
Using these parameter values, we simulated 2 independent data sets. First, we simulated an experiment by Burgess et al. (2010), which is identical to the 2008 experiment except for the use of 0.5-mg instead of 3.0-mg doses. Then, to investigate the effects of a light-dark cycle on the melatonin PRC, we simulated the Lewy et al. (1992, 1998) protocol in which baseline DLMO was assessed on day 1, followed by a week of protocol acclimation with placebo. On day 7, pretreatment DLMO was obtained followed by 2 days of placebo (days 8 and 9), 4 days of 0.5 mg melatonin (days 10–13), and posttreatment DLMO measurement on day 14. With the exception of DLMO measurement days (1, 7, and 14), subjects were at home in uncontrolled and unrecorded light exposure environments. For individuals previously adapted to dim light (e.g., in inpatient experiments), the dynamic range of the circadian phase shifting response to light falls between 0 and 1000 lux (Zeitzer et al., 2000); we therefore simulate light intensities from this range. Light-dark cycles simulated had 16 h of 5, 50, or 500 lux with 8 h of 0 lux in each simulated 24-h day. The parameter set was estimated using the least-squares data fitting method described above.
RESULTS
Pharmacokinetics Results
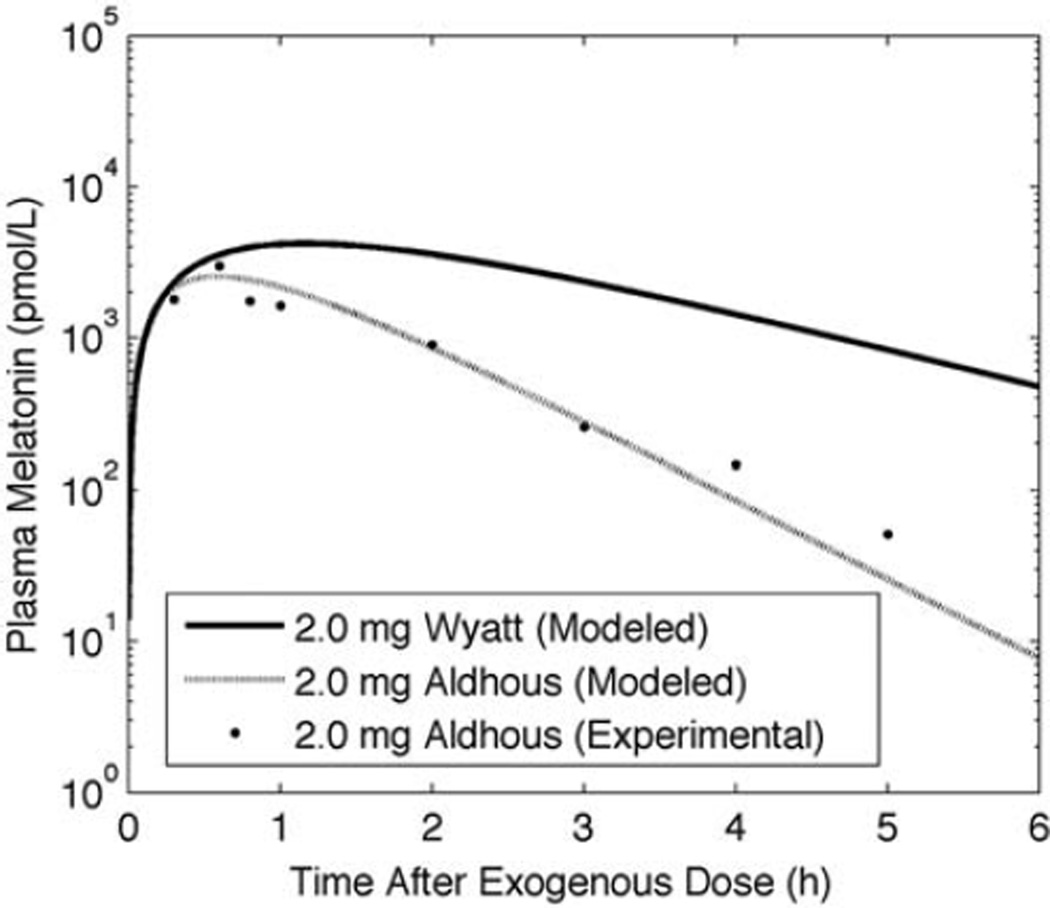
Simulated and experimental (Wyatt et al., 2006) pharmacokinetics results for 0.3-mg and 5.0-mg data are shown in Figure 2. For the gelatin capsule preparation modeled here, we use ε = 0.1, βAP= 1.62 × 10−4 sec−1, and βCP= 3.35 × 10−4 sec−1 to achieve a 100-min time to peak and 100-min half-life with peak melatonin concentration following a 0.3-mg and 5.0-mg dose of 5 × 102 and 104 pmol/L, respectively. Simulations of the Wyatt et al. (2006) and the Aldhous et al. (1985) oral doses of gelatin capsule melatonin are shown in Figure 3. The Aldhous et al. preparation has a faster time to peak, faster clearance rate, and greater preabsorption metabolism than the Wyatt et al. preparation, with ε = 0.03, βAP = 6.67 × 10−4 sec−1, and βCP = 3.35 × 10−4 sec−1, representing a time to peak of ~50 min, a half-life of ~40 min, and a peak melatonin concentration following a 2.0-mg dose of 1.15 × 103 pmol/L. We assessed model sensitivity to these parameters. Increasing βCP by 20% decreased time to peak by 10% and half-life by 18%. Increasing βAP by 20% decreased time to peak by 7% and half-life by 9%.
Figure 2.
Experimental (symbols, from Wyatt et al. 2006) and modeled (lines) plasma melatonin concentrations over 7 h following 5.0-mg and 0.3-mg doses of oral melatonin.
Figure 3.
Simulated pharmacokinetic profiles following the Aldhous (1985) (dashed line) and Wyatt (2006) (solid line) 2.0-mg gelatin-capsule melatonin doses. Experimental data from Aldhous et al. (1985) indicated by symbols.
PRC Results
To verify that a phase response is indeed present, we simulated zero phase response (i.e., a horizontal line) at all phases. The adjusted R2 value was 0.616 when phase shifts were simulated using the model and only 0.321 when zero phase shifts were simulated. We therefore proceeded with the model for all simulations. We note that the uncertainty in the original data is not reported, thus limiting our data fitting comparison to that of the residual sums for different simulations.
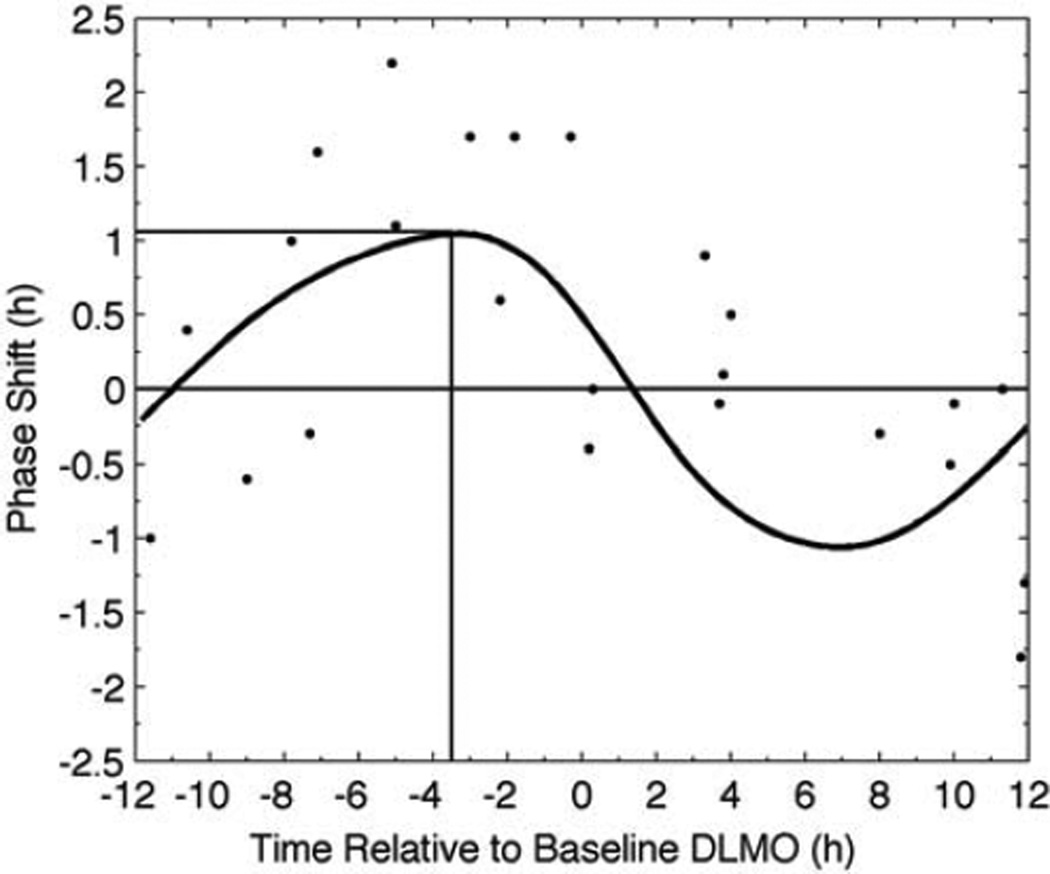
Simulated and experimental PRC data for the 3.0-mg dose are shown in Figure 4. Exogenous melatonin administered around the time of DLMO causes negligible phase resetting. Doses given prior to DLMO (left of 0 h in the figure) cause phase advances, whereas doses given after DLMO (right of 0 h in the figure) cause phase delays. The model thus predicts type 1 resetting to 3.0 mg of exogenous melatonin.
Figure 4.
Melatonin PRC for 3 consecutive daily doses of 3.0 mg of oral melatonin. Data extracted from Burgess et al. (2008) are represented as symbols; model output is represented by the solid curve. The vertical line marks the stimulus time required for maximum phase advance (horizontal line). The thin, solid line across the figure demarks a phase shift of 0 h.
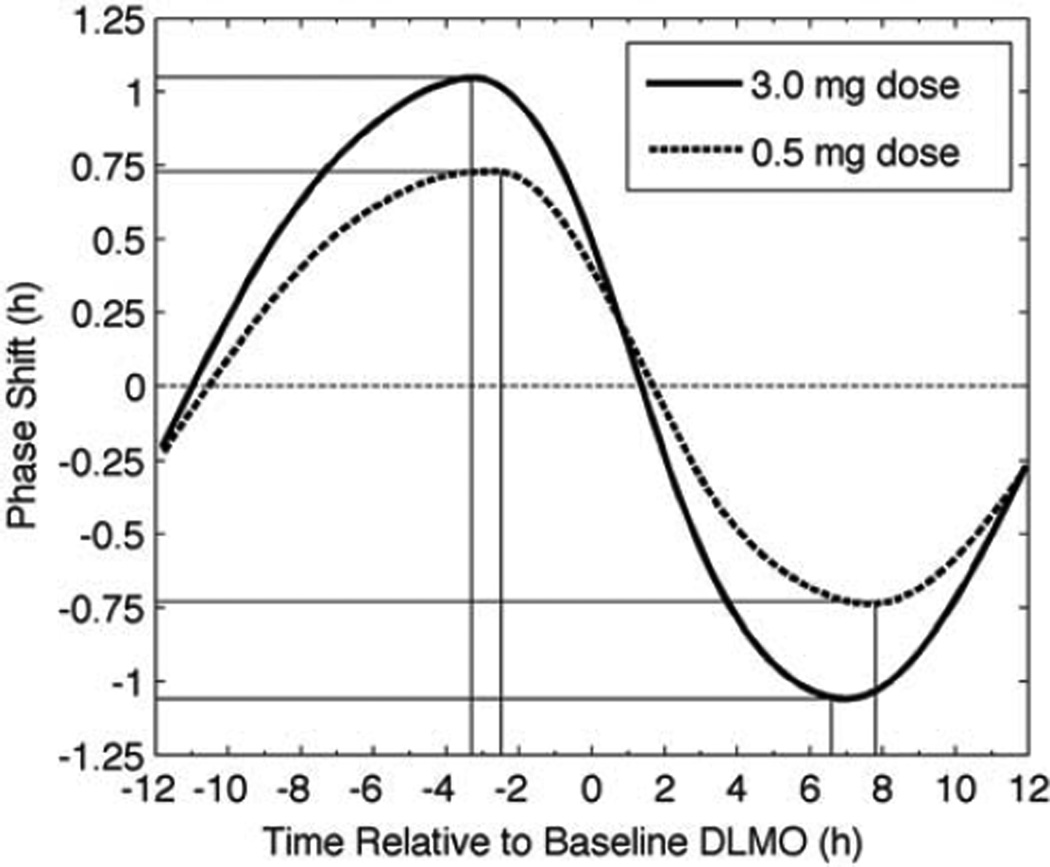
In a more recent experiment, Burgess et al. (2010) showed that compared with a 3.0-mg dose, a 0.5-mg dose of the same preparation results in a slightly lower peak that occurs at a slightly later phase. The model correctly predicted these findings without modification to model parameters (Figure 5).
Figure 5.
Simulated PRCs for 3 consecutive daily doses of 3.0 mg (solid line) and 0.5 mg (dashed line) of melatonin. The vertical lines mark timing required for the peak phase advance and phase delay (horizontal lines) for each PRC. The horizontal straight, dashed line at zero shows zero phase shift.
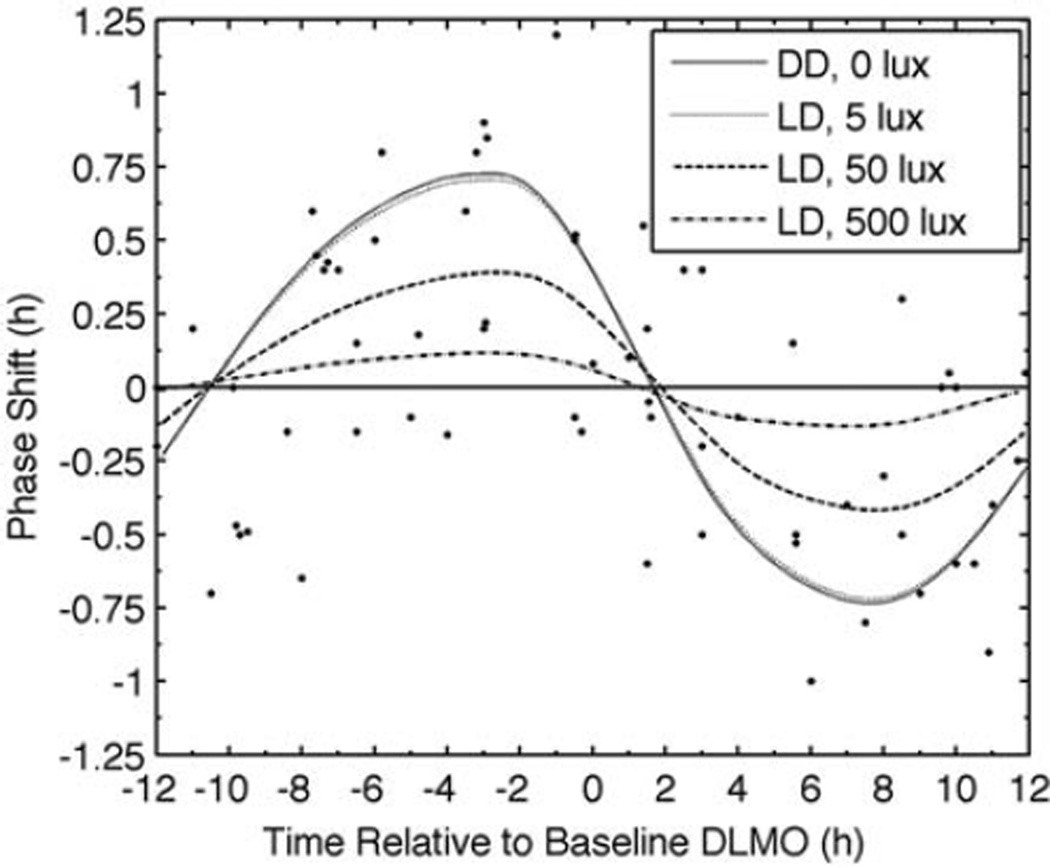
Since Lewy et al. (1998) did not control light exposure, and light is a stronger phase-shifting stimulus than is melatonin, the simulations of that protocol were performed with 4 different light levels during the wake episodes (Figure 6). As light intensity decreases, the PRC peak occurs earlier and at higher amplitude, similar to the effects observed when increasing exogenous melatonin dose (Figure 5). Higher light intensities reduce melatonin-induced phase shifts due to light’s entraining effects, which may lock the rhythm to a stable phase.
Figure 6.
Simulated PRC for 4 consecutive doses of 0.5 mg of exogenous melatonin. Symbols represent experimental data (Lewy et al. 1998). The 4 curves show results from constant darkness (DD; 0 lux) and 3 light levels (5, 50, and 500 lux) within a light-dark (LD) cycle of 16 h light and 8 h dark. Note that PRCs for DD and 5 lux conditions overlap. The horizontal straight, solid line at zero shows zero phase shift.
DISCUSSION
This article presents the first physiologically based mathematical model of diurnal variations in melatonin that includes the phase-shifting effects of exogenous doses of melatonin. The model was shown here to accurately reproduce melatonin’s pharmacokinetics and PRC.
Many equations presented in the Materials and Methods section were adapted from a previous model (St. Hilaire et al., 2007b), as is appropriate when a model is extended to add additional terms. In Equation 7, light suppression of melatonin is approximated by a simple linear function. The functional form used for suppression makes little difference here, as we are modeling phase shifts. However, in future we may opt to use a more realistic saturating suppression function.
Although model parameters presented in this article were optimized to fit the data of Burgess et al. (2008), the model fit at least 1 other PRC (Lewy et al., 1998). The Lewy et al. (1998) PRC was similar to but lower in amplitude than that of Burgess et al. (2008). We showed that this difference possibly can be explained by the uncontrolled light exposures that participants received in this study. Although there were likely interindividual variations in daily light exposure, we showed that a 16:8 LD cycle of 50 lux during wake and 0 lux during sleep fits the Lewy et al. data (R2 = 0.74) using the same pharmacokinetic parameters used to fit the Burgess et al. data. The ability to incorporate light-dark exposures in addition to doses will be significant when applying the model to real-world situations in which variable light-dark cycles are present. Further optimization of light intensity during wake is not warranted because of the assumed large variation in subjects’ timing and intensity of light exposures. Although we cannot rule out differences in pharmacokinetics, clearance rates, or sensitivity to exogenous melatonin, they are not required to reproduce Lewy et al.’s results.
We showed that the model simulates different oral melatonin preparations by varying the fraction of melatonin metabolized preabsorption, ε, and the rate of absorption, βAP, which along with the clearance rate, βCP, determine time to peak and physiological half-life. Although the model can be manipulated to fit the Wyatt et al. (2006) and Aldhous et al. (1985) data by changing the clearance rate, manipulating the model in that way makes less physiological sense; all melatonin molecules should be cleared from the blood plasma by the same mechanism, regardless of initial preparation. We therefore consider clearance rate (βCP) to be independent of preparation. We note that to model the 2 preparations shown here, modifications within only a single order of magnitude were needed for ε and βAP.
One prediction of our model is that different preparations result in different PRCs. We note that although preliminary studies attempted to demonstrate this effect (Aldhous et al., 1985), the data sets are highly variable. Because of large interindividual variability in same-dose response, an ideal pharmacokinetic data set would measure the pharmacokinetics of different preparations in the same subjects. To our knowledge, no such data set exists.
We showed in this article that our model simulates expected phase shifts with different oral preparations and doses. However, we have not addressed interindividual variability, which may account for some between-studies differences, including differences ascribed to preparations. The variability of PRC data in which each point is from a different individual is suggestive of large differences in responses to the same dose, even at the same circadian phase. Developing methods to enable the model to predict an individual’s response would be valuable. As one step, the fixed 5 L of blood volume used in this version of the model could become a variable modified for each individual.
Melatonin preparation type is important in interpreting the PRC for at least 2 reasons. (1) Slowly metabolized preparations or doses would be expected to activate melatonin receptors across a broader range of circadian phases than just the circadian phase of administration. (2) For plasma concentrations greater than ~1000 pmol/L, melatonin receptors are saturated (Dollins et al., 1994). Therefore, we posit that when melatonin infuses into the bloodstream quickly, causing high melatonin concentrations, a large proportion of that melatonin will be broken down and cleared without acting at the receptor level. Using the pharmacokinetic profile of gelatin capsules from Aldhous et al. (1985) and fitting to the Burgess et al (2008) data, we predicted that Burgess et al. (2008) used gelatin capsules in their study. More direct comparison between the Aldhous et al. (1985) and Wyatt et al. (2006) data is not possible due to the low number of data points in the Aldhous et al. study. After these predictions, we confirmed via personal communication (2011) that both Burgess et al. (2008) and Wyatt et al. (2006) used gelatin melatonin capsules. Although most studies do not report preparation used, a literature search revealed that corn oil was listed more frequently than was gelatin until the mid-1980s, after which gelatin became the primary preparation listed in chronobiology. We note that preparation variation likely exists even among preparations of a single class (e.g., gelatin). Since preparation used is important in interpreting pharmacokinetic and PRC data, we encourage researchers of future publications to provide this information.
Both experimental and modeling results demonstrate a nonlinear dose response in the melatonin PRC, with only about 40% increased amplitude for a 500% larger dose. We note that the amplitude reported by Burgess et al. (2008, 2010) based on a dual harmonic fit indicates a ~4% increase in amplitude (2.8 h in the case of the 0.5-mg PRC and 2.9 h phase shift in the case of the 3.0-mg PRC). Our results may be different because we fit our model to the data points without using a dual harmonic curve.
In addition to the difference in amplitude, the 3.0-mg PRC is phase advanced relative to the 0.5-mg PRC. This result can be understood in terms of time spent with H > Hsat for each dose. In both cases, the dose is absorbed rapidly (exceeding Hsat in <30 min), as seen in Figure 2. The time taken to fall below Hsat differs significantly between the 2 doses, taking about 6 h for the 0.5-mg dose and about 11 h for the 3.0-mg dose. The 3.0-mg dose therefore activates melatonin receptors over a different range of circadian phases than the 0.5-mg dose, resulting in its PRC being advanced relative to the 0.5-mg dose.
Light has the strongest effect on the circadian pacemaker, but other stimuli such as meals and locomotion also affect the circadian rhythm (St. Hilaire et al., 2007a). We tested our model with the nonphotic drive of St. Hilaire et al. (2007a) but found it to have a negligible effect on the resultant PRC (data not shown) and therefore excluded it from this work. Nonphotic drives could play an important role in achieving entrainment with and without exogenous melatonin in blind individuals, which we could model in future work. One potential source of variability not modeled here is down-regulation of melatonin receptors after repeated exposure to superphysiological exogenous doses (Lockley et al., 2000). There are not yet sufficient data to speak to the strength of this effect, but it may be important for modeling entrainment by daily doses.
Our present findings suggest 2 model additions of possible merit. The first is to combine our model with a sleep-wake model to include the hypnotic effects of melatonin. One candidate model is that of Phillips and Robinson (2007), which has already been adapted to model the effects of caffeine on sleep (Puckeridge et al., 2011) and has been combined with the circadian model used here (Phillips et al., 2011). The second potential addition to our model is to incorporate the pharmacokinetics and phase-shifting ability of Ramelteon, a new melatonin-like drug designed to be physiologically similar to melatonin but possibly stronger and more receptor selective (Miyamoto et al., 2004).
Aside from light, melatonin is the most widely used chronobiotic agent, with potential applications to jet lag, insomnia, circadian rhythm sleep disorders, shift work, and circadian entrainment of blind individuals. Side effects from low levels of exogenous melatonin are minimal (Herxheimer and Petrie, 2002). However, melatonin is unregulated in the United States, and therefore there are no guarantees of purity or potency of over-the-counter preparations; indeed, potentially dangerous impurities have been reported (Williamson et al., 1998). Very high doses of even pure melatonin can in rare cases have negative side effects, especially with repeated doses, including depression, cognitive alteration, tremor, fatigue, headache, and somnolence (de Lourdes et al., 2000) and may saturate receptors without causing additional phase resetting effects. Therefore, maximizing phase shifting effects via careful timing rather than higher dosage has potential therapeutic benefit.
By creating this dynamic model, we can manipulate the dose time and dose size to predict the best dosing procedure to produce any phase shift. This model therefore provides the initial basis for ultimately predicting and optimizing melatonin use in real-world environments.
ACKNOWLEDGMENTS
Research supported by NIH P01-AG009975, K24-HL105664 (E.B.K.), T32-HL07901 (M.S.H.), R01-HL114088, and RC2-HL101340 and by NSBRI through NASA NCC 9-58 HPF01603, HFP02802, and PF02101 (A.J.K.P.).
Footnotes
CONFLICT OF INTEREST STATEMENT
In 2010–2011, E.B.K. received investigator-initiated research support from Respironics and an unrestricted gift to the BWH from Sony Corporation. In 2011, A.J.K.P. consulted for Zeo, Inc.
REFERENCES
- Aldhous M, Franey C, Wright J, Arendt J. Plasma concentrations of melatonin in man following oral absorption of different preparations. Br J Clin Pharmacol. 1985;19:517–521. doi: 10.1111/j.1365-2125.1985.tb02679.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown EN, Choe Y, Shanahan TL, Czeisler CA. A mathematical model of diurnal variations and comparison to plasma melatonin levels. Am J Physiol Soc. 1997;272:E506–E516. doi: 10.1152/ajpendo.1997.272.3.E506. [DOI] [PubMed] [Google Scholar]
- Burgess HJ, Revell VL, Eastman CI. A three pulse phase response curve to three milligrams of melatonin in humans. J Physiol. 2008;586:639–647. doi: 10.1113/jphysiol.2007.143180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess HJ, Revell VL, Molina TA, Eastman CI. Human phase response curves to three days of daily melatonin: 0.5 mg versus 3.0 mg. J Clin Endocrinol Metab. 2010;95:3325–3331. doi: 10.1210/jc.2009-2590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claustrat B, Brun J, Chazot G. The basic physiology and pathophysiology of melatonin. Sleep Med Rev. 2005;9:11–24. doi: 10.1016/j.smrv.2004.08.001. [DOI] [PubMed] [Google Scholar]
- Czeisler CA, Khalsa SBS. The human circadian timing system and sleep-wake regulation. In: Kryger MH, Roth T, Dement WC, editors. Principles and Practice of Sleep Medicine. 3rd ed. Philadelphia, PA: WB Saunders; 2000. pp. 353–375. [Google Scholar]
- Deacon S, Arendt J. Melatonin-induced temperature suppression and its acute phase-shifting effects correlate in a dose-dependent manner in humans. Brain Res. 1995;688:77–85. doi: 10.1016/0006-8993(95)96872-i. [DOI] [PubMed] [Google Scholar]
- de Lourdes M, Seabra V, Bignotto M, Pinto LR, Tufik S. Randomized, double-blind clinical trial, controlled with placebo, of the toxicology of chronic mela-tonin treatment. J Pineal Res. 2000;29:193–200. doi: 10.1034/j.1600-0633.2002.290401.x. [DOI] [PubMed] [Google Scholar]
- Dollins AB, Zhdanova IV, Wurtman RJ, Lynch HJ, Deng MH. Effect of inducing nocturnal serum melatonin concentrations in daytime on sleep, mood, body temperature, and performance. Proc Natl Acad Sci U S A. 1994;91:1824–1828. doi: 10.1073/pnas.91.5.1824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forger DB, Jewett ME, Kronauer RE. A simpler model of the human circadian pacemaker. J Biol Rhythms. 1999;14:532–537. doi: 10.1177/074873099129000867. [DOI] [PubMed] [Google Scholar]
- Herxheimer A, Petrie KJ. Melatonin for the prevention and treatment of jet lag. Cochrane Database Syst Rev. 2002;2 doi: 10.1002/14651858.CD001520. CD001520. [DOI] [PubMed] [Google Scholar]
- Hui Y, Hastings MH, Maywood ES, Ebling FJP. Photoperiodic regulation of glutamatergic simulation of secretion of leuteinizing hormone in male Syrian hamsters. J Reprod Fert. 1992;95:935–946. doi: 10.1530/jrf.0.0950935. [DOI] [PubMed] [Google Scholar]
- Khalsa SBS, Jewett ME, Cajochen C, Czeisler CA. A phase response curve to single pulse bright light pulses in human subjects. J Physiol. 2003;3:945–952. doi: 10.1113/jphysiol.2003.040477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klerman EB, Gershengorn HB, Duffy JF, Kronauer RE. Comparisons of the variability of three markers of the human circadian pacemaker. J Biol Rhythms. 2002;17:181–193. doi: 10.1177/074873002129002474. [DOI] [PubMed] [Google Scholar]
- Kronauer RE. A quantitative model for the effects of light on the amplitude and phase of the deep circadian pacemaker, based on human data. Proceedings of the Tenth European Congress on Sleep Research. Sleep. 1990;90:306–309. [Google Scholar]
- Kronauer RE, Forger DB, Jewett ME. Quantifying human circadian pacemaker response to brief, extended, and repeated light stimuli over the photopic range. J Biol Rhythms. 1999;14:501–516. doi: 10.1177/074873099129001073. [DOI] [PubMed] [Google Scholar]
- Lewy AJ, Ahmed S, Jackson JML, Sack RL. Melatonin shifts human circadian rhythms according to a phase-response curve. Chronobiol Int. 1992;9:380–392. doi: 10.3109/07420529209064550. [DOI] [PubMed] [Google Scholar]
- Lewy AJ, Bauer VK, Ahmed S, Thomas KH, Cutler NL, Singer CM, Moffit MT, Sack RL. The human phase response curve (PRC) to melatonin is about 12 hours out of phase with the PRC to light. Chronobiol Int. 1998;15:71–83. doi: 10.3109/07420529808998671. [DOI] [PubMed] [Google Scholar]
- Lockley SW, Skene DJ, James K, Thapan K, Wright J, Arendt J. Melatonin administration can entrain the free-running circadian system of blind subjects. J Endocrinol. 2000;164:R1–R6. doi: 10.1677/joe.0.164r001. [DOI] [PubMed] [Google Scholar]
- Miyamoto M, Nishikawa H, Doken Y, Hirai K, Uchikawa O, Ohkawa S. The sleep-promoting action of ramelteon (TAK-375) in freely moving cats. Sleep. 2004;27:1319–1325. doi: 10.1093/sleep/27.7.1319. [DOI] [PubMed] [Google Scholar]
- Nadler SB, Hidalgo JH, Block T. Prediction of blood volume in normal human adults. Surgery. 1962;51:224–232. [PubMed] [Google Scholar]
- Phillips AJK, Robinson PA. A quantitative model of sleep-wake dynamics based on the physiology of the brainstem ascending arousal system. J Biol Rhythms. 2007;22:167–179. doi: 10.1177/0748730406297512. [DOI] [PubMed] [Google Scholar]
- Phillips AJK, Czeisler CA, Klerman EB. Revisiting spontaneous internal desynchrony using a quantitative model of sleep physiology. J Biol Rhythms. 2011;26:441–453. doi: 10.1177/0748730411414163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puckeridge M, Fulcher BD, Phillips AJK, Robinson PA. Incorporation of caffeine into a quantitative model of fatigue and sleep. J Theor Biol. 2011;273:44–54. doi: 10.1016/j.jtbi.2010.12.018. [DOI] [PubMed] [Google Scholar]
- Reppert SM, Weaver DR, Rivkees SA, Stopa EG. Putative melatonin receptors in a human biological clock. Science. 1988;242:78–81. doi: 10.1126/science.2845576. [DOI] [PubMed] [Google Scholar]
- Rusak B. The role of the suprachiasmatic nuclei in the generation of circadian rhythms in the Golden Hamster, Mesocricetus Auratus. J Comp Physiol B. 1977;118:145–164. [Google Scholar]
- Sanchez-Barcelo EJ, Mediavilla MD, Tan DX, Reiter RJ. Clinical uses of melatonin: evaluation of human trials. Curr Med Chem. 2010;17:2070–2095. doi: 10.2174/092986710791233689. [DOI] [PubMed] [Google Scholar]
- St. Hilaire MA, Klerman EB, Khalsa SBS, Wright KP, Czeisler CA, Kronauer RE. Addition of a non-photic component to a light-based mathematical model of the human circadian pacemaker. J Biol Rhythms. 2007a;247:583–599. doi: 10.1016/j.jtbi.2007.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- St. Hilaire MA, Gronfier C, Zeitzer JM, Klerman EB. A physiologically based mathematical model of melato-nin including ocular light suppression and interactions with the circadian pacemaker. J Pineal Res. 2007b;43:294–304. doi: 10.1111/j.1600-079X.2007.00477.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone BM, Turner C, Mills SL, Nicholson AN. Hypnotic activity of melatonin. Sleep. 2000;23:663–669. [PubMed] [Google Scholar]
- Waldhauser F, Waldhauser M, Lieberman HR, Deng Mei-Hua, Lynch HJ, Wurtman RJ. Bioavailability of oral melatonin in humans. J Neuroendocrinol. 1984;39:307–313. doi: 10.1159/000123997. [DOI] [PubMed] [Google Scholar]
- Williamson BL, Tomlinson AJ, Mishra PK, Gleich GJ, Naylor S. Structural characterization of contaminants found in commercial preparations of melatonin: similarities to case-related compounds from L-tryptophan associated with eosinophilia-myalgia syndrome. Chem Res Toxicol. 1998;11:234–240. doi: 10.1021/tx970202h. [DOI] [PubMed] [Google Scholar]
- Winfree AT. The Geometry of Biological Time, Biomathematics. Volume 8. New York: Springer-Verlag; 1980. [Google Scholar]
- Wyatt JK, Dijk DJ, Ritz-de Cecco A, Ronda JM, Czeisler CA. Sleep-facilitating effect of exogenous melatonin in healthy young men and women is circadian-phase dependent. Sleep. 2006;29:606–607. doi: 10.1093/sleep/29.5.609. [DOI] [PubMed] [Google Scholar]
- Zhdanova IV, Wurtman RJ, Lynch HJ, Ives JR, Dollins AB, Morabito C, Matheson JK, Schomer DL. Sleep-inducing effects of low doses of melatonin ingested in the evening. Clin Pharmacol Ther. 1995;57:552–558. doi: 10.1016/0009-9236(95)90040-3. [DOI] [PubMed] [Google Scholar]
- Zhdanova IV. Melatonin as a hypnotic: pro. Sleep Med Rev. 2005;9:51–65. doi: 10.1016/j.smrv.2004.04.003. [DOI] [PubMed] [Google Scholar]
- Zaidan R, Geoffriau M, Brun J, Taillard J, Bureau C, Cazot G, Claustrat B. Melatonin is able to influence its secretion in humans: descriptions of a phase-response curve. Neuroendocrinology. 1994;60:105–112. doi: 10.1159/000126726. [DOI] [PubMed] [Google Scholar]
- Zeitzer JM, Dijk DJ, Kronauer RE, Brown EN, Czeisler CA. Sensitivity of the human circadian pacemaker to nocturnal light: melatonin phase resetting and suppression. J Physiol. 2000;526:695–702. doi: 10.1111/j.1469-7793.2000.00695.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zucker I, Rusak B, King RG. Neural bases for circadian rhythms in rodent behavior. Adv Psychobiol. 1976;3:35–74. [PubMed] [Google Scholar]