Ab initio calculations and validation of the pH-dependent structures of the His37-Trp41 quartet, the heart of acid activation and proton conductance in the M2 protein of Influenza A virus

Abstract

The M2 protein of Influenza A virus forms a homotetrameric proton channel activated by low pH. The His37-Trp41 quartet is the heart of acid activation and proton conductance, but the functional mechanism is still controversial. We carried out ab initio calculations to model the pH-dependent structures of the His37-Trp41 quartet. In our model at neutral pH, the four His37 residues are configured into a pair of dimers; in each dimer, a proton is shared between Nδ1 on one residue and Nε2 on the other, and, under the restraint of the backbone, the two imidazole rings are nearly parallel, in contrast to a perpendicular arrangement for a free imidazole-imidazolium dimer. Within each dimer the +1 charge is highly delocalized, contributing to its stabilization in a low dielectric environment. The Nδ1-H-Nε2 strong hydrogen bonds result in significantly downfield shifted Nδ1 and Nε2 chemical shifts (at 169.7 and 167.6 ppm, respectively), in good agreement with experiments. In our model at acidic pH (where the channel becomes activated), a third proton binds to an imidazole-imidazolium dimer; the imidazole rings rotate away (each by ~55°) from each other, destroying the dimer structure. The two imidazoliums are stabilized by hydrogen bonds with water molecules and a cation-π interaction with Trp41. The Raman spectra calculated for the His37-Trp41 quartet at neutral and acidic pH are in agreement with experiments. Our calculations support an activation and conductance mechanism in which a hydronium ion from the N-terminal side passes a proton to an imidazole-imidazolium dimer; when the Trp41 gate is open, relaying of a proton onto a water molecule from the C-terminal side then allows the imidazole-imidazolium dimer to reform and be ready for the next round of proton conductance.

Introduction

The M2 protein of influenza A virus forms a homotetrameric proton-selective channel that is activated by low pH.^{1, 2} Each monomer, with 97 residues, forms a transmembrane (TM) helix (residues 26–46) and an amphipathic helix (residues 47–62).³ The TM helices of the tetramer line the channel pore, whereas the amphipathic helices reside in the viral membrane inner interfacial region (Fig. 1a). Two drugs, amantadine and rimantadine, inhibit channel activity by blocking the pore, but a drug-resistant mutation (S31N) has become prevalent in recent seasonal flus as well as the 2009 swine flu pandemic.⁴ Designing drugs that can withstand drug-resistant mutations requires a deeper understanding on the mechanism of acid activation and proton conductance.⁵ The heart of the functional mechanism is the His37-Trp41 quartet.^6–8 It is established that His37 is the pH sensor⁶ and Trp41 is the primary gate,⁹ but the details of acid activation and proton conductance have been controversial. Here we report ab initio calculations of the pH-dependent structures of the His37-Trp41 quartet and their validation against experimental data, in an effort to delineate an activation and conductance mechanism.

Fig. 1.

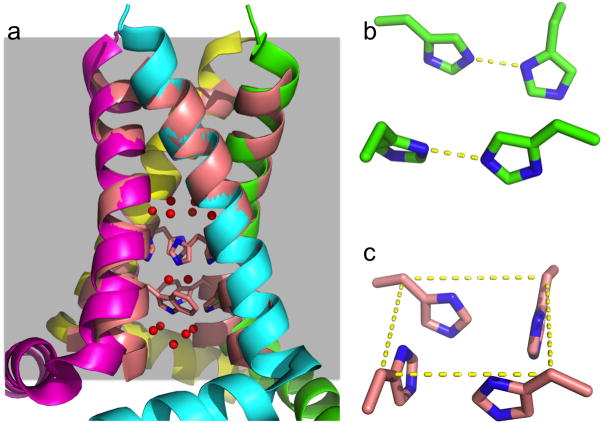
ssNMR and X-ray structures of the M2 conductance domain and the TM domain (PDB entries 2L0J and 3LBW). (a) Cα alignment of the two structures using residues 25–41 (2L0J with four chains in magenta, cyan, green, and yellow; 3LBW with all chains in pink). The His37 and Trp41 sidechains (sticks with C and N atoms in pink and blue, respectively) and the three water layers (red spheres) in 3LBW are also shown. A gray shaded band indicates the membrane. (b) The all-parallel imidazole-imidazolium dimers configuration of the His37 tetrad in 2L0J. (c) The box-like arrangement in 3LBW. The four His37 Cγ atoms are connected by dashed lines to indicate the top of the box.

A model for acid activation and proton conductance, originated from computational studies,^10–13 posits that protonation of His37 residues leads to their repulsion, creating an open pore with a continuous water wire for proton conduction. The proton conductance calculated from such a model was 53 pS,¹³ or 3 × 10⁸ protons per second. However, conductance measurements, especially more recent ones using liposome preparations, place the maximum conductance at ~3 × 10² protons per second.^{8, 14–18} The six orders of magnitude discrepancy casts doubt on this gating model.

An alternative model was proposed by Pinto et al.,¹⁹ in which the His37 tetrad relays the proton from the N-terminal side to the C-terminal side. It was speculated that, after proton release, an imidazole ring flip brings the His37 residue(s) to the initial conformation. It was not clear whether or how His37 residues work cooperatively. The model does provide an explanation for the high proton selectivity of the M2 channel.

An important development toward elucidating the functional mechanism of the M2 proton channel was the determination of the pK_as of the His37 tetrad, by measuring the solid-state NMR (ssNMR) spectra of His37 ¹⁵Nδ1 and ¹⁵Nε2 as a function of pH.⁷ At neutral pH, both ¹⁵Nδ1 and ¹⁵Nε2 showed significantly downfield-shifted resonances (at 167 and 162 ppm, respectively, compared to 147 and 144 ppm for a typical imidazole and 156 and 153 ppm for a typical imidazolium). The significant downfield shifts are characteristic of a strong, low-barrier hydrogen bond between Nδ1 and Nε2, as seen in imidazole- imidazolium crystals.²⁰ The pK_as of the His37 tetrad were determined to be 8.2, 8.2, 6.3, and < 5.0. That the first two pK_as are high and identical shows that the His37 tetrad can form a pair of imidazole-imidazolium dimers with high proton affinity and cooperatively. The third pK_a coincides with the pH for acid activation,^{1, 2} suggesting that the uptake of the third proton opens the channel.

We recently determined the structure of the M2 conductance domain (residues 22–62) in lipid bilayers by ssNMR spectroscopy and restrained molecular dynamics simulations [Protein Data Bank (PDB) entry 2L0J; Fig. 1a].⁸ The sidechain conformation of the His37-Trp41 quartet was modeled by quantum mechanics/molecular mechanics (QM/MM) calculations under the restraint of the backbone structure. Guided by the ssNMR data indicating a strong inter-ring hydrogen bond,⁷ our optimized structure has the His37 residues forming a pair of imidazole-imidazolium dimers, with the imidazole rings parallel within each dimer and also between the dimers (Fig. 1b). We also suggested likely motions of the His37-Trp41 quartet when the third proton is added from the N-terminal side and subsequently released to the C-terminal side, thus filling in some possible details of the proton relay mechanism. We further developed this mechanism into a mathematical model for calculating proton conductance.²¹ From either side of the membrane, proton binding to the His37 tetrad was modeled as a diffusion-controlled reaction. Once bound, the proton can be released to either side of the membrane. This model^{22, 23} predicts proton conductance in the observed range (i.e., up to 3 × 10² protons per second) and quantitatively reproduces the observed current-voltage and current-pH relations,^{2, 24} as well as a 2-fold decrease in current when the solvent is changed from H₂O to D₂O observed by Mould et al.14

A high-resolution (1.65 Å) structure of the M2 TM domain has now been determined by X-ray crystallography (PDB entry 3LBW).²⁵ The backbone conformation of this crystal structure is very similar to that of the ssNMR structure determined in lipid bilayers (Cα RMSD of just 0.6 Å for residues 25–41), with a slightly tighter TM helix packing in 3LBW toward the C-termini, perhaps due to the missing amphipathic helices or the crystalline environment. However, the sidechain conformation of the His37-Trp41 quartet in 3LBW is very different from that in 2L0J. Instead of the all-parallel imidazole-imidazolium dimers that we determined for the His37 tetrad (Fig. 1b), the imidazole rings in 3LBW are arranged into a box, with adjacent rings perpendicular to each other and the Cε1 atom of one ring directed at the face of the other ring (Fig. 1c).

In the present study we carried out ab initio calculations to model the pH-dependent structures of the His37-Trp41 quartet. We also calculated NMR and Raman spectroscopic properties to enable validation by experimental data. We found that the box-like arrangement of the His37 tetrad cannot produce the significantly downfield-shifted resonances of ¹⁵Nδ1 and ¹⁵Nε2 observed at neutral pH. In contrast, the conformation comprising a pair of imidazole-imidazolium dimers, re-calculated here using the X-ray backbone structure for restraint, produced chemical shifts in good agreement with experiments.⁷ We further modeled the structures of the His37-Trp41 quartet bound with a third proton, when the Trp41 primary gate is either closed or open. The Raman spectra calculated for the His37-Trp41 quartet at both neutral and acidic pH are also in good agreement with experiments.²⁶ Our calculations of the pH-dependent structures of the His37-Trp41 quartet support a mechanism in which the uptake of a proton from a hydronium ion from the N-terminal side breaks an imidazole-imidazolium dimer. The two imidazoliums rotate away from each other, and become stabilized by hydrogen bonds with water molecules and by a cation-π interaction with Trp41. When the Trp41 gate is open, release of a proton to a water molecule on the C-terminal side allows the imidazole-imidazolium dimer to reform and be ready for the next round of proton transport.

Results and discussion

His37 residues at high and low pH

At very high (> 8.2) and very low (< 5.0) pH, the His37 sidechains of the M2 protein would be individually deprotonated and protonated, with 0 and +1 charges, respectively. Although these species are not expected to be involved directly in the proton transport mechanism, they do serve as references for understanding the peculiar structural and spectroscopic properties of the His37 tetrad at intermediate pH. We modeled these two species as 4-methylimidazole and 4-methylimidazolium, respectively (A1 or A1′ and A2 in Fig. 2). In the channel pore, they are likely to be stabilized by hydrogen bonding with water molecules (or similar interactions with surrounding polar groups of the protein). We explicitly modeled these hydrogen-bonding interactions.

Fig. 2.

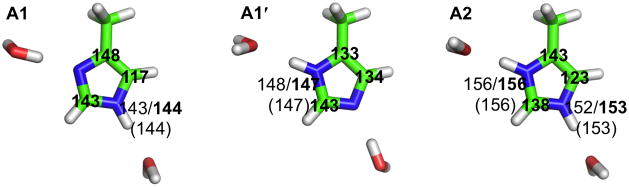
Models of the His37 residues at high pH (A1 and A1′) and low pH (A2). The chemical shifts calculated using MP2 and DFT are shown in regular and bold fonts, respectively; the experimental values are shown in parentheses. For the carbons, only DFT results are shown; MP2 results have the same qualitative differences among A1, A1′, and A2.

We calculated the chemical shielding for A1, A1′, and A2 using either density functional theory (DFT) or second-order Møller-Plesset perturbation (MP2) method. The latter method accounts for long-range dispersion interactions. The calculated results for nitrogens (σ_N) showed strong correlation with the observed chemical shifts (δ_N) of His37 15Nε2 and ¹⁵Nδ1 at high (144 and 147 ppm) and low pH (153 and 156 ppm).⁷ The R² of the linear regression analysis was 0.98 and 1.0, respectively, for the MP2- and DFT-based results. The resulting parameters in the linear relation δ_N = a + bσ_N were a = 204.67 and b = −0.63 for the MP2 method and a = 183.63 and b = −0.53 for the DFT method. Following other studies,^{27, 28} these linear relations are used below to convert calculated Nε2 and Nδ1 chemical shieldings into chemical shifts for other model systems. The 9 ppm downfield shift of the His37 Nε2 and Nδ1 at low pH relative to the counterparts at high pH is captured by our calculations, and can be attributed to stronger hydrogen bond interactions (with water) by the charged species (A2) relative to the neutral species (A1 and A1′), in line with observations on related compounds.^{20, 29–32} Compared to A1 and A1′, the donor-acceptor distances (d_N-O) in A2 showed small but significant shortening (2.9–3.0 Å versus 2.8 Å). A similar increase in hydrogen bonding strength in charged species has been noted in previous studies.^{33, 34}

The differences in calculated Cβ, Cδ2, and Cε1 chemical shifts among A1, A1′, and A2 show characteristic trends. (For carbons, we did not linearly scale the calculated chemical shifts against experimental values, hence our focus is on the qualitative side, specifically on the directions of changes among different species.) These species represent three imidazole tautomers, commonly denoted as τ, π, and Im⁺, respectively. Relative to the Im⁺ tautomer A2, Cδ is downfield-shifted in A1 but upfield-shifted in A1′; Cδ2 is upfield-shifted in A1 but downfield-shifted in A1′; and Cε1 is downfield-shifted in both A1 and A1′. These trends, including the anti-correlation between Cδ and Cδ2 chemical shifts, are consistent with the tautomer dependence observed previously.²⁸ As also noted in that study, interactions with neighboring groups can further change the chemical shifts. The latter effects will be prominent in the systems considered next.

The imidazole-imidazolium dimer

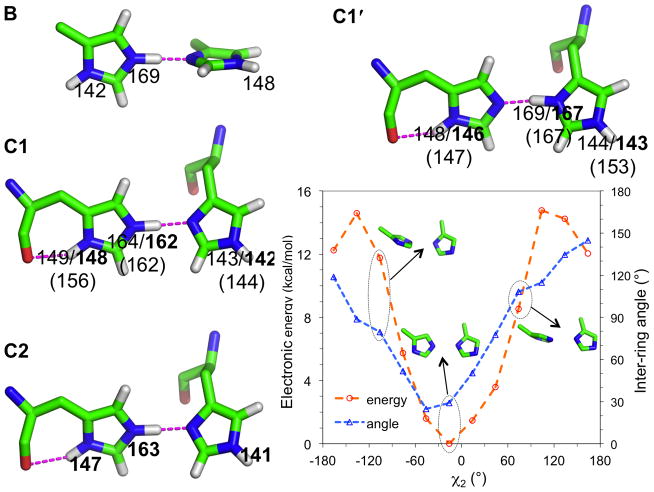
To provide context for characterizing the His37-Trp41 quartet in the confines of the M2 backbone structure, we first carried out structural and chemical shift calculations on a dimer (B in Fig. 3), formed by an imidazolium (A2) and an imidazole (A1) sharing a proton between Nε2 of the first ring and Nδ1 of the second ring. In the optimized model, the distance between the Cγ atoms is 7.0 Å, and, in agreement with a previous calculation,³⁵ the two imidazole rings are orthogonal to each other. The donor-acceptor distance between the inter-ring hydrogen bond is 2.7 Å, indicating strong hydrogen bonding. In the crystal structure of imidazole imidazolium perchlorate, the same 2.7 Å donor-acceptor distance was observed, though the two rings were rotated with respect to each other about the inter-ring Nε2-Nδ1 pseudobond by 55°.³⁶ The moderate deviation from an orthogonal arrangement possibly reflects molecular packing in the crystal structure. The energy barrier (MP2 electronic energy) for transferring the proton from the Nε2 donor to the Nδ1 acceptor in B is only 0.1 kcal/mol; after correcting for (DFT) vibrational free energy (at 298 K), the barrier energy even becomes slightly negative, −1.5 kcal/mol. These results show that the proton resides in a nearly flat-bottomed potential well and can thus move freely between the two nitrogens.³⁵ The binding energy (with vibrational free energy correction) of B is −20 kcal/mol, similar to those for other systems where low-barrier hydrogen bonds are implicated.^{37, 38}

Fig. 3.

Structural models and nitrogen chemical shifts of the imidazole-imidazolium dimer. The models are optimized without restraint (B) and with the restraint of the 2L0J backbone (C1 and C1′) or 3LBW backbone (C2). Intramolecular and intermolecular hydrogen bonds are indicated by dashed lines. The chemical shifts shown follow the convention of Fig. 2. For C1, the dependence of the electronic energy on the inter-ring angle (sampled by varying the χ₂ torsion angle of the left ring) is also shown.

Along with the short donor-acceptor distance and the substantial binding energy, the calculated chemical shift, at 169 ppm, for the hydrogen donor, Nε2, is 17 ppm downfield-shifted relative to the counterpart in A2, again indicating strong interring hydrogen bonding in B. Indeed, by comparing the chemical shifts of the A1–A2 and B model systems, it is clear that only the inter-ring hydrogen bonding produces such a significant downfield shift. The nitrogens that hydrogen bond to water molecules have resonances much farther upfield.

In contrast to the orthogonal inter-ring orientation in B, the optimized model of the imidazole-imidazolium dimer restrained by the M2 backbone structure of either 2L0J or 3LBW has nearly co-planar rings (inter-ring angles at 29°–40° for C1, C1′, and C2; Fig. 3). This dimer conformation is similar to what we previously determined in the context of the His37-Trp41 quartet (Fig. 1b),⁸ suggesting that it has intrinsic stability. The inter-ring hydrogen bond distances, between Nε2 and Nδ1, in C1, C1′, and C2 are all 2.7 Å. The energy barrier for transferring the proton is again low (0.3 kcal/mol (with vibrational free energy correction) for C1). C1 and C1′ are structurally nearly identical (both with a Cγ-Cγ distance of 6.9 Å, compared a value of 6.8 Å for C2), differing only in the placement of the proton involved in the inter-ring hydrogen, consistent with this hydrogen bond having a low energy barrier. In all the three models, an additional hydrogen bond is formed between Nδ1 of the first ring and the backbone carbonyl. The chemical shifts of Nε2, the hydrogen donor in C1 and C2, calculated by DFT and MP2 are 162–164 ppm, in good agreement with the experimental value of 162 ppm.⁷ Similarly, the chemical shifts of Nδ1, the hydrogen donor in C1′, calculated by DFT and MP2 are 167–169 ppm, in good agreement with the experimental value of 167 ppm.⁷

To ascertain that the nearly co-planar inter-ring orientation corresponds to the global energy minimum of the imidazole-imidazolium dimer under the restraint of the backbone structure, we scanned the electronic energy of C1 while sampling the inter-ring angle by changing the χ₂ angle of the first histidine. The results, displayed in Fig. 3, show that the 29° inter-ring angle (corresponding to χ₂ = −16°) is indeed the global minimum. The two conformations with an orthogonal inter-ring orientation (χ₂ = −106° and 74°; the latter mimicking B) have electronic energies that are 11.8 and 8.5 kcal/mol higher. Compared to C1, the conformation with the first ring flipped 180° is a local minimum, with an energy ~10 kcal/mol higher. The large energy difference between the two conformations with a co-planar inter-ring orientation for C1 is in contrast to the nearly identical energies of the counterparts for B. The χ₂ = −16° conformation is favored over the 180° flip at least in part due to the Nδ1-carbonyl hydrogen bond (Fig. 3). With this sidechain-backbone hydrogen bond, the NH groups not participating in the inter-ring hydrogen bond are both positioned below the latter hydrogen bond. This positioning will have additional significance in stabilizing the His37-Trp41 quartet and in the functional mechanism of M2, as discussed below.

The His37-Trp41 quartet at neutral pH

To model the protein environment of the His37 tetrad more realistically, we previously optimized the structure of the His37-Trp41 quartet with the backbone heavy atoms fixed.⁸ Here we repeated the optimization using the 3LBW backbone for the TM domain,²⁵ to show that the all-parallel imidazole-imidazolium dimers configuration of the His37 tetrad is compatible with the latter backbone structure, and to provide evidence that only this configuration, not the box-like configuration, is consistent with structural validation experiments in lipid bilayers. Included in the present structural optimization were 13 crystal waters (divided into three layers; Fig. 1a). To model the neutral pH condition, two diagonal histidines are in the Im⁺ tautomeric form, and the remaining diagonal histidines are in either the τ or π tautomeric form. Initial values of the sidechain χ₁ and χ₂ torsion angles of the histidine and tryptophan residues were either directly those in 3LBW or similar to those in 2L0J. The His37 tautomeric forms, χ ₁ and χ₂ angles, and calculated chemical shifts of the optimized models are listed in Table 1.

Table 1.

Tautomers, torsion angles, and isotropic chemical shifts of the His37 tetrad in D1–D4^a

	D1	D2	D2′	D3	D4
Tauto-	τ/τ	Im+/Im+	π/π	Im+/Im+	Im+/Im+
mer	Im+/Im+	τ/τ	Im+/Im+	τ/Im+	τ/Im+
χ1 (°)	−170/−165	−173/−170	−167/−168	−165/−178	−166/−179
	−168/−161	−164/−165	−164/−166	−163/179	−164/−177
χ2	−178/−165	−7/−8	−10/−9	−11/64	−9/56
	175/170	−100/−93	−95/−93	−91/−135	−88/−158
Cα (ppm)64/64		64/63	64/63	64/69	64/67
	63/64	74/74	74/74	75/66	74/64
Cγ	40/40	39/35	40/37	36/33	36/32
	39/36	39/39	36/37	40/38	40/38
Cβ	146/146	136/139	134/135	140/141	140/139
	139/142	148/148	143/141	148/140	147/139
Cδ2	125/125	125/128	131/128	130/125	129/120
	123/127	119/121	120/120	123/132	124/132
Cε1	139/139	144/137	140/138	136/148	138/145
	140/138	143/141	144/140	143/130	143/132
Nδ1b	−/−	146/146	144/145	149/148	149/149
	159/157	−/−	169/170	−/157	−/154
Nε2	149/148	167/168	−/−	162/156	167/159
	157/149	151/152	153/153	154/153	153/158

^aIn each entry, the first two tautomers or numbers refer to those for chains A and C, and the last two refer to those for chains B and D.

^bThe linear scaling relation for nitrogen chemical shifts were obtained using only nuclei covalently bonded to a hydrogen. For N not covalently bonded to a hydrogen, no reliable results were available.

D1 is a direct optimization of the 3LBW structure, which was putatively in the doubly protonated (+2 charge) state.²⁵ We chose the Im⁺ tautomer for chains B and D and the τ tautomer for chains A and C. The optimized sidechain conformation is very close to the initial structure, with a heavy atom RMSD of just 0.2 Å. In this box-like structure, both χ₁ and χ₂ in each His37 residue are ~180° (Table 1). The Cε1H bond of each His37 projects into the center of a neighboring His37 ring in a clockwise fashion (top view; Fig. 1c), forming a relatively weak interaction. Each Nδ1 points upward whereas each Nε2 points downward. All the Nδ1 atoms form hydrogen bonds with water above; two Nε2 atoms (in chains A and B) also form hydrogen bonds with water below while the other two Nε2H bonds project into Trp41 indoles. The hydrogen bonding with water was thought to provide significant stabilization.^{25, 39} The 5-membered ring (and the Nε1H bond in particular) of each Trp41 indole extends toward the central pore.

D2 is a re-calculation of the 2L0J sidechain conformation for the His37-Trp41 quartet using the 3LBW backbone structure but manually adjusted χ1 and χ2 angles for His37 and Trp41 before optimization. Very similar to 2L0J, the His37 residues in D2 form a pair of imidazole-imidazolium dimers (Fig. 4), though the Cγ-Cγ distances within the D2 dimers, 6.9–7.0 Å, are slightly shorter than those, 7.1–7.2 Å, in 2L0J (see Supplementary Table S1 for further comparison), in line with the somewhat tighter helix packing in 3LBW. A main difference of D2 from D1 is in the His37 χ₂ angles (Table 1), which are now ~−10° for chains A and C (Im⁺ tautomer) and ~−95° for chains B and D (τ tautomer). The inter-ring angles in the A–B and C–D dimers are ~20°, indicating that the rings become slightly more co-planar in the tetramer context relative to the isolated dimer C2. Concomitantly, the inter-ring hydrogen donor-acceptor distances are reduced slightly, to 2.6 Å.

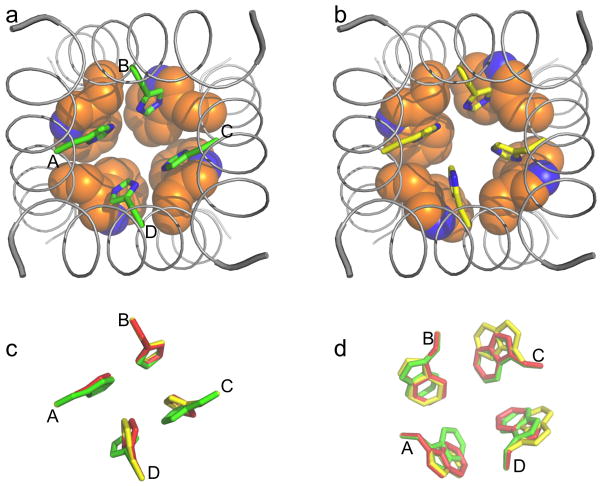
Fig. 4.

Models of the His37-Trp41 quartet under neutral and acidic pH. (a) D2 (+2 charge), representing the histidine-locked state at neutral pH. (b) D4 (+3 charge), representing the conducting state at acidic pH. His37 sidechains are in stick mode and Trp41 sidechains are in space-filling mode; the backbone structure of the TM domain (from 3LBW) is also shown. (c) and (d): Superposition of the His37 and Trp41 sidechains in D2 (green), D3 (+3 charge; red), and D4 (yellow). These conformations mainly differ in His37 χ₂ angles of chains C and D and Trp41 χ₁ angles of chains A, C, and D.

As a result of the differences in χ₂ angles, instead of the box defined by D1, where each His37 ring lines one sidewall (Fig. 1c), the two rings of one dimer in D2 line one sidewall and the two rings of the second dimer line the opposite sidewall. Moreover, the top of the D1 box, defined by the four Cγ atoms, has nearly a square shape (with side length 6.8 Å), consistent with 4-fold symmetry, but the D2 top has more of a rectangular shape [with longer side lengths within the dimers than between the dimers (6.9–7.0 Å versus 6.7–6.8 Å)], conforming to 2-fold symmetry. Another key difference between D1 and D2 is the interactions that the nitrogens of the His37 rings are engaged in. As noted above, six of the eight nitrogens in D1 hydrogen bond to water. In D2, one nitrogen from each ring (Nε2 in chains A and C and Nδ1 in chains B and D) is engaged in inter-ring hydrogen bonding. The other NH bond in each ring projects downward, forming either a hydrogen bond, in the case of Nδ1 in chains A and C, with the backbone carbonyl of the same chain, or an interaction, in the case of Nε2 in chains B and D, with the indole ring of a neighboring chain. The water molecules included in the optimization form weak hydrogen bonds with CH groups on the His37 rings (see Fig. 6 below). As in 2L0J, the nitrogens in D2 are thus fully engaged and not available either to accept a proton from water above or to release a proton to water below. It is for this reason that we have referred to the pair of imidazole-imidazolium dimers as forming the histidine-locked state.⁸

Fig. 6.

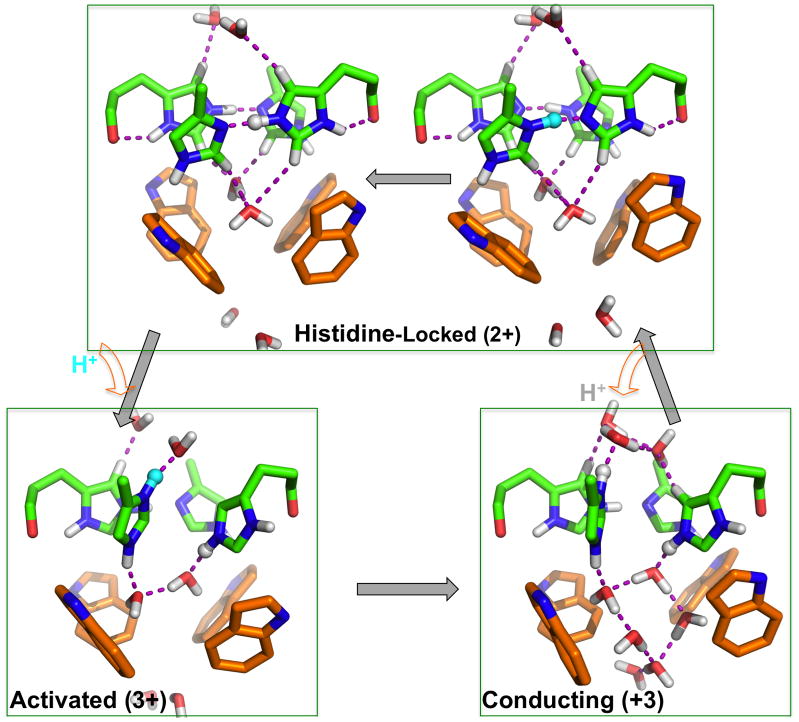
A proposed acid activation and proton conductance mechanism delineated by the D2–D4 models of the His37-Trp41 quartet. Hydrogen bonds involving the imidazole rings and between water molecules are indicated by dashed lines. At acidic pH, addition of a proton (cyan sphere) breaks an imidazole-imidazolium dimer and positions the previously shared proton (gray sphere) toward water below. Occasional opening of the Trp41 gate allows the release of the latter proton to the water chain underneath and the reformation of the imidazole-imidazolium dimer, now sharing the added proton.

In addition to the differences in His37 χ₂ angles between D1 and D2, the Trp41 χ₂ angles are also changed, from ~70° in D1 to ~−100° in D2, corresponding to a nearly 180° flip of the indoles, along with small changes in the Trp41 χ₁ angles (from ~180° to 150°). The flip places the 6-membered ring of each indole toward the central pore, such that the indoles form a tighter seal beneath the His37 tetrad in D2.

To investigate whether the water molecules included in the optimization have a significant effect on the D2 model, we re-optimized D2 after removing all the water molecules. There is very little structural change, with an RMSD of only 0.1 Å for the His37 sidechains (0.5 Å when the Trp41 sidechains are included). This provides further evidence for the intrinsic stability of the imidazole-imidazolium dimer and reinforces the notion that the pair of imidazole-imidazolium dimers formed by the His37 tetrad is well protected from water. This is in contrast to D1, which relies on hydrogen bonding with water for stability.

By moving the protons from Nε2 in chains A and C to Nδ1 in chains B and D before the optimization for D2, we obtained the isomeric model D2′. Except for the placement of the two protons, the D2 and D2′ isomers are nearly structurally identical (see Table 1 for sidechain torsion angles), just like the situation for the dimeric isomers C1 and C1′.

The D2 and D2′ isomers represent functional conformations at neutral pH

Does D2 (and its isomer D2′) or D1 better capture the structure of the doubly protonated His37-Trp41 quartet in the functional environment, i.e., lipid bilayers? Below we present extensive validation against available ssNMR data, which strongly favors D2 over D1.

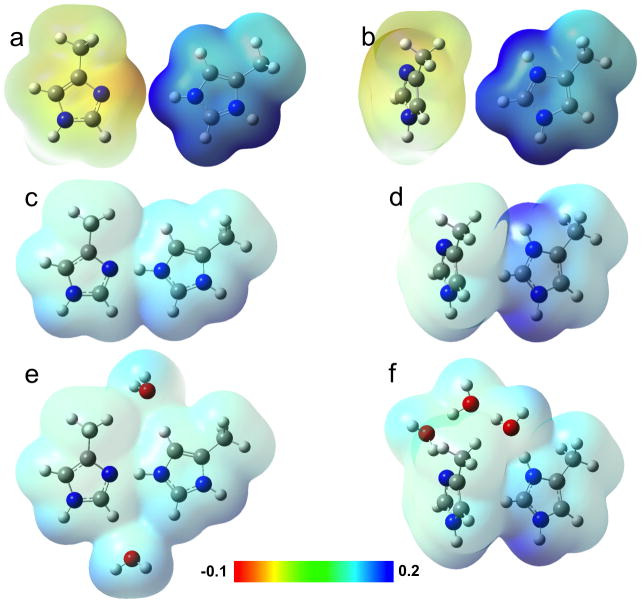
The high values of the first two pK_as determined by ssNMR spectroscopy⁷ show that the His37 tetrad has high affinity for the two protons. Potentially the +2 charge inside the low dielectric environment of lipid membranes can be a significant destabilizing force, which could be mitigated by charge delocalization. Relative to the neutral imidazole, the electrostatic surface of an isolated imidazolium indicated highly concentrated positive charges around Nδ1H and Nε2H (Fig. 5a,b). However, as shown in Fig. 5c, each imidazole-imidazolium dimer in D2 displays a nearly uniform, low electrostatic potential surface, indicating strong delocalization of the +1 charge in each dimer over all its atoms. In contrast, the electrostatic potential surface of a pair of neighboring imidazole and imidazolium in D1 shows significant charge concentration on the imidazolium Nδ1H and Nε2H (Fig. 5d), similar to the situation in an isolated imidazolium and indicating the ineffectiveness of the Cε1H-imidazole interaction in delocalizing charge. Acharya et al.²⁵ argued that the water clusters above and below the His37 sidechains can help delocalzie the charge. When two water molecules weakly hydrogen bonded to the CH groups of an imidazole-imidazolium dimer in D2 are included, there is some redistribution of the already delocalized charge (Fig. 5e). However, in D1, only two of the His37 sidechains are hydrogen bonded to water below, since only a limited number of water molecules can be accommodated in the spacing between the His37 sidechains and the Trp41 indoles. The imidazolium that interacts with an indole instead has considerable charge concentrated on the Nε2H group, even as the water cluster above provides charge delocalization for the Nδ1H group (Fig. 5f).

Fig. 5.

Contrasting charge distributions in D2 and D1. In (a) and (b), electrostatic potential surfaces calculated separately for an imidazole (left) and for an imidazolium (right) are arranged in the orientation of a pair in D2 or D1, to serve as references. The corresponding surfaces of an imidazole-imidazolium dimer in D2, without and with two surrounding water molecules, are shown in (c) and (e); those of a pair of neighboring imidazole and imidazolium in D1, without and with three water molecules at the top, are shown in (d) and (f). The electrostatic potentials are displayed on the isodensity surface; the scale is in atomic units.

Nishimura et al.⁴⁰ obtained information about the His37 sidechain orientation at neutral pH by determining the ¹⁵Nδ1–¹H dipolar splitting and the ¹⁵Nδ1 anisotropic chemical shift in oriented samples. The results were 2.0 ± 0.3 kHz and 226 ± 10 ppm, respectively (the latter referenced to liquid ammonia). The small dipolar splitting indicates that the angle (θ₃) of the Nδ1H bond vector of the His37 sidechain (in the Im⁺ tautomer) with respect to the pore axis is near the magic angle of 54.7°. In our D2 model, the Nδ1H bond vectors in chains A and C (in the Im⁺ tautomer) have θ₃ = 60.6° and 60.9°, respectively. The calculated dipolar splitting is 3.0 kHz, in good agreement the experimental value. The calculated Nδ1 anisotropic chemical shift is 212 ppm, also in good agreement with the experimental value. In contrast, in the D1 model, the Nδ1H bond vectors in chains B and D (in the Im⁺ tautomer) nearly aligns with the pore axis (θ₃ = 22.0° and 24.9°, respectively), resulting in a significantly overestimated dipolar splitting of 16.0 kHz. The calculated Nδ1 anisotropic chemical shift, 250 ppm, also deviates significantly from the experimental value.

Nishimura et al.⁴⁰ further obtained information about the relative orientation between His37 and Trp41 sidechains by recording the dephasing of the Trp41 ¹³Cδ REDOR intensity by His37 ¹⁵Nδ1. The dephasing could be explained by a single dipolar interaction at ~3.9 Å. In the D2 model, Trp41 Cδ in chain B (or D) has distances of 4.4 and 5.4 Å, respectively, from the Nδ1 atoms of chains A and B (or C and D). The multiple dipolar interactions could perhaps account for the observed dephasing. In comparison, in D1 the shortest Cβ-Nδ1 distance is 5.3 Å, and the next distance is ~7 Å.

Chemical shifts determined by ssNMR spectroscopy provide exquisite probes of the chemical environments of nuclei in a membrane-bound protein. In our previous study⁷ two significantly downfield-shifted resonances, at 162 ppm for ¹⁵Nε2 and 167 ppm for ¹⁵Nδ1, were observed at neutral pH, and were interpreted as indicating a strong Nε2-H-Nδ1 inter-ring hydrogen bond. The calculations on the imidazole-imidazolium dimer here confirm this interpretation. The calculated chemical shifts of the D2 and D2′ models of the His37-Trp41 quartet (Table 1) again show that the inter-ring strong hydrogen bonds give rise to the significant downfield shifts. When the Nε2 nuclei have the shared protons covalently bonded to them (as in chains A and C of D2), their chemical shifts are 167.6 ± 0.7 ppm; when the protons are moved to the Nδ1 nuclei (as in chains B and D of D2′), the chemical shifts of the latter nuclei are 169.7 ± 0.5 ppm. These still are in good agreement with the observed values. In contrast, no such significantly downfield shifted resonances are predicted for the D1 model, which have nitrogen chemical shifts similar to those in the A1-A2 model systems forming hydrogen bonds with water molecules.

Recently two sets of ¹³C resonances for the His37-Trp41 quartet have been observed.^41–43 The ¹³C isotropic chemical shifts of the two forms have been fully assigned by Can et al.⁴² His37 in one form relative to the other has a 3 ppm upfield shift for Cα, 6 ppm downfield shift for Cβ, 4 ppm downfield shift for Cδ2, and slight shifts (≤ 1 ppm) for Cγ and Cε1. These trends are reproduced by our chemical shift calculations for D2 with the exception of the Cδ site, where the assignment in Can et al. appears to be counter to the experimental literature for histidine.^{28, 44} As listed in Table 1, relative to chains B and D, His37 residues in chains A and C have an 11 ppm upfield shift for Cα, 11 ppm upfield shift for Cβ, 7 ppm downfield shift for Cδ2, and much smaller shifts (≤ 2 ppm) for Cγ and Cε1. The results are very similar for D2′. In contrast, in line with a 4-fold symmetric structure, no significant differences in chemical shifts are found between the chains of D1 for all His37 carbons except for Cδ (with a 6 ppm difference between chains in different tautomers). For Trp41, the observed resonances showed discernible but small differences (< 2 ppm) between the two forms for Cα and Cγ and no significant differences for the rest of the sidechain.⁴² Our calculations also found very similar Trp41 chemical shifts for the four chains in D2 and D2′.

A recent assessment of membrane protein structures (including those of the M2 protein) suggests that membrane mimetics used for sample preparations in structure determination can significantly influence the protein structures.⁴⁵ The detergent-based crystalline environment of 3LBW perhaps helps trap the His37 sidechains in a box-like conformation. However, in the membrane environment where M2 functions, the all-parallel dimers conformation is essential for channel function.⁴⁶

The His37-Trp41 quartet at acidic pH: the activated and conducting States

At pH ~6, the His37 tetrad starts to be triply protonated⁷ and the M2 proton channel becomes activated.^{1, 2} As our D3 model shows (Fig. 4c), the uptake of the third proton (on chain D) breaks the Nε2-H-Nδ1 hydrogen bond in the C–D imidazolium-imidazole dimer, with the imidazole rings rotating ~70° (chain C) and ~40° (chain D) in opposite directions, while the other dimer remains intact. In this “activated” state (Fig. 6), the newly added proton (to Nδ1 of chain D) forms a hydrogen bond with a water molecule above, and the Nε2H group of the same ring forms a hydrogen bond with a water molecule below (resulting in a hydrogen bonding pattern reminiscent of D1). Meanwhile the former partner, i.e., the imidazolium of chain C, tilts downward such that its Nε2H group forms a hydrogen bond with the second water molecule below and the whole ring forms a cation-π interaction with the Trp 41 indole of chain D (Fig. 6 and 7b).

Fig. 7.

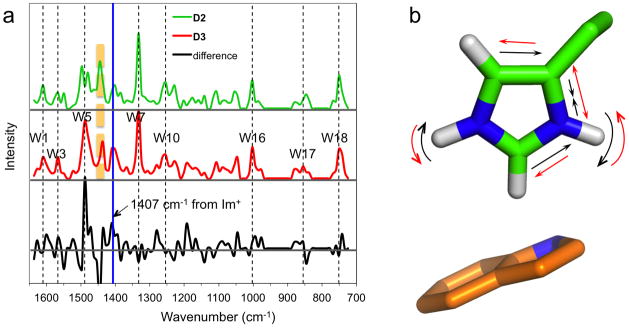
Calculated Raman spectra of the D2 and D3 models and the 1407 cm⁻¹ mode. (a) Raman spectra of D2 and D3, representing the His37-Trp41 quartet at pH 7.4 and 5.4, respectively, and the difference spectrum highlighting the 1407 cm⁻¹ band (blue line). The band immediate to the left (orange dash) is from imidazoliums of chains A and C (in D2) or chains A and D (in D3). Other bands assignable to Trp41 modes are also indicated (black dashes). (b) Normal mode corresponding to the 1407 cm⁻¹ band. The imidazolium is that of chain C; the indole underneath is that of chain D.

As we envisioned,⁸ in the activated state, the four Trp41 indoles still form a tight seal below the His37 residues (Fig. 4d and 6). It is only when the indoles occasionally swing open that water molecules from the C-terminal side connect with the second water layer, allowing the Nε2 of chain C to release its proton to the newly formed water chain. This “conducting” state is represented by our D4 model (Fig. 4b-d and 6). We emphasize that at acidic pH the triply protonated His37-Trp41 quartet spends most of the time in the activated state and makes only infrequent transitions to the conducting state. This assumption is directly supported by the observation that Cu²⁺ applied from the extracellular side strongly inhibits the proton flux, very likely via coordination with the His37 tetrad,⁴⁷ but Cu²⁺ applied from the intracellular side has little effect on the proton flux, presumably because the Trp41 gate, closed most of the time, blocks Cu²⁺ access from below.⁹ Infrequent opening of the Trp41 gate was incorporated as an essential component in our mathematical model for conductance calculations and helps explain key experimental results such as the maximum conductance rate.^{21, 22}

Because of the significant charge delocalization within an imidazole-imidazolium dimer noted above, the nominal cation-π interaction formed between an imidazolium in D2′ (via Nε2H of chain B or D) with a Trp41 indole should be relatively weak. So the first bona fide cation-π interaction is the one introduced in D3 by breaking the C–D dimer. This provides an explanation for the pH-dependent Trp41 fluorescence quenching observed by Czabotar et al.⁴⁸ It is known that a histidine in the Im+ tautomer is generally a much more effective quencher of tryptophan fluorescence. Yet Czabotar et al. found that the Trp41 fluorescence is unchanged from pH 8 to ~6. This is the pH range in which the first two protons are added,⁷ but as we just explained the resulting imidazoliums are not expected to be more effective than an imidazole in fluorescence quenching. As the pH was further reduced to 5, Czabotar et al. found a significant increase in Trp41 fluorescence quenching, which we can attribute to the cation-π interaction formed after the breakup of the C–D dimer.

Our D2 and D3 models are further validated by the Raman spectra of the M2 TM domain at pH 7.4 and 5.4 determined by Okada et al.²⁶ We calculated the Raman spectra of D2 and D3 to provide quantitative interpretation of the experimental results at these two pH values. These calculations reproduced the known tryptophan bands (Fig. 7a). More importantly, in agreement with the experimental results, they yielded a band at 1407 cm⁻¹ that becomes significantly more prominent in D3. Okada et al. attributed that band to a protonated His37 that is interacting with Trp41. Indeed, our 1407 cm⁻¹ band is due to a normal mode localized to the imidazolium of chain C, which, as already noted, forms a cation-π interaction with Trp41 of chain D (Fig. 7b). The mode involves the contraction/expansion of the CβNδ1 bond along with the swing of the Nδ1H and Nε2H bonds in the imidazole plane.

The acid activation and proton conductance mechanism

Based on the D2-like structure determined for 2L0J, we previously proposed a mechanism for acid activation and proton conductance in M2.⁸ With the newly calculated D3 and D4 models and the extensive validation presented above, we can now delineate this mechanism with atomic details and more certainty (Fig. 6). At neutral pH, the nitrogens of the His37 imidazole rings are all engaged in the histidine-locked state, thus preventing proton translocation across the His37 tetrad. When the viral exterior is acidified, a proton in a hydronium ion above the His37 tetrad can transfer to an Nδ1 that was forming an inter-ring hydrogen bond with an Nε2, thus breaking the imidazole-imidazolium dimer. The Nδ1 tilts up to accept the proton from the water molecule above, positioning the Nε2H group of the same ring downward for a hydrogen bond with a water molecule below, while the just disengaged Nε2H of the neighboring ring tilts downward for a hydrogen bond with the second water molecule below. The two imidazolium rings rotate away from each other (by 55° ± 15° each) to minimize charge repulsion and are further stabilized by a cation-π interaction with Trp41.

The two disengaged imidazoliums hold onto an excess proton, except on rare occasions when the Trp41 indoles swing open (by ~30° decrease in χ₁) to allow the water underneath to form a continuous chain. The indole dynamics may be coupled to backbone motions, such as helix kinking around a Gly34 residue,⁴⁹ that widen the pore at the level of the indoles, thereby providing room for their radially outward swinging. The proton on the Nε2H group disengaged from the neighboring Nδ1 (the latter now bonded to the added proton) is then released to the water below. Thereafter the newly deprotonated Nε2 reform a hydrogen bond with the neighboring Nδ1H, restoring the imidazole-imidazolium dimer.

In each round of proton translocation from the N-terminal side to the C-terminal side the His37-Trp41 quartet thus cycles from the histidine-locked state through the activated state and the conducting state back to the histidine-locked state. Right before the attack by a hydronium ion the proton in the initial Nδ1-H-Nε2 hydrogen bond is located on the Nε2 but right after the proton release the proton in the restored Nδ1-H-Nε2 hydrogen bond is located on the Nδ1. The low energy barrier between the isomers allows the proton to easily hop from the Nδ1 to the Nε2, fully recovering the initial state so that a new round of proton conductance can begin.

Both experimental and computational studies suggest that proton dissociation from the His37 tetrad (resulting in the +2 charge state) is the rate-limiting step for proton conductance.^{17, 22, 49,50} In our conductance mechanism (Fig. 6), to recover the +2 charge state, the proton has to be transferred to the water chain underneath and the imidazole rings have to rotate toward each other to reform the dimer. Our preliminary calculation indicates that it is energetically much more favorable to have the proton hop before the rings rotate (to avoid charge-charge repulsion; Supplementary Fig. S1). This results in an intermediate that is about 2 kcal/mol higher in energy. Thereafter the rotation of the rings encounters an additonal barrier of about 8 kcal/mol. In the transition state, Nε2 of chain C and Nδ1 of chain D are not sufficiently close to form a strong hydrogen bond between them but are close enough to prevent them from forming good hydrogen bonds with water. The calcultated total energy barrier of about 10 kcal/mol is broadly consistent with those estimated from the temperature dependences of both the proton conductance rate¹⁵ and the His37 sidechain rotational dynamics.⁵⁰

The D2–D4 models described above are calculated using the 3LBW backbone for restraint, in order to facilitate the discrimination of two alternative sidechain configurations, D1 and D2, by the experimental data. As noted in the Introduction, the backbone structure of 3LBW is very similar to that of our ssNMR structure 2L0J. Consequently very similar D2–D4 models are obtained when either backbone structure was used for restraint (see Supplementary Table S1 for comparison). These models for the states along the proton conductance cycle provide important atomic details, but preserve the basic framework of the mechanism that we originally proposed.⁸ This mechanistic framework was the basis of our mathematical model for calculating proton conductance.^21–23 That these calculations quantitatively reproduce key experimental results, including the maximum conductance rate, current-pH and current-voltage relations, as well as solvent isotope effect, provides strong support of the mechanism delineated here.

Conclusion

In this study we have used ab initio calculations to model the structures of the His37-Trp41 quartet in the states along the proton conductance cycle of the Influenza A M2 protein. We have presented extensive validation of these structural models against experimental results, including chemical shifts and other ssNMR data that provide sensitive chemical and geometrical information, and pH-dependent Raman spectra and Trp41 fluorescence quenching. These models add important atomic details to a mechanism for acid activation and proton conductance. This mechanism is supported by the ability of a resulting mathematical model to reproduce key experimental results on proton conductance.

The validation of the imidazole-imidazolium dimers configuration for the His37 tetrad at neutral pH, as captured by the D2 model, is particular compelling. It is worth noting that the significant stabilization afforded by the inter-ring low-barrier hydrogen bonds, the resulting considerable charge delocalization, and the 2-fold (instead of 4-fold) symmetry, suspected previously,⁴² are all produced by our ab initio calculations. Additional validation and refinement of the structural model for the activated state will further tighten the mechanistic description for an important drug target.

Computational methods

Model systems

The pH-dependent structures of the His37-Trp41 quartet were studied by using different model systems. Specifically, the structure of His37 at high pH (above 8.2) was modeled by 4-methylimidazole (with either Nε2 or Nδ1 protonated, corresponding to the τ or π tautomer; shown as A1 and A1′ in Fig. 2), whereas the structure at low pH (below 5.0) was modeled by 4-methylimidazolium (i.e., with both Nε2 and Nδ1 protonated, corresponding to the Im⁺ tautomer; shown as A2 in Fig. 2). These imidazole and imidazolium molecules were hydrogen bonded to two water molecules, with protonated Nε2 and Nδ1 as donors and unprotonated Nδ1 and Nε2 as acceptors. Nδ1 and Nε2 chemical shifts calculated on these two model systems were used as benchmarks. The main focus of the present study was the structures of the His37-Trp41 quartet at neutral pH, where the His37 tetrad is doubly protonated and the channel is closed, and at pH ~6, where the His37 tetrad is triply protonated and the channel becomes activated.

The imidazole-imidazolium dimer was of special interest and we explored its conformations in four model systems in addition to the His37-Trp41 quartet. The first, shown as B in Fig. 3, was the A2–A1 dimer (without any water molecule); a hydrogen bond was formed between the protonated Nε2 of the first ring (Im+ tautomer) and the unprotonated Nδ1 of the second ring (τ tautomer). In the optimization of this model system (described below), all the atoms were free to move. The second and third model systems, shown as C1 and C1′ in Fig. 3, consisted of a histidine in the Im+ tautomeric form with a histidine in either the τ or π tautomeric form; the backbone heavy atoms were fixed to the positions in our recent ssNMR structure (chains A and B in PDB 2L0J), with the broken bonds of each histidine backbone saturated with hydrogens. C1, like B, has the Im⁺-τ combination and forms a hydrogen bond between the protonated Nε2 of the first ring and the unprotonated Nδ1 of the second ring. In C1′, the proton is moved from the Nε2 to the Nδ1, resulting in the π-Im⁺ combination. The fourth model system (shown as C2 in Fig. 3) was similar to C1, except that the backbones of the histidines were taken from the recent X-ray structure (chains C and D in PDB 3LBW) and the sidechains were rotated to approximate the conformations in C1 before optimization. These model systems served as references for investigating how the backbone restraints affected the sidechain conformations and whether a second dimer had significant effects on the conformation and chemical shifts of the first dimer.

The full His37-Trp41 quartet systems, D1–D4, studied here were comprised of His37, Leu38, Leu40, and Trp41, plus 13 water molecules. All had backbone heavy atoms fixed to the positions in the X-ray structure 3LBW, and the broken backbone bonds saturated with hydrogens. D1 was an optimization of the X-ray structure, with the His37 tetrad arranged in the box-like configuration. To model the structure at neutral pH, the histidine sidechains of chains B and D are in the Im⁺ tautomeric form but those of chains A and C are in the τ tautomeric form. In this case the 13 water molecules were from the X-ray structure, and were arranged into 3 layers, located above the His37 tetrad, between the His37 and Trp41 residues, and below the Trp41 residues, with 6, 2, and 5 water molecules, respectively (Fig. 1a).

D2 was a re-calculation of the structure for the His37-Trp41 quartet at neutral pH reported previously (Fig. 1),⁸ here using the backbone restraint and the water molecules of the X-ray structure 3LBW. To prepare D2 for optimization, we manually rotated the χ1 and χ2 angles of His37 and Trp41 to approximate the previous structure.⁸ In D2, the histidine sidechains of chains A and C in the Im⁺ tautomeric form but those of chains B and D are in the τ tautomeric form. We also optimized the model when the protons were moved from the Nε2 positions in chains A and C to the Nδ1 positions in chains B and D, leading to D2′. In addition, to examine the influence of the water molecules, we also re-optimized D2 after removing them.

Electrostatic potential surfaces were calculated for isolated imidazole (A1) and imidazolium (A2) and for sub-systems of D1 and D2 including the His37 sidechains in two neighboring chains, plus three or two water molecules when specified. All the broken bonds in the sub-systems were saturated with hydrogens.

To model the structure for the His37-Trp41 quartet in the activated state, we added a proton to the Nδ1 of chain D in a D2-like model; optimization produced D3 with a triply protonated His37 tetrad. To further model the conducting state, in which the water molecules in the second and third layers form a continuous chain, before optimization we manually rotated the Trp41 indoles slightly and moved some water molecules to the space created so the two layers of water molecules became connected.

We used subsets of the D2 and D3 models for calculating the Raman spectra. The systems (referred to as E1 and E2) included in each chain His37, the amino group of Leu38 (so that the peptide bond could be kept), and the Trp41 sidechain, as well as the 6 and 2 water molecules in the top and middle layers. All the broken bonds were saturated with hydrogens.

Quantum chemical calculations

All the calculations were done using the Gaussian 03 package.⁵¹ Geometries of A1, A1′, A2, and B were fully optimized using B3LYP DFT^52–54 with the 6–311++G(2d,p) basis set. The same method was used for optimizing C1, C1′, and C2, except in these cases the backbone heavy atoms were fixed. For C1, starting from the optimized model, we also scanned the χ₂ (i.e., Cα-Cγ-Cβ-Nδ1) torsion angle of the first histidine to explore how the electronic energy changed as the inter-ring angle was changed. In the optimized C1 model, the Cγ-Cδ bond of the first histidine is nearly parallel to the inter-ring Nε2-Nδ1 pseudobond (Fig. 3), so varying the χ₂ angle was a convenient way to sample the inter-ring angle.

For the full His37-Trp41 quartet systems D1–D4, the ONIOM protocol⁵⁵ was used for structural optimization. In this protocol, each system was divided into two layers. The inner layer, including His37, the amino group of Leu38, Trp41, and the carboxyl group of Leu40 in each chain, as well as the 13 water molecules, was treated by B3LYP/6-31G(d,p). The number of atoms in the inner layer was 229 and 230 in the systems with doubly- and triply-protonated His37 tetrads, respectively. The outer layer, comprised of the rest part of each system with 144 atoms, was treated by the AM1 semi-empirical method. These systems were optimized with all the backbone heavy atoms fixed.

The gauge-independent atomic orbital (GIAO) method^56–59 was used for NMR chemical shift calculations. For classes A–C model systems, both DFT and the MP2 method were used, with the 6–311++G(2d,p) basis set. For the class D model systems, B3LYP/6-311++G(2d,p) and AM1 were used for inner and outer layers, respectively, to calculate the chemical shieldings. For carbons, the isotropic chemical shielding (σ_C) from the Gaussian output was converted to the chemical shift (δ_C) according to δ_C = σ_DSS – σ_C, where σ_DSS is the average methyl carbon chemical shielding calculated on 4,4-dimethyl-4-silapentane-1-sulfonic acid (DSS). For nitrogens, the chemical shielding (σ_N) was converted to the chemical shift (δ_N) via linear scaling: δ_N = a + bσ_N ^25,26 where a and b are fitting parameters. The four class-A Nδ1 and Nε2 positions bonded to a hydrogen, shown in Fig. 2, were used for fitting.

For calculating the Raman spectra, hydrogen positions in E1 and E2 were first optimized by using B3LYP/6-31G(d,p) (with all heavy atoms fixed). Vibrational analysis was then performed on the whole systems. To compensate for the neglect of anharmonicity effects, a scale factor of 0.9648 was used to correct the fundamental vibrational frequencies.⁶⁰ For the electrostatic potential surfaces, single-point calculations were done at the MP2/6-31G(d,p) level.

In order to reflect the dielectric environment of the M2 proton channel as a membrane protein and to reduce computational cost, all the calculations were performed in gas phase.

Calculation of His37 ¹⁵Nδ1-¹H dipolar coupling and ¹⁵Nδ1 anisotropic chemical shift

Following Im and Brooks⁶¹ and our previous work,⁴⁹ the dipolar splitting (ν) was calculated according to ν = ν_//P₂(cosθ₃), where ν_//= 20.58 was the maximum splitting determined by Ramamoorthy et al.,⁶² θ₃ as already defined is the angle between the Nδ1H bond vector and the pore axis, and P₂(x) = (3×2 – 1)/2 is the second-order Legendre polynomial. The anisotropic chemical shift (δ_ani) was calculated according to δ_ani = δ₁₁cos²θ₁ + δ₂₂cos²θ₂ +δ₃₃cos²θ₃, where δ₁₁ = 77 ppm, δ₂₂ = 203 ppm, and δ₃₃ = 260 ppm (referenced to liquid ammonia) are the principal values of the chemical shift tensor of Im⁺ histidine Nδ1 determined by Ramamoorthy et al.⁶². The third principal axes is along the Nδ1H bond vector (at angle θ₃ from the pore axis); the second principal axis lies in the imidazole ring whereas the first principal axis is perpendicular to it (making angles θ₂ and θ₁ from the pore axis).