Characterizing the ear canal acoustic reflectance and impedance by pole-zero fitting

Abstract

This study characterizes middle ear complex acoustic reflectance (CAR) and impedance by fitting poles and zeros to real-ear measurements. The goal of this work is to establish a quantitative connection between pole-zero locations and the underlying physical properties of CAR data. Most previous studies have analyzed CAR magnitude; while the magnitude accounts for reflected power, it does not encode latency information. Thus, an analysis that studies the real and imaginary parts of the data together could be more powerful. Pole-zero fitting of CAR data is examined using data compiled from various studies, dating back to Voss and Allen (1994). Recent CAR measurements were taken using a middle ear acoustic power analyzer (MEPA) system (HearID, Mimosa Acoustics), which makes complex acoustic impedance and reflectance measurements in the ear canal over the 0.2 to 6.0 kHz frequency range. Pole-zero fits to measurements over this range are achieved with an average RMS relative error of less than 3% using 12 poles. Factoring the reflectance fit into its all-pass and minimum-phase components approximates the effect of the ear canal, allowing for comparison across measurements. It was found that individual CAR magnitude variations for normal middle ears in the 1 to 4 kHz range often give rise to closely-placed pole-zero pairs, and that the locations of the poles and zeros in the s-plane may differ between normal and pathological middle ears. This study establishes a methodology for examining the physical and mathematical properties of CAR using a concise parametric model. Pole-zero modeling shows promise for precise parameterization of CAR data and for identification of middle ear pathologies.

1. Introduction

1.1. Background

Acoustic reflectance measurements and their clinical applications have been the subject of many recent studies. These studies have shown that power reflectance, the magnitude squared of the complex acoustic reflectance¹ (CAR), shows distinct and often systematic variations between pathological and normal middle ears (e.g. Feeney et al., 2003; Allen et al., 2005; Hunter et al., 2010). Studies by Voss et al. (2012) and Nakajima et al. (2012) have investigated the efficacy of reflectance measurements for differential diagnosis of middle ear pathology. Laser doppler vibrometry is the current standard for presurgical differentiation between ossicular fixation, ossicular discontinuity, and third window disorders (Rosowski et al., 2003, 2008). Nakajima et al. concluded that power reflectance performed as well as laser doppler vibrometry, both in combination with audiometry. This is a valuable result, because CAR measurements can be performed using the United States Food and Drug Adminstration (FDA) approved HearID system (Mimsosa Acoustics), which costs an order of magnitude less than the laser Doppler vibrometer (≈ 10, 000 vs. 100, 000 USD) and requires less training to operate (Nakajima et al., 2012). Voss et al. systematically manipulated cadaver ears to isolate the effects of various pathologies in differing degrees of severity, and studied the CAR response. They also concluded that power reflectance may be a strong supplement to audiometry for the diagnosis of certain pathologies.

CAR and impedance are measured at ambient pressure by a probe conétaining a calibrated microphone and receiver, sealed in the ear canal. The probe is calibrated using a multi-cavity least squares procedure (Allen, 1986) to find the acoustic Thévenin equivalent parameters of the source. A stimulus is emitted by the probe and the complex cavity pressure response is measured. From the calibration pressure responses, the acoustic impedance, reflectance, and related quantities (admittance, power reflectance, etc.) may be calculated. The CAR Γ(f) is equal to the ratio of the reflected to incident wave pressure at the microphone, located in the ear canal, as a function of frequency. The magnitude squared of the reflectance |Γ(f)|² represents the relative acoustic power reflected back to the ear canal from the middle and inner ears. The power reflectance is related to conductive hearing functionality and is therefore relevant to clinical assessment of the middle ear. The complex acoustic impedance Z(ω) and reflectance Γ(ω) as functions of frequency (ω = 2πf) are related by

$$\mathrm{\Gamma }(\omega )=\frac{\frac{Z(\omega )}{r_0}-1}{\frac{Z(\omega )}{r_0}+1},$$ (1)

where r₀ = ρc/A is the surge resistance, ρ is the density of air, c is the speed of sound, and A is the area of the ear canal.

The clinical utility of CAR depends on its capacity to discern normal from pathological results, thus requires a method for comparison of the measurements across ears. Direct comparison of CAR is complicated because the probe insertion depth L varies across subjects. This variation has a large effect on the reflectance phase and the complex acoustic impedance. The ear canal is frequently modeled as a rigid-walled tube of uniform area and distance L between the probe tip and the tympanic membrane² (TM). Under this assumption, the relationship between the CAR at the probe and at the TM becomes

$${\mathrm{\Gamma }}_{probe}(\omega )={\mathrm{\Gamma }}_{TM}(\omega )e^{-j\frac{2L}{c}\omega }.$$ (2)

In many cases this is not a realistic model, particularly because of variation in the ear canal area A(x) with distance x (Farmer-Fedor and Rabbitt, 2002). However, consideration of the CAR magnitude (or the power reflectance |Γ(ω)|²) is highly effective, because when the approximation in Eq. 2 can be made,

$$|{\mathrm{\Gamma }}_{probe}(\omega )|=|{\mathrm{\Gamma }}_{TM}(\omega )|.$$ (3)

Eliminating the variation due to insertion depth by using the CAR magnitude or power reflectance allows for comparison across measurements. The relationship in Eq. 3 was experimentally verified by Voss et al. (2008).

Variation due to the ear canal confounds phase information associated with the eardrum and ossicles, but taking the magnitude of the CAR eliminates all relevant phase information. An analysis of the complex data could be more powerful and generalizable if the canal effect can be accounted for in a rigorous manner, without eliminating all phase data. This study seeks to develop a method for concise parametric characterization of CAR measurements, with the ultimate goal of improving and automating differential diagnosis of middle ear pathology. This is accomplished by fitting poles and zeros to the complex data.

1.2. Pole-Zero Fitting

Poles and zeros may be expressed in terms of a rational polynomial fraction, as the roots of the denominator and numerator, respectively. Such a function will have the form

$$F(s)=\frac{b_{N_z}{s}^{N_z}+b_{N_z-1}{s}^{N_z-1}+\dots +b_{1}s+b_0}{s^{N_p}+a_{N_p-1}{s}^{N_p-1}+\dots +a_{1}s+a_0}=b_{N_z}\frac{{\prod }_{m=1}^{N_z}(s-z_m)}{{\prod }_{n=1}^{N_p}(s-p_n)},$$ (4)

where s is the complex frequency variable (s = σ + jω), a_i and b_i are the polynomial coefficients, N_p is the number of poles, N_z is the number of zeros, p_n are the poles, and z_m are the zeros. Poles and zeros are a familiar concept as related to impedance, but considering Eq. 1 we see that the reflectance may also have poles and zeros via a simple algebraic transformation.

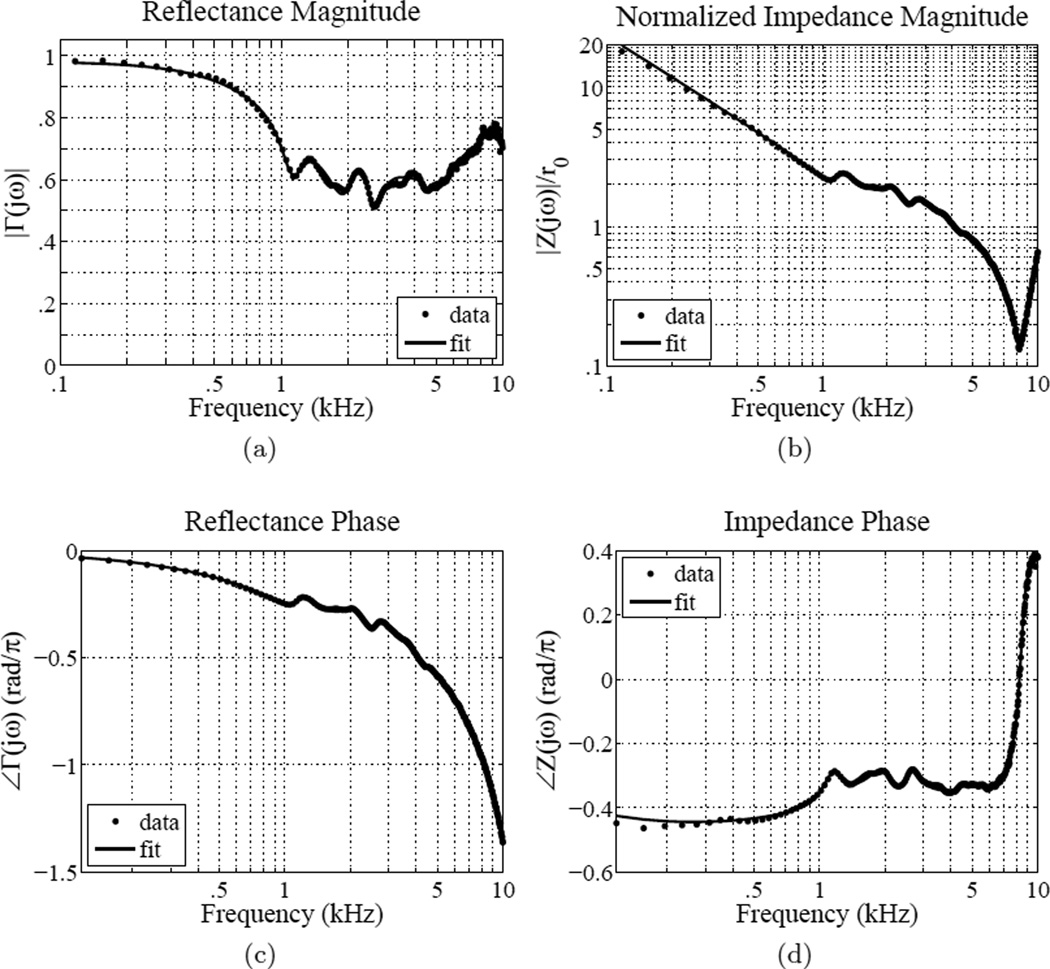
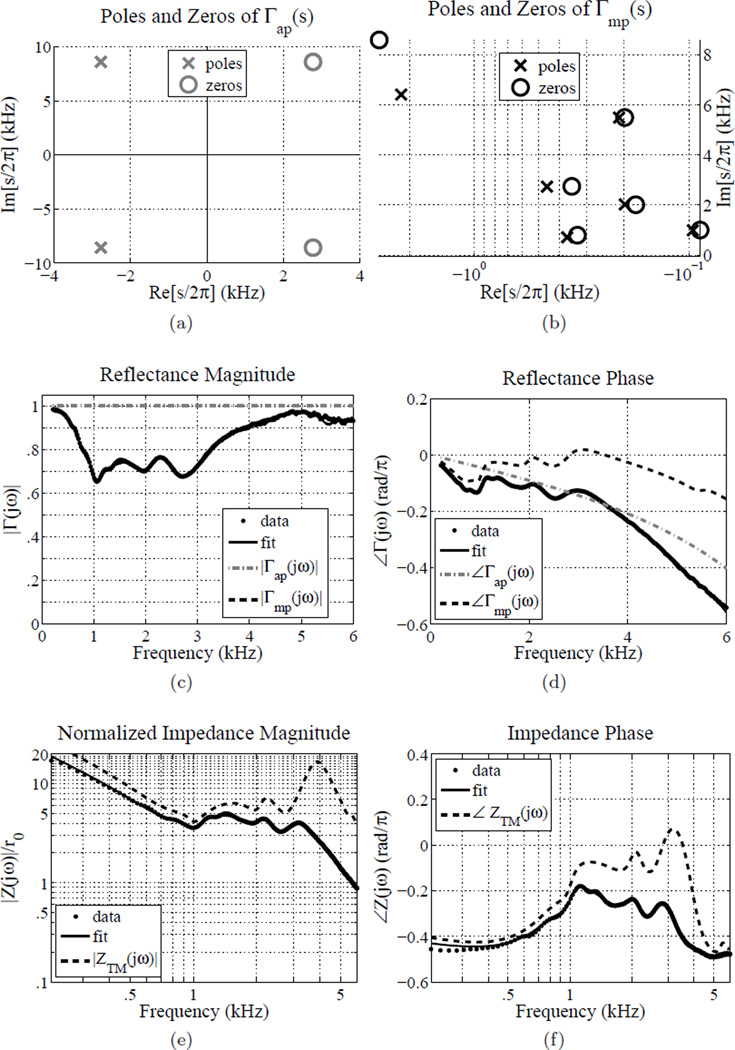
An example CAR measurement and preview fit is displayed in Fig. 1. This is a normal ear, subject #7 of Voss and Allen (1994). The fit is performed on reflectance domain data, and achieves an RMS relative error of 2.5%. Magnitude vs. frequency (Figs. 1a, 1b), and phase vs. frequency (Figs. 1c, 1d) are shown for both the reflectance and impedance. Effects of the ear canal are particularly noticeable in the magnitude impedance and reflectance phase graphs (the magnitude impedance is dominated by the canal standing wave, and the reflectance phase is nearly linear).

Figure 1.

Voss and Allen (1994) subject #7; example data and fit for a normal ear. (a) Reflectance magnitude, (b) impedance magnitude, (c) reflectance phase, (d) impedance phase. The fit was performed over 0.1 to 10 kHz, yielding 18 poles and 18 zeros with an RMS relative error of 2.5% (MSE = −31.9 dB).

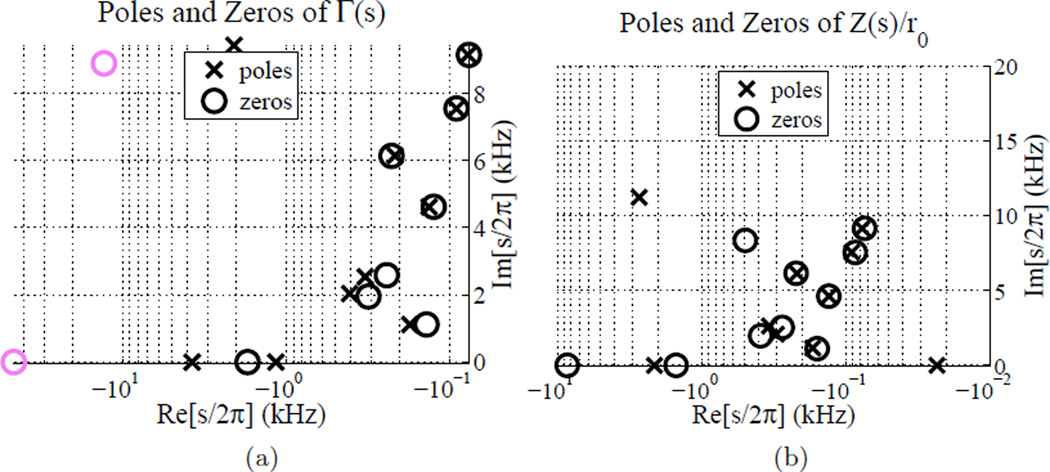
Figure 2 shows the poles and zeros that produce the fit shown in Fig. 1. The Z-domain poles have been calculated from the fitted Γ-domain poles via Eq. 1. It is very important to note that the pole-zero plots of Γ(s) (Fig. 2a) and Z(s) (Fig. 2b) are shown only via the fourth quadrant of the complex plane. All poles and zeros with non-zero ℑ[s] components have complex conjugates in quadrant three, not shown. Pink poles and zeros are actually located in the positive real s-plane, but have been inverted over the jω axis so that pole-zero locations may be more easily viewed using a log ℜ[s] axis. Thus these plots, though limited to one quadrant, completely describe the set of poles and zeros for a given fit. It was found that this procedure greatly aids the viewing of these pole zero plots.

Figure 2.

Voss and Allen (1994) subject #7; example pole-zero fit for a normal ear. (a) Poles and zeros of Γ(s), (b) poles and zeros of Z(s). The fit was performed over 0.1 to 10 kHz, yielding 18 poles and 18 zeros with an RMS relative error of 2.5% (MSE = −31.9 dB). Pink poles and zeros are actually located in the positive real s-plane, but have been inverted over the jω axis so that pole-zero locations may be more easily viewed using a log ℜ[s] axis.

Considering the magnitude reflectance, we see that the fine structure minima and maxima in the mid-frequency range is fit by a group of three pole-zero pairs with ℑ[s] values in that range. Considering the pole-zero plot of the impedance Z(s), note the solitary pole on the real axis close to the origin (σ = −23 Hz), as characterized by a stiffness at low frequencies. The ℜ[s] component of a pole or zero is determined by damping in the middle ear system. Poles and zeros with smaller damping have a larger effect on the response. Thus, this pole has a stronger effect than the other zeros and poles on the real axis. Using these pole-zero fits, we ultimately hope to be able to better model the physics of the CAR and impedance measurements.

It is important to note that pole-zero fitting of CAR data cannot be accomplished by autoregressive moving-average (ARMA) modeling because the time domain signal Γ(t) = ℱ⁻¹{Γ(ω)} (where ℱ⁻¹ denotes the inverse Fourier transform) is not available. CAR is measured as a function of frequency, and measurement noise below 100 or 200 Hz typically prevents the accurate calculation of an inverse FFT. Instead, a method developed by Gustavsen and Semlyen (1999) is used to fit CAR data directly in the frequency domain. This procedure finds a rational approximation of the data as a function of complex frequency, using a vector fitting method. Such pole-zero fits capture magnitude and phase characteristics of the CAR measurements with a small set of parameters, and with a low RMS relative error. This procedure is desribed next, along with our results and their diagnostic implications.

2. Methods

The CAR data sets examined in this paper were compiled from previous studies. A population of normal ears was drawn from Voss and Allen (1994) and Rosowski et al. (2012). Fourteen CAR measurements of ten ears (4 retest measurements) were collected in vivo up to 15 kHz by Voss and Allen (1994), using a measurement system described in their paper. Fifty-eight CAR measurements (and 58 retest measurements) were collected in vivo over a frequency range of 0.2 to 6 kHz, using the Mimosa Acoustics HearID system (Rosowski et al., 2012). These 58 “strictly normal” ears were required to meet specific audiometric criteria in order to be included in the study.

Pathological CAR data were drawn from Voss et al. (2012) and Nakajima et al. (2012). The Voss et al. (2012) CAR measurements were collected from cadaver preparations, which were manipulated to simulate static pressure disorders in the ME cavity (positive and negative), middle ear fluid, fixed stapes, disarticulated incudo-stapedial joints, as well as TM perfora tions. The cadaver ears were also measured in their normal (no simulated pathology) state. The Nakajima et al. (2012) CAR measurements were collected in vivo from patients with confirmed stapes fixation due to otosclerosis, ossicular discontinuity, and superior semicircular canal dehiscence. These data were also collected using the Mimosa HearID (FDA approved) system.

2.1. Fitting Procedure

Rational approximations to the CAR data as a function of frequency (ω = 2πf) were calculated using a vector fitting procedure developed by Gustavsen and Semylen (1999). This procedure is reproduced here for the reader’s benefit. F̂(s), where s = σ + jω is the complex frequency variable, will be used to denote the complex frequency domain fit, and F(ω) will be used to denote the frequency domain data. It is important to note that the data is only available as a function of ω, thus the data is related to the fitted function by F(ω) ≈ F̂(s)|_s=jω. When F̂(s) is evaluated along the jω axis of the complex s-plane, it parametrically approximates the observed data. Because the middle ear is not a lossless system, the poles and zeros of the fit are typically located off the jω axis (have non-zero σ); thus F̂(s)|_s=jω typically has minima and maxima instead of zero and infinite values.

The data is fit to a residue expansion of the form

$$\mathrm{F̂}(s)=\sum _{i=1}^{N_p}\frac{C_i}{s-A_i}+D+Es.$$ (5)

Constants D and E are real quantities, while the constant poles and residues, A_i and C_i, are either real or occur in complex conjugate pairs. Note that if E is nonzero, the numerator order (N_z) will be one greater than the denominator order (N_z = N_p + 1). Similarly, if E is zero the numerator and denominator orders are equal (N_z = N_p), and if both D and E are zero the numerator order is one less than the denominator order (N_z = N_p − 1). Equation 5 is nonlinear in its unknowns, because the unknown poles A_i appear in the denominator.

The vector fitting procedure is a two step process, which converts a nonlinear least squares problem to a linear least squares problem by introducing an unknown scaling function with known poles. This procedure is described at length in appendix Appendix A. It is possible to fit poles and zeros not only to the complex reflectance Γ(ω), but also to the impedance Z(ω) and the admittance Y (ω) = 1/Z(ω). The poles and zeros of each fit may then be transformed between domains using Eq. 1. For example, one may estimate the poles and zeros in the impedance domain based on a fit performed in the reflectance domain.

Throughout this paper, we will describe goodness of fit using a mean squared error³ (MSE) metric presented in decibels, relative to the L2 norm of the signal as follows

$$\mathrm{M}\mathrm{S}\mathrm{E}(\mathrm{d}\mathrm{B})=10{\text{log}}_{10}\left[\frac{\sum {|F(\omega )-\mathrm{F̂}(j\omega )|}^2}{\sum {|F(\omega )|}^2}\right].$$ (6)

A MSE of −30 dB corresponds to an RMS relative error of 3.16%. The example fit for subject #7 from the Voss and Allen (1994) study, shown in Figs. 1 and 2 was performed in the reflectance domain over the 0.1 to 10 kHz frequency range. Using an MSE tolerance of −30 dB, a fit of order N_p = 14 and N_z = 15 was found with an MSE of −31.6 dB and E = −1.9 × 10⁻⁶. Because E was close to 0, the data was re-fit with E forced to 0, yielding an MSE of −31.9 dB for N_p = N_z = 18 after 18 iterations. For comparison, when the data was fit with order N_p = 18 and N_z = 19 over 18 iterations, an MSE of −30.6 dB (1.3 dB worse) was achieved with E = −1.0 × 10⁻⁶. In this example fit, there are several poles and zeros that appear to be overlapping, due to the small extrema from high frequency noise in the data. Eliminating the pole-zero pairs at ℑ[s] ≈ 7.5 kHz and ℑ[s] ≈ 9 kHz from the fit increases the MSE to −31.5 dB, a tolerable change of about 0.1 dB, and does not increase the corresponding impedance domain MSE.

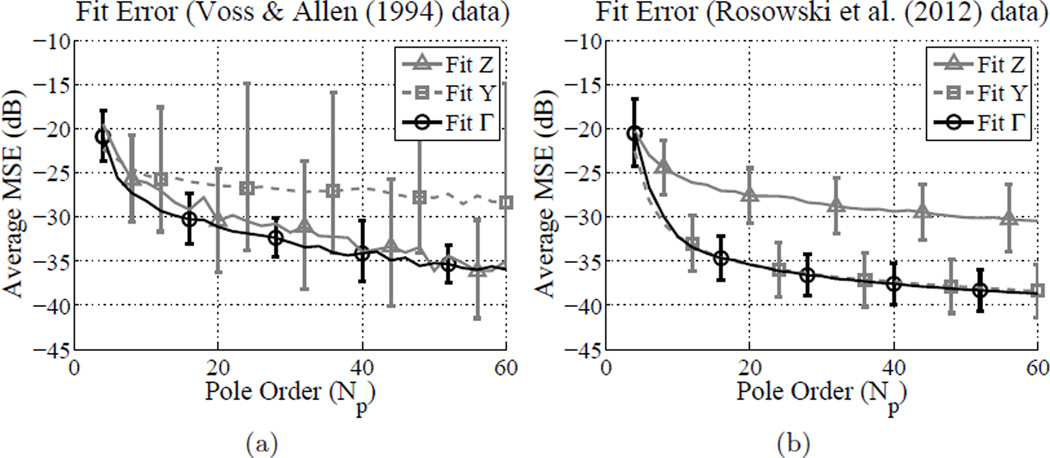
An error analysis of the fitting procedure is given in Fig. 3. Average MSE vs. pole order is plotted in different domains for pole-zero fits to two data sets of normal middle ears. Figure 3b shows the average MSE for fits over 0.1 to 10 kHz to 14 measurements of normal ears made by Voss and Allen (1994). Figure 3a shows the average MSE for fits over 0.2 to 6 kHz to 112 measurements of normal ears made by Rosowski et al. (2012). Error bars show ±1 standard deviation of the average. It is apparent that the fit error saturates after about 10 to 20 poles, as the algorithm begins to fit the measurement noise. Figure 3a shows higher average MSEs than Fig. 3b. This is primarily because the Voss and Allen (1994) measurements were fit over a larger frequency range, including more noise than the Rosowski et al. (2012) measurements. Discrepancies between goodness of fit in the impedance and admittance domains for these two data sets are due to the frequency range of the fit and noise. Because of the typical shape of the impedance response, low frequency noise has a larger effect on error in the impedance domain, and high frequency noise has a larger effect on error in the admittance domain. There are differing amounts of low and high frequency noise between the 0.1 to 10 kHz and the 0.2 to 6 kHz ranges, causing differences in impedance domain error relative to admittance domain error.

Figure 3.

Fit error evaluation across the Z, Y and Γdomains for different data sets (18 iterations). Lines show the average MSE (dB) for each domain, with error bars indicating one standard deviation. (a) 14 measurements of normal ears (Voss and Allen, 1994) fit over the 0.1 to 10 kHz range, (b) 112 measurements of normal ears (Rosowski et al., 2012) fit over the 0.2 to 6 kHz range.

Considering Fig. 3, the fitting procedure consistently performs best in the reflectance domain. Additionally, for diagnostic applications it is desirable to have the best possible fit to the magnitude reflectance. While the impedance magnitude and phase are both dominated by the ear canal response, in the reflectance domain only the phase is significantly affected by the ear canal. It is preferable to achieve the best fit to the magnitude reflectance, which shows diagnostic promise. Additionally, the dynamic range of the reflectance is much smaller than that of the impedance, typically spanning less than about 10 dB, whereas the impedance may span 20 to 40 dB (1 to 2 orders of magnitude). Due to the nature of the least squares procedure, the small magnitude data points of Z(ω) inadvertently receive less emphasis in the fitting procedure than the data points with larger magnitude. Thus, fitting to the impedance may provide a better approximation to low frequency data (where the magnitude is large, as in Fig. 1b), but will yield a poorer fit in the mid-frequency region of the reflectance magnitude. This range, typically about 1 to 5 kHz (Allen et al., 2005; Rosowski et al., 2012), shows individual variation of fine structure minima and maxima for normal middle ears. To appropriately characterize the reflectance it is necessary to capture these minima and maxima. Fitting the data in the reflectance domain gives approximately equal weight to the error across frequencies. Fitting 112 measurements over the 0.2 to 6 kHz range in the reflectance domain, an average RMS relative error of 2.13 ± 0.73% is achieved with 12 poles for 18 iterations of the fitting algorithm. Fitting the data over a larger frequency range typically requires more poles.

Typically, fits to the CAR yield values of E close to zero, as in the example fit to Voss and Allen (1994) subject #7 discussed previously. Typically, |E| is very small for fits to both normal and pathological measurements, averaging on the order of 10⁻⁵ for fits with N_p < 20. For higher pole orders there is more variation in the value of |E|, which is to be expected as the number of fitting parameters increases. Average |E| values are similar for normal and pathological data sets, indicating that this is a property of the reflectance and not a property of middle ear functionality. These results suggest that E should be forced to 0 during the fitting procedure, enforcing a relative pole-zero order of N_p = N_z. For most fits, forcing E to be zero has a negligible affect on the error; often this effect may be remedied by adding a few more poles. However, the average value of |D| is on the order of 1 for fits with N_p < 20, so it is not negligible. Thus, it is important to allow D to be non-zero when fitting the reflectance.

When the fitting procedure is performed in the reflectance domain, all fits to Γ(ω) are stable (all poles are in the left half s plane) because stability is enforced by the algorithm. However, when the fit is transformed to the impedance domain by the relation in Eq. 1, stability is not ensured. If E is allowed to be nonzero, out of the fits performed to 112 measurements of Γ(ω) over 0.2 to 6 kHz (Rosowski et al., 2012) with a −30 dB MSE tolerance, no fits are stable when transformed to the impedance domain. With E = 0 and all other conditions the same, 59 fits are stable in the impedance domain. All of these fits are also minimum phase in the impedance domain, meaning that the zeros of Ẑ(s) reside in the left half s plane as well as the poles, ensuring that both the impedance and admittance are causal and stable. Of the fits to Γ(ω) that are unstable in the impedance domain, 46 have a single pole on the real axis in the right half s plane causing the instability. That pole has a mean value of ℜ[s]/2π = 17.78 Hz with a standard deviation of 12.17 Hz. This is approximately at the origin of the s plane, characterizing the low frequency stiffness of Z(ω) for normal middle ears. The remaining fits to Γ(ω) with unstable Ẑ(s) have higher pole orders and may need more careful attention during the fitting procedure (e.g. there are many or large noise peaks causing misbehavior of the fit between the impedance and reflectance domains). Note that the positive real condition for an impedance (Brune, 1931) is stricter than the minimum phase condition. Due to noise, some CAR measurements have |Γ(ω)| > 1, corresponding to ℜ{Z(ω)} < 0 for some ω. Typically, fits to these measurements will share this property.

2.2. Comparing Across Measurements

Considering the CAR instead of its magnitude re-introduces the problem of comparing CAR measurements, because of the effect of the ear canal on the complex response. This effect is difficult to extract, particularly because the limited frequency range of the measurements does not allow for a good estimate of the ear canal length between the probe and the TM. Even though measurements are available to 15 kHz for the Voss and Allen (1994) study, there is high frequency noise in the data that makes it difficult to accurately estimate L.

Using the Weiner factorization technique

$$\mathrm{\Gamma ̂}(s)={\mathrm{\Gamma ̂}}_{ap}(s){\mathrm{\Gamma ̂}}_{mp}(s),$$ (7)

where Γ̂_ap(s) is the all-pass component and Γ̂_mp(s) is the minimum-phase component of the pole-zero fit Γ̂ (s), it is possible to preserve the magnitude reflectance while removing some undesirable variability in the complex measurement. To construct Γ̂_ap(s), poles are introduced in the left half s plane to mirror the zeros of Γ̂ (s) in the right half s plane (e.g. the same distance from the jω axis). The minimum-phase component Γ̂_mp(s) contains all singularities of Γ̂ (s) that are in the left half s plane, and zeros at the same locations as the poles of Γ̂_ap(s). This process yields unique functions Γ̂_ap(s) and Γ̂_mp(s), and ensures that Γ̂ (s) = Γ̂_ap(s)Γ̂ _mp(s). These functions have the properties |Γ̂_ap(s)| = 1 and |Γ̂_mp(s)| = |Γ̂ (s)|. The reflectance magnitude is maintained in the minimum-phase component of the fit, and the component of the reflectance that is uniformly lossless across frequency, including any pure delay, is removed. This works well assuming negligible losses in the ear canal.

From this factorization it is possible to solve for the TM impedance fit

$${Ẑ}_{TM}(s)=r_0\frac{1+{\mathrm{\Gamma ̂}}_{mp}(s)}{1-{\mathrm{\Gamma ̂}}_{mp}(s)}$$ (8)

using Eq. 1. In many cases the all-pass component of the factorization has an approximately linear phase (constant group delay), resulting in a robust estimate of L in Eq. 2. In these cases, the TM impedance estimate is similar to the “propagated impedance” function described by Voss and Allen (1994), calculated by removing a pure delay from the reflectance. Removing ear canal delay eliminates the deep “standing wave” notch in the impedance magnitude that is characteristic of the ear canal (Scheperle et al., 2008; Withnell et al., 2009). When Γ̂_ap(s) gives a good approximation to the ear canal pure delay

$${\mathrm{\Gamma ̂}}_{mp}(s)\approx {\mathrm{\Gamma }}_{TM}(s).$$ (9)

3. Results

3.1. Factorization of Γ̂ (s)

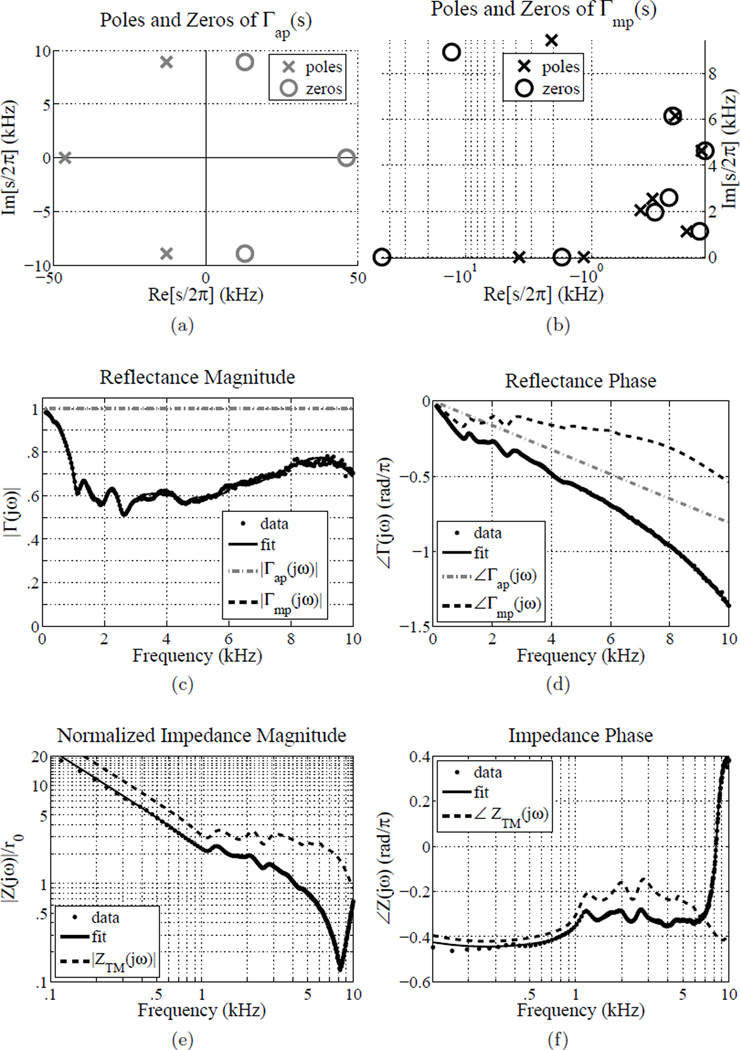
An example factorization is shown in Fig. 4, for subject #7 from Figs. 1 and 2. Before factorization, the overlapping pole-zero pairs at 7.5 and 9 kHz were removed. Figures 4a and 4b show the resulting poles and zeros of the all-pass and minimum-phase components of Γ̂ (s).

Figure 4.

Voss and Allen (1994) subject #7; example of a factored reflectance fit. (a) Poles and zeros of Γ_ap(s), (b) poles and zeros of Γ_mp(s), (c) reflectance magnitude, (d) reflectance phase, (e) impedance magnitude, (f) impedance phase. Note that Γ_mp(s) has no poles or zeros in the positive real s-plane, thus the fit is completely described by 4^th quadrant of the s-plane (shown in (b)) without any plotting tricks. All 4 quadrants of the s-plane are shown in plot (a) to allow the reader to view the symmetry of |Γ_ap(s)|. The fit was performed over 0.1 to 10 kHz, yielding N_p = 18 and N_z = 18 with an RMS relative error of 2.5% (MSE = −31.9 dB) as shown in Fig. ??; the pole-zero pairs at ℑ[s] ≈ 7.5 kHz and ℑ[s] ≈ 9 kHz were removed, yielding a MSE of −31.5 dB and N_p = 14 and N_z = 14.

The reflectance phase and the phases of the all-pass and minimum-phase components of Γ̂ (s) are shown in Fig. 4d. For this fit the phase of Γ̂_ap(s) is approximately linear, meaning that the group delay is approximately constant,

$$\tau (\omega )=-\frac{d\varphi (\omega )}{d\omega }\approx \frac{2L}{c},$$ (10)

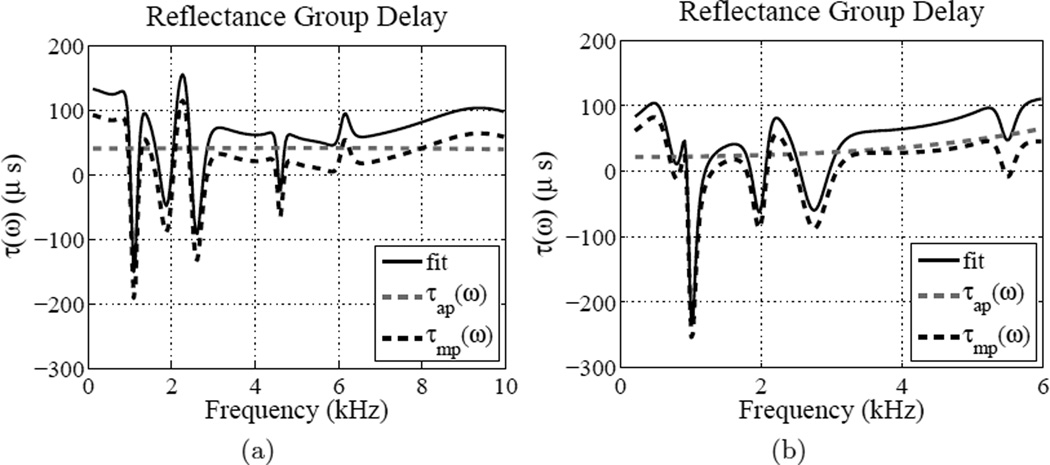
where ϕ (ω) is the phase. For subject #7 (Voss and Allen, 1994), the group delay of Γ̂_ap(_s) has a mean value of τ̄ = 40.39 µs, with a standard deviation of 0.45 µs. Taking L̂ = τ̄ c/2, the estimated length L̂ is 7.0 mm. This is a reasonable estimate for the residual length of the canal, given that Voss and Allen estimate the length of the foam plug plus probe at 1.5 cm, and the typical total ear canal length between the opening and center of the TM is about 2.35 cm (Fletcher, 1925). The TM impedance and phase are shown in Figs. 4e and 4f. Removing an approximately constant 40.39 µs of delay across frequency from the reflectance fit Γ̂(s) removes the deep notch in Ẑ_TM(ω).

A second example factorization is shown in Fig. 5. This is cadaver ear 12R from the Voss et al. (2012) study, in its normal (no simulated pathology) state. Unlike measurements made in vivo, CAR measurements of cadaver ears typically have a much shorter probe to TM distance L due to the nature of the preparation. For this ear, the group delay of the reflectance all-pass component does not appear to be constant. The group delays of the fit Γ̂(s) and its components Γ̂_mp(s) and Γ̂_ap(s) are shown in Fig. 6b, along with a similar plot from Voss and Allen (1994) subject 7 (Fig. 6a). For the Voss et al. (2012) ear 12R the mean group delay is 33.97 µs over the entire frequency range of the fit, with a standard deviation of 12.20 µs. This group delay is not constant, and appears to have the most frequency dependence between 4 and 6 kHz. If it is assumed that the constant portion of the group delay is representative of any pure delay in the canal, the minimum value of the group delay of Γ̂_ap(s) over the 0.2 to 6 kHz range (min(τ_ap) = 21.73 µs) yields the estimate L̂ ≈ 3.8 mm, which is short compared to L̂ for the in vivo measurement. Variation of the all-pass group delay with frequency may be accounted for by non-uniform area of the ear canal, or lossless mass-stiffness properties of the TM and middle ear. The TM in particular may contribute a significant amount of lossless delay (Puria and Allen, 1998; Parent and Allen, 2010).

Figure 5.

Voss and Allen (1994) subject #7; example of a factored reflectance fit.(a) Poles and zeros of Γ_ap(s), (b) poles and zeros of Γ_mp(s), (c) reflectance magnitude, (d) reflectance phase, (e) impedance magnitude, (f) impedance phase. Note that Γ_mp(s) has no poles or zeros in the positive real s-plane, thus the fit is completely described by 4^th quadrant of the s-plane (shown in (b)) without any plotting tricks. All 4 quadrants of the s-plane are shown in plot (a) to allow the reader to view the symmetry of |Γ_ap(s)|. The fit was performed over 0.2 to 6 kHz, yielding N_p = 12 and N_z = 12 with a MSE = −35.8 dB.

Figure 6.

Group delay of the fit Γ̂(s), and its factors Γ̂_mp(s) and Γ̂_ap(s). (a) Voss and Allen (1994) subject #7, (b) Voss et al. (2012) ear 12R (‘normal’ middle ear state).

3.2. Normal Ears

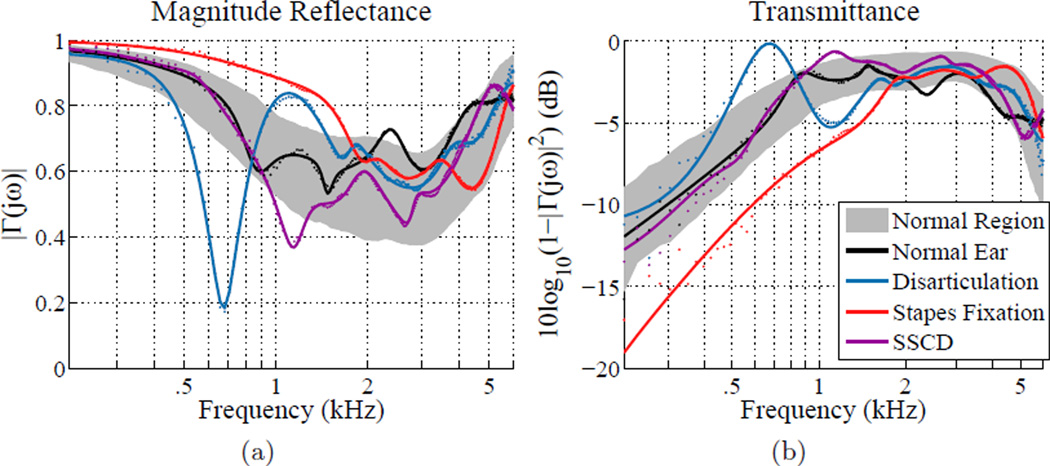
Figures 7 and 8 show a summary of fits to 4 measurements of ears with varying conditions (normal + 3 pathologies). Figure 7 shows a reflectance summary, while Fig. 8 shows a sensitivity analysis of key poles and zeros for each measurement. In this section we will focus on the normal ear measurement (plotted in black in Fig. 7), ear 22L of the Rosowski et al. (2012) study of normal ears. This fit was performed on reflectance domain data with E = 0, achieving an MSE of −35.6 dB with 12 poles and 12 zeros. The resulting poles and zeros of Γ̂_mp(s) are shown in Fig. 8a (right). The magnitude reflectance |Γ̂_mp(jω)| = |Γ̂ (jω)| is plotted in Fig. 7a. Normative data, plus or minus 1 standard deviation for 112 measurements of normal ears (Rosowski et al., 2012), is shown as the shaded grey region. Ear 22L falls within this normal region.

Figure 7.

A comparison of normal and pathological ears. (a) Power reflectance |Γ(jω)|², (b) transmittance level (dB). Grey region shows the normative region for the Rosowski et al. (2012) study of normal ears (±1 standard deviation). The black data points and line show the data and fit for normal ear 22L of Rosowski et al. (2012). The blue, red, and purple show the data and fit for stapes fixation ear 62L, disarticulation ear 28L, and SSCD ear 52L of Nakajima et al. (2012).

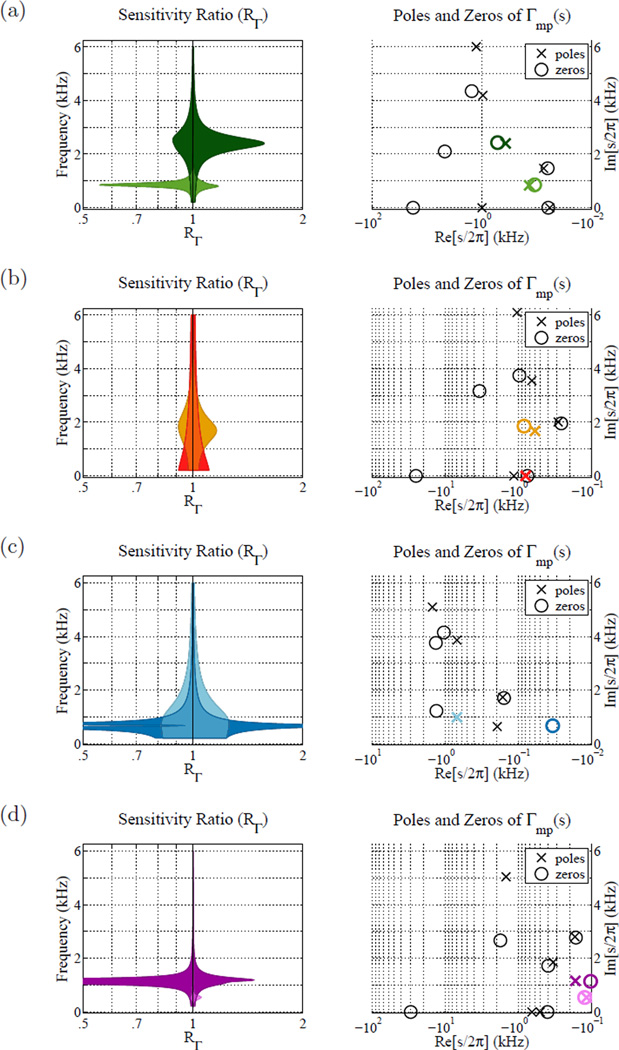
Figure 8.

Sensitivity analysis of poles and zeros for the ears shown in Fig. 7. Each subplot shows the pole-zero plot Γ_mp(s) of the fit (left), and the corresponding sensitivity analysis of the highlighted poles (right). The sensitivity analysis represents a ratio of modified reflectance magnitude |Γ(jω)| to the original fit, given a slight variation in the location of the highlighted pole, zero, or pole-zero pair. Each sensitivity plot shows two different color-coded analyses. Notice that the frequency axes are aligned for each pair of plots. (a) Normal ear, (b) stapes fixation, (c) disarticulation, (d) SSCD.

Figure 7b shows the power transmittance (Allen et al., 2005; Rosowski et al., 2012; Liu et al., 2008) defined as

$$\text{Power Transmittance}(\mathrm{d}\mathrm{B})\equiv 10{\text{log}}_{10}(1-|\mathrm{\Gamma }(j\omega ){|}^2).$$ (11)

The mean and normative region of the transmittance for normal middle ears have a very distinct shape. Rosowski et al. (2012) characterize the rising slope as 15 dB per decade and the falling slope as −23 dB per decade, with a flat region occurring between about 1 and 4 kHz. This is a useful way to characterize reflectance data, because deviations of the power absorbance from normal are more easily recognized, and are closely related to hearing sensitivity (Allen et al., 2005).

Figure 8a (left) shows a sensitivity analysis of poles and zeros from Fig. 8a (right). Figure 8a (left) displays a ratios of the modified magnitude reflectance to the original |Γ̂ _mp(jω)| shown in Fig. 7a for two different color-coded sensitivity analyses. For each sensitivity analysis, the reflectance is modified by shifting a pole-zero pair of Γ̂_mp(s) on the s plane, and the minimum and maximum range of the modified magnitude reflectance to the magnitude reflectance ratio R_Γ is shown for a 10% shift of the color coded singularity. Pole-zero pairs are shifted as a unit about their 2-dimensional centers. Sensitivity regions show the minimum and maximum values of the ratio

$$R_{\mathrm{\Gamma }}=\frac{|{\mathrm{\Gamma ̂}}_{mp}(s+\epsilon (s))|}{|{\mathrm{\Gamma ̂}}_{mp}(s)|}$$ (12)

out of 1000 shifts of the chosen pole, zero, or pair (s_k) by

$$\epsilon (s)=\{\begin{array}{cc}0.1\left|\frac{1}{N}{\sum }_{k=1}^N{s}_k\right|e^{j\mathrm{\Theta }}\hfill & \text{for}s=s_k\hfill \\ 0\hfill & \text{else}\hfill \end{array}$$ (13)

where Θ is a random variable distributed as 𝒰 (−π, π).

Considering Fig. 8a (left), the light green region shows a sensitivity anal ysis of the pole-zero pair at 1 kHz, and the dark green region shows a sensitivity analysis of the pole-zero pair at 2.5 kHz. Note that the frequency axis of the sensitivity plot is aligned with that of the pole-zero plot for comparison. According to Fig. 8a (left), the reflectance magnitude is only significantly affected by variations of the pair location in the frequency neighborhood where each pair resides. This indicates that the exact location and curvature of the minima and maxima in those frequency regions are determined by the corresponding pole-zero pairs. This is similar to the observation in section 1.2 that the fine structure minima and maxima in the mid-frequency range of |Γ (ω)| (Voss and Allen (1994) subject #7) are fit by pole-zero pairs in the same ℑ[s] range. Thus, the individually varying fine structure minima and maxima in the 1 to 5 kHz range (Allen et al., 2005; Rosowski et al., 2012) are characterized primarily by pole-zero pairs with ℑ[s] values in that range.

3.3. Pathological Ears

A similar sensitivity analysis to that presented in Fig. 8a for a normal ear is applied to pathological ears from the Nakajima et al. (2012) study. A representative measurement has been chosen for each pathology, including stapes fixation (Fig. 7 red, Fig. 8b), ossicular disarticulation (Fig. 7 blue, Fig. 8c), and superior semicircular canal dehiscence⁴ (SSCD) (Fig. 7 purple, Fig. 8d).

3.3.1. Stapes Fixation

The red fit curve and data points in Figs. 7a and 7b show an example CAR measurement (patient ear 62L,Nakajima et al. (2012)) for a patient with confirmed stapes fixation due to otosclerosis, in the presence of an intact TM and aerated middle ear. The reflectance domain fit has N_p = 10, N_z = 10, and an MSE of −40.3 dB. The transmittance (Fig. 7b) and magnitude reflectance (Fig. 7a) for this ear fall significantly outside of the normative regions.

Stapes fixation due to otosclerosis is best characterized by an increased middle ear stiffness (Feeney et al., 2003; Allen et al., 2005; Nakajima et al., 2012). This typically results in an elevated reflectance magnitude at low frequencies, corresponding to a right shift of the low-frequency sloping region of the transmittance (Allen et al., 2005). This behavior is apparent in Fig. 7b, where the transmittance curve for ear 62L is significantly shifted to the right of the normative region at low frequencies. The sensitivity plot in Fig. 8b (left) emphasizes low frequency singularities, due to the unusual behavior of the magnitude reflectance at low frequencies.

The red region of Fig. 8b (left) shows a sensitivity analysis of the pole of Γ̂_mp(s) on the real axis, closest to the origin. The movement of this pole affects the magnitude reflectance at low frequencies up to about 2 kHz. Moving this pole towards the origin should strengthen its effect, increasing the magnitude reflectance at low frequencies, and moving it away from the origin will decrease the magnitude reflectance at low frequencies. The gold region shows the sensitivity analysis for the pole-zero pair at about 1.75 kHz. While its largest effect occurs in the frequency neighborhood where the pair resides, movement of this pole-zero pair also affects the magnitude reflectance at low frequencies. This pair appears to characterize the ‘break-point’ of the transmittance, where the transition between the initial slope and the relatively flat region occurs For normal ears, this breakpoint occurs significantly lower in frequency, around 1 kHz.

3.3.2. Ossicular Discontinuity

The blue fit curve and data points in Figs. 7a and 7b show an example CAR measurement (patient ear 28L, Nakajima et al. (2012)) for a patient with confirmed ossicular discontinuity, in the presence of an intact TM and aerated middle ear. The reflectance domain fit has N_p = 10, N_Z = 10, and an MSE of −31.3 dB. The transmittance (Fig. 7b) and magnitude reflectance (Fig. 7a) for this ear also fall outside the normative regions, but the nature of this variation is quite different from that due to stapes fixation.

Ossicular discontinuity typically causes a zero in the magnitude reflectance between 0.5 and 0.8 kHz, indicating a narrow-band (tuned) resonance (Nakajima et al., 2012). This is visible in the case of ear 28L, which has a deep notch in the reflectance magnitude at about 700 Hz and a corresponding elevated transmittance in that frequency region. The transmittance does not have a normal breakpoint at 1 kHz. The poles and zeros of Γ̂_mp(s) correspondingly show an abnormal behavior in this range. In Figs. 4b, 5b and 8a (right), showing Γ̂_mp(s) for normal ears, there is typically a pole-zero pair with very close proximity to each other at 1 kHz. Figure 8b indicates that this pair may partially characterize the breakpoint between the low frequency slope and the flat region of the transmittance, though for stapes fixation this pair occurs significantly above 1 kHz. In this case of ossicular discontinuity there are poles and zeros at and below 1 kHz, but they are not tightly paired.

Figure 8c (left) shows a sensitivity analysis when poles and zeros close to 1 kHz are varied by ±10%. The darker blue region indicates that the strong zero at about 700 Hz characterizes the deep notch in the magnitude reflectance. The magnitude reflectance is very sensitive to the location of this zero, experiencing sharp relative dips when it is moved higher or lower in frequency. The lighter blue shows the sensitivity of the magnitude reflectance to the pole at 1 kHz. Not only does this pole affect the magnitude reflectance in the 1 kHz region where the magnitude reflectance is higher than average, but it has a significant (seemingly uniform) effect on the magnitude reflectance for all frequencies below about 2 kHz.

3.3.3. Superior Semicircular Canal Dehiscence (SSCD)

The purple fit curve and data points in Figs. 7a and 7b show an example CAR measurement (patient ear 52L, Nakajima et al. (2012)) for a patient with confirmed SSCD, in the presence of an intact TM and aerated middle ear. The reflectance domain fit has N_p = 12, N_z = 12, and an MSE of −34.3 dB. The transmittance (Fig. 7b) and magnitude reflectance (Fig. 7a) for this ear fall slightly outside the normative regions around 1 kHz.

SSCD typically shows a similar variation from normal to that caused by ossicular discontinuity, though not as extreme (Nakajima et al., 2012). In Fig. 7a there is a slight dip in the reflectance at 1 kHz, corresponding to a slight elevation of the transmittance at that frequency (Fig. 7b), relative to the normal middle ear region. Comparing this with the blue curves for ossicular discontinuity, the effect is similar but not as pronounced, and the notch occurs in a slightly higher frequency range around 1 kHz. Because the variation in the magnitude reflectance is observed at low frequencies around 1 kHz, the sensitivity of poles and zeros in that region is analyzed.

Figure 8d (left) shows the sensitivity analysis for the pole-zero pairs at 500 Hz and 1 kHz in Fig. 8d (right). The darker purple region shows that shifting the pole-zero pair at 1 kHz causes large variations in the magnitude reflectance in that frequency neighborhood. Notice that the zero of this pair is significantly closer to the imaginary s axis than the pole, increasing its relative strength (effect on the reflectance). This zero, and its distance from the pole, affects the depth of the minimum in the magnitude reflectance at 1 kHz. The pole-zero pair also characterizes the nature of the breakpoint in the transmittance between the initial slope and the flat region. The lighter purple region of Fig. 8d (left) shows the effect of the pole zero pair at 500 Hz on the magnitude reflectance. Shifting this pole-zero pair causes a variation in the reflectance magnitude around that frequency. However, the effect is not very pronounced; the pole and zero are very close together, and appear to be fitting a small noise peak in this frequency region. In fact, this effect is so small compared to the effect of the 1 kHz pole-zero pair, that the lighter purple region is hard to see.

4. Discussion

4.1. Limitations

The pole-zero fitting method is limited by the data provided, and will typically not be valid outside that frequency range. Because the reflectance is not known at higher or lower frequencies, the calculation of Γ̂_ap(s) is inherently imperfect. Additionally, the relative order of the fitting procedure is determined by high frequency behavior.

It is also important to note that the data is slightly impacted by the estimation of the surge resistance r₀ (Eq. 1). For the MEPA system, the canal area A is set according to the foam tip size used. It has been shown that small variations in the ear canal area relative to the calibration cavity area, within 20%, cause a negligible change in the reflectance measurement (Keefe et al., 1992; Voss and Allen, 1994). However, this will have a small affect on the CAR function and the pole-zero locations of its approximation. If Ẑ(s) ≡ N(s)/D(s) then

$$\mathrm{\Gamma ̂}(s)=\frac{N(s)-r_{0}D(s)}{N(s)+r_{0}D(s)}.$$ (14)

Thus, inaccuracy in the estimate of the surge resistance r₀ will cause inaccuracies in the poles and zeros, especially those with large |s| values.

4.2. Relative Order (N_z vs. N_p)

A relative fit order of N_z = N_p + 1 indicates a linear behavior of the data at high frequencies, a relative order of N_z = N_p indicates a constant behavior, and N_z = _Np #x002212; 1 indicates that the data goes to zero at high frequencies. Recall that the relative order is determined by zero or nonzero values of the fit parameters E and D. Thus, imperfect calculations of these parameters may not reflect the true order of the reflectance or impedance of the middle ear. For instance, the reflectance function should be zero at time t = 0 (Rasetshwane and Neely, 2011). In the Laplace transform of the fit Γ̂(s), a non-zero fit parameter D will be a delta function at t = 0. For the 112 Rosowski et al. (2012) measurements, the reflectance is fit with a small D. On average, the magnitude of D for those measurements (N_p = 12, _Nz = 12) is 0.833 ± 0.371.

If the value of D is a good approximation, it may be used to estimate the inaccuracy in r₀. Considering the time domain form of Eq. 1, at time t = 0

$$\varsigma (0)={\mathrm{r̄}}_0=r_0\frac{1+\gamma (0)}{1-\gamma (0)}.$$ (15)

Theoretically Γ(0) = 0, such that r̄0 = r₀. If r₀ is estimated incorrectly by the measurement tool, then the corrected surge resistance is

$${\mathrm{r̄}}_0=r_0\frac{1+D}{1-D}.$$ (16)

The relative order of the impedance Z(s) must have the property |N_z − N_p| ≤ 1, because it is an input impedance. This property need not be true in the reflectance domain, though for a polynomial fraction approximation N_z < N_p must hold in order for the time-domain reflectance to be 0 at t = 0. However, considering Eq. 14, a pole-zero representation of Ẑ(s) will yield an equal order (N_p = N_z) approximation of Γ(s) if there are no cancellations of powers of s.

4.3. Applications

The fitting algorithm is fast, and may be easily implemented in a reflectance measurement system. Ultimately, it should allow for more robust automated classification than visual assessment or correlations between magnitude reflectance values and audiometric measurements. Pole-zero fitting is advantageous because it condenses the entire complex response to a small set of parameters, without extensive processing of the magnitude reflectance (e.g. a somewhat arbitrary choice of the frequency points over which to average the magnitude CAR). However, further study is needed to meet this objective. Using larger volumes of normal and pathological CAR data, in combination with known physical characteristics of normal and pathological middle ears, the complex data must be further studied, and classification strategies sought.

Pole-zero fits may also be used to synthesize network models of the complex impedance (e.g. Brune (1931)). However, such RLC networks will not necessarily be unique. Networks synthesized from pole-zeros fits of CAR measurements will often lack direct physical interpretations, such as the Zwislocki (1962), Kringlebotn (1988), or Parent and Allen (2010) models. However, they may have utility for analyzing CAR data.

4.4. Summary

This study establishes a methodology for examining the physical and mathematical properties of CAR data using pole-zero fitting. Pole-zero fits can characterize CAR data with low error and small number of parameters. While considering the complex data reintroduces the effect of variation in the probe-TM distance, measurements may be effectively compared across ears by factoring the reflectance fit into its minimum-phase and all-pass components. The magnitude of the minimum-phase component of the CAR is equal to the reflectance magnitude, thus preserving the current diagnostic standard. In this preliminary investigation, it was found that pole-zero locations show distinct pole-zero pairs in the mid-frequency region of individual variation for normal ears, and may systematically differ for various pathologies, similar to the magnitude reflectance. Pole-zero modeling shows promise for mathematically characterizing CAR data in order to enable improved automated identification of middle ear pathology using a noninvasive, yet relatively low cost measurement system.

Appendix A

Vector Fitting

The vector fitting procedure is a two step process, which converts a nonlinear least squares problem to a linear least squares problem by introducing an unknown scaling function κ(s), having known poles a_i, defined by Gustavsen and Semlyen (1999) as

$$\left[\begin{array}{c}\hfill (\kappa ·\mathrm{F̂})(s)\hfill \\ \hfill \kappa (s)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\sum }_{i=1}^{N_p}\frac{{\mathrm{c̃}}_i}{s-a_i}+\mathrm{d̃}+ẽs\hfill \\ \hfill {\sum }_{i=1}^{N_p}\frac{{\mathrm{b̃}}_i}{s-a_i}+1\hfill \end{array}\right].$$ (A.1)

This vector system of equations consists of two relations which are linear in their unknowns c̃_i, d̃, ẽ, and b̃_i. Both κ(s) and (κ ·F̂)(s) share the same known poles a_i. These are the ‘starting poles’ of the algorithm; their selection is described briefly in section ??. The vector fitting method relates the system of equations in Eq. A.1 to the measured data F(ω) via

$$\kappa (j\omega )·F(\omega )\approx (\kappa ·\mathrm{F̂})(j\omega ).$$ (A.2)

When evaluated over the many available frequency points of F(ω), Eq. A.2 results in a overdetermined linear problem in the unknowns c̃_i, d̃, ẽ, and b̃_i. The data can then be approximated by

$$\mathrm{F̂}(j\omega )=\frac{(\kappa ·\mathrm{F̂})(j\omega )}{\kappa (j\omega )},$$ (A.3)

given the estimated values of c̃_i, d̃, ẽ, and b_i.

Because (κ · F̂)(s) and κ(s) share the same poles there is a perfect cancellation in Eq. A.3, thus the zeros of κ(s) become the poles of F̂(s). One may see this by considering the product form of Eq. A.1

$$\left[\begin{array}{c}\hfill (\kappa ·\mathrm{F̂})(s)\hfill \\ \hfill \kappa (s)\hfill \end{array}\right]=\left[\begin{array}{c}\hfill \frac{ẽ{\prod }_{i=1}^{N_p+1}(s-{\mathrm{\varsigma ̃}}_i)}{{\prod }_{i=1}^{N_p}(s-a_i)}\hfill \\ \hfill \frac{{\prod }_{i=1}^{N_p}(s-{ẑ}_i)}{{\prod }_{i=1}^{N_p}(s-a_i)}\hfill \end{array}\right],$$ (A.4)

where ζ̃_i are the zeros of (κ · F̂)(s) and z̃_i are the zeros of κ(s). Combining Eqs. A.3 and A.4 yields

$$\mathrm{F̂}(s)=\frac{ẽ{\prod }_{i=1}^{N_p+1}(s-{\mathrm{\varsigma ̃}}_i)}{{\prod }_{i=1}^{N_p}(s-{\mathrm{z̃}}_i)}.$$ (A.5)

Thus, the zeros of the scaling function κ(s) become the poles of the fitted function F̂(s) (Eq. 5) such that A_i = z̃_i. Gustavsen and Semlyen observe that it is more accurate to calculate the remaining quantities C_i, D, and E by recalculating the values of c̃_i, d̃, ẽ, and b̃_i, using z̃_i as the starting poles. Once this has been accomplished, it is possible to equate C_i = c̃_i, D = d̃, and E = ẽ.

An appropriate selection of starting poles is necessary for the convergence of the vector fitting method. For a function with resonance peaks, such as the reflectance, Gustavsen and Semlyen (1999) suggest that the starting poles come in complex conjugate pairs and be linearly distributed over the frequency range of the data. Pole pairs of the form

$$a_k=-{\alpha }_k\pm j{\beta }_k,$$ (A.6)

with ${\alpha }_k=\frac{{\beta }_k}{100}$, are advised for suitable performance of the algorithm. This is necessary as the linear problem can become ill-conditioned if the starting poles are real. Large differences between the starting poles and the best fit poles of the response can cause large differences between κ(s) and (κ · F̂)(s) that result in poor least squares solutions (Gustavsen and Semlyen, 1999).

As the starting poles a_i approach their optimal locations, the scaling function κ(s) will approach 1 (the calculated zeros z̃_i of κ(s) converge to the ai values). The method may be used iteratively to converge on the best fit, by setting the starting poles equal to the new poles at each iteration (Gustavsen and Semlyen, 1999). If the least squares procedure returns unstable poles (ℜ[z̃_i] > 0), their real parts are reflected to the left-half s plane before the next iteration. Due to this, the error will not always decrease monotonically with iteration. Depending on the application, it may also be beneficial to impose properties other than stability. For instance, one might force the impedance to be minimum phase, instead of merely stable. This can be done by inverting the real part of any zero that appears in the right half s-plane, similar to the procedure for enforcing stability of the poles. Such a constraint may cause an increase in error, but could have utility for physical modeling.

The fit error can depend on the starting pole values due to the noise in the data. Additionally, due to the nature of the fit, the smoothness of the reflectance function and the number of available parameters, there exist multiple non-unique fits yielding reasonable fit errors (e.g. within a certain MSE tolerance). Thus the poles (of an already low error fit) may vary with iteration, causing non-monotonic behavior of the error. Typically, significant MSE improvement over the first few iterations occurs only for low pole orders (e.g. N_p < 10). For high pole orders (e.g. N_p > 20) the fitting procedure achieves close to its lowest MSE within the first iteration. When the order is reasonably high, the starting poles better cover the entire frequency range, causing the fit to converge very quickly. For low orders of poles, more iterations are necessary to move the poles toward their best fit locations.