Data-Driven Learning of Q-Matrix

Abstract

The recent surge of interests in cognitive assessment has led to developments of novel statistical models for diagnostic classification. Central to many such models is the well-known Q-matrix, which specifies the item–attribute relationships. This article proposes a data-driven approach to identification of the Q-matrix and estimation of related model parameters. A key ingredient is a flexible T-matrix that relates the Q-matrix to response patterns. The flexibility of the T-matrix allows the construction of a natural criterion function as well as a computationally amenable algorithm. Simulations results are presented to demonstrate usefulness and applicability of the proposed method. Extension to handling of the Q-matrix with partial information is presented. The proposed method also provides a platform on which important statistical issues, such as hypothesis testing and model selection, may be formally addressed.

Diagnostic classification models (DCMs) are an important statistical tool in cognitive diagnosis and can be employed in a number of disciplines, including educational assessment and clinical psychology (Rupp & Templin, 2008b; Rupp, Templin, & Henson, 2010). A key component in many such models is the so-called Q-matrix, which specifies item–attribute relationships, so that responses to items can reveal the attribute configurations of the respondents. K. Tatsuoka (1983, 2009) proposed the simple and easy-to-use rule space method for Q-matrix-based classifications.

Different DCMs can be built around the Q-matrix. One simple and widely studied model among them is the DINA model (Deterministic Input, Noisy output “AND” gate; see Junker & Sijtsma, 2001). Other important developments can be found in K. Tatsuoka (1985); DiBello, Stout, and Roussos (1995); Junker and Sijtsma (2001); Hartz (2002); C. Tatsuoka (2002); Leighton, Gierl, and Hunka (2004); von Davier (2005); Templin (2006); Templin and Henson (2006); and Chiu, Douglas, and Li (2009). Rupp et al. (2010) contains a comprehensive summary of many classical and recent developments.

There is a growing literature on the statistical inference of Q-matrix-based DCMs that addresses the issues of item parameters estimation when the Q-matrix is prespecified (Henson & Templin, 2005; Roussos, Templin, & Henson, 2007; Rupp, 2002; Stout, 2007). Having a correctly specified Q-matrix is crucial for parameter estimation (such as the slipping, guessing probability, and the attribute distribution) and for the identification of participants’ underlying attributes. As a result, these approaches are sensitive to the choice of the Q-matrix (de la Torre, 2008; de la Torre & Douglas, 2004; Rupp & Templin, 2008a). For instance, a misspecified Q-matrix may lead to substantial lack of fit and, consequently, erroneous attribute identification. Thus, it is desirable to be able to detect misspecification and to obtain a data-driven Q-matrix.

In this article, the authors consider the estimation problem of the Q-matrix. In particular, they introduce an estimator of the Q-matrix under the setting of the DINA model. The proposed estimator only uses the information of dependence structure of the responses (to items) and does not rely on information about the attribute distribution, or the slipping, or guessing parameters. The definition of these concepts will be provided in the text momentarily. Nonetheless, if additional information is available such as a parametric form of the attribute distribution or partial information about the Q-matrix, the estimation procedure is flexible enough to incorporate those structures. Such information, if correct, can substantially improve the efficiency of the estimator, enhance the identifiability of the Q-matrix, and reduce the computational complexity. In addition to the construction of the estimator, computational algorithms and simulation studies are also provided to assess the performance of the proposed procedure.

It is worth pointing out that this method is in fact generic in the sense that it can be adapted to cover a large class of DCMs besides the DINA model. In particular, the procedure is implementable to the DINO (Deterministic Input, Noisy output “OR” gate) model, the NIDA (Noisy Inputs, Deterministic “AND” Gate) model, and the NIDO (Noisy Inputs, Deterministic “OR” Gate), model among others. In addition to the estimation of the Q-matrix, the authors emphasize that the main idea behind the derivations forms a principled inference framework. For instance, during the course of the description of the estimation procedure, necessary conditions for a correctly specified Q-matrix are naturally derived. Such conditions can be used to form appropriate statistics for hypothesis testing and model diagnosis. In connection to that, additional developments (e.g., the asymptotic distributions of the corresponding statistics) are needed, but they are not the focus of the current study. Therefore, the proposed framework can potentially serve as a principled inference tool for the Q-matrix in DCMs.

This article is organized as follows: the section Estimation of the Q-Matrix is a presentation of the estimation procedures and the corresponding algorithms. Section on Simulation includes simulation studies to assess the performance of the proposed estimation methods. Some discussions are given in the last section.

Estimation of the Q-Matrix

The situation that N participants taking a test consisting of J items would be considered. The responses are binary, so that the data will be an N × J matrix with entries being 0 or 1. The DCM to be considered for such data envisions K attributes that are related to both the participants and the items.

Model Setup and Notations

The following notation and specifications are needed to describe the DCMs.

Responses to items

There are J items and R = (R¹, …, R^J)^T is used to denote the vector of responses to them, where, for each j, R^j is a binary variable taking 0 or 1 and superscript T denotes transpose.

Attribute profile

There are K attributes and α = (α₁, …, α_K)^T is used to denote the vector of attributes, where α_k = 1 or 0, indicating the presence or absence of the k th attribute, k = 1, …, K.

Note that both α and R are participant-specific. Throughout this article, it is assumed that the number of attributes K is known and that the number of items J is observed.

Q-matrix

This describes the link between the items and the attributes. In particular, Q = (Q_jk)_{J × K} is an J × K matrix with binary entries. For each j and k, Q_jk = 1 indicates that item j requires attribute k and Q_jk = 0 otherwise.

Let ξ^j(α, Q) denote the ideal response, which indicates whether a participant possessing attribute profile α is capable of providing a positive response to item j if the item–attribute relationship is specified by matrix Q. Different ideal response structures give rise to different DCMs. For instance,

$${\mathrm{\xi }}_{\mathrm{D}\mathrm{I}\mathrm{N}\mathrm{A}}^j(\mathbf{\alpha },Q)=\mathbf{1}({\mathrm{\alpha }}_k\ge Q_{jk}\mathit{\text{for all}}k=1,\dots ,K)$$ (1)

is associated with the DINA model, where 1 is the usual indicator function. The DINA model assumes conjunctive relationship among attributes; that is, it is necessary to possess all the attributes indicated by the Q-matrix to be capable of providing a positive response to an item. In addition, having additional unnecessary attributes does not compensate for a lack of the necessary attributes. To simplify the notation, ${\mathrm{\xi }}_{\mathrm{D}\mathrm{I}\mathrm{N}\mathrm{A}}^j={\mathrm{\xi }}^j$.

The last ingredient of the model specification is related to the so-called slipping and guessing parameters (Junker & Sijtsma, 2001). The concept is due to Macready and Dayton (1977) for mastery testing; see also van der Linden (1978). The slipping parameter is the probability that a participant (with attribute profile α) responds negatively to an item if the ideal response to that item ξ(α, Q) = 1; similarly, the guessing parameter refers to the probability that a participant responds positively if his or her ideal response ξ(α, Q) = 0. s is used to denote the slipping probability and g to denote the guessing probability (with corresponding subscript indicating different items). In the discussion, it is more convenient to work with the complement of the slipping parameter. Therefore, c = 1 − s is defined to be the probability of answering correctly, with s_j, g_j, and c_j being the corresponding item-specific notation. Given a specific participant’s profile α, the response to item j under the DINA model follows a Bernoulli distribution:

$$P(R^j=1|Q,\mathbf{\alpha },c_j,g_j)=c_j^{{\mathrm{\xi }}^j(\mathbf{\alpha },Q)}{g}_j^{{1-\mathrm{\xi }}^j(\mathbf{\alpha },Q)}.$$ (2)

In addition, conditional on α, (R¹, …, R^J) are jointly independent.

Last, subscripts are used to indicate different participants. For instance, $R_r={(R_r^1,\dots ,R_r^J)}^{\mathrm{T}}$ is the response vector of participant r. Similarly, α_r is the attribute vector of participant r. With N participants, R₁, …, R_N is observed but not α₁, …, α_N. It is further assumed that the attribute profiles are independent and identically distributed (i.i.d.) such that

$$P({\mathbf{\alpha }}_r=\mathbf{\alpha })=p_{\mathbf{\alpha }},$$

and let p = (p_α : α ∈ {0, 1}^K), c = (c₁, …, c_J), and g = (g₁, …, g_J). Thus, the model specification is finished.

Estimation of the Q-Matrix

Intuition

The participants’ attribute profiles are not directly observed. Thus, the estimator of the Q-matrix is built only on the information contained in the response vectors, R₁, …, R_N. The estimation of the Q-matrix is based on an assessment of how well a given matrix Q fits the data. Throughout the discussion, Q is used to denote the true matrix that generates the data and Q′ to denote a generic J by K matrix with binary entries. In particular, each Q-matrix along with the corresponding parameters (Q′, p, c, g) determines the distribution of the response vector R given by

$$P(R|Q\prime ,p,c,g)=\sum _{\mathbf{\alpha }}{p}_{\mathbf{\alpha }}\prod _{j=1}^{J}P(R^j|Q\prime ,\mathbf{\alpha },c,g).$$ (3)

Consider the (observed) empirical distribution

$$\widehat{P}(R)=\frac{1}{N}\sum _{i=1}^{N}I(R_i=R).$$ (4)

If the Q-matrix and the other parameters, (Q′, p, c, g), are correctly specified, the empirical distribution in (4) eventually converges to (3) as the sample size (the number of participants) becomes large. The estimator is then constructed based on this observation.

The T-matrix

The T-matrix is central to the construction of the estimator. It is another representation of the Q-matrix and serves as a connection between the observed response distribution and the model structure. In particular, it sets up a linear dependence between the attribute distribution and the response distribution. It is a tool that allows the expression of the probabilities in (3) in terms of matrix products. Each row vector of the T-matrix is specified first. For each item j, recall that

$$P(R^j=1|Q\prime ,p,c,g)=\sum _{\mathbf{\alpha }}{p}_{\mathbf{\alpha }}P(R^j=1|Q\prime ,\mathbf{\alpha },c,g),$$ (5)

where P(R^j = 1|Q′, α, c, g) = (c_j − g_j)ξ^j(α, Q′) + g_j. If a row vector B_{Q′, c, g}(j) of length 2^K containing the probabilities P(R^j = 1|Q′, α, c, g) for all αs is created and those elements are arranged in an appropriate order, then for all j, Equation 5 can be written in the form of a matrix product

$$\sum _{\mathbf{\alpha }}{p}_{\mathbf{\alpha }}P(R^j=1|Q\prime ,\mathbf{\alpha },c,g)=B_{Q\prime ,c,g}(j)p,$$

where p is the column vector containing the probabilities p_α. Similarly, for each pair of items, it may established that the probability of responding positively to both items j₁ and j₂ is

$$P(R^{j_1}=1,R^{j_2}=1|Q\prime ,p,c,g)=\sum _{\mathbf{\alpha }}{p}_{\mathbf{\alpha }}P(R^{j_1}=1|Q\prime ,\mathbf{\alpha },c,g)P(R^{j_2}=1|Q\prime ,\mathbf{\alpha },c,g)=B_{Q\prime ,c,g}(j_1,j_2)p,$$

where B_{Q′, c, g} (j₁, j₂) is a row vector containing the probabilities P(R^j₁ = 1|Q′, α, c, g) P(R^j₂ = 1|Q′, α, c, g) for each α. Note that each element of B_{Q′, c, g}(j₁, j₂) is the product of the corresponding elements of B_{Q′, c, g}(j₁) and B_{Q′, c, g}(j₂). With a completely analogous construction,

$$P(R^{j_1}=1,\dots ,R^{j_1}=1|Q\prime ,p,c,g)=B_{Q\prime ,c,g}(j_1,\dots ,j_l)p$$

for each combination of distinct (j₁, …, j_l). Similarly, B_{Q′, c, g}(j₁, …, j_l) is the element-by-element product of B_{Q′, c, g}(j₁), …, B_{Q′, c, g}(j_l). From a computational point of view, one only needs to construct the B_{Q′, c, g}(j)’s for each individual item j and then take products to obtain the corresponding combinations.

The T-matrix has 2^K columns. Each row vector of the T-matrix is one of the vectors B_{Q′, c, g}(j₁, …, j_l), that is, the T-matrix is a stack of B-vectors

$$T_{c,g}(Q\prime )=\left(\begin{array}{c}{B}_{Q\prime ,c,g}(1)\\ ⋮\\ B_{Q\prime ,c,g}(J)\\ B_{Q\prime ,c,g}(1,2)\\ ⋮\end{array}\right).$$

By the definition of the B-vectors,

$$T_{c,g}(Q\prime )p=\left(\begin{array}{c}P(R^1=1|Q\prime ,p,c,g)\\ ⋮\\ P(R^J=1|Q\prime ,p,c,g)\\ P(R^1=1,R^2=1|Q\prime ,p,c,g)\\ ⋮\end{array}\right),$$ (6)

is a vector containing the corresponding probabilities associated with a particular set of parameters (Q′, c, g , p). β is the vector containing the probabilities (corresponding to those in Equation 6) of the empirical distribution, for example, the first element of β is $\frac{1}{N}{\sum }_{i=1}^N\mathbf{1}(R_i^1=1)$ and the (J + 1)th element is $\frac{1}{N}{\sum }_{i=1}^N\mathbf{1}(R_i^1=1,R_i^2=1)$. With a large sample and a set of correctly specified parameters (Q, c, g , p),

$$\mathrm{\beta }\to T_{c,g}(Q)p$$ (7)

almost surely as N → ∞.

An illustrative example

To aid the understanding of the T-matrix, one simple example is provided. Suppose that two attributes have to be tested. The population is naturally divided into four strata. The corresponding contingency table of attributes is

	Attribute 2
Attribute 1	p00	p01
	p10	p11

Let vector p = (p₀₀, p₁₀, p₀₁, p₁₁)^T contain all the corresponding probabilities in this particular order. Consider an exam containing three problems and admitting the following Q-matrix,

$$Q=\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 1\end{array}\right).$$ (8)

To simplify the discussion, the case that c_i = 1 and g_i = 0 is considered; that is, there is no chance of slipping or guessing. Thus, the response R is completely determined by the attribute profile α. Under this simplified situation, if the Q-matrix is correctly specified, the following identities are obtained:

$$p_{10}+p_{11}=N_1/N,p_{01}+p_{11}=N_2/N,p_{11}=N_3/N,$$

where $N_j={\sum }_{r=1}^{N}I(R_i^j=1)$ is the total number-correct responses to item j. The corresponding T-matrix and β-vector are created as follows:

$$T_{c,g}(Q)=\left(\begin{array}{cccc}0& 1& 0& 1\\ 0& 0& 1& 1\\ 0& 0& 0& 1\end{array}\right),\mathrm{\beta }=\left(\begin{array}{c}{N}_1/N\\ N_2/N\\ N_3/N\end{array}\right).$$ (9)

The first column of T_{c, g}(Q) corresponds to the zero attribute profile, the second corresponds to α = (1, 0), the third corresponds to α = (0, 1), and the last corresponds to α = (0, 1). The first row of T(Q) corresponds to item one, the second to two, and the third to three. Note that the T-matrix changes as the Q-matrix changes. For instance, for an alternative matrix

$$Q\prime =\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 1\end{array}\right),$$

the corresponding T-matrix would be

$$T_{c,g}(Q\prime )=\left(\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& 1& 1\\ 0& 1& 0& 1\end{array}\right);$$ (10)

while the β-vector remains.

To illustrate this idea, consider the matrix in Equation 8. With a correctly specified Q-matrix, it can be established that

$$T_{c,g}(Q)p=\mathrm{\beta }.$$ (11)

Note that the β-vector is directly observed and the attribute distribution p is not. Thus, the preceding display suggests that a necessary condition for a correctly specified Q-matrix is that the preceding linear equations (with p being the variable) has a solution subject to the natural condition that Σ_αp_α = 1.

If for any misspecified Q-matrix, Equation 11 does not have any solution, then the Q-matrix is identifiable. Otherwise, more constraints may be included in the T-matrix to enhance the identifiability. For instance, the combination of items one and two may be considered; that is,

$$p_{11}=N_{1\wedge 2}/N,$$ (12)

where $N_{1\wedge 2}={\sum }_{i=1}^N\mathbf{1}(R_i^1=1,R_i^2=1)$. The preceding identity also suggests that people who are able to solve Problem 3 must have both attributes and therefore are able to solve both Problems 1 and 2; that is, N₃ = N_1∧2. Certainly, this is not necessarily respected in the real data, though it is a logical conclusion. The slipping and guessing parameters are introduced to account for such disparities. With the additional constraint in (12) included, the corresponding T-matrix and β-vector should be

$$T_{c,g}(Q)=\left(\begin{array}{cccc}0& 1& 0& 1\\ 0& 0& 1& 1\\ 0& 0& 0& 1\\ 0& 0& 0& 1\end{array}\right),\mathrm{\beta }=\left(\begin{array}{c}{N}_1/N\\ N_2/N\\ N_3/N\\ N_{1\wedge 2}/N\end{array}\right).$$ (13)

Similarly, one may include other (linear) constraints in the T-matrix that correspond to combinations of distinct items.

Objective function and estimation of the Q-matrix

Based on the preceding construction and the discussions, an objective function is introduced,

$$S_{c,g,p}(Q)=|T_{c,g}(Q)p-\mathrm{\beta }|,$$ (14)

where | · | is the Euclidean distance. If all the parameters are correctly specified, it is expected that S_{c , g , p}(Q) → 0 as N → ∞. A natural estimator of the Q-matrix would be

$$\widehat{Q}=\text{arg}\underset{Q\prime }{\text{inf}}{S}_{c,g,p}(Q\prime ).$$

Dealing with the unknown parameters

Most of the time, the parameters (c, g , p) are unknown. Under these situations, the profiled objective functions are considered:

$$S(Q\prime )=\underset{c,g,p}{\text{inf}}{S}_{c,g,p}(Q\prime ),$$ (15)

where the minimization is subject to the natural constraints that c_i, g_i, p_α ∈ [0, 1] and Σ_αp_α = 1. Then, the corresponding estimator is

$$\widehat{Q}=\text{arg}\underset{Q\prime }{\text{inf}}S(Q\prime ).$$ (16)

The minimization of p in Equation 15 consists of a quadratic optimization with linear constraints, and therefore can be done efficiently. The minimization with respect to c and g is usually not straightforward. One may alternatively replace the minimization by other estimators (such as the maximum likelihood estimator [MLE]) (ĉ(Q′), ĝ(Q′), p̂(Q′)). Thus, the objective function becomes

$$\widehat{S}(Q\prime )=S_{\widehat{c}(Q\prime ),\widehat{g}(Q\prime ),\widehat{p}(Q\prime )}(Q\prime ).$$ (17)

The corresponding estimator is

$$\tilde{Q}=\text{arg}\underset{Q\prime }{\text{inf}}\widehat{S}(Q\prime ).$$ (18)

This alternative allows certain flexibility in the estimation procedure. The S-function in Equation 17 is usually easier to compute. Therefore, the estimator (Equation 18) is often used and a hill-climbing algorithm to compute Q̃ is given in the next subsection.

• Remark 1: Conceptually, all the combinations (j₁, …, j_l) for l = 1, …, J may be included in the T-matrix, which results in a T-matrix of 2^J − 1 rows. Such a T-matrix is called saturated. The corresponding vector β contains all the information of the observed responses. However, from a practical point of view, to ensure a convergence of when the T-matrix is saturated, it is necessary to have sample size N>>2^J. That is, the sample size needs to be sufficiently large so that the count in each cell of the J-way contingency table is nonzero. Unfortunately, such a large sample is usually not achievable even for a reasonable number of items, for example, J = 20. Furthermore, to construct a matrix of 2^J row typically induces a substantial computational overhead.

With this concern, all combinations of items in the T-matrix are not typically included. A practical suggestion is to include, in an ascending order, 1-way, 2-way combinations, and so on, until the number of rows of the T-matrix reaches N/10. Generally speaking, combinations of fewer items are included first, followed by those of more items. In the simulation study presented later, a T-matrix including at least up to (K + 1)-way combinations performs well empirically. For the corresponding theoretical analysis, see Liu, Xu, and Ying (2011).

Computations

In this subsection, the computation of the estimator is considered. In particular, the estimator in Equation 18 and the objective function (Equation 17) are considered. Let (ĉ, ĝ, p̂) be the MLE. The computation of the MLEs can be done efficiently by the expectation–maximization (EM) algorithm (de la Torre, 2009; Dempster, Laird, & Rubin, 1977). Furthermore, the optimization of Equations 16 and 18 is considered.

The optimization of a general nonlinear discrete function is a very challenging problem. A simple-minded search of the entire space consists of evaluating the function S up to 2^{J × K} times. In the current setting, an a priori Q-matrix, denoted by Q₀, is usually available. It is expected that Q₀ is reasonably close to the true matrix Q.

For each Q′, let U_j(Q′) be the set of J × K matrices that are identical to Q′ except for the jth row (item). Then the algorithm is described as follows:

• Algorithm 1: Choose a starting point Q(0) = Q₀. For each iteration m, given the matrix from the previous iteration Q(m − 1), the following steps are performed:

  1. Let

     $$Q_j=\text{arg}\underset{Q\prime \in U_j(Q(m-1))}{\text{inf}}S(Q\prime ).$$ (19)
  2. Let j_* = arg inf_j S(Q_j).
  3. Let Q(m) =Q_j*.

Repeat Steps 1 to 3 until Q(m) = Q(m − 1).

At each step m, the algorithm considers updating one of the J items. In particular, if the jth item is updated, the Q-matrix for the next iteration would be Q_j. Then, Q(m) is set to be the Q_j* that admits the smallest objective function among all the Q_js. The optimization (Equation 19) consists of evaluating the function S up to 2^K times. Thus, the total computation complexity of each iteration is J × 2^K evaluations of S.

• Remark 2: The simulation study in the next section shows that if Q₀ is different from Q by 3 items (out of 20 items) Algorithm 1 has a very high chance of recovering the true matrix with reasonably large samples.

Simulation

In this section, simulation studies are conducted to illustrate the performance of the proposed method. The data from the DINA model are generated under different settings and the estimated Q-matrix and the true Q-matrix are compared.

Estimation of the Q-Matrix With No Special Structure

The simulation setting

To start with, a 20 × 3 Q-matrix (J = 20 items and K = 3 attributes) is considered, denoted by Q₁, given by

$$Q_1=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\\ 1& 1& 0\\ 1& 0& 1\\ 1& 0& 1\\ 0& 1& 1\\ 1& 0& 1\\ 0& 1& 1\\ 1& 1& 0\\ 0& 1& 1\\ 1& 0& 1\\ 0& 1& 1\\ 1& 1& 1\end{array}\right).$$ (20)

The attributes are generated from a uniform distribution; that is,

$$p_{\mathbf{\alpha }}=2^{-K}.$$

The slipping parameters and the guessing parameters are set to be s_i = g_i = 0.2 for all items. In addition, for each sample size N = 500, 1,000, 2,000, and 4,000, 100 data sets were generated under such a setting.

To reduce the computational complexity, the T-matrix contains combinations of up to 4 items. More generally, the simulation study shows that a T-matrix containing all the (K + 1) (and lower) combinations delivers good estimates. Algorithm 1 is implemented with a starting Q-matrix Q₀ specified as follows. The Q₀ is constructed based on the true matrix Q by misspecifying 3 items. In particular, 3 items out of the total 20 items are randomly selected without replacement. For each of the selected items, the corresponding row of Q₀ is sampled uniformly from all the possible K dimensional binary vectors excluding the true vector (of Q) and the zero vector. That is, each of these rows is a uniform sample of 2^K − 2 vectors. Thus, it is guaranteed that Q₀ does not have zero vectors and is different from Q by precisely 3 items. The simulation results are given by the first row of Table 1. The columns “Q̂ = Q” and “Q̂ ≠ Q” contains the frequencies of the events “Q̂ = Q” and “Q̂ ≠ Q,” respectively. Based on 100 independent simulations, Q̂ recovers the true Q-matrix 98 times when the sample size is 500. For larger samples, the estimate Q̂ never misses the true Q-matrix.

Table 1.

Numbers of Correctly Estimated Q-Matrices Out of 100 Simulations With N = 500, 1,000, 2,000, and 4,000 for Q₁, Q₂, and Q₃

	N = 500		N = 1,000		N = 2,000		N = 4,000
	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q
Q1	94	6	100	0	100	0	100	0
Q2	82	18	100	0	100	0	100	0
Q3	38	62	98	2	100	0	100	0

The data from Q-matrices with four and five attributes are simulated:

$$Q_2=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ 1& 1& 0& 0\\ 1& 0& 1& 0\\ 1& 0& 0& 1\\ 0& 1& 1& 0\\ 0& 1& 0& 1\\ 0& 0& 1& 1\\ 1& 1& 1& 0\\ 1& 1& 0& 1\\ 1& 0& 1& 1\\ 0& 1& 1& 1\\ 1& 1& 1& 1\\ 1& 1& 1& 1\end{array}\right),Q_3=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\\ 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\\ 1& 1& 0& 0& 0\\ 1& 0& 1& 0& 0\\ 1& 0& 0& 1& 0\\ 1& 0& 0& 0& 1\\ 0& 1& 1& 0& 0\\ 0& 1& 0& 1& 0\\ 0& 1& 0& 0& 1\\ 0& 0& 1& 1& 0\\ 0& 0& 1& 0& 1\\ 0& 0& 0& 1& 1\end{array}\right).$$ (21)

With exactly the same settings, the results are given by the corresponding rows in the Table 1. The estimator performs well except for the cases where N = 500. This is mainly because the sample size is small relative to the dimension K.

An improved estimation procedure for small samples

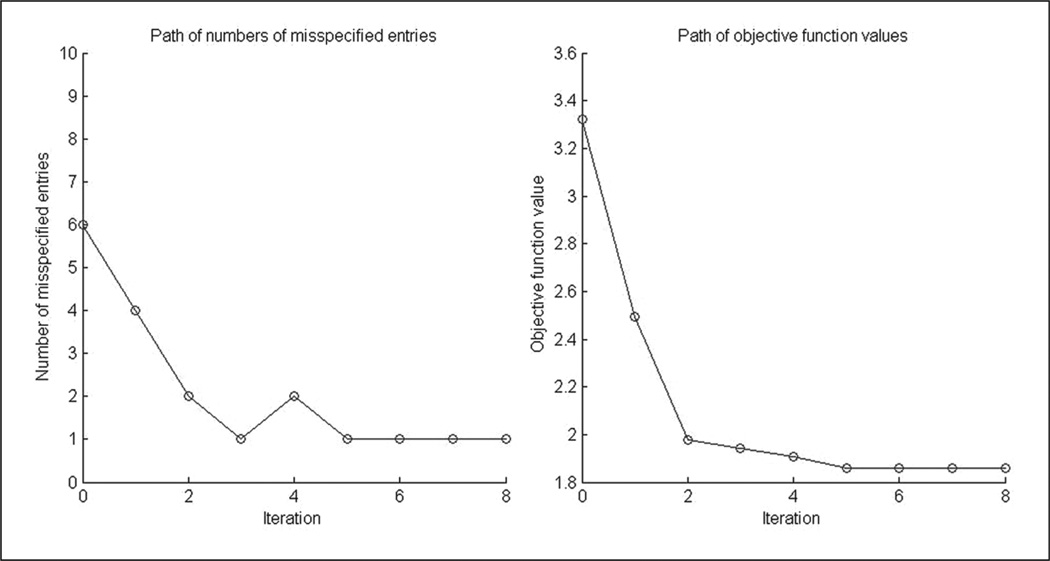
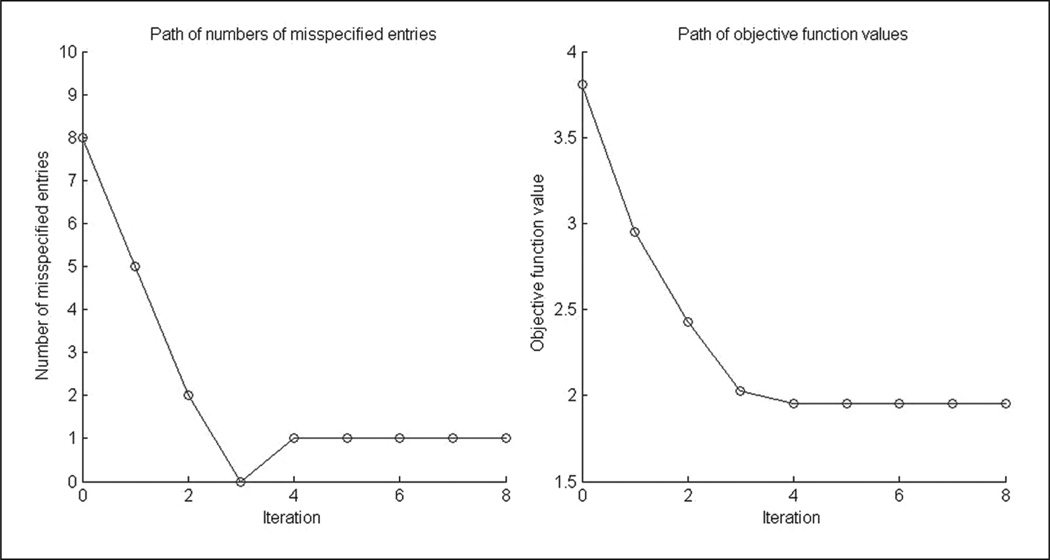
The data sets generated according to Q₂ and Q₃ with N = 500 when the estimator Q̂ did not perform as well as other situations are investigated. In particular, the cases when Q̂ ≠ Q are considered. It is observed that Q-matrices with more misspecified entries do not necessarily admit larger S values. In some cases, Q does not minimize the objective function S; nonetheless, S(Q) is not much larger than the global minimum inf_Q′ S(Q′). Figures 1 and 2 show two typical cases. For each of the two figures, two plots are provided. The x-axis shows the number of iterations of the optimization algorithm. The y-axis of the left plot shows the number of misspecified entries of Q(m) at iteration m; the plot on the right shows the objective function S(Q(m)). For the case shown in Figure 1, the algorithm just misses the true Q-matrix by one entry; for the case in Figure 2, the algorithm in fact passes the true Q-matrix and moves to another one. Both cases show that the true Q-matrix does not minimize the objective function S. In fact, the values of the S function have basically dropped to a very low level after three iterations. The algorithm tends to correct one misspecified item at each of the first 2 iterations. After Iteration 3, the reduction of the S function is marginal, and there are several Q-matrices that fits the data approximately equally well. For such situations where there are several matrices whose S values are close to the global minimum, careful investigation of all those matrices and selection of the most sensible one from a practical point of view are recommended.

Figure 1.

Results of a simulated data set with N = 500 and K = 5, for which the estimated Q-matrix does not pass the true one

Figure 2.

Results of a simulated data set with N = 500 and K = 5, for which the estimated Q-matrix passes the true one but does not converge to it

Motivated by this, a modified algorithm with an early stopping rule is considered, that is, the algorithm is stopped when the reduction of the S-function value is below some threshold. In particular, a threshold value of 4:5% of S(Q_m−1) at the m-th iteration is chosen. With this early stopping rule, the estimator for Q₂ and Q₃ can be improved substantially. The results based on the same samples as in Table 1 are shown in Table 2 which shows much high frequency of recovering the true Q-matrix.

Table 2.

The Results of Algorithm With an Early Stopping Rule for Q₂ and Q₃ Based on the Same Samples as in Table 1

	N = 500
	Q̂ = Q	Q̂ ≠ Q
Q = Q2	94	6
Q = Q3	70	30

When attribute profile α follows a nonuniform distribution

The situation where the attribute profile α follows a nonuniform distribution is considered. A similar setting as in Chiu et al. (2009) is adopted, where attributes are correlated and unequal prevalence. A multivariate probit model is assumed. In particular, for each participant, let θ = (θ₁, …, θ_k) be the underlying ability following a multivariate normal distribution MVN(0, Σ), where the covariance matrix Σ has unit variance and common correlation ρ taking values of 0.05, 0.15, and 0.25. Then the attribute profile α = (α₁, …, α_K) is determined by

$${\mathrm{\alpha }}_k=\{\begin{array}{cc}1& \mathit{\text{if}}{\mathrm{\theta }}_k\ge {\mathrm{\Phi }}^{-1}\left(\frac{k}{K+1}\right)\\ 0& \mathit{\text{otherwise}}\end{array}.$$

The other settings are similar as the previous simulations. The true Q-matrix given as in Equation 20 and K = 3 is considered. The slipping and guessing parameters are set to be 0:2. In all, 100 independent data sets are generated. Table 3 shows the frequency of Q₁ being recovered by the estimator (after applying a similar early stopping method introduced in the previous subsection). The more correlated the attributes are, the more difficult it is to estimate a Q-matrix. This is mostly because the samples are unevenly distributed over the 2^K possible attribute profiles, and thus, the “effective sample size” becomes smaller.

Table 3.

Numbers of Correctly Estimated Q₁ out of 100 Simulations With N = 500, 1,000, 2,000, and 4,000 for Different ρ Values

	N = 1,000		N = 2,000		N = 4,000
	Q̂ = Q1	Q̂ ≠ Q1	Q̂ = Q1	Q̂ = Q1	Q̂ ≠ Q1	Q̂ = Q1
ρ = 0.05	78	22	98	2	100	0
ρ = 0.15	71	29	94	6	99	1
ρ = 0.25	41	59	76	24	95	5

Estimation of the Q-Matrix With Partial Information

In this subsection, the situation where partial knowledge is available for the Q-matrix is considered. Consider one of the situations discussed in the next section. Consider a J × K Q-matrix where, among the total J items, the attribute requirements of J − 1 items are known. Of interest is learning the Jth item. In this simulation, let J = 2K + 1. The first 2K rows of Q are known to form two complete matrices; that is,

$$Q=\left(\begin{array}{c}{I}_K\\ I_K\\ V_J\end{array}\right),$$

where I_K is the identity matrix of dimension K and V_J is the row corresponding to the J-th item to be learnt. The corresponding estimator becomes

$$\widehat{Q}=\text{arg}\underset{Q\prime \in U_J(Q)}{\text{inf}}S(Q\prime ),$$

where U_J(Q) is defined in the Computations section, as the set of Q-matrices identical to Q for the first J − 1 rows.

With a similar setting to the previous simulations, the slipping and guessing parameters are set to be 0.2 and the population is set to be uniform, that is, p_α = 2^−K. For each combination of K = 3, 4, and 5, different V_J s are considered. A total of 100 independent data sets are generated. Table 4 shows the frequency of V_J being recovered by the estimator. One empirical finding is that the more “1”s V_J contains, the more difficult it is to estimate V_J.

Table 4.

Numbers of Correctly Estimated Q-Matrices Out of 100 Simulations With K = 3, 4, 5

	N = 250		N = 500		N = 1,000		N = 2,000
VJ	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q
(1 0 0)	91	9	98	2	100	0	100	0
(1 1 0)	82	18	97	3	99	1	100	0
(1 1 1)	70	30	83	17	100	0	100	0
	N = 500		N = 1,000		N = 2,000		N = 4,000
VJ	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q
(1 0 0 0)	91	9	98	2	100	0	100	0
(1 1 0 0)	84	16	94	6	100	0	100	0
(1 1 1 0)	71	29	87	13	99	1	100	0
(1 1 1 1)	39	61	62	38	94	6	100	0
	N = 1,000		N = 2,000		N = 4,000		N = 8,000
VJ	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q	Q̂ = Q	Q̂ ≠ Q
(1 0 0 0 0)	95	5	100	0	100	0	100	0
(1 1 0 0 0)	88	12	99	1	100	0	100	0
(1 1 1 0 0)	77	23	98	2	100	0	100	0
(1 1 1 1 0)	47	53	76	24	92	8	100	0
(1 1 1 1 1)a	29	71	37	63	56	44	88	12

^aIn the case of (1 1 1 1 1), Q̂ recovers Q 100 times when N = 12,000.

Discussions

Estimation of the Q-matrix for other DCMs

The differences among DCMs lie mostly in their ideal response structures and the distribution of the response vectors implied by the Q-matrices. The distribution of response vector R takes an additive form as in (3) if responses to different items are conditionally independent given the attribute profile α. With such a structure, one can construct the corresponding B-vectors that contain the corresponding conditional probabilities of the response vectors given each attribute profile α. Furthermore, a T-matrix is constructed by stacking all the B-vectors and an S-function is defined as the L² distance between the observed frequencies and those implied by the Q matrix. An estimator is then obtained by minimizing the S-function. Thus, this estimation procedure can be applied to other DCMs. For instance, one immediate extension of the current estimation procedure is to the DINO model.

Incorporating available information in the estimation procedure

Sometimes partial information is available for the parameters (Q, c, g, p). For instance, it is often reasonable to assume that some entries of the Q-matrix are known. Suppose the attributes are separated into “hard” and “soft” ones. By “hard,” it means those that are concrete and easily recognizable in a given problem, and by “soft,” it means those that are subtle and not obvious. It is then assumed that entries in columns which correspond to “hard” attributes are known. Alternatively, there may be a subset of items whose attribute requirements are known, while the item–attribute relationships of all other items need to be learnt, for example, when new items need to be calibrated according to the existing ones. Furthermore, even if an estimated Q-matrix may not be an appropriate replacement of the a priori Q-matrix provided by the “expert” (such as exam makers), it can serve as validation as well as a method of calibration using existing knowledge about the Q-matrix. When such information is available and correct, computation can be substantially reduced. This is because the optimization, for instance, that in Equation 18, can be performed subject to existing knowledge of the Q-matrix. In particular, once the attribute requirements of a subset of J − 1 items are known, one can calibrate other items, one at a time, using those known items. More specifically, consider a J × K matrix Q*, the first J − 1 items of which are known. The last item is estimated by Q̂ = arg sup_{Q′∈UJ(Q*)} S(Q′), that is, the S-function is minimized subject to the knowledge about the first J − 1 items. Note that this optimization requires 2^K evaluations of the S-function and is therefore efficient. Thus, to calibrate M items, the total computation complexity is O(M × 2^K), which is typically of a manageable order.

Information about other parameters such as c, g , and p can also be included in the estimation procedure. For instance, the attribute population is typically modeled to admit certain parametric form such as a log-linear model with certain interactions (Henson & Templin, 2005; von Davier & Yamamoto, 2004; Xu & von Davier, 2008). This type of information can be incorporated in to the definition of Equations 15 and 17, where the minimization and estimation of (c, g , p) can be subject to additional parametric form or constraints. Such addition information is helpful enhancing the identifiability of the Q-matrix.

Theoretical properties of the estimator

Under restrictive conditions, the theoretical properties of the proposed methods have been established in Liu et al. (2011), which assumes the following conditions hold. First, the guessing parameters for all items are known. In the definition of the objective function (Equation 17), ĝ is replaced by the true guessing parameters. Second, the true Q-matrix is complete, that is, for each attribute k, there exists an item that only requires this particular attribute. Equivalently, there exist K rows in Q such that the corresponding submatrix is diagonal. Together with a few other technical conditions, it is shown that with probability converging to 1, Q̂ (and Q̃) is the same as the true matrix Q up to a column permutation. Two matrices Q₁~Q₂ are written if they differ only by a column permutation. Permuting the columns of a Q-matrix is equivalent to relabeling the attributes. The data do not contain information about the specific meaning of the attributes. In this sense, the two matrices Q₁ and Q₂ cannot be distinguished based on the data if Q₁~Q₂. Therefore, results of the form P(Q̂~Q) → 1 are the strongest type that one may expect. In addition, the binary relationship “~” is an equivalence relationship. The corresponding quotient set is the finest resolution possibly identifiable based on the data.

Under weaker conditions, such as absence of completeness in the Q-matrix or the presence of unknown guessing parameter, the identifiability of the Q-matrix may be weaker, which corresponds to a coarser quotient set. One empirical finding is that Q-matrices with more diversified items tend to be easier to identify. For instance, one simple yet surprising example of a nonidentifiable Q-matrix is that

$$Q=\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 0\end{array}\right).$$

with slipping and guessing probabilities being 0:2 for all items and p_α = 1/4 for all α. This Q-matrix cannot be distinguished from

$$Q\prime =\left(\begin{array}{cc}1& 0\\ 0& 1\\ 1& 1\end{array}\right);$$

that is, one can find another set of slipping, guessing probabilities and $p_{\mathbf{\alpha }}^{\prime }$ that implies the same distribution of the response vector.

Model Validation

The proposed framework is applicable to not only the estimation of the Q-matrix but also the validation of an existing Q-matrix. If the Q-matrix is correctly specified and the assumptions of the DINA model are in place, then one may expect

$$|\mathrm{\beta }-T_{\widehat{c},\widehat{g}}(Q)p|\to 0$$

in probability as N → ∞. The above convergence requires no additional conditions to establish the consistency of Q̂ and Q̃ (such as completeness or diversified attribute distribution). In fact, it suffices that the responses are conditionally independent given the attributes and (ĉ, ĝ) are consistent estimators of (c, g). Then, one may expect that

$$\widehat{S}(Q)\to 0.$$

If the convergence rate of the estimators (ĉ, ĝ) is known, for instance, (ĉ − c, ĝ − g) = O_p(N^−1/2), then a necessary condition for a correctly specified Q-matrix is that S_{ĉ, ĝ}(Q) = O_p (N^−1/2). The asymptotic distribution of S depends on the specific form of (ĉ, ĝ). Consequently, checking the closeness of S to zero forms a procedure for validation of the existing knowledge of the Q-matrix and the DINA model assumption.

Sample size

As the simulation results show, the estimator misses the true Q-matrix with non-ignorable probability (more than 50%). This probability is substantially reduced (to 2%) when the sample size is increased to N = 1, 000. This suggests that a practically large sample N should be at least 30 × 2^K. Note that the K binary attributes partition the population into 2^K groups. To have the estimator yield reasonably accurate estimate, there should be on average at least 30 samples in each group. In addition, performance of the estimator maybe further affected by the underlying attribute distribution. For instance, if the attributes are very correlated, the probabilities of certain attributes will be substantially smaller than others. For such cases, estimation for some rows in the Q-matrix (those corresponding to the small probability attributes) will be less accurate. For such situations, the “effective sample size” is even smaller.

Computation

The optimization of S(Q) over the space of J × K binary matrices is a nontrivial problem. This is a substantial computational load if J and K are reasonably large. This computation might be reduced by splitting the Q-matrix into small submatrices. For typical statistical models, dividing the parameter space is usually not possible. The Q-matrix adopts a particular structure with which there is certain independence among items so that splitting the Q-matrix is valid. Similar techniques have been employed in the literature, such as chapter 8.6 in the K. Tatsuoka (2009) with large-scale empirical studies in that chapter. In particular, for instance, if there are 100 items, one can handle such a situation as follows. First, split the 100 items into 20 groups (possibly with overlapping items between groups if necessary); then apply the estimator to each of the 20 groups of items, respectively. This is equivalent to breaking a big 100 × K Q-matrix into 20 smaller matrices and estimating each of them separately. Last, combine the 20 estimated submatrices together to form a single estimate. Given that the computation for smaller scale matrices is much easier than those big ones, the splitting approach reduces the computation overhead. Nonetheless, developing a fast computation algorithm is an important line of future research.

Summary

As a concluding remark, it is emphasized that learning the Q-matrix based on the data is an important problem even if a priori knowledge is sometimes available. In this study, an estimation procedure of the Q-matrix is proposed under the setting of the DINA model. This method can also be adapted to the DINO model that is considered as the dual model of the DINA model. Simulation study shows that the estimator performs well when the sample size is reasonably large.