A microfluidic platform for generating large-scale nearly identical human microphysiological system arrays

Abstract

This paper reports a polydimethylsiloxane microfluidic model system that can develop an array of nearly identical human microtissues with interconnected vascular networks. The microfluidic system design is based on an analogy with an electric circuit, applying resistive circuit concepts to design pressure dividers in serially-connected microtissue chambers. A long microchannel (550, 620 and 775 mm) creates a resistive circuit with a large hydraulic resistance. Two media reservoirs with a large cross-sectional area and of different heights are connected to the entrance and exit of the long microchannel to serve as a pressure source, and create a near constant pressure drop along the long microchannel. Microtissue chambers (0.12 μl) serve as a two-terminal resistive component with an input impedance > 50-fold larger than the long microchannel. Connecting each microtissue chamber to two different positions along the long microchannel creates a series of pressure dividers. Each microtissue chamber enables a controlled pressure drop of a segment of the microchannel without altering the hydrodynamic behaviour of the microchannel. The result is a controlled and predictable microphysiological environment within the microchamber. Interstitial flow, a mechanical cue for stimulating vasculogenesis, was verified by finite element simulation and experiments. The simplicity of this design enabled the development of multiple microtissue arrays (5, 12, and 30 microtissues) by co-culturing endothelial cells, stromal cells, and fibrin within the microchambers over two and three week periods. This methodology enables the culturing of a large array of microtissues with interconnected vascular networks for biological studies and applications such as drug development.

Introduction

Recent advances in microfluidic technology have enabled the in vitro study of cellular behaviours in 3-D microenvironments.^1-2 By designing the microfluidic system to control both the flow and concentration profiles of the constituents, the mechanical and chemical environment in a small volume can be controlled temporally and spatially. Based on these unique capabilities, microsystems that simulate in vivo physiological microenvironments have been demonstrated for studying endothelial cell migration,³ angiogenesis,^4,5 flow in single capillaries,⁶ and flow in a network of endothelial-lined channels.^7-8 However, in order to perform large-scale parallel assays with 3-D tissues, it is critical to develop a microfluidic array platform with a user-friendly interface. Current microfluidic methodologies and systems (e.g. on-chip passive pumps) pose major limitations to grow 3-D microtissues in a high-throughput fashion. In these systems, considerable pressure loss takes place in a short amount of time (ranging from minutes to a day).^9-10 Constant adjustment of these passive pumps is needed to maintain the 3-D tissue microenvironments, both mechanically and chemically. On the other hand, active pumping systems are bulky and typically do not provide a user-friendly interface. Furthermore, the set up time and complex fluid manifolds make it challenging for large-scale applications.^11-12 For example, it is not possible to rapidly change medium through the microfluidic system without influencing or interrupting the created 3-D microenvironment. Thus, a microfluidic model system that can control 3-D microenvironments in large-scale arrays for long culturing times (weeks and above) and with a simple user-interface (as simple as changing the medium of a culture dish) would be a major stepping stone for in depth tissue engineering studies.

In this paper, we present an in vitro model system that can generate multiple human microtissues with a self-assembled and connected microvascular network that are nearly identical. The user interface is simple and can be used in regular tissue culture incubators. Instead of constructing an artificial substrate^6-8 or controlling concentration gradients of chemical stimuli,^4-5 our system provides proper microphysiological conditions to allow endothelial cells to self-assemble (vasculogenesis) into a vascular network by controlling interstitial flow. Interstitial flow ranging from 0.5 to 10 μm/s stimulates the vasculogenic process mechanically,^13-16 and also manipulates the spatial concentration of growth factors and morphogens.

The physiological microenvironment can be controlled using the concept of a pressure divider and a resistive circuit, applying principles used in the design of electric circuits.¹⁷ This analogy has been used by others to design proportional networks¹⁸ and serial networks¹⁹ for serial dilution, as well as pyramidal networks for creating concentration gradients.²⁰ A microfluidic resistance network has also been applied to culture cells in a large array,²¹ and to control the number of trapped cells for controlling the size of embryoid bodies.²² In the present work, multiple human microtissues with a continuous and connected (within and between chambers) microvascular network were developed over two to three weeks, and the physiological microenvironment was verified by finite element simulation. Using this microfluidic platform, metabolically active microtissues with perfused microvascular networks were demonstrated. The detailed experimental findings of the perfused vascular network were presented in a separate paper.²³ Herein, we present the design, modelling, and simulation of a microfluidic platform for producing arrays of nearly identical microtissues. The methodology of the presented platform forms the basis of new high-throughput tissue culture systems for studying tumour metastasis, drug discovery, vascular disease, and chemical toxicity.

Materials and methods

A Design of microfluidic network

The basic design is a long, square (100 μm by 100 μm) cross-sectional microchannel with culture media flowing at low Reynolds number (<<1) driven by a pressure difference between the source (P_S) and the end of the channel (P_E). A steady-state incompressible Navier-Stokes equation with homogeneous viscosity can be applied to derive the velocity and pressure distribution within the channels and the microtissue chambers. Since a long (relative to the size of the microchambers; 1 mm by 2 mm by 0.1 mm in diamond shape) microchannel was used in this study (550, 620 and 775 mm), a fully developed laminar flow could be assumed. Thus, the Hagen–Poiseuille law can be used to describe the fully developed laminar flow throughout the long microchannel, and is generalized to ΔP = R_TQ,¹⁷ where ΔP = P_S - P_E, and R_T and Q are the total hydraulic resistance and volumetric flow rate. The long microchannel can then be considered as a series of microchannel segments connected to each other, and each segment can be lumped into an equivalent hydraulic resistor R_i. This arrangement is analogous to Ohm's law of linear electric circuits. Furthermore, if the pressure gradient along the long microchannel is constant, pressure dividers in the microfluidic channel become analogous to voltage dividers in electric circuit design.

Using this configuration, the specific pressure drop across a microtissue chamber can be achieved by applying the design concept of a voltmeter.²⁴ To accurately measure the voltage drop across a component of an electric circuit, the voltmeter connects a large resistor in series with a Galvanometer in parallel to the electric component to measure the voltage across it. Thus, a very low current is drawn from the electric circuit without altering the voltages or currents in the circuit. Following the same design concept, the long microfluidic channel and the microtissue chamber can be considered as the electric circuit and the voltmeter, respectively. However, different from the purpose of a voltmeter, the “measured pressure” is used as the “driving pressure” for creating a physiological environment in the microtissue chamber.

To realize this design, the microtissue chamber was designed to have high input impedance with two communication pores, which served as a two-terminal resistive loading component. By connecting the communication pores at different positions along the long microchannel, the pressure drop across the microtissue chamber can be controlled using the concept of the voltage divider. Furthermore, since only a very small amount of media flows into the microtissue chamber, a constant pressure drop along the long microchannel is maintained. This concept has been applied previously to capture the full physiological range of mass transport in 3-D tissue cultures to study vasculogenesis.¹⁶

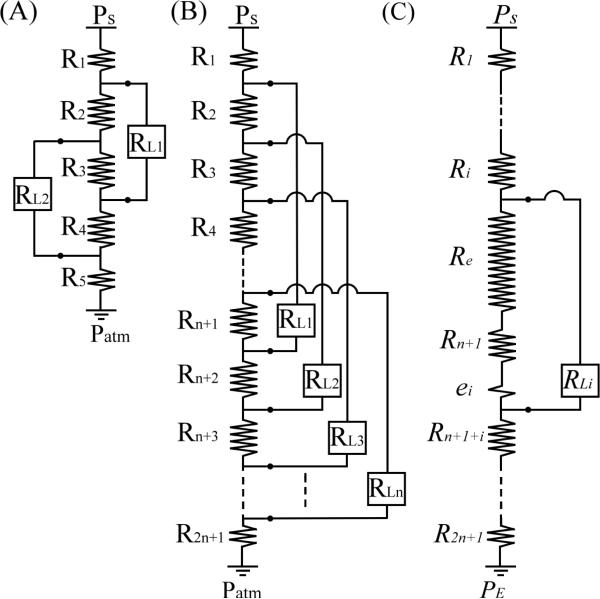
Figure 1(A) shows the basic design concept, where the constant pressure drop (ΔP_L1) across the first two-terminal component (microtissue chamber R_L1) can be written as:

$$\Delta P_{L1}=\frac{[(R_2+R_3)∕∕R_L]\Delta P}{R_1+[(R_2+R_3)∕∕R_L]+R_4+R_5},\text{where}$$ (1)

$$\Delta P_{L1}\approx \frac{R_2+R_3}{R_1+R_2+R_3+R_4+R_5}\Delta P,\text{when}[(R_2+R_3)∕R_L]<<1.$$ (2)

Similarly, the constant pressure drop of the second two-terminal component (microtissue chamber R_L2) can be written as:

$$\Delta P_{L2}=\frac{[(R_3+R_4)∕∕R_L]\Delta P}{R_1+R_2+[(R_3+R_4)∕∕R_L]+R_5},\text{where}$$ (3)

$$\Delta P_{L2}\approx \frac{R_3+R_4}{R_1+R_2+R_3+R_4+R_5}\Delta P,\text{when}[(R_3+R_4)∕R_L]<<1.$$ (4)

where // is a symbol to represent the equivalent resistance of resistors connected in parallel. If the microchannel segments are equal in length, then the resistance of R₂, R₃, and R₄ are equal in magnitude, R. The constant pressure drop applied to both microtissue chambers becomes identical and can be written as:

$$\Delta P_{Li}\approx \frac{2R}{R_1+3R+R_5}\Delta P,\text{when}R<<R_L,$$ (5)

where subscript i = 1 or 2. By using this design strategy, multiple microtissue chambers with high input impedance (R_L) can be connected evenly along a long microfluidic channel at equal distances from each other. As a result, the pressure drop across each microtissue chamber is identical. Figure 1(B) shows an equivalent circuit of n microtissue chambers connected to a long microchannel separated into 2n+1 hydraulic resistors, where R₁ and R_2n+1 are the hydraulic resistors of the entrance and the exit portions of the long microchannel, and R₂ = R₃ = • • • = R_2n = R. The pressure drop ΔP_L across each microchamber (R_Li) can be written as

$$\Delta P_L=[\left(\sum _{i=1}^n{R}_{i+1}\right)∕\left(\sum _{j=1}^{2n+1}{R}_j\right)]\Delta P=\frac{nR}{R_T}\Delta P,$$ (6)

where R_T is the total hydraulic resistance of the long microchannel, and ΔP = P_s - P_E. Note also that the same concept can be applied to create different pressure drops by connecting the two terminals of microchambers to a long microchannel with different separation distances. This enables a spectrum of physiological conditions to be realized on one microfluidic platform. An example verifying this alternate design and simulation is discussed in the supplementary document.

Fig. 1.

Equivalent circuits of (A) a microchannel connected by two external loadings (R_L1 & R_L2), (B) a long microchannel connected by n external loadings with equal pressure drop, and (C) the lumped resisters (R_e & e_i) between the i^th external loading.

With the design described here, only a limited number of microchambers can fit on the microfluidic platform due to the need to route the long microchannel around the microchambers. In order to bypass the need to maintain each segment of the long microchannel to be the same (R₂ = R₃ = • • • = R_2n = R), the hydraulic resistor R_n+1 between the two terminals of every microchamber can be increased to dominate the resistive circuit. For example, if R₃ is dominant [Fig. 1(A)], the difference between R₂ and R₄ can be ignored, and Eq (5) can be modified to describe pressure drops in both resistors.

$$\Delta P_{Li}=\frac{R_3+R+e}{R_1+R_3+R+e+R_5}\Delta P\approx \frac{R_3+R}{R_1+R_3+R+R_5}\Delta P,\text{when}{R}_L>>R_3>>R>e,$$ (7)

where e is the small variation of resistance generated from slight length variations between R₂ and R₄. With this design principle, the variation of hydraulic resistors of each segment of a large resistance circuit can be neglected. The pressure drop ΔP_Li of the i^th microchamber (R_Li) can be simplified to

$$\Delta P_{Li}=\frac{\sum _{c=i}^{n-1}{R}_{c+1}+R_{n+1}+\sum _{d=n+2}^{n+i}{R}_d}{\sum _{a=1}^n{R}_a+R_{n+1}+\sum _{b=n+2}^{2n+1}{R}_b}\Delta P=\frac{R_{n+1}+R_e+e_i}{R_T}\Delta P\approx \frac{R_{eq}}{R_T}\Delta P,$$ (8)

where R_e + e_i is a lumped resistor from other microchannel segments between two terminals [Fig. 1(C)], e_i is the small variation of resistance generated from slight length variations for each i^th microchamber, R_n+1 >> R_e ≈ (n-1)R > e_i, and R_eq = R_n+1 + R_e. By using this method, the pressure drop across all microchambers is nearly identical and a large array of nearly identical microchambers can be realized.

B High input impedance microtissue chamber design

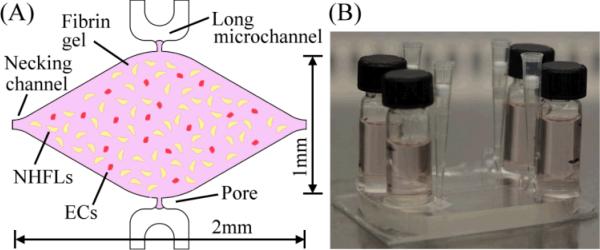
Figure 2(A) shows the basic design of the microtissue chamber, which is filled with a fibrin gel seeded with stromal cells (normal human lung fibroblasts, NHLFs) and endothelial cells (ECs) (see below) to form a 3-D tissue construct. Stromal cells are required for the development of stable microvessels.²⁵

Fig. 2.

(A) Conceptual illustrations of the high impedance 3-D microtissue chamber, where cell construct is formed by fibrin gel seeded with ECs and NHFLs, (B) a picture of the microfluidic platform and media reservoirs.

Based on our design methodology, two key requirements must be considered for the microchamber: 1) a high input impedance, and 2) a proper physiological microenvironment for initiating and maintaining vasculogenesis. The high input impedance was created by combining the hydraulic permeability of the porous matrix with small cross-section communication pores [30 μm by 100 μm, Fig. 2(A)]. The hydraulic impedance (R_Li) between the two communication pores was more than 50-fold higher than the total hydraulic impedance of the long microchannel R_T. This allowed the microtissue chamber to be connected to any two arbitrary positions along the long microchannel without influencing the resistive circuit. Since the pressure drop along the long microchannel served as a constant pressure source to the microtissue chamber, the pressure drop inside the microchamber was determined solely by the distance between the two communication pores along the microchannel. The constant pressure was achieved by using the large hydraulic resistance of the microchannel itself and two media reservoirs with a large cross-sectional area (12.5mm in diameter) connected to the entrance and exit of the long microchannel [Fig. 2(B)]. The maximum rate of pressure drop was only 20 μm/hr.

The physiological environment to stimulate vasculogenic process was created by manipulating the mass transport in the microtissue chamber. The mechanical stimulus, interstitial flow, was introduced and controlled by the pressure drop across the microtissue chamber. The nutrient supply was controlled by the diamond shaped and millimeter-sized microchamber [Fig. 2(A), height 100μm]. In order to control the oxygen supply, the thickness of the top PDMS was larger than 8 mm to provide a long diffusion length for oxygen,²⁶ and a 1 mm thick glass slide was bonded to the bottom PDMS sheet to block oxygen diffusion from the bottom. Thus, the majority of oxygen supplied to the 3-D cell construct was from the small communication pore positioned at the high pressure side, and delivered throughout the microchamber by the resulting interstitial flow. Moreover, to mimic physiological oxygen levels in adult tissue, the microplatform was cultured under 5% oxygen, thus maintaining the oxygen level inside the long microchannel and media reservoirs was at approximately 5%. Under this microphysiological environment, the 3-D cell constructs initiated vasculogensis and the formation of a continuous vascular network. Furthermore, the diamond-shaped microchamber provided a symmetrical chamber to balance the contractile force generated by the stromal cells in the microtissue. The necking channels shown in Fig. 2(A) were used to load the cell-matrix solution, and they also served to connect multiple microchambers in series for large scale loading. In addition, these necking channels also minimized the influence of vasculogenic stimuli from adjacent microchambers. Finally, the concept of a capillary burst valve was used for the design of communication pores to inhibit leaking of the fibrin solution into the microfluidic channel during loading as previously described.^{16, 23,27}

C Cell culture and cell-matrix preparation

Endothelial colony forming cell-derived endothelial cells (ECFC-ECs) were isolated from cordblood²⁸ and expanded on gelatin-coated flasks in endothelial growth medium-2 (EGM-2, Lonza). Normal lung human fibroblasts (NHLFs, Lonza) were cultured in fibroblast growth media (Lonza). ECFC-ECs (ECs, used at passages 4-7) and NHLFs (used at passage 3-5) were both grown in a 37 °C / 5% CO₂ / 20% O₂ incubator in 100% humidified air. The cell-matrix solution was prepared by dissolving bovine fibrinogen (Sigma-Aldrich) in DPBS (10 mg/ml), and ECs (5×10⁶ cells/mL) and NHLFs (2.5×10⁶ cells/mL) were suspended in the fibrinogen solution at a ratio of 2:1. Thrombin (50 U/ml) was then added to the cell-matrix solution for a final concentration of 3 U/ml. This allowed the gel to be fully polymerized within 30 minutes after being pipetted into the microtissue chambers. Fully supplemented EGM-2 media and 20% oxygen tension was supplied through the long microchannel for the first 12 hours. Then, the fully supplemented media was replaced by EGM-2 without VEGF and bFGF, and the levels of the media in the two media reservoirs were levelled to the constant pressure drop ΔP of the resistive network. The microfluidic platform was then placed in a 5% O₂ incubator for 2 to 3 weeks to allow cell constructs to develop into microtissues with a continuous vascular network. The media levels of the two media reservoirs were adjusted every other day to maintain a constant ΔP. The cell nuclei and developed microvessels were then fixed and stained with DAPI (nuclear) and anti-CD31 (ECs) antibody for imaging.

D Finite Element Simulation

As previously described, we used finite element simulation to estimate the hydraulic resistances of the designed microfluidic network.¹⁶ Briefly, COMSOL Multiphysics® 3.5a was used to simulate the mass transport induced in each microchamber. The incompressible Navier-Stokes equation was used to perform the steady-state analysis of the 3-D microfluidic models. No-slip boundary condition was applied to all surfaces except the entrance and exit of the long microchannel. Simulated velocity field was saved, and used to solve the time-dependent convection and diffusion problem for mass transfer. Dextran at 1 mol•m^–3 concentration (diffusion coefficient of 7×10⁻¹¹ m²/s) was simulated flowing from the entrance into the long microchannel. The dynamic viscosity and density of water were 0.748 mPa•s and 1 kg/m³. The porosity and permeability of fibrin gel were estimated to be 0.99 and 1.5×10⁻¹³ m² by using the Brinkman equation.^15-16 These parameters were retrieved from the best fitted parameters used in our previous published paper.¹⁶

E Microfabrication of the PDMS microfluidic platfrom

A 100 μm thick SU-8 100 (Micro Chem) was first spun on a cleaned silicon wafer [RCA-1 cleaned and 2% HF (Hydrofluoric acid) dipped]. A single mask photolithography process was then employed to create the master mold for the long microchannel, communication pores, and microchambers. The SU-8 molds were silanized with trichlorosilane (C₈H₄Cl₃F1₃Si), and a 10-to-1 mixture of PDMS prepolymer and curing agent (Dow Corning) was cast on the SU-8 mold. A cured PDMS microfluidic network was then demolded, and plasma bonded to a 1mm thick PDMS sheet that was itself plasma bonded to a 1 mm thick glass slide. Two glass vials with the bottom cleaved were then glued to the entrance and exit of the long microchannel using a PDMS mixture and then cured in an 85 °C oven for 4 hours. The finished microfluidic platform was then sterilized at 121 °C for 20 minutes.

Results and Discussion

A Multi-microtissue platform based on pressure divider

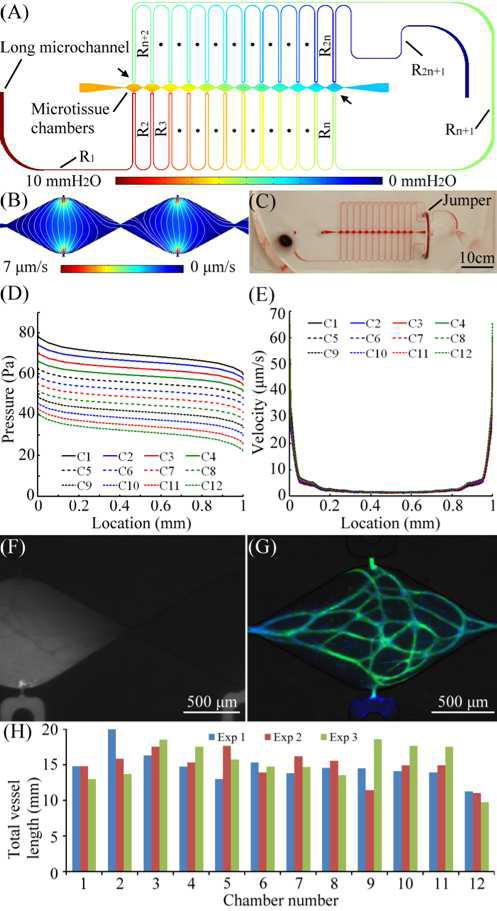
Figures 3(A) and 3(B) shows the design and finite element simulated pressure field of a microtissue platform based on the equivalent circuit presented in Fig. 1(B) and Eq. (6). A total of 12 microtissue chambers and a 550 mm long microchannel were used for this microplatform. The total pressure drop ΔP across the long microchannel was maintained at 10 mmH₂O (98.1 Pa). The simulated hydraulic resistances were R_T = 122.5×10¹² Pa•s/m³, R_i = 4.42×10¹²Pa•s/m³ with a standard deviation of 0.29×10¹² Pa•s/m³. The average hydraulic resistance R_Li of each microchamber was 5094×10¹² Pa•s/m³, which was large enough to have negligible influence on the resistive circuit of the long microchannel (i.e., R_Li >> R_T). Notice that the microchannel segment [R_n+1 specified between two arrows; Fig. 3 (A)]between all of the two communication pores of each microtissue chamber could not have a similar length to other microchannel segments (R_i) between adjacent microchambers, its hydraulic resistance was 3.56 times higher (15.75×10¹² Pa•s/m³). A microfluidic jumper made by a short silicone tube was added in its path to minimize the length of this segment [see the fabricated PDMS device shown in Fig. 3(C)]. In addition, this jumper allowed breaking up the long microchannel in to two, and had one segment on each side of the microtissue chambers. This design offered the capability to minimize the amount of shear stress exerted on exposed fibrin gel at the pores while media entered the long microchannel during loading. The jumper can also be removed for additional investigation of the system following the development of the human microtissues which required the pressure on either side of the microtissue to be decoupled.

Fig. 3.

(A) Microfluidic configuration and the simulated pressure field of the multi-microtissue platform, (B) simulated velocity field and pattern of interstitial flow (white lines), (C) the microtissue platform, (D) & (E) the pressure field and velocity field of each microtissue chamber, (F) the distribution of dextran flowing into a microchamber, (G) one of the 12 developed human microtissues, where microvascular network and nuclei were labeled with CD31 (green) and DAPI (blue). (H) total vessel lengths of each microtissue chamber from three independent experiments.

The calculated hydraulic resistance of the microchannel segment connected in parallel with each microchamber was 0.51R_T with standard deviation of 0.014. It is more than 80 times smaller than the input impedance of the microtissue chamber (R_Li). Thus, a very small amount of media flows into the microtissue chamber. This demonstrates the voltmeter analogy, as the pressure drop across each microtissue chamber was nearly identical. Figure 3(B) shows the simulated velocity field and pattern of interstitial flow (streamlines) of two consecutive microtissue chambers which have essentially identical velocity fields. Figures 3(D) and 3(E) are the simulated pressure field and velocity field of each microtissue chamber starting from the communication high pressure pore at (0 mm) and ending at the low pressure pore (1 mm). These data lines are numbered C1 to C12 sequentially to represent microtissue chambers from the left to right order shown in Fig 3(A). It is evident from Fig 3(D) that the magnitude of hydraulic pressure applied to each communication pore decreases with a near constant value while having a similar pressure gradient within the microtissue. This design results in a nearly identical velocity field in all the microtissue chambers [Fig. 3(E)]. Further, the range of interstitial flow was controlled in the range that was identified for stimulating vasculogenic process.^13-16 In Fig. 3(E), the velocity of interstitial flow is between 1.18 μm/s to 7.10μm/s over the majority of the microchamber (90%), but increases to 65 μm/s near the communication pores due the narrow opening of the pore and rapidly expanding field for flow. Since this central line has the highest velocity profile in the microchamber, the range of created interstitial flow in the majority of the chamber is controlled below 7.1 μm/s.

The effect of the necking channel was also verified by observing the velocity profiles of adjacent microtissue chambers [Fig 3(B)]. The velocity of mass transport in the necking channel was approximately 10⁻⁸ μm/s; thus, there is essentially zero communication between adjacent microchambers. This effect was verified experimentally by flowing fluorescein isothiocyanate (FITC) dextran (Sigma Aldrich, 70 kDa MW) in the long microchannel [Fig 3(F)]. The FITC dextran is transported from bottom to top direction, but not to the adjacent microtissue chamber. Note also that the microvessel network is visible as dark lines demonstrating that the 70 kDa MW FITC-dextran does not penetrate the microvessel through the basal surface. This phenomenon was also observed with 150 kDa dextran (data not shown).²³ Finally, all 12 microtissue chambers developed an interconnected of microvessels after 2-week and 3-week culture. Figure 3(G) shows the developed vascular network in two of the 12 microtissues. The microvascular network and nuclei were stained with CD-31 anti-body (green) and DAPI (blue). Figure 3(H) shows 3 independent experiments characterized by measuring the total vessel length of each microtissue chamber after a 3-week culture. The average total vessel length for the experiments are 14.85 mm (Exp1; standard deviation = 2.47 mm), 14.95 mm (Exp2; standard deviation = 2.3 mm), and 15.42 mm (Exp3; standard deviation = 2.68 mm), respectively.

B Multi-microtissue platform with a high hydraulic resistance

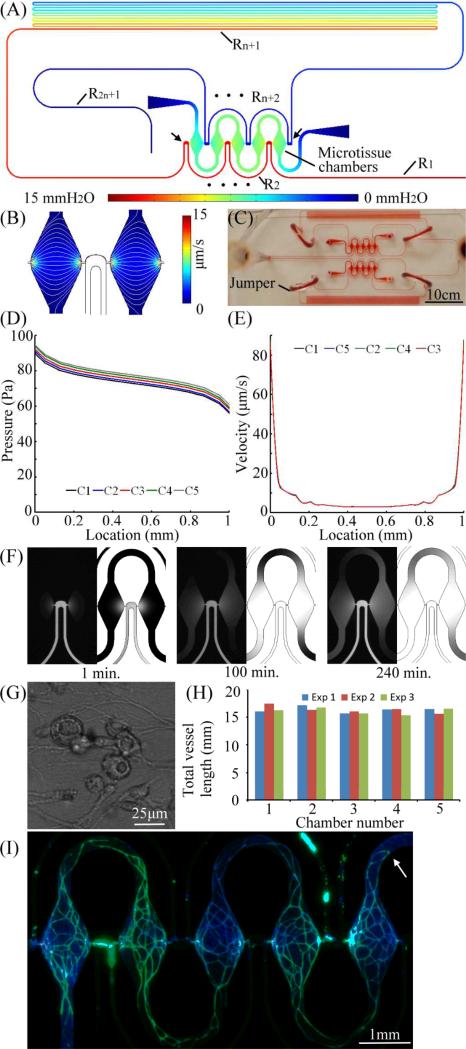
Figure 4 shows an alternate design, and finite element simulated pressure field, of a microtissue platform based on a large resistor R_n+1 [Eq. (8)]. Five microtissue chambers are connected along a 620 mm long microchannel. The length of the microchannel segment between the two communication pores of the first and last microtissue chambers was increased to 560 mm long such that a very large resistance separated them [R_n+1 of 92.6×10¹² Pa•s/m³, Fig. 4(A); specified between two arrows]. This was 62.4 times larger than each microchannel segment R_i, where R_e = 3.64×10¹² Pa•s/m³ and 0.9×10¹² < e_i < 1.1×10¹² Pa•s/m³ [Fig. 1(C)]. Since R_n+1 was nearly 93 times larger than e_i, the variations in hydraulic resistance between two terminals of each microchamber could be neglected. The approximation presented in Eq. (8) could then be applied. The calculated hydraulic resistance R_Li of each microchamber was 6273×10¹² Pa•s/m³ and thus was also significantly higher than the long microchannel. The calculated hydraulic resistance of the microchannel segment in parallel with each microchamber was 0.86R_T with a standard deviation of 0.0076. The total pressure drop ΔP of the long microchannel was maintained at 15 mmH₂O (147.1 Pa). The finite element simulated velocity field and the pattern of interstitial flow are shown in Fig. 4(B), and the microfabricated microplatform is shown in Fig. 4(C). The simulated pressure field and velocity field of each microtissue chamber are shown in Fig. 4(D) and 4(E), respectively. The simulated pressure field clearly demonstrates that by introducing a long segment of microchannel between the two communication pores of every microtissue chamber, a high hydraulic resistance R_n+1 is introduced and dominates the pressure divider [Eq. (8)]. The magnitude of pressure applied to the communication pores was thus nearly the same to every microtissue chamber, and a nearly identical velocity profile was created [Fig. 4(E)]. Note also that induced interstitial flow is within the identified physiological range for stimulating vasculogenesis.^13-16 Similar to the first microtissue platform (Fig. 3), the velocity of interstitial flow was controlled between 2.88 μm/s and 10.00 μm/s in 80% of the central area. The remaining 20% area was increased to 95 μm/s due to the narrow pore and rapidly enlarging cross-sectional area. The interstitial flow is controlled below 10 μm/s in the majority of the microchamber.

Fig. 4.

(A) Microfluidic configuration and the simulated pressure field of the multi-microtissue platform with a dominated hydraulic resistor R_n+1, (B) simulated velocity field and pattern of interstitial flow (white lines), (C) the microtissue platform, (D) & (E) the pressure field and velocity field of each microtissue chamber, (F) time-lapse distributions of dextran flowing into two microchamber and corresponding simulated results at 1, 100, and 240 min, (G) vacuoles found after 12-hour culture, and (H) total vessel lengths of each microtissue chamber from three independent experiments, (I) a fluorescent image of developed 5 human microtissues, where microvascular network and nuclei were labeled with CD31(green) and DAPI (blue).

The simulation results verified nearly equal pressure drop ΔP_L across each microchamber. To visualize the distribution of nutrient supply from the communication pore at high pressure, fluorescent dextran (70 kDa) was introduced into the long microchannel under identical ΔP. The time for dextran to fill the whole microchamber was approximately 10 hours [Fig. 4(F); left panel experimental results, right panel simulated result for each time point]. This result demonstrates that similar microphysiological environments can be created within microtissue chambers with negligible influence from adjacent chambers. Note that the U-shaped necking channel between microtissue chambers can significantly suppress the interaction from adjacent chambers. Evidence of initiation of vasculogenesis was verified by vacuole formation within 12-hours of culture [Fig. 4(G)].²⁹

Fully developed (i.e, continuous) microvascular networks were found in all microtissue chambers after two weeks in culture. Figure 4(H) shows 3 independent experiments characterized by measuring the total vessel length of each microtissue chamber after a 2-week culture. The average total vessel length for the experiments are 16.38 mm (Exp1; standard deviation = 0.55 mm), 16.41 mm (Exp2; standard deviation =0.68 mm), and 16.13 mm (Exp3; standard deviation =0.60 mm), respectively. Figure 4(I) shows a fluorescent image of the five microtissues developed in this microplatform, where microvessels and nuclei were stained with anti-CD31 (green) and DAPI (blue), respectively. Furthermore, the necking channels connected to the loading pipette tips (first and last microchamber) minimized the influence of the cell suspension remaining in the tips (white arrows). Thus, each microtissue chamber can be considered as an independent environment, and both cell and tissue level (i.e., microvessel network) phenotype can be investigated in parallel.

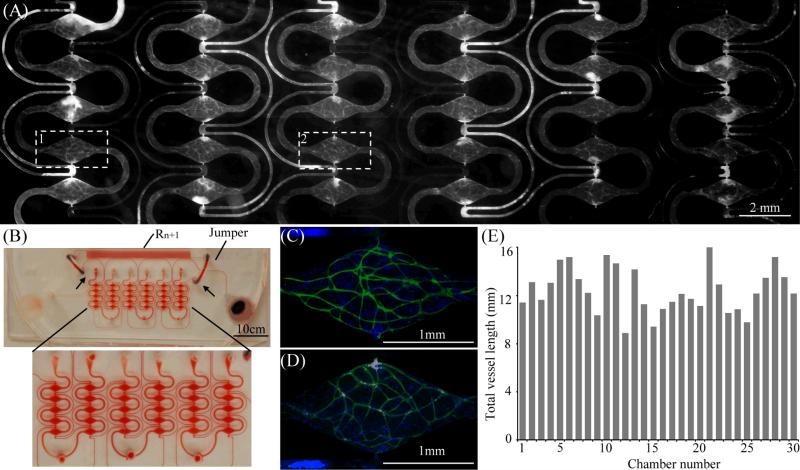
C A large-scale multi-microtissue platform

Utilizing the design criteria shown in Fig. 4 and Eq. (8), a microtissue platform with a larger array of 30 microtissue chambers was designed. The total length of the long microchannel was 775 mm. Fig. 5(A) shows a fluorescent image of a 2-week cultured microtissue array taken by a digital camera. The developed microvascular network was labelled with CD31 anti-body (white). Fig 5(B) shows the microfabricated microfluidic platform (filled with red dye for demonstration) and a zoomed-in image of 30 microtissue chambers. The 30 microtissues were created by 3 separate loadings of cell-matrix suspensions from the 3 bottom loading holes. With this microplatform, 30 microtissues with a continuous vascular network were formed after two weeks in culture [Fig. 5(A)]. Figures 5(C) and 5(D) represent two of the microchambers at higher magnification (white rectangles in Fig 5A labeled “1” and “2”). Figure 5(E) shows the measured total vessel length of each microtissue chamber shown in Fig. 5(A). The average total length is 12.46 mm and the standard deviation is 1.87mm. This experimental result demonstrated that a larger array of microtissue chambers with nearly identical physiological environmentscan be created simultaneously to create nearly identical microvessel networks in parallel.

Fig. 5.

(A) A Fluorescent image of the microtissues developed by the high throughput microtissue platform, where the microvessels were stained with CD-31. (B) The high throughput mictotissue platform, (C) and (D) are fluorescent images of two microtissues (4X magnification), where microvascular network and nuclei were labeled with CD31 (green) and DAPI (blue), (E) total vessel lengths of each microtissue chamber.

Conclusions

We present a novel microfluidic model system that can develop nearly identical multiple human microtissues in parallel on a PDMS microplatform by controlling the mechanical and chemical microphysiological environment. For our application, we used the device to create self-assembled and continuous microvascular networks over two and three weeks in culture in three different designs that consisted of 5, 12, and 30 microtissues. The experimental and theoretical results demonstrate that the platform design can control the major determinants of vasculogenesis [interstitial flow in the physiological range (0.5 to 10 μm/s)] in every microtissue chamber.^13-16

The microfluidic system is flexible and can be generalized to create a host of physiological environments for tissue engineering applications. First, the nearly identical mechanical and chemical environments can manipulated and controlled to create parallel investigation of microtissue development. Second, the composition of the cell-matrix suspension can be selectively seeded to investigate the impact of cell type or matrix composition. Third, as suggested in the supplementary document, the magnitude of the pressure gradient in microchambers need not be identical in all chambers, but can be manipulated to generate different physiological conditions. This can be realized by utilizing a long microchannel with different separation lengths. Using this method, 3-D cellular behaviours in response to different physiological conditions can be investigated simultaneously on one microfluidic platform. This method is simple, and can be easily adapted to essentially all current microfluidic systems for creating a specific microphysiological environment for 3-D tissue engineering studies.

The platform design is based on an analogy between an electrical circuit and a microfluidic network. Two microfluidic components were used to create the microfluidic model system. The first is a microchannel that spans several hundred millimeters and serves as a constant pressure source for each microtissue chamber. The second is the millimeter-sized microtissue chamber with high input impedance. The microchamber draws a very small flow while using the measured pressure drop to control the internal microenvironment. The method introduced here provides a simple and straightforward means to createnearly identical microphysiological environments in an array of microtissue chambers. This microplatform and its application can potentially impact such fields as tumour metastasis, drug discovery, vascular disease, and chemical toxicity.