Using Discrete-time Event History Fertility Models to Simulate Total Fertility Rates and Other Fertility Measures

Abstract

Event history models, also known as hazard models, are commonly used in analyses of fertility. One drawback of event history models is that the conditional probabilities (hazards) estimated by event history models do not readily translate into summary measures, particularly for models of repeatable events, like childbirth. In this paper, we describe how to translate the results of discrete-time event history models of all births into well-known summary fertility measures: simulated age- and parity-specific fertility rates, parity progression ratios (PPRs), and the total fertility rate (TFR). The method incorporates all birth intervals, but permits the hazard functions to vary across parities. It also can simulate values for groups defined by both fixed and time-varying covariates, such as marital or employment life histories. We demonstrate the method using an example from the National Survey of Family Growth (NSFG) and provide an accompanying data file and Stata program.

Event history models, also known as hazard models, are commonly used in analyses of fertility. Provided that retrospective or prospective fertility histories are available, such models offer many advantages over analyses of cross sectional measures (such as children ever born). Event history models potentially provide richer information about the age at first birth and subsequent birth spacing because they account for both the occurrence and timing of births. They also appropriately handle right censoring because they take into account the duration of exposure to the risk of childbearing, thus permitting analyses to include women at all stages of their reproductive lives. Finally, they permit researchers to incorporate critical time-varying predictors, such as employment, educational, and marital statuses, into analyses.

One drawback of event history models, however, is that they are difficult to translate into meaningful information about lifetime childbearing or birth spacing. Such information is important for those interested in making comparisons across groups, cohorts, or time periods, while controlling for compositional differences related to fertility, such as marital status, age, or education. In this paper, we show how to convert the results of pooled discrete-time event history models of all births into well-known fertility measures, including simulated age- and parity-specific fertility rates, parity progression ratios (PPRs), and total fertility rates (TFRs). Age- and parity-specific fertility rates provide detailed information on the number and timing of births across the reproductive life course. PPRs are important indicators of spacing and stopping behaviors and childlessness. Finally, the TFR is the most commonly-used measure of fertility. It provides an estimate of the total number of children the average woman will have in her reproductive lifetime if she experienced all current age-specific fertility rates.

The key advantage of the method we present is that it permits researchers to compare groups on these common-used fertility measures while statistically controlling for differences on other characteristics associated with childbearing. In doing so, the method provides a comprehensive picture of women’s fertility experiences across the entire reproductive life course. This goes beyond most descriptive and multivariate fertility analyses, which tend to be confined to births of specific parities (e.g., first births) and only rarely consider all births (e.g., first, second, third births, etc.) simultaneously (Guzzo and Hayford 2011; Schellekens 2009; Carter 2000; Brand and Davis 2011; Goldstein, White, and Goldstein 1997; and White et al. 2008). Additionally, the method can simulate values for groups defined by both fixed and time-varying covariates. This is helpful for assessing how life course trajectories can delay (or accelerate) births and eventually reduce (or increase) completed fertility. For example, one could estimate the effects of delayed marriage on completed fertility by comparing simulated TFRs for women who married at age 35 with their peers, who are similar on all characteristics except that they married at age 20.

We build on prior methods developed for estimating multistate life tables based on event history models (e.g., Cai et al. 2010; Lee and Rendall 2001). Of particular relevance, Retherford and his colleagues (2010) demonstrated how to use complimentary log-log event history models to estimate PPRs, the total marital fertility rate, and the TFR for women in the Philippines by parity and across periods and cohorts. Our major contribution is to provide a highly accessible exposition of these methods for readers who are familiar with event history analysis and descriptive fertility measures, but may be less cognizant of the conceptual linkages between event history models, life tables, and common summary fertility measures. Going beyond prior work, we also offer ideas about how to model multiple parities, incorporate time-varying variables as predictors, simulate the full range of fertility measures (ASFRs, TFRs, PPR, and parity-specific ASFRs and TFRs), and estimate bootstrapped standard errors for these fertility measures. Throughout the article, we illustrate the methods with data and analyses on fertility differentials by race and marital status in the United States. While informative, the examples are not intended to stand on their own as substantive contributions to the literature. Importantly, our simulated results are consistent with national estimates produced by the National Center for Vital Statistics

In what follows, we first describe the data and measures used in our examples. Next, we explain how single-event event history models are related to single-decrement life tables using an illustration drawn from the National Survey of Family Growth (NSFG). This section provides an orientation on the linkage between event history analysis and single-decrement life tables, but can be skipped by readers who are already familiar with these methods (see also Singer and Willett (2003) and Teachman and Hayward (1993) for more rigorous treatments of these methods). We next discuss the extension of single-decrement methods to multiple parities. Again, we illustrate the method with an example from the NSFG. Consistent with our goal for accessibility, we rely on one of the most common event history models used and promoted by population scientists: the discrete-time model estimated with logistic regression (Allison 1995; Singer and Willett 2003). Nevertheless, it would be possible to develop a similar approach for other kinds of event history models (e.g., Cox Models, complimentary log-log, etc.). Although we discuss the method as relevant for fertility, it could be applied to any event history analysis in which multiple events per individual are modeled (e.g., marriages, arrests, poverty spells, etc.).

Data and Measures

To simulate fertility measures from event history model estimates, it is necessary to model the occurrence and timing of births. Therefore, a fertility history recording the precise timing of each birth is required (ideally month and year), such as is available in the NSFG or the Demographic and Health Surveys. In data sources like these, older women are able to report a complete fertility history, but younger women may report a partial or unfinished fertility history. Younger women may have more children in the future, but they are right-censored by the survey. This is perfectly acceptable because event history models take into account the fact that older women spent more time at risk of childbearing than younger women.

To generate the examples provided in this paper, we used the continuous collection of the NSFG (2006–2010). We used NSFG over other data sets because the NSFG is a nationally representative, cross-sectional survey of reproductive age women in the United States conducted by the National Center for Health Statistics (NCHS) and is the principle source of fertility behavior in the United States. As the primary fertility survey in the United States, the NSFG collects information on the respondent’s race/ethnicity, complete fertility histories, and other socio-demographic controls such as marriage history, and serves as the national source of “statistics on family formation, growth, and dissolution” (CDC 2012ⁱ). When available, the recoded variables, rather than the raw variables, were used in the analysis as recommended by the NCHS (Lepkowski et al. 2010).

For simplicity, we limited the sample to two major racial-ethnic groups in the United States, U.S.-born non-Hispanic black and white women. The analytic sample was further limited to those with full information on the sample variables. After listwise deletion, the final sample included 7,164 women. We then organized the analytic data file into “person-year” records, with one data record for each year of age a woman is at risk of having a birth (i.e., from age 15, the earliest reported age at first birth, to age 44 or age at censorship/survey date, whichever is younger; N = 120,825 person-years).

Weighted means for the variables used in the analysis are shown in Table 1. The dependent variable is a dichotomous indicator of whether or not a woman had a single live birth in the age interval, x to x+1ⁱⁱ. We selected at least one time-constant and one time-varying predictor to illustrate how the method handles these different types of independent variables. Each are critical predictors of fertility. Time-constant predictors assume the same value across all person-year records for an individual, and for our examples, we selected race (non-Hispanic black and white), and religion (no religion, Catholic, Protestant, and other). Values for time-varying predictors may change across ages for a given individual. We included three time-varying predictors in our examples: age, marital status, and educational attainmentⁱⁱⁱ.

Table 1.

Weighted Sample Means (by Age for Time-varying Variables)

	Birthsa (% per year)	Years of Educa	Marrieda (%)	% Black	Religious Affiliation (%)
					No Religion	Catholic	Protestant	Other Religion
All Ages	7.1	12.6	29.9	17.1	17.8	17.9	56.7	7.5
15	0.9	8.0	0.1
16	2.1	9.0	0.3
17	3.8	9.9	0.7
18	5.8	10.9	1.9
19	7.4	11.7	4.6
20	9.1	12.4	8.8
21	8.9	12.9	13.4
22	9.5	13.3	18.4
23	9.4	13.7	23.6
24	10.1	13.9	29.6
25	9.1	14.0	36.0
26	10.4	14.0	40.9
27	9.9	14.0	46.4
28	10.9	14.1	50.6
29	10.7	14.0	52.6
30	10.8	14.0	56.7
31	10.1	14.0	59.5
32	9.4	14.0	61.6
33	9.1	14.0	62.4
34	7.0	14.0	63.7
35	6.5	13.9	63.9
36	5.1	13.9	65.2
37	4.1	13.9	66.1
38	2.4	13.9	65.2
39	2.9	13.8	65.5
40	0.9	13.7	64.0
41	0.7	13.6	63.9
42	1.0	13.7	62.4
43	0.1	13.8	61.6
44	0.0	13.9	61.9

^aTime-varying variable

Data: National Survey of Family Growth 2006–2010

Sample: U.S.-born non-Hispanic black and white women age 15–44 (7,164 women; 120,825 person-year records)

Age is coded in five-year categories: 15–19; 20–24; 25–29; 30–34; 35–39; and 40–44. We used five-year age categories, rather than single-year, because five-year age groups are commonly used when calculating age-specific fertility rates. Additionally, our data did not include enough cases to yield stable estimates for single-year age groups, particularly at higher parities. Nevertheless, it would be possible to use single-year age groups or alternative age classifications for larger samples, particularly for the “additive” model (see “Step 1: Model Estimation” below). We provide a brief discussion of the effects of age coding in the Conclusion and provide an Appendix with a more detailed description of how the results change when we coded age in single- rather than five-year categories. Marital status is a dichotomous indicator of whether or not a woman is married at the beginning of the interval; any status other than married is coded zero. Years of education are the number of completed years of formal school (not counting preschool) a woman has received at the beginning of each person-year interval.

Section 1: Hazard Models and Life Tables for Non-Repeated Events

Event history models are conceptually linked to life tables. Life tables were first developed by demographers to estimate how mortality reduces the size of a cohort as it ages. Event history models of non-repeated events, like first births, are directly analogous to single-decrement life tables (Singer and Willett 2003). In both, cohorts are conceptualized as being exposed to risk of an event. The age pattern of this risk in an event history analysis is referred to as the hazard function. It is notated as q_x in a life table as the probability of the event at age x. Once cohort members experience the event in question, such as a first birth, they exit the risk pool, leaving behind an ever-diminishing group at risk. The survival function in an event history analysis represents the depletion of the cohort by age, or the proportion remaining at risk of the event. It is notated as l_x in a life table. Finally, the number of events, or unconditional probability of the event, experienced by the cohort at each age x is denoted as d_x in a life table.

Event history models estimate the associations of predictors with the timing and occurrence of events, a key advantage over life tables. That is, they allow us to estimate how the hazard of the event differs across subgroups (such as marital status) or varies across values of a covariate (such as education), in addition to producing standard errors around the estimates. Event history model coefficients specifically estimate the association of predictors with the hazard of the event, which is the conditional probability of the event occurring in a narrow time window (typically a year) given that it has not already occurred. For example, in a model of first births, the hazard is the probability of a first birth occurring at age x given that the woman has not yet had a birth. Because people are often interested in lifetime patterns of fertility (e.g., median age at first birth), researchers often use event history life tables to transform event history coefficients into simulated birth histories for selected groups.

To illustrate, we estimated a simple discrete-time hazard model (Allison 1989) of first birth based on fertility histories in the NSFG, and then used the results to generate a life table of first birth. The hazard model of first birth is a logistic regression model predicting whether a first birth occurred in each person-year interval. As noted above, we used logistic regression because of its wide use by demographers for modeling discrete outcomes (DeMaris 1992) and event history analysis (Allison 1989; Singer and Willett 2003). The analytic sample is confined to person-year records falling within the first birth interval (i.e., from age 15 until age at first birth, age 44, or censorship by the survey, whichever comes first). The estimated model coefficients are (from the 1^st parity fully-interactive model in Table 3):

$$\begin{array}{l}\text{logit}(\text{pr}[\text{first}\text{birth}\text{age}\text{x}\mid \text{no}\text{earlier}\text{birth}])=-3.29+0.45(\text{age}20-24)+0.17(\text{age}25-\\ 29)+0.11(\text{age}30-34)-0.53(\text{age}35-39)-2.31(\text{age}40-44)+0.00(\text{no}\text{religion})-\\ 0.20(\text{Catholic})-0.19(\text{other}\text{religion})+0.75(\text{black})-0.02(\text{education})+1.84(\text{married}).\end{array}$$

Table 3.

Additive, partially-interactive, and fully-interactive models of fertility

	Additive Model	Partially-interactive Model	Fully-interactive Model
			1st parity	2nd parity	3rd+ parity
Age 15–19 (ref.)
Age 20–24	0.52 ***	0.52 ***	0.45 ***	−0.10	0.44
Age 25–29	0.24 **	0.42 ***	0.17	−0.45 **	−0.21
Age 30–34	0.01	0.43 ***	0.11	−0.66 ***	−0.58
Age 35–39	−0.79 ***	−0.18	−0.53 **	−1.18 ***	−1.63 ***
Age 40–44	−2.63 ***	−1.93 ***	−2.31 ***	−2.83 ***	−3.67 ***
First Parity (ref.)
Second Parity	0.65 ***	1.32 ***
× 20–24		−0.59 ***
x 25–29		−0.84 ***
× 30–34		−1.04 ***
× 35–39		−0.96 ***
× 40–44		−0.85
Third+ parity	−0.17 **	0.60
× 20–24		−0.16
× 25–29		−0.81 *
× 30–34		−1.22 **
× 35–39		−1.69 ***
× 40–44		−1.95 **
Protestant (ref.)
No Religion	−0.04	−0.05	0.00	−0.11	−0.09
Catholic	−0.09	−0.09	−0.20 **	0.02	0.16
Other Religion	0.02	0.04	−0.19 *	0.06	0.71 ***
Black (vs. NH-white)	0.55 ***	0.52 ***	0.75 ***	0.12	0.34 ***
Years of Education	0.00	0.00	−0.02	0.03	0.03
Married	1.24 ***	1.21 ***	1.84 ***	0.85 ***	0.23 *
Intercept	−3.38 ***	−3.41 ***	−3.29 ***	−2.16 ***	−2.74 ***
N	120,825	120,825	78,428	20,096	22,301

Model Comparisons	df	Chi-square	p-value
Partially-interactive vs. Additive	10	290	0.000 ***
Fully-interactive vs. Partially-interactive	10	656	0.000 ***

^*p<0.05

^**p<0.01

^***p<0.001

Data and Sample: See Table 1.

Using race as an example, the results suggest that the hazard, or conditional probability, of birth among black women is 2.11 times as high as it is among white women (exp(0.75)=2.11).

To express this difference in more concrete terms, we used the model estimates to generate a life table for two hypothetical groups: black and white women with the mean marital status, educational attainment, and religious affiliations. This involved two steps. First, we generated predicted hazards for these two groups across all ages, shown in the q_x columns in Table 2. These were calculated by substituting values (i.e. weighted age-specific mean years of education, marital status, and religion, shown in Table 1) into the event history model (shown in Table 3) to obtain predicted log-odds. The predicted log-odds are then transformed into predicted hazards (i.e., q_x). For example, for a black woman age 15, the predicted hazard is 0.060, and is obtained as follows:

$$\begin{array}{l}\text{Predicted}\text{log}-\text{odds}=-3.29+0.00(0.178[\text{proportion}\text{no}\text{religion}])-0.20(.179\\ [\text{proportion}\text{Catholic}])-0.19(0.075[\text{proportion}\text{other}\text{religion}])-0.02(8[\text{mean}\\ \text{education}\text{at}\text{age}15])+1.84(0.001[\text{proportion}\text{married}\text{at}\text{age}15])+0.75[\text{black}]=-2.75;\\ \text{Predicted}\text{hazard}=exp(-2.75)/(1+exp(-2.75))=\mathrm{0.060.}\end{array}$$

Table 2.

Life table of first birth, simulated for black and white women with mean educational attainment, marital status, and religious affiliations

Age	White Women			Black women
	Hazard of 1st birth qx	Proportion at risk of 1st birth Ix	Unconditional Prob. of 1st birth dx	Hazard of 1st birth qx	Proportion at risk of 1st birth Ix	Unconditional Prob. of 1st birth dx
15	0.029	1.000	0.029	0.060	1.000	0.060
16	0.029	0.971	0.028	0.059	0.940	0.056
17	0.029	0.942	0.027	0.059	0.884	0.052
18	0.029	0.915	0.026	0.059	0.832	0.049
19	0.030	0.889	0.026	0.061	0.783	0.048
20	0.049	0.863	0.042	0.097	0.736	0.072
21	0.052	0.821	0.043	0.104	0.664	0.069
22	0.057	0.778	0.044	0.112	0.595	0.067
23	0.061	0.734	0.045	0.121	0.528	0.064
24	0.068	0.689	0.047	0.133	0.464	0.062
25	0.058	0.642	0.037	0.116	0.402	0.046
26	0.064	0.604	0.038	0.125	0.356	0.045
27	0.070	0.566	0.040	0.137	0.311	0.043
28	0.075	0.526	0.039	0.146	0.269	0.039
29	0.078	0.487	0.038	0.150	0.230	0.035
30	0.078	0.449	0.035	0.152	0.195	0.030
31	0.082	0.414	0.034	0.159	0.165	0.026
32	0.085	0.380	0.032	0.164	0.139	0.023
33	0.086	0.348	0.030	0.166	0.116	0.019
34	0.088	0.317	0.028	0.170	0.097	0.016
35	0.049	0.289	0.014	0.098	0.080	0.008
36	0.050	0.275	0.014	0.100	0.073	0.007
37	0.051	0.261	0.013	0.102	0.065	0.007
38	0.050	0.248	0.012	0.100	0.059	0.006
39	0.051	0.236	0.012	0.101	0.053	0.005
40	0.009	0.224	0.002	0.018	0.047	0.001
41	0.009	0.222	0.002	0.018	0.047	0.001
42	0.008	0.220	0.002	0.018	0.046	0.001
43	0.008	0.218	0.002	0.017	0.045	0.001
44	0.008	0.216	0.002	0.017	0.044	0.001
45		0.214			0.043

Data and Sample: See Table 1.

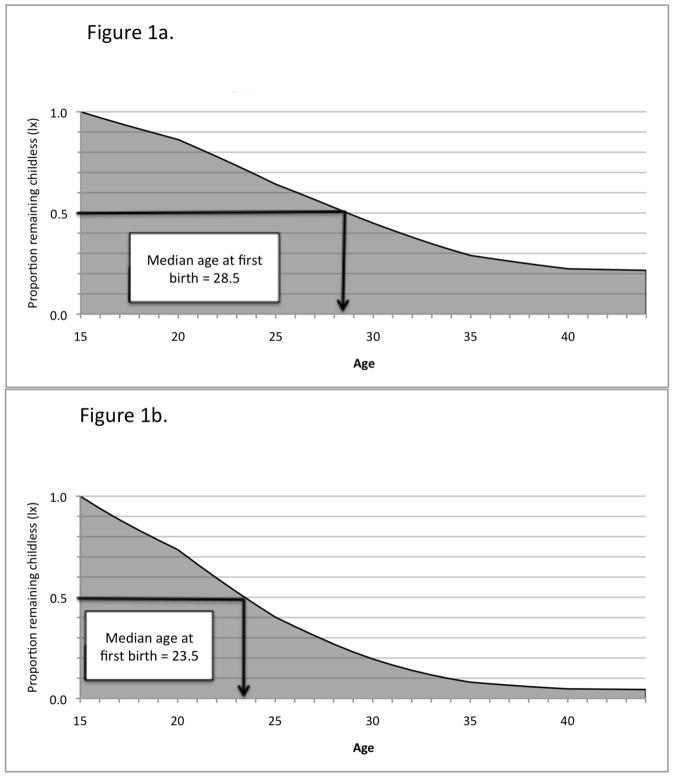
Second, we used the predicted hazards to calculate the proportion of women estimated to remain at risk of the event by exact age x, shown in the l_x column in Table 2 and graphed in Figure 1. At very young ages (e.g., 15), all are childless, so l₁₅ is set equal to 1.0. The expected proportion of women having births from age x to x+1 is given in the d_x column, and it is calculated as the product of l_x and q_x: d_x = l_x * q_x. As the cohort ages from one year to the next, the proportion remaining at risk declines by the proportion who had a birth the year before: l_x+1 = l_x − d_x. Finally, the proportion estimated to have had a first birth by age x is 1 − l_x; and those remaining childless is l_x

Figure 1.

Figure 1a. Simulated proportion of white women who remain childless with mean education. marital status, and religious affiliation

Figure 1b. Simulated proportion of black women who remain childless with mean education. marital status, and religious affiliation

The results show that if women experienced the predicted hazards for women with the mean marital status, educational, and religious affiliation, the simulated median age of first birth (i.e., the age at which half the cohort has had a first birth) would be about 28.5 for whites and 23.5 for blacks. Median rather than mean age at first birth is preferred because not all birth times are observed (Singer and Willett 2003:337). Additionally, among white women, 13.7% (1−.863) would have a birth prior to age 20, 35.8% by age 25, and 78.5% by their 45^th birthday, leaving 21.4% childless by age 45^iv. Among black women, the respective percentages would be much higher: 26.4%, 59.8%, and 95.7%, leaving only 4.3% childless by their 45^th birthday.

It is important to recognize that these estimates of childlessness differ from national vital statistics estimates because they are “standardized” rather than observed. To demonstrate this point, we compiled period measures of the percentage childless published by NCHS for non-Hispanic white and black women for 2010, 2000, and 1990 (Martin et al. 2002; Martin et al. 2012; NCHS 1994). This two-decade period roughly corresponds with the time the women in our sample were having children. The published results show average childlessness rates of 20% for non-Hispanic white women and 19% for black women. This is similar to our simulated rates for white women (21.4%),but much higher than our simulated rates for black women (4.3%). The reason is that the simulation assigns mean levels of the control variables to each group. In particular, black women are much less likely to marry than average^v, and marriage is positively associated with fertility. If black women were given average marital status patterns, this would result in much lower rates of childlessness than observed. In fact, when we simulate levels of childlessness for black women alone and assign them black means on the control variables, we obtain much a higher rate (16%).

Section 2: Hazard Models and Life Tables for Repeated Events

The methods described above work for non-repeated events like first births, but cannot be directly applied to repeatable events, like all births. The reason is that, in hazard models of multiple parities, the underlying life table model is no longer a single-decrement process. Rather, the underlying life table has multiple, sequenced events: women can have several births, but do not enter the “risk set” of having the next higher order birth unless they have already had earlier parity births. Because of their underlying complexity, the hazard in models of multiple parities has an even narrower interpretation than in models predicting only first births. It is conditional not only on not already having had a j^th birth, but also on already having had the previous (j-1^th) birth. Therefore, the coefficients provide an estimate of a group’s relative risk of having a birth among those in the same age/parity window. Models of repeated events can be used to generate a large set of predicted hazards of having a birth by both age and parity. However, translating these predicted conditional probabilities into overall assessments of the timing or total number of births is not straightforward and can limit their utility in research. In what follows, we outline a methodology for doing this and provide a simple empirical example. The method involves three major steps: (1) model estimation; (2) generation of predicted hazards for selected groups; and (3) generation of fertility life tables for multiple parities. The Stata programs and data file used to generate the example are available on-line at www.[link to be determined].

Step 1. Model Estimation

We first use a discrete-time event history model to model the occurrence and timing of births. As described by Allison (1989; 1995), this model uses logistic regression to estimate the log-odds of a birth occurring in each person-year interval as a function of the woman’s age category, and non-time-varying and time-varying characteristics. In the case of multiple events, one may pool all birth intervals in the same analysis provided that appropriate steps are taken to account for the clustering of births within individual women (Allison 1995; Cleves et al. 2008)^vi.

There are several possible ways to handle multiple birth intervals (parity greater than one). At the simplest level, one can estimate an additive model that includes birth interval (i.e., parity) as one of the time-varying independent variables:

$$\mathit{Additive}\mathit{Model}:\text{Logit}({\text{b}}_{\text{x}}=1)=\text{a}+{\text{j}}_{\text{x}}+{\underset{\_}{\text{A}}}_{\text{x}}{\text{B}}_1+{\underset{\_}{\text{C}}\text{B}}_2+{\underset{\_}{\text{C}}}_{\text{x}}{\text{B}}_3$$

where:

• b_x = birth occurred at age x

• j_x = birth interval j at age x (range: 1-J). The j^th birth interval starts in the person-year following the j-1^th birth, and ends in the person-year of the j^th birth or censorship.

• A_x = vector of dummy variables indicating membership in 5-year age category at age x (note: other age intervals or age functions are possible)

• C = vector of time-fixed control variables

• C_x = vector of time-varying control variables

This model allows the levels of the underlying hazard function to differ across birth intervals, but assumes that the shape of the hazard function (i.e., the age pattern given by B₁) does not vary by birth interval. One advantage of this model is that, even with modest sample sizes, it has the power to estimate coefficients for very detailed (e.g., single-year) age categories because it effectively combines cases from all parities together, albeit at the expense of obscuring differences by parity. In our example the vector, C, time-fixed control variables include religion and race. The C_x vector of time-varying control variables includes years of education and marital status.

To relax the assumption that the shape of the hazard function is identical across parities, one can include interaction terms between birth intervals and age categories:

$$\mathit{Partially}-\mathit{Interactive}\mathit{Model}:\text{Logit}({\text{b}}_{\text{x}}=1)=\text{a}+{\text{j}}_{\text{x}}+{\underset{\_}{\text{A}}}_{\text{x}}{\text{B}}_1+{\underset{\_}{\text{C}}\text{B}}_2+{\underset{\_}{\text{C}}}_{\text{x}}{\text{B}}_3+({\text{j}}_{\text{x}}\ast {\underset{\_}{\text{A}}}_{\text{x}}){\text{B}}_6$$

This model allows both the level and shape of the hazard function (i.e., age pattern of the hazard of childbearing) to vary by birth interval. For example, if first births were heavily concentrated around age 25, but subsequent births were more flatly distributed across subsequent ages, this model would detect these parity differences. The variables included in this model are the same as the additive model with the inclusion of an interaction term (j_x* A_x) between the birth interval j at age x and the dummy variable indicating membership in the 5-year age category at age x. A chi-square test indicates whether the partially-interactive model fits the data better than the additive model^vii. One drawback of this model is that some interaction terms are likely to drop out altogether for age-parity combinations with few or no events (e.g., young ages and high parities). This problem can be handled by combining higher order parities into a single category (e.g., 3 or more), using less detailed age categories (e.g., five- rather than single-year age groups), or both.

Finally, to allow the effects of all covariates to vary across birth intervals, one can estimate a fully-interactive model:

$$\mathit{Fully}-\mathit{Interactive}\mathit{Model}:\text{Logit}({\text{b}}_{\text{xj}}=1)={\text{a}}_{\text{j}}+{\underset{\_}{\text{A}}}_{\text{x}}{\text{B}}_{1\text{j}}+{\underset{\_}{\text{C}}\text{B}}_{2\text{j}}+{\underset{\_}{\text{C}}}_{\text{x}}{\text{B}}_{3\text{j}},\mathit{for}\mathit{each}{j}^{th}\mathit{birth}\mathit{interval}.$$

This model is estimated separately for each birth interval; higher birth intervals can be combined if sample sizes become too small. This model is the most flexible of the three described. If racial-ethnic groups had similar first birth, but different spacing and stopping patterns, for example, this model would capture these differences. The fully-interactive model includes the same variables as the additive model with the vector C time-fixed and the vector C_x time-varying covariates. One can use a chi-square test to test whether the fully-interactive model fits better than the partially-interactive model^viii. This model has the same limitation of the partially-interactive model: some of the age coefficients are likely to have extreme values or drop out for age-parity combinations with few or no events. Again, this problem must be handled by either combining higher order parities into a single category or by using less detailed age categories, particularly for the higher-parity models.

To illustrate, we estimated the additive, partially-interactive, and fully-interactive models for our NSFG sample while adjusting for the clustering of observations within individual women. To account for the NSFG’s stratified sampling design, the models are weighted with a normalized sampling weight^ix. Weighting the models helps ensure that the simulated fertility measures (when evaluated at sample means) approximate those observed in the population^x. Because of low cell sizes at higher parities, we top-coded our measure of parity at 3-or-more births. The results are shown in Table 3. The chi-square test clearly indicates that the fully-interactive model fits the data significantly better than the partially-interactive model, which in turn, fits the data better than the additive model. This is also evident by significant age-parity interactions in the partially-interactive model and several of the coefficients vary across parities in the fully-interactive model.

Focusing on the effects of race and marital status in the best-fitting fully-interactive model, the hazard of first birth for black women is 2.1 (exp(0.75)) times as large as among white women and their hazard for third-or-higher-order births is 1.4 (exp(0.34)) times as large. The hazard of a second birth for black women is no different from white women. Additionally, the hazard for married women is 6.3 (exp(1.84)) times greater as unmarried women for first births, 2.3 (exp(0.85)) times greater for second births, and 1.3 (exp(0.23)) times greater for third-or-higher-order births.

Step 2. Generating Predicted Hazards

After fitting the hazard model, one can use the results to obtain predicted hazards, q_x, of having a birth at each year of age and parity for selected groups of interest (i.e., groups k = 1 to K). For example, if we were interested in obtaining predicted values for women with varying marital status histories, one group might be women who never married while another group might be women who married at age 25. To hold other factors constant, all other predictors must be set to the same values across all groups (often the mean). In general, the predicted probability of a birth at age x, birth interval j, for group k is obtained by inserting values for C and C_x (to identify groups 1 to K) for each combination of age (x) and parity (j) into the estimated model.

The first step is to calculate the predicted log-odds for all values of age, parity, and groups (x, j, and k, respectively). For example, for each of the fully-interactive models estimated for each j^th birth interval, values for A_x, C, and C_x need to be replaced with values corresponding to each combination of x and k:

$$\text{Predicted}\text{logged}-{\text{odds}}_{\text{xjk}}={\text{a}}_{\text{j}}+{\underset{\_}{\text{A}}}_{\text{x}}{\text{B}}_{1\text{j}}+{\underset{\_}{\text{C}}\text{B}}_{2\text{j}}+{\underset{\_}{\text{C}}}_{\text{x}}{\text{B}}_{3\text{j}}$$

The second step is to convert the predicted log-odds to predicted hazards for each combination of x, j, and k;

$${\text{q}}_{\text{xjk}}=exp(\text{predicted}\text{log}-{\text{odds}}_{\text{xjk}})/[1+exp(\text{predicted}\text{log}-{\text{odds}}_{\text{xjk}})]$$

As an illustration, Table 4 displays the predicted hazards (q_x) for the first and second parities for white women with the mean marital status and religious affiliations. These predicted hazards serve as the key inputs for the other components of a fertility life table, which are discussed in the next section. The predicted hazard of first birth at age 20 is 0.049, and is obtained by inserting age-specific sample means (see Table 1) into the fully-interactive first parity model as follows:

$$\begin{array}{l}\text{Predicted}log-\text{odds}=-3.29+0.45(\text{age}20-24)+0.00(0.178[\text{proportion}\text{no}\text{religion}])\\ -0.20(0.179[\text{proportion}\text{Catholic}])-0.19(.075[\text{proportion}\text{other}\text{religion}])-\\ 0.02(12.4[\text{mean}\text{education}\text{at}\text{age}20])+1.84(0.088[\text{proportion}\text{married}\text{at}\text{age}20])=-2.97;\\ \text{Predicted}\text{hazard}=exp(-2.97)/(1+exp(-2.97))=\mathrm{0.049.}\end{array}$$

Table 4.

Partial multi-parity fertility life table simulated for white women with mean educational attainment, marital status, and religious affiliation. Based on fully-interactive model (Table 3)

x	Parity 1			Parity 2
	Predicted Hazard of birth qx,1	Proportion at risk of birth Ix 1	Unconditional Prob. of birth dx,1	Predicted Hazard of birth qx,2	Proportion at risk of birth Ix,2	Unconditional Prob. of birth dx,2
15	0.029	1.000	0.029	0.125	0.000	0.002
16	0.029	0.971	0.028	0.128	0.028	0.005
17	0.029	0.942	0.027	0.132	0.050	0.008
18	0.029	0.915	0.026	0.136	0.069	0.011
19	0.030	0.889	0.026	0.142	0.084	0.014
20	0.049	0.862	0.042	0.137	0.097	0.016
21	0.052	0.821	0.043	0.143	0.123	0.021
22	0.056	0.778	0.044	0.150	0.145	0.025
23	0.061	0.734	0.045	0.157	0.164	0.029
24	0.068	0.689	0.047	0.165	0.180	0.033
25	0.058	0.642	0.037	0.128	0.193	0.027
26	0.063	0.605	0.038	0.133	0.203	0.030
27	0.070	0.566	0.039	0.138	0.212	0.032
28	0.075	0.527	0.039	0.142	0.219	0.034
29	0.077	0.488	0.038	0.145	0.225	0.035
30	0.078	0.450	0.035	0.125	0.227	0.031
31	0.082	0.415	0.034	0.127	0.232	0.032
32	0.085	0.381	0.032	0.129	0.234	0.032
33	0.087	0.348	0.030	0.130	0.235	0.032
34	0.088	0.318	0.028	0.131	0.232	0.032
35	0.050	0.290	0.014	0.083	0.228	0.019
36	0.051	0.276	0.014	0.083	0.223	0.019
37	0.052	0.262	0.014	0.084	0.218	0.019
38	0.051	0.248	0.013	0.083	0.213	0.018
39	0.052	0.235	0.012	0.083	0.207	0.018
40	0.009	0.223	0.002	0.017	0.202	0.003
41	0.009	0.221	0.002	0.017	0.200	0.003
42	0.009	0.219	0.002	0.016	0.199	0.003
43	0.008	0.217	0.002	0.016	0.197	0.003
44	0.009	0.216	0.002	0.016	0.196	0.003

Data and Sample: See Table 1.

These calculations were repeated for each combination of age (x) and parity (j). The predicted hazards in Table 4 are similar for each 5-year age block (e.g., 15 to 19, 20 to 24, etc.) because we modeled age effects using a set of dummy variables for 5-year age categories. They differ slightly because the mean values for age-specific time-varying predictors change values across ages. If we had modeled age with single-year age groups, we would obtain different q_xjk values for each single year of age.

Step 3. Generating Fertility Life Tables for Multiple Parities

To convert the predicted hazards to fertility measures like the TFR, it is necessary to construct a sequential multi-decrement life table. The life table models report how many children women in a synthetic cohort are likely to have, by parity at each age, throughout their entire reproductive lifetime, if they experienced all of the predicted probabilities produced by the event history model. If the predicted probabilities pertain to a particular group (e.g., women who never married), then the life table will produce estimates of the simulated number and timing of births for women with these characteristics.

As noted above, Table 4 displays a portion of a fertility life table for the first two parities from age 15 to 45 for white women with mean values on education, marital status, and religious affiliation. The complete life table is much larger with the maximum number of births observed in our sample, 11.

The x column denotes exact age for the synthetic cohort.

The q_xj columns show the hazard of having a j^th birth;, the probability of having a j^th birth between age x and x+1, given that the j^th birth has not yet occurred, but that the j−1^th birth has occurred before age x. For example, at her 18^th birthday, a young woman has a 0.029 probability of having a first birth before she turns 19, if she has never had a birth before. She has a 0.136 probability of having a second birth, if she already had a first, but not yet a second. These values are the predicted hazards generated from the discrete-time event history models (i.e., q_xjk). They are the only inputs required to produce the life table.

The l_xj columns indicate the proportion of the entire synthetic cohort at risk of having the j^th birth at exact age x. Because the entire cohort at age 15 is “at risk” of having a first birth (because none of the women in our sample had a birth at an earlier age), l_15(j=1) is set equal to 1.0. The proportion at risk of having a first birth declines as first births occur. Additionally, the proportion at risk of a second birth is smaller because it includes only those who have already had a first birth, but not yet a second birth.

The d_xj columns give the unconditional probability of a j^th birth between age x and x+1. In other words, it is the proportion of all women in the synthetic cohort who have a j^th birth during the age x to x+1 interval.

These three columns are related in the following ways. For the first parity, we use the following set of equations. For the youngest age group (x = 15):

$$\begin{array}{l}{\text{l}}_{15,1}=1.0\\ {\text{d}}_{15,1}={\text{q}}_{15,1}.\end{array}$$

l_15,1 is set to 1.0 because 100% of women age 15 in our simulated cohort are at risk of a first birth because none have had a first birth yet. The proportion in the cohort having a first birth at age 15 (d_15,1) is simply the conditional probability having a first birth at age 15 (q_15,1). For all older ages, (x > 15):

$$\begin{array}{l}{\text{l}}_{\text{x},1}={\text{l}}_{\text{x}-1,1}-{\text{d}}_{\text{x}-1,1}.\\ {\text{d}}_{\text{x},1}={\text{q}}_{\text{x},1}{\text{l}}_{\text{x},1}\end{array}$$

The women at risk of having a first birth at the beginning of the age interval x (l_x,1) is the number originally at risk at beginning of the previous age interval (l_x-1,1) minus those who had a first birth during the previous age interval (d_x-1,1). The proportion in the cohort having a first birth between age x and x+1 (d_x,1) is the product of the hazard of having a first birth (q_x,1) and the share of women at risk of having a first birth (l_x,1) at age x.

For subsequent parities j, we use a slightly modified set of equations. For the first age group (x = 15):

$$\begin{array}{l}{\text{l}}_{15,\text{j}}=0\\ {\text{d}}_{15,\text{j}}={\text{q}}_{15,\text{j}}({\text{d}}_{15,\text{j}-1}/2).\end{array}$$

For example, in the case of the 2^nd parity (j = 2), the proportion of women in the synthetic cohort at exact age 15 at risk of having 2^nd birth (l_15,2) is zero because none could possibly have already had a first birth before exact age 15, and one has to have had a first birth before being at risk of having a second. The proportion that has a 2^nd birth at age 15 (d_15,2) is equal to the product of the conditional probability of having a 2^nd birth at age 15 (q_15,2) and the proportion at risk (half of those who had a first birth when they were 15; we count only half because we assume that first births occurred evenly throughout the year, leaving on average half the year remaining at risk for second^xi).

For all older ages (x > 15):

$$\begin{array}{l}{\text{l}}_{\text{x},\text{j}}={\text{l}}_{\text{x}-1,\text{j}}-{\text{d}}_{\text{x}-1,\text{j}}+{\text{d}}_{\text{x}-1,\text{j}-1}\\ {\text{d}}_{\text{x},\text{j}}={\text{q}}_{\text{x},\text{j}}[{\text{l}}_{\text{x},\text{j}}+({\text{d}}_{\text{x},\text{j}-1}/2)]\end{array}$$

Again, in the case of the 2^nd parity (j = 2), the proportion of women at risk of having a 2^nd birth at exact age x (l_x,2) is the proportion who were at risk of a 2^nd birth at the beginning of the previous age interval (i.e., women who previously had a first birth but not yet a 2^nd by age x-1 [l_x-1,2]) minus the share among them who had a 2^nd birth during the x-1 age interval (d_x-1,2), plus those who had a first birth during the previous age interval (d_x-1,1).

The proportion of women in the synthetic cohort that has a second birth between age x and x+1 (d_x,2) is the product of the proportion at risk and the conditional hazard of having a 2^nd birth at age x (q_x,2). Here, the proportion at risk includes those who were at risk of having a second birth at the beginning of the age interval (l_x,2), plus half of the proportion who had a first birth within the same age interval (d_x,1/2).

Importantly, the d_xj columns can be used to estimate various summary measures of fertility. If we sum d_xj across all ages (summing down columns), we estimate the proportion of women in the synthetic cohort who ever had a j^th birth in their reproductive lifetime, or the parity-specific TFR:

$${\text{TFR}}_{\text{j}}=\sum _{\text{x}=10}^{49}{\text{d}}_{\text{xj}}$$

We can construct a series of PPRs (i.e., the probability of progressing to the next higher parity) from these:

$${\text{PPR}}_{\text{j}}=\frac{{\text{TFR}}_{\text{j}}}{{\text{TFR}}_{\text{j}-1}}$$

$$\text{where}{\text{TFR}}_0=1.$$

For example, the PPR for parity 1 is the probability of ever having a first birth; PPR for parity 2 is the probability of ever having a 2^nd birth among those who had a 1^st birth, and PPR for parity k is the probability of having a k^th birth among those who had k-1 births.

If we sum d_xj across all parities j (summing across rows), we obtain the proportion of women having any parity birth at age x, or age-specific fertility rates:

$${\text{f}}_{\text{x}}=\sum _{\text{j}=1}^{\omega }{\text{d}}_{\text{xj}}$$

Finally, if we sum f_x, we obtain the TFR, or the expected number of children born to women if they experienced all of the predicted age- and parity-specific birth hazards:

$$\text{TFR}=\sum _{\text{x}=10}^{49}{\text{f}}_{\text{x}}$$

Standard Errors

Although alternative approaches have been used (Lynch and Brown 2010 and Lee and Rendall 2001), it is increasingly common to sample with replacement from the data to obtain bootstrapped standard error estimates of life table components (Cai et al. 2010; Rendall et al. forthcoming; Poi 2004). Here, we used Stata’s bootstrap routine to draw 500 replicate samples with N observations from the data, where N is the same number as in the full sample We sampled by person-level clusters (i.e., taking all person-year observations for each sampled individual) rather than sampling person-year records independently. We estimated the models for each of the 500 replicate samples and used the results to estimate the life table components. The mean across the 500 replicates provided the expected value of the life table components and the standard deviation provided an estimate of the standard error. The average TFR and standard deviation stabilize by about the 250^th replication (results available upon request).

Example: Predicted fertility measures by race and marital status

We simulated fertility measures for black and white women while holding the other time-constant predictor, religion, at its sample mean and the time-varying predictors, marital status and education, at their age-specific sample means. We summarize the results in Figure 2 and Table 5.

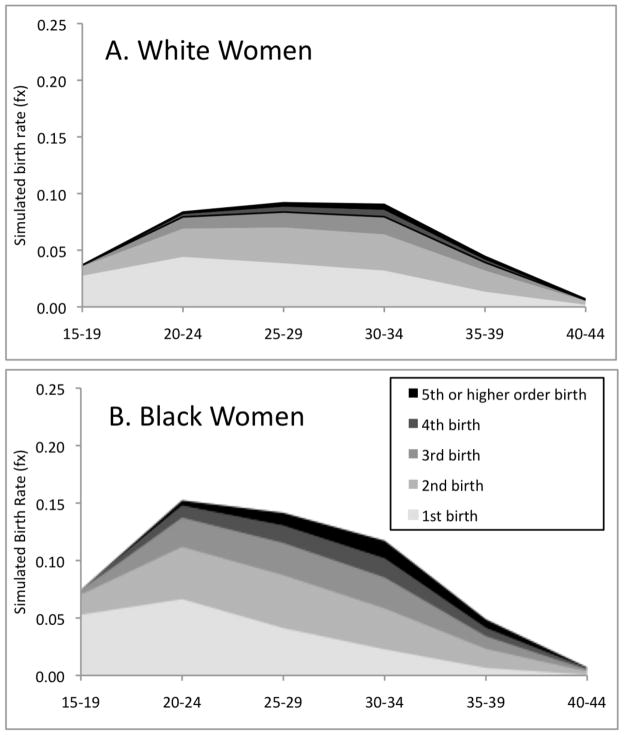
Figure 2.

Simulated parity- and age-specific fertility rates, white and black women, based on fully-interactive hazard model (Table 3)

Data and Sample: See Table 1.

Table 5.

Simulated total fertility rate and parity progression ratios for black and white women and by marital status history, based on fully-interactive hazard model (Table 3)

	White	Black	Marital Status History
			Never Married	Married age 20+	Married age 25+	Married age 25–34a
Simulated Total Fertility Rate
Average number of lifetime births
1st parity	0.79 (0.01)	0.96 (0.01)	0.57 (0.02)	0.98 (0.00)	0.95 (0.01)	0.92 (0.01)
2nd parity	0.59 (0.02)	0.82 (0.02)	0.39 (0.02)	0.93 (0.01)	0.82 (0.02)	0.76 (0.02)
3rd parity	0.25 (0.01)	0.48 (0.02)	0.18 (0.01)	0.57 (0.02)	0.37 (0.02)	0.35 (0.01)
4th parity	0.10 (0.01)	0.25 (0.02)	0.08 (0.01)	0.28 (0.02)	0.14 (0.01)	0.14 (0.01)
5th or higher parity	0.05 (0.01)	0.20 (0.03)	0.04 (0.01)	0.18 (0.02)	0.07 (0.01)	0.07 (0.01)
All parities	1.77 (0.04)	2.71 (0.09)	1.27 (0.04)	2.94 (0.06)	2.36 (0.04)	2.24 (0.04)
Simulated Parity Progression Ratios
Probability of progression from:
No births to 1st parity	0.79 (0.01)	0.96 (0.01)	0.57 (0.02)	0.98 (0.00)	0.95 (0.01)	0.92 (0.01)
1st to 2nd parity	0.75 (0.02)	0.86 (0.02)	0.68 (0.02)	0.94 (0.01)	0.86 (0.01)	0.83 (0.01)
2nd to 3rd parity	0.42 (0.02)	0.58 (0.02)	0.46 (0.02)	0.61 (0.02)	0.45 (0.02)	0.46 (0.02)
3rd to 4th parity	0.39 (0.02)	0.53 (0.02)	0.43 (0.02)	0.50 (0.02)	0.39 (0.01)	0.39 (0.01)
4th to 5th or higher parity	0.51 (0.03)	0.80 (0.07)	0.56 (0.05)	0.64 (0.04)	0.52 (0.03)	0.51 (0.03)

^aMarried continously between ages 25 and 34

Notes: All other covariates held at their mean. Bootstrapped SEs in parentheses.

Data and Sample: See Table 1.

Simulated age- and parity-specific fertility rates for black and white women are displayed in Figure 2. Both groups show the typical age pattern with the highest fertility rates occurring for women aged 20 to 34. However, black women exhibit much higher fertility than their white peers, especially at younger ages and at higher parities. These patterns also appear in the simulated TFRs and PPRs shown in Table 5. For example, nearly all (96%) black women are simulated to have a birth in their lifetime compared with only 79 percent of white women. The TFRs and PPRs further indicate that black women are more likely to continue to have subsequent births at all parities. Overall, after controlling for marital status history, educational attainment, and religious affiliation, black women are simulated to have nearly one more birth than white women in their lifetimes (2.71 versus 1.77 births). The standard errors suggest that this difference is statistically significant; it is much larger than twice the standard error of the difference (2 * SE-diff = 2 * sqrt(0.09²+0.04²) = 0.20). Like the simulated rates of childlessness in our example on first births, it is important to recognize that these TFR estimates are standardized and thus differ from national vital statistics estimates (Martin et al. 2002; Martin et al. 2012; NCHS 1994). For example, the observed TFR for black women averaged around 2.26 between 1990 and 2010, while our simulated TFR is 2.71. The simulated TFR is higher primarily because it assigns black women average means on the control variables (a result that is primarily driven by marital status). In fact, when we assign black women black-specific means, we obtained a simulated TFR (2.25) that is much closer to the observed rate (2.26).

To illustrate the method for a time-varying predictor, we generated simulated fertility measures for four groups of women with various marital status histories: (1) never married, (2) married age 20+, (3) married age 25+, and (4) married age 25–34. Again, we hold the remaining time-constant predictors, race and religion, at their sample means and the time-varying predictor, education, at its age-specific sample mean. Simulated age-, parity-specific fertility rates for the four marital status groups are shown in Table 5 and displayed in Figure 3.

Figure 3.

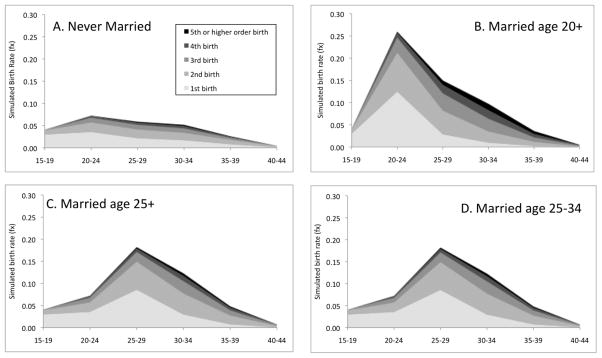
Simulated parity- and age-specific fertility rates, by marital status history, based on fully-interactive hazard model (Table 3)

Data and Sample: See Table 1.

Never-married women exhibit very low and flat age patterns, while the other groups exhibit elevated fertility rates following marriage. Women who marry at age 20 exhibit much higher lifetime fertility than women who marry at age 25. As married women, they are exposed to the highest age-specific fertility rates between ages 20 and 24. But the fertility pattern of women who were married at age 25 and older is nearly identical to the pattern among those who were married between the ages of 25 and 34, largely because fertility rates are low for all groups after age 35. These patterns appear in the simulated TFRs and PPRs shown in Table 5. For example, a little more than half (57%) of never-married women are simulated to ever have a birth, much less than women who married at any age. Among ever-married women, age at marriage is moderately related to childlessness. Nearly all (98%) women who marry at age 20 are simulated to ever have a birth, compared with 95 percent among those marrying at age 25, and 92% among those married between the ages of 25 and 34. Interestingly, among women who already had two births, the probability of progressing to third or higher-order births is similar across all groups, except those marrying at very young ages. In other words, fertility behaviors at higher parities appear to be less associated with marriage than lower-parity fertility which is also evident in the fully-interactive models. Overall, after controlling for race, educational attainment, and religious affiliation, never-married women are simulated to have only 1.27 lifetime births compared with 2.94, 2.36, and 2.24 among women who were married age 20+, 25+, and 25–34, respectively.

Conclusions

In this paper, we presented a method for translating multiple-birth hazard model coefficients into simulated fertility measures, including age-specific fertility rates, TFRs, and PPRs. The key advantage of the method is that it permits comparisons of the timing and number of lifetime births across groups while controlling for other characteristics. For example, one could use the method to simulate TFRs for various racial and ethnic groups while holding constant a large set of fixed and time-varying characteristics, such as social class origins, educational attainment, and marriage and employment history.

It is crucial to recognize that the simulated measures and standard errors generated from the life tables are only as good as the data and model on which they are based. For example, it is important to take into account how the model predictors vary across parities. This was clear in our NSFG example as the fully-interactive model fit the data significantly better than the additive and partially-interactive models. The consequence of selecting the less optimal model can be seen in comparisons of simulated fertility measures across model specifications. For example, the simulated TFR for white women is lower (1.61) when generated from the worst-fitting additive model than the better-fitting partially-interactive model (1.71), which is in turn lower than the TFR generated from the best-fitting fully-interactive model (1.77) (results not shown but available).

Another potential concern is that many data sources, including the NSFG, include only a few time-varying covariates, so important predictors of fertility like school enrollment, labor force participation, and involvement in sexual relationships outside of marriage may be missing from the hazard model. Indeed, the differences we observed between black and white women in simulated total lifetime fertility might be driven by these unmeasured factors. In other words, the summary measures of interest to many researchers are only as good as the discrete time hazard models used as the inputs for the life tables. Related to this concern, the relationships estimated by the model and the simulated fertility measures may not be causal. For example, we estimated much higher lifetime fertility for ever-married women than never-married women. However, this difference may be due to the selection of women with higher fertility intentions into marriage rather than (or in addition to) the effects of marriage on fertility.

Additionally, sample size may limit age and parity detail one may plausibly use. In our examples, we used five-year age categories because of limitations in sample size, particularly at higher parities. But in supplementary analyses, we assessed how the results would differ if we had coded age with single-year categories. Described in Appendix A, these analyses suggest that additional detail by age may not be worthwhile if the sample size is not large enough to support it. First, summary measures (TFRs and PPRs) were not very sensitive to age coding, particularly for groups defined by non-time-varying variables. Additionally, while single-year age categories may reveal real age patterns that are missed when using larger age categories, they also has the potential to produce erratic, implausible age patterns in the simulated ASFRs. Related to this point, it is important to avoid simulating results that extend beyond the ranges observed in the data. If one attempts to simulate results outside of the observed data or where there exist few actual cases, the multistate life table will not be able to reproduce the true values resulting in biased estimates (Cai et al. 2010). In general, the closer substituted values are to the sample means, the more accurate are the estimates.

Finally, our NSFG example involved fertility, but the method could be applied to other repeated events. For example, criminologists are often interested in modeling the occurrence and timing of arrests. One could use multiple-event hazard models and life tables to simulate estimates of the age pattern and cumulative number of lifetime arrests for selected groups while controlling for other key variables known to be associated with arrests. Such information could be helpful for discerning between groups for whom delinquency tends to be concentrated in adolescence and groups for whom criminal activity extends into adulthood. This may provide useful information for designing interventions and deterrence programs. A similar type of analysis could be conducted on marriages, with the intent of identifying how marriage patterns differ across groups (e.g., no marriage, late marriage, multiple marriages). Researchers could use the method to produce summary measures on the total number of marriages a woman might experience in her lifetime and the probability of transitioning from a first marriage to a subsequent. Overall, the methodology described here offers many practical advantages for those seeking to translate the repeated or multi-event hazard model estimates into interpretable summary measures, rather than relying on cumbersome conditional hazards.

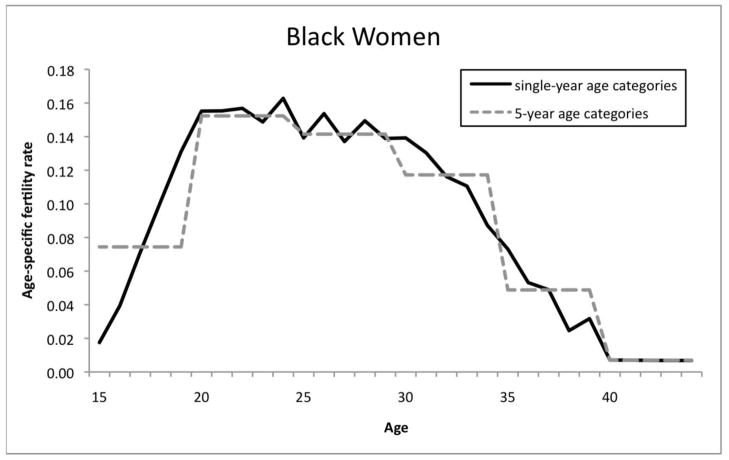
Appendix Figure 1.

Effects of Age Coding on simulated age-specific fertility rates for black women, based on fully-interactive hazard model

Data and Sample: See Table 1.

Appendix Table 1.

Fully-interactive models of fertility, with age coded in single years

	1st parity	2nd parity	3rd+ parity
Age (15 = ref in 1st parity model; 15–19 = ref in 2nd & 3rd + parity models)
16	0.87 ***	---	---
17	1.54 ***	---	---
18	1.97 ***	---	---
19	2.29 ***	---	---
20	2.38 ***	0.04	0.54
21	2.14 ***	−0.07	0.86 *
22	2.13 ***	−0.02	0.42
23	2.05 ***	−0.15	0.19
24	2.04 ***	−0.29	0.37
25	1.83 ***	−0.44*	0.01
26	2.05 ***	−0.43 *	−0.05
27	1.95 ***	−0.47 *	−0.39
28	2.02 ***	−0.48 **	−0.23
29	2.08 ***	−0.49 **	−0.45
30	2.15 ***	−0.54 **	−0.48
31	1.99 ***	−0.70 ***	−0.43
32	1.84 ***	−0.68 **	−0.59
33	1.79 ***	−0.57 **	−0.71
34	1.53 ***	−1.01 ***	−0.84 *
35	1.77 ***	−1.01 ***	−1.17 **
36	1.49 ***	−0.97 ***	−1.76 ***
37	0.53	−1.18 ***	−1.53 ***
38	0.78	−1.76 ***	−2.45 ***
39	0.56	−1.54 ***	−2.00 ***
40–44	−0.55	−2.84 ***	−3.70 ***
Protestant (ref.)	---	---	---
No Religion	0.01	−0.11	−0.10
Catholic	−0.18 *	0.02	0.17
Other Religion	−0.15	0.06	0.71 ***
Black (vs. NH-white)	0.75 ***	0.12	0.34 ***
Years of Education	−0.08 ***	0.03 *	0.04
Married	1.84 ***	0.86 ***	0.25 **
Intercept	−4.14 ***	−2.20***	−2.80 ***
N	78,428	20,096	22,294

^*p<0.05

^**p<0.01

^***p<0.001

Data and Sample: See Table 1.

Appendix Table 2.

Effects of age coding on simulated total fertility rate and parity progression ratios for black women and women married age 25+, based on fully-interactive hazard model (bootstrapped SEs)

	Black Women		Married age 25 +
	5-yr age categories	single-year age	5-yr age categories	single-year age
Simulated Total Fertility Rate
Average number of lifetime births
1st parity	0.96 (0.01)	0.96 (0.01)	0.95 (0.01)	0.95 (0.01)
2nd parity	0.82 (0.02)	0.82 (0.02)	0.82 (0.02)	0.83 (0.01)
3rd parity	0.48 (0.02)	0.48 (0.02)	0.37 (0.02)	0.37 (0.01)
4th parity	0.25 (0.02)	0.25 (0.02)	0.14 (0.01)	0.14 (0.01)
5th or higher parity	0.20 (0.03)	0.20 (0.03)	0.07 (0.01)	0.07 (0.01)
All parities	2.71 (0.09)	2.71 (0.09)	2.36 (0.04)	2.37
Simulated Parity Proqression Ratios
Probability of progression from:
No births to 1st parity	0.96 (0.01)	0.96 (0.01)	0.95 (0.01)	0.95 (0.01)
1st to 2nd parity	0.86 (0.02)	0.86 (0.02)	0.86 (0.01)	0.87 (0.01)
2nd to 3rd parity	0.58 (0.02)	0.58 (0.02)	0.45 (0.02)	0.45 (0.02)
3rd to 4th parity	0.53 (0.02)	0.53 (0.02)	0.39 (0.01)	0.39 (0.01)
4th to 5th or higher parity	0.80 (0.07)	0.79 (0.07)	0.52 (0.03)	0.52 (0.03)

All other covariates held at their mean

Data and Sample: See Table 1.

Appendix A. Sensitivity to Age Coding

We used five-year age categories in our analyses because of limitations in sample size, particularly at higher parities. How would the results differ if we had coded age with single-year categories? To answer this question, we re-estimated the fully-interactive model, only this time, we used single-year age dummy variables. The model coefficients are shown in Appendix Table 1. The results illustrate the analytic challenges of using single- rather than five-year age groups. First, we were forced to code ages 40–44 with a single five-year category because there were so few births for these ages. Additionally, age groups 15–19 had to be combined in 2nd and 3rd+ parity models, again because there were no events for some parity-single-age combinations.

We next assessed how the simulated TFRs and PPRs differed by age coding. Appendix Table 2 compares the results based on five- and single-year age categories for black women and women married 25+ (with each group assessed at mean levels of model covariates). As shown, the results are nearly identical for black women and for women married 25+. They were also nearly identical for white women and other marital status groups (results not shown).

Finally, it is clear that the single-year coding provides greater detail for simulated age-specific fertility rates. This is shown in Appendix Figure 1, which graphs the age-specific fertility rates for all parities among black women based on single- and five-year age categories. When age is coded in single years, important details within the five-year age groups can be seen. For example, single-year fertility rates are very low for 15 year-olds but steadily increase across the 15–19 age category. However, the single-year rates can also be erratic and may not reflect actual age patterns. An example is the zig-zag pattern from ages 24 to 30.