Delay accuracy in bat sonar is related to the reciprocal of normalized echo bandwidth, or Q

Abstract

Big brown bats (Eptesicus fuscus) emit wideband, frequency-modulated biosonar sounds and perceive the distance to objects from the delay of echoes. Bats remember delays and patterns of delay from one broadcast to the next, and they may rely on delays to perceive target scenes. While emitting a series of broadcasts, they can detect very small changes in delay based on their estimates of delay for successive echoes, which are derived from an auditory time/frequency representation of frequency-modulated sounds. To understand how bats perceive objects, we need to know how information distributed across the time/frequency surface is brought together to estimate delay. To assess this transformation, we measured how alteration of the frequency content of echoes affects the sharpness of the bat's delay estimates from the distribution of errors in a psychophysical task for detecting changes in delay. For unrestricted echo frequency content and high echo signal-to-noise ratio, bats can detect extremely small changes in delay of about 10 ns. When echo bandwidth is restricted by filtering out low or high frequencies, the bat's delay acuity declines in relation to the reciprocal of relative echo bandwidth, expressed as Q, which also is the relative width of the target impulse response in cycles rather than time. This normalized-time dimension may be efficient for target classification if it leads to target shape being displayed independent of size. This relation may originate from cochlear transduction by parallel frequency channels with active amplification, which creates the auditory time/frequency representation itself.

To perceive their surroundings, echolocating bats transform acoustic information from biosonar echoes into spatial representations of objects (1, 2). Here, we report new information about the bat's internal representation of sonar targets, that is, the bat's sonar images (3), as manifested in the relation between echo-delay acuity and the frequency content of echoes. Big brown bats, Eptesicus fuscus (4), broadcast wideband, multiple-harmonic, downward-sweeping, frequency-modulated (FM) biosonar sounds covering frequencies from 22 to 100 kHz (3, 5, 6), and they perceive objects from echoes of these sounds that return to their ears. Bats determine target distance, or range, from the delay of echoes, which is 5.8 ms/m (7-9). In principle, the high center frequency (f_c = ≈60 kHz) and wide bandwidth (Δf = ≈80 kHz) of the big brown bat's FM signals can support very accurate determination of delay (10, 11). For echoes with unrestricted bandwidths, these bats can detect changes in echo delay as small as 10-40 ns (12, 13). To understand how the broad frequency content of the signals is marshaled to achieve such fine temporal hyperacuity (12), we measured delay accuracy while filtering out progressively greater portions of the low-frequency or the high-frequency end of the echo spectrum. We found that the bat's delay accuracy deteriorates as frequencies are removed from echoes, but not in proportion to the reciprocal of echo bandwidth (1/Δf) or center frequency (1/f_c) as predicted from sonar receiver theory (10, 11, 14-15). Instead, accuracy declines consistently with Q (= f_c/Δf), which is the reciprocal of the bandwidth relative to frequency (Δf/f_c). The value of Q is a well known quantity that represents the sharpness (“quality”) of the filtering imposed on echoes independent of frequency, but it also is the relative width of the target impulse response in number of cycles or peaks (16). From previous experimental results, big brown bats appear to perceive the shape of targets in terms of the distribution of reflecting points along the range axis (3, 8), which is equivalent to the distribution of peaks in the target's impulse response. By expressing the bandwidth of echoes normalized to frequency, and thus the time-extent of the impulse response in normalized, or dimensionless, time, the bat may display shape as the number of parts in the target independent of their actual time separations. This efficient abstract representation may be responsible for the demonstrated abilities of echolocating bats to classify rapidly moving targets in multiple-object “scenes” (3, 8).

Methods

Jittered-Echo Procedure. To measure the accuracy of delay perception for different echo bandwidths, we used an experimental method that required the bat to broadcast a series of sonar sounds and compare the delays of successive echoes to determine whether they change. Bats were trained to sit on an elevated Y-shaped platform and broadcast sonar sounds into two microphones located 20 cm away on the platform arms, about 40° apart to the bat's left and right (12, 13). The signals from the microphones were amplified, filtered with adjustable analog band-pass filters (see below), electronically delayed, and then delivered back to the bat as artificially generated “echoes” from corresponding loudspeakers located next to the microphones. The delay of the echoes from one side (left or right, randomly changed from trial to trial) was alternated back and forth (“jittered”) between two values from one broadcast to the next. The delay of echoes from the other side was kept stationary. The bat received echoes at a succession of delays from both sides and then chose the side with the jittering echoes by moving forward onto the correct arm of the platform to receive a food reward (12, 13). The big brown bat's sonar sounds were moderately directional (17), so that the signals picked up by the microphones varied in amplitude by ±10 dB according to the aim of the bat's head, which scanned back and forth during each trial. An electronic comparator determined which microphone received the stronger version of each signal and activated only the loudspeaker on that side of the apparatus (12, 13). Consequently, only one electronic echo was delivered back to the bat for each broadcast. The bat had to remember the delays of successive echoes to determine whether they jittered, while scanning with its head to activate first one channel and then the other to find the jittering stimuli. The bat's delay accuracy in this jitter-detection task was measured by reducing the size of the jitter interval in small steps from an easily detected amount to progressively smaller amounts, until the bat's left-right choice performance declined from ≈90-95% correct to ≈50% (chance). The bat's threshold was measured at 75% correct responses. In the jitter experiments we report here, we altered the frequency settings on the electronic filters used to pass the bat's signals from the microphones to the delay-lines and then determined the bat's threshold separately for each filter condition.

Echo Delays. The delay supplied by the delay-line in each channel was switched automatically back and forth from one value to another each time the bat emitted a sound, so that the electronically simulated echoes jittered between two delays while the bat emitted a series of sounds. On any given trial, the left (or right) channel returned echoes that jittered in delay, while the other channel returned echoes that had a fixed delay. We used a mean delay of 3,275 μs for both jittering and fixed echoes, and we varied the delay of the jittering echoes around this mean by amounts from ≈30 μs down to zero in small steps to measure the bat's threshold for detecting the jitter (12, 13). The experiments reported here involved delay changes of 0-80 ns in 5-ns steps, which were produced by analog delay-lines in series with digital delay-lines to achieve overall electronic delays of ≈2 ms (for details, see ref. 13). To regulate the signal-to-noise ratio of echoes (d = 49 dB), a low level of wideband random noise was added independently to the electronic echoes in the left and right channels just before the loudspeakers, so that the electronically manipulated echoes always arrived in a fixed background of noise.

Echo Frequency Content. At close range, the big brown bat's sonar sounds contain roughly equal spectral levels from 25 to 90 kHz, and our experiments involved electronic modification of spectral levels in echoes of these sounds. The bat's sounds traveled over an air-path of only 20 cm out to the microphones and 20 cm back from the loudspeakers, while the bulk of the stimulus delay was generated electronically by devices with a flat frequency response from 20 to 100 kHz, so there was negligible atmospheric absorption to modify the spectrum of the stimuli beyond our intended manipulations. The frequency content of stimulus echoes delivered to the bat was regulated by setting high-pass (HP), low-pass (LP), or band-pass (BP) analog electronic filters (24 dB/octave Butterworth) to remove progressively greater segments of the original 22-100 kHz broadcast bandwidth. The 12 different filter conditions for our experiments were wideband (15-100 kHz), HP (20-80 kHz, 25-80 kHz, 30-80 kHz, and 35-80 kHz), LP (20-80 kHz, 20-75 kHz, 20-70 kHz, 20-65 kHz, 20-60 kHz, and 20-55 kHz), and BP (50-60 kHz). Taking into account the frequency-response of the loudspeakers, the corresponding raw echo bandwidths (Δf) were wideband (65 kHz), HP (60, 55, 50, and 45 kHz), LP (60, 55, 50, 45, 40, and 35 kHz), and BP (≈5 kHz), which includes consideration of the sharp 50-kHz spectral notch introduced by the bat's external ear (18). Corresponding raw echo center frequencies (f_c) were wideband (47.5 kHz), HP (50, 52.5, 55, and 57.5 kHz), LP (50, 47.5, 45, 42.5, 40, and 37.5 kHz), and BP (55 kHz). Note that these values were derived entirely from the filter HP and LP dial settings in kHz, not measured from the signals themselves. An alternate series of measurements of bandwidth were made by digital processing of the stimuli (see below).

Results and Discussion

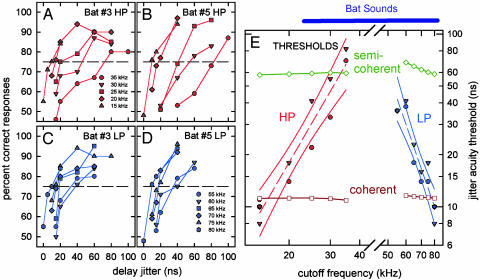
Jitter-Detection Thresholds. Fig. 1A shows the performance of two big brown bats detecting different amounts of jitter in experiments with HP filtering (Fig. 1 A and B; red) or LP filtering (Fig. 1 C and D; blue) to restrict the frequency content of echoes (see legends in Fig. 1 A and D). For each filter condition, the psychophysical curves yielded well defined thresholds that were dependent on the frequency settings of the electronic filters (Fig. 1E). The thresholds became higher as frequencies were removed, with the bats declining in delay accuracy from ≈10 ns to ≈80 ns for the HP conditions and from ≈10 ns to ≈40 ns for the LP conditions. In jitter experiments, the bat's thresholds for detecting changes in delay were small fractions of a microsecond, which seemed impossible for the animal to achieve, so attention was then focused on what (presumably spectral) artifact other than change in delay itself must be the cue for the bat's performance (19, 20). However, acoustic calibrations plus several control procedures built into the experimental design have established that the thresholds were not derived from perception of nondelay artifacts (13, 21), and that they represented a hyperacuity for delay (12). During experiments, we monitored the bat's broadcasts with an oscilloscope and a real-time spectrogram display; the bats were not observed to change the duration or amplitude of their sounds across conditions. Emitted-amplitude compensation by big brown bats is a weak effect that requires large changes of 10-30 dB to be made in echoes to elicit broadcast amplitude changes of only a few decibels (22).

Fig. 1.

Performance (percentage correct) for two big brown bats detecting different amounts of jitter in echo delay. (A and B) HP filter conditions (HP; red); (C and D) LP filter conditions (LP; blue) (40-60 trials per data point). Keys in A and D show 3-dB HP or LP cutoff frequency settings on filters. (E) Composite plot of bats' thresholds at 75% correct responses for different filter settings on horizontal axis (dashed red and blue lines show linear regression and solid lines show 99% confidence limits). Predicted thresholds for optimal receiver with coherent (open squares, brown line) and semicoherent (open diamonds, green line) processing of FM echoes in HP and LP conditions. Purple horizontal bar at top shows frequency range of bat sounds passed through the loudspeakers.

Theoretical Echo-Delay Accuracy. The accuracy of delay determination in sonar is limited by the signal-to-noise ratio of echoes, and by the reciprocal of their bandwidth as defined in a special way. According to the theory of optimal receivers (14-15), maximum echo delay accuracy (minimum standard deviation of the delay estimate, σ) is achieved by a matched filter that incorporates full knowledge of the original broadcast and can be expressed as σ = (2πBd)^-1, where B is echo bandwidth and d is the signal-to-noise ratio, defined as 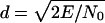(a dimensionless quantity, where E is the total energy of the echo and N₀ is the energy spectral density of the noise). The bandwidth term is specified in two ways according to the receiver model used to estimate delay. The “coherent” receiver computes the crosscorrelation function of the pulse and the echo and estimates echo delay as the time corresponding to the maximum peak in the fine structure of the crosscorrelation function. For the coherent receiver, echo bandwidth is given by root-mean-square (RMS) bandwidth, defined as 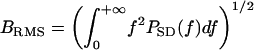, where P_SD(f) is the power spectral density of the pulse. The “semicoherent” receiver estimates echo delay as the time corresponding to the maximum of the envelope of the crosscorrelation function between the pulse and the echo. For the semicoherent receiver, echo bandwidth is given by the centralized RMS (CRMS) bandwidth, defined as 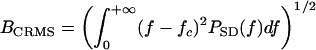, where 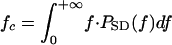is the center frequency of the echo. The two different versions of bandwidth are related as .

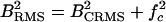We measured RMS bandwidth (B_RMS) and CRMS bandwidth (B_CRMS) of the stimuli by digitally sampling bat-like FM signals passed through the filters, determining the target transfer function with or without the loudspeaker frequency response, and measuring the 3-dB cutoff frequencies of the signals returned to the bat. From the numerical values of B_RMS and B_CRMS, we predicted the jitter thresholds by using either coherent crosscorrelation with phase (where B = B_RMS) or semicoherent crosscorrelation with just the envelope (where B = B_CRMS). Fig. 1E plots the predicted HP and LP thresholds along with the measured thresholds from the bats. Predicted semicoherent thresholds (green diamonds) were ≈55-70 ns over the filter conditions of the experiments. In contrast, the bats' thresholds (HP and LP data in Fig. 1E) extended systematically down to 10 ns for echoes whose frequencies were progressively less limited by the filters. Predicted coherent thresholds (brown squares) were 11-12 ns for both HP and LP experiments. We found little difference between coherent crosscorrelation by using the original wideband bat signal as a template (nonadaptive matched filtering over the full broadcast bandwidth) as in Fig. 1E, and by using a band-limited version of the original signal, where the spectrum of the template was adjusted to contain only the frequencies passed through the filters (adaptive matched filtering over the restricted band for each condition). The bats' thresholds dipped slightly below the predicted coherent thresholds for unrestricted echo bandwidths but rose progressively higher than coherent thresholds when more and more frequencies were removed from echoes. This result implies that the bat coherently processed echoes that contain the full frequency spectrum of broadcast sounds (11), but when frequencies were removed, the bat's acuity declined too steeply to be explained by coherent processing of the remaining frequencies.

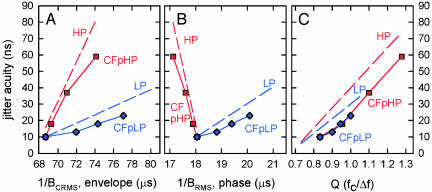
Quantifying Echo Frequency Content. The filter dial settings in the HP and LP experiments controlled the electronic channels that deliver the stimuli to the bat, controlling, in effect, the transfer function of the sonar target being simulated by the filters. We estimated the nominal 3-dB bandwidth of the channel transfer function from the difference between the high and low electronic-filter settings (Δf), and the nominal center frequency (f_c) was given as the mean of these frequencies. The bats' thresholds from Fig. 1E are replotted in Fig. 2 against the reciprocal of echo bandwidth (1/Δf; Fig. 2 A) and the reciprocal of echo center frequency (1/f_c; Fig. 2B). Threshold values are proportional to the reciprocals of both of these stimulus parameters, but the respective regression lines in Fig. 2 have different slopes for the HP conditions (red) and LP conditions (blue). With respect either to bandwidth or center frequency from the filter dial settings, the bats appeared to treat the HP and LP conditions as belonging to different experiments, not as two manipulations in the same experiment. The relations between HP or LP filtering and the bats' jitter thresholds were substantially the same with respect to measured values of 1/B_CRMS (Fig. 2D) and 1/B_RMS (Fig. 2E) as they were for estimates of 1/Δf (Fig. 2 A) and 1/f_c (Fig. 2B) derived from filter dial settings. The regression lines for HP conditions (Fig. 2D; red) and LP conditions (Fig. 2E; blue) still differ in their slopes, as though they were derived from different experiments. Thus, the difference in slope between HP and LP experiments (Fig. 2) does not depend on what method, filter settings or digital processing, is used to determine the bandwidth of the stimuli. The foregoing values are for absolute bandwidth in Hertz, whereas the relative bandwidth is the ratio of bandwidth to center frequency (Δf/f_c). When the bats' thresholds were replotted in terms of the reciprocal of relative bandwidth (f_c/Δf) in Fig. 2C, the regression lines for the HP and LP experiments were the same. Now, the bats appeared to treat the HP and LP conditions as being two different manipulations of just one experiment.

Fig. 2.

Jitter thresholds from Fig. 1E (bat 3, triangles; bat 5, circles) for different filter conditions (HP, red; LP, blue; BP, green). Data points shown with dashed regression lines and solid-line 99% confidence intervals. Measured thresholds are plotted against the reciprocal of echo bandwidth from filter settings (1/Δf) (A), the reciprocal of center frequency from filter settings (1/f_c) (B), echo Q from filter settings (f_c/Δf) (C), the reciprocal of CRMS bandwidth (B_CRMS) (D), the reciprocal of RMS bandwidth (B_RMS) (E), and echo Q as in C but with different scales to show BP condition (BP, green) (F). The value of Q is the reciprocal of normalized bandwidth for the target as a filter, and thus is normalized time-width for the target impulse response.

The reciprocal of relative bandwidth is the Quality Factor, Q (= f_c/Δf), which expresses the relative sharpness of an electronic filter's tuning as derived from its transfer function (16). For a given center frequency (f_c), sharper tuning (smaller Δf) means larger Q, or higher filter quality, because a sharper filter is more discriminative for its tuned frequency. Although the numerical value of Q is intended to measure frequency tuning, it also inversely describes a filter's impulse response in terms of the number of cycles the filter “rings” when the input is a single, sharp pulse. For example, a filter with a Q of 5 has a transfer function 5 times narrower than its center frequency, which is good for discriminating the tuned frequency from other frequencies, but it also has five peaks in its impulse response, which is a poor replica of the original pulse's single peak. Thus, higher filter quality for better discrimination of the tuned frequency means more ringing or less faithful reproduction of a sharp pulse. A sonar target can be conceived as a “filter” whose input is the incident sonar sound and whose output is the reflected echo. The target's transfer function shows its reflective strength at different frequencies, and its frequency selectivity can be expressed as a value of Q if the transfer function is created by tuning to a restricted range of frequencies in the incident sound. In our experiments, the ratio Q = f_c/Δf gives the relative sharpness of frequency tuning for the pass-band bounded by different HP and LP filter settings.

The values of Q used in our HP and LP experiments ranged from ≈0.7 to 1.3 (Fig. 2C), which represent minimal amounts of frequency selectivity consistent with echoes that might plausibly be received by bats in natural conditions. Substantially sharper filtering of echoes, that is, higher Q values than shown in Fig. 2C, would be environmentally unrealistic, because when natural targets in air are ensonified by wideband sounds they return wideband echoes, not echoes containing just a single narrow frequency band (resonance is not a dominant feature of small targets in air) (23). Nevertheless, to evaluate the robustness of the auditory computations underlying echo processing, we wanted to know whether the relation between delay acuity and Q in Fig. 2C holds true for more exaggerated tuning. Accordingly, we carried out the same jitter threshold experiment for echoes that were BP filtered to a narrow frequency band ≈55 kHz. Filter dial settings were 50 kHz HP and 60 kHz LP, which nominally gives f_c = 55 kHz, Δf = 10 kHz, and Q = 5.5. However, notch-rejection filtering was present in the bat's external ear at 50 kHz (18), which truncates the low-frequency end of echo spectra to about 55 kHz instead of 50 kHz. This restricts the effective stimulus frequencies for the BP condition to ≈55-60 kHz, so f_c = 57 kHz, Δf = 5 kHz, and Q = 11. Jitter detection thresholds for the same two big brown bats in the BP experiment are shown in Fig. 2F (green data points). Also shown in Fig. 2F is a single regression line derived from all of the data plotted against only the lower values of Q in Fig. 2C (green dashed line, with solid 99% confidence limits). The thresholds of the bats in the BP experiment for stimuli with a Q value of ≈11 were predicted by the regression line for thresholds in experiments with Q values of only 0.7-1.3, indicating that the relation of the bat's delay accuracy to Q is robust well outside of the range used in the HP and LP experiments.

Auditory Time/Frequency Representation. The mechanical action of the bat's cochlea disperses ultrasonic frequencies to sequential locations along the organ of Corti, creating many parallel frequency-tuned channels which segment the wideband FM sweeps of echoes into numerous overlapping time/frequency “slices” (24). Within these channels, neural transduction generates single spikes that register the times-of-occurrence of different frequencies in the sweeps (25-27). At higher levels of the auditory pathway, it is likely that volleys of spikes with different latencies representing the same time/frequency slices are used to make multiple estimates of echo delay (28). Each frequency thus may count for more delay precision than would be expected from the bandwidth alone, in which case the slope for deterioration of delay acuity ought to be steeper than the slope for ordinary coherent predictions (as in Fig. 1E), because removal of any one frequency segment removes more than one estimate of delay.

Each cochlear filter (CF) is a cascade of passive mechanical tuning and active electromechanical tuning and amplification (29, 30). Because of the active component, if the amplitude of an acoustic stimulus decreases at some particular frequency, the amount of gain and associated sharpness of tuning in cochlear channels tuned to that stimulus frequency almost immediately increases to compensate, so that the levels of excitation delivered by receptor cells to afferent neurons are compressed into a narrow range of only 5-15 dB for stimulus ranges up to as much as 50 dB (29, 30). For wideband sounds that span many frequency channels, auditory representation of fine details or sharp edges in the sound's spectrum would be smeared by the broad V-shape and overlap of auditory tuning curves compared to the narrow rectangular frequency bins of digital signal processing. The cochlear active process would boost gain at frequencies where the acoustic spectrum is weak, so the spectral profile actually registered ought to differ from that of the sound itself. Moreover, this equalization would be imperfect because of spectral smearing from the V-shaped tuning curves and overlap of the filters. We assumed that active gain compensation occurs in the bat's inner ear when the amplitude of echoes is reduced at the low-frequency or high-frequency end of the spectrum by the HP or LP conditions. This compensation would tend to flatten the echo spectrum as well as boost the background noise at those frequencies where the HP or LP conditions weakened the echoes, leading to higher gain. We modeled the CFs in bat's auditory periphery, incorporating an active process, and then tested the model as an alternative to the crosscorrelation receiver for generating predictions of delay accuracy. For this CF model, we used N parallel BP filters with biologically realistic V-shaped transfer functions (31) of the form W(f) = [1 + ({f - f₀}/0.12f₀)ν]^-1, where f₀ is the center frequency of each filter. To approximate existing physiological tuning data from FM bats (31), we set the slope of the high-frequency skirt (ν = 1.75 if f ≤ f₀) to be twice that of the low-frequency skirt (ν = 3.5 if f > f₀). The gains of individual filters at f₀ were adjusted to amplify the parts of the echo spectrum that had been attenuated by the HP or LP electronic filters (thus also increasing the background noise passing through these filters), and the resulting filter outputs were applied to estimating echo delay.

The problem of deciding whether the delay of successive echoes is jittered or not is equivalent to estimating the impulse response of the electronically simulated target (32, 33). For any one echo, this impulse response consists of a single, delayed delta function with different delays for jitter and no jitter. If C_est(f) is the receiver's estimate of the channel transfer function C(f), then the receiver's estimate of the effective signal spectrum is U(f)C_est(f), where U(f) is the Fourier transform of the transmitted signal. The optimum receiver for minimum mean-square error estimation of the target impulse response is

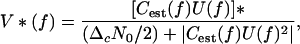where Δ_c is the expected duration of the target impulse response, and N₀ is the spectral density of the noise in Watts/Hz. We assume that C_est (f) is obtained by passing C(f) through a set of filters that are frequency translated, scaled versions of a window function W(f), i.e., 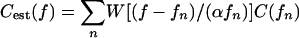, where α is a constant and the intervals between frequency samples f_n are small relative to the bandwidth of W(f), which implies that the filters are highly overlapping. The computed performance degradation for various values of the cutoff frequency is very sensitive to the shape of the window function W(f) that is used to obtain C_est(f), but the physiologically reasonable low-frequency (ν = 3.5) and high-frequency (ν = 1.75) window-function slopes gave good fits to the observed declines in delay accuracy.

Fig. 3 A and B shows the predicted jitter thresholds from the auditory CF model for the HP and LP conditions (CFpHP, red; CFpLP, blue). Whether plotted against the reciprocal of B_CRMS (Fig. 3A) or the reciprocal of B_RMS (Fig. 3B), the auditory CF model's predictions are aligned with the bats' thresholds. The predicted thresholds have coherent delay accuracy of ≈10 ns when the frequency content of echoes is unrestricted, and they decline sharply in accuracy when progressively more frequencies are removed from echoes at either the low-frequency or the high-frequency end of the spectrum. Moreover, the slopes of the CF-predicted thresholds are markedly different for the HP and LP experiments, closely paralleling the regression lines for the bats' thresholds. Most importantly, when the CF model's performance is replotted against echo Q in Fig. 3C, the predicted thresholds for HP and LP conditions fall along the same line, as though they were now being displayed on the axis the bat's receiver creates for representing delay.

Fig. 3.

Predicted thresholds in HP and LP experiments for CF model (CFpHP, red squares; CFpLP, blue diamonds) as plotted against 1/B_CRMS (A), against 1/B_RMS (B), and against Q (C). Dashed lines are regression lines of bats' HP (red) and LP (blue) thresholds from Fig. 2. The measured thresholds and the CF predicted thresholds have similar slope relations for HP and LP conditions relative to bandwidths or Q, indicating that the inner ear's coding scheme may be responsible for the unusual changes in the bats' thresholds, including the consistency of the relation to Q.

Conclusions

The bandwidth term in the bat's version of the equation for sonar delay accuracy, σ = (2πBd)^-1, is the reciprocal of echo bandwidth normalized to frequency, not the reciprocal of bandwidth itself (Fig. 2). The bats' Q-related performance in HP, LP, and BP experiments implies use of the number of wavelengths or cycles in the target impulse response, not the duration in units of time, to characterize the distribution of echo arrival-times along the axis of delay, or range. We found that a receiver model incorporating the two most salient physiological features of the auditory time/frequency representation (V-shaped tuning curves with different high- and low-frequency slopes, and an active process for compressive gain nonlinearity) replicates the relations between the bat's delay thresholds, echo bandwidth, and Q. Bats perform exceptionally well in tasks requiring classification of targets by shape by using a small number of echoes (34), and it is possible to transform time/frequency information to depict target shape from delays (35-38). Knowing that the underlying reciprocal relation is to relative bandwidth, Q, not absolute bandwidth, B, gives new insights into the nature of this transformation.