Abstract
A microfluidic device using on-chip passive pumping was characterized for use as a particle counter. Flow occurred due to a Young-Laplace pressure gradient between two 1.2 mm diameter inlets and a 4 mm diameter reservoir when 0.5μ L fluid droplets were applied to the inlets using a micropipette. Polystyrene particles (10μm diameter) were enumerated using the resistive pulse technique. Particle counts using passive pumping were within 13% of counts from a device using syringe pumping. All pumping methods produced particle counts that were within 16% of those obtained with a hemocytometer. The effect of intermediate wash steps on particle counts within the passive pumping device was determined. Zero, one, or two wash droplets were loaded after the first of two sample droplets. No statistical difference was detected in the mean particle counts among the loading patterns (p > 0.05). Hydrodynamic focusing using passive pumping was also demonstrated.
Keywords: Microfluidics, Resistive Pulse, Colloid, Enumeration
1 Introduction
Much work has been done to develop microfluidic systems that can enumerate particles in a colloidal suspension via the resistive pulse (i.e., Coulter) method. A microfluidic resistive pulse counter is appealing because of the many benefits that would result if successfully implemented: reduced sample volume, simplified operation, high throughput via parallelization, portability, and low unit cost, among others. Biomedical applications – hematological diagnostics in particular – would benefit the most from a microfluidic particle counter Larsen et al (1997); Koch et al (1999); Nieuwenhuis et al (2004); Chun et al (2005); Jagtiani et al (2006); Zhe et al (2007); Wu et al (2008a); Zheng et al (2008); Scott et al (2008); Wang et al (2008); Wu et al (2008b); Rodriguez-Trujillo et al (2008). Other microfluidic discrete particle detection applications such as enumeration of nanoscale polymer beads Saleh and Sohn (2002) or single molecules Saleh and Sohn (2003a) and antigen-antibody binding Saleh and Sohn (2003b); Carbonaro and Sohn (2005) have also been demonstrated. Detailed particle information (cell volume Ateya et al (2005), particle shape Arndt et al (2004), bacterial taxa Benazzi et al (2007)) can be obtained from suspended particle samples using a capacitance bridge Sohn et al (2000) or a lock-in amplifier Benazzi et al (2007). To date, most research efforts have focused on improving detection sensitivity or throughput, but pumping fluid through the particle counter requires substantial off-chip infrastructure in the form of tubing and syringe pumps, ultimately limiting the portability and increasing the cost of the device. An ideal pumping method for a portable particle counter would be self-contained on-chip and require minimal external equipment and energy.
Passive pumping offers an attractive approach because the surface tension contained within a single liquid droplet is harnessed to pump fluid through a microfluidic device. Only a syringe or micropipette is required to deliver the droplets. Flow induced by passive pumping has recently been characterized Berthier and Beebe (2007); Berthier et al (2008); Ju et al (2008); Chen et al (2009) and used in various applications: viral assay Zhu et al (2009), cell culture Meyvantsson et al (2008), and spatiotemporal control of concentration gradients Du et al (2009). While traditional pumping methods deliver carefully regulated and in some cases non-pulsatile flow, they all rely on external pumps or energy sources to generate physical forces on the chip to induce pumping Tüdös et al (2001). Passive pumping offers a simple and low-cost method of fluid transport with precise control over sample size and easy manipulation of the sample.
In this paper we describe the first integration of passive pumping with a microfluidic resistive pulse particle counter. Passive pumping was used to transport and hydrodynamically focus particles. Results generated from the passive pumping device were compared to a microfluidic resistive pulse counter that used a syringe pump. Output from both pumping methods was very similar, suggesting that passive pumping is a viable alternative to using syringe pumps for developing microfluidic devices in which cost, complexity, and sample volume must be minimized.
2 Theory
Passive pumping uses the pressure gradient that exists between two physically connected droplets of different radii Walker and Beebe (2002); Berthier and Beebe (2007). This method of flow is described by the Young-Laplace equation, in which the internal pressure of a droplet (P) can be described using the surface free energy (γ) and the drop radius (R):
| (1) |
The internal pressure of a small drop is greater than that of a large drop; connecting the two via a microfluidic channel will result in fluid flow. Fluid is directed by creating inlets with diameters smaller than their corresponding reservoirs or outlets. The pressure difference along a microchannel depends on the difference in radius between the pumping (inlet) port and the outlet port. Assuming the outlet port has a pressure of essentially zero due to its large radius, a 1.2 mm diameter inlet port, with a 0.5μL droplet, generates a pressure difference of approximately 240Pa. To maximize the pressure gradient caused by surface tension, hydrophilic fluids should be paired with hydrophobic inlet surface materials or vice versa.
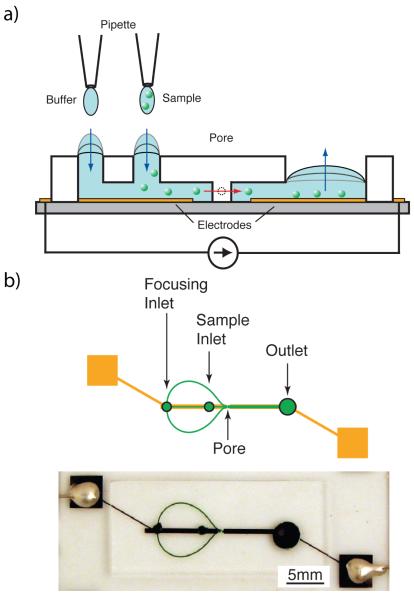
Resistive pulse detection is a well-established method of particle enumeration Coulter (1953). This method relies on the difference in conductivity between the particles and their surrounding solvent. When a particle is forced through an insulating pore while suspended in an electrically conductive medium, the electrical resistance of the pore briefly changes. Two electrodes on either side of the pore provide a constant excitation current. A rapid change in potential across the electrodes indicates that a particle has traversed the pore. In this way, pulses can be recorded and counted to determine the number of particles in a sample solution. For a more thorough treatment of resistive pulse detection, see DeBlois and Bean DeBlois and Bean (1970). Figure 1 illustrates our experimental setup and shows how passive pumping can be combined with resistive pulse detection to obviate the need for external pumps.
Fig. 1.
(a) A micropipette applies a small volume of fluid to the focusing and sample inlets. These inlets possess a higher internal pressure than the large reservoir drop. Due to this pressure gradient, fluid moves downstream towards the reservoir until the pressures equilibrate. Particles suspended in the sample fluid traverse the pore as they move downstream. The electrical resistance of the device is briefly changed while a particle is in the pore, yielding a detectable voltage pulse. (b) Focusing channels are used to align the particles before they traverse the pore, resulting in a more consistent signal. To minimize leaking, electrodes were fabricated lengthwise down the channel, stopping a short distance (100μm) on either side of the pore.
3 Device Design & Fabrication
The microfluidic device consisted of a glass substrate patterned with thin film Ti/Pt electrodes and a polydimethylsiloxane (PDMS) mold. The metal electrodes were fabricated by first cleaning a 2″x3″ glass microscope slide (Corning Inc., Corning NY) with piranha solution (H2SO4:H2O2, 7:3) for ten minutes, then rinsing in DI water for five minutes and drying with nitrogen. Hexamethyldisilazane (HMDS, Sigma, St. Louis, MO) was applied to the glass slide (3500RPM, 30s) as an adhesion layer. A positive photoresist (AZ1518, AZ Electronic Materials Corp., Somerville, NJ) was then spin-coated onto the slide and soft baked (100°C for 60s). Using a photomask, the resist was exposed to UV light (Canon PLA-501FA, Tokyo, Japan). The unwanted resist was then developed away using MF CD-26 developer (Microchem Corp., Newton MA). The slide was then hard baked for 50s at 100°C. Titanium (10nm) and platinum (100nm) were sputtered onto the slide using a custom DC/RF magnetron sputter system. Liftoff was performed by submerging the slide in methanol and placing it in an ultrasonic bath for 30 minutes.
The master for the PDMS mold was created by patterning negative photoresist (SU-8 2025, Microchem Corp., Newton MA) on a silicon wafer. The resist was spun to 35μm thickness, soft baked, selectively exposed to UV using a photomask, and post-exposure baked. The unexposed resist was dissolved using developer (SU-8 Developer, Microchem Corp., Newton MA). The wafer was then hard-baked. PDMS (Sylgard 184 Elastomer, Dow Corning, Midland, MI) components were mixed (base:curing agent, 10:1), degassed, and poured into a foil liner holding the wafer. To minimize inlet volumes only 5g of PDMS was used to coat a single 3″ wafer, which yielded a 1.5mm thick layer of PDMS. After pouring the PDMS, the wafer was tilted from side to side until the entire surface was coated and then placed on a level surface for 5 minutes. The mold was cured by baking at 125°C for 15min. The PDMS mold was then removed from the wafer and cut to size. Two identical molds were made: one for the passive pumping device and one for the continuous flow (syringe pump) device. All inlets were cored out using an 18 gauge (1.2mm diameter) dispensing syringe. The reservoir for the passive pumping device was 4mm in diameter and was made with a cork borer. The outlet for the continuous flow device was 1.2mm in diameter to allow for the attachment of a PDMS connector which was in turn attached via tubing to a syringe pump Mohanty et al (2006).
The PDMS molds were treated with oxygen plasma and irreversibly bonded to the glass slides. The connector was also plasma bonded to the outlet of the syringe pump driven device. While the PDMS channels were still hydrophilic, the device was first filled with 0.005%w/v Tween-20 solution, then flushed with 0.9%w/v saline (NaCl) solution. Treatment with Tween-20 solution reduced adhesion between polystyrene particles and glass. The saline was used because of its good conductivity relative to polystyrene and because it is nearly isotonic with mammalian cells. Saline was added to the two inlet ports until the meniscus was flush with the PDMS surface. The outlet reservoir in the passive pumping device was only partially filled to minimize effects from hydrostatic pressure. Tygon tubing (Tygon S-50-HL, Cole-Palmer, Vernon Hills, IL) was inserted into the connector outlet of the continuous flow device.
All channels were 35μm tall. The focusing and central channels were 200μm wide. The pore measured 15μm wide by 60μm long. The electrodes were 750μm wide and they were spaced 200μm apart.
4 Method
Sample Preparation
A sample solution was prepared by first passing a solution containing 10μm diameter monodisperse polystyrene beads (Polysciences, Warrington, PA) through a 12μm polycarbonate filter (Millipore, Ireland) to remove any large particles or debris. The beads were resuspended by vortexing and agitating rapidly with a micropipette and then manually counted with a hemocytometer. Saline solution was added to the bead suspension to obtain a final concentration of approximately 7,600 beads/μL.
Passive Pumping Technique
A micropipette was used to add 0.5μL droplets to the inlets of the passive pumping device. Droplets of either sample solution or saline were added approximately every 120s, but not before the pumping droplets were exhausted (i.e., flush with surface of the device). The total sample solution volume used for each experiment was 1.0μL. Samples were loaded by placing a 0.5μL droplet of saline on the focusing inlet followed by a 0.5μL droplet of sample solution on the sample inlet. Saline was loaded first to prevent back-flow of the sample solution. Intermediate wash steps were performed by placing a droplet of saline on the focusing inlet followed by a droplet on the sample inlet. At the end of each experiment, ten wash steps (a total of 10μL, or 5μL per inlet) were performed to ensure that the entire sample had flowed through the device.
The volume of wash solution needed was determined using the equation: Warrick et al (2007):
| (2) |
where α is the fraction of particles washed away by fluid, ζ is a geometric parameter, Vchan is the channel volume, Vt is the treatment (droplet) volume applied to the pumping port, and n is the number of times the droplet is applied. For channels with a cylindrical cross-section, ζ = 0.25; ζ is a measure of fluid replacement that depends on channel geometry. We used α = 1.0 since we assume all particles are washed away. Thus, clearing the sample inlet to 5% of the original bead concentration(ϕ = 95%) is possible with a single (n = 1) saline bolus of about 8.5μL (Vt = 8.5μL), assuming a sample inlet port height of 1.5mm and diameter of 1.2mm. To allow for variations in device geometry, 10μL of saline was used as mentioned above. Five microliters of saline were dispensed onto the sample and focusing inlets in 0.5μL droplets.
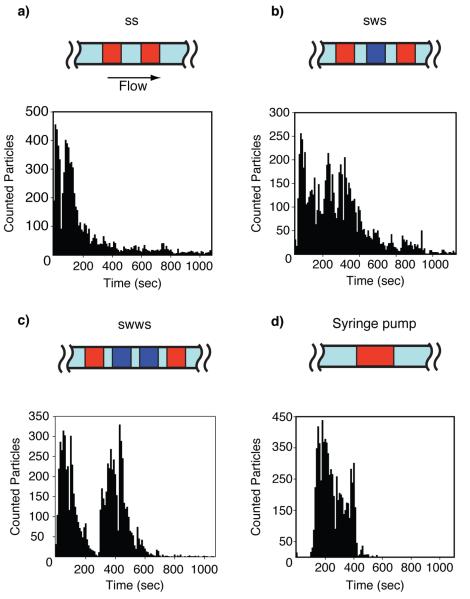
Because the sample solution is delivered to the passive pumping device in two 0.5μL droplets, we investigated the effect intermediate saline droplets had on total particle count. Figure 3 shows the three saline (wash) drop patterns used, with the syringe pump as a control. Each protocol was characterized three times (n = 3). When an aggregate of beads clogged the pore, gentle tapping on the device removed the clog. This temporary disruption of device volume affected the voltage readings, so voltage recordings during those events were omitted. These disruptions represented a small (< 1%) fraction of data points.
Fig. 3.
Pulse counts versus time for passive pumping devices using the droplet patterns (a) SS, (b) SWS, (c) SWWS. (d) A syringe pump was used for the control. Distinct peaks that exponentially decay can be seen in the passive pumping histograms, representing the bolus of particles from each sample droplet. The continuous flow of the syringe pump resulted in a well-defined bolus of particles. S = sample droplet. W = wash (saline) droplet.
Passive Drop Hydrodynamic Focusing
Fluorescence microscopy was used to validate hydrodynamic focusing in the passive pumping device. Deionized water was applied to the focusing inlet, and a solution of fluorescein in deionized water was loaded into the sample inlet. After the sample drops were loaded, a FITC image of the focusing region was captured for each drop ratio. The intensity of identical cross-sectional regions was examined and a threshold of approximately half of the maximal intensity was selected. The ratio of central stream width to channel width was determined by measuring the width of the region with intensity values above the threshold then dividing by the total width of the cross-sectional region.
Syringe Pump Device
A microfluidic device connected to a syringe pump in withdraw mode was used as an experimental control. One microliter of saline was loaded onto the focusing inlet, followed immediately by 1μL of sample onto the sample inlet. A 1mL syringe filled with saline and connected to the outlet via tubing was placed on the syringe pump. Fluid was withdrawn from the device at a flow rate of 1μL/min. Instead of performing 10 wash steps at the end of each experiment as in the passive pumping setup, 300μL of saline was pooled on top of the device, covering both inlets. The saline was allowed to flow through the device for 10 minutes.
Detection Circuit
The Ti/Pt electrodes were connected to the detection circuit by wires bonded using silver conductive epoxy. A constant DC voltage of 1.2V yielded pulses that could be distinguished from baseline noise using a LabView (National Instruments, Austin, TX) peak detection algorithm. A minimal DC voltage was selected to preserve the electrodes for prolonged operation Gencoglu and Minerick (2009). Because maximal pore occlusion causes a very small (≤15%) Gawad et al (2001) relative change in the total device resistance (≈ 100kΩ), the constant DC voltage can be approximated as a constant current supply.
The detection circuit consisted of three main stages. (1) The first component was the device connected in series with the DC voltage supply; the device can be modeled as a variable resistor. (2) A voltage follower (TL081, Texas Instruments) isolated the detection circuit from the device so that no current entered the amplifiers. DC components in the voltage follower output were removed by the high pass filter (15Hz cutoff frequency) preceding the first stage amplifier. (3) The second stage amplifier (TL082, Texas Instruments) had a gain of 3,300. Frequencies above 1kHz were attenuated by the op-amp’s frequency response. A data acquisition board (National Instruments USB-6122, Austin, TX) connected to a desktop computer collected the voltage output of the second stage amplifier. A custom-written LabView program recorded the voltage output and performed peak detection in real-time.
5 Results & Discussion
Hydrodynamic focusing reduces particle trajectory variability through the pore and reduces the chances for pore clogging, both of which improve signal quality by making the voltage peaks more consistent. Microfluidic methods for hydrodynamic focusing have been reported before Nieuwenhuis et al (2004); Simonnet and Groisman (2006); Chang et al (2007); Hairer and Vellekoop (2007); Yang and Hsieh (2007); Rodriguez-Trujillo et al (2008); Scott et al (2008); Watkins et al (2009), but none have used passive pumping. As shown in Figure 2, the relative radii of droplets on the focusing and sample inlets affects the width of the outer focusing streams and the inner sample stream.
Fig. 2.
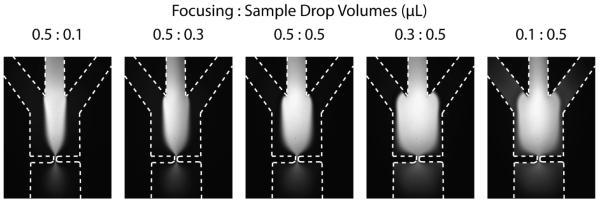
FITC images of hydrodynamic focusing (HDF) for ratios of focusing droplet volume to sample droplet volume. Drops of deionized water were applied to the focusing inlet, and a solution of fluorescein in deionized water was loaded into the sample inlet. The focusing drop fed the outer two side channels simultaneously, while the sample drop fed the central channel. Due to channel design, the fluidic resistance is approximately equal between the focusing inlet and the pore and between the sample inlet and the pore. When the focusing drop has a larger radius than the sample drop, the focusing streams are wider due to a higher pressure. When the ratio is reversed, the sample stream is wider than the focusing streams.
The channel resistance between the sample inlet and pore was the same as between the focusing inlet and the pore. Thus, the combined width of the outer focusing streams and the width of the sample stream were proportional to the pressures generated by their respective droplets. When equal droplet volumes were used half of the channel width was occupied by the sample stream; the remaining half of the channel width (the outer 25% on either side of the sample stream) was occupied by the focusing streams, as shown in Figure 2. The other droplet ratios show similar changes in stream width. The stream widths remain proportionally the same as they traverse the pore, so focusing happens regardless of the relative droplet volumes. The tradeoff is that less focusing happens before particles reach the pore for wider sample streams. In the interest of consistency, a ratio of 0.5:0.5 was used for all subsequent experiments.
Saline wash (W) droplets were inserted between sample (S) droplets in three different patterns to determine their effect on particle count (Figure 3). Hydrodynamic focusing was maintained throughout. The passive pumping flow rate was greatest when the drop was first applied to the inlet (≈ 2.35μL/min) and decreased over time as the droplet volume was depleted. Application of another droplet immediately elevated the flow rate again. Thus, over time the fluid flow rate generated by passive pumping resembled a sawtooth wave, which in turn altered particle counting rate over time. This effect is most pronounced in Figure 3a and 3c. In contrast, particles counted using continuous flow experienced a steep increase once the bolus of particles reached the pore and then monotonically decreased as the sample was depleted. The sawtooth shape is less apparent in Figure 3b. Possible reasons for this anomaly include particle clogging and human error in the application of wash and sample drops that might disrupt the direction of flow. Particles were detected earlier using the passive pumping method because the volumetric flow rate for passive pumping is initially higher than the fixed 1μL/min rate of the syringe pump. Among the passive pumping strategies, zero wash steps was the most effective, as discussed below. The SS passive pumping device successfully counted 95% of the beads in under fifteen minutes (11±3 minutes), with the first 50% of the beads counted in under 6 minutes. The syringe pump device counted 95% of the beads in 10 minutes (8±1 minutes), and the first 50% were counted in 4 minutes. Passive pumping achieved counting rates up to 45 beads/sec with the fastest rates occurring at the beginning of the test.
The repeatability of the three passive pumping protocols was compared to the continuous flow (syringe pump) device. A two-sample Student’s t-test was performed to determine if the different protocols yielded particle counts with equal means. The mean particle count for zero wash steps (7267 ± 350) was not significantly different from the particle count for one wash step (7166 ± 673; p < 0.05) or those for two wash steps (7690 ± 178; p < 0.05). Mean counts were not significantly different for any of the passive pumping protocols compared to continuous pumping (p < 0.05). The variation in particle counts is most likely due to the inherent error in counting particles using a hemocytometer, the variability in bead distribution in the sample solution, and counting errors caused by multiple particles coincident in the pore. The results suggest that there is no advantage to adding wash droplets between sample droplets because doing so did not ensure better sample flushing or counting efficiency.
The voltage pulse amplitudes generated from the different methods were also compared. Voltage pulses corresponded directly with beads passing through the pore. An example of signal output is shown in Figure 4. The average voltage pulse amplitudes for beads passing through the pore in protocols with zero, one, and two wash steps are shown in Table 1. The syringe pump again served as a control. The mean voltage pulse amplitude for all pumping methods was approximately equal for all of the pumping methods tested. The coefficient of variance of voltage pulse amplitudes varied for each pumping protocol (zero: 6%, one: 1.6%, two: 17.9%, syringe pump: 12%); the particle diameters had a coefficient of variance of 4%. This slight discrepancy can be attributed to multiple particles coincident in the pore or slightly off-centered beads traversing the pore.
Fig. 4.
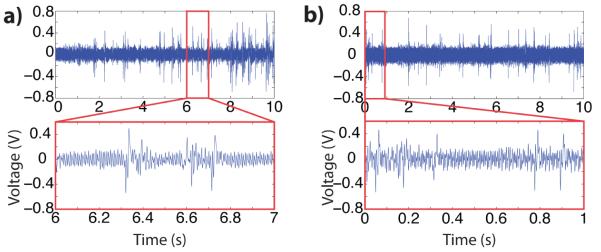
Ten-second voltage recordings for (a) passive pumping with zero wash droplets between samples and (b) syringe pump generating a 1μL/min flow rate. Insets: detail of one-second interval.
Table 1.
Comparison of voltage pulse statistics for each pumping technique. Zero, one, and two saline wash droplets were introduced between the two sample drops in the passive pumping device. All measurements are sample means plus/minus one standard deviation with n = 3. A hemocytometer was used to determine the initial sample particle concentration (7,600beads/μL).
| Pumping Method | Pulse Count | Pulse Amplitude (V) |
|---|---|---|
| SS | 7267±350 | 0.314±0.019 |
| SWS | 7166±673 | 0.312±0.005 |
| SWWS | 7690±178 | 0.346±0.062 |
| Syringe Pump | 7392±227 | 0.331±0.040 |
The results show that a microfluidic particle counter based on passive pumping is as effective as one based on syringe pumping. In all passive pumping experiments the sample counts were within 13% of the sample count obtained using the syringe pump and within 16% of the count obtained using the hemocytometer. For 10μm diameter beads, flow rates generated from 0.5μL droplets were sufficient to thoroughly flush a 1.0μL sample volume through the device in under twenty minutes. Higher flow rates could be achieved by increasing the difference between inlet and reservoir diameters or by increasing channel cross sectional areas.
6 Conclusion
Passive pumping is a direct and effective way to pump fluid through a microfluidic device. Hydrodynamic focusing can be implemented in a passive pumping platform. Careful channel design and droplet measurement could potentially yield highly controllable focusing results.
Within the context of point-of-care or diagnostic microfluidic devices, passive pumping has several benefits: ease of use, minimal infrastructure requirements, portability, and low cost. The use of sample droplets for pumping facilitates the use of smaller sample volumes, which are advantageous for biological assays (e.g., a blood sample). As the number of microfluidic control elements based on the inherent physics of the micro-scale continue to grow, future miniaturized devices stand to proliferate due to decreased complexity and cost.
For increased portability, the entire experimental device could ultimately be condensed into a hand-held point-of-use tool by replacing the desktop computer with a battery-powered micro-controller programmed with a pulse detection algorithm. The low-voltage excitation signal could also be battery-powered.
A few simple changes could further improve passive pumping device performance. The counting rate for passive flow could be drastically increased if multiple pores and electrically-isolated electrodes were operated in parallel. Fluid flow rate through the device could also be increased by implementing a hydrodynamic focusing regiment based on the clever use of laminar flow Rodriguez-Trujillo et al (2007); Watkins et al (2009); Mao et al (2009).
Contributor Information
Amy L. McPherson, Department of Biomedical Engineering, North Carolina State University, Raleigh & University of North Carolina at Chapel Hill, NC, Tel.: 919-513-8253 Fax: 919-513-3814 almcpher@ncsu.edu
Glenn M. Walker, Department of Biomedical Engineering, North Carolina State University, Raleigh & University of North Carolina at Chapel Hill, NC, Tel.: 919-513-4390 Fax: 919-513-3814 gmwalker@ncsu.edu
References
- Arndt S, Seebach J, Psathaki K, Galla H, Wegener J. Bioelectrical impedance assay to monitor changes in cell shape during apoptosis. Biosens Bioelectron. 2004;19(6):583–594. doi: 10.1016/s0956-5663(03)00269-0. [DOI] [PubMed] [Google Scholar]
- Ateya D, Sachs F, Gottlieb P, Besch S, Hua S. Volume cytometry: Microfluidic sensor for high-throughput screening in real time. Analytical Chemistry. 2005;77(5):1290–1294. doi: 10.1021/ac048799a. [DOI] [PubMed] [Google Scholar]
- Benazzi G, Holmes D, Sun T, Mowlem MC, Morgan H. Discrimination and analysis of phytoplankton using a microfluidic cytometer. IET Nanobiotechnol. 2007;1(6):94–101. doi: 10.1049/iet-nbt:20070020. [DOI] [PubMed] [Google Scholar]
- Berthier E, Beebe DJ. Flow rate analysis of a surface tension driven passive micropump. Lab Chip. 2007;7(11):1475–1478. doi: 10.1039/b707637a. [DOI] [PubMed] [Google Scholar]
- Berthier E, Warrick J, Yu H, Beebe D. Managing evaporation for more robust microscale assays part 2. characterization of convection and diffusion for cell biology. Lab Chip. 2008;8(6):860. doi: 10.1039/b717423c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carbonaro A, Sohn L. A resistive-pulse sensor chip for multianalyte immunoassays. Lab Chip. 2005;5(10):1155–1160. doi: 10.1039/b504827c. [DOI] [PubMed] [Google Scholar]
- Chang C, Hsiung S, Lee G. Micro flow cytometer chip integrated with micropumps/micro-valves for multi-wavelength cell counting and sorting. Jpn J Appl Phys. 2007;46(5A):3126–3134. [Google Scholar]
- Chen I, Eckstein E, Lindner E. Computation of transient flow rates in passive pumping micro-fluidic systems. Lab Chip. 2009;9(1):107–114. doi: 10.1039/b808660e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chun H, Chung T, Kim H. Cytometry and velocimetry on a microfluidic chip using polyelectrolytic salt bridges. Anal Chem. 2005;77(8):2490–2495. doi: 10.1021/ac048535o. [DOI] [PubMed] [Google Scholar]
- Coulter W. Means for counting particles suspended in a fluid. 2,656,508 US Patent. 1953
- DeBlois R, Bean C. Counting and sizing of submicron particles by the resistive pulse technique. Rev Sci Instrum. 1970;41:909–916. [Google Scholar]
- Du Y, Shim J, Vidula M, Hancock M, Lo E, Chung B, Borenstein J, Khabiry M, Cropek D, Khademhosseini A. Rapid generation of spatially and temporally controllable long-range concentration gradients in a microfluidic device. Lab Chip. 2009;9(6):761–767. doi: 10.1039/b815990d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gawad S, Schild L, Renaud P. Micromachined impedance spectroscopy flow cytometer for cell analysis and particle sizing. Lab Chip. 2001;1(1):76–82. doi: 10.1039/b103933b. [DOI] [PubMed] [Google Scholar]
- Gencoglu A, Minerick A. Chemical and morphological changes on platinum microelectrode surfaces in AC and DC fields with biological buffer solutions. Lab Chip. 2009;9(13):1866–73. doi: 10.1039/b820126a. [DOI] [PubMed] [Google Scholar]
- Hairer G, Vellekoop M. Experiments on hydrodynamic focusing of non coaxial sheath flows. Sensors 2006 5th IEEE Conference on.2007. pp. 431–434. [Google Scholar]
- Jagtiani AV, Sawant R, Zhe J. A label-free high throughput resistive-pulse sensor for simultaneous differentiation and measurement of multiple particle-laden analytes. J Micromech Microeng. 2006;16(8):1530–1539. [Google Scholar]
- Ju J, Park J, Kim K, Kim H, Berthier E, Beebe D, Lee S. Backward flow in a surface tension driven micropump. J Micromech Microeng. 2008;18(8):087,002. [Google Scholar]
- Koch M, Evans A, Brunnschweiler A. Design and fabrication of a micromachined Coulter counter. J Micromech Microeng. 1999;9(2):159–161. [Google Scholar]
- Larsen U, Blankenstein G, Branebjerg J. Microchip Coulter particle counter. Solid State Sensors and Actuators, 1997 TRANSDUCERS’ 97 Chicago. 1997 International Conference on.1997. pp. 1319–1322. [Google Scholar]
- Mao X, Lin S, Dong C, Huang T. Single-layer planar on-chip flow cytometer using microfluidic drifting based three-dimensional (3D) hydrodynamic focusing. Lab on a Chip. 2009;9(11):1583–1589. doi: 10.1039/b820138b. [DOI] [PubMed] [Google Scholar]
- Meyvantsson I, Warrick J, Hayes S, Skoien A, Beebe D. Automated cell culture in high density tubeless microfluidic device arrays. Lab on a Chip. 2008;8(5):717–724. doi: 10.1039/b715375a. [DOI] [PubMed] [Google Scholar]
- Mohanty S, Beebe D, Mensing G. [October 2009];Chips & tips: PDMS connectors for macro to microfluidic interfacing. Lab Chip. 2006 http://www.rsc.org/Publishing/Journals/lc/PDMS_connector.asp.1.
- Nieuwenhuis J, Kohl F, Bastemeijer J, Sarro P, Vellekoop M. Integrated Coulter counter based on 2-dimensional liquid aperture control. Sensor Actuat B-Chem. 2004;102(1):44–50. [Google Scholar]
- Rodriguez-Trujillo R, Mills CA, Samitier J, Gomila G. Low cost micro-coulter counter with hydrodynamic focusing. Microfluid Nanofluid. 2007;3(2):171–176. [Google Scholar]
- Rodriguez-Trujillo R, Castillo-Fernandez O, Garrido M, Arundell M, Valencia A, Gomila G. High-speed particle detection in a micro-Coulter counter with two-dimensional adjustable aperture. Biosens Bioelectron. 2008;24(2):290–296. doi: 10.1016/j.bios.2008.04.005. [DOI] [PubMed] [Google Scholar]
- Saleh O, Sohn L. Correcting off-axis effects in an on-chip resistive-pulse analyzer. Rev Sci Instrum. 2002;73(12):4396–4398. [Google Scholar]
- Saleh O, Sohn L. An artificial nanopore for molecular sensing. Nano Lett. 2003a;3:37–38. [Google Scholar]
- Saleh O, Sohn L. Direct detection of antibody-antigen binding using an on-chip artificial pore. P Natl Acad Sci USA. 2003b;100(3):820–824. doi: 10.1073/pnas.0337563100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott R, Sethu P, Harnett CK. Three-dimensional hydrodynamic focusing in a microfluidic Coulter counter. Rev Sci Instrum. 2008;79(4):046–104. doi: 10.1063/1.2900010. [DOI] [PubMed] [Google Scholar]
- Simonnet C, Groisman A. High-throughput and high-resolution flow cytometry in molded microfluidic devices. Analytical Chemistry. 2006;78:5653–5663. doi: 10.1021/ac060340o. [DOI] [PubMed] [Google Scholar]
- Sohn L, Saleh O, Facer G, Beavis A, Allan R, Notterman D. Capacitance cytometry: Measuring biological cells one by one. P Natl Acad Sci USA. 2000;97:10,687–10,690. doi: 10.1073/pnas.200361297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tüdös A, Besselink G, Schasfoort R. Trends in miniaturized total analysis systems for point-of-care testing in clinical chemistry. Lab Chip. 2001;1(2):83–95. doi: 10.1039/b106958f. [DOI] [PubMed] [Google Scholar]
- Walker G, Beebe D. A passive pumping method for microfluidic devices. Lab Chip. 2002;2(3):131–134. doi: 10.1039/b204381e. [DOI] [PubMed] [Google Scholar]
- Wang Y, Kang Y, Xu D, Chon C, Barnett L, Kalams S, Li D, Li D. On-chip counting the number and the percentage of CD4+ T lymphocytes. Lab Chip. 2008;8(2):309–315. doi: 10.1039/b713932b. [DOI] [PubMed] [Google Scholar]
- Warrick J, Meyvantsson I, Ju J, Beebe DJ. High-throughput microfluidics: improved sample treatment and washing over standard wells. Lab Chip. 2007;7(3):316–321. doi: 10.1039/b613350a. [DOI] [PubMed] [Google Scholar]
- Watkins N, Venkatesan B, Toner M, Rodriguez W, Bashir R. A robust electrical microcytometer with 3-dimensional hydrofocusing. Lab Chip. 2009;9(22):3177–3184. doi: 10.1039/b912214a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu X, Chon C, Wang Y, Kang Y, Li D. Simultaneous particle counting and detecting on a chip. Lab Chip. 2008a;8(11):1943–1949. doi: 10.1039/b804319a. [DOI] [PubMed] [Google Scholar]
- Wu X, Kang Y, Wang YN, Xu D, Li D, Li D. Microfluidic differential resistive pulse sensors. Electrophoresis. 2008b;29(13):2754–2759. doi: 10.1002/elps.200700912. [DOI] [PubMed] [Google Scholar]
- Yang A, Hsieh W. Hydrodynamic focusing investigation in a micro-flow cytometer. Biomed Microdevices. 2007;123:672–679. doi: 10.1007/s10544-006-9003-9. [DOI] [PubMed] [Google Scholar]
- Zhe J, Jagtiani A, Dutta P, Hu J, Carletta J. A micromachined high throughput Coulter counter for bioparticle detection and counting. J Micromech Microeng. 2007;17(2):304–313. [Google Scholar]
- Zheng S, Liu M, Tai YC. Micro Coulter counters with platinum black electroplated electrodes for human blood cell sensing. Biomed Microdevices. 2008;10(2):221–231. doi: 10.1007/s10544-007-9128-5. [DOI] [PubMed] [Google Scholar]
- Zhu Y, Warrick J, Haubert K, Beebe D, Yin J. Infection on a chip: a microscale platform for simple and sensitive cell-based virus assays. Biomed Microdevices. 2009;11(3):565–570. doi: 10.1007/s10544-008-9263-7. [DOI] [PMC free article] [PubMed] [Google Scholar]