Comparing Neural-Network Scoring Functions and the State of the Art: Applications to Common Library Screening

Abstract

We compare established docking programs, AutoDock Vina and Schrödinger’s Glide, to the recently published NNScore scoring functions. As expected, the best protocol to use in a virtual-screening project is highly dependent on the target receptor being studied. However, the mean screening performance obtained when candidate ligands are docked with Vina and rescored with NNScore 1.0 is not statistically different than the mean performance obtained when docking and scoring with Glide. We further demonstrate that the Vina and NNScore docking scores both correlate with chemical properties like small-molecule size and polarizability. Compensating for these potential biases leads to improvements in virtual screen performance. Composite NNScore-based scoring functions suited to a specific receptor further improve performance. We are hopeful that the current study will prove useful for those interested in computer-aided drug design.

Introduction

Because of the high cost and time requirements associated with traditional high-throughput screens, many researchers now use computational methods to prefilter candidate ligands prior to experimental testing. A number of ligand-based computational techniques for identifying likely binders have been utilized. These include 2D screening with fingerprints,¹⁻³ shape-based screening,^4,5 and pharmacophore matching,⁶ which identify potential actives by comparing their atomic connectivities, three-dimensional shapes, and three-dimensional pharmacophores to those of known ligands, respectively.

When structural information about a macromolecular drug target is known (e.g., from X-ray crystallography or NMR), computer docking programs are often used to identify candidate ligands. These programs position three-dimensional models of small molecules into models of target binding pockets; associated scoring functions subsequently predict the binding affinities of these “posed” candidate ligands. While certainly useful as an enrichment tool, docking has not yet reached its full potential. In part, the inaccuracies inherent in this technique stem from factors that are independent of the scoring function itself. For example, most docking programs do not account for full receptor flexibility, despite the fact that flexibility plays a critical role in modern theories of small-molecule binding (e.g., induced-fit^7,8 and population-shift⁹⁻¹² models). Indeed, efforts to account for receptor flexibility have proven effective and have led to the identification of a number of experimentally validated ligands.^8,13,14 Similarly, most docking programs do not account for binding-pocket water molecules, which can in some cases play critical roles in mediating receptor–ligand interactions.¹⁵ Even a “perfect” docking program would fail to identify true ligands when presented with sterically incompatible binding-pocket conformations and/or pockets devoid of crucial water molecules.

However, some of the inaccuracies associated with computer docking are intrinsic to the scoring functions themselves. In recent years, much work has been directed toward improving these functions without sacrificing speed.^16,17 Some of our own recent efforts have focused on training neural networks to rapidly predict the binding energies of protein–ligand complexes leading to the creation of two neural-network-based scoring functions, NNScore 1.0¹⁸ and NNScore 2.0.¹⁹ Neural networks are computer models that mimic, albeit inadequately, the microscopic architecture and organization of the brain. Biological neurons and synapses are simulated in silico as “neurodes” and “connections.” Data to be analyzed is encoded on an input layer of neurodes, triggering a cascade of signals that propagates through the network. Both the organization and number of the neurodes as well as the weights (i.e., strengths) assigned to each neurode–neurode connection serve to modify the initial input signal during propagation. The cascade eventually reaches an output layer of artificial neurons, where an analysis of the original input signal is ultimately encoded.

In the NNScore implementations, the strengths of the connections between neurodes were varied until the networks could reliably predict binding affinity when given descriptors of a ligand–receptor complex. For NNScore 1.0, these descriptors included the number of protein–ligand close contacts, categorized by AutoDock atom types; the electrostatic energy of those close contacts; the number of ligand atoms of each atom type; and the number of ligand rotatable bonds. For NNScore 2.0, the input additionally included the descriptors provided by the BINANA algorithm²⁰ (counts of the number of hydrophobic, π–π, hydrogen-bond, and salt-bridge interactions), as well as the components of the Vina scoring function (steric, hydrophobic, hydrogen-bond, and ligand-rotatable-bond terms).²¹

While some efforts have been made to demonstrate the favorable performance of these neural-network scoring functions, these efforts focused on a limited number of systems, and the neural-network functions were not directly compared to top-tier proprietary docking programs like Schrödinger’s Glide.²²⁻²⁵ In the current work, we use AutoDock Vina²¹ and Glide^26,27 to dock the diverse compounds of the NCI diversity set III, a popular compound library available through the National Cancer Institute (NCI), into the 40 protein receptors of the Directory of Useful Decoys (DUD).²⁸ Additionally, Vina- and Glide-docked poses are reevaluated using NNScore 1.0 and 2.0. The mean screening performance obtained when candidate ligands are docked with Vina and rescored with NNScore 1.0 is not statistically different than the mean performance obtained when docking and scoring with Glide. This is particularly noteworthy given that Glide, while state of the art, is expensive and has a restrictive token system. In contrast, AutoDock Vina and NNScore 1.0 are both free and open source.

Additionally, we note a correlation between certain chemical properties and the associated docking scores, suggesting systematic bias. For both Vina and NNScore, docking scores tended to correlate with small-molecule chemical properties like size and polarizability, regardless of the target receptor. Compensating in part for these potential biases improves virtual-screen performance. Creating composite scoring functions suited to a specific receptor can improve performance further still.

Though the mean screening performances of Glide and (Vina + NNScore 1.0) over all 40 DUD receptors are not statistically different, our results do confirm what has been found by others: the best scoring function to use for a specific pharmacological target, be it Vina, NNScore, or Glide, is highly system dependent.^23,29−32 Positive controls (known inhibitors), when available, should be included in virtual screens to ensure that the docking protocol chosen is suited to the system at hand. However, when positive controls are not available, we recommend (Vina + NNScore 1.0) as a potential alternative to proprietary docking programs like Schrödinger’s Glide.

Materials and Methods

Receptor Preparation

The 40 protein receptors of the DUD²⁸ were downloaded from the DUD website (http://dud.docking.org/). All ligands and water molecules were removed. Hydrogen atoms were added to the protein structures (neutral pH) and hydrogen bonds were optimized using Schrödinger Maestro’s Protein Preparation Wizard.⁶¹ These processed models were then converted to the AutoDock PDBQT format with MGLTools 1.5.4³³ for use in the Vina and NNScore screens.

Ligand Preparation

Models of ligands known to bind to the 40 DUD receptors were likewise downloaded from the DUD website. Additionally, the compounds of the NCI diversity set III were obtained from the website of the NCI/NIH Developmental Therapeutics program (http://dtp.nci.nih.gov/). All these small molecules were processed with Schrödinger’s LigPrep module to generate models with appropriate tautomeric, isomeric, and ionization states for pH values ranging from 5.0 to 9.0. These models were ultimately converted to the PDBQT format using MGLTools 1.5.4³³ for use in the Vina and NNScore screens, and to the SDF format for use in the Glide screens. A few molecular models could not be generated; 1560 NCI models were ultimately used in the virtual screens.

Docking Parameters

For Vina docking, the default parameters were used. All ligands were docked into regions (boxes) centered on the respective receptor binding pockets. The centers and dimensions of the boxes were taken from the DUD. Edge lengths ranged from 35.9 to 50.0 Å, and box volumes ranged from 56,365.8 to 88,845.5 ų. Each Vina docking generated multiple poses. For the Vina analysis, the best-scoring pose as judged by the Vina docking score was used. For the NNScore analysis, all Vina poses were reevaluated with NNScore 1.0¹⁸ and NNScore 2.0,¹⁹ and the best-scoring Vina pose as judged by NNScore was considered for subsequent analysis. In the case of NNScore 1.0, the original programmers provided 24 neural networks that were particularly adept at identifying potent ligands when given descriptors of crystallographic ligand–receptor complexes. The final NN1 scores for each docking were derived by averaging the output of these 24 networks.

For Glide docking, parameters similar to the defaults were likewise used. The docking grid was defined by two cubes centered on the DUD-specified active sites. The inner cube, with 14 Å edges, imposed restrictions on the location of the ligand center, and the outer cube, with 45 Å edges, imposed restrictions on the location of all ligand atoms. For each system, both the positive controls and the compounds of the NCI diversity set III were first docked with Glide HTVS. To test more advanced Glide docking protocols, the top 50% of these compounds were subsequently docked with Glide SP, and the top 25% of the remaining compounds were docked with Glide XP.³⁴ Glide-HTVS- and Glide-XP-docked models were also rescored with NNScore 1.0 and 2.0. The default parameters were again used for both.

In all screens, where there were multiple models of a distinct compound due to alternate tautomeric, stereoisomeric, or protonation states, the best-scoring model was selected, and all others were discarded.

Calculating Molecular Properties

Molecular properties were calculated using Schrödinger’s Maestro suite. Compounds were processed with LigPrep to optimize geometry and ensure electrical neutrality. QikProp was then used to calculate molecular properties.

Assessing the Performance of the Virtual Screens

Receiver operating characteristic (ROC³⁵) curves can be generated when performing virtual screens of compound libraries that include known binders. Following docking and scoring, the compounds are ordered by their docking scores. A moving cutoff is then employed that sweeps from the best predicted binder to the worst. At each cutoff, the list of compounds is partitioned. The compounds above the cutoff are tentatively considered to be binders, and the compounds below are considered to be nonbinders. If all compounds not known to be binders are considered decoys, true and false positive rates can then be calculated for each partition. The ROC curve is generated by plotting all (false positive rate, true positive rate) points. ROC or partial ROC curves were calculated for all screens. The trapezoidal rule was used to determine the areas under these curves.

ROC curves assess the performance of a virtual screen from the best predicted binder to the worst. In practice, however, computational chemists are typically interested in the top-ranked compounds. One useful way to assess the top-performing ligands is to determine the true positive rate for a given fixed false positive rate.³⁶ In the current work, we identify the true positive rate when the false positive rate is fixed at 5%. When required to facilitate the optimization of this metric, the ROC curve was smoothed using a linear interpolation as implemented in NumPy/SciPy.³⁷⁻⁴¹

The ROC curves generated using the multi-tiered (HTVS-SP-XP) Glide protocol against dihydrofolate reductase and epidermal growth factor receptor were not complete enough to calculate the early-performance metric. To maintain equal sample sizes for the ANOVA and t-test analyses, all screens against these two receptors were discarded when appropriate, regardless of the docking scoring protocol used. Mean and median early-performance metrics over all 40 DUD receptors were calculated using all available screen results.

Results and Discussion

The purpose of the current study is two-fold. First, we perform a systematic comparison of common AutoDock Vina,²¹ NNScore,^18,19 and Glide protocols. In this study, a “protocol” refers to the two-step process used to computationally identify potential ligands. First, a compound model must be placed within a model of the binding pocket. Second, the binding affinity of that posed compound must be estimated. These two steps are called docking and scoring, respectively, and are often combined into a single algorithm. Vina and Glide, for example, both dock and score potential ligands; NNScore 1.0 and 2.0 only score (or rescore).

We compare two neural-network docking scoring protocols, Vina–NNScore-1.0 and Vina–NNScore-2.0 (henceforth abbreviated Vina-NN1 and Vina-NN2, respectively) and several popular protocols that are based exclusively on either Vina or Glide. We show that while the performance of these docking schemes is highly receptor dependent, the mean screening performances of the Vina-NN1 and Glide protocols are not statistically different.²²⁻²⁵

Second, we demonstrate that there are biases in most of the docking protocols studied, as has been demonstrated for other scoring functions.^23,29−32 Correcting for these biases improves the performance of the Vina-NN1 protocol further.

Testing Docking Protocols: Receptor, Active, and Decoy Selection

In order to compare multiple docking protocols, it is useful to perform a series of “mock” virtual screens that draw from compound libraries containing both known ligands (“actives”) and presumed decoy molecules. As the actives are known a priori, screen performance can be assessed by examining the ability of a given docking protocol to accurately separate out actives from decoys. The performance of a given protocol is often receptor specific; consequently, it is prudent to perform multiple screens into many diverse receptors when attempting to assess global utility.

The Directory of Useful Decoys (DUD),²⁸ an excellent resource for facilitating these assessments, contains 40 diverse protein receptors and 2950 known actives. For each active, the DUD contains 36 topologically distinct presumed decoys that are by design chemically similar to the known inhibitors, as judged by metrics like molecular weight, cLogP, and the number of hydrogen-bonding groups. In the current work, we use the DUD receptors and known active compounds to assess several docking protocols; however, rather than using the DUD decoy molecules, we instead used 1560 models of compounds from the NCI diversity set III (presumed decoys), a set of publically available, diverse, drug-like molecules provided by the National Cancer Institute free of charge.

Without wishing to in any way disparage the DUD decoy set, which is certainly useful in many contexts, it is important to understand why we opted to use the NCI compounds as decoys instead. Factors that influence molecular binding can be divided into two general categories: those that are ligand specific (i.e., independent of the receptor) and those that are binding specific (i.e., dependent on specific receptor–ligand interactions). The number of ligand rotatable bonds is a good example of a ligand-specific factor, as the immobility of highly flexible ligands that generally occurs upon binding is thought to be entropically unfavorable, independent of the receptor. In contrast, receptor–ligand complementarity of hydrogen-bond donors and acceptors is a good example of a binding-specific factor, as it depends specifically on interactions between the ligand and the receptor. In predicting ligand binding, it is prudent to consider both ligand- and binding-specific factors.

The DUD decoys were specifically selected so as to be chemically similar to known actives; they consequently may lack the chemical heterogeneity that one would see in a set of compounds selected with diversity in mind (e.g., the NCI diversity set). On one hand, it is certainly possible that some scoring functions may be inappropriately biased in their assessment of ligand-specific factors. What if, for example, a scoring function inappropriately assigns better docking scores to compounds with larger dipole moments independent of the receptor, and coincidentally, the actives being screened tend to have larger dipole moments than the decoys? The idea of controlling for this inappropriate bias by intentionally selecting decoy molecules with dipole moments similar to those of the actives certainly has its appeal.

On the other hand, insufficient chemical heterogeneity in the decoys may unfairly bias the evaluation of scoring functions that rely on valid assessments of ligand-specific factors. What if, for example, a scoring function correctly considers the number of ligand rotatable bonds in assessing the likelihood of binding but the actives and decoys all have the same number of rotatable bonds? Such a scoring function would be inappropriately penalized because its ability to utilize information about ligand rotatable bonds would be underexploited. Indeed, these types of concerns have lead others to use modified versions of the DUD decoy set.^42,43 Of note, Vina includes one ligand-specific term in its scoring function (number of rotatable bonds),²¹ and the NNScore functions include additional ligand-specific terms related to the number of ligand atom types.^18,19 Consequently, while we believe convincing arguments can be made in favor of using the DUD decoys, in the current work, we opted to use the NCI compounds as decoys instead.

A separate issue related to decoy selection must also be addressed. High-throughput screens typically have hit rates that range from 0.1% to 1.0%;⁴⁴⁻⁵⁰ it is therefore reasonable to assume that for each DUD protein, the NCI set contains between 1 and 16 “decoys” that are in fact actives. A similar assumption underlies the set of DUD decoys, which have likewise not been explicitly tested to rule out binding. Possible inaccuracies in comparison metrics introduced by these kinds of assumptions are at least in part ameliorated by the fact that all the docking scoring protocols being compared are subject to the same assumption. Furthermore, the NCI set used in the current project may well have fewer true binders than the widely used DUD set, given that the DUD decoys were, as mentioned above, carefully chosen to be chemically similar to the DUD actives.

Comparing Docking Protocols: ROC Curves

Having selected the receptors, actives, and decoys, we next turn to the question of how best to evaluate virtual-screening performance. Among the many methods that have been considered,^36,51 receiver operating characteristic (ROC) curves are appealing because they are independent of the ratio of actives vs inactives and have desirable statistical properties. The area under the ROC curve (ROC-AUC) is thought to correspond to the probability that a known binder picked at random will rank higher than a known nonbinder picked at random.

To compare docking scoring protocols using the ROC-AUC metric, we docked NCI decoys and DUD actives into the 40 DUD receptors using AutoDock Vina²⁸ and Glide HTVS, a state of the art, fast docking algorithm designed specifically for screening large libraries. The Vina-docked poses were then rescored with NNScore 1.0¹⁸ and NNScore 2.0.¹⁹

The more rigorous Glide SP and Glide XP docking protocols were not used at this juncture because, while impressively precise, they are not as well suited for use in high-throughput virtual screens. Given that an average of 1634 compounds had to be docked into each of the 40 DUD receptors (74 DUD actives and 1560 NCI decoys), 65,350 individual dockings were required to test each docking protocol. We note that others have similarly eschewed an exclusive use of Glide SP/XP for projects requiring comparable numbers of individual dockings.⁵²

As has been shown previously,^{19,23,29−32} our results demonstrate that the ideal docking protocol for a given project is highly system dependent. For example, when the screens were assessed by the ROC-AUC metric, Vina–Vina performed better than Vina–NN1, Vina–NN2, and HTVS–HTVS for docking into the progesterone receptor and glycinamide ribonucleotide transformylase. Vina–NN1 performed best for docking into hydroxymethylglutaryl–CoA reductase and the glucocorticoid receptor. Vina–NN2 performed best for docking into epidermal growth factor receptor and platelet-derived growth factor receptor kinase. HTVS–HTVS performed best for docking into adenosine deaminase and AmpC β-lactamase (Table 1).

Table 1. Areas under ROC Curves (ROC-AUC).

receptor	Vina–Vina	Vina–NN1	Vina–NN2	HTVS–HTVS
angiotensin-converting enzyme	0.48	0.69	0.54	0.45
acetylcholinesterase	0.81	0.90	0.80	0.87
adenosine deaminase	0.29	0.48	0.60	0.74
aldose reductase	0.57	0.63	0.59	0.61
AmpC β-lactamase	0.62	0.45	0.66	0.86
androgen receptor	0.67	0.87	0.71	0.88
cyclin-dependent kinase 2	0.71	0.77	0.72	0.65
catechol O-methyltransferase	0.52	0.43	0.62	0.71
cyclooxygenase-1	0.58	0.61	0.62	0.69
cyclooxygenase-2	0.63	0.89	0.79	0.88
dihydrofolate reductase	0.78	0.88	0.85	0.71
epidermal growth factor receptor	0.71	0.76	0.83	0.68
estrogen receptor agonist	0.83	0.91	0.89	0.95
estrogen receptor antagonist	0.90	0.98	0.97	0.89
fibroblast growth factor receptor kinase	0.84	0.92	0.83	0.40
factor Xa	0.93	0.95	0.93	0.76
glycinamide ribonucleotide transformylase	0.93	0.88	0.85	0.51
glycogen phosphorylase β	0.38	0.26	0.25	0.68
glucocorticoid receptor	0.65	0.93	0.71	0.71
HIV protease	0.90	0.98	0.95	0.71
HIV reverse transcriptase	0.45	0.72	0.69	0.73
hydroxymethylglutaryl–CoA reductase	0.55	0.86	0.68	0.30
human heat shock protein 90	0.62	0.90	0.81	0.78
enoyl ACP reductase	0.81	0.81	0.86	0.67
mineralocorticoid receptor	0.59	0.81	0.82	0.92
neuraminidase	0.55	0.56	0.68	0.91
P38 mitogen activated protein	0.87	0.90	0.92	0.79
poly(ADP-ribose) polymerase	0.77	0.73	0.53	0.95
phosphodiesterase 5	0.82	0.87	0.88	0.78
platelet-derived growth factor receptor kinase	0.80	0.75	0.87	0.60
purine nucleoside phosphorylase	0.60	0.70	0.65	0.81
peroxisome proliferator activated receptor γ	0.94	0.96	0.97	0.73
progesterone receptor	0.72	0.66	0.67	0.63
retinoic X receptor α	0.59	0.93	0.87	0.98
S-adenosyl-homocysteine hydrolase	0.73	0.59	0.58	0.92
tyrosine kinase SRC	0.82	0.83	0.88	0.68
thrombin	0.92	0.95	0.93	0.84
thymidine kinase	0.46	0.63	0.60	0.53
trypsin	0.80	0.96	0.92	0.78
vascular endothelial growth factor receptor	0.84	0.81	0.88	0.61
average	0.70	0.78	0.76	0.73
median	0.72	0.82	0.81	0.73

Given that NN2 considers features of molecular binding that NN1 neglects, it is curious that for many individual receptors Vina–NN1 performs substantially better than Vina–NN2 (Table 2). One common criticism of neural networks is that, unlike some other machine-learning techniques, they are essentially “black boxes”; it is difficult to impossible to determine precisely how they come to their ultimate conclusions. Though speculative, we suspect two factors explain the favorable performance of Vina–NN1. First, the additional features of molecular binding that NN2 explicitly considers may not provide additional information over what NN1 can infer implicitly. For example, in estimating binding affinity, NN2 explicitly considers the number π–π stacking interactions; however, NN1 might be able to implicitly infer π–π stacking by considering the number of receptor and ligand aromatic carbon atoms that are in close proximity. Second, NN1 and NN2 assess ligand potency very differently. NN1 is trained to return a binary response: good binder or poor binder. In contrast, NN2 is trained to return a range of scores roughly equivalent to pK_i or pIC₅₀ values. It may be that binary classification is more effective than continuous classification in this case. Future versions of NNScore currently in development will return to the binary-classification paradigm.

Table 2. True Positive Rates When the False Positive Rates Are Fixed at 5%.

receptors	Vina–Vina	Vina–NN1	Vina–NN2	HTVS–HTVS	HTVS–SP–XP	HTVS–SP–XP–NN1	HTVS–SP–XP–NN2	composite (general)	composite (independent)
angiotensin-converting enzyme	0.04	0.25	0.02	0.10	0.08	0.10	0.06	0.24	0.44
acetylcholinesterase	0.40	0.64	0.25	0.74	0.69	0.69	0.65	0.51	0.66
adenosine deaminase	0.01	0.05	0.08	0.43	0.57	0.39	0.30	0.34	0.72
aldose reductase	0.02	0.05	0.16	0.08	0.08	0.04	0.08	0.05	0.70
AmpC β-lactamase	0.02	0.01	0.06	0.24	0.24	0.29	0.29	0.04	0.76
androgen receptor	0.12	0.39	0.25	0.54	0.54	0.57	0.46	0.20	0.39
cyclin-dependent kinase 2	0.09	0.18	0.15	0.10	0.25	0.21	0.13	0.49	0.48
catechol O-methyltransferase	0.14	0.05	0.13	0.00	0.09	0.09	0.09	0.36	1.00
cyclooxygenase-1	0.03	0.07	0.03	0.06	0.20	0.24	0.24	0.05	0.30
cyclooxygenase-2	0.07	0.45	0.24	0.70		0.11	0.59	0.09	0.48
dihydrofolate reductase	0.08	0.31	0.27	0.00		0.88	0.88	0.83	0.59
epidermal growth factor receptor	0.01	0.09	0.27	0.15	0.28	0.28	0.26	0.27	0.53
estrogen receptor agonist	0.45	0.40	0.48	0.79	0.69	0.79	0.66	0.54	0.38
estrogen receptor antagonist	0.42	0.99	0.74	0.73	0.77	0.82	0.82	0.87	1.00
fibroblast growth factor receptor kinase	0.17	0.49	0.23	0.06	0.08	0.09	0.11	0.69	0.71
factor Xa	0.77	0.74	0.55	0.38	0.58	0.57	0.57	0.78	0.79
glycinamide ribonucleotide transformylase	0.50	0.48	0.04	0.00	0.86	0.86	0.81	1.00	1.00
glycogen phosphorylase β	0.02	0.02	0.01	0.11	0.17	0.06	0.00	0.39	0.75
glucocorticoid receptor	0.08	0.70	0.16	0.30	0.15	0.12	0.10	0.61	0.71
HIV protease	0.50	0.97	0.66	0.32	0.49	0.53	0.57	0.64	0.98
HIV reverse transcriptase	0.07	0.09	0.18	0.38	0.30	0.20	0.28	0.29	0.53
hydroxymethylglutaryl–CoA reductase	0.06	0.22	0.02	0.00	0.03	0.03	0.00	0.33	0.83
human heat shock protein 90	0.01	0.24	0.23	0.13	0.17	0.13	0.21	0.85	0.73
enoyl ACP reductase	0.35	0.16	0.47	0.21	0.26	0.25	0.28	0.27	0.49
mineralocorticoid receptor	0.21	0.22	0.44	0.91	0.60	0.67	0.60	1.00	0.55
neuraminidase	0.02	0.05	0.03	0.81	0.90	0.69	0.65	0.47	0.95
P38 mitogen-activated protein	0.46	0.53	0.53	0.43	0.46	0.48	0.47	0.43	0.48
poly(ADP-ribose) polymerase	0.06	0.10	0.05	0.67	0.45	0.52	0.30	0.29	0.33
phosphodiesterase 5	0.26	0.42	0.46	0.32	0.31	0.39	0.35	0.55	0.64
platelet-derived growth factor receptor kinase	0.20	0.18	0.46	0.09	0.08	0.10	0.11	0.32	0.40
purine nucleoside phosphorylase	0.06	0.17	0.16	0.56	0.48	0.40	0.40	0.33	0.88
peroxisome proliferator activated receptor γ	0.82	0.81	0.87	0.41	0.62	0.58	0.57	0.78	0.97
progesterone receptor	0.10	0.31	0.14	0.05	0.00	0.04	0.00	0.16	0.35
retinoic X receptor α	0.20	0.74	0.42	0.80	0.50	0.45	0.45	1.00	1.00
S-adenosyl-homocysteine hydrolase	0.03	0.05	0.02	0.73	0.48	0.09	0.42	0.44	0.82
tyrosine kinase SRC	0.11	0.30	0.25	0.33	0.48	0.44	0.50	0.44	0.60
thrombin	0.65	0.74	0.60	0.46	0.77	0.78	0.77	0.95	0.84
thymidine kinase	0.01	0.15	0.08	0.09	0.14	0.14	0.09	0.36	0.76
trypsin	0.48	0.88	0.46	0.45	0.80	0.77	0.80	0.73	1.00
vascular endothelial growth factor receptor	0.24	0.25	0.50	0.27	0.27	0.27	0.33	0.33	0.66
average	0.21	0.35	0.28	0.35	0.39	0.38	0.38	0.48	0.68
median	0.10	0.25	0.24	0.32	0.38	0.34	0.34	0.43	0.70

Setting the specific details of virtual screens against individual proteins aside, the best way of assessing the global utility of a docking scoring function is to consider its performance over multiple diverse receptors. When the average area under the ROC curve calculated over all 40 DUD receptors was considered, Vina–NN1 and Vina–NN2 outperformed Vina–Vina and HTVS–HTVS. To determine whether or not this difference was statistically significant, we used a technique called analysis of variance (ANOVA).⁵³ ANOVA asserts the null hypothesis that the means of multiple samples are equal (i.e., that multiple samples are drawn from populations with the same mean). In this sense, ANOVA is similar to the t-test, which is limited to two samples. When assessing multiple samples, one might be tempted to simply perform multiple t-tests between all sample pairs; however, each t-test carries with it the risk of incorrectly rejecting the null hypothesis (i.e., committing a type I error by rejecting the conclusion that two samples have statistically equal means when in fact they are statistically equal). As more and more t-tests are performed, the chances of committing this error increase. ANOVA avoids the problem by considering multiple samples in conjunction rather than pairwise.

Both ANOVA and the t-test allow one to assess the degree of statistical significance via a p value. The p value in this case represents the probability that the multiple samples could have means that differ to the degree observed or greater, given that the null hypothesis is true (i.e., given that the samples are drawn from populations with equal means). If p < 0.05, the null hypothesis is rejected.

ANOVA analysis suggested that the mean screening performances of the Vina–NN1, Vina–NN2, Vina–Vina, and HTVS–HTVS protocols were not statistically different (p = 0.16, not quite the 0.05 required to reject the null hypothesis). Clearly, known inhibitors, when available, should be included in a virtual screen and used to determine which docking scoring protocol is best suited to the specific system at hand. In the absence of any information about known binders, however, we recommend docking with Vina and rescoring with NNScore 1.0, as that protocol did have the highest ROC-AUC mean and median performances.

Comparing Docking Protocols: The Metric of Early Performance

Though the ROC-AUC metric is frequently used to evaluate virtual-screening performance, some have criticized its use because it assesses that performance by considering all screened compounds from the best predicted binder to the worst.⁵⁴ In practice, computational chemists are most interested in the top-ranked compounds, the ones that will be subsequently submitted for experimental validation. It is therefore the initial portion of the ROC curve, some argue, that ought to be of primary interest. A number of performance metrics have been proposed to address this issue (e.g., the BEDROC metric⁵⁴ derived from a modified ROC curve that weights top-ranked compounds). Additionally, Hawkins et al.³⁶ recently suggested a simple approach using the “metric of early performance based on the ROC curve.” In this scheme, one analyzes a ROC curve to determine the true positive rate for a fixed false positive rate (5% in the current work).

We used the metric of early performance to compare the Vina-, NNScore-, and HTVS-based protocols to a common multi-tiered Glide protocol (HTVS–SP–XP)³⁴ that has been used extensively in the literature (see, for example, refs (52), (55), (56), and (57)). The top 50% best ligands as judged by the HTVS–HTVS protocol were subsequently redocked with Glide SP. The top 25% of the Glide-SP compounds were then redocked with Glide XP. These XP-docked poses were additionally rescored with NNScore 1.0¹⁸ and NNScore 2.0¹⁹ to facilitate comparison.

We note that the multi-tiered HTVS–SP–XP approach is best suited for docking large compound libraries. Admittedly, the analysis herein described required that only 1634 compounds be docked into each DUD receptor on average, suggesting that Glide-SP or -XP docking alone might have been feasible. However, as mentioned above, because we considered all 40 DUD receptors simultaneously, 65,350 dockings would have ultimately been required had the multi-tiered approach been abandoned. Others have similarly turned to multi-tiered Glide protocols for projects requiring comparable numbers of individual dockings.⁵²

Many compounds were filtered out in the initial HTVS and SP steps of the HTVS–SP–XP protocol and so were never docked/scored using Glide XP. Consequently, it was not possible to calculate a complete ROC curve for the HTVS–SP–XP protocol. However, by assuming that compounds filtered out in the preliminary HTVS and SP steps truly were poor binders (the reasoning implicit in the multi-tiered approach), it was possible to generate the arguably paramount initial portion of the ROC curve.

While individual results were system dependent, Vina–NN1 and Vina–NN2 again performed better on average than Vina–Vina as judged by the average early-performance metric (Table 2). Surprisingly, the mean performances of the HTVS–HTVS, HTVS–SP–XP, and Vina–NN1 protocols were not statistically different (ANOVA, p = 0.72). In contrast, t-tests comparing the mean performance of the HTVS–SP–XP protocol to that of the Vina–Vina and Vina–NN2 protocols led us to reject the null hypothesis of equivalence (t-test, p = 0.002 and 0.049, respectively). HTVS–SP–XP performed better, on average, than Vina–Vina and Vina–NN2.

To further compare the Glide XP and NNScore scoring functions, we reevaluated the HTVS–SP–XP poses with NNScore 1.0 and 2.0. As expected, early performance was highly system dependent. Nevertheless, ANOVA demonstrated that the mean performances of the HTVS–SP–XP, HTVS–SP–XP–NN1, and HTVS–SP–XP–NN2 protocols were not statistically different (p = 0.88). The mean performances of HTVS–SP–XP–NN1 and Vina–NN1 were likewise not statistically different (t-test, p = 0.70).

Correlations between Molecular Properties and Docking Scores: Artifactual or Physical?

In hopes of further improving virtual-screening accuracy, we next sought to specifically characterize scoring-function biases. Schrödinger’s QikProp program was used to analyze the screened compounds (known inhibitors and putative decoys). A statistical correlation between certain chemical properties and the average rank of each compound across all 40 DUD receptors was noted. Vina–Vina, Vina–NN1, and Vina–NN2 scores tended to correlate with properties associated with molecular size (molecular weight, total solvent accessible surface area, volume, number of ring atoms, and number of heteroatoms) and polarizability (Table 3). It is interesting that both Vina and the neural-network scoring functions demonstrated similar trends, even though they evaluate ligand binding using very different methodologies. Others have identified similar biases in the FlexX and Gold docking programs.⁵⁸ The HTVS–HTVS and HTVS–SP–XP protocols did not exhibit these biases to the same extent (Table 3). For the interested reader, we provide a real-world example of how scoring-function biases can affect screening results in the Supporting Information.

Table 3. R² (Goodness of Fit) Values Associated with Correlations between Average Rank Over All 40 Receptors and Selected NCI Small-Molecule Chemical Properties, As Determined Using Schrödinger’s Qikprop^a.

Qikprop Property	Vina–Vina	Vina–NN1	Vina–NN2	HTVS–HTVS	HTVS–SP–XP
molecular weight	0.45	0.42	0.48	0.03	0.20
solvent-accessible surface area (Å2)	0.43	0.48	0.44	0.02	0.15
solvent-accessible volume (Å3)	0.44	0.52	0.45	0.02	0.16
polarizability (Å3)	0.57	0.52	0.54	0.05	0.10
predicted hexadecane/gas partition coefficient	0.56	0.41	0.51	0.06	0.24
number of atoms in rings	0.70	0.32	0.50	0.23	0.07
number of heteroatoms	0.57	0.50	0.49	0.05	0.21

^aFor the HTVS–SP–XP protocol, only ligands that were scored using Glide XP in at least 10 out of 40 receptors were considered. In the end, this amounted to about 200 ligands.

These potentially artifactual correlations between ligand properties and docking scores may result in part from a general neglect of penalty terms that ought to be associated with binding (e.g., ligand desolvation, trapping binding-site waters, etc.). We do not mean to imply that Vina and NNScore neglect penalty terms entirely. The Vina scoring function, for example, has three steric-interaction terms.²¹ Additionally, NNScore may be able to implicitly account for some penalty terms as well; information about energetically unfavorable buried polar groups, for example, could potentially be extracted from the pairwise receptor–ligand atom-type information that NNScore considers. Nevertheless, both Vina and NNScore are likely “blind” to many important penalty phenomena. Indeed, Glide-based protocols may perform well relative to many other scoring functions²⁴ because they better account for these penalties, as evidenced by the fact that HTVS and XP scores are not strongly correlated with molecular weight (Table 3). Future versions of NNScore currently being developed will consider three-dimensional descriptions of ligand–receptor binding and so may be even more effective than current implementations.

On the other hand, one must consider the possibility that at least a portion of these scoring-function “biases” in fact represent accurate characterizations of small-molecule binding. To this end, we tested whether or not correlations exist between the molecular properties and experimentally measured binding affinities of known ligands independent of receptor. All the binding data deposited in the Binding MOAD database as of March 2013 was considered.⁵⁹ In total, 2081 entries representing 1598 unique compounds had both known structures and precise or approximate K_i measurements (i.e., measurements described as “=” or “≈”). We were ultimately able to calculate molecular properties for 1531 of these compounds.

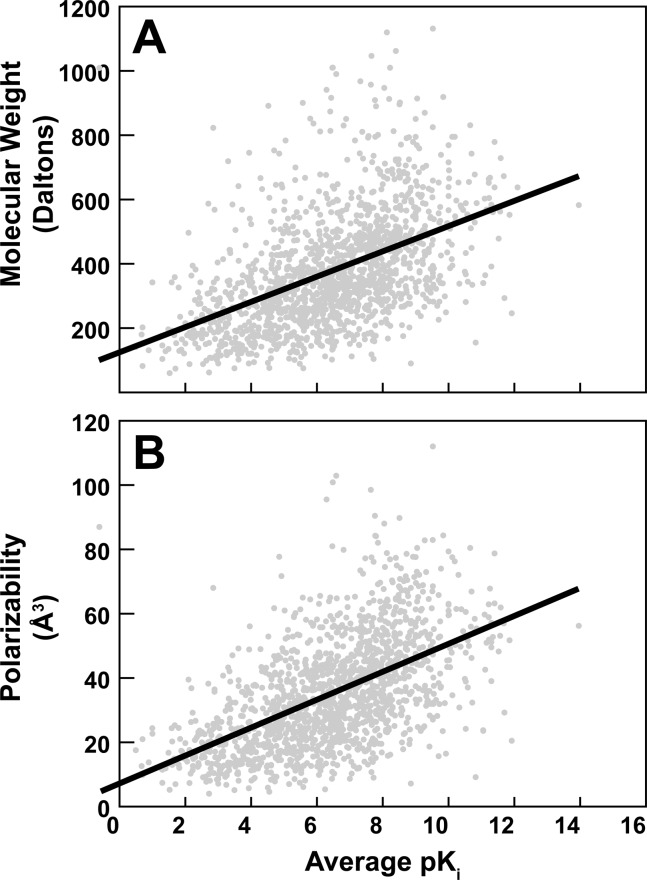
Interestingly, both molecular weight and polarizabiliy were correlated with the experimentally measured pK_i values; these molecular properties are plotted as a function of average pK_i (independent of receptor) in Figure 1A and B, respectively. Linear regression suggested that the relationship between molecular weight and pK_i was MW = 39.2710 (pK_i) + 122.1835, with a R² value of 0.23. A t-test on the slope coefficient yielded a p-value of 0.0, leading us to reject the null hypothesis that there is no true relationship between pK_i and molecular weight (i.e., that the true slope coefficient is 0). Similarly, the regression equation describing the relationship between polarizability and pK_i was pol = 4.3326 (pK_i) + 7.3163, with a R² value of 0.30. A t-test on the slope coefficient of this regression similarly produced a p-value of 0.0; the hypothesis that polarizability and pK_i are not correlated was thus similarly rejected.

Figure 1.

Molecular properties vs average experimentally measured pK_i values independent of the receptor. Linear regression is shown as a bolded line. (A) Molecular weight. (B) Polarizability.

Subjectively, the notion that ligand binding may be in part dependent on factors that are entirely ligand centric has some appeal. For example, while it is certainly true that in the absence of ligand–binding-site complementarity bigger is not necessarily better, larger molecules may well have more interacting moieties on average that serve to enhance potency if complementarity is assumed. On the other hand, it may be that the noted correlations between molecular properties and experimentally measured pK_i values are more reflective of traditional and perhaps flawed approaches to medicinal chemistry than of actual physical phenomena. For example, during the drug-optimization process, molecules do tend to increase in size.⁶⁰ Regardless, our goal ought to be to compensate for true biases while maintaining correlations that reflect actual physical phenomena.

Compensating for Bias: General-Purpose Scoring Functions

To compensate for potential scoring-function biases, we considered 15 relevant QikProp properties for each NCI decoy and known DUD inhibitor: accptHB (estimated number of hydrogen-bond acceptors), CIQPlogS (predicted aqueous solubility), dipole (computed ligand dipole moment), donorHB (estimated number of hydrogen-bond donors), SASA (total solvent accessible surface area, Ų), FISA (hydrophilic component of the SASA, Ų), FOSA (hydrophobic component of the SASA, Ų), mol_MW (molecular weight, daltons), nonHatm (number of heavy atoms), PISA (π component of the SASA, Ų), QPlogPC16 (predicted hexadecane/gas partition coefficient), QPlogPo/w (predicted octanol/water partition coefficient), Qppolrz (predicted polarizability, ų), rotor (number of rotatable bonds), and volume (total solvent-accessible volume, ų). Composite scoring functions were considered of the form

where NN1 is the Vina–NN1 score, P_i is the i^th chemical property (listed above), and C_i is a coefficient associated with that property.

A stepwise selection method was used to identify the composite scoring functions that best improved screen performance. First, training sets were generated for each DUD receptor by randomly selecting 75% of the associated known actives and merging them with the set of all NCI decoys. Similar testing sets were generated using the remaining known actives. All 15 coefficients were initially set to 0.0 so that the composite and Vina–NN1 scores were identical. The downhill simplex algorithm (SciPy) was then used to adjust the coefficients so as to maximize the average screen performance over all 40 training sets. Once training was complete, the resulting composite scoring function was then evaluated by calculating the average early-performance metric over the 40 testing sets, now without adjusting the coefficients.

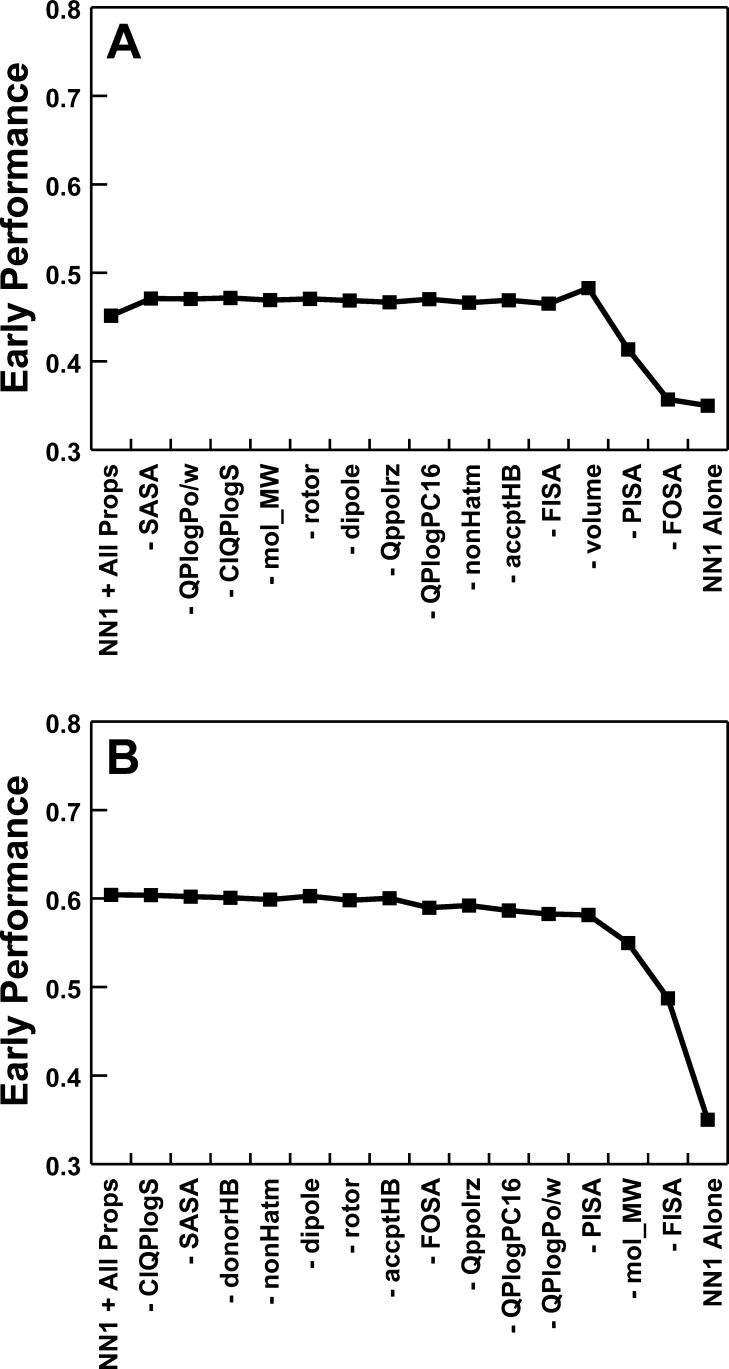
The above protocol was repeated; each time, a different coefficient was fixed at 0.0 so that the associated chemical property was essentially ignored. The single chemical property that when discounted was associated with the smallest drop in the average screen performance over the 40 testing sets was identified. A new set of 14 chemical properties was generated by excluding this chemical property. In total, this elimination step was repeated 15 times until no additional chemical properties remained (Figure 2A).

Figure 2.

Screen performance when composite scoring functions were used. In each graph, the leftmost data point describes the average performance over all 40 DUD receptors when a composite function that incorporates the Vina–NN1 score together with 15 small-molecule properties is used. Advancing rightward, composite functions are used that progressively incorporate fewer chemical properties. The rightmost data point shows screen performance when Vina–NN1 alone is used. (A) Single general-purpose function. (B) Independent composite scoring functions generated for each receptor.

A general-purpose scoring function was identified by considering the minimum number of chemical properties required to maintain optimal early performance (Figure 2A). Specifically, when the compounds were ranked by (NN1 + 0.1093 × donorHB + 0.0011 × FOSA + 0.0008 × PISA), the average early-performance metric over all 40 receptors was 0.48, substantially improved over the 0.35 obtained with Vina–NN1 alone. A t-test in fact required that we reject the notion that the mean performances of these two screens were statistically equal (p = 0.04) (Table 2, composite/general).

Given that we opted to use decoys that were not necessarily chemically similar to the DUD actives, it was especially important to ensure that the above general-purpose scoring function was not overtrained. For example, consider the hypothetical possibility that the decoys and DUD actives all have fewer than three and more than four hydrogen-bond donors, respectively. It would be possible to identify the actives using ligand-specific factors alone, independent of any important ligand–receptor interactions.

On the other hand, some ligand-specific factors (e.g., the number of rotatable bonds) may well be legitimately useful for distinguishing actives from decoys. It is not unreasonable to expect some genuine enrichment when compounds are ranked by a scoring function comprised exclusively of ligand-specific terms; nevertheless, one would expect that screen performance would improve further still when additional binding-specific terms (e.g., the NNScore) are included.

To ensure that actives were not being identified based on their chemical properties alone, we generated a second scoring function of the same form (0.1093 × donorHB + 0.0603 × FOSA + 0.0458 × PISA), comprised exclusively of the ligand-specific terms of the parent general-purpose function. The average early-performance metric over all 40 receptors when the ligands were ranked by this ligand-specific scoring function was 0.22. A t-test required that we reject the null hypothesis that the mean performances of the ligand-specific scoring function and its parent function were statistically equivalent (p = 0.00005), suggesting that the general-purpose function achieved its enhanced performance by considering both ligand-specific and binding-specific factors.

Compensating for Bias: Receptor-Specific Scoring Functions

The implicit assumption behind the creation of any general-purpose scoring function is that a single function can perform optimally across any number of receptors; however, given the demonstrated system dependence of scoring functions in general, this supposition is not likely to be correct. We therefore repeated the above scoring-function optimizations, now generating an independent composite scoring function for each receptor (Figure 2B).

The average early-performance metric over the 40 receptors was substantially improved when receptor-specific scoring functions that included terms for FISA, mol_MW, and volume were employed (0.68). A t-test required us to reject the null hypothesis that the mean early-performance metrics of this scoring function and the general-purpose scoring function described above were statistically equivalent (p = 0.00073; Table 2, composite/individual). An analogous scoring function containing only ligand-specific terms was also generated, as above. Again, we rejected the null hypothesis that the mean performances of the ligand-specific scoring function and its parent function with the additional NN1 term were statistically equivalent (0.53 vs 0.68, p = 0.01).

It is not necessarily our purpose to provide specific composite functions for others to use in their virtual screens; rather, we wish to demonstrate the general utility of deriving such functions when positive controls (known inhibitors) are available. A composite scoring function tailored to a specific receptor and designed to optimize the ranking of known inhibitors can potentially enhance virtual-screening performance.

Conclusion

The performance of a docking scoring protocol is highly dependent on the specific receptor being studied. When possible, positive controls (known binders) should be included in the screen so many different protocols can be tested. However, in the absence of known ligands and when a free, open source, general-purpose solution is sought, docking with AutoDock Vina and rescoring with NNScore 1.0 is an excellent option. We are hopeful that this work will help guide computational chemists in their efforts to best utilize computer-docking programs.

Supporting Information Available

Real-world example of how scoring-function biases can affect screening results. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States