Fast and accurate fitting of relaxation dispersion data using the flexible software package GLOVE

Abstract

Relaxation dispersion spectroscopy is one of the most widely used techniques for the analysis of protein dynamics. To obtain a detailed understanding of the protein function from the view point of dynamics, it is essential to fit relaxation dispersion data accurately. The grid search method is commonly used for relaxation dispersion curve fits, but it does not always find the global minimum that provides the best-fit parameter set. Also, the fitting quality does not always improve with increase of the grid size although the computational time becomes longer. This is because relaxation dispersion curve fitting suffers from a local minimum problem, which is a general problem in non-linear least squares curve fitting. Therefore, in order to fit relaxation dispersion data rapidly and accurately, we developed a new fitting program called GLOVE that minimizes global and local parameters alternately, and incorporates a Monte-Carlo minimization method that enables fitting parameters to pass through local minima with low computational cost. GLOVE also implements a random search method, which sets up initial parameter values randomly within user-defined ranges. We demonstrate here that the combined use of the three methods can find the global minimum more rapidly and more accurately than grid search alone.

Introduction

Analysis of protein dynamics is a highly topical area that aims at an understanding of the detailed mechanisms by which proteins function (Karplus 2010). Relaxation dispersion NMR spectroscopy is one of the most powerful techniques available for quantitation of protein dynamics (Tollinger et al. 2001; Loria et al. 1999), providing site-specific information on chemical (conformational) exchange processes in proteins on μs–ms time scales. Detailed insights into the thermodynamics and kinetics of many important biological processes, including enzyme catalysis (Bhabha et al. 2011; Henzler-Wildman et al. 2007; Boehr et al. 2006), protein-protein interaction (Vallurupalli et al. 2008; Sugase et al. 2007a; Sugase et al. 2007b), and protein folding (Yanagi et al. 2012; Meinhold DW and Wright PE 2011), have been obtained from relaxation dispersion experiments. An advantage of this method is that it can probe low-populated excited states that are invisible to conventional biophysical methods. Structural information on the invisible excited state is also obtained in the form of the chemical shift differences between the ground and excited states. Remarkable progress has recently been made in development of methods for determination of three-dimensional structures of low-populated (excited) states using the chemical shift differences obtained from relaxation dispersion experiments as conformational restraints (Neudecker et al. 2012; Bouvignies et al. 2011).

Needless to say, it is crucial to fit relaxation dispersion data accurately for a good understanding of protein functions in the light of a dynamic structure. Several computer programs to analyze relaxation dispersion data have become publicly available, such as GUARDD (Kleckner and Foster 2011), NESSY (Bieri and Gooley 2011), CATIA (http://pound.med.utoronto.ca/~flemming/catia/), and CPMGFit (http://cpmcnet.columbia.edu/dept/gsas/biochem/labs/palmer/software/cpmgfit.html). These programs fit relaxation dispersion curves to the theoretical equation using the Levenberg-Marquardt algorithm or the interior-point algorithm (Press et al. 2007). Although these algorithms are widely used for non-linear least square fitting, a common drawback is that they often become trapped in local minima, resulting in incorrect fitted parameters. This issue is more serious in global fits, in which some parameters, such as the exchange rate and population in relaxation dispersion curve fitting, are shared among multiple datasets (e.g. dispersion data for multiple residues), because more local minima exist in the parameter space. (Note that the terms “global” and “local” are used for both the minimum least-squares errors and for fitting parameters in this paper. The terms “global minimum” and “local minimum” represent the minimum least-squares errors, and “global parameter” and local parameter” represent fitting parameters.) To find the global minimum that provides the best-fit parameter values, the dataset should be fitted multiple times from different initial parameter sets within a certain parameter space. To explore the whole parameter space, the aforementioned programs use the grid search method, in which each parameter range is divided by a user-specified grid size, and the dataset is fitted from the parameter sets on all grid points. The grid search, however, fails to find the global minimum in cases where there is a local minimum between the global minimum and the grid point nearest to it. Whether such a local minimum exists or not depends on how large the parameter ranges are and how many grid points are defined. To avoid such local minima, the grid sizes should be sufficiently large. An increase in the grid size, however, requires longer computational time. Grid sizes are usually uniformly increased for all parameters because it is difficult to determine which parameter requires a larger grid size before the fit. The grid search is usually time-consuming, particularly for global fits because of the large number of local minima. Therefore an alternative method that can pass through local minima is desirable, to find the global minimum with lower computational cost.

Here, we demonstrate fast and accurate fitting of relaxation dispersion data using a newly developed software package GLOVE (global and local optimization of variable expressions). GLOVE, a non-linear least square-fitting program utilizing the Levenberg–Marquardt algorithm, is capable of hybrid local and global fits of relaxation dispersion data. To enable the fitting parameters to pass through local minima, we implemented a new fitting method that minimizes global parameters and local parameters alternately. Using this method, a parameter set that becomes trapped in a local minimum during the minimization of the global parameters can be further minimized in the subsequent minimization of local parameters. In the following round of the minimization process, the global parameters will also be further minimized. Although this minimization method is powerful, it cannot minimize a parameter set trapped in local minima of both global and local parameters. Thus, we also incorporated the Monte Carlo-minimization method (Metropolis et al. 1953; Kirkpatrick S 1983; Li and Scheraga 1987) within GLOVE, which can pass through local minima by adding random values to the parameter set, followed by additional minimization. Moreover, the grid search method and the random search method, which selects initial parameter values randomly from within the user-defined ranges, were also implemented in GLOVE. We fitted experimental relaxation dispersion data using these methods and several combinations of them. None of the fits using solely a grid search found the global minimum, whereas almost of all fits converged to the global minimum as long as the new minimization method was used at the end of the fits. Furthermore, starting Monte Carlo-minimization from a local minimum found by random search reached the global minimum more rapidly than other methods.

Theory and Methods

The GLOVE program

In what follows, characters written in Courier New represent the GLOVE related computational words such as command, keywords, and options used in the command lines, GLOVE input files or GLOVE output files.

GLOVE is a command line C++ program developed to solve non-linear least square problems rapidly and accurately utilizing the Levenberg–Marquardt algorithm (LMA). For relaxation dispersion curve fitting, LMA minimizes iteratively the following target function:

$${\chi }^2=\sum _{i=1}^N{\left(\frac{R_2^{i,exp}-R_2^{i,\text{calc}}}{{\sigma }^i}\right)}^2,$$ (1)

where R₂^i,exp and R₂^i,calc are experimental and calculated effective R₂ relaxation rates, R₂^eff, respectively, and σⁱ is the estimated experimental uncertainty described below.

GLOVE has five methods (ONE, ONEEX, GRID, RANDOM, and MCMIN) to set up initial parameter values, which are subsequently minimized using LMA. These methods can be run sequentially in any order, and the same method can be repeated. The best-fit parameter set that provides the lowest χ² value is stored in the memory, and is replaced with a better parameter set whenever one is found during a fit.

ONE is a single point minimization starting from the lowest limit, or an initial value optionally defined in the input file. Global and local parameters are separated, and they are minimized alternately. Once the minimization becomes trapped in a local minimum, usually during the minimization of global parameters, the fit stops. ONEEX is the same as ONE except that the fit does not stop until both global and local parameters become stuck in local minima. In the case of global fits, ONEEX provides better results than ONE, but it is much slower to converge than ONE. The GRID, RANDOM and MCMIN methods adopt the same stopping condition as ONE because these methods are designed to search the parameter space rapidly at the initial and middle stages of a fit.

GRID represents the grid search method. It was designed to search global parameters and local parameters separately for a global fit. Initially, global parameters are fixed to a grid point, and local parameters of each dataset are optimized using the grid search algorithm. Subsequently, the global parameters are unfixed, and all parameters including global parameters are minimized starting from the optimized local parameters. This process is repeated until all grid points of the global parameters have been examined.

RANDOM and MCMIN correspond to the random search method and the Monte Carlo-minimization method, respectively. RANDOM chooses initial values randomly from the user-defined parameter range, followed by minimization. It is used for searching the global minimum roughly from the whole parameter space. The fit using RANDOM is repeated by the user-defined iterations. In contrast to RANDOM, MCMIN is used for searching more finely for the global minimum, starting from the vicinity of the current best-fit parameter set found by RANDOM (or other methods). A detailed description of MCMIN is given in the next section.

The Monte Carlo minimization

The Monte Carlo-minimization method is a version of the simulated annealing protocol utilizing the Metropolis criterion (Metropolis et al. 1953; Kirkpatrick S 1983). It has been successfully applied by Scheraga and co-workers to find the minimum energy structure in a peptide folding simulation (Li and Scheraga 1987) by randomly changing a dihedral angle among all the variable dihedral angles, followed by energy minimization to bypass large energy barriers. The energy-minimized conformation is examined by the Metropolis criterion to compare it with the previously accepted conformation. The GLOVE version of the Monte Carlo-minimization (MCMIN) defines the initial parameter values as the current best-fit parameter values plus or minus random values that distribute in a Gaussian manner, enabling the parameter set to pass through a local minimum (Figure 1). The new parameter set is minimized using LMA, and is accepted if χ² is smaller than that of the current best-fit parameter set. The MCMIN calculation continues to run as long as MCMIN finds a better parameter set (passes through a local minimum) within the user-specified number of iterations, typically set to more than 5. Namely, the iteration count of the MCMIN calculation is reset to 0 if χ² decreases. The amplitudes of the random values are controlled by a scaling factor defined in the GLOVE input file. Note that it is important to choose an appropriate scaling factor to minimize χ² efficiently. If the scaling factor is too small, local minima cannot be passed through. On the other hand, if the scaling factor is too large, the new parameter set becomes quite different from the current best-fit parameter set, resulting in a significant increase in χ². To find the global minimum rapidly and accurately, MCMIN should be run repeatedly with successive reductions in the scaling factor. At the initial stage of fitting, the fitting parameters are usually far from the best-fit values, and thus the scaling factor should be set to a large value. At later stages, the variation of the parameters should be smaller as the parameters approach the global minimum.

Figure 1.

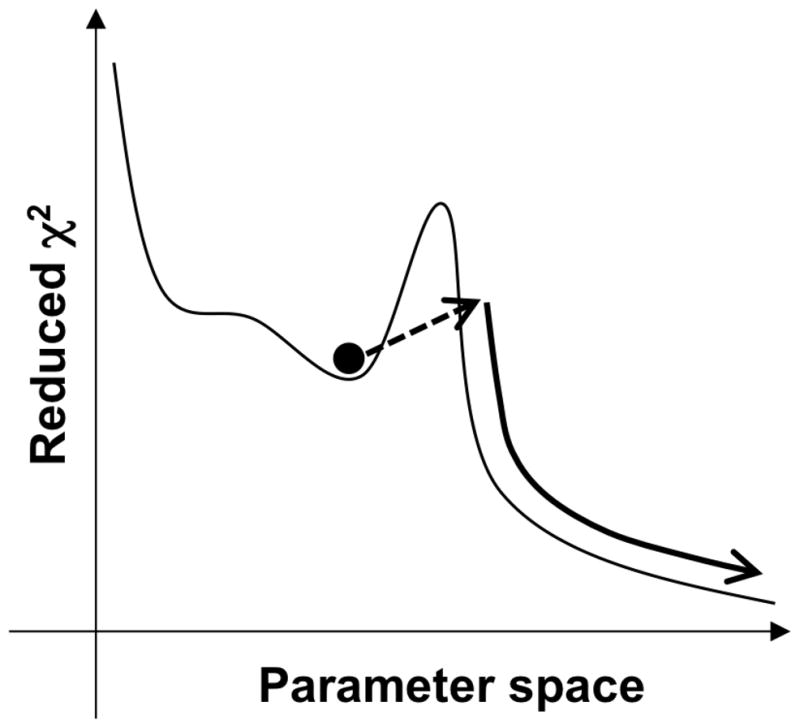
Schematic representation of the Monte-Carlo minimization method implemented in GLOVE. The dashed line arrow represents the Monte-Carlo process that adds random values to the current best fit parameters, enabling the parameters to pass through a local minimum. The reduced χ² value usually increases in this step. The new parameter set is subsequently minimized as represented by the curved solid arrow.

Fitting model for a two-state exchange

Although GLOVE incorporates many fitting models, including two- and three-state exchange models, here we describe the Carver and Richards equation (Carver and Richards 1972), which is most frequently used for relaxation dispersion curve fitting, and its implementation in GLOVE. Other fitting models are described in Supporting Information.

The Carver and Richards equation, called Richards in GLOVE, calculates well-approximated R₂^eff values for all exchange regimes of a two-state exchange model ( $\text{A}\underset{k_{\text{BA}}}{\overset{k_{\text{AB}}}{\rightleftarrows }}\text{B}$) under the experimentally accessible condition. The original equation is represented as

$$\begin{array}{l}{R}_2^{\text{eff}}=\frac{1}{2}\left\{R_{2\text{A}}^0+R_{2\text{B}}^0+k_{\text{AB}}+k_{\text{BA}}-\frac{1}{{\tau }_{\text{CP}}}{cosh}^{-1}\left[D_{+}cosh{\eta }_{+}-D_{-}cos{\eta }_{-}\right]\right\}\\ D_{\pm }=\frac{1}{2}\left[\pm 1+\frac{\mathrm{\Psi }+2\mathrm{\Delta }{\omega }^2}{\sqrt{{\mathrm{\Psi }}^2+{\xi }^2}}\right]\\ {\eta }_{\pm }={\tau }_{\text{CP}}\sqrt{\frac{1}{2}\pm \mathrm{\Psi }+\sqrt{{\mathrm{\Psi }}^2+{\xi }^2}}\\ \mathrm{\Psi }=R_{2\text{A}}^0-R_{2\text{B}}^0+k_{\text{AB}}-{k_{\text{BA}}}^2-\mathrm{\Delta }{\omega }^2+4k_{\text{AB}}{k}_{\text{BA}}\\ \xi =2\mathrm{\Delta }\omega R_{2\text{A}}^0-R_{2\text{B}}^0+k_{\text{AB}}-k_{\text{BA}},\end{array}$$ (2)

where Δω represents the chemical shift difference between the two states in units of rad·s⁻¹, R_2A⁰ and R_2B⁰ represents intrinsic transverse relaxation rates of the states A and B, respectively. Although the intrinsic transverse relaxation rates of the two states can be different, they are usually assumed to be the same, i.e., R₂⁰ = R_2A⁰ = R_2B⁰. The assumption has little effect upon the analysis of the exchange when the exchange rate is much faster than the difference between R_2A⁰ and R_2B⁰ (k_ex ≫|R_2A⁰ − R_2B⁰|). In addition to the assumption on R₂⁰, GLOVE adopts k_ex (sum of the forward and backward rates, k_AB + k_BA) and p_Ap_B (product of the two populations, p_A × p_B) instead of k_AB and k_BA to reduce the parameter spaces around the commutable k_AB and k_BA, enhancing the computational efficiency and stability. The population of state B, designated as the lower-populated state, is calculated according to the formula $p_{\text{B}}=1-\sqrt{1-4p_{\text{A}}{p}_{\text{B}}}/2$. The exact equation used in GLOVE is represented as

$$\begin{array}{l}{R}_2^{\text{eff}}=R_2^0+\frac{1}{2}\left\{k_{\text{ex}}-\frac{1}{{\tau }_{\text{CP}}}{cosh}^{-1}\left[D_{+}cosh{\eta }_{+}-D_{-}cos{\eta }_{-}\right]\right\}\\ D_{\pm }=\frac{1}{2}\left[\pm 1+\frac{\mathrm{\Psi }+2\mathrm{\Delta }{\omega }^2}{\sqrt{{\mathrm{\Psi }}^2+{\xi }^2}}\right]\\ {\eta }_{\pm }={\tau }_{\text{CP}}\sqrt{\frac{1}{2}\pm \mathrm{\Psi }+\sqrt{{\mathrm{\Psi }}^2+{\xi }^2}}\\ \mathrm{\Psi }=k_{\text{ex}}^2-\mathrm{\Delta }{\omega }^2\\ \xi =2\mathrm{\Delta }\omega k_{\text{ex}}\sqrt{1-4p_{\text{A}}{p}_{\text{B}}}.\end{array}$$ (3)

Partial derivatives of R₂^eff with respect to all fitting parameters are calculated analytically for LMA in GLOVE, and therefore the fit is faster than would be the case where they are derived numerically according to:

$$\frac{\partial R_2^{\text{eff}}}{\partial x}=\frac{fx+\mathrm{\Delta }-fx}{\mathrm{\Delta }},$$ (4)

where x represents a fitting parameter and Δ is a small value.

Processing relaxation dispersion data using the GLOVE software package

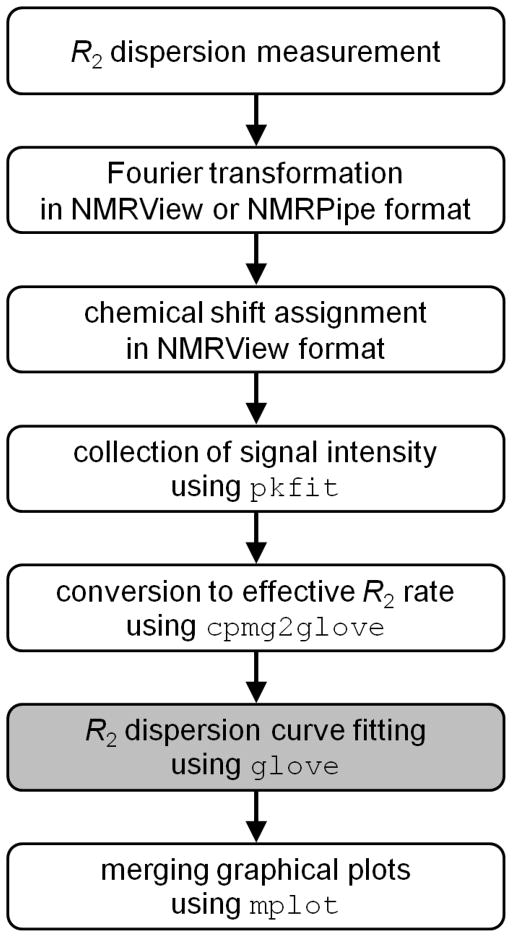
We now describe briefly how R₂ relaxation dispersion data are processed using the GLOVE software package, together with some important tips (Figure 2). Relaxation dispersion spectra are measured using a Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence with a constant relaxation time of T_CPMG (Vallurupalli et al. 2008). All spectra are processed with the same parameters: solvent suppression, apodizations, Fourier transformation, phase correction and baseline correction. It should be noted that the order of the baseline correction should be minimum; otherwise, intensities of small signals might be modified significantly. Linear prediction should not be used since it is not suitable for quantitative analysis of NMR data.

Figure 2.

Procedure for the analysis of relaxation dispersion data. The programs included in the GLOVE software package are shown in Courier New font. The main part of the data fitting using the GLOVE program, whose executable command is glove, is shown as the grey background.

Integrated peak intensities of non-overlapped peaks are obtained typically as a sum of intensities at 3 × 3 grid points centered on the peak top. This can be achieved using the program pkfit included in the GLOVE software package. An error in a peak intensity, ε_I, is evaluated from the standard deviation of noise amplitudes in each spectrum and differences in peak intensities of duplicated spectra. A pkfit output file contains the magnetic field B₀ (in units of MHz), T_CPMG (s), 1/τ_CP (s⁻¹), and peak intensities of all resonances at each 1/τ_CP value. τ_CP represents the delay between successive 180° pulses in the CPMG pulse train. It should be noted that some research groups define τ_CPMG as a half delay between two 180 pulses, and use ν_CPMG = 1/(4τ_CPMG) instead of 1/τ_CP for the horizontal axis of a relaxation dispersion plot. ν_CPMG can be converted to 1/τ_CP according to the equation: 1/τ_CP = 2ν_CPMG. R₂^eff rates are calculated from the obtained peak intensities using the program cpmg2glove according to the formula:

$$R_2^{\text{eff}}{\tau }_{\text{CP}}=-\frac{1}{T_{\text{CPMG}}}ln\left(\frac{I{\tau }_{\text{CP}}}{I_0}\right),$$ (5)

where I(τ_CP) represents peak intensity at a particular τ_CP delay, and I₀ is the intensity in the reference spectrum. An error of R₂^eff is calculated from ε_I as (Ishima and Torchia 2005)

$${\sigma }^i=\frac{{\epsilon }_I}{I{\tau }_{\text{CP}}\times T_{\text{CPMG}}}.$$ (6)

The program cpmg2glove creates a GLOVE input file, which contains fitting procedure, fitting parameters, and experimental data, from single or multiple sets of intensities measured under different experimental conditions, such as magnetic field, temperature, and sample concentration.

GLOVE fits the relaxation dispersion data according to the input file, and outputs a summary of the result in a text file and graphical plots in the Xmgr or Grace format (http://plasma-gate.weizmann.ac.il/Grace/). Although GLOVE creates an Xmgr file for each resonance (residue) in the dataset, these can be merged into a single PDF file with a reduced graph size using the program mplot to facilitate comparisons of the relaxation dispersion profiles. GLOVE also reports a reduced χ² value (χ² divided by the degrees-of-freedom) to the standard output, or a monitor, in real time during a fit. Standard deviations of fitting parameters are calculated using the covariance matrix method by default, and optionally calculated using the Monte Carlo and/or jackknife methods (Press et al. 2007; Mosteller and Tukey 1968).

Demonstration of relaxation dispersion curve fitting

To demonstrate the performance of GLOVE, we fitted 110 (= 55 resonances × 2 magnetic fields) ¹⁵N R₂ relaxation dispersion profiles of the KIX domain of CREB-binding protein. KIX is known to interconvert with a non-native conformation through a two-state exchange mechanism (Schanda et al. 2008). The relaxation dispersion data were recorded previously (Matsuki et al. 2011) on Bruker DRX600 and DMX750 spectrometers at 25°C using 0.5 mM [¹⁵N]-KIX. Two-dimensional data sets with 1024 × 64 (t₂ × t₁) complex points were acquired at τ_CP = 10, 5, 3.33, 2.5, 2.0, 1.66, 1.43, 1.25, 1.0, 0.83, 0.71, 0.63, 0.55, 0.50, 0.4, and 0.33 ms with a constant relaxation time of T_CPMG = 40 ms.

We tested the fitting speed and the accuracy using the methods ONE, ONEEX, and GRID, and the combination of the methods GRID+ONEEX, RANDOM+ONEEX, MCMIN+ONEEX, and RANDOM+MCMIN+ONEEX. It should be noted that we always validate newly developed fitting methods and models using synthetic data with and without random noise. In the case of the combined method RANDOM+MCMIN+ONEEX, which shows the best performance as described below, the best-fit parameters were identical to the input parameters if no error was added to the synthetic data. Even with 5% random error of effective R₂ rates, we confirmed that the best-fit parameters were in excellent agreement with the input parameters (Supporting Table S1).

All the relaxation dispersion profiles of KIX were globally fitted to Equation 3, in which k_ex and p_Ap_B were specified as global parameters. Parameter ranges were set to 100–2500 for Δω, 5–4000 for k_ex, and 0.005–0.09 for p_Ap_B. The initial R₂⁰ rate was estimated as the lowest R₂^eff rate of each relaxation dispersion dataset. The minimization using ONE, ONEEX and MCMIN started from the lower limits of the parameters. For GRID, the fitting tests were conducted for grid sizes of Δω, k_ex, p_Ap_B ranging from 2 to 20. The iterations of RANDOM and MCMIN were set to 20 and 5, respectively when they were used solely or combined with ONEEX, and the iteration of RANDOM was set to 5 when it was used in combination with MCMIN. MCMIN was repeated three times, reducing the scaling factor sequentially from 0.1 to 0.001 by a factor of 0.1. RANDOM and MCMIN use random number generators, providing different results every time; therefore, the fitting tests using RANDOM or MCMIN were repeated ten times, and the average and standard deviations of the reduced χ² and computational time were calculated. Standard deviations of the fitted parameters were estimated using the covariance matrix method.

All tests were performed on Apple iMac with dual 3.4 GHz Intel Core i7 processors using the GLOVE executable binary compiled by the Intel C++ compiler.

Results and Discussion

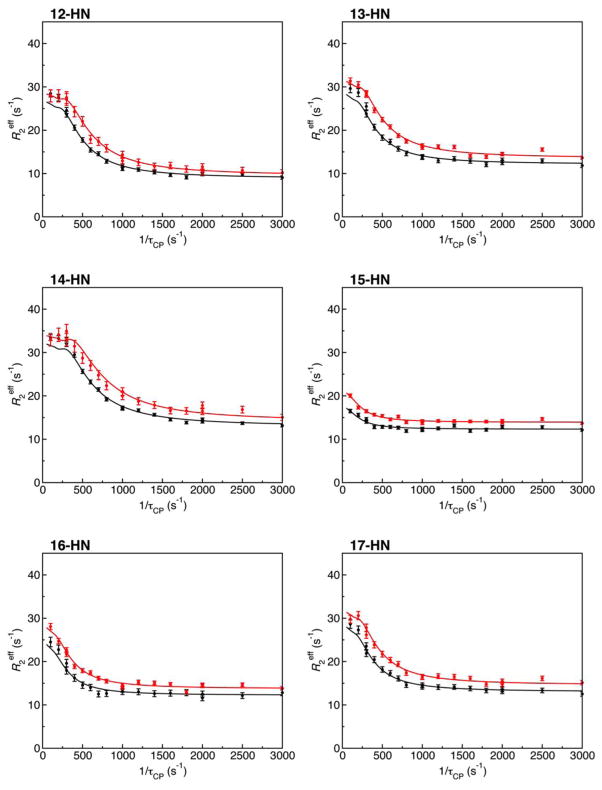
To address which method or which combination of methods fits the data the most rapidly and most accurately, we carried out global fits of 110 relaxation dispersion profiles of KIX using the methods implemented in GLOVE and combinations of them. Since the reduced χ² value converged to 1.45047 as the lowest value in many tests, we considered this value to be the global minimum. The global parameters k_ex and p_Ap_B converged to 600 ± 5 s⁻¹ and 0.0343 ± 0.0002, respectively when the reduced χ² value was 1.45047. Thus, these values were considered to be the best-fit parameter values. Figure 3 shows representative relaxation dispersion profiles and the best-fit curves. The graphical plots were created in PDF format using the GLOVE software package, and were not modified except for the file format conversion.

Figure 3.

Representative ¹⁵N relaxation dispersion profiles for KIX with the best-fit curves. The relaxation dispersion data were collected at ¹⁵N frequencies of 60.83 MHz (black line) and 76.01 MHz (red line). The plots were initially created by GLOVE for individual residues, and merged using mplot into a single PDF file. The numbers followed by “-HN” on the upper left of the plots are the residue number.

The fitting protocol ONE, which is a single point minimization starting from the lower limits of the parameters, could not find the global minimum (Table 1). This outcome means that relaxation dispersion curve fitting has a local minimum problem, and thus, well estimated initial values or multiple fits from different initial parameters are required to find the global minimum. ONEEX provided a smaller reduced χ² value than ONE, but it also failed to find the global minimum, and the computational time was very long. ONEEX should not be used for the initial stage of a fit although ONEEX shows a very good performance at the final stage of a fit, as described below.

Table 1.

Speed and accuracy tests of relaxation dispersion curve fitting

Method	Reduced χ2 valuea	Computational time (s)
ONE	14.9719	0.3
ONEEX	9.82986	1036
RANDOM	2.06638 (0.78064)	62 (9)d
+ ONEEXb	→ 1.45047 (0)c
RANDOM	3.70891 (0.84149)	38 (12)d
+ MCMIN	→ 1.45052 (0.00008)
+ ONEEXb	→ 1.45047 (0)c
MCMIN	9.54153 (3.05157)	2924 (2398)d
+ ONEEXb	→ 8.93963 (3.12073)c

^aThe initial reduced χ² value is 88.7611.

^bThe tests were repeated ten times

^cThe average of the reduced χ² values after each method is shown with the standard deviation in parentheses. The arrows indicates that the fitting parameters were sequentially minimized using the method written on the same line in the Method column

^dThe average total computational time is shown with the standard deviation in parentheses.

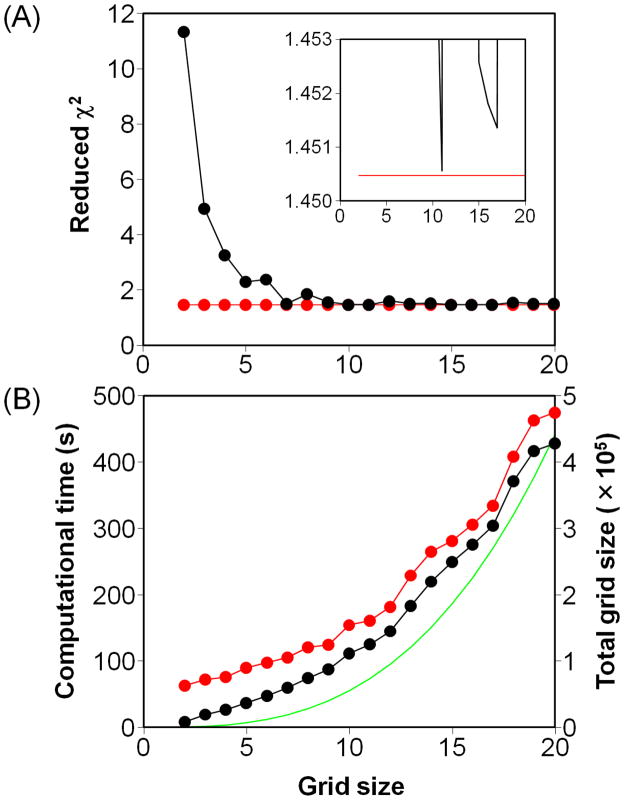
We then focused on the grid search method, which is commonly used by other programs to fit relaxation dispersion data, and examined how many grid sizes are required to find the global minimum by fitting the test data with grid sizes ranging from 2 to 20. However, none of the fits reached the global minimum (Figure 4A). A grid size of 11 provided the lowest reduced χ² value of 1.45056, which is very slightly higher than that of the global minimum. The resulting global parameters k_ex and p_Ap_B (603 ± 5 s⁻¹ and 0.0342 ± 0.0002, respectively) were the same as the best-fit values within the uncertainties. However, when the grid size was increased from 11 to 18, the fitted k_ex and p_Ap_B (515 ± 5 s⁻¹ and 0.0366 ± 0.0002) were obviously far from the best-fit values. Note that the fitting quality (reduced χ² value) did not always improve with the increase of grid size although the computational time increased collinearly with the total grid size (Figure 4B). Interestingly, application of ONEEX following GRID always reached the global minimum with an additional computational time of less than 1 minute (Figure 4A). Therefore, ONEEX is suitable to use at the final stage of a fit to converge the parameters to the global minimum.

Figure 4.

Fitting accuracy and speed using the grid search method. (A) The reduced χ² values of the fits using the methods GRID (black) and GRID+ONEEX (red) plotted against the grid size. The inset is an enlarged view of the same plot. The symbols have been omitted for clarity. (B) The computational time for the fits using GRID (black) and GRID+ONEEX (red) plotted against the grid size. The vertical scale is shown on the left-hand side of the plot. The green line represents the total grid size N^total, whose vertical scale is shown on the right-hand side of the plot. N^total is calculated as: $N^{\mathit{total}}=\prod _i{N}_i^{\text{global}}\sum _j\prod _k{N}_{j,k}^{\text{local}}$, where N_i^global and N_j,k^local represents the grid sizes of the i-th global parameter and the k-th local parameter in the j-th dataset, respectively.

Fits using RANDOM or MCMIN alone failed to find the global minimum, despite the fact that the fits were repeated ten times for each method (Table 1). However, if ONEEX was used after RANDOM, the fits always converged to the global minimum. Furthermore, the combined method RANDOM+MCMIN+ONEEX found the global minimum much faster than any other method. On the other hand, the fit starting with MCMIN followed by ONEEX resulted in larger reduced χ² values, and the computational time was extremely long. The reason is twofold. Firstly, MCMIN was designed to optimize the parameters more finely than RANDOM, and the tests started from the lower limits of the parameters that are far from the best-fit values, hence MCMIN failed to find the global minimum. Nevertheless, the combined method MCMIN+ONEEX could find the global minimum if an additional MCMIN calculation with 10 iterations and scale of 1 was added prior to the MCMIN+ONEEX calculation; however, this MCMIN+MCMIN+ONEEX calculation did not search the parameter space as efficiently as RANDOM+MCMIN+ONEEX (data not shown). Secondly, ONEEX takes a long time to converge to a global or local minimum. Indeed, the computational time of the combined methods including ONEEX was spent mainly on the ONEEX stage. Therefore, before the ONEEX calculation, the fitting parameters should be optimized to be as close as possible to the global minimum in order to shorten the computational time. The reason why the computational time of RANDOM+MCMIN+ONEEX was shorter than that of the other methods is that the reduced χ² value before ONEEX was the smallest.

Using the combined method RANDOM+MCMIN+ONEEX, we have already succeeded in fitting a large number of relaxation dispersion datasets (Bhabha et al. 2011; Meinhold DW and Wright PE 2011; Sugase et al. 2007b; Boehr et al. 2006), including fits of a three-state exchange model which describes coupled folding and binding processes of an intrinsically disordered protein (Sugase et al. 2007a). This combined method should be widely applicable to the analysis of relaxation dispersion data. Furthermore, GLOVE was developed to solve general non-linear least-square problems, and has built-in functions for the analysis of CLEANEX-PM (Hwang TL et al. 1998), and R₁ and R₂ relaxation data. Of course, the combined RANDOM+MCMIN+ONEEX method will also be useful for fitting such data. Since other functions can readily be added, GLOVE will undoubtedly find wide applications for the analysis of a broad range of experimental data.

For a computer required for GLOVE, we used a relatively fast computer in performing the above tests of GLOVE. For comparison, we also ran a test fit using the GLOVE executable binary compiled by g++ for RANDOM+MCMIN+ONEEX, which showed the best performance in finding the global minimum, on an old and slow computer (Cygwin running on Windows Vista PC with a 2.2 GHz Intel Core2 Duo processor). This test was repeated ten times, but always converged to the global minimum with a computational time of 202 ± 52 second. As this computational time would still be tolerable, GLOVE could be used on a broad range of computers.