Abstract
Purpose
In 2D SENSE-accelerated 3D Cartesian acquisition, the net acceleration factor R is the product of the two individual accelerations, R = RY × RZ. Acceleration Apportionment tailors acceleration parameters (RY, RZ) to improve parallel imaging performance on a patient- and coil-specific basis and is demonstrated in contrast-enhanced MR angiography.
Methods
A performance metric is defined based on coil sensitivity information which identifies the (RY, RZ) pair that optimally trades off image quality with scan time reduction on a patient-specific basis. Acceleration Apportionment is evaluated using retrospective analysis of contrast-enhanced MR angiography studies, and prospective studies in which optimally apportioned parameters are compared with standard acceleration parameters.
Results
The retrospective studies show strong variability in optimal acceleration parameters between anatomic regions and between patients. Prospective application of apportionment to foot contrast-enhanced MR angiography with an 8-channel receiver array provides a 20% increase in net acceleration with improved contrast-to-noise ratio. Application to 16-channel contrast-enhanced MR angiography of the feet and calves suggests 10% acceleration increase to R > 13 and no contrast-to-noise ratio loss. The specific implementation allows the optimum (RY, RZ) pair to be determined within one minute.
Conclusion
Optimum 2D SENSE acceleration parameters can be automatically chosen on a per-exam basis to allow improved performance without disrupting the clinical workflow.
Keywords: parallel imaging, GPU, SENSE, accelerated
Parallel imaging using two-dimensional (2D) techniques was initially described a decade ago (1) and, in recent years, has been used in various applications of three-dimensional Fourier transformation acquisition, perhaps most notably in 3D contrast-enhanced MR angiography (CE-MRA) (2–8). Just as for one-dimensional (1D) acceleration, 2D acceleration is implemented by increasing the distance between samples in k-space, but in two phase-encode directions rather than one. Specific to SENSE acceleration, a model-based image-space-based parallel imaging framework, two other specific characteristics of the 1D implementation can be extended to the 2D case. First, regions within the field of view (FOV) which are known to have zero magnetization, typically the air outside the object under study, can be forced to have zero signal in the SENSE-unfolded image and thereby reduce signal-to-noise ratio (SNR) loss in the unfolding process (9). Second, because acceleration is implemented by simply adjusting the incremental spacings along the kY and kZ directions, the accelerations along these directions, defined here as RY and RZ, respectively, can assume non-integer values. The net SENSE acceleration R is the product: R = RY × RZ.
The above aspects of SENSE acceleration provide more flexibility in selecting the desired acceleration factors for the 2D vs. the 1D case. The fraction of the volume of a 3D FOV actually filled by an object depends on the anatomy under study, but is often no more than about 60% and even considerably smaller for some anatomic regions. It is generally not obvious how the zero magnetization regions in such a case can be exploited by appropriate choice of RY and RZ. Also, for a given target overall acceleration R, there are many pairs (RY, RZ), or “R-pairs,” for which R ≈ RY × RZ, but again it is generally not clear beforehand which specific R-pair is best to use. This uncertainty in selecting (RY, RZ) is further compounded in applications such as contemporary accelerated 3D CEMRA where acceleration factors of R = 6–8 or higher are routinely used (10–14). That is to say, the region over RY−RZ “acceleration” space in which high quality images can be generated is much broader than if, say, practical overall acceleration factors were limited to R < 4.
Previously, the Controlled Aliasing In Parallel Imaging Results IN Higher Acceleration (CAIPIRINHA) technique (15,16) has been presented as a means to improve acceleration performance for a given R by making aliasing more benign through adjustment of the 2D SENSE under-sampling kernel to shift the directions of aliasing. CAI-PIRINHA has been further generalized (17). In contrast, the purpose of this work is to develop Acceleration Apportionment in which the acceleration values (RY, RZ) themselves are altered rather than the undersampling lattice pattern. Specifically, we illustrate the potential gains available when RY and RZ are allowed to vary for a given R, show how the choice of an optimum R-pair depends upon the subject, and describe an algorithm for selecting patient-specific RY and RZ based on a quality metric calculated from the subject-specific 3D g-factor map. We also describe an implementation for determining the optimum R-pair within one minute after acquisition of the coil sensitivity images, allowing incorporation into the subsequent accelerated scan. The feasibility of the method is demonstrated in CE-MRA studies of the lower extremities.
METHODS
Filling Percentages
As a prelude to this study, the fraction of the 3D FOV filled by the object was determined for several different anatomic regions. Data sets collected from previous in vivo 2D SENSE-accelerated 3D CE-MRA studies of the abdomen (18), calves (12), and feet (19) were used for this analysis. For each region, 10 consecutive studies were evaluated. In each case, the 3D FOV was noted. Also, the volume of the object within each FOV was determined using a simple masking process used routinely in SENSE reconstruction (9) for detection of the object edge. Finally, by taking the ratio of the volume of the 3D masked object with the full FOV volume, the percentage filling of the FOV was determined. In all cases, the FOV was chosen to encompass the object with minimal empty space. Results of this analysis in Table 1 show that the mean filling percentages are 55% (abdomen), 44% (calves), and 20% (feet).
Table 1.
Fractional FOV Filling Percentages for n = 10 Studies for Each of Three Anatomic Regions
| Mean (%) | Min–Max (%) | |
|---|---|---|
| Feet | 20 | 15–23 |
| Calves | 44 | 30–53 |
| Abdomen | 55 | 51–67 |
In all cases, the 3D FOV was chosen to be tight to the anatomy.
Aliasing Maps and Example of Apportionment
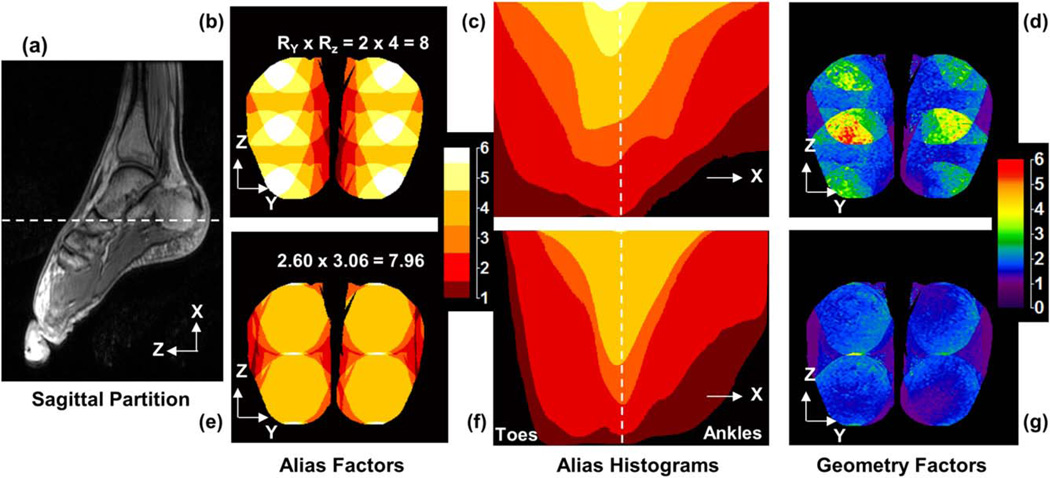
Evaluation of a candidate R-pair for a specific accelerated imaging application can be done in various ways, and this is commonly done using the g-factor, a measure of the noise amplification due to the unfolding process (9). Another measure which can provide some intuitive insight is the level of aliasing. An alias map is defined as an image of the number of aliases occurring in the SENSE-accelerated acquisition for a specific (RY, RZ) combination. This is illustrated in Figure 1. Figure 1a is a single 1 mm thick sagittal partition taken from a 3D volume acquisition of the feet typically used for the generation of coil sensitivity data for a subsequent SENSE-accelerated study. The full sagittal FOV is shown, and the right-left FOV was similarly chosen to tightly encompass the object. The white dashed line in (a) defines an axial plane through the feet, intersecting the heels, the axial level with approximately the greatest percent filling of the object. The acceleration directions are in the axial plane: phase encode (Y) is left-right (L/R) and partition encode (Z) is anterior-posterior (A/P). Figure 1b is the alias map of the axial level defined in (a) using a 2D SENSE acceleration of R = RY × RZ = 2 × 4. Figure 1c shows a volume histogram plot of the number of aliases for each pixel per axial slice, with the abscissa on the plot corresponding to the superior-inferior (S/I) position of the axial slice in the 3D volume. Again the dashed line in (c) corresponds to the level identified in (a) and shown in (b). Figure 1d is the g-factor map of the same axial slice at the acceleration noted in (b).
FIG. 1.
Demonstration of the potential value of Acceleration Apportionment in 2D SENSE accelerated acquisitions. a: A single 1-mm-thick sagittal partition of the foot taken from a 3D volume acquisition. The white dashed line denotes the axial level imaged in (b, d, e, g) and corresponds to the level similarly identified in (c, f). b: Alias map for a standard RY × RZ = 2 × 4 = 8 acceleration at the axial level identified. c: Volume histogram plot of the aliasing count population for the entire volume, and (d) g-factor image of the axial level for standard acceleration. When acceleration factors are alternately chosen to be 2.60 × 3.06, giving the same R ≈ 8 net acceleration, the corresponding results in (e–g) all show improvement.
The potential value of Acceleration Apportionment is illustrated in Figure 1e–g. Again starting with the masked images of the feet, the effect of various assumed acceleration pairs (RY, RZ) on the aliasing map was studied by trial and error, keeping R ≈ 8. The sequence of 6-fold aliasing regions along the Z direction in Figure 1b suggests that RZ is higher than desired and might be reduced for increased RY. Figure 1e shows the aliasing map for the same axial slice in (b) but with RY × RZ = 2.60 × 3.06 × 7.96 ≈ 8. Note that the regions of 6-fold and 5-fold aliasing of (b) have been substantially reduced. Figure 1f–g shows, respectively, the volume histogram plot and the g-factor map of the axial slice of (e). Note the reduced overall aliasing (f vs. c) and reduced g-factors (g vs. d) provided by the modified RY and RZ values, with equivalent R ≈ 8.
Optimization of R-Pair Selection
The goal of Acceleration Apportionment is to determine that (RY, RZ) pair which provides optimum 2D acceleration performance according to some criterion, or cost function. Ideally, the optimization is performed before the accelerated study itself so that the study can benefit from use of the optimum acceleration factors.
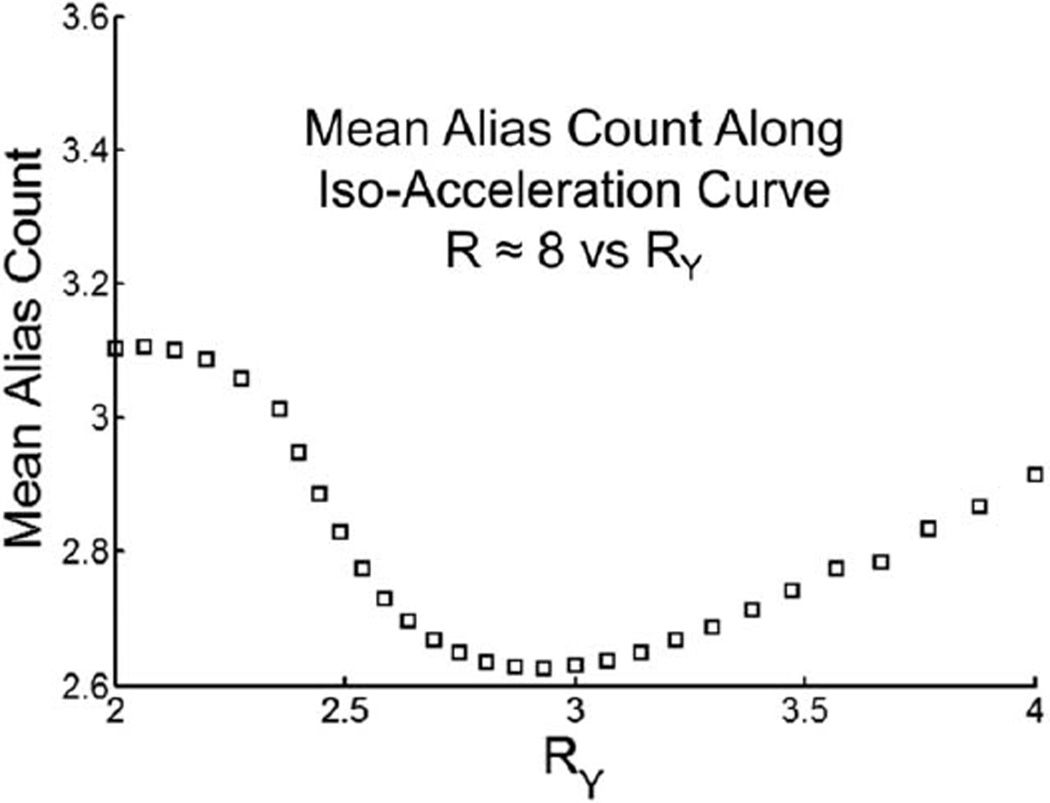
We indicate at the outset that there are several plausible measures of performance that may be used as a criterion for optimization. As an example, suppose that the cost function is defined as the mean aliasing factor over the 3D volume of interest; i.e., the mean value of the functions in Figure 1c,f subject to the overall 2D SENSE acceleration R being fixed at R = 8. The result of this is shown in Figure 2 for the specific CE-MRA study used in Figure 1. The abscissa is a measure of the value of RY along the curve RY × RZ ≈ 8 in RY−RZ space. The quantization along RY is due to the number of measured phase encodes in the accelerated direction (NY/RY) needing to be integer, where NY is the number of measured encodes in the unaccelerated scan (264 in this example). Similar quantization restrictions apply to RZ. As seen, the optimum using this cost function occurs in the vicinity of RY = 3, with (RY, RZ) = (2.93, 2.67) providing the lowest mean alias count.
FIG. 2.
A plot of the mean alias count of the 3D foot exam displayed in Figure 1 for each R-pair comprising net acceleration R ≈ 8 parameterized against RY. Note the minimum at RY = 2.93, RZ = 2.67.
Although use of the aliasing factor as the cost function may provide intuitive insight, using the g-factor calculated from the masked coil sensitivity images is advantageous as it takes into account both the patient-specific anatomy as well as the receiver coil performance. Moreover, the sensitivity maps used for computing the g-factor are generally acquired before the accelerated study, such as in 3D CE-MRA. In this work, we restricted the cost function CF(RY, RZ) to be of the form:
| [1] |
where it is understood that f(g) is some function of the (3D) g-factor map for the specific (RY, RZ) under consideration. CF attempts to balance image quality (f(g)) with speed (RY × RZ), and implicit in Eq. [1] is equal weighting of each.
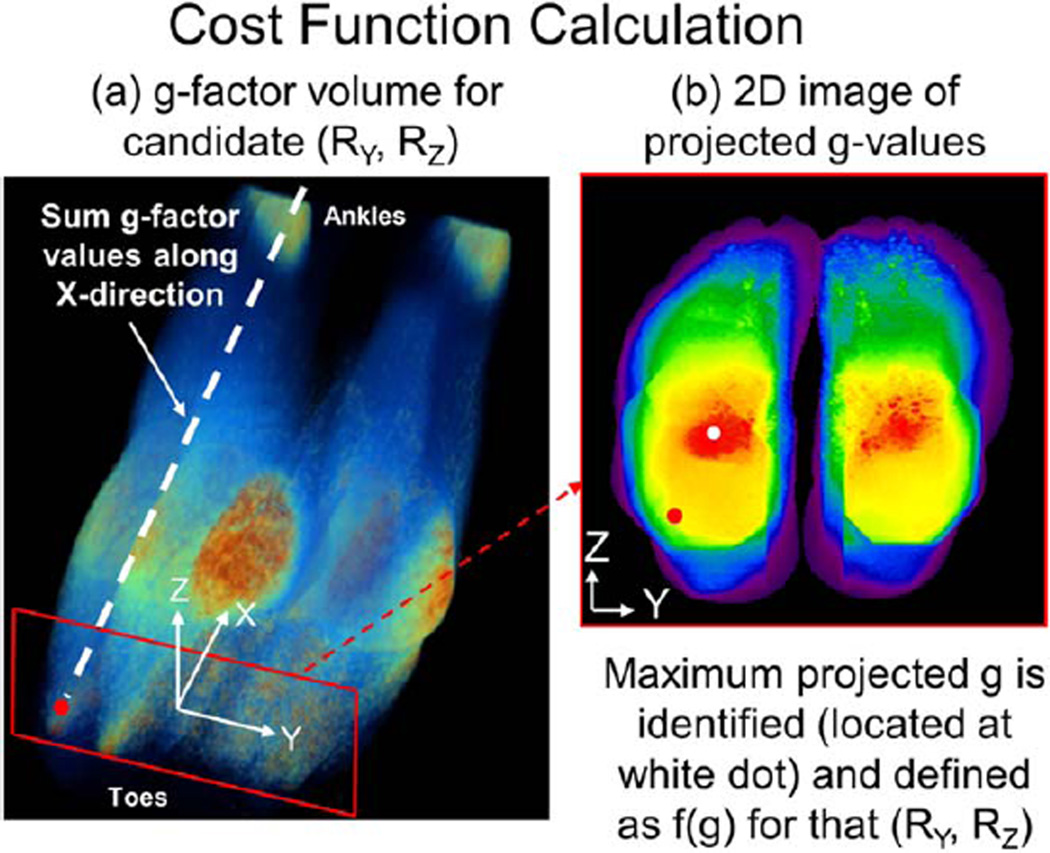
Generation of a scalar metric f(g) based on the g-factor volume requires some consideration. In our preliminary testing, the mean and median g-value of the volume did not respond with large enough variation to adequately discriminate R-pairs with good vs. poor g-factor performance. Conversely, use of a single point operator like the maximum g-value of the volume was too easily influenced by noise in the calibration data. For this work, a hybrid method was devised to generate the quality metric f(g). This is illustrated in Figure 3 for a study of the feet. Starting with coil sensitivity images, the g-factor is calculated over the volume of interest for some candidate (RY = 2, RZ = 4). Next the g-factor image is summed along the frequency (X) direction (a) to produce a 2D image in the phase encoding (Y-Z) plane (b). The maximum value within that image gives a single value metric f(g), which is relatively insensitive to calibration data noise, yet highlights areas of high noise amplification. Dividing this value by the corresponding proposed R as in Eq. [1] produces the CF. This process is repeated for each R-pair considered, and that R-pair which minimizes the cost function is chosen as optimum.
FIG. 3.
Illustration of the generation of f(g) for RY = 2, RZ = 4 for a 8-channel foot study. a: For this specific R-pair, the g-factor volume is calculated and then projected along the frequency direction. b: The maximum of the resultant 2D image located at the white dot is chosen to represent the image quality metric value f(g) generated using that R-pair.
Retrospective Evaluation of In Vivo Studies
Ten sets each of abdomen, calf, and foot studies described above for studying filling percentages were further analyzed to assess optimization of acceleration factors. In all cases, a minimum of eight coil elements had been used previously for R = 8 2D SENSE accelerated studies, and the coil sensitivity information was available for retrospective calculation and optimization of the cost function described above. With the acceleration fixed at R ≈ 8, the R-pair which provided the lowest cost function value was determined for each study. The analysis was then expanded to allow a broader search over the RY−RZ plane to allow different, and possibly higher, net acceleration values. For this work, the precision in sampling the RY and RZ values was ~0.1.
Prospective In Vivo Experiments
To assess the potential of Acceleration Apportionment to provide improvement in performance of acquisitions which are already highly accelerated, the method was studied in 3D time-resolved CE-MRA exams of the feet of three healthy volunteers, and the calves of a fourth volunteer. All studies were performed under a protocol approved by the Institutional Review Board of the institution, and all subjects provided written consent. All studies were done on a 3.0 T MRI system (GE Signa, v14–22, GE Healthcare, Waukesha, WI). Each volunteer was imaged twice, with a minimum of one day between sessions to allow clearance of contrast. For each session, the volunteer was injected with 20 mL of MultiHance (Bracco Diagnostics, Princeton, NJ) at 3 mL/s with a 20 mL saline flush at 3 mL/s. In the first session, the subject was imaged with a previously reported “reference” acceleration. In the second session, the acceleration parameters were selected to test Acceleration Apportionment.
The CE-MRA exams were performed using a spoiled gradient echo sequence with ±62.50 kHz readout bandwidth and a 30° flip angle. Other sequence parameters are shown in Table 2. Coil calibration data was acquired using a similar sequence, but with a coarser 2.66 × 2.66 × 2.00 mm voxel size, ±31.25 kHz readout bandwidth, and a 10° flip angle. For the CE-MRA scans, an image time series was generated using the view sharing method of Ref. 12, and the frame time and temporal footprint (10) are noted.
Table 2.
Summary of Acquisition Parameters for Prospective In Vivo Studies of Acceleration Apportionment
| Volunteer no. | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Anatomic region | Feet | Feet | Feet | Calves |
| No. coil elements | 8 | 8 | 16 | 16 |
| Field of view | ||||
| S/I (X) × L/R (Y) × A/P (Z) (cm3) | 30.0 × 19.8 × 25.6 | 30 × 19.8 × 25.6 | 30.0 × 24.0 × 24 | 42.0 × 33.6 × 16.0 |
| Spatial resolution | ||||
| S/I (X) × L/R (Y) × A/P (Z) (mm3) | 0.75 × 0.75 × 1.00 | 0.75 × 0.75 × 1.00 | 0.75 × 0.75 × 0.9375 | 1.00 × 1.00 × 1.00 |
| TR/TE (ms/ms) | 6.37/2.82 | 5.76/2.64 | 5.76/2.64 | 6.14/2.80 |
| RY × RZ = R | ||||
| Reference | 2 × 4 = 8 | 2 × 4 = 8 | 3 × 4 = 12 | 6 × 2 = 12 |
| Apportioned | 2.87 × 3.37 = 9.67 | 3.06 × 3.37 = 10.31 | 3.90 × 3.55 = 13.85 | 5.42 × 2.50 = 13.55 |
| Frame time | ||||
| Reference (s) | 7.2 | 6.6 | 5.4 | 4.4 |
| Apportioned (s) | 6.2 | 5.2 | 4.7 | 3.9 |
| Temporal footprint | ||||
| Reference (s) | 27.0 | 24.2 | 19.6 | 15.6 |
| Apportioned (s) | 22.6 | 18.9 | 17.0 | 13.8 |
| Figure | 7 | – | – | 8 |
For Volunteers 1 and 2, the coil was comprised of two anterior and two posterior elements of area 27.1 × 10.5 cm2 and two left and two right elements of area 27.1 × 14.3 cm2. For Volunteer 3, a 16 element circumferential array using four different coil element shapes was used. For Volunteer 4, the coil was comprised of 16 elements, each of area 40 × 7.2 cm2.
All studies used coil arrays developed in our laboratory. Each array was comprised of 8–16 elements, connected in a linear fashion, first element to second element, second to third, etc., and wrapped around the target anatomy with the last element connected to the first element to totally circumscribe the FOV. The array design for the 8-channel receiver is illustrated in Figure E2 of Ref. 12 and pictured in Figure 3 of Ref. 19. The size of the individual elements is shown in Table 2. These coil arrays have routinely allowed CE-MRA with 2D SENSE acceleration of R = 8.
For Volunteers 1 and 2, the reference acceleration was RY × RZ = 2 × 4 = 8. This was developed for use with similar linear arrays in the calves (12), and adapted for use in forming high quality images of the feet (19,20). For Volunteers 3 and 4, 16-element receiver coils with similar design considerations for the feet and calves, respectively, were used with reference accelerations, RY × RZ = 3 × 4 = 12 for the feet and RY × RZ = 6 × 2 = 12 for the calves. These references were chosen to assess performance at acceleration factors not yet demonstrated for clinical use for these regions.
The apportioned acceleration parameters for Volunteer 1 were selected by trial-and-error to show feasibility of apportionment before the development of the full CF methodology. Acceleration parameters of Volunteers 2–4 were determined by minimizing the CF described above.
Results from all four prospective studies were evaluated for image quality based on vessel contrast-to-noise ratio (CNR) measurement. For each subject, 11 segments from major vessels were identified throughout the 3D volume, identical segments for both the reference and apportioned studies. Using the subtracted axial images from the peak arterial contrast time frame, the mean signal intensity from the vessel segment was measured with a 10, 5, or 3 pixel region of interest depending on vessel size. The standard deviation of a ~400 pixel region of interest of contrast-free subtracted tissue near the vessel segment was measured as the noise. The ratio of the mean signal to the noise measurement was calculated as the CNR. Statistical significance of the CNR change between the reference and apportioned studies was tested using the paired t-test (21).
Determination of Optimum R-Pair
Calculation of the g-factor-based cost function is computationally expensive due to the matrix inversions required for each set of aliased voxels in the reconstructed volume. On an eight-node dual-processor cluster currently used for real-time 3D image reconstruction using 2D SENSE and homodyne processing (22), it takes ~1.2 s to calculate the cost function for a single R-pair for a typical 3D FOV. If RY and RZ are both allowed to have values ranging from ~2.0 to 5.0 with an increment of 0.05, then the total number of R-pairs considered is 3600, leading to an overall optimization time of greater than 1 h.
For Acceleration Apportionment to be practical, it is desirable for the optimum R-pair to be determined within seconds after the coil sensitivity data are acquired, thereby allowing the optimum values to be incorporated into the subsequent accelerated acquisition. To this end, hardware consisting of a dual hex-core processing node and an nVidia Tesla C2050 general-purpose graphics processing unit was made accessible online to the MRI scanner. Computation of the CF for an individual R-pair was reduced to the range of 20–40 ms, with 40 ms necessary if the acceleration considered was as high as R = 20 for a receiver array with as many as 16 coil elements. This reduced the overall time of the search to about 1 min. This rapid implementation was used for Volunteers 2–4.
RESULTS
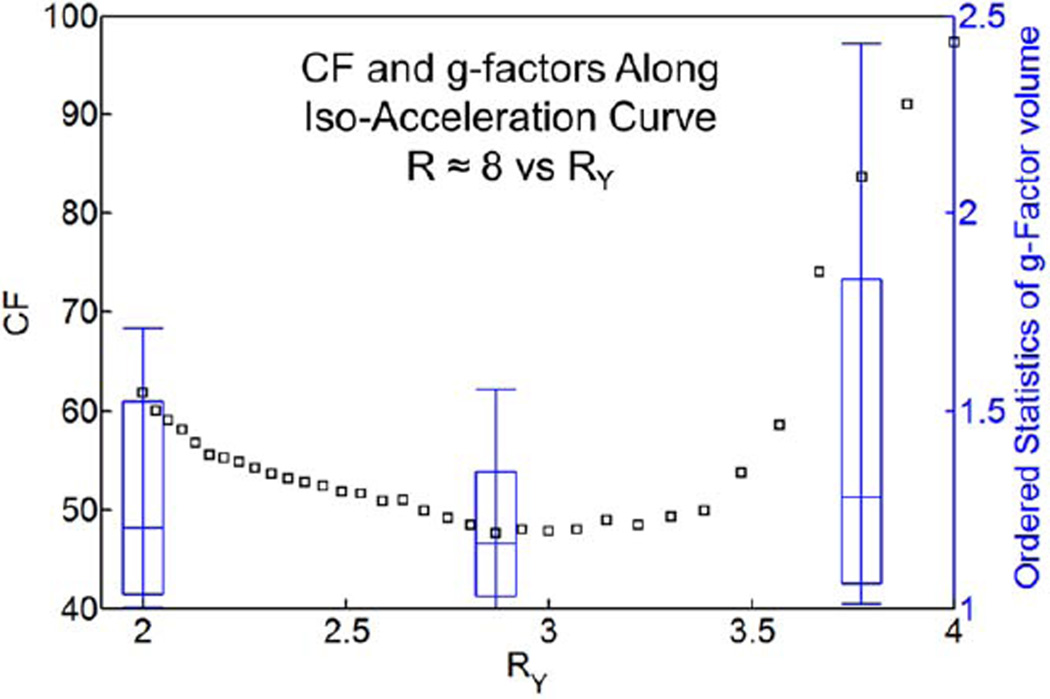
Figure 4 is a plot of the cost function defined above in Eq. [1] for Volunteer 1 for those (RY, RZ) pairs which provide net acceleration R = RY × RZ ≈ 8. RY values are chosen along the abscissa at increments of ~0.1 units, again with subtle quantization effects as described previously. However, there is a clear minimum in the curve occurring for RY = 2.87, corresponding to RZ = 8/RY = 2.84. Also shown using the right ordinate in Figure 4 are box-and-whisker plots of the g-factors for the specific R-pairs of (2, 4), (2.87, 2.84), and (3.77, 2.10).
FIG. 4.
The cost function for Volunteer 1 with R ≈ 8 is plotted against RY, with RZ implied such that R ≈ 8. The box-and-whisker plots represent the 10th, 25th, median, 75th, and 90th percentiles of the g-factor volume as calculated with the accelerations indicated by the x-position of the box plot. Note the favorable g-factor statistics at the RY value corresponding to the minimum CF.
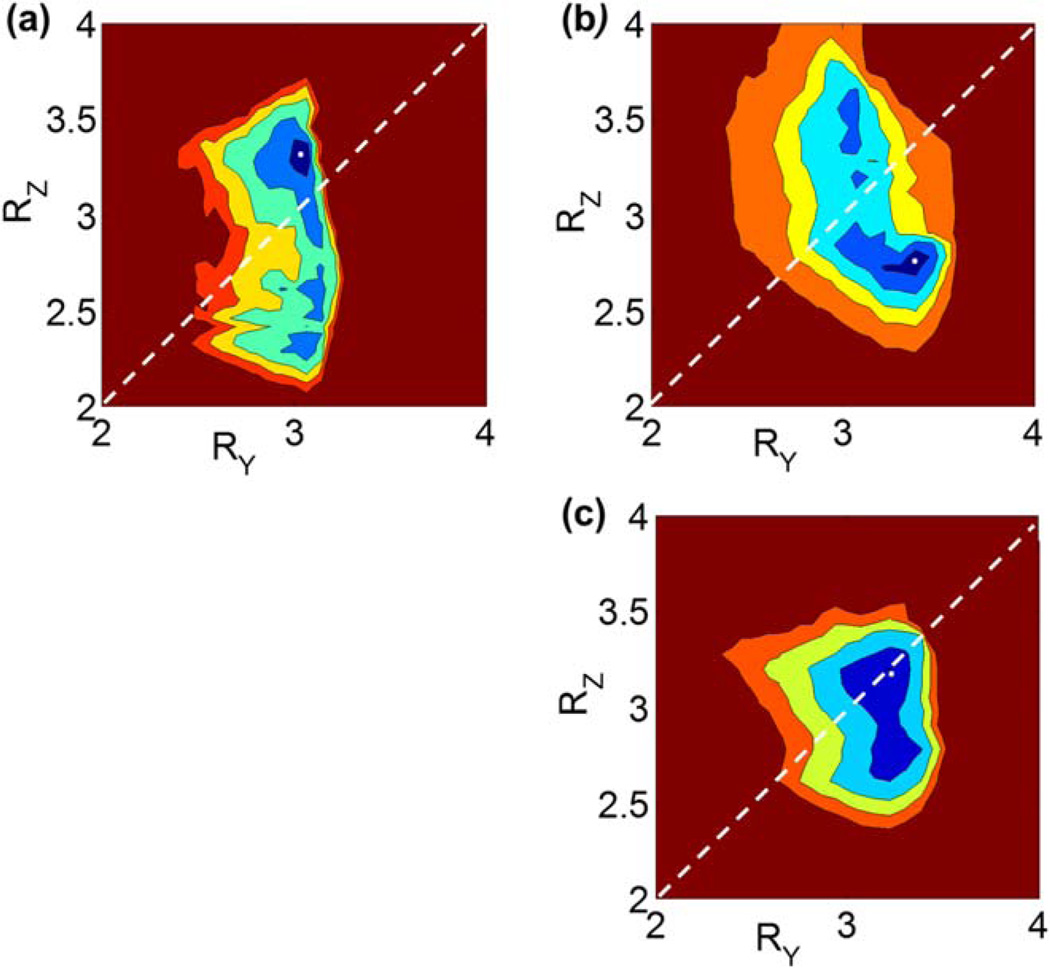
Figure 5 is a comparison of the images of the cost function CF in RY−RZ space for three representative CEMRA foot exams studied retrospectively. Each exam shows a specific minimum in the cost function identified by the white dot in the blue region, corresponding to the unique R-pair which provides optimum exam performance for that subject. Note the different optima for the three subjects and, further, that none of these corresponds to the reference (RY = 2, RZ = 4) R-pair used previously.
FIG. 5.
a–c: Visualization of relative cost function behavior in the form of contour plots over RY−RZ space for three representative 3D exams of the feet. Note the minima are unique to each exam despite identical coil array and acquisition parameters.
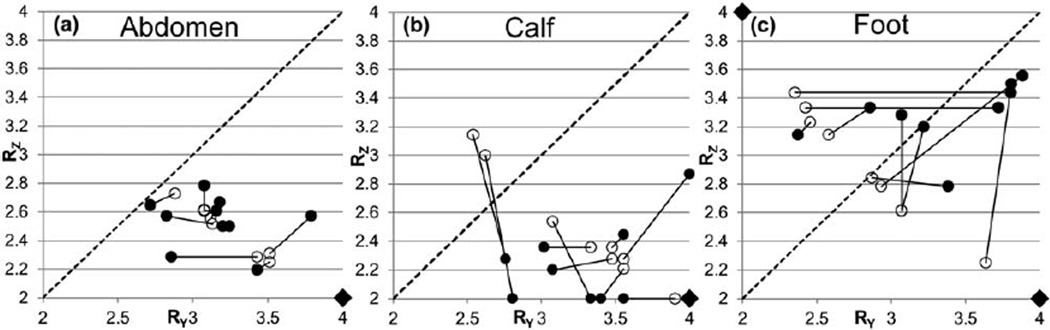
Figure 6 shows results from the retrospective analysis of abdomen (a), calf (b), and foot (c) studies. In each case, an open circle indicates the R-pair that minimizes the cost function along the iso-acceleration curve R = 8 for one of the 10 studies, while the linked filled circle indicates the optimum R-pair for that subject when R is allowed to have arbitrary values. The line RY = RZ is also shown for reference. Note that the optimum R-pairs cluster differently in RY−RZ space for each anatomic region.
FIG. 6.
Plots of the optimum R-pairs for 10 3D studies each of the abdomen (a), calves (b), and feet (c). For each study, the optimum R-pair for fixed R ≈ 8 is identified by an open circle, and the optimum R-pair as identified across all RY−RZ space is identified by the linked closed circle. Note variability between subjects, precluding a dictionary-based approach for selection of advantageous acceleration based solely on anatomy. The diagonal line marks RY = RZ. Diamonds mark the reference acceleration values. In all cases, L/R is the Y direction, and A/P is the Z direction.
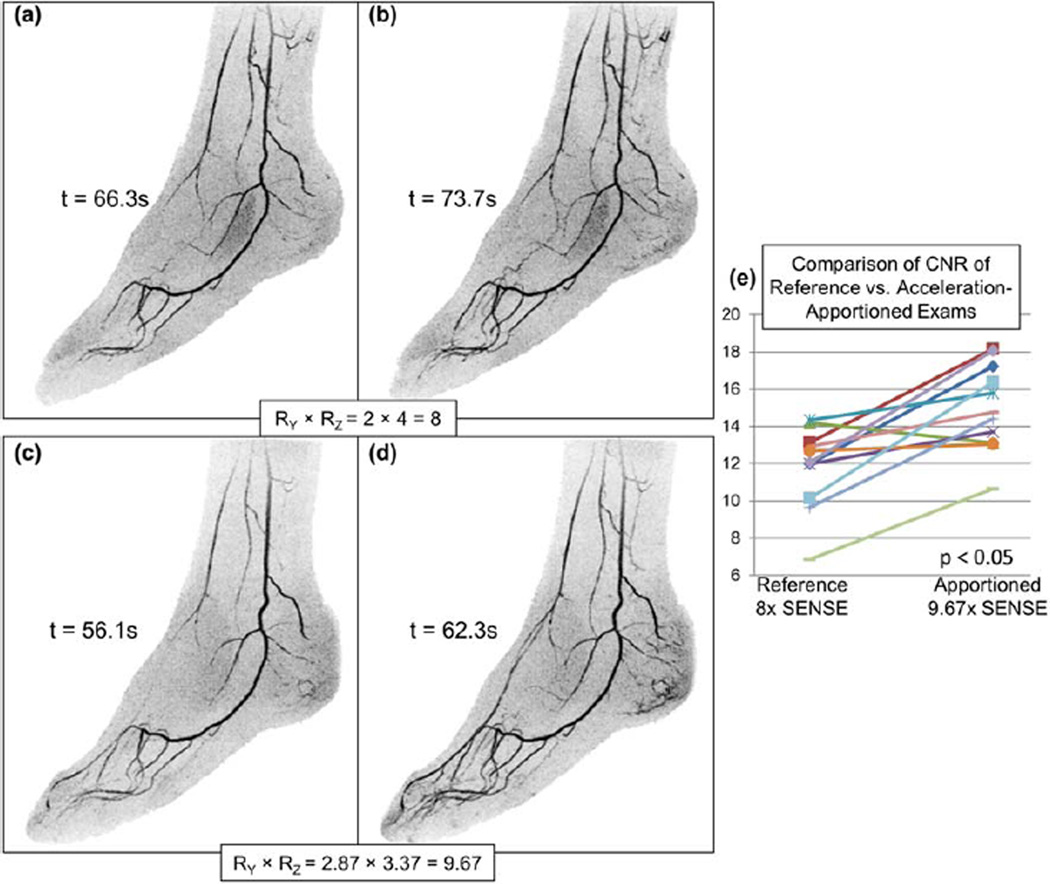
Figure 7 shows results from Volunteer 1 of the prospective study. The frames presented for the apportioned case (c, d, RY × RZ = 2.87 × 3.37 = 9.67) were selected to approximately match the arterial phases for the reference case (a, b, RY × RZ = 2 × 4 = 8). Acceleration exceeding R = 8 is allowed because superposition of pixels of known zero signal, such as air outside the subject but within the acquired FOV, does not contribute to aliasing. The ~10 s difference in contrast injection-to-arrival times for the two studies is due to normal day-to-day intra-subject variability. As stated earlier, the R-pair used to generate (c, d) was selected by trial and error. Figure 7e shows CNR measurements for the 11 vessel segments which for this volunteer show statistically significant improvement (P < 0.05) for the apportioned case.
FIG. 7.
Example of effective Acceleration Apportionment. a and b: Sagittal MIP images from consecutive time frames acquired using a reference acceleration R = 2 × 4 = 8. c and d: These images were generated 2 days later on the same subject using optimized factors R = 2.87 × 3.38 = 9.67. e: This image is a comparison of vessel-to-background CNR measurements from 11 vessel segments selected throughout the 3D FOV. The times shown in (a–d) are post start of contrast injection.
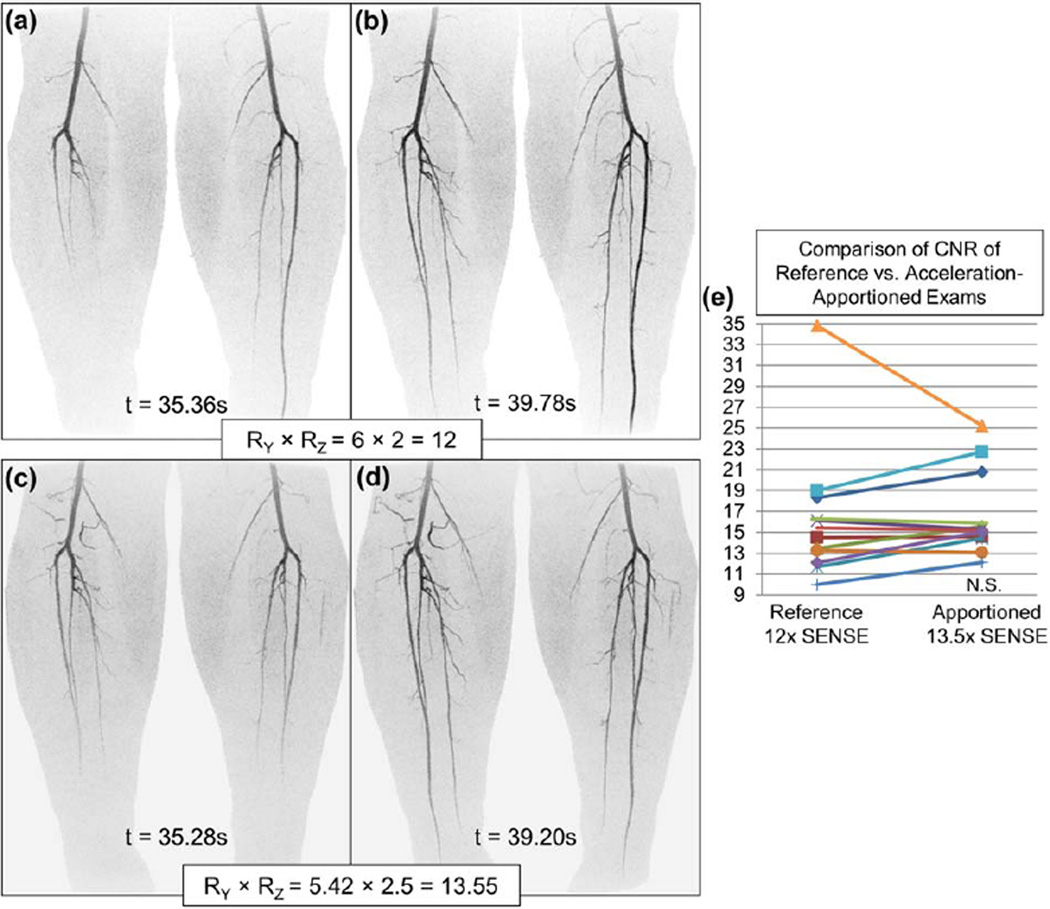
Figure 8 shows results from Volunteer 4, a study of the calves using a 16-element receiver coil, for the reference acceleration RY × RZ = 6 × 2 = 12 (a, b) and the apportioned study at RY × RZ = 5.42 × 2.5 = 13.55 (c, d). Use of Acceleration Apportionment reduced the update time for a 3D volume from 4.4 s to 3.9 s. The CNR measurements in (e) show a nonsignificant difference (P > 0.05) with a 10% increase in R for the apportioned study.
FIG. 8.
Images from Volunteer 4, an apportioned calf exam using a prototype 16-channel calf coil, (a, b) are coronal MIPs using RY × RZ = 6 × 2 = 12 as well as (c, d) using apportioned RY × RZ = 5.42 × 2.50 = 13.55. The apportioned acceleration factors were generated approximately one minute after the conclusion of the coil sensitivity data acquisition using the general-purpose graphics processing unit compute system. e: A CNR comparison of vessel segments.
CNR measurements for Volunteer 2 showed a statistically significant (P < 0.05) improvement for the apportioned vs. reference study. Volunteer 3 showed a nonsignificant change in CNR for the apportioned vs. reference study.
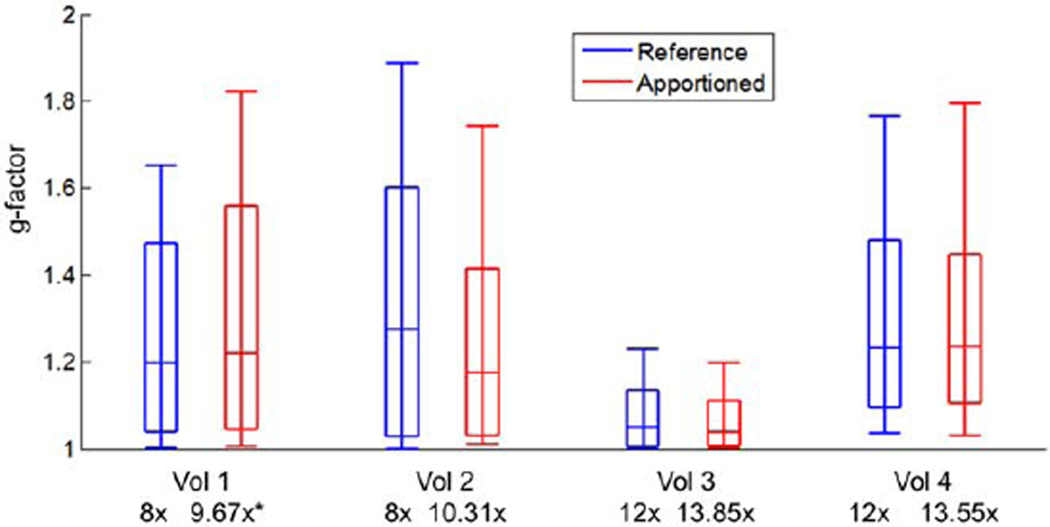
Figure 9 shows g-factor box plots and demonstrates reduced g-factors at the 50th, 75th, and 90th percentiles for apportioned vs. reference accelerations for Volunteers 2 and 3, and comparable g-factors for Volunteer 4. Volunteer 1 shows somewhat less favorable g-factors, most likely due to the trial-and-error determination of the acceleration parameters. In all of these cases, the increased acceleration was used to reduce the image update time.
FIG. 9.
g-factor statistics from Volunteers 1–4. Reported are the 10th, 25th, Median, 75th, and 90th percentile g-factors of the entire volume at the reported acceleration factors. Volunteers 2–4 were apportioned using the automated cost function minimization, and resulted in higher acceleration and commensurate faster update times with equivalent or lower g-factor statistics relative to reference accelerations. *The apportionment for Volunteer 1 was done by trial and error, and although higher acceleration was obtained, the g-factor statistics are somewhat less favorable for the apportioned vs. reference studies.
DISCUSSION
We have shown how the individual acceleration factors RY and RZ for 2D SENSE parallel acquisition can be optimized on a patient-specific basis by taking into account the body habitus and the relationship of the receiver coil array to the patient. Analysis of previous CE-MRA studies has shown variability of optimum accelerations from anatomic region to region and from patient to patient. We have shown the feasibility in prospective CE-MRA studies of the extremities that Acceleration Apportionment can provide a ~20% increase in acceleration over the nominal R = 8 used with an 8-element array and a ~10–15% increase over the R = 12 used with a 16-element array with comparable or reduced g-factor noise statistics. In all cases, vessel-to-background CNR was maintained or improved.
The (RY, RZ) pair that provides optimum performance can be determined prior to and thus used within the subsequent accelerated scan. Coil sensitivity images are acquired before a SENSE-accelerated acquisition. This calibration data is not only necessary for the SENSE unfolding but it is also useful in determining the extent of the object filling the FOV, the alias counts, and the g-factors for a particular set of accelerations. The described method allows for these considerations to be incorporated into calculation of the cost function, and minimization of the cost function results in the (RY, RZ) pair providing optimum performance.
The basis of any optimization lies in the definition of and subsequent minimization of a cost function. Our definition of the CF is arbitrary, but we believe it is sensible to somehow balance speed with image quality. The g-factor-based cost function considers coil response and quality of SENSE unfolding when evaluating overall image quality, as opposed to simply using raw alias maps. The specific function f(g) of Eq. [1] used a hybrid averaging-maximum approach to reject noisy calibration data while maintaining sensitivity to changes in image quality with each (RY, RZ). We acknowledge that other cost functions may be more effective than the one used in this work. We also note that we have not taken into consideration within the cost function the √R SNR undersampling penalty due to reduced signal averaging.
The calculation of the cost function is not computationally trivial, primarily due to the matrix inversions required to synthesize the g-factor maps. If the search for the optimum R-pair is to be done within some prescribed time, then both the computation time per R-pair and the total number of R-pairs tested should be considered. Moving from an advanced CPU-based computation cluster to a single general-purpose graphics processing unit reduced computation time of the cost function in Eq. [1] to under 40 ms. The implementation described here provides optimum acceleration factors for a given patient and coil array in a time similar to that for the “pre-scan” calibration of RF excitation angle. Due to the separable nature of the computation, use of additional GPUs is expected to provide a near-linear time reduction.
We believe that 3D CE-MRA is a useful application of Acceleration Apportionment, as the high acceleration factors previously demonstrated to be effective in CE-MRA allow considerable latitude in determining the most favorable R-pair for each situation. Moreover, time-resolved CE-MRA has been shown to be well suited to precalibrated parallel imaging methods (10), as the exam is generally run out over a dozen or more 3D time-resolved volumes, reusing the same calibration data for each. Acceleration Apportionment is not limited to CE-MRA, as any exam using 2D-SENSE acceleration may benefit from the proposed methodology with an appropriate adaption in choice of cost function likely with R < 8.
The sampling pattern adjustment proposed here changes the spacing between points in the kY−kZ plane. It is fundamentally different from the previously described CAIPIRIHNA pattern (16), which seeks to shift aliasing directions in a manner advantageous to SENSE acceleration, similarly making use of empty space within the FOV. We recognize that a combination of Acceleration Apportionment and CAIPIRIHNA may yield even higher parallel imaging performance than either provides separately.
There are multiple plausible extensions to this work. The methodology described here might be used for rapid determination of the optimum CAIPIRINHA kernel for a given R. Also, it is conceivable that a prescan before an auto-calibrated parallel imaging method such as GRAPPA (23) may be able to identify the best autocalibration kernel based on some quality evaluation of the k-space weights. Additionally, this method could possibly be applied to the selection of which available coil elements in a coil array to use for a specified FOV.
This work has a number of limitations. The number of prospective studies done was relatively limited. Many of these initial studies were undertaken in the lower extremity, a situation in which the large amount of empty space in the image volume allows for “free” SENSE acceleration. However, Acceleration Apportionment also appears to be useful for application to anatomy which more fully fills the FOV, as shown in Figure 6a for abdominal exams. Another limit is that the method used to minimize the cost function was a rudimentary search over extensive RY−RZ space, and application of standard optimization techniques (24) may provide better search efficiency.
In summary, a methodology for optimizing 2D SENSE acceleration parameters based on the interaction of the body habitus of the individual patient and the receiver coil array has been described. An automated system for rapidly determining the optimum acceleration parameters and incorporating them into the subsequent accelerated scan has been demonstrated.
ACKNOWLEDGMENTS
The authors acknowledge Kathy Brown, Dr. James Glockner, Dr. John Huston, and Dr. Phillip Young for invaluable assistance.
Grant sponsor: NIH; Grant number: EB000212, HL070620, RR018898.
REFERENCES
- 1.Weiger M, Pruessmann KP, Boesiger P. 2D SENSE for faster 3D MRI. Magma. 2002;14:10–19. doi: 10.1007/BF02668182. [DOI] [PubMed] [Google Scholar]
- 2.Weiger M, Pruessmann KP, Kassner A, Roditi G, Lawton T, Reid A, Boesiger P. Contrast-enhanced 3D MRA using SENSE. J Magn Reson Imaging. 2000;12:671–677. doi: 10.1002/1522-2586(200011)12:5<671::aid-jmri3>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 3.Hu HH, Madhuranthakam AJ, Kruger DG, Huston J, III, Riederer SJ. Improved venous suppression and spatial resolution with SENSE in elliptical centric 3D contrast-enhanced MR angiography. Magn Reson Med. 2004;52:761–765. doi: 10.1002/mrm.20216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hu HH, Madhuranthakam AJ, Kruger DG, Glockner JF, Riederer SJ. Combination of 2D sensitivity encoding and 2D partial Fourier techniques for improved acceleration in 3D contrast-enhanced MR angiography. Magn Reson Med. 2006;55:16–22. doi: 10.1002/mrm.20742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Meckel S, Mekle R, Taschner C, Haller S, Scheffler K, Radue E-W, Wetzel S. Time-resolved 3D contrast-enhanced MRA with GRAPPA on a 1.5-T system for imaging of craniocervical vascular disease: initial experience. Neuroradiology. 2006;48:291–299. doi: 10.1007/s00234-006-0052-9. [DOI] [PubMed] [Google Scholar]
- 6.Zhang H, Maki JH, Prince MR. 3D contrast-enhanced MR angiography. J Magn Reson Imaging. 2007;25:13–25. doi: 10.1002/jmri.20767. [DOI] [PubMed] [Google Scholar]
- 7.Lim RP, Shapiro M, Wang EY, et al. 3D time-resolved MR angiography (MRA) of the carotid arteries with time-resolved imaging with stochastic trajectories: comparison with 3D contrast-enhanced bolus-chase MRA and 3D time-of-flight MRA. Am J Neuroradiol. 2008;29:1847–1854. doi: 10.3174/ajnr.A1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fenchel M, Doering J, Seeger A, Kramer U, Rittig K, Klumpp B, Claussen CD, Miller S. Ultrafast whole-body MR angiography with two-dimensional parallel imaging at 3.0 T: feasibility study. Radiology. 2009;250:254–263. doi: 10.1148/radiol.2501080494. [DOI] [PubMed] [Google Scholar]
- 9.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 10.Haider CR, Hu HH, Campeau NG, Huston J, III, Riederer SJ. 3D high temporal and spatial resolution contrast-enhanced MR angiography of the whole brain. Magn Reson Med. 2008;60:749–760. doi: 10.1002/mrm.21675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hadizadeh DR, von Falkenhausen M, Gieseke J, Meyer B, Urbach H, Hoogeveen R, Schild HH, Willinek WA. Cerebral arteriovenous aalformation: Spetzler-Martin classification at subsecond-temporal-resolution four-dimensional MR angiography compared with that at DSA. Radiology. 2008;246:205–213. doi: 10.1148/radiol.2453061684. [DOI] [PubMed] [Google Scholar]
- 12.Haider CR, Glockner JF, Stanson AW, Riederer SJ. Peripheral vasculature: high-temporal- and high-spatial-resolution three-dimensional contrast-enhanced MR angiography. Radiology. 2009;253:831–843. doi: 10.1148/radiol.2533081744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kukuk GM, Hadizadeh DR, Gieseke J, et al. Highly undersampled supraaortic MRA at 3.0 T: initial results with parallel imaging in two directions using a 16-channel neurovascular coil and parallel imaging factors up to 16. Magn Reson Imaging. 2010;28:1311–1318. doi: 10.1016/j.mri.2010.06.008. [DOI] [PubMed] [Google Scholar]
- 14.Mostardi PM, Young PM, McKusick MA, Riederer SJ. High temporal and spatial resolution imaging of peripheral vascular malformations. J Magn Reson Imaging. 2012;36:933–942. doi: 10.1002/jmri.23714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med. 2005;53:684–691. doi: 10.1002/mrm.20401. [DOI] [PubMed] [Google Scholar]
- 16.Breuer FA, Blaimer M, Mueller MF, Seiberlich N, Heidemann RM, Griswold MA, Jakob PM. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA) Magn Reson Med. 2006;55:549–556. doi: 10.1002/mrm.20787. [DOI] [PubMed] [Google Scholar]
- 17.Wu B, Millane RP, Watts R, Bones PJ. Improved matrix inversion in image plane parallel MRI. Magn Reson Imaging. 2009;27:942–953. doi: 10.1016/j.mri.2009.01.017. [DOI] [PubMed] [Google Scholar]
- 18.Mostardi PM, Glockner JF, Young PM, Riederer SJ. Contrast-enhanced MR angiography of the abdomen with highly accelerated acquisition techniques. Radiology. 2011;261:587–597. doi: 10.1148/radiol.11110242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Haider CR, Riederer SJ, Borisch EA, et al. High temporal and spatial resolution 3D time-resolved contrast-enhanced magnetic resonance angiography of the hands and feet. J Magn Reson Imaging. 2011;34:2–12. doi: 10.1002/jmri.22469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Johnson CP, Borisch EA, Glockner JF, Young PM, Riederer SJ. Time-resolved dual-station calf–foot three-dimensional bolus chase MR angiography with fluoroscopic tracking. J Magn Reson Imaging. 2012;36:1168–1178. doi: 10.1002/jmri.23739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Rosner B. Fundamentals of biostatistics. xix. Pacific Grove, CA: Duxbury; 2000. p. 792. [Google Scholar]
- 22.Johnson CP, Haider CR, Borisch EA, Glockner JF, Riederer SJ. Time-resolved bolus-chase MR angiography with real-time triggering of table motion. Magn Reson Med. 2010;64:629–637. doi: 10.1002/mrm.22537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn Reson Med. 2002;47:1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- 24.Nelder J, Mead R. A simplex method for function minimization. Comput J. 1965;7:308–313. [Google Scholar]